李占山^1,2, 宋志扬¹, 花昀峤³
1. 吉林大学 软件学院, 吉林 长春 130012;
2. 吉林大学 计算机科学与技术学院, 吉林 长春 130012;
3. 吉林大学 资产管理处, 吉林 长春 130012
收稿日期：2022-05-24
基金项目：国家自然科学基金资助项目(61802056)；吉林省自然科学基金资助项目(20180101043JC)；吉林省发展和改革委员会产业技术研究与开发项目(2019C053-9)。
作者简介：李占山(1966-), 男, 吉林公主岭人, 吉林大学教授, 博士生导师。

摘要：为了解决目前基于分解的多模态多目标优化算法存在种群搜索能力不足, 子种群中存在无用解和距离度量不具有普适性等问题, 提出了一种基于自适应搜索的多模态多目标优化算法MOEA/D-AS.首先，该方法通过减少平均子种群的个体数量, 进而增加参考向量的数量.其次, 根据子种群当前状态自适应分配子种群的个体数量.最后, 使用引入了局部种群信息的清除距离作为维护子种群的依据.将提出的算法与4种算法在2019年CEC多模态多目标测试问题和大规模多模态多目标测试问题上进行对比实验, 实验结果表明, 提出的算法可以有效解决多模态多目标优化问题.
关键词：多模态多目标优化算法自适应搜索子种群局部信息清除距离
A Multi-modal Multi-objective Optimization Algorithm Based on Adaptive Search
LI Zhan-shan^1,2, SONG Zhi-yang¹, HUA Yun-qiao³
1. School of Software, Jilin University, Changchun 130012, China;
2. School of Computer Science and Technology, Jilin University, Changchun 130012, China;
3. Asset Management Division, Jilin University, Changchun 130012, China
Corresponding author: HUA Yun-qiao, E-mail:122794833@qq.com.

Abstract: The current decomposition-based multi-modal multi-objective optimization algorithms have insufficient population search capability, useless solutions in sub-populations, and a non-universal distance metric. To address these issues, an adaptive search multi-modal multi-objective optimization algorithm MOEA/D-AS is proposed. Firstly, this method increases the number of reference vectors by reducing the size of the average sub-population. Secondly, the sub-populations are reallocated according to the current state of the sub-populations in the iteration. Finally, a clear distance based on local population information is introduced as the basis for modifying the sub-populations. The proposed algorithm is compared with four algorithms on the 2019 CEC multi-modal multi-objective test problems and the large-scale multi-modal multi-objective test problems for experiments. The experimental results show that the proposed algorithm can effectively solve the multi-modal multi-objective optimization problems.
Key words: multi-modal multi-objective optimization algorithmadaptive searchsub-populationlocal informationclear distance
多目标优化问题需要多目标优化算法同时权衡多个目标, 并在目标空间中找到逼近帕累托前沿的非支配解的集合, 这样的集合在决策空间中称为帕累托最优解集.多目标优化算法计算得到的帕累托最优解集在目标空间中的收敛性和多样性可以得到保证, 但在决策空间中的收敛性和多样性没有得到过多关注.如果算法能够提供目标值相似但在决策空间中不同的解, 决策者就可以作出更多的选择, 因此设计解决这类问题的算法具有极其重要的意义.多模态多目标优化问题(multi-modal multi-objective optimization problems, MMOPs)需要找到在决策空间中与帕累托最优解目标值相同的所有等价解^[1].进化算法可以在一次运行中获取多个解, 并且还可以在算法设计中平衡算法开发和勘探能力^[2], 因此通常使用多模态多目标进化算法(multi-modal multi-objective evolutionary algorithms, MMEAs)解决MMOPs.
在过去的十几年内, 许多****提出了不同的MMEAs及改进, 主要分为三大类：基于帕累托支配、基于分解和基于存档.
基于支配的MP-MMEA^[3]使用合并和分割操作以自适应调整子种群的数量, 使用引导向量让各个种群独立进化, 所以在高维空间中表现优秀.基于帕累托支配的MMEAs的特点是参数较少、搜索能力强、不易陷入局部最优解和时间复杂度较低等.但随着目标数的增加, 帕累托支配关系给予种群的环境选择压力急剧降低, 同时因为拥挤距离的作用减弱, 种群在进化早期已经失去了多样性^[4], 难以处理4个目标及以上的超多目标优化问题.
基于分解的MMEAs中参考向量的邻域间接确定了种群的拓扑结构, 构成了在多模态单目标优化算法中常用的小生境技术^[5]；在多目标优化问题中, 分解策略在高维目标空间中表现出了良好的性能^[6]；相对于支配关系来说, 使用聚合函数可以更好地解决目标数增加的问题, 因此基于分解的MMEAs在处理MMOPs时具有一定的优势.
基于档案的TriMOEA-TA&R^[7]首先使用决策变量分析技术检测与收敛相关的决策变量, 将其加入到收敛档案中进行优化；使用聚类策略和新的清除策略提高多样性.该类算法的特点是在某些测试问题中性能优异, 时间复杂度较低, 但基于档案的MMEAs参数过多, 其效果依赖于测试集.
本文提出了一种基于分解和自适应搜索的多模态多目标优化算法，命名为MOEA/D-AS(adaptive search)算法, 引入了自适应机制和档案机制, 设计了新的维护子种群的操作, 改进了相关度量, 并提高了其鲁棒性.实验结果表明, MOEA/D-AS算法可以有效解决MMOPs.
1 相关工作基于分解的MMEAs参考了多目标优化算法MOEA/D^[8].如图 1a所示, MOEA/D算法使用一组参考向量将具有M个目标的问题分解为N个单目标子问题进行独立求解.图中f₁, f₂为该问题的优化目标.如图 1b~1c所示箭头线为参考向量, 每个参考向量都对应1个子种群, 子种群上的圆表示个体, 每个子种群保留多个解意味着可以保留等价解.在种群进化过程中, 子种群产生后代后, 找到在决策空间的子种群中距离相近的2个个体.通过聚合函数计算2个个体的聚合函数值, 淘汰聚合函数值较差的解, 进而解决MMOPs.
图 1(Fig. 1)

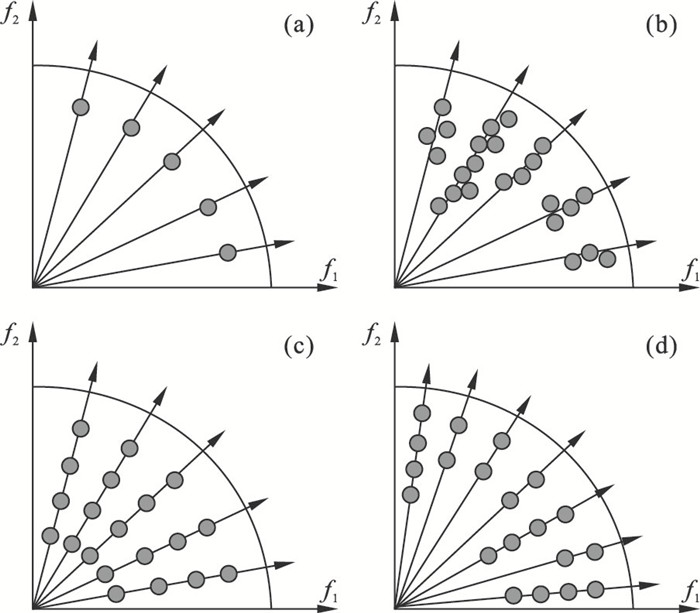图 1 基于分解的MMEAs图解Fig.1 Illustration of the decomposition-based MMEAs (a)—MOEA/D; (b)—MOEA/D-AD; (c)—MOEA/D-MM; (d)—MOEA/D-AS.

MOEA/D-AD^[9]设计了增加和删除算法对子问题对应的子种群进行维护, 子种群中可以保留多个个体, 如图 1b所示.MOEA/D-AD参考向量的数量等于种群个体数量, 并且每个子种群中解的数量将会逐渐增加, 而它们大多数都是无用解, 这些无用解占据了算法的搜索资源, 降低了算法的搜索能力.经过最终选择过程得到的输出种群也无法保证决策空间的收敛性和多样性, 无法保证找到足够多的等价解.
MOEA/D-MM^[10]为子种群分配固定数量的解, 如图 1c所示, 提高了算法寻找等价解的能力, 其性能优于MOEA/D-AD.参考向量数量的减少会降低目标空间的收敛性和多样性, 降低搜索能力.在解决具有不同等价解数目的问题时, 不是每个子种群中的每个个体都能够达到理想状态, 即子种群中的每个个体都找到一个不同的等价解, 子种群中仍会存在部分无用解.另外, 依靠清除半径σ并不适合判断2个个体是否相近, 其难以解决搜索空间巨大的问题, 因为当种群分布稀疏时σ值较大, 算法难以保证决策空间的收敛性和多样性.
针对目前基于分解的MMEAs存在搜索能力较弱、子种群中存在无用解、决策空间的多样性不足的问题, 本文提出了MOEA/D-AS算法(见图 1d), 引入了自适应机制和档案机制, 设计了子种群的增加和删除策略, 及时去除子种群中的无用解, 增加参考向量的数量, 进而提高算法的搜索能力和找到更多等价解的能力.改进了在基于分解的MMEAs中常用的距离度量, 提出了新度量——清除距离, 该度量具有较好的鲁棒性, 可以提高种群在决策空间中的收敛性和多样性.
2 MOEA/D-AS算法2.1 自适应机制在MOEA中参考向量的设置决定了算法的搜索方向, 在一定程度上决定了算法的搜索能力和最终解集的分布.在基于分解的MMEAs中, 参考向量的数量|ω|=N/C, 其中N是种群个体数量, C是平均每个子种群能够包含个体的平均值.参考向量的数量减少, 会导致算法搜索能力和目标空间的多样性降低.MOEA/D-AS算法如图 1d所示, 自适应机制需要根据子种群的状态重新分配其大小, 进而降低C的平均值, 增加参考向量的数量.图 1d中的种群大小和图 1c中的种群大小相同, 但参考向量的数量多于图 1c中的参考向量的数量.
假定对于最小化问题, 本文设计了2个指标评价子种群的状态, 第1个指标为平均距离D.如式(1)所示, 第k个子种群的平均距离D_k为

(1)

式中: k={1, 2, …，|ω|}; μ_k为第k个子种群中个体集合; d(μ_ki, μ_kj)表示在决策空间中μ_k的第i个解与第j个解之间的欧氏距离.
第2个指标为平均聚合函数值T.基于分解的MMEAs常用的分解方法有加权和法、切比雪夫法和PBI法.其中加权和法的权重系数难以确定, PBI法需要设定θ值, 切比雪夫法不需要参数设置, 并且可以有效处理非凸帕累托前沿的问题.因此本文中使用切比雪夫法聚合函数.如式(2)所示, 第k个子种群的平均聚合函数值T_k为

(2)

式中: 维度i={1, 2, …，M}; ω_k是参考向量集中的第k个参考向量; z_i^*为理想点, 是所有解中每个目标值分量最小值组成的坐标.
由于D和T的尺度差异很大, 那么使用D和T在评估子种群状态时, 任何1个度量起到主导作用均会使决策空间或目标空间丧失多样性^[11].式(3)和式(4)中对D和T值进行归一化：

(3)

式中: D_min是D的最小值；D_max是D的最大值; D_nork表示第k个子种群的归一化平均距离, 其大小表征了决策空间中第k个子种群的拥挤程度, 该值越大表示子种群表现越不拥挤.

(4)

式中: T_min是T的最小值; T_max是T的最大值; T_nork表示第k个子种群的归一化平均聚合函数值, 其大小表征了目标空间中第k个子种群中个体的收敛情况, 该值越大表示子种群越接近真实帕累托前沿.
可以根据D_nork和T_nork来计算第k个子种群的得分, 公式为

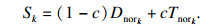(5)

得分的计算兼顾了子种群在决策空间和目标空间中的分布状态, S_k越大表示第k个子种群内解的平均距离越远或平均聚合函数值越小, 即子种群中的解越接近理想状态.在决策空间和目标空间中更偏向于在决策空间获取更均匀的解, 因此建议控制参数c的取值范围为[0.1, 0.4].表 1介绍了如何根据每个子种群的得分重新调整子种群个体数量.
表 1(Table 1)

表 1 计算子种群个体数量Table 1 Calculation of sub-population size 输入：子种群中个体数量的上界Umax和下界Umin；控制参数c. 输出：各子种群的个体数量集合m. ??1.计算每个子种群的得分 ??2.将得分排名前50%的种群个体数量设置为Umax ??3.将得分排名后50%的种群个体数量设置为Umin

表 1 计算子种群个体数量 Table 1 Calculation of sub-population size

2.2 档案机制过去的研究表明, 引入档案可以提高基于分解的多目标优化算法的性能^[12].本文尝试将其引入到基于分解的MMEA中, 以防止优秀个体丢失.每个参考向量都对应一个档案, 以维护种群的多样性.档案在所有完成一次环境选择后需要进行快速非支配排序^[13], 及时去除被支配的无用解, 提高算法运行效率.
2.3 子种群维护操作在算法迭代过程中, 各子种群的个体数量是不断变化的, 意味着需要对子种群中的个体进行补充和去除.子种群中的个体去除操作见表 2, 本文使用了MOEA/D-MM算法的处理框架, 区别在于使用了新的度量——清除距离, 并需要把淘汰的解存入档案中.子种群进行补充的操作见表 3.
表 2(Table 2)

表 2 去除子种群中多余的解Table 2 Removal of redundant solutions from sub-populations 输入：第k个子种群的个体数量mk；清除距离r；当前第k个子种群μk；第k个子种群的档案. 输出：更新后的子种群μk. ??1.while |μk|>mk ??2. ??找到μk中欧氏距离最近的2个解i和j ??3. ??if d(i, j) < r ??4. ????删除聚合函数值最差的解 ??5. ??else ??6. ????将μk中聚合函数值最差的解移除 ??7. ??end if ??8. ??将淘汰的解放入档案中 ??9.end while

表 2 去除子种群中多余的解 Table 2 Removal of redundant solutions from sub-populations

表 3(Table 3)

表 3 补充子种群中的解Table 3 Supplement of the solution in sub-populations 输入：第k个子种群的个体数量mk；清除距离r；当前第k个子种群μk；第k个子种群的档案. 输出：更新后的子种群μk. ??1.while |μk| < mk ??2. ??if档案为空 ??3. ????随机产生一个新解加入μk ??4. ??else ??5. ????从当前第k个子问题的档案中, 选择与当前子种群中的欧氏距离较远但目标值较优的个体进行补充. ??6. ??end if ??7.end while

表 3 补充子种群中的解 Table 3 Supplement of the solution in sub-populations

2.4 清除距离在基于分解的MMEA中, MOEA/D-AD和MOEA/D-MM中均有与清除距离类似的概念.在MOEA/D-AD中的概念为相邻^[9], 种群中任意2个个体X_i和X_j是否相邻需要判断X_i是否在与X_j欧氏距离最近的第L个个体中, L为0.1×N, N为种群个体数量.在MOEA/D-MM中的概念为清除半径σ^[10], σ的大小为决策空间中与X_i最近的第L个个体的距离和的平均值, L为0.1×N, 其中i={1, 2, …, N}, N为种群个体数量. 这两种度量决定了种群在决策空间中的收敛性和多样性：度量值过小, 算法只会去除聚合函数值最差的个体；度量值过大, 算法会去除已经找到的等价解.
在基于分解的MMEAs中, 每个子种群只与其邻域中的个体进行交配, 从而间接地形成了小生境结构, 这种结构在处理多模态问题时十分常见, 比如MO_Ring_PSO_SCD^[14]中的环形拓扑, 环形拓扑、小生境技术减缓了种群信息的传递速度, 能够提高种群的多样性.然而上述相邻和清除半径σ度量均从全局种群中提取信息, 忽略了拓扑结构中隐含的局部种群信息.为此, 本文提出了改进的距离度量——清除距离r, 旨在提高这一重要度量的鲁棒性.计算清除距离需要使用2.1节中计算出的N个子种群的平均距离D={D₁, D₂, …, D_N}.对D进行升序排序, 得到D_sort.使用式(6)计算得到清除距离r为

(6)

式中，mean表示取均值, 即计算排名前c₁个D_sort的平均值，得到清除距离r, 建议c₁取值为2.
2.5 算法整体框架MOEA/D-AS算法的框架见表 4.
表 4(Table 4)

表 4 MOEA/D-AS框架Table 4 The framework of MOEA/D-AS 输入：子种群中个体数量的上界Umax和下界Umin；控制参数c和c1; 种群个体数量N. 输出：最终种群. ??1.初始化参考向量及其邻域、子种群 ??2.计算理想点z* ??3. while not terminate do ??4. ??计算清除距离r ??5. ??对每个参考向量: ??6. ????从邻域和当前子种群中选取父母, 通过SBX交叉和多项式变异产生子解, 更新理想点 ??7. ????使用表 2中算法删除子种群中多余个体 ??8. ??end for ??9. ??对存档进行快速非支配排序 ??10. ??使用表 1中算法重新计算子种群个体数量m ??11. ??使用表 2，表 3中算法补充或删除子种群个体 ??12. end while ??13.对当前种群进行最终选择

表 4 MOEA/D-AS框架 Table 4 The framework of MOEA/D-AS

在最终选择过程中, 首先, 将子种群个体数量设置为U_max, 之后补充子种群.然后, 对种群进行快速非支配排序.最后, 若当前子种群个体数量大于N, 则找到种群中欧氏距离最近的一对个体, 随机删除其中一个, 重复这个过程, 直至满足当前子种群个体数量小于或等于N.
假定种群个体数量为N, 目标数为M, 函数评价次数为F, 子种群个体数量平均值为C.MOEA/D-MM算法总时间复杂度近似为O(FMN²); MOEA/D算法总时间复杂度近似为O(FMN²); 设MOEA/D-AS算法运行中档案大小为p×N, 则MOEA/D-AS算法总时间复杂度近似为O((1+p²)×FMN²).另外, MP-MMEA算法总时间复杂度近似为O(FMN²); TriMOEA-TA&R算法总时间复杂度近似为O(FMN²).综上所述, 本文算法时间复杂度与目前各主流算法处在同一量级.
3 实验结果与分析3.1 数据集与对比算法多模态多目标优化是近几年来进化计算中的新领域, 本文使用了经典的2019年CEC多模态多目标测试问题^[15]全面测试算法性能.其中部分测试问题没有使用, 它们涉及局部和全局最优解共存问题, 而本文实验中所有算法目标为定位帕累托等价最优解集.目前有很多MMEAs用于解决少于三维或三目标的MMOPs, 但在实际优化问题中, 会出现决策维度和目标较多的问题, 因此使用大规模多模态多目标测试问题^[16]检验算法的性能是必要的.表 5列出了所使用测试问题的名称、维度、目标数、等价解数、PS形状和PF形状.
表 5(Table 5)

表 5 多模态多目标优化问题特点Table 5 The distinction of multi-modal multi-objective problems 测试问题 维度 目标数 等价解数 PS形状 PF形状 SYM-PART 2 2 9 线性 凸形 Omni 3 2 27 线性 凸形 MMF1 2 2 2 非线性 凸形 MMF1z 2 2 2 非线性 凸形 MMF2 2 2 2 非线性 凸形 MMF3 2 2 2 非线性 凸形 MMF4 2 2 4 非线性 凹形 MMF5 2 2 4 非线性 凸形 MMF6 2 2 4 非线性 凸形 MMF7 2 2 2 非线性 凸形 PolygonD2M6 2 6 4 非线性 凹形 PolygonD4M6 4 6 4 非线性 凸形 PolygonD6M6 6 6 4 非线性 凸形 PolygonD8M6 8 6 4 非线性 凸形 PolygonD10M6 10 6 4 非线性 凹形 Polygon1D2M6 2 6 9 非线性 凹形 Polygon1D4M6 4 6 9 非线性 凸形 Polygon1D6M6 6 6 9 非线性 凸形 Polygon1D8M6 8 6 9 非线性 凸形 Polygon1D10M6 10 6 9 非线性 凹形

表 5 多模态多目标优化问题特点 Table 5 The distinction of multi-modal multi-objective problems

为了比较MOEA/D-AS算法的性能, 本文引入了不同类型的、最新的或具有代表性的MMEAs进行对比实验, 包括：最先进的基于帕累托支配的多模态多目标进化算法MP-MMEA^[3], 最新的基于分解的多模态多目标进化算法MOEA/D-MM^[10], 具有代表性的基于存档的多模态多目标进化算法TriMOEA-TA&R^[7].同时, 根据领域惯例, 引入了传统多目标优化算法MOEA/D^[8]进行比较.所有实验结果由算法在每一个测试用例上独立运行30次得到, 并利用Wilconxon’s rank sum test统计和比较算法之间水平α=0.05的显著性差异.
3.2 评估指标及实验参数3.2.1 评估指标本文采用了度量多目标优化算法的性能指标IGD^[17]来检验MMEAs在目标空间中的分布性与收敛性.计算IGD值时, 目标值相同但在决策空间不同的解会被视为同一个解, 所以IGD无法检验决策空间的收敛性和分布性.IGDX^[17]可以检验决策空间的分布性与收敛性, IGDX是使用IGD扩展得到的, IGD值越小, 表示算法得到的解集映射到目标空间后越贴近帕累托最优解集.IGDX值越小，表示算法在决策空间中得到的解集越贴近帕累托最优解集.IGD和IGDX的计算公式为

(7)

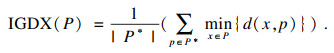(8)

式中: f(x)和f(p)表示x和p在目标空间中的目标值；d(x, p)是x与p之间的欧氏距离, p是算法获得的决策空间中的解集; P^*是一组参考点.
3.2.2 算法参数设置本次实验的算法实现和运行均在Platemo v3.2^[18]上进行, 所有算法参数均使用平台提供的默认值, 聚合函数均使用切比雪夫聚合函数.其余参数设置如下：种群个体数量N取300, 最大评价次数取10⁵, 在MOEA/D-AS算法中, U_max取4, U_min取2, 控制参数c取0.3, 控制参数c₁取2.
在表 6中, 当c=0.3时, 与c取0.1, 0.2, 0.4的结果没有较大区别, 因为3/2/15, 4/1/15, 2/1/17与c=0.3的结果相比, 大部分结果是等价的, 即c取[0.1, 0.4]时, 算法整体表现较好.c取[0.6, 0.9]时的结果为0/3/17, 0/4/16, 2/8/10, 1/8/11, IGDX值劣于c=0.3时的测试问题数量逐步上升, 优于c=0.3时的测试问题数量较少, 因此在该区间的算法效果不如c=0.3.这是因为控制参数c能够控制D_nork和Tnor_k占据得分中的比例, 当c取[0.1, 0.4]时得分的计算比较看重决策空间中种群的状态, 即D_nork的占比较高, 实验结果与预期相符.因此, 建议c值取[0.1, 0.4].
表 6(Table 6)

表 6 控制参数c取不同值时与c=0.3时进行IGDX指标上的对比实验Table 6 Comparative experiment on IGDX with c=0.3 when different values of control parameter c are taken c 0.1 0.2 0.4 0.5 0.6 0.7 0.8 0.9 优/劣/等于 3/2/15 4/1/15 2/1/17 1/3/16 0/3/17 0/4/16 2/8/10 1/8/11 注：由于篇幅有限, 具体实验结果没有在表格中体现, 仅列出c取不同值时算法明显优于、劣于和等于c=0.3时的测试问题总数量.

表 6 控制参数c取不同值时与c=0.3时进行IGDX指标上的对比实验 Table 6 Comparative experiment on IGDX with c=0.3 when different values of control parameter c are taken

同理, 在表 7中, 当c₁=2时, 其结果明显优于c₁取其他值, 尤其是当c₁=1时的结果为2/14/4, 说明在20个测试问题中有14个测试问题的结果差于c₁=2时的结果.这是因为, 当c₁=1时, 清除距离r的计算受到极值影响.当c₁取3, 4, 5时, 清除距离r不能够准确反映出种群当前的拥挤状况, 无法为种群进化提供指导, 实验结果与预期相符, 因此建议c₁取2.
表 7(Table 7)

表 7 控制参数c1取不同值时与c1=2时进行IGDX指标上的对比实验Table 7 Comparative experiment on IGDX with c1=2 when different values of control parameter c1 are taken c1 1 3 4 5 优/劣/等于 2/14/4 0/4/16 0/3/17 1/7/12 注：由于篇幅有限, 具体实验结果没有在表格中体现, 仅列出c1取不同值时算法明显优于、劣于和等于c1=2时的测试问题总数量.

表 7 控制参数c1取不同值时与c1=2时进行IGDX指标上的对比实验 Table 7 Comparative experiment on IGDX with c1=2 when different values of control parameter c1 are taken

3.3 实验结果与分析表 8和表 9分别给出了5种算法在不同测试问题中得到的IGDX和IGD的平均值、标准差, 结果后的括号中给出了5种算法在当前测试问题上的排名, 最后一行给出总平均排名, 即单个算法在所有数据集上获得的综合排名除以测试问题的数量.
表 8(Table 8)

表 8 MOEA/D-AS算法与其他4种算法IGDX指标的比较结果Table 8 Comparison results of IGDX between MOEA/D-AS algorithm and other four algorithms 测试问题 MP-MMEA(2021) TriMOEA-TA&R(2019) MOEA/D-MM(2020) MOEA/D(2007) MOEA/D-AS SYM-PART 3.515 9±1.26(4)- 1.333 1±0.977(3)- 0.639 1±0.718(2)= 13.378±2.65(5)- 0.343 9±0.347(1) Omni 0.294 5±0.111(3)- 0.434 3±0.161(4)- 0.223 2±0.111(2)- 3.296 4±0.665(5)- 0.168 6±0.080 4(1) MMF1 0.044 7±0.003 6(3)- 0.040 2±0.001 79(2)- 0.052 0±0.002 43(4)- 0.118 4±0.040 6(5)- 0.038 6±0.001 5(1) MMF1z 0.048 9±0.009 5(4)- 0.039 0±0.006 43(3)- 0.036 4±0.002 08(2)- 0.177 6±0.083 9(5)- 0.027 3±0.001 43(1) MMF2 0.014 4±0.005 4(3)- 0.034 7±0.044 2(4)- 0.012 8±0.001 03(2)- 0.297 0±0.12(5)- 0.010 2±0.001 08(1) MMF3 0.013 7±0.005 7(3)- 0.021 6±0.011 3(4)- 0.011 6±0.000 77(2)- 0.137 7±0.046(5)- 0.009 7±0.000 63(1) MMF4 0.046 3±0.013 8(4)- 0.040 6±0.103(3)- 0.020 4±0.001 62(1)= 0.314 2±0.093 4(5)- 0.021 5±0.004 08(2) MMF5 0.085 0±0.010 3(4)- 0.057 3±0.013 5(1)+ 0.071 2±0.002 1(2)= 0.288 5±0.094 1(5)- 0.072 6±0.006 72(3) MMF6 0.086 8±0.011 3(4)- 0.048 1±0.001 7(1)+ 0.061 6±0.001 82(2)= 0.223 6±0.057 6(5)- 0.062 7±0.005 25(3) MMF7 0.026 8±0.003 4(4)- 0.024 8±0.021 8(2)= 0.026 5±0.001 44(3)- 0.105 7±0.057 2(5)- 0.019 0±0.000 94(1) PolygonD2M6 0.161 4±0.011 6(2)- 0.834 4±0.432(5)- 0.308 1±0.055 2(4)- 0.169 9±0.015 7(3)- 0.102 3±0.001 5(1) PolygonD4M6 3.490 3±1.17(4)- 3.392 8±1.29(3)- 2.800 2±1.44(2)- 4.545 1±0.86(5)- 0.334 1±0.113(1) PolygonD6M6 6.275 2±0.106(4)- 5.811 1±1.1(3)- 4.569 4±1.5(2)- 6.425 5±0.086 6(5)- 2.993 2±1.48(1) PolygonD8M6 7.476± 0.132(3)- 7.505 3±0.513(4)- 6.896 4±1.36(2)- 7.524±0.097 9(5)- 4.446 8±0.984(1) PolygonD10M6 8.629 9±0.151(5)- 8.614 3±0.164(4)- 8.166 1±1.16(2)- 8.538 9±0.080 3(3)- 6.229 6±1.42(1) Polygon1D2M6 0.261 5±0.016 6(2)- 0.633 0±0.568(5)- 0.574 4±0.196(4)- 0.397 37±0.041 8(3)- 0.248±0.01(1) Polygon1D4M6 4.096 9±1.84(4)- 2.271 9±1.21(2)- 3.987 9±1.8(3)- 4.301 8±1.68(5)- 1.702 6±1.28(1) Polygon1D6M6 9.755 1±0.713(5)- 7.010 1±2.17(2)- 7.169 1±2.01(3)- 8.731 2±1.62(4)- 4.468 7±1.17(1) Polygon1D8M6 11.649±0.13(5)- 9.138 2±1.74(3)- 9.119 4±2.03(2)- 10.676±1.5(4)- 6.121 1±0.884(1) Polygon1D10M6 13.256±0.12(5)- 11.936±1.8(3)- 11.368±1.97(2)- 12.485±1.5(4)- 7.591 7±0.878(1) +/-/= 0/20/0(3.7) 2/17/1(3.0) 0/16/4(2.4) 0/20/0(4.5) (1.2) 注: “+/-/=”是当前算法明显优于、劣于和等于MOEA/D-AS算法结果的测试问题数量；每个问题的最优解用灰色填充, 次优解用加粗字体标出.

表 8 MOEA/D-AS算法与其他4种算法IGDX指标的比较结果 Table 8 Comparison results of IGDX between MOEA/D-AS algorithm and other four algorithms

表 9(Table 9)

表 9 MOEA/D-AS算法与其他4种算法IGD指标的比较结果Table 9 Comparison results of IGD between MOEA/D-AS algorithm and other four algorithms 测试问题 MP-MMEA(2021) TriMOEA-TA&R(2019) MOEA/D-MM(2020) MOEA/D(2007) MOEA/D-AS SYM-PART 0.022 5±0.004 6(2)+ 0.028 0±0.003 25(4)- 0.032 1±0.005 6(5)- 0.017 7±0.001 9(1)+ 0.024 1±0.006 1(3) Omni 0.009 9±0.001 5(1)+ 0.017 9±0.002 9(3)= 0.025 2±0.004 3(5)- 0.011 6±0.003 7(2)+ 0.017 9±0.003 7(4) MMF1 0.002 4±0.000 1(2)+ 0.003 1±0.000 1(4)- 0.004 2±0.000 1(5)- 0.001 3±0.000 1(1)+ 0.002 8±0.000 1(3) MMF1z 0.002 3±0.000 1(2)+ 0.003 2±0.000 1(4)- 0.004 1±0.000 2(5)- 0.001 2±0.000 1(1)+ 0.002 7±0.000 1(3) MMF2 0.004 5±0.000 6(1)+ 0.018 2±0.058 2(5)- 0.008 0±0.000 7(3)- 0.008 2±0.008 9(4)- 0.006 4±0.000 6(2) MMF3 0.005 2±0.000 3(1)+ 0.006 8±0.001 8(3)+ 0.008 5±0.000 4(5)- 0.006 0±0.004 0(2)+ 0.007 2±0.000 5(4) MMF4 0.003 5±0.000 3(3)- 0.015 2±0.045 9(5)- 0.004 3±0.000 1(4)- 0.001 3±0.000 1(1)+ 0.002 7±0.000 1(2) MMF5 0.002 4±0.000 1(2)+ 0.003 0±0.002 06(4)- 0.003 7±0.000 2(5)- 0.001 4±0.000 1(1)+ 0.002 8±0.000 1(3) MMF6 0.002 3±0.000 1(2)+ 0.002 6±0.000 1(3)+ 0.003 6±0.000 1(5)- 0.001 3±0.000 1(1)+ 0.002 8±0.000 1(4) MMF7 0.002 4±0.000 1(2)+ 0.003 8±0.001 3(4)- 0.004 5±0.000 1(5)- 0.001 3±0.000 1(1)+ 0.003 0±0.000 1(3) PolygonD2M6 0.134 0±0.007 6(3)- 0.450 0±0.033 6(5)- 0.193 4±0.007 0(4)- 0.111 0±0.001 4(1)+ 0.115 4±0.002 5(2) PolygonD4M6 0.232 7±0.021 6(3)- 0.544 0±0.065 3(5)- 0.318 2±0.012 3(4)- 0.163 9±0.005 6(1)+ 0.182 8±0.009 7(2) PolygonD6M6 0.396 6±0.086 2(3)- 0.532 7±0.036 6(5)- 0.492 6±0.033 8(4)- 0.245 5±0.012 4(1)+ 0.296 8±0.016 4(2) PolygonD8M6 0.547 1±0.071 9(3)- 0.569 7±0.066 7(4)- 0.689 8±0.050 2(5)- 0.328 3±0.022 8(1)+ 0.471 7±0.044 0(2) PolygonD10M6 0.777 0±0.140 0(4)- 0.664 7±0.065 9(3)= 0.942 1±0.071 2(5)- 0.428 3±0.025 3(1)+ 0.644 8±0.081 1(2) Polygon1D2M6 0.243 2±0.008 5(1)+ 0.439 5±0.070 4(4)- 0.448 1±0.031 2(5)- 0.322 8±0.008 1(3)- 0.284 5±0.011 1(2) Polygon1D4M6 0.439 1±0.017 7(1)+ 0.664 4±0.149 0(4)- 0.742 6±0.064 7(5)- 0.586 3±0.102 0(3)- 0.521 8±0.062 5(2) Polygon1D6M6 0.628 3±0.014 4(1)+ 0.949 0±0.150(4)- 0.953 0±0.094 0(5)- 0.854 5±0.117 0(3)- 0.715 6±0.116 0(2) Polygon1D8M6 0.764 6±0.025 7(1)+ 1.172 8±0.178 0(5)- 1.110 0±0.120 0(4)- 1.011 4±0.133 0(3)- 0.925 8±0.141 0(2) Polygon1D10M6 0.923 5±0.024 8(1)+ 1.390 7±0.200 0(5)- 1.316 7±0.135 0(4)- 1.206 1±0.099 0(3)- 1.104 1±0.112 0(2) +/-/= 14/0/6(1.9) 2/16/2(4.1) 0/20/0(4.6) 14/0/6(1.7) (2.5) 注：“+/-/=”是当前算法明显优于、劣于和等于MOEA/D-AS算法结果的测试问题数量；每个问题的最优解用灰色填充, 次优解用加粗字体标出.

表 9 MOEA/D-AS算法与其他4种算法IGD指标的比较结果 Table 9 Comparison results of IGD between MOEA/D-AS algorithm and other four algorithms

由表 8和表 9可以看出MOEA/D-AS算法明显优于大部分多模态多目标算法.MOEA/D-AS算法得到的标准差在大多数测试问题上都比其他MMEAs得到的结果小, 说明MOEA/D-AS算法表现稳定. MOEA/D-AS算法的IGDX和IGD值排名显著高于TriMOEA-TA&R算法和MOEA/D-MM算法, 说明MOEA/D-AS算法能够比大多数MMEAs更有效地解决MMOPs.
与最先进的MP-MMEA算法相比, MOEA/D-AS算法的IGDX值较优, 其平均排名为1.2, 而MP-MMEA平均排名仅为3.7, 是4种MMEAs中效果最差的.但MP-MMEA算法的IGD值则较优秀, 平均排名为1.9, 而MOEA/D-AS算法的平均排名略低, 为2.5, 但MOEA/D-AS算法结果大都是次优解.这说明在决策空间和目标空间中, MP-MMEAs算法更偏重维护目标空间中的性能, 而MOEA/D-AS算法更偏重维护决策空间中的性能.但是对于MMEAs来说, 维护决策空间的性能更重要, 如果决策者更需要算法保证目标空间中的性能, 不妨使用MOEA/D等多目标优化算法.因此MOEA/D-AS算法性能优于MP-MMEA算法, 其性能达到了与最先进的MMEAs相当水平.
另外, 本文提供了与经典的多目标优化算法比较结果, 这印证了算法设计的“没有免费午餐”原则.MMEA算法保证了决策空间中的收敛性和多样性, 会在某种程度上降低算法在目标空间中的收敛性和多样性, 多目标优化算法MOEA/D其IGD值平均排名为1.7, IGDX值平均排名为4.5, 但MOEA/D算法没有能力保存等价解.换句话说, MOEA/D无法解决多模态多目标优化问题, 其IGDX指标没有意义.
通过深入分析在决策空间中不同类型测试问题对算法性能的影响, 可以得出：
1) MOEA/D-AS适合处理等价解数目较多的问题, 并且表现稳定.根据表 5中对测试问题的介绍, 其中Omni测试问题存在27个等价解；SYM-PART测试问题具有9个等价解；6目标的Polygon和Polygon1测试问题分别具有4个和9个等价解, 而MOEA/D-AS算法均取得了最优的IGDX值.MOEA/D-AS算法在处理等价解数目较多的问题时具有显著优势, 原因是MOEA/D-AS算法在子种群个体数量分配时, 为表现最佳的半数子种群分配了较多的搜索资源, 使种群尽量均匀分布在各个帕累托最优解的等价解上, 这样使后代更有希望找到新的等价解.
2) MOEA/D-AS适合处理具有复杂PS形状的问题, 并且表现非常稳定、不易受到局部最优解影响.测试问题MMF1, MMF2, MMF3和MMF7在决策空间内有着复杂的PS形状.在这4个测试问题中, MOEA/D-AS均取得了最优的IGDX值, 并且其标准差明显优于其他算法的标准差.MOEA/D-AS算法具有很强的搜索能力, 运行稳定且不易受到局部最优解的影响.原因是其自适应机制间接增加了参考向量的数量, 提高了算法的搜索能力, 防止算法陷入局部最优解, 而档案机制可以有效防止优秀个体丢失.
3) MOEA/D-AS更适合处理搜索空间较大、决策维度较多、目标数较多和等价解间距较大的MMOPs.本文算法在大规模多模态多目标测试问题中的IGDX指标上表现出最佳性能: 原因一是算法搜索能力较强; 原因二是使用清除距离r比使用清除半径σ表现稳定.在PolygonD2M6测试问题中, MOEA/D-MM算法运行过程中的清除半径σ的平均值为20.36，均方差为1.62.MOEA/D-AS算法运行过程中的清除距离r的平均值为5.02，均方差为0.66.PolygonD2M6测试问题中相邻等价解间的距离为5, 清除距离r与该间距非常接近, 且均方差更小, 证明了使用局部种群信息改进的距离度量——清除距离r具有较好的鲁棒性.
4 结语针对目前基于分解的多模态多目标优化算法存在种群搜索能力不足, 子种群中包含无用解和距离度量不具有普适性的问题, 本文提出了基于分解和自适应搜索的多模态多目标算法MOEA/D-AS.在算法初始化阶段, 通过降低每个子种群中解数量的平均值, 增加参考向量的数量, 提高种群的搜索能力.根据每个子种群的归一化平均距离和归一化平均聚合函数值重新分配各个子种群中解的数量, 使种群能够根据当前状态自适应分配搜索资源.使用清除距离作为维护子种群中解的依据, 它具有更好的鲁棒性, 并且提高了算法的性能.实验表明, MOEA/D-AS算法可以有效解决多模态多目标优化问题, 且性能与最先进的多模态多目标算法相比具有竞争力.
参考文献

[1]	Tanabe R, Ishibuchi H. A review of evolutionary multimodal multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(1): 193-200. DOI:10.1109/TEVC.2019.2909744
[2]	李占山, 刘兆赓, 俞寅, 等. 量子化信息素蚁群优化特征选择算法[J]. 东北大学学报(自然科学版), 2020, 41(1): 17-22. (Li Zhan-shan, Liu Zhao-geng, Yu Yin, et al. A quantized pheromone ant colony optimization algorithm for feature selection[J]. Journal of Northeastern University(Natural Science), 2020, 41(1): 17-22.)
[3]	Tian Y, Liu R C, Zhang X Y, et al. A multipopulation evolutionary algorithm for solving large-scale multimodal multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2021, 25(3): 405-418. DOI:10.1109/TEVC.2020.3044711
[4]	Nguyen B H, Xue B, Andreae P, et al. Multiple reference points-based decomposition for multiobjective feature selection in classification: static and dynamic mechanisms[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(1): 170-184. DOI:10.1109/TEVC.2019.2913831
[5]	Huang T, Gong Y J, Kwong S, et al. A niching memetic algorithm for multi-solution traveling salesman problem[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(3): 508-522.
[6]	Yuan Y, Xu H, Wang B, et al. Balancing convergence and diversity in decomposition-based many-objective optimizers[J]. IEEE Transactions on Evolutionary Computation, 2016, 20(2): 180-198. DOI:10.1109/TEVC.2015.2443001
[7]	Liu Y P, Yen G, Gong D. A multimodal multiobjective evolutionary algorithm using two-archive and recombination strategies[J]. IEEE Transactions on Evolutionary Computation, 2019, 23(4): 660-674. DOI:10.1109/TEVC.2018.2879406
[8]	Zhang Q F, Li H. MOEA/D: a multi-objective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759
[9]	Tanabe R, Ishibuchi H. A decomposition-based evolutionary algorithm for multi-modal multi-objective optimization[C]// Proceedings of Parallel Problem Solving from Nature-PPSN. Coimbra: Springer International Publishing, 2018: 249-261.
[10]	Peng Y M, Ishibuchi H. A decomposition-based large-scale multi-modal multi-objective optimization algorithm[EB/OL]. (2020-09-03)[2021-12-26]. https://ieeexplore.ieee.org/document/9185674.
[11]	Liu Y P, Ishibuchi H, Yen G G, et al. On the normalization in evolutionary multi-modal multi-objective optimization[EB/OL]. (2020-09-03)[2021-12-25]. https://ieeexplore.ieee.org/document/9185899.
[12]	Ma X L, Yu Y N, Li X D, et al. A survey of weight vector adjustment methods for decomposition-based multiobjective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(4): 634-649. DOI:10.1109/TEVC.2020.2978158
[13]	Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017
[14]	Yue C T, Qu B Y, Liang J. A multiobjective particle swarm optimizer using ring topology for solving multimodal multi-objective problems[J]. IEEE Transactions on Evolutionary Computation, 2018, 22(5): 805-817. DOI:10.1109/TEVC.2017.2754271
[15]	Li G Q, Wang W L, Chen H L, et al. A SHADE-based multimodal multi-objective evolutionary algorithm with fitness sharing[J]. Applied Intelligence, 2021, 51(12): 8720-8752. DOI:10.1007/s10489-021-02299-1
[16]	Tanabe R, Ishibuchi H. A niching indicator-based multi-modal many-objective optimizer[J]. Swarm and Evolutionary Computation, 2019, 49(1): 134-146.
[17]	Zhou A, Zhang Q, Jin Y. Approximating the set of pareto-optimal solutions in both the decision and objective spaces by an estimation of distribution algorithm[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 1167-1189. DOI:10.1109/TEVC.2009.2021467
[18]	Tian Y, Cheng R, Zhang X Y, et al. PlatEMO: a Matlab platform for evolutionary multi-objective optimization[J]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87. DOI:10.1109/MCI.2017.2742868