
 , 曲兴超, 李柏涛, 苏晶
, 曲兴超, 李柏涛, 苏晶 东北大学 机械工程与自动化学院,辽宁 沈阳 110819
收稿日期:2022-05-25
基金项目:国家重点研发计划项目(2020YFB2007802); 中央高校基本科研业务费专项资金资助项目(N2103025)。
作者简介:李小彭(1976-), 男, 江西宁都人, 东北大学教授, 博士生导师。
摘要:以风力发电机球轴承为研究对象,提出了凹坑形式的轴电流损伤模型,分析该损伤对轴承动力学特性的影响规律.利用半正弦和分段激励函数建立了一个含长度、宽度和深度的损伤模型,用于描述轴电流的不同损伤程度;建立了含轴电流损伤的轴承动力学模型,来研究损伤凹坑的大小和形状及外载荷对轴承的振动特性影响;通过轴承的接触分析,研究了轴电流损伤程度对轴承载荷分布的影响;将仿真结果和实验对比,验证了模型的正确性.研究结果表明:所提出的模型可以准确地描述由凹坑形式的轴电流损伤导致的冲击激励与周期性变化现象;随着轴电流损伤程度的增大,轴承的振动响应和接触力变大,系统趋于不稳定.
关键词:轴电流损伤模型轴承载荷动力学
Dynamic Modeling and Property Analysis of Ball Bearings with Shaft Current Damage
LI Xiao-peng

 , QU Xing-chao, LI Bai-tao, SU Jing
, QU Xing-chao, LI Bai-tao, SU Jing School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LI Xiao-peng, E-mail: xpli@me.neu.edu.cn.
Abstract: Aimed at the wind turbine ball bearings, a shaft current damage model in the form of pits is proposed to investigate the influence of the shaft current pit damage on the bearings' dynamic characteristics. A damage model with length, width and depth is established based on the half-sine and piecewise excitation functions to describe the different damage degrees of the shaft current. The dynamic model of the bearings with shaft current damage is built to study the influence of the pit size, the pit shape and the external load on the vibration properties of the bearings. The effect of the shaft current damage with different damage degrees on the load distribution of the bearings is investigated by the contact analysis. The correctness of the proposed model is verified by comparing the results from the numerical simulation and the experiment. The results show that the shock excitation and the periodic phenomenon caused by the shaft current pit damage can be accurately described by the proposed model. With the shaft current damage increasing, the vibration response and the contact force of the bearings increase, and the stability becomes worse.
Key words: shaft currentdamage modelbearingloaddynamics
在电气驱动的背景下,随着大型风力发电机单机容量的逐渐提高,变流器和电气控制系统的复杂化,约50 % 的电机故障是由于滚动轴承发生了损坏;在损坏的轴承中,25 % 的轴承损伤是由轴电流造成的,其轴电流问题是加速轴承退化的主要起因[1-2].电机运行时,由于磁场不平衡,在轴承和轴之间会形成轴电压,当轴电压超出轴承油膜电压的最小阈值时,将会在油膜薄弱的位置击穿并形成轴电流,其接触表面瞬间熔化并形成较小的电腐蚀凹坑.在机械载荷和疲劳磨损的作用下,损伤日益加剧,轴承性能逐渐退化,甚至失效[3].
近年来,在工业生产中密切关注因轴电流导致发电机轴承故障的问题,国内外的许多****对轴电流产生的原因、轴承损伤形貌、轴承损伤近似评估以及振动检测等进行了相关研究,其中对发电机的振动监测是最常用、最可靠的轴承损伤检测方法之一[4-7].Loos等[8]分析了变频器在变速驱动中导致电机和轴承形成电流通道的原因,通过实验证明了轴电流是导致轴承形成损伤的主要起因.Liu[9]研究了高频电流通道导致变频电机轴承早期失效的主要原因,并对滚道表面的轴电流损伤凹坑形貌进行了分析.Xie等[10]开展了轴承电腐蚀试验,研究了轴承表面在弱电流下的损伤行为.通过对滚道表面的损伤凹坑观察,发现其凹坑形状上宽下窄,形似于三角形或梯形.Xu等[11]基于位移激励变化性质,提出了轴承内、外滚道和滚动体的局部缺陷模型,研究了缺陷大小与缺陷角度对刚度的变化情况.刘静等[12]研究了滚动体和滚道之间是非理想赫兹线性接触,对故障的滚动轴承进行动力学建模,分析了不同的缺陷宽度尺寸对系统振动特性的影响.Patel等[13]考虑深沟球轴承滚道中的单个和多个缺陷,其于矩形缺陷模型,建立了缺陷轴承的动力学模型,未考虑滚动体通过损伤凹坑的接触状态.马辉等[14]引入矩形缺陷来模拟轴承滚道局部剥落缺陷,并建立了含局部剥落的轴承有限元模型,分析了故障边缘的等效应力.Qin等[15]考虑故障的耦合效应和分段效应,基于半正弦激励函数,建立了含局部故障的球轴承动力学模型,但未考虑损伤缺陷宽度对系统振动特性的影响规律.
本文以风力发电机轴承为研究对象,针对凹坑形式的轴电流损伤,利用半正弦和分段激励函数对轴电流损伤凹坑进行描述.建立含轴电流损伤的深沟球轴承动力学模型,分析损伤凹坑的尺寸和形状对系统的振动特性影响,并研究不同外载荷作用下轴承加速度信号变化规律.通过轴承的接触研究,分析了不同程度的轴电流损伤对轴承载荷分布的影响.最后,开展了损伤轴承的振动实验,采集加速度信号并与数值仿真结果进行比较,验证了动力学模型的准确性.
1 含轴电流损伤的轴承动力学模型1.1 轴电流损伤模型轴电流是造成风力发电机轴承损伤的主要原因之一[3],当电机内部形成电流通道的瞬间,会使轴承滚道与滚动体的接触表面形成较小的电腐蚀凹坑[10-11],当滚动体通过局部凹坑时,将使轴承系统产生相应的冲击和振动,振动的特征取决于滚动体与滚道损伤位置的接触情况.针对不同的轴电流损伤凹坑形式,为了准确地描述轴电流损伤凹坑特征,本文通过半正弦和分段激励函数建立了一个含长L、宽B和高H的三维损伤凹坑模型,进而去描述滚道及滚动体上不同程度的轴电流损伤,其中损伤凹坑的长度L为滚动体滚动方向,轴电流损伤凹坑描述如图 1所示.
图 1(Fig. 1)
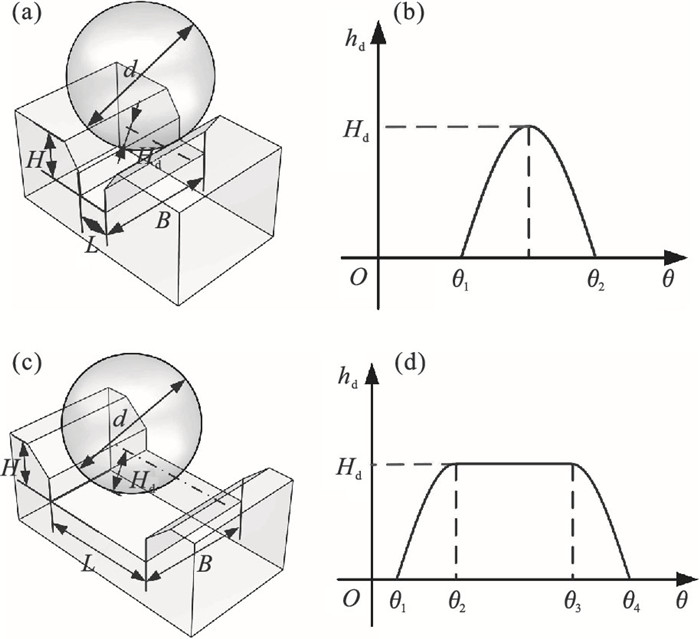 | 图 1 轴电流损伤凹坑描述示意图Fig.1 Schematic diagram of the shaft current damage pits (a)—半正弦类型损伤;(b)—半正弦激励函数;(c)—分段类型损伤;(d)—分段激励函数. |
当轴承滚道及滚动体存在轴电流损伤凹坑时,定义滚动体直径与轴电流损伤凹坑的尺寸比为
 | (1) |
 | (2) |
滚动体通过不同形状和尺寸的轴电流损伤凹坑所产生的激励不同,根据滚动体直径与轴电流损伤凹坑的尺寸比以及凹坑的长宽比,将损伤激励形式分为三种类型.第一种类型的损伤程度较小,如图 1a所示,其滚动体直径大于损伤凹坑尺寸且损伤凹坑长小于等于宽(κbd>1,ηd≤1);这种损伤类型采用图 1b中的半正弦激励函数来描述滚动体通过损伤位置时位移激励瞬间增大又逐渐减小的状态.当损伤程度为第二、三种类型时,如图 1c所示,即滚动体直径大于损伤凹坑尺寸且损伤凹坑长大于宽(κbd>1,ηd>1)或滚动体直径小于等于损伤凹坑尺寸(κbd≤1);这两种损伤类型均采用图 1d中的分段激励函数来描述滚动体通过损伤位置时位移激励突然增大并在短暂时间内保持最大激励不变,然后逐渐减小.
根据上述三种损伤激励形式,定义轴电流损伤模型为
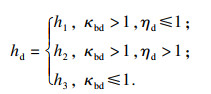 | (3) |
在式(3)中,h1的函数表达式为
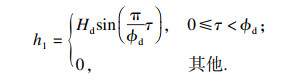 | (4) |
轴承滚动体与轴电流损伤缺陷之间的角位置定义,如图 2所示.图中θdi和θdo分别为内、外滚道损伤位置相对Y轴的夹角,?di和?do分别为内、外滚道上的损伤缺陷角度.
图 2(Fig. 2)
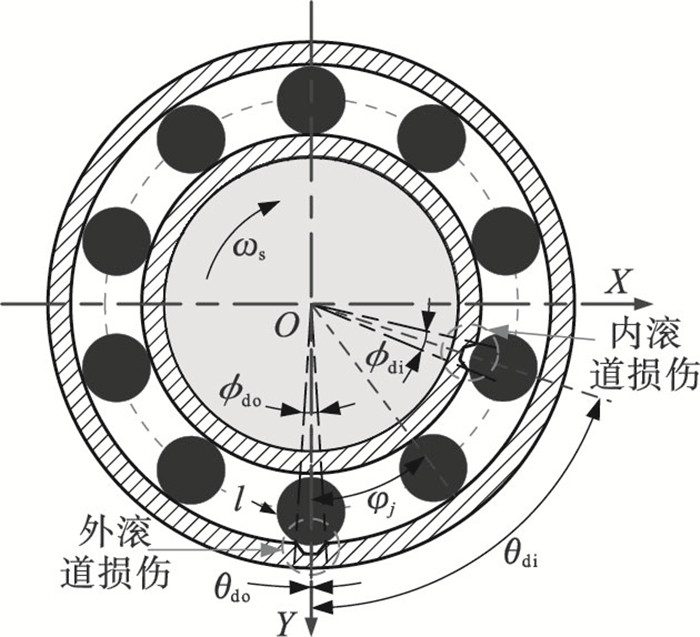 | 图 2 滚动体与损伤的角位置定义Fig.2 Angular position definition of the rolling body and damage |
因此,第j滚动体与内、外滚道之间的夹角为
 | (5) |
滚动体与不同损伤凹坑的接触状态,如图 3所示.根据滚动体与轴电流损伤凹坑接触时的几何位置关系,进而得到损伤缺陷角度?d,滚动体在损伤区域的理论位移ΔH以及实际位移Hd.
图 3(Fig. 3)
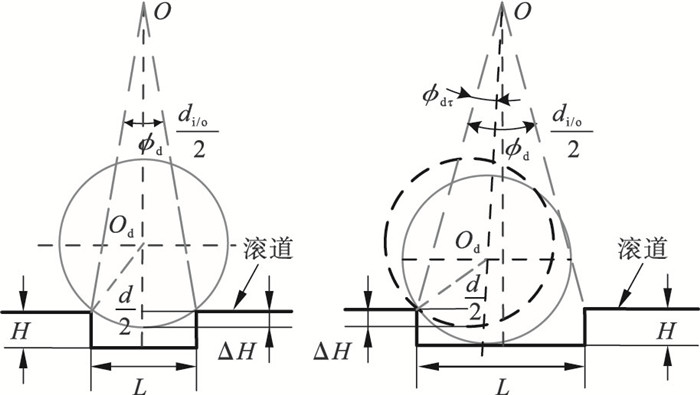 | 图 3 滚动体与不同损伤凹坑的接触状态Fig.3 Contact state between the rolling body and different damage pits |
则轴承内、外滚道的损伤缺陷角度为
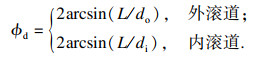 | (6) |
滚动体通过损伤区域的理论位移为
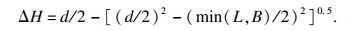 | (7) |
 | (8) |
 | (9) |
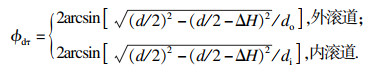 | (10) |
图 4(Fig. 4)
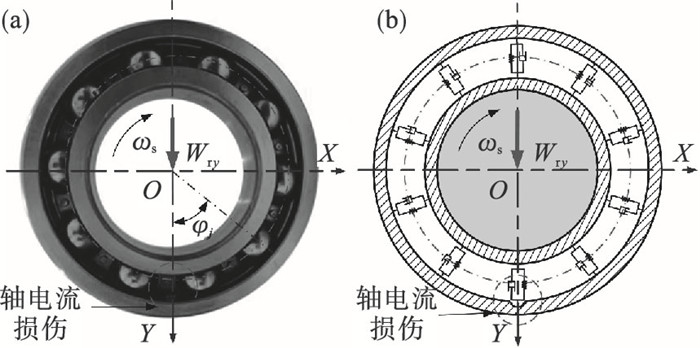 | 图 4 轴电流损伤轴承动力学模型示意图Fig.4 Schematic diagram of the dynamic model of bearings with shaft current damage (a)—实物图;(b)—模型图. |
根据Hertz接触理论,推导了轴电流损伤轴承的接触力表达式为
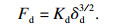 | (11) |
滚动体与损伤滚道的接触变形为
 | (12) |
当滚动体与损伤滚道接触时,其接触刚度为
 | (13) |
 | (14) |
根据摩擦力产生的条件,当滚动体进入轴承的承载区域时,滚动体与内、外滚道因相互接触产生了摩擦力,其摩擦力的表达式为
 | (15) |
在深沟球轴承中,当滚动体与轴承滚道相互接触时,X和Y方向上产生的摩擦力为
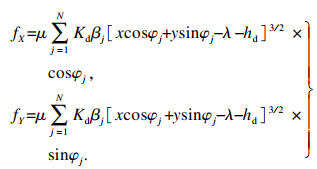 | (16) |
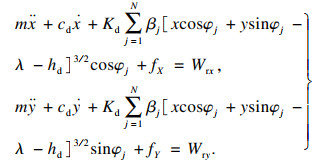 | (17) |
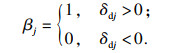 | (18) |
分析含轴电流损伤的深沟球轴承的振动响应时,数值仿真所采用的模型参数如表 1所示.
表 1(Table 1)
| 表 1 DGB 6210轴承尺寸参数 Table 1 Geometric dimension parameters of DGB 6210 |
2.1 轴电流损伤大小对轴承系统的影响为了研究轴电流损伤凹坑尺寸对系统响应的影响规律,令损伤凹坑宽度大于等于长度,选取损伤凹坑的深度H为0.1 mm,长度L等于宽度B分别为0.1,0.3和0.5 mm,通过对含轴电流损伤轴承的动力学方程求解,获得了损伤轴承的Y方向振动响应信号,如图 5所示.
图 5(Fig. 5)
 | 图 5 轴电流损伤凹坑尺寸对轴承振动响应的影响Fig.5 Effect of the pit size of shaft current damage on bearings' vibration response (a)—L=B=0.1 mm时域图; (b)—L=B=0.3 mm时域图; (c)—L=B=0.5 mm时域图; (d)—L=B=0.1 mm包络谱图; (e)—L=B=0.3 mm包络谱图; (f)—L=B=0.5 mm包络谱图. |
从图 5的振动加速度响应中可以看出,在滚动体通过损伤位置时,系统出现了明显的冲击现象,加速度突增随后系统响应出现衰减的趋势,随着滚动体依次进入损伤位置,轴承外滚道的加速度信号呈现出周期性变化.由于轴电流损伤的大小和形状不同,导致振动加速度响应的幅值和波形不同.随着损伤尺寸的增大,滚动体通过损伤位置时会产生较大的冲击,在时域图上可以看到明显的幅值变化.从包络谱图上可以得到,系统响应的频率成分为fbo,2fbo,3fbo和4fbo,其中fbo为102.2 Hz,为外圈损伤特征频率.当轴电流损伤尺寸增大时,系统响应的主要频率成分基本不变,但频率对应的幅值增大且系统加速度信号出现多次谐波,代表系统趋于不稳定.
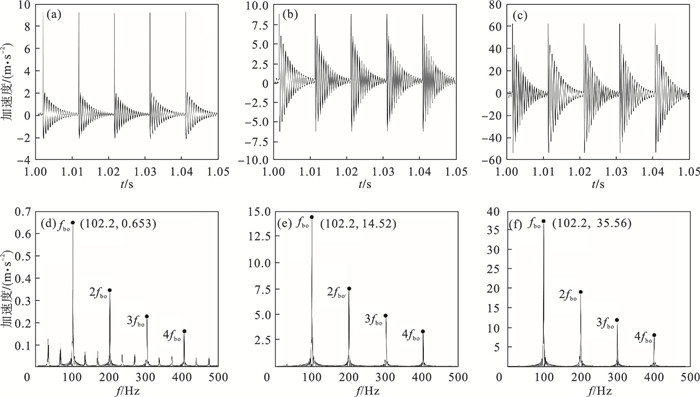
其次,为了研究轴电流损伤凹坑的长度L与宽度B对系统加速度响应的影响,令损伤凹坑长度大于宽度,选取凹坑的深度H为0.1 mm,长度L依次为0.3,0.5和0.5 mm,宽度B依次为0.1,0.1和0.3 mm,得到了损伤轴承的轴承加速度信号,如图 6所示.
图 6(Fig. 6)
 | 图 6 轴电流损伤凹坑长度L与宽度B对轴承加速度信号的影响Fig.6 Effect of the length L and width B of shaft current damage pits on bearings' acceleration signal (a)—L=0.3 mm,B=0.1 mm时域图; (b)—L=0.5 mm,B=0.1 mm时域图; (c)—L=0.5 mm,B=0.3 mm时域图. |
对比图 6a和图 6b可以看出,随着轴电流损伤凹坑长度L的增加,滚动体通过损伤位置时也会产生一定的周期性冲击,但其振动加速度的幅值增长趋势相对较小且波形发生了改变.这说明轴电流损伤凹坑长度对系统的振动幅值影响较小.对比图 6b和图 6 c可知,随着轴电流损伤凹坑宽度B的增加,时域波形变化趋势基本相同,但加速度幅值明显增大且变化更剧烈.结果表明,轴电流损伤宽度对系统响应影响较大,使系统振动增大,不利于轴承稳定.
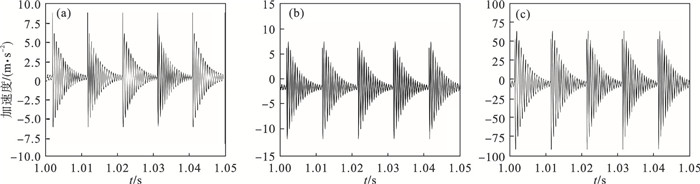
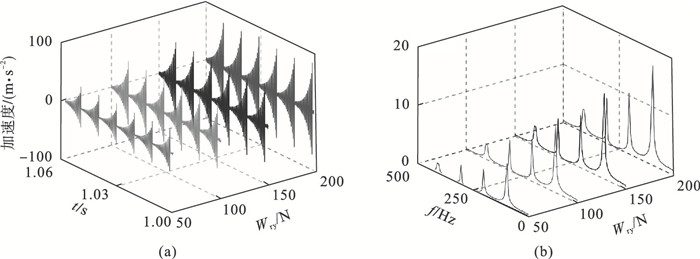
2.2 外载荷对轴承的振动特性影响为了研究外载荷对轴电流损伤轴承振动特性的影响规律,分别选取长度L=0.3 mm、宽度B=0.3 mm和深度H=0.1 mm,以及长度L=0.5 mm、宽度B=0.3 mm和深度H=0.1 mm的不同损伤.当外载荷作用分量Wrx=0 N和Wry=50,100,150和200 N,转速为1 500 r/min时,分析外载荷对轴承振动特性的影响,如图 7和图 8所示.
图 7(Fig. 7)
 | 图 7 外载荷对轴承振动特性的影响(L=0.3 mm,B=0.3 mm和H=0.1 mm)Fig.7 Effect of the external load on bearings'vibration characteristics(L =0.3 mm, B =0.3 mm and H =0.1 mm) (a)—加速度时域图;(b)—加速度包络谱图. |
图 8(Fig. 8)
 | 图 8 外载荷对轴承振动特性的影响(L=0.5 mm,B=0.3 mm和H=0.1 mm)Fig.8 Effect of the external load on bearings' vibration characteristics(L=0.5 mm, B=0.3 mm and H=0.1 mm) (a)—加速度时域图;(b)—加速度包络谱图. |
从图 7和图 8的振动加速度响应曲线和包络谱中可以看到,加速度波形和幅值大小随外载荷的增加而变大.这说明由于外载荷的增加,滚动体与滚道之间的接触力也随之变大,当滚动体通过损伤区域时所产生的冲击和碰撞现象更加明显,轴承的振动响应变化就越大.当外载荷在一定范围变化时,对比图 7和图 8的不同轴承损伤形式下的振动响应,可以看出图 8的振动响应幅值变化较大.这是因为当损伤长度相对增加时,在外载荷的作用力下,滚子与滚道之间接触面积和接触力也相对变大,振动响应也就随之变大.
3 轴电流损伤轴承的载荷分布轴承外滚道存在轴电流损伤凹坑,其损伤缺陷的初始位置角为0,损伤长度L=0.1 mm,宽度B=0.1 mm和深度H=0.1 mm,轴承以1 500 r/min的转速转动,径向负载Wry=100 N,通过式(11)对轴电流损伤轴承的接触力进行分析,如图 9所示.
图 9(Fig. 9)
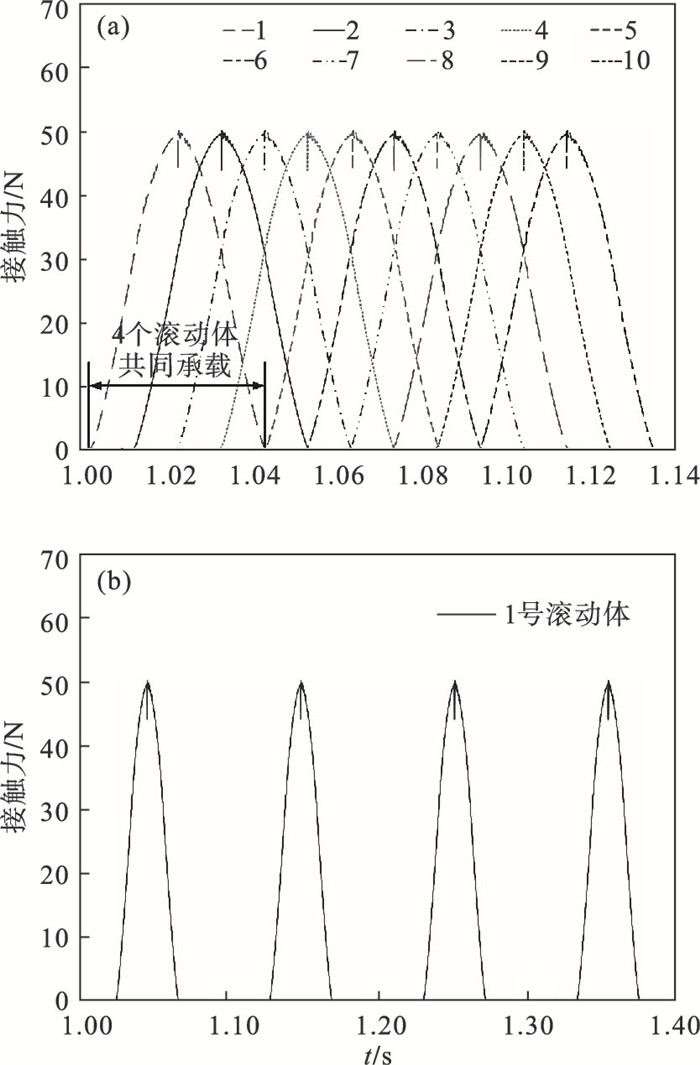 | 图 9 轴电流损伤轴承的接触力分布Fig.9 Load distribution of the shaft current damage bearings (a)—滚动体与外滚道的接触力情况;(b)—1号滚动体与外滚道的接触力变化情况. |
从图 9a中可以看出,在轴承的受载区域内,10个滚动体中最多存在4个滚动体同时出现在承载区,其单个滚动体与滚道之间的接触力最大值约为50 N.图 9b为1号滚动体与轴承外滚道之间的接触力,从图上可以看出,随着时间的变化,1号滚动体呈现出周期性进入或者离开轴承的承载区域和损伤区域.
轴承外加径向负载Wry为100 N,转速ns为1 500 r/min时的工况下,研究了轴电流损伤大小对轴承动态载荷分布的影响规律,如图 10所示.
图 10(Fig. 10)
 | 图 10 轴电流损伤大小对轴承动态载荷分布的影响规律Fig.10 Influence law of the shaft current damage on dynamic load distribution of bearings (a)—L=0.1 mm, B=0.1 mm; (b)—L=0.3 mm, B=0.3 mm; (c)—L=0.5 mm, B=0.3 mm; (d)—L=0.5 mm, B=0.5 mm; (e)—L=2 mm, B=0.5 mm; (f)—L=6 mm, B=0.5 mm. |
从图 10中可以看到,滚动体依次通过轴承的非承载区、承载区、损伤区,承载区和非承载区.当滚动体通过损伤位置时,轴承会产生相应的冲击力和接触力突变情况.从一系列的损伤轴承载荷分布图中可以看出,随着轴电流损伤的不断增大,冲击力也不断增大,滚动体与滚道之间的载荷分布波动变大,轴承在损伤区域的承载能力在不断减小,当损伤缺陷达到一定程度时,位于损伤区域的滚动体将会丧失承载能力.
4 实验验证为了验证建立的含轴电流损伤轴承的动力学模型,在如图 11所示的ABLT-1A轴承疲劳实验机上对DGB 6210损伤轴承开展了实验,通过DHDAS动态信号采集仪器和加速度传感器,对轴承的Y方向振动信号进行了测量.
图 11(Fig. 11)
 | 图 11 ABLT-1A轴承疲劳实验机Fig.11 ABLT-1Abearing fatigue testing machine |
在实验机的转轴上安装了4个同型号的轴承,1,3,4号为健康轴承,2号为损伤轴承并径向加载1 000 N,转速ns为1 500 r/min,通过加速度传感器测得了系统的振动响应.
从图 12和图 13的仿真与实验对比图中可以看出,在时域图上,波形变化趋势基本相同,均存在着明显的冲击现象且呈现出周期性变化;随着轴电流损伤尺寸的增大,仿真与实验的时域波形变化更加剧烈,并且加速度响应幅值显著增大.在频域图上,仿真与实验信号的频率成分基本一致,两者均能反映出轴承外圈损伤特征频率且分为fbo,2fbo,3fbo和4fbo;第一组仿真与实验的结果表明,损伤特征频率fbo分别为102.2 Hz和101.0 Hz,相对误差为1.17 %;同上,第二组损伤特征频率fbo分别为102.2 Hz和100.7 Hz,相对误差为1.47 %;两组不同损伤下的外圈损伤特征频率的相对误差较小,因此结果可以被认为是可靠的.
图 12(Fig. 12)
 | 图 12 仿真与实验对比图(L=0.3 mm,B=0.3 mm和H=0.1 mm)Fig.12 Comparison of thenumerical simulation and the experiment(L=0.3 mm, B=0.3 mm and H=0.1 mm) (a)—仿真加速度响应;(b)—仿真加速度包络谱;(c)—实验加速度响应;(d)—实验加速度包络谱. |
图 13(Fig. 13)
 | 图 13 仿真与实验对比图(L=0.5 mm,B=0.3 mm和H=0.1 mm)Fig.13 Comparison of the simulation and the experiment(L=0.5 mm, B=0.3 mm and H=0.1 mm) (a)—仿真加速度响应;(b)—仿真加速度包络谱;(c)—实验加速度响应;(d)—实验加速度包络谱. |
另外,仿真与实验结果还存在着较小的误差和差异,主要来源于模型的假设因素、轴承安装精度以及外界环境因素等,后续将尽可能地减少这些误差来源,以提高仿真和实验的精度.综上所述,模型仿真和实验结果具有很好的吻合度,证明了本文所建立的动力学模型的准确性.
5 结论1) 当滚动体通过轴电流损伤凹坑时,加速度信号出现明显的突增现象,随后呈现衰减趋势且随时间进行周期性变化.随着凹坑尺寸的增大,振动响应幅值增加,其主要频率成分基本不变,次频响应增加,系统运行更加不稳定.
2) 随着轴电流损伤凹坑的尺寸不断增大,冲击力也不断增大,滚动体与滚道之间的载荷分布波动很大,轴承在损伤区域的承载能力在不断减小,当损伤缺陷达到一定程度时,位于损伤区域的滚动体将会完全丧失承载能力.
3) 通过对比模型仿真和实验数据的结果可以看到,两者吻合度较好,在时域信号上均存在着明显的冲击现象且呈现出周期性的变化,波形变化趋势基本相同,频率成分基本一致,验证了本文模型的准确性.
参考文献
| [1] | Plazenet T, Boileau T, Caironi C, et al. A comprehensive study on shaft voltages and bearing currents in rotating machines[J]. IEEE Transactions on Industry Applications, 2018, 54(4): 3749-3759. DOI:10.1109/TIA.2018.2818663 |
| [2] | Kudelina K, Vaimann T, Rass lkin A, et al. Induction motor bearing currents-causes and damages[C]//2021 28th International Workshop on Electric Drives: Improving Reliability of Electric Drives(IWED). Moscow: IEEE, 2021: 1-5. |
| [3] | 孟宪文. 风力发电机轴承轴电流损伤研究[D]. 湘潭: 湖南科技大学, 2016. (Meng Xian-wen. Research on bearing shaft current damage of wind turbine[D]. Xiangtan: Hunan University of Science and Technology, 2016. ) |
| [4] | Qiu C D, Wu X B, Xu C Q, et al. An approximate estimation approach of fault size for spalled ball bearing in induction motor by tracking multiple vibration frequencies in current[J]. Sensors, 2020, 20(6): 1631. DOI:10.3390/s20061631 |
| [5] | Raadnui S, Kleesuwan S. Electrical pitting wear debris analysis of grease-lubricated rolling element bearings[J]. Wear, 2011, 271(9/10): 1707-1718. |
| [6] | Wang J, Peng Y Y, Qiao W. Current-aided order tracking of vibration signals for bearing fault diagnosis of direct-drive wind turbines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6336-6346. DOI:10.1109/TIE.2016.2571258 |
| [7] | Prudhom A, Antonino-Daviu J, Razik H, et al. Time-frequency vibration analysis for the detection of motor damages caused by bearing currents[J]. Mechanical Systems and Signal Processing, 2017, 84: 747-762. DOI:10.1016/j.ymssp.2015.12.008 |
| [8] | Loos J, Bergmann I, Goss M. Influence of high electrical currents on WEC formation in rolling bearings[J]. Tribology Transactions, 2021, 64(4): 708-720. DOI:10.1080/10402004.2021.1909789 |
| [9] | Liu W. The prevalent motor bearing premature failures due to the high frequency electric current passage[J]. Engineering Failure Analysis, 2014, 45: 118-127. DOI:10.1016/j.engfailanal.2014.06.021 |
| [10] | Xie G X, Luo J B, Guo D, et al. Damages on the lubricated surfaces in bearings under the influence of weak electrical currents[J]. Science China Technological Sciences, 2013, 56(12): 2979-2987. DOI:10.1007/s11431-013-5399-7 |
| [11] | Xu H Y, He D, Ma H, et al. A method for calculating radial time-varying stiffness of flexible cylindrical roller bearings with localized defects[J]. Engineering Failure Analysis, 2021, 128: 105590. DOI:10.1016/j.engfailanal.2021.105590 |
| [12] | 刘静, 邵毅敏, 秦晓猛, 等. 基于非理想Hertz线接触特性的圆柱滚子轴承局部故障动力学建模[J]. 机械工程学报, 2014, 50(1): 91-97. (Liu Jing, Shao Yi-min, Qin Xiao-meng, et al. Dynamic modeling on localized defect of cylindrical roller bearing based on non-Hertz line contact characteristics[J]. Journal of Mechanical Engineering, 2014, 50(1): 91-97.) |
| [13] | Patel V N, Tandon N, Pandey R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races[J]. Journal of Tribology, 2010, 132(4): 041101-041111. DOI:10.1115/1.4002333 |
| [14] | 马辉, 李鸿飞, 俞昆, 等. 含局部故障的滚动轴承动力学建模及振动分析[J]. 东北大学学报(自然科学版), 2020, 41(3): 343-348. (Ma Hui, Li Hong-fei, Yu Kun, et al. Dynamic modeling and vibration analysis of rolling bearing with local faults[J]. Journal of Northeastern University(Natural Science), 2020, 41(3): 343-348.) |
| [15] | Qin Y, Cao F, Wang Y, et al. Dynamics modelling for deep groove ball bearings with local faults based on coupled and segmented displacement excitation[J]. Journal of Sound and Vibration, 2019, 447: 1-19. DOI:10.1016/j.jsv.2019.01.048 |
