, 张鹏1, 李红雷1, 吕中1 1. 东北大学 机械工程与自动化学院，辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室，辽宁 沈阳 110819
收稿日期：2022-08-29
基金项目：国家自然科学基金资助项目(51975110)；“兴辽英才计划”项目(XLYC1907171)；中央高校基本科研业务费专项资金资助项目(N2003005，N21003005)。
作者简介：黄贤振(1982-), 男, 山东定陶人, 东北大学教授, 博士生导师。
摘要：预紧量对轴承的运行状态和使用寿命有着重要的影响.为了保证主轴轴承的合理装配，需要确定轴承的零游隙位置.首先，采用厚壁圆筒理论计算了轴承游隙的变化量，从而确定轴承的零游隙位置.而后，建立了轴承零游隙的有限元位移模型，提出了一种更加准确的零游隙位置计算方法.考虑到随机因素的影响，提出了Kriging代理模型的方法，分析了风电主轴轴承零游隙下内外圈位置的概率分布特性.最后，数值算例表明，Kriging模型预测的最大误差在0.1 % 以内，表明所提出的方法具有较高的精度和适用性.
关键词：风力发电机主轴轴承概率分析有限元模型Kriging代理模型
Probability Analysis of Zero Clearance Position of Wind Turbine Spindle Bearings
HUANG Xian-zhen1,2
, ZHANG Peng1, LI Hong-lei1, LYU Zhong1 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems, Ministry of Education, Northeastern University, Shenyang 110819, China
Corresponding author: HUANG Xian-zhen, E-mail: xzhhuang@mail.neu.edu.cn.
Abstract: The preload greatly affects the operating state and service life of bearings. To ensure the reasonable assembly of the spindle bearings, the position of zero clearance for the bearings needs to be determined. Firstly, the variation of clearance is calculated by using the thick-walled cylinder theory to determine the zero clearance position of the bearings. Then, the finite element displacement model of bearing zero clearance is established, and a more accurate calculation method of zero clearance position is proposed. Considering the influence of random factors, the Kriging surrogate model is proposed to analyze the probability distribution characteristics of the inner and outer ring positions under the zero clearance of wind turbine spindle bearings. Finally, numerical examples show that the maximum error predicted by the Kriging model is within 0.1 %, indicating that the proposed method has higher accuracy and applicability.
Key words: wind turbinespindle bearingprobability analysisfinite element modelKriging surrogate model
风力发电机主轴轴承是风力发电机组的关键部件，其运行状态的好坏直接关系到整个机组的运行效率与安全.风力发电机主轴轴承安装在10 m以上的高空, 其安装和更换极为不便且成本较高，这对轴承的寿命和可靠性提出了更高的要求.主轴轴承所受载荷状况复杂, 且受风力影响会发生振动.为了减少滚动工作面的微动磨损，轴承采取过盈配合的方式安装在主轴及轴承座上.而轴承游隙对轴承的承载能力、工作性能以及疲劳寿命等有着重大影响.因此，为了保障风力发电机主轴轴承的合理装配，研究主轴轴承的零游隙位置具有重要意义.
国内外****已经对风力发电机轴承作了大量研究.Liu等[1]对风电轴承的失效模式及故障诊断方法进行了综述，轴承套圈与安装轴或轴承座间的微动磨损会导致轴承的失效.Zheng等[2]采用非赫兹理论和切片技术分析了无齿轮风电主轴轴承的内部载荷和接触压力分布.Aguirrebeitia等[3]通过建立风电四接触点回转轴承的几何理论模型和有限元模型，研究了预紧力对轴承静态承载能力的影响.He等[4]建立了风电回转支承的试验台，提出了一种使用小样本试验测试轴承疲劳寿命的方法.Chen等[5]建立了考虑轴承套圈弹性的风电叶片轴承计算模型，研究了负游隙对接触应力的影响.Zheng等[6]在振荡外载荷和转速条件下，分析了直驱风电双列圆锥滚子轴承的疲劳寿命.Zhang等[7]建立了考虑复合载荷的风电双列回转球轴承的力学模型，研究了球与滚道的接触特性.轴承内外圈的过盈量会改变轴承的游隙，这对轴承的使用寿命和工作性能有着重大影响.Oswald等[8]通过分析不同等级的轴承过盈配合，确定了环向应力对角接触和深沟球轴承疲劳寿命的影响.Zhang等[9]提出了不同预紧机制下球轴承的刚度比较模型，详细讨论了内圈过盈量、转速和径向载荷对轴承特性的影响.Yu等[10]建立了滚动轴承的工作游隙模型，对结果进行了可靠性分析.
本文针对风电主轴轴承进行研究，为了使得轴承在装配后达到零游隙位置，分别通过理论计算和有限元建模的方法，分析了内外圈在装配时应在轴向提前移动的具体位置，以便在装配完成后圆锥滚子轴承的外圈与滚子达到刚好接触的状态.此外，考虑到轴承、主轴在加工装配的随机性，基于Monte-Carlo(MC)模拟，提出Kriging代理模型的方法对零游隙下轴承内外圈在轴向的移动位置进行了概率分布预测，预测结果可为工程实际中轴承的零游隙位置提供理论参考.
1 风力发电机主轴轴承的零游隙位置分析现代风力发电机主轴由定轴和转轴两个部分组成，如图 1所示.定轴固定在塔架上，转轴通过轮毂与叶片相连，转轴和定轴之间通过轴承支撑并传递力矩.在装配过程中，为了防止发生微动疲劳，轴承内圈与定轴、轴承外圈与转轴一般采取过盈配合的方式固定连接.由于弹性变形的影响，轴承内圈会产生径向膨胀，轴承外圈会产生径向收缩.从而内外圈和滚子的接触面产生挤压，表现为滚子和滚道表面接触应力的增加，从而影响轴承的使用寿命.为了尽可能消除内外圈变形带来的负面影响，减少由于挤压而造成的接触应力，需要使轴承在装配后达到零游隙位置，由于圆锥滚子轴承的内外圈是可分离结构，在轴承装配时，将轴承的内外圈在轴向提前错开一定的位置.在装配完成后，在施加过盈量的作用下，由于内外圈的膨胀和收缩，使得轴承滚子和外圈刚好接触，从而使轴承达到零游隙位置.
图 1(Fig. 1)
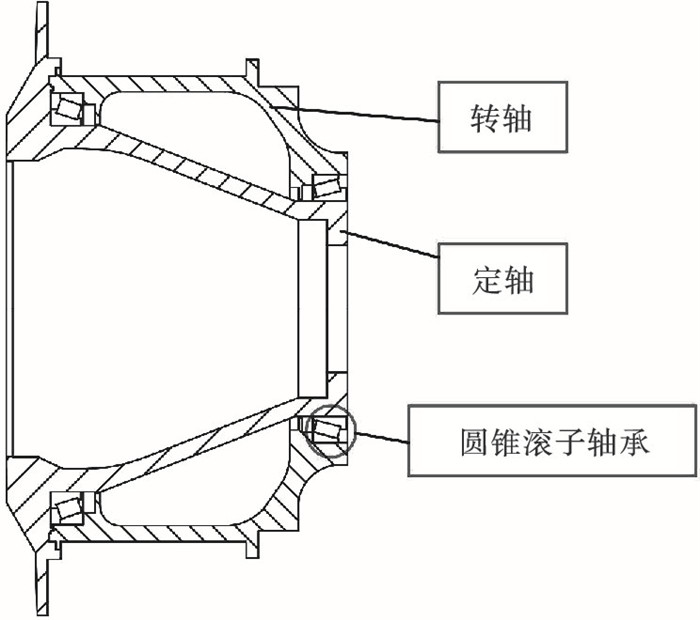 | 图 1 两点支撑式风力发电机Fig.1 Two-point support wind turbine |
如图 2所示，图 2b为零游隙位置示意图.为了施加合理的预紧量，使轴承处于最佳工作状态，需要先确定轴承的零游隙位置.
图 2(Fig. 2)
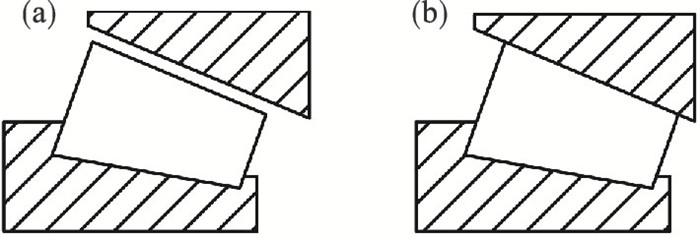 | 图 2 轴承游隙位置示意图Fig.2 Schematic diagram of bearing clearance position (a)—正游隙；(b)—零游隙. |
1.1 基于厚壁圆筒理论的轴承游隙计算轴承内外圈与定轴和转轴的过盈配合，会使内圈产生径向膨胀，外圈产生径向收缩，而引起轴承径向游隙的减小.如图 3所示，为了分析轴承内外圈的径向膨胀和收缩量，可将它们简化为圆筒.
图 3(Fig. 3)
 | 图 3 厚壁圆筒受力简图Fig.3 Sketch of force on thick-walled cylinder |
假设圆筒内部受到的压力为pi，外部受到的压力为po，那么由厚壁圆筒理论可知，在径向的变化量为
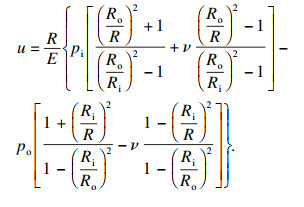 | (1) |
如图 4所示，由两个过盈配合的圆筒相互作用，产生的径向变形量为[11]
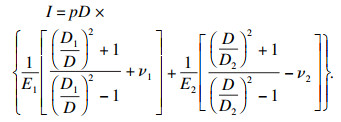 | (2) |
 | 图 4 过盈配合圆筒示意图Fig.4 Schematic diagram of interference fit cylinder |
式中：E1和E2分别为两个圆筒的弹性模量；D为内外圆筒过盈配合后的共同直径；D1和D2分别为过盈配合的两个圆筒的内外直径；p是由过盈配合产生的作用压力；ν1和ν2分别为两个圆筒的泊松比.
在径向变形量(过盈量)I确定的情况下，由式(2)推导确定压力p：
 | (3) |
 | (4) |
同理，由轴承外圈与风力发电机转轴过盈配合产生的轴承外圈内径收缩量为
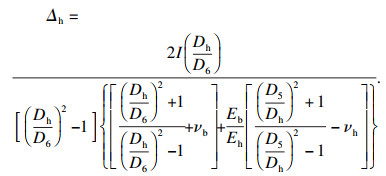 | (5) |
那么，轴承与风力发电机过盈配合安装后，轴承径向游隙的变化量为
 | (6) |
1.2 基于有限元的轴承零游隙位置分析基于厚壁圆筒理论的风力发电机主轴轴承游隙变化量分析方法是将轴承内外圈和风力发电机定转轴简化为壁厚均匀的圆筒，而在工程实际中风力发电机的结构十分复杂，上述简化将造成较大的计算误差.为了解决这一问题，本节将基于有限元理论，提出一种新的风力发电机主轴轴承零游隙位置的分析方法，用以计算装配时内外圈需要在轴向提前移动的相对位置，使得轴承装配后能够达到零游隙位置.
由于轴承、定轴和转轴均为中心对称模型，所以可对模型进行切分，截取只包含一个滚子的装配组件进行有限元分析，如图 5所示.为避免计算困难，对模型进行了简化，忽略一些倒角、圆角等微小结构.
图 5(Fig. 5)
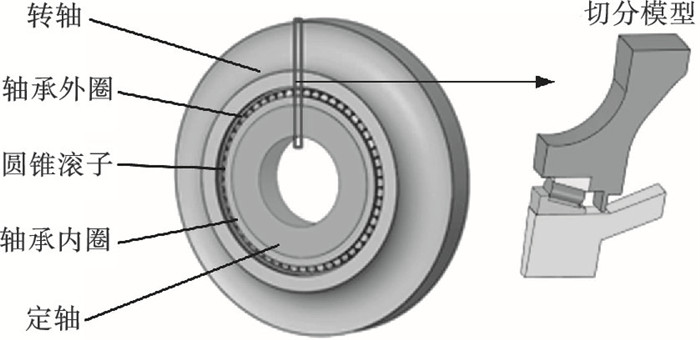 | 图 5 轴承装配体及切分模型Fig.5 Bearing assembly and segmentation model |
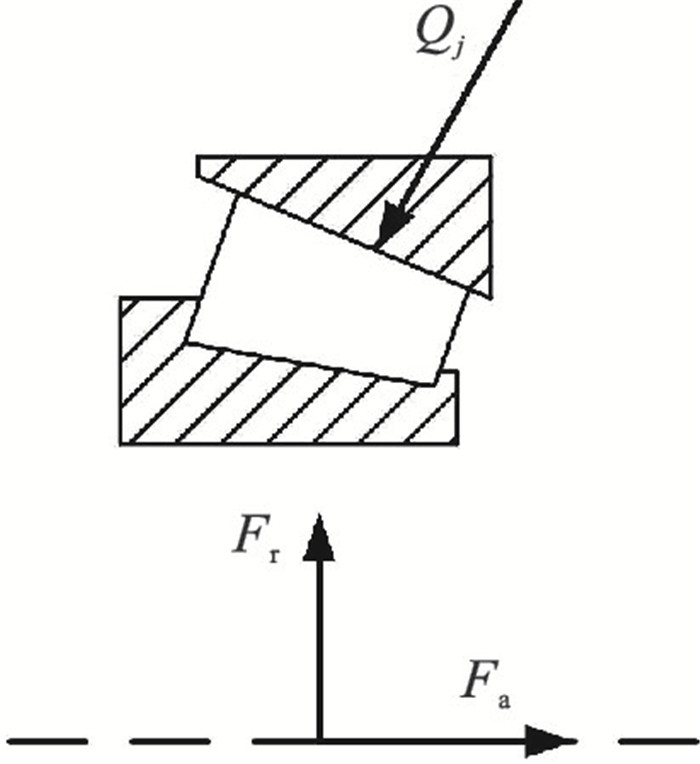
当轴承与风力发电机定轴及转轴过盈配合时，轴承内外圈在发生径向膨胀和收缩的同时还会发生轴向伸缩.为了模拟轴承实际过盈的情况，确定游隙为零时内外圈的位置，需要确定所施加的有限元边界条件.如图 6所示，对轴承整体进行静力学分析.在实际工作中，轴向载荷Fa、径向载荷Fr通过轴施加在轴承的内圈上，将内圈及滚子视为受力体，求外圈的法向接触应力Qj(j=1, 2，…，Z)与Fr，Fa的平衡.
 | (7) |
 | 图 6 轴承受力分析示意图Fig.6 Schematic diagram of bearing force analysis 1—施加轴承外圈过盈量；2—摩擦接触f0；3—摩擦接触f1；4—固定定轴底端自由度；5—摩擦接触f2；6—摩擦接触f3；7—施加轴承内圈过盈量；8—固定定轴底端自由度；9, 12—无摩擦约束；10—固定滚子Z方向自由度；11—摩擦接触f4. |
式中：α为滚子与外圈的接触角；Z为滚动体个数；ψj为各滚子所处的方位角.
这里对轴承在过盈状态下游隙恰好为零时的位置情况进行分析，并不施加轴向、径向载荷，即Fr，Fa都为零，由受力平衡得，轴承外圈与轴承滚子处于恰好接触却无作用力的临界状态.此时，轴承内外圈与风力发电机主轴接触面间的轴向摩擦力为零.此处不考虑摩擦是为了在施加过盈量后，轴承内外圈能够在轴向实现自由滑动，从而将轴承内外圈在径向的膨胀收缩变形释放掉.此时内外圈在轴向的相对位置即是装配时内外圈需要提前移动的位置.
基于以上静力学分析，为了模拟轴承的零游隙状态，需要在有限元模型中对接触副和约束条件进行设置.如图 7所示，轴承内外圈与风电主轴接触面设置为摩擦接触，摩擦系数设置为零，即f0，f3为0.滚子和轴承内外圈滚道间设置为摩擦接触，为了体现轴承内外圈轴向自由位移，减小摩擦力的影响，将其余摩擦系数统一设为一个微小量，即f1，f2，f4为0.002.同时固定转轴和定轴的底端自由度，限制转轴和定轴在各个方向的移动和转动.对滚子施加绕y方向的转动约束，限制滚子的周向运动.在轴承内外圈以及定轴和转轴的侧面设置无摩擦约束，以设置装配体的对称边界.
图 7(Fig. 7)
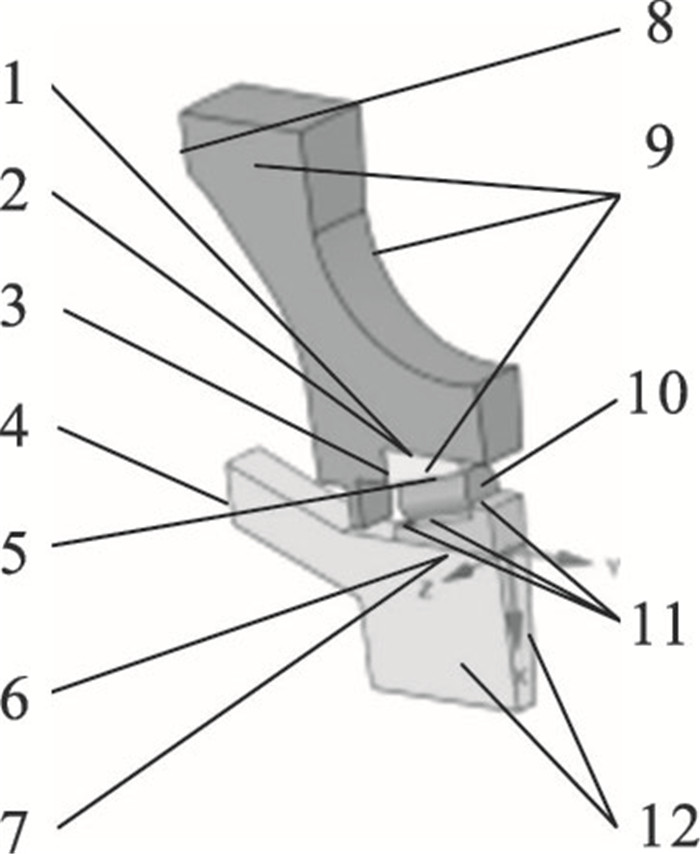 | 图 7 边界条件设定Fig.7 Boundary condition setting |
在施加轴承外圈与转轴过盈量为122.5 μm，轴承内圈与定轴过盈量为100 μm的条件下，对模型进行网格划分，设置边界条件进行有限元分析，经过求解得到有限元结果.如图 8所示，提取轴承外圈小端面轴向位移、轴承内圈大端面轴向位移、轴承内圈接触面径向位移和轴承外圈接触面径向位移等分析结果，以便于确定内外圈在轴向的具体位置.
图 8(Fig. 8)
 | 图 8 轴承内外圈径向、轴向位移示意图Fig.8 Schematic diagram of radial and axial displacement of inner and outer ring of bearings |
选取内外圈接触面沿路径的中间面作为有限元的计算截面, 轴承内外圈及转轴的等效半径如图 9所示.由内圈膨胀量(内圈径向位移)和外圈收缩量(外圈径向位移)，即可得到轴承径向游隙变化量Ca.从而，轴承轴向游隙变化量为
 | (8) |
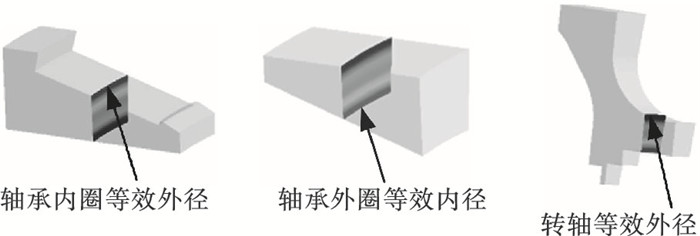 | 图 9 等效半径示意图Fig.9 Schematic diagram of equivalent radius |
式中：β为轴承接触角.由建模过程可知，轴承轴向游隙变化量C与转轴和定轴的弹性模量EQ、转轴和定轴的密度ρQ、轴承内外圈的弹性模量EG、轴承内外圈的密度ρG、轴承内圈厚度Ti、滚子长度L、轴承外圈厚度To等参数有关，是关于它们的函数C(EQ, ρQ, EG, ρG, Ti, L, To).
2 主轴轴承零游隙位置概率分析在工程实际中，由于随机因素(如加工误差、温度变化、材料劣化等)的影响，轴承和风力发电机主轴结构参数和材料参数X =[EQ ρQ EG ρG Ti L To]T具有一定分散性[12].因此，在装配过程中，即使所施加给轴承内外圈的过盈量固定，为了使风力发电机主轴轴承在装配后达到零游隙位置而提前移动的内外圈位置也具有一定的随机性.此时内外圈移动位置呈现概率分布的特点.因此，为了最大概率能够使得轴承外圈和滚子实现刚好接触的状态，本文在有限元模型的基础上对轴承内外圈在轴向移动的相对位置进行了概率分析，以找到内外圈移动概率最大的位置点，以这一位置点进行轴承的装配，可以尽可能消除轴承过盈对游隙的影响，最大概率地使轴承在装配后达到零游隙位置.在得到轴承的零游隙位置后，可以在零游隙位置的基础上施加合适的预紧量，使得轴承在工作时能够达到较长的使用寿命.
本文采用MC模拟方法，由基本随机变量的概率密度函数fX(x) 产生N组随机样本xj(j=1, 2, …, N)，将N组随机样本代入有限元分析模型中，即获取轴承内外圈轴向和径向位移样本.对样本进行统计分析，即可得到内外圈轴向和径向位移的均值、方差、概率密度和概率分布函数等概率统计特征.
基于MC的概率分析方法，需要产生大量的样本才能真实反映轴承内外圈位置的概率分布特性.而轴承内外圈位移的有限元分析需要大量的计算量、较为耗时，难以在有限元分析模型的基础上直接开展MC分析[13].为了提高计算效率，减少运行时间，可采用Kriging代理模型的方法，而后开展MC模拟分析.Kriging模型作为一种代理模型，可以根据少量的有限元模拟数据完成建立，并能够快速预测其他设计点的响应.相对于用有限元法或蒙特卡洛模拟法求解的工程问题，Kriging模型极大地节约了计算时间和成本.其次，在随机变量一定的变化范围内，Kriging模型具有较高的预测精度.
采用Kriging方法，可以将轴承内外圈的位移表示为
 | (9) |
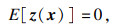 | (10) |
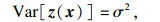 | (11) |
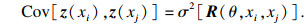 | (12) |
根据Kriging理论，未知点x处的响应预测值为
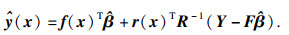 | (13) |
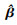
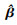
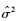
 | (14) |
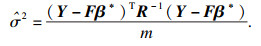 | (15) |
图 10(Fig. 10)
 | 图 10 Kriging轴承零游隙位置预测流程图Fig.10 Flow chart of Kriging bearing zero clearance position prediction |
3 数值算例某风力发电机轴承主轴单元采用单列圆锥滚子轴承，轴承与主轴的结构参数和材料参数公称值如表 1所示.由于随机因素的影响，轴承和主轴参数具有随机性，具体分布特征如表 2所示.
表 1(Table 1)
 表 1 模型结构参数Table 1 Structural parameters of the model
| 表 1 模型结构参数 Table 1 Structural parameters of the model |
表 2(Table 2)
表 2 轴承参数的分布特征Table 2 Distribution characteristics of bearing parameters
| 表 2 轴承参数的分布特征 Table 2 Distribution characteristics of bearing parameters |
在轴承内圈与定轴之间和轴承外圈与转轴之间分别施加6组过盈量，采用厚壁圆筒理论和有限元方法计算获得轴承外圈径向收缩量，内圈径向膨胀量及内外圈轴向位移量，轴承施加过盈量情况如表 3所示，结果如图 11~图 13所示.由图 11可以发现，基于厚壁圆筒理论的轴承外圈径向收缩量计算精度较低，存在较大误差.由图 12、图 13可知，两种方法获得的内圈径向膨胀量和内外圈轴向位移量结果较为一致.
表 3(Table 3)
表 3 施加的过盈量Table 3 Interference fit amount applied μm
| 表 3 施加的过盈量 Table 3 Interference fit amount applied μm |
图 11(Fig. 11)
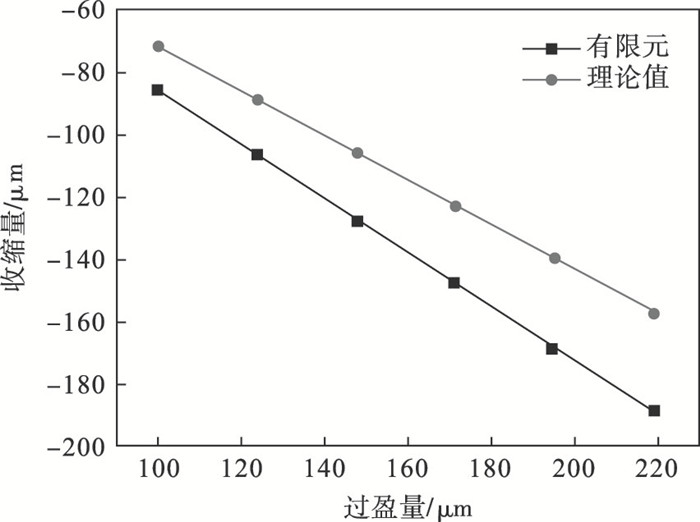 | 图 11 轴承外圈径向收缩量对比Fig.11 Comparison of radial shrinkage of the bearing outer ring |
图 12(Fig. 12)
 | 图 12 轴承内圈径向膨胀量对比Fig.12 Comparison of radial expansion of the bearing inner ring |
图 13(Fig. 13)
 | 图 13 轴承内外圈轴向位移对比Fig.13 Comparison of axial displacements of bearing inner and outer rings |
为了开展零游隙下轴承内外圈位置的概率分析，基于随机变量的概率分布特性，采用拉丁超立方方法抽取500组随机参数样本，将其中400组样本代入有限元模型进行计算，获取随机主轴轴承的内外圈轴向和径向位移样本.采用Kriging模型拟合随机参数与轴承内外圈轴向位移的函数关系.将剩余100组样本代入有限元模型进行计算，获取随机主轴轴承外圈的轴向位移用以验证Kriging模型的拟合精度.如图 14所示，Kriging模型的拟合精度较高，可以用于分析零游隙下风力发电机主轴轴承内外圈位置的概率分布特性.
图 14(Fig. 14)
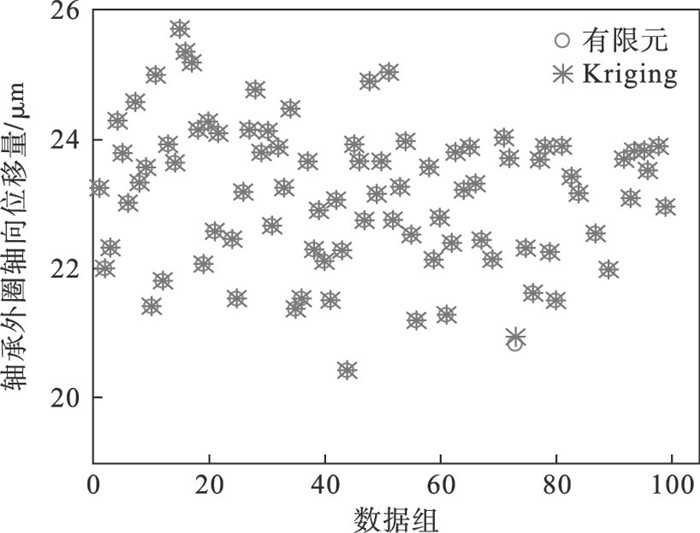 | 图 14 Kriging模型误差Fig.14 Error results of the Kriging model |
在轴承外圈与转轴之间施加过盈量为100 μm，转轴内圈与定轴之间施加过盈量为122.5 μm条件下，基于MC模拟抽取1 000组随机变量样本，将其代入建立好的Kriging模型和前文建立的有限元模型中进行计算，得到轴承内外圈的轴向位移样本.将两者轴向位移的概率密度和累计概率分布进行了比较，如图 15~图 18所示.同时，通过计算得到了两者的均值，对比结果如表 4所示.
图 15(Fig. 15)
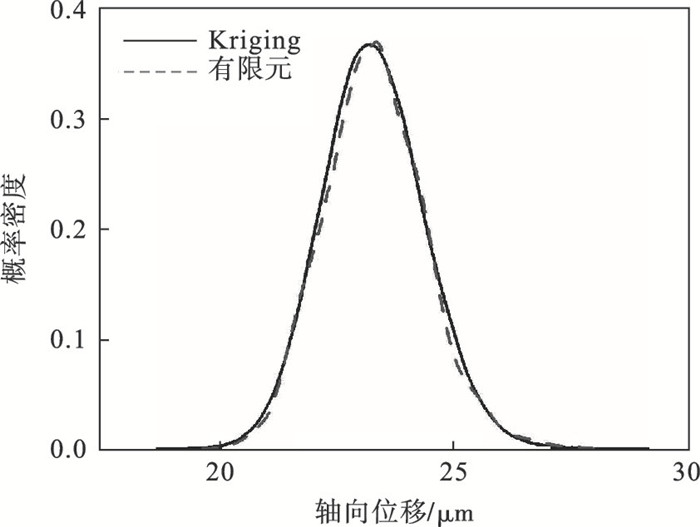 | 图 15 轴承外圈轴向位移概率密度曲线Fig.15 Probability density curves of axial displacement of bearing outer ring |
图 16(Fig. 16)
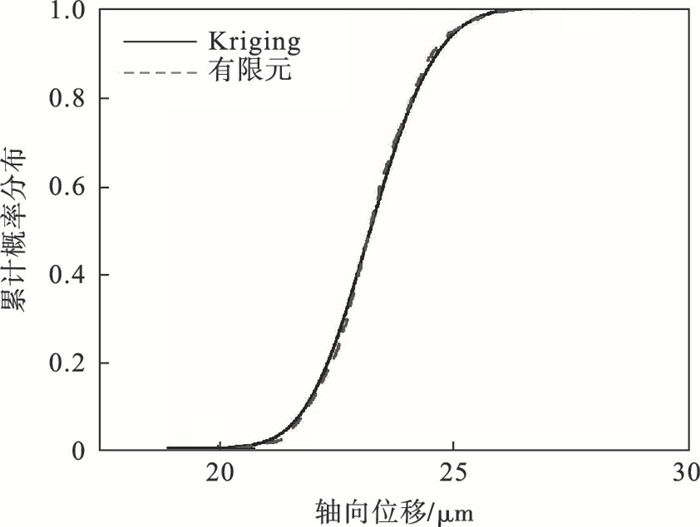 | 图 16 轴承外圈轴向位移累计概率分布曲线Fig.16 Cumulative probability distribution curves of axial displacement of the bearing outer ring |
图 17(Fig. 17)
 | 图 17 轴承内圈轴向位移概率密度曲线Fig.17 Probability density curves of axial displacement of the bearing inner ring |
图 18(Fig. 18)
 | 图 18 轴承内圈轴向位移累计概率分布曲线Fig.18 Cumulative probability distribution curves of axial displacement of the bearing inner ring |
表 4(Table 4)
表 4 Kriging和有限元均值结果对比Table 4 Comparison of mean results of the Kriging and finite element
| 表 4 Kriging和有限元均值结果对比 Table 4 Comparison of mean results of the Kriging and finite element | ||||||||||||||
从两者的概率密度曲线和累计概率分布曲线以及均值对比结果可以看出，轴承内外圈轴向位移的Kriging模型预测结果与有限元直接计算得到的结果基本一致，验证了Kriging模型的正确性，表明所构建的Kriging模型适用于预测装配轴承内外圈移动位置的分布.
4 结论1) 本文建立了风力发电机主轴轴承零游隙位置的有限元模型，通过计算过盈状态下轴承内外圈的径向和轴向位移，从而找到轴承在装配时提前在轴向移动的相对位置，使轴承在装配后刚好达到零游隙位置.此模型可用于计算实际轴承的复杂装配体，改进了理论方法只能计算规则厚壁圆筒的情况，在工程实际中比理论方法更具实用性.
2) 考虑到轴承和主轴在加工装配过程中参数的随机性，本文在有限元模型的基础上对轴承在装配时内外圈在轴向提前移动的相对位置进行了概率分析.从而找到内外圈移动位置概率最大处的点，以这一位置点进行装配，可以最大概率使轴承在装配后刚好达到零游隙位置.为了提高计算效率，减少计算时间，本文建立了Kriging模型来代替原始的有限元模型，基于MC模拟，预测了在轴承装配时内外圈提前在轴向移动位置的概率分布.在工程实际中，为风力发电机主轴轴承的装配提供理论指导.
参考文献
| [1] | Liu Z P, Zhang L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings[J]. Measurement, 2020, 149: 107002. DOI:10.1016/j.measurement.2019.107002 |
| [2] | Zheng J Y, Ji J C, Yin S, et al. Internal loads and contact pressure distributions on the main shaft bearing in a modern gearless wind turbine[J]. Tribology International, 2020, 141: 105960. DOI:10.1016/j.triboint.2019.105960 |
| [3] | Aguirrebeitia J, Plaza J, Abasolo M, et al. Effect of the preload in the general static load-carrying capacity of four-contact-point slewing bearings for wind turbine generators: theoretical model and finite element calculations[J]. Wind Energy, 2014, 17(10): 1605-1621. DOI:10.1002/we.1656 |
| [4] | He P Y, Hong R J, Wang H, et al. Fatigue life analysis of slewing bearings in wind turbines[J]. International Journal of Fatigue, 2018, 111: 233-242. DOI:10.1016/j.ijfatigue.2018.02.024 |
| [5] | Chen L, Zhang Y P, Xia X T. Contact stress and deformation of blade bearing in wind turbine[C]//2010 International Conference on Measuring Technology and Mechatronics Automation. Changsha, 2010: 833-836. |
| [6] | Zheng J Y, Ji J C, Yin S, et al. Fatigue life analysis of double-row tapered roller bearing in a modern wind turbine under oscillating external load and speed[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(15): 3116-3130. DOI:10.1177/0954406220911966 |
| [7] | Zhang H W, Chen S G, Dou Y T, et al. Mechanical model and contact properties of double row slewing ball bearing for wind turbine[J]. Reviews on Advanced Materials Science, 2021, 60(1): 112-126. DOI:10.1515/rams-2021-0017 |
| [8] | Oswald F B, Zaretsky E V, Poplawski J V. Interference-fit life factors for ball bearings[J]. Tribology Transactions, 2010, 54(1): 1-20. DOI:10.1080/10402004.2010.512428 |
| [9] | Zhang J H, Fang B, Zhu Y S, et al. A comparative study and stiffness analysis of angular contact ball bearings under different preload mechanisms[J]. Mechanism and Machine Theory, 2017, 115: 1-17. DOI:10.1016/j.mechmachtheory.2017.03.012 |
| [10] | Yu A D, Huang H Z, Li H, et al. Reliability analysis of rolling bearings considering internal clearance[J]. Journal of Mechanical Science and Technology, 2020, 34(10): 3963-3971. DOI:10.1007/s12206-020-2206-9 |
| [11] | Harris T A, Kotzalas M N. Advanced concepts of bearing technology: rolling bearing analysis[M]. New York: CRC Press, 2006: 51-54. |
| [12] | 冯吉路, 孙志礼, 许二丰, 等. 轴承结构参数的随机性对轴承刚度灵敏度的影响[J]. 东北大学学报(自然科学版), 2017, 38(6): 823-827. (Feng Ji-lu, Sun Zhi-li, Xu Er-feng, et al. Influence of randomness of structure parameters for bearings on its stiffness sensitivity[J]. Journal of Northeastern University(Natural Science), 2017, 38(6): 823-827.) |
| [13] | Lyu Z Y, Lu Z Z, Wang P. A new learning function for Kriging and its applications to solve reliability problems in engineering[J]. Computers & Mathematics with Applications, 2015, 70(5): 1182-1197. |
