
 , 李高瑞
, 李高瑞 大连理工大学 机械工程学院,辽宁 大连 116024
收稿日期:2022-05-24
基金项目:国家重点研发计划项目(2018YFB1306700);辽宁省自然科学基金资助项目(2021-MS-300);辽宁省教育厅科研基金资助项目(LJKZ0526)。
作者简介:霍军周(1979-),男,山西运城人,大连理工大学教授,博士生导师。
摘要:为解决恶劣工况下全断面硬岩隧道掘进机(tunnel boring machine,TBM)关键主承力结构应变监测难、监测不准的难题,提出了一种基于BP神经网络和有限元分析的TBM刀盘关键位置应变重构方法.首先,通过静、动力学有限元分析确定了TBM刀盘关键位置,并提取了刀盘典型易损特征子结构.其次,基于有限元技术和实验设计(design of experiments,DOE)方法,分别进行了标准件和特征子结构多载荷下静力学有限元分析,并构建了载荷-应变数据库.最后,运用BP神经网络建立了标准样件和刀盘特征子结构的应变重构模型,并进行了标准样件的实验验证.结果表明,重构应变的平均误差为10%,验证了方法的可行性,为TBM刀盘复杂结构的应变重构提供了一种可行的方法.
关键词:TBM刀盘特征子结构应变重构BP神经网络实验设计
Strain Reconstruction of TBM Cutterhead at Key Positions Based on BP Neural Network
HUO Jun-zhou, GE Li-han, ZHANG Zhan-ge

 , LI Gao-rui
, LI Gao-rui School of Mechanical Engineering, Dalian University of Technology, Dalian 116024, China
Corresponding author: ZHANG Zhan-ge, E-mail: nicege@163.com.
Abstract: To solve the problem of difficult and inaccurate strain monitoring of the key main load-bearing structures of the full face hard rock tunnel boring machine(TBM)under harsh working conditions, a strain reconstruction method for key positions of the TBM cutterhead based on BP neural network and finite element analysis was proposed. Firstly, the key vulnerable positions of the TBM cutterhead were determined through static and dynamic finite element analysis, and the typical vulnerable feature substructures of the cutterhead were extracted. Secondly, the static finite element analysis of standard parts and feature substructures under multiple loads was carried out based on the design of experiments(DOE), and the load-strain database was constructed. Finally, a strain reconstruction model for the standard sample and cutterhead feature substructure was established using BP neural network, and experimental verification of the standard samples were conducted. The results showed that the average error of the reconstructed strains is 10%, which verifies the feasibility of the method and provides a feasible method for strain reconstruction of complex TBM cutterhead.
Key words: TBM cutterheadfeature substructuresstrain reconstructionBP neural networkdesign of experiments
TBM常用于长距离(2 500 m以上)、大埋深的隧道建设,刀盘滚刀不断挤压破碎高硬度围岩(250 MPa以上),工况恶劣.刀盘作为TBM的关键主承力结构,其结构复杂,由大量厚钢板栓焊而成.滚刀破岩过程中,刀盘承受多向不确定的强冲击大载荷,由于主承力结构复杂,导致了复杂载荷作用下刀盘内部的力流传递规律复杂多变,结构极易损坏,损伤位置多且分布位置不确定[1].TBM刀盘内部空间狭小,且伴随着高压涌水、泥浆冲刷、岩碴冲击等恶劣工作环境,使得刀盘关键位置的应变难以检测,而应变信息又是评估刀盘损伤及寿命预测的重要依据.因此,依据少量关键结构处的应变信息对刀盘整体结构的应变场进行精确的重构具有重要意义,能够为刀盘的寿命评估提供可靠依据.
国内外****针对应变场的重构提出了多种方法.在Colombo等[2]提出的利用逆有限元法(inverse finite element method, IFEM)进行应变检测的基础上,文献[3-4]基于逆有限元法与变形理论实现了三维结构较高精度的变形重构.文献[5-7]使用模态分析方法实现了静态和振动载荷下复杂结构变形重建.文献[8-11]基于传统Ko位移理论对多向载荷作用下的复杂结构多向位移场进行了重构计算和实验验证, 表现出较高的重构精度.Wang等[12]基于FGB传感器,通过对多项式系数的重构实现应变分布的重构, 大大提高了重构的速度.
上述研究工作对于薄壁结构以及规则几何形状零件的应变重构进行了深入的研究,实现了对该类模型结构的高精度应变场重构.然而,面对结构复杂且厚度较大的模型,上述研究方法对于整体应变场的重构能力存在一定欠缺.BP神经网络是处理复杂非线性问题的一种有效方法,能够建立输入和未被发现过程条件下输出数据之间的关系,从有限测量点应变信息反演出完整应变场,从而应用于复杂结构模型的应变场重构.本文提出一种新的刀盘应变重构方法,运用有限元技术和实验设计(design of experiments,DOE)方法进行结构多级载荷作用下的静力学分析,基于BP神经网络的应变重构方法,重构了整体结构的应变场,经过关键位置实际应变信息的修正,使得重构应变场更为精确,这为刀盘关键结构寿命的快速准确评估和预测奠定了基础.
1 理论和方法基于BP神经网络的TBM刀盘关键位置应变重构方法以及验证流程如图 1所示.
图 1(Fig. 1)
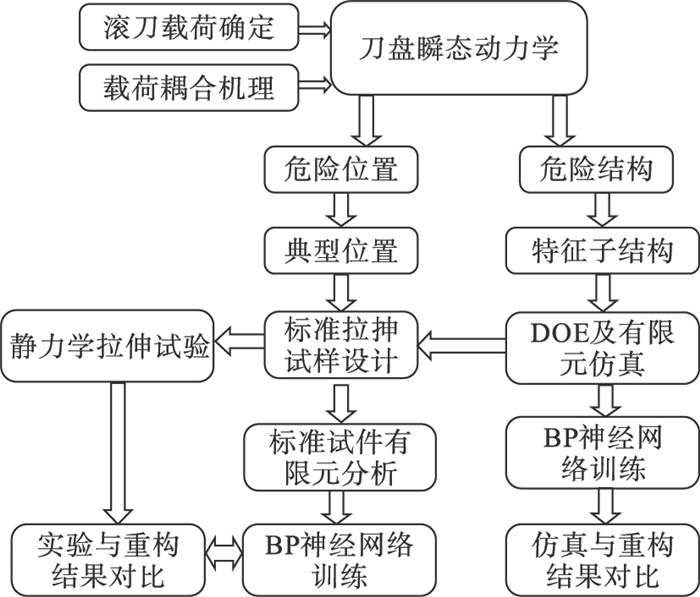 | 图 1 TBM刀盘关键位置应变重构及验证流程Fig.1 Process of strain reconstruction and verification of TBM cutterhead's key positions |
首先,为确定多源不确定的强冲击滚刀破岩载荷作用下TBM刀盘的危险薄弱位置,根据TBM实际服役工况,对滚刀破岩载荷以及多源多向滚刀载荷的耦合加载机理进行了研究.同时,考虑到TBM刀盘的装配特点,进行TBM刀盘的瞬态动力学分析.
其次,基于瞬态动力学分析结果,确定TBM刀盘危险位置,并根据TBM刀盘结构特点提取危险位置的特征子结构.对于特征子结构采用有限元仿真与DOE,确定对危险薄弱位置影响较大的载荷因素.进一步,以特征件有限元分析应变、位置和载荷数据作为数据库,基于BP神经网络进行了载荷-应变重构模型的训练,并与仿真结果进行对比.
然后,基于特征件DOE得到的实验结果,在特征样件应力最大位置处最敏感方向提取标准拉伸实验样件.对该实验样件进行静力学有限元分析,基于有限元数据,对该实验样件进行了应变重构.设计静力学拉伸实验,通过对比重构应变、实验应变以及有限元仿真应变对重构方法进行验证.
最后,基于提出的应变重构模型,将节点坐标数据以及载荷等作为BP神经网络训练的输入,三向应变数据作为输出,对TBM刀盘在实际服役载荷下关键薄弱位置的应变快速重构模型进行训练.同时,设计实验样件,搭建应变检测系统对关键位置的应变进行采集.使用实测的应变数据对基于BP神经网络的应变重构模型进行修正,与实测应变数据对比验证该方法的可行性.
1.1 刀盘模型瞬态动力学分析由于刀盘结构复杂、且承受空间多点随机冲击载荷,仅开展静力学分析无法全面了解刀盘的实际承载及其应力、变形状态.因此,为确定TBM刀盘实际服役过程中易损伤位置,基于实际动态载荷,对刀盘进行瞬态动力学分析[13-14].
1.1.1 载荷分析刀盘所受载荷为滚刀破岩时产生的反作用力,包括法向力FN,侧向力FS,滚动力FR,如图 2所示.
图 2(Fig. 2)
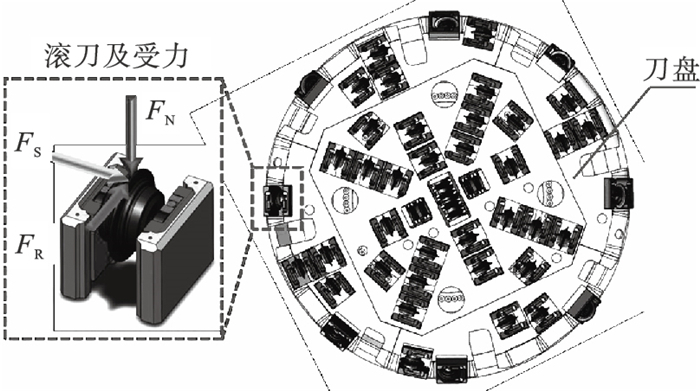 | 图 2 TBM刀盘、滚刀和破岩载荷Fig.2 TBM cutterhead, cutters, rock loads |
针对滚刀破岩机理以及滚刀破岩载荷的研究,国内外****提出了不同的滚刀受力预测模型,目前国内外应用最多的滚刀破岩法向力和滚动力模型是美国科罗拉多矿业大学提出的CSM预测模型.该模型是科罗拉多矿业大学基于理论分析和实验测试相结合得到的滚刀破岩载荷预测模型,能够实现滚刀破岩法向载荷和滚动载荷的准确预测.该模型涉及参数包括岩石物理性质、刀具几何形状、刀具半径(盘形滚刀半径)、刀尖宽度(刃宽)、切割间距和侵入深度,作用于盘形滚刀的合力:
 | (1) |
 | (2) |
 | (3) |
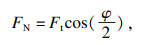 | (4) |
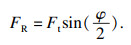 | (5) |
CSM模型只可以计算法向力FN和滚动力FR,滚刀破岩侧向力多采用秋三藤三郎模型[15],计算公式如下:
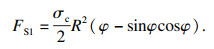 | (6) |
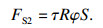 | (7) |
本文研究对象为辽西北引水工程实际服役的TBM刀盘,刀盘和滚刀结构如图 2所示.在实际服役过程中,刀盘额定转速为6 r/min.根据实测围岩参数及TBM滚刀参数计算得到滚刀破岩的法向力、滚动力和侧向力,基于实验滚刀破岩载荷,修正得到实际工况下的滚刀动态破岩载荷,如图 3所示.其中,名义载荷条件下,所有滚刀法向载荷均值为315 kN,指向刀盘;滚动力均值为47.25 kN,和刀盘旋转方向相反;侧向力均值为31.5 kN,指向刀盘外.
图 3(Fig. 3)
 | 图 3 滚刀动态破岩载荷Fig.3 Dynamic rock breaking loads of the cutter (a)—滚刀垂向力;(b)—滚刀滚动力;(c)—滚刀侧向力. |
以刀盘旋转一周为一个周期,在瞬态动力学分析中模拟刀盘旋转一周关键结构的力流变化,加载时间为10 s,载荷如图 3所示.
1.1.2 TBM刀盘有限元分析由TBM主机系统的装配关系可知,TBM刀盘与主轴承和支撑架通过螺栓连接为一个整体,支撑架通过支护油缸和护盾支撑在岩壁上,支撑架的后端和主梁通过法兰连接.因此,对于刀盘系统的约束边界设置如图 4所示,其中,支撑架的上下盖板和左右支撑设置为固定约束,支撑架和主梁连接法兰设置为固定约束,所有螺栓连接处设置预紧力.
图 4(Fig. 4)
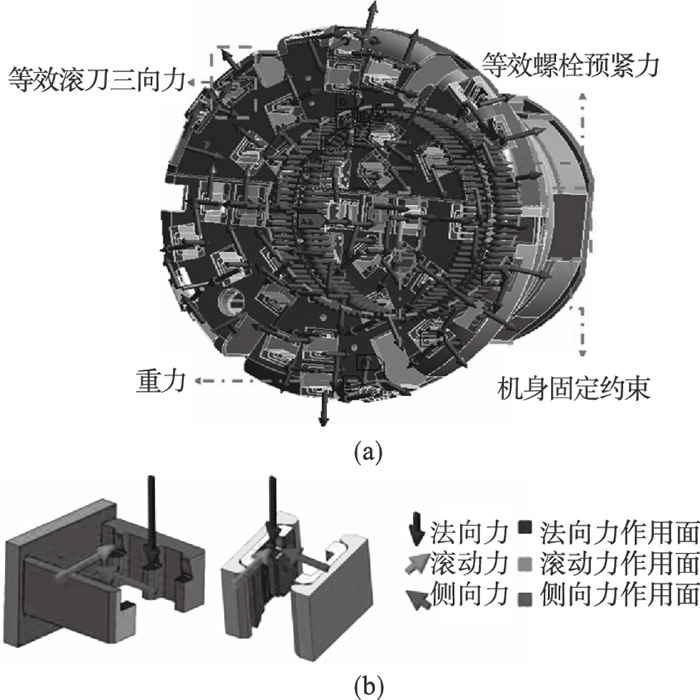 | 图 4 刀盘瞬态动力学有限元分析Fig.4 Transient dynamic finite element analysis of the cutterhead (a)—TBM刀盘的载荷和边界;(b)—滚刀载荷加载. |
滚刀载荷施加在刀座上,位置如图 4所示;刀盘分体通过螺栓连接,螺栓预紧力为440 kN;刀盘法兰的螺栓预紧力为920 kN;重力朝下;刀盘材料为Q345D.
1.1.3 结果分析通过刀盘瞬态动力学分析,得到刀盘在动态破岩载荷作用下的力流变化,刀盘的瞬时最大等效应力如图 5所示.
图 5(Fig. 5)
 | 图 5 筋板应力云图Fig.5 Rib stress cloud map |
在刀盘破岩的一个周期内,刀盘等效应力为55~68.75 MPa(安全系数4~5)的区域包括筋板与中间面板接触的尖角处、筋板与中间面板接触的棱边处,应力超过55 MPa的体积跟随刀盘的旋转时刻发生变化,体积最大为0.298 4×107 mm3.等效应力为36.7~55 MPa的区域体积最大为0.406×108 mm3,最小为0.339 5×108 mm3.最大应力处于筋板下角尖角处.
根据瞬态动力学分析的应力分布,确定了刀盘的危险薄弱位置以及区域,其中各个筋板位置的等效应力最大.通过现场统计的数据进行对比,各筋板和面板的焊接位置较易出现裂纹失效,综上,确定筋板靠近面板的边缘为刀盘的最薄弱位置,筋板应力云图如图 5所示.
1.2 DOE正交试验设计及模拟实验根据瞬态动力学结果确定TBM刀盘的薄弱位置后,提取薄弱位置处的特征子结构进行分析.为探明三向载荷对该位置力流传递的影响,设计正交试验[14],提取关键试验因素.因此,本节通过有限元分析与正交试验相结合,进行各个水平各个因素的多组模拟实验.
1.2.1 模拟实验方案为确定三向载荷中占比最大的影响因素,以法向力、滚动力、侧向力为试验因素,并根据实际载荷上下限确定3个试验因素,如表 1所示.
表 1(Table 1)
| 表 1 试验水平-因素 Table 1 Experimental level and factor? | |||||||||||||||||||||||||||||||||||||||||||||||||
3个试验因素影响筋板特征件应力状态及变形情况.每个试验因素包含3个试验水平,若对所有水平、所有因素进行组合试验,共需要33=27组试验,工作量较大、耗费时间较长.采用L9(32)正交试验进行设计,如表 2所示.
表 2(Table 2)
| 表 2 正交试验方案 Table 2 Orthogonal experimental plan |
对于上述试验方案,使用Ansys workbench参数化平台进行静力学有限元仿真分析.计算得到薄弱位置的最大等效应力以及最大变形量如表 3所示.
表 3(Table 3)
| 表 3 正交试验载荷的有限元分析结果 Table 3 Finite element analysis results of orthogonal experimental loads |
1.2.2 试验结果分析根据统计学理论对试验数据进行分析,通过计算法向力、滚动力、侧向力对最大等效应力的极差值,得到3个试验因素中对最大等效应力影响最大的因素.
以法向力相关的3个水平为例,将各因素1水平的结果求和并求平均值,如式(8)~式(10)所示:
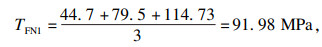 | (8) |
 | (9) |
 | (10) |
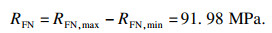 | (11) |
基于各个试验因素载荷作用下薄弱位置的等效应力及最大变形量,计算得到各项等效应力均值以及各项极差,如表 4所示.
表 4(Table 4)
| 表 4 试验因素对模拟实验结果影响的极差 Table 4 Range influence of experimental factors on simulated experimental results |
根据极差判断原则:极差越大,对应因素越重要.根据表 4可以确定法向力对应的等效应力在各个因素中数值最大,即法向力是影响筋板特征件等效应力的主要因素.
1.3 BP神经网络构建BP网络的学习过程是一种误差修正型学习算法,由正向传播和反向传播组成.在正向传播过程中,输入信号从输入层通过作用函数后, 逐层向隐含层、输出层传播,每一层神经元沿原来的连接通路返回,通过修改各层神经元的连接权值,使得输出误差信号最小.
理论上已经证明,3层BP神经网络可以以任意精度逼近任意连续函数,当学习不连续函数时则需4层神经网络.而面对复杂问题时,3层网络的隐含层节点数过多后,会影响计算效率和精度,此时需要增加层数以减少各层节点数.一般来说,BP神经网络的预测精度会随层数的增加而有所提高,但层数增加后会导致其结构复杂化,并且会影响神经网络训练效率、降低泛化(预测)能力.本文数据来源于标准拉伸试样在弹性阶段不同载荷水平加载后产生的节点应变值,随着载荷的变化,应变值近似线性增加,三层神经网络即可保证快速精确收敛.
神经网络的构建包括神经网络模型层数、各层(输入层、隐含层、输出层)的节点数及激活函数等.本文模型具体结构如图 6所示,输入层节点xi包含4个,分别为拉伸载荷F、X坐标、Y坐标和Z坐标;隐含层节点包含8个,其中第j个节点的输入为nj,输出为oj;输入层第i个节点到隐含层第j个节点的连接权值为wij;隐含层阈值为αi,激活函数为f;隐含层第j个节点到输出层第k个节点的连接权值为wjk;输出层阈值为bk, 激活函数为g;ek为返回误差.
图 6(Fig. 6)
 | 图 6 BP神经网络结构图Fig.6 Structure of BP neural network |
隐含层第j个节点的输入为
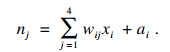 | (12) |
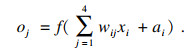 | (13) |
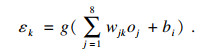 | (14) |
对于BP神经网络,误差的判定是通过二次型误差准则函数ek来表示.
 | (15) |
而在误差的反向传播过程中,通过梯度下降法修正权值,使输出与目标之间的误差达到允许值.输入层第i个节点到隐含层第j个节点以及隐含层第j个节点到输出层第k个节点的权值修正过程为
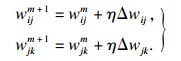 | (16) |
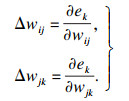 | (17) |
1.4 筋板易损位置主应力方向应变重构1.4.1 标准样件刀盘关键结构比较复杂,为实现刀盘关键薄弱位置应变重构,基于瞬态动力学和静力学分析,确定了筋板易损位置的力流以及主应力方向.因此,在刀盘筋板薄弱位置沿着主应力的方向提取标准样件,基于标准样件的拉伸应变来等效筋板易损位置主应力方向上的应变,进行筋板易损位置主应力方向的应变重构.标准样件的结构、尺寸以及力学性能如图 7和表 5所示.
图 7(Fig. 7)
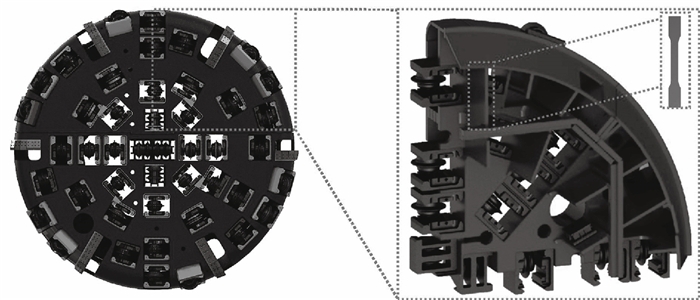 | 图 7 关键结构及试件位置Fig.7 Critical structure and position of the specimen |
表 5(Table 5)
| 表 5 试样基本属性 Table 5 Basic properties of the specimen |
1.4.2 标准样件有限元分析在ANSYS软件中建立标准力学拉伸试件模型,拉伸试件的参数如表 5所示.在Workbench进行有限元求解.其中,一端夹持区域的两个面设置为固定约束,另一端夹持区域的两个面限制除拉伸方向的自由度.载荷加载于拉伸方向自由端的夹持面上.
为保证BP神经网络训练精度,在刀盘筋板易损位置的承力范围内随机生成20组不同应力载荷,保证其处于材料的弹性范围内.将最大应力载荷和最小应力载荷转换为标准样件的力载荷并取整.其中,最小载荷不小于1 kN,最大载荷不大于20 kN.
1.4.3 标准样件应变重构基于标准样件有限元分析应变结果,提取标准样件各节点的坐标、三向应变和等效应变,构建标准样件位置和力学性能数据库,以节点三维坐标和单轴载荷作为输入,节点等效应变作为输出,基于BP神经网络训练得到标准样件快速应变重构模型.
1.5 复杂载荷下筋板易损位置应变重构由瞬态动力学分析可知,在多源随机载荷作用下刀盘关键承力筋板结构的受力状态实时变化,为实现刀盘关键承力结构的应变检测,需要建立多向载荷作用下的筋板结构应变重构模型.因此,考虑筋板的不确定受力,将筋板的受力等效为3个方向上的力,进行不同载荷作用下的筋板有限元分析.其中筋板的约束根据筋板在刀盘位置和连接进行设定.载荷根据滚刀三向力规律进行设计,在服役载荷范围内随机生成2 000组不同三向载荷,进行筋板静力学有限元分析.提取不同载荷作用下筋板节点的空间坐标和等效应变.建立三向载荷作用下的筋板载荷、位置和应变的数据库.基于提出的应变重构方法对筋板三向载荷作用下的应变重构模型进行训练,建立复杂载荷作用下筋板结构应变快速重构模型.
2 实验设计为验证本文提出的应变重构模型的可行性和准确性.设计了标准样件应变重构验证实验,如图 8所示.实验系统主要由力学拉伸试样、WDM-100万能拉伸实验机、无线应变采集系统、上位机计算机等组成.其中,无线应变采集系统主要用于监测位置应变信息的采集,并将应变信息传输至计算机进行应变信息的记录和分析.
图 8(Fig. 8)
 | 图 8 标准件应变检测Fig.8 Standard specimen strain detection |
应变检测系统中的应变片布置方案如图 8所示:根据实际受力情况,在标准样件非夹持区域的3个面上分别设置4个测点, 测点间相距24 mm.进行8级载荷下标准样件的应变检测.通过对比12个测点的实测应变和由BP神经网络重构所得应变,对本文提出的应变重构方法进行验证.
3 实验结果与对比分析3.1 标准样件重构应变和有限元应变对比基于训练得到的标准样件应变重构模型,在标准样件上随机选取100个节点,并将此100个节点的坐标和载荷代入重构模型中,计算得到该100个节点的BP重构应变.BP重构和有限元仿真等效应变对比如图 9所示.通过对比分析,BP重构等效应变和有限元仿真的等效应变的误差在0.05 % 以下,重构应变的精度能够满足需求.
图 9(Fig. 9)
 | 图 9 BP神经网络重构应变与有限元应变对比Fig.9 Comparison between BP neural network reconstruction strain and finite element strain |
3.2 筋板结构件应变重构验证为验证重构方法对于复杂载荷作用下复杂结构的可行性和准确性,基于筋板有限元分析数据库训练建立的筋板三向载荷作用下的等效应力重构模型,计算在确定载荷作用下筋板结构的重构等效应变,与有限元分析结果进行对比验证模型的准确性.
首先,对三向力均为2 kN作用下的筋板进行静力学有限元分析,在薄弱位置区域随机选取30个点,并导出节点坐标和节点的等效应变.
将三向力以及30个节点的坐标作为输入,代入到建立的筋板应变重构模型中,得到30个节点的重构应变,如图 10所示.通过比对可知,本文提出方法计算的应变与有限元仿真等效应变值的平均误差为3%,最大奇异点误差为8%.用本文方法计算的应变具有较好的重构精度,可以满足复杂模型应变重构的精度需要.
图 10(Fig. 10)
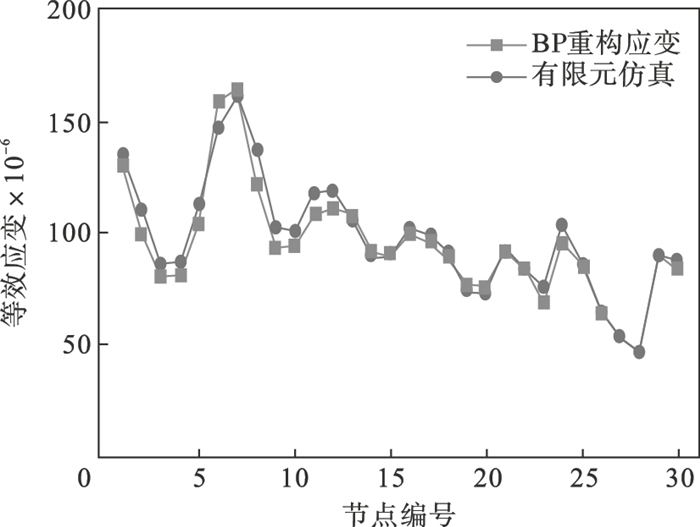 | 图 10 筋板易损位置重构应变与有限元应变对比Fig.10 Comparison of reconstructed strain and finite element strain at the vulnerable positions of rib plates |
3.3 标准样件应变实测验证实验方案如图 8所示,设计了8组标准试样拉伸实验载荷,所有拉伸力保证了拉伸试样的等效应力的大小均处于Q345D材料的弹性阶段,实验载荷分别为6,8,10,12,14,16,18和20 kN.实时采集12个测点的应变,提取稳定后的应变值作为该载荷作用下的应变,用于重构应变的验证,如图 11~图 13所示.
图 11(Fig. 11)
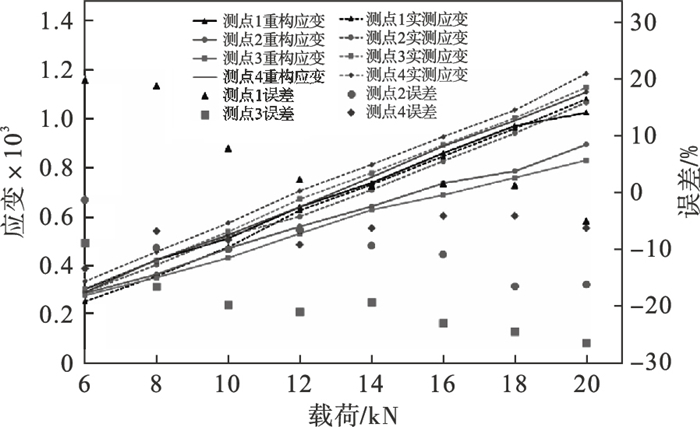 | 图 11 X方向应变对比Fig.11 Comparison of strain in X direction |
图 12(Fig. 12)
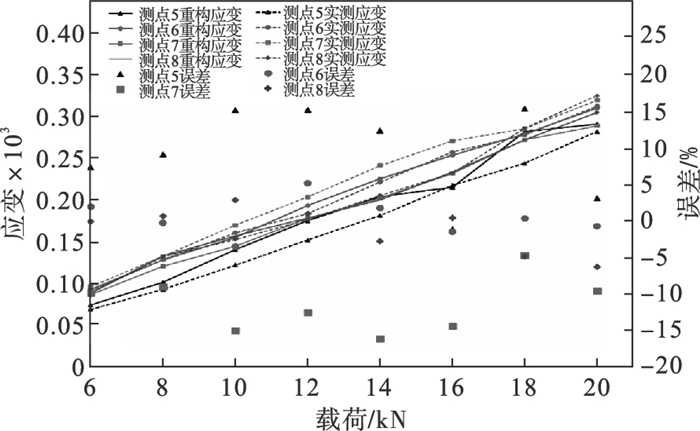 | 图 12 Y方向应变对比Fig.12 Comparison of strain in Y direction |
图 13(Fig. 13)
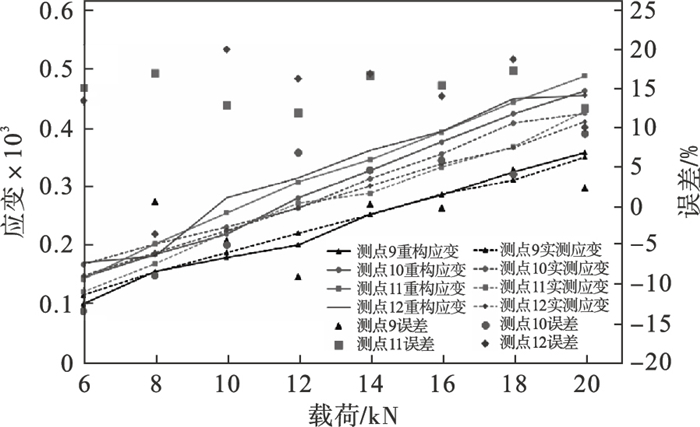 | 图 13 Z方向应变对比Fig.13 Comparison of strain in Z direction |
由图 11~图 13可知,实测应变值与重构应变值最大误差在20% 左右,其中,除少量误差达20% 外,其余各测点实测应变和重构应变的误差均在15% 以内.
误差的原因为
1) 由于神经网络的训练数据来源于有限元分析,有限元分析和实际的误差导致了重构误差较大.
2) 应变片粘贴导致的误差.由于应变片粘贴无法做到完全贴合,且应变片可能会在变形后略微脱落,导致测量值偏小.应变片在粘贴过程中的粘贴位置误差可能导致应变采集误差,这也是造成实验误差的一个因素.
4 结论1) 研究了多源不确定滚刀破岩载荷的计算方法,根据瞬态动力学、DOE设计等技术,确定刀盘的易损位置、典型结构,确定了筋板和法兰面应力集中处为易损薄弱位置,确定了滚刀法向力为刀盘损伤的主要因素.
2) 提出了一种基于BP神经网络和有限元DOE的应变重构方法,通过标准件的重构应变验证,基于有限元分析数据和实验数据建立的BP神经网络的应变重构模型的误差在10% 以内,验证了本文提出方法的有效性和准确性.
3) 基于提出的应变重构方法,对筋板特征子结构的应变进行了重构,与实测应变的对比表明:基于有限元分析数据和实验数据建立的BP神经网络模型对于复杂载荷作用下的复杂筋板结构的重构应变误差在10% 以内,实现了TBM刀盘复杂主承力筋板结构在复杂载荷作用下的应变场重构.满足了工程实际需求,可以作为TBM刀盘寿命预测的依据.
参考文献
| [1] | 杨博文, 霍军周, 张伟, 等. 服役结构超前载荷实时预测方法的研究[J]. 东北大学学报(自然科学版), 2022, 43(4): 541-550. (Yang Bo-wen, Huo Jun-zhou, Zhang Wei, et al. Research on real-time overload prediction method of in-service structures[J]. Journal of Northeastern University(Natural Science), 2022, 43(4): 541-550.) |
| [2] | Colombo L, Sbarufatti C, Giglio M. Definition of a load adaptive baseline by inverse finite element method for structural damage identification[J]. Mechanical Systems and Signal Processing, 2019, 120: 584-607. DOI:10.1016/j.ymssp.2018.10.041 |
| [3] | 付书山, 孙广开, 何彦霖, 等. 基于逆有限元的机翼蒙皮变形监测方法仿真研究[J]. 航空制造技术, 2022, 65(6): 107-114. (Fu Shu-shan, Sun Guang-kai, He Yan-lin, et al. Simulation study on wing skin deformation monitoring based on inverse finite element method[J]. Aerospace Manufacturing Technology, 2022, 65(6): 107-114.) |
| [4] | 潘兴琳, 保宏, 张旭东. 基于模糊的框架变形重构的应变测量修正[J]. 振动·测试与诊断, 2018, 38(2): 360-364, 423. (Pan Xing-lin, Bao Hong, Zhang Xu-dong. Updating measurement strain for the elastic deformation of 3-d frame structure using fuzzy method[J]. Journal of Vibration, Measurement & Diagnosis, 2018, 38(2): 360-364, 423.) |
| [5] | Yu M, Guo J J, Lee K M. A modal expansion method for displacement and strain field reconstruction of a thin-wall component during machining[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(3): 1028-1037. DOI:10.1109/TMECH.2018.2790922 |
| [6] | Alexandros I, Rasoul S, Wout W, et al. A modal decomposition and expansion approach for prediction of dynamic responses on a monopile offshore wind turbine using a limited number of vibration sensors[J]. Mechanical Systems and Signal Processing, 2016, 68/69(7): 84-104. |
| [7] | 敖春燕, 乔百杰, 刘美茹, 等. 基于非接触式测量的旋转叶片动应变重构方法[J]. 航空动力学报, 2020, 35(3): 569-580. (Ao Chun-yan, Qiao Bai-jie, Liu Mei-ru, et al. Dynamic strain reconstruction method of rotating blades based on no-contact measurement[J]. Journal of Aerospace Power, 2020, 35(3): 569-580.) |
| [8] | 冯荻, 梁冰, 刘坤. 基于应变监测的升降舵壁板变形重构方法[J]. 计测技术, 2020, 40(1): 12-18. (Feng Di, Liang Bing, Liu Kun. Deformation reconstruction method of elevator assembly based on strain monitoring[J]. Metrology & Measurement Technology, 2020, 40(1): 12-18.) |
| [9] | 胡明月, 吴邵庆, 董萼良. 基于实测应变的典型热防护结构位移场实时重构[J]. 东南大学学报(自然科学版), 2021, 51(4): 664-671. (Hu Ming-yue, Wu Shao-qing, Dong E-liang. Real-time displacement field reconstruction of typical thermal protection structures based on measured strain[J]. Journal of Southeast University(Natural Science Edition), 2021, 51(4): 664-671.) |
| [10] | 赵飞飞, 曹开拓, 保宏, 等. Timoshenko梁的变形场重构及传感器位置优化[J]. 机械工程学报, 2020, 56(20): 1-11. (Zhao Fei-fei, Cao Kai-tuo, Bao Hong, et al. Deformation field reconstruction of Timoshenko beam and optimization of sensor placement[J]. Journal of Mechanical Engineering, 2020, 56(20): 1-11.) |
| [11] | Esposito M, Gherlone M. Composite wing box deformed-shape reconstruction based on measured strains: optimization and comparison of existing approaches[J]. Aerospace Science and Technology, 2020, 99: 14-21. |
| [12] | Wang J, Wang Z F, Sui Q M, et al. Study of FBG strain distribution reconstruction based on improved genetic algorithm dual constraint[J]. Chinese Journal of Lasers, 2012, 39: 12-22. |
| [13] | Huo J Z, Xu Z H, Meng Z C, et al. Coupled modeling and dynamic characteristics of TBM cutter head system under uncertain factors[J]. Mechanical Systems and Signal Processing, 2020, 140: 106-114. |
| [14] | Huo J Z, Wu H Y, Sun W, et al. Electromechanical coupling dynamics of TBM main drive system[J]. Nonlinear Dynamic, 2017, 90: 2687-2710. |
| [15] | 曹岩. 全断面掘进机滚刀数值模拟及布置规律优化研究[D]. 沈阳: 东北大学, 2011. (Cao Yan. Numerical simulation and cutter layout design study of full-face tunnel boring machine[D]. Shenyang: Northeastern University, 2011. ) |
