赵永, 焦诗卉, 赵乾百
东北大学 资源与土木工程学院，辽宁 沈阳 110819
收稿日期：2022-05-22
基金项目：国家自然科学基金资助项目(52004052)；中央高校基本科研业务费专项资金资助项目(N2101027)。
作者简介：赵永(1991-)，男，山东临沂人，东北大学讲师，博士。

摘要：微震监测是保证矿山安全生产的有效手段，微震信号识别精度直接影响着微震事件的判定及分析结果.鉴于此，以夏甸金矿微震监测数据作为样本，建立了基于Mel频谱和长短时记忆(long short-term memory, LSTM)神经网络与深度卷积神经网络(deep convolutional neural networks, DCNN)混合的矿山微震信号识别模型.首先对监测信号进行预处理，利用Mel时频谱降低干扰频段的权重并减小样本尺寸.然后利用LSTM和DCNN模型分别提取信号的时间特征及空间特征.通过多种模型的对比分析，结果表明本文提出的Mel-LSTM-DCNN混合模型对微震信号识别准确率最高.该模型为矿山准确识别微震信号提供参考.
关键词：神经网络深度学习信号识别微震监测Mel频谱
Hybrid Recognition Model of Microseismic Signals for Mining Based on Mel Spectrum and LSTM-DCNN
ZHAO Yong, JIAO Shi-hui, ZHAO Qian-bai
School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: JIAO Shi-hui, E-mail: jiaoshihui0206@126.com.

Abstract: Microseismic monitoring can ensure safe production in mines, and the accuracy of microseismic signal recognition directly affects the analysis of microseismic events. The microseismic monitoring data of Xiadian Gold Mine were used as samples to establish a mining microseismic signal recognition model based on Mel spectrum and a combination of long short-term memory(LSTM)and deep convolutional neural networks(DCNN). Firstly, the monitoring signal was preprocessed, and the Mel time spectrum was used to reduce the weight of the interference frequency band and sample size. Then, LSTM and DCNN models were employed to extract the temporal and spatial features of the signal, respectively. Through comparative analysis of multiple models, the results showed that the proposed Mel-LSTM-DCNN hybrid model has the highest accuracy in identifying microseismic signals. The model proposed provides reference for accurately identifying microseismic signals in mines.
Key words: neural networkdeep learningsignal identificationmicroseismic monitoringMel spectrum
工程岩体在采动条件下产生渐进损伤，释放出弹性波并形成微震事件.微震信号中蕴含了关于矿岩损伤破坏过程及机理的重要信息.因此，可以利用微震监测技术对岩体产生的微震事件进行分析，从而达到监测岩体稳定状态的目的.微震监测技术发展迅速，已广泛应用于矿山^[1]、深埋隧道^[2-3]、边坡^[4-5]等多个工程领域.由于岩石破裂信号为非线性随机信号，且井下开采环境复杂，传感器接收到的信号中通常混杂着爆破、机械振动等干扰信息，微震事件的筛选难度大大增加.因此，如何从诸多波形信号中识别出有效的岩石破裂信号是利用微震技术有效解译岩体破坏的基础.
深度学习是机器学习领域一个新的研究方向，相较于传统的识别方法，它的特征提取能力更加出色，在各领域取得了巨大成功.卷积神经网络(convolutional neural networks，CNN)是深度学习的主要模型之一.近几年，其特征学习能力得到广泛的关注与认可，并依托计算机与大数据技术的进步而快速发展^[6]，在图像分类^[7]、心脑电波^[8]等方面都取得了突破性成果.CNN中各层节点采用局部连接，且同一层神经元的连接权重共享，相比于传统神经网络模型，其复杂度更低、权值数量更少，可以大大地减少训练时所需的参数数量.这些特性提高了训练效率并降低了计算机的性能要求，对处理大数据问题带来了颠覆性的益处.深度卷积神经网络(deep convolutional neural networks，DCNN)即采用多个卷积层进行深度卷积，能够更好地发挥CNN的空间提取能力.但DCNN方法无法明确模拟时间关系，不适合处理时间序列问题.递归神经网络(recurrent neural network，RNN)考虑了相邻步长时间之间的输入信息的序列关系，能够记忆历史信息，更加适合处理微震波形的拾取问题.在反向传播过程中，RNN由于需要训练的参数较多，会随着模型深度的增加而出现梯度消失和梯度爆炸的情况^[9].为了解决这个问题，Hochreiter等^[10]提出了长短时记忆(long short-term memory，LSTM)神经网络.目前，LSTM在大量与时序信号有关的领域，例如交通速度预测^[11]、电力负荷预测^[12]等都取得了较好的效果.
Mel刻度于20世纪30年代被提出.该方法将信号的原频域调整至新刻度，即得到Mel频谱.Mel频谱已被广泛应用于各种音频^[13]、声纹^[14]的识别或故障诊断^[15]，均取得了良好的效果.本文利用该方法对监测信号进行前处理，这将提高微震信号识别模型的学习效果.
本文以夏甸金矿实际岩体破裂微震监测数据为依托，对岩石破裂、爆破和机械振动三种主要信号进行了智能识别研究，提出一种基于Mel频谱和LSTM-DCNN的矿山微震信号识别方法.首先将信号数据映射至Mel频谱，以此作为深度学习的数据集.然后构建LSTM-DCNN微震信号识别模型，调整模型参数.最后，利用现场实测数据进行测试，检验所提出方法的有效性.
1 工程背景夏甸金矿位于中国“黄金之都”招远市，是中国十大黄金生产矿山之一.夏甸金矿目前的开采深度为800 m，是中国深部采矿作业的典型.为了实现高效开采的经济和安全目标，在矿井-700 m的地下设置了一个试验采场对采场结构进行优化试验，并使用矿山常用的IMS微震监测系统分布在试验采场附近，以监测试验采场的稳定性.根据现场的主要条件，在测试采场-692 m和-700 m的次级水平附近分布了6个微震传感器(5个单分量检波器和1个三分量检波器，带宽为9~2 000 Hz，灵敏度为(80±8)V·m^-1·s^-1，在-692 m的子层上分布4个，-700 m的子层上分布2个，详见图 1).根据现场记录的爆破时间和地点，人工选择爆破信号作为模板，确定爆破信号.然后收集在矿井没有进行爆破且机械振动信号很少时获得的信号，手动筛选岩石破裂信号.这些信号用作识别所有监控信号的参考.最后，对机械设备运行过程中监测到的信号进行分析，并在此基础上对所有监测信号进行人工识别，以确定机械信号.据此，从2015年12月11日至2016年2月29日，夏甸金矿采前、采中、采后从微震监测系统共采集7 564个信号，包括3 465个岩石破裂信号、2 381个爆破信号和1 718个机械振动信号.微震监控系统中记录的上述三种常见信号类型如图 2所示.
图 1(Fig. 1)

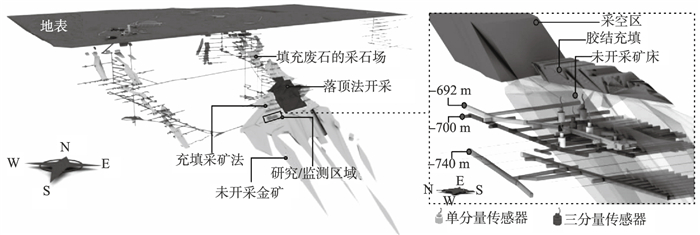图 1 夏甸金矿三维模型Fig.1 Three-dimensional model of the Xiadian Gold Mine

图 2(Fig. 2)

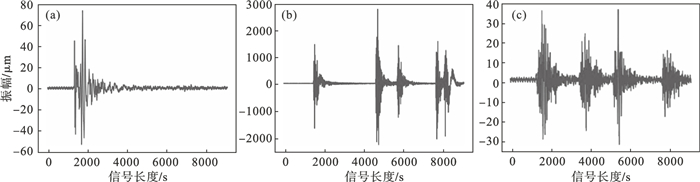图 2 三类信号波形图Fig.2 Waveforms of three kinds of signals (a)—岩石破裂信号; (b)—爆破信号; (c)—机械振动信号.

2 微震信号识别模型的建立本节综合Mel频谱、DCNN和LSTM模型，提出了一种新的信号混合识别模型Mel-LSTM-DCNN. 预处理部分统一了三类信号的数量及长度.将80% 的信号用于训练，20% 的信号用于测试，最终得到混合模型对三类信号的识别精度.数据处理流程见图 3.
图 3(Fig. 3)

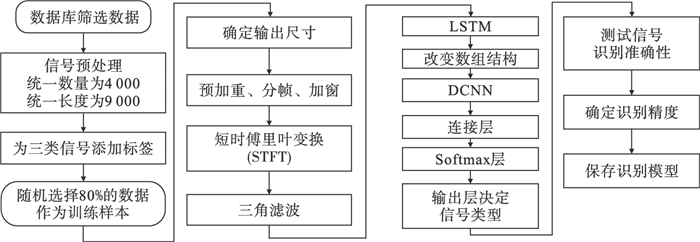图 3 数据处理流程Fig.3 Flowchart of data processing

2.1 预处理数据集由7 564个样本组成，其中岩石破裂信号3 465个，爆破信号2 381个，机械振动信号1 718个.有研究指出，均衡分布产生了最佳性能.因此，通过仔细分析监测信号，手动建立包含三种信号的信号数据库.从数据库筛选的信号长度不等，截取信号长度为9 000，使三种类型信号具有相同长度.三种信号数量不同，使用重采样来增加样本，得到三种具有相同长度的信号各4 000个.
所测信号信噪比分布如图 4所示.计算式为

(1)

图 4(Fig. 4)

图 4 三种信号信噪比分布图Fig.4 Distribution of signal-to-noise ratio for three kinds of signals

式中：R_SN为所测信号信噪比；P_s为有用信号功率；P_n为噪声信号功率.
由图 4可知，本文所使用信号信噪比均小于30 dB；统计可得有52% 的岩石破裂信号、45% 的爆破信号、46% 的机械振动信号的信噪比小于0 dB.信号信噪比总体偏低，可以更好验证模型精度.
2.2 Mel频谱设定输出尺寸为256×128.首先对信号预加重、分帧和加窗；对每帧信号进行短时傅里叶变换，得到短时幅度谱.再使用Mel滤波(Melfilter)将声纹时频谱变换到Mel标度(Mel scale)下的Mel时频谱.Mel标度与频率的转换关系如式(2)、式(3)所示.Mel时频谱可以通过刻度的非线性映射提高对低频率的感知，以此降低干扰频段的权重，并且Mel时频谱可以在保留监测信号特征的前提下减小样本的尺寸，提高模型训练速度及识别速度.

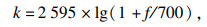(2)

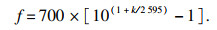(3)

式中：k为信号的Mel标度频率，Hz；f为信号的正常标度频率，Hz，0≤f≤22 050.
短时幅度谱通过Mel滤波器组得到Mel频谱.使用等高三角形滤波器组对时频谱进行滤波操作，该等高三角形滤波器组的函数如下：

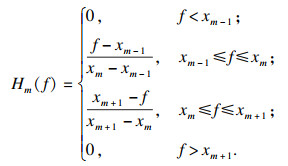(4)

式中：x为滤波器的中心频率；1＜m＜M，M为滤波器数量.
本文使用Mel滤波对微震信号时频谱图进行降维处理，并进行特征提取.通过将时频谱矩阵与Mel滤波器组矩阵相乘，再取对数，得到Mel时频谱.
2.3 深度学习神经网络信号识别模型2.3.1 LSTM长短期记忆网络LSTM模型采用三种“门”的设计来避开梯度爆炸和长期依赖的问题.该网络的每一次循环都用到了前一次循环的信息，所以每一个输出状态都受到了之前状态的影响，这也表示LSTM网络能够更好地记住长期的规律，适用于时间序列预测的问题，同时也适用于微震信号识别问题.
如图 5所示，该网络主要结构为三个“门”.
图 5(Fig. 5)

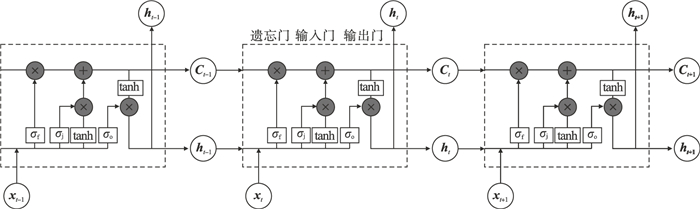图 5 LSTM模型结构Fig.5 LSTM model structure

1) 遗忘门.此阶段用来控制前一时刻的储存单元C_t-1有多少信息能够保存到当前时刻储存单元C_t中，即选择性忘记.σ层通过上一时刻隐藏状态h_t-1与t时刻输入x_t得到一个0到1之间的值，作为上一层细胞状态被遗忘的概率，视为C_t-1记忆的衰减系数，记作f_t.遗忘门的表达式为

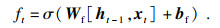(5)

式中：W_f为遗忘门的权重矩阵；[h_t-1, x_t]表示h_t-1和x_t的连接；b_f为遗忘门的偏置项.
2) 输入门.此阶段用来控制x_t有多少信息保存到C_t中，即选择性“记忆”.输入门的一部分决定哪些信息需要更新，即遗忘门中选择忘掉的部分.该部分将x_t与上一时刻隐藏状态h_t-1进行线性组合，然后通过σ层激活得到i_t.另一部分将h_t-1与x_t通过一个tanh层生成一个向量，得到备选的用来更新的内容.接下来两部分联合将状态C_t-1更新为C_t.输入门更新过程公式为

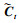
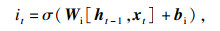(6)

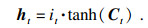(7)

式中：W_i为输入门的权重矩阵；b_i为输入门的偏置项.
每一次循环都用到了前一次循环的信息C_t-1与h_t-1，因此每一个输出状态都会受到之前状态的影响，所以LSTM具有记忆长期历史信息的能力.
2.3.2 DCNN深度卷积神经网络常见的卷积神经网络(CNN)一般由输入层、卷积层、池化层、全连接层和输出层构成.其主要结构如图 6所示.
图 6(Fig. 6)

图 6 DCNN模型结构Fig.6 DCNN model structure

1) 卷积层.卷积层进行卷积运算，主要负责提取特征.卷积层由一组滤波器(二维数字矩阵)组成.
2) 池化层.池化层也称为下采样层，其作用是：在保留有用信息的基础上逐步减小特征图的维数，提高网络的计算速度.根据需求，通常会取若干个卷积层和池化层交替设置^[16].池化操作后，特征图的分辨率降低，但依旧能较好地保持描述的特征.池化层可以缩小长和高方向上的空间运算，减少模型的计算量，使网络具有一定的抗噪能力.
3) 全连接层.全连接层由大量的神经元组成.全连接层中的每个神经元都与上一层中的所有神经元相连.该层的目的是对卷积层或池化层后高度抽象化特征进行整合，然后进行归一化.全连接的核心操作就是通过矩阵向量乘积，将一个特征空间线性变换到另一个特征空间.
2.4 LSTM-DCNN本文所构建的混合模型主要由LSTM和DCNN两部分组成，如图 7所示.其中，LSTM用于接收从Mel频谱图提取特征的输出，并利用其在时序上具有的记忆特性准确提取时间序列特征，以作为后者的输入；DCNN用于底层表达及抽取重构空间的空间特征信息.本文使用三层LSTM神经网络，深度卷积部分采用6个卷积层、4个池化层.为了降低网络记住训练数据特定特征的可能性，为最后一个全连接层的输入添加一个小的丢弃率.具体网络结构见表 1.目前，并没有成熟的理论可以定量给出所需的网络层数和神经元数，本文中LSTM-DCNN的网络结构参数由试错法确定.
图 7(Fig. 7)

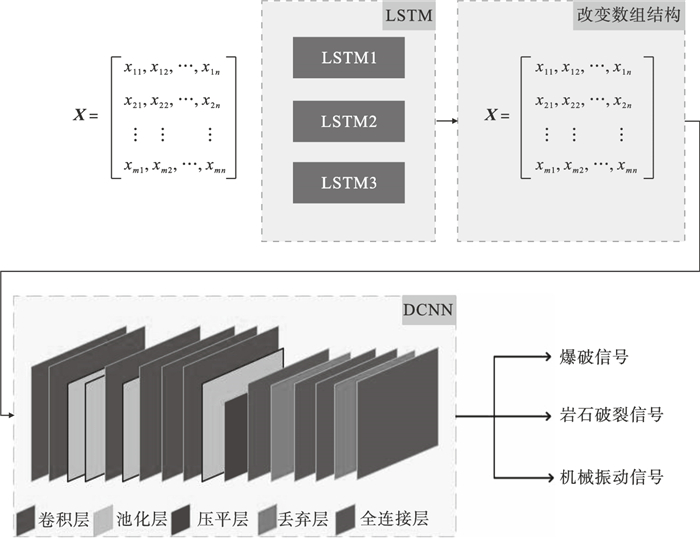图 7 LSTM-DCNN模型结构Fig.7 Structure of LSTM-DCNN model

表 1(Table 1)

表 1 LSTM-DCNN识别模型网络结构Table 1 Network structure of LSTM-DCNN identification model 序号 层 激活函数 输出尺寸 卷积核 1 LSTM1 — 256×128×3 — 2 LSTM2 — 256×128×3 — 3 LSTM3 — 256×128×3 — 4 改变数组结构 — 128×128×1 — 5 卷积层1 ReLU 32×32×96 3×3 6 卷积层2 ReLU 16×16×96 3×3 7 最大池化层1 — 8×8×96 2×2 8 最大池化层2 — 4×4×96 2×2 9 卷积层3 ReLU 4×4×256 3×3 10 最大池化层3 — 16×16×8 2×2 11 卷积层4 ReLU 2×2×256 3×3 12 卷积层5 ReLU 2×2×384 3×3 13 卷积层6 ReLU 2×2×256 3×3 14 最大池化层4 — 1×1×256 2×2 15 压平层 — 256 — 16 全连接层1 ReLU 2 048 — 17 丢弃层1 — 2 048 — 18 全连接层2 ReLU 2 048 — 19 全连接层3 ReLU 100 — 20 丢弃层2 — 100 — 21 全连接层4 Softmax 3 — 22 输出层 — — —

表 1 LSTM-DCNN识别模型网络结构 Table 1 Network structure of LSTM-DCNN identification model

3 结果对比及分析图 8显示了LSTM-DCNN模型的训练和测试迭代的准确度和损失函数变化.准确度表示波形被准确识别的概率，而损失函数反映了模型的学习效果.损失值越小，训练效果越好.训练和测试的最终准确率分别为100% 和97.88%.可以看出，LSTM-DCNN模型在训练和验证方面都表现良好.
图 8(Fig. 8)

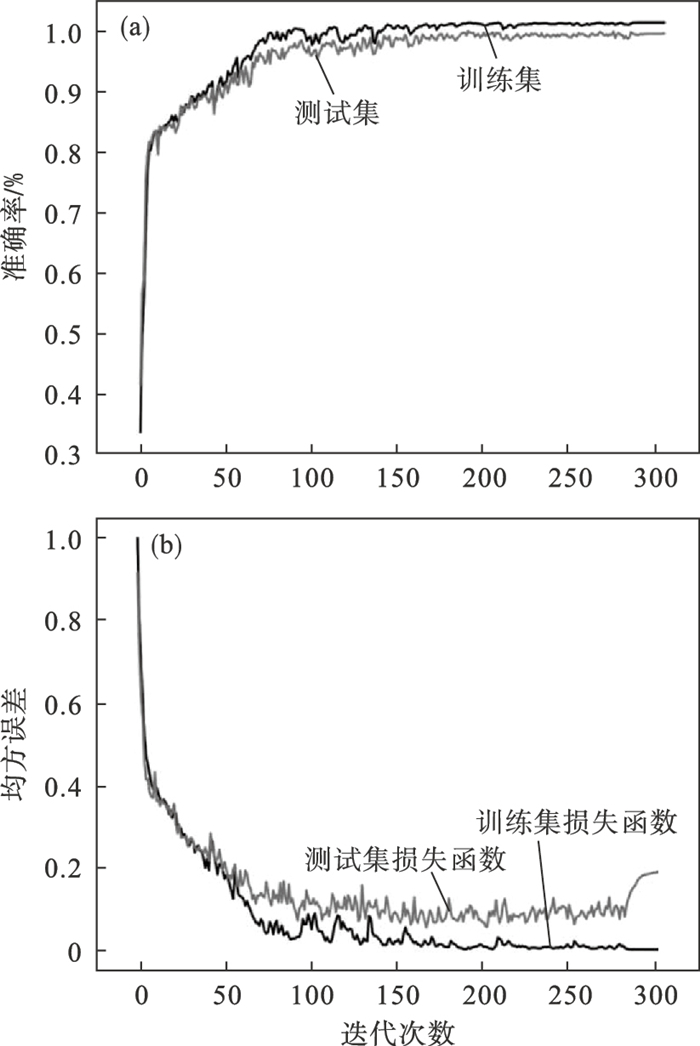图 8 LSTM-DCNN识别模型准确率及损失函数Fig.8 Accuracy and loss function of LSTM-DCNN recognition model (a)—识别准确率；(b)—损失函数.

为确定准确的识别结果并验证LSTM-DCNN识别模型，本文使用5次交叉验证来训练模型.为验证LSTM-DCNN识别模型与其他网络模型相比的识别性能，还对DCNN，LSTM和BP(back propagation)模型进行了5次交叉验证，结果见表 2.DCNN的输入是由原始监控信号通过STFT方法转换的时频图像.LSTM和BP的输入是由Mel方法转换的时频序列.
表 2(Table 2)

表 2 4种神经网络的信号识别准确率(每种信号4 000个)Table 2 Signal recognition accuracy of four neural network methods(4 000 signals of each type)? % 模型 信号类型 测试1 测试2 测试3 测试4 测试5 平均值 LSTM-DCNN 岩石破裂 99.6 99.6 99.5 99.7 99.9 99.66 爆破 94.4 95.2 96.0 97.2 97.1 95.98 机械振动 98.1 98.8 96.4 98.4 98.0 97.94 总计 97.38 97.92 97.29 98.46 98.33 97.88 LSTM 岩石破裂 97.6 98.3 97.6 98.1 98.0 97.92 爆破 91.0 88.8 91.0 86.4 88.8 89.20 机械振动 90.2 89.7 90.2 93.3 92.1 91.1 总计 92.96 92.33 92.96 82.62 93.00 88.77 DCNN 岩石破裂 97.5 96.5 96.6 95.8 96.7 96.62 爆破 93.6 97.1 96.8 95.8 95.0 95.76 机械振动 99.4 90.3 90.3 88.3 97.2 93.10 总计 96.82 94.67 94.62 93.38 96.33 95.16 BP 岩石破裂 81.6 88.6 89.0 84.5 91.5 87.04 爆破 69.8 76.0 53.6 68.5 57.1 65.00 机械振动 71.1 73.5 79.2 71.4 69.9 73.02 总计 79.11 79.25 79.32 80.56 78.79 79.41

表 2 4种神经网络的信号识别准确率(每种信号4 000个) Table 2 Signal recognition accuracy of four neural network methods(4 000 signals of each type)?

从表 2可以看出，5次交叉验证下LSTM-DCNN模型的总体平均以及单种信号的识别性能标准差均小于其他模型.即本文提出的LSTM-DCNN模型识别性能是稳定的.LSTM和DCNN模型都优于BP模型.此外，从表 2中可以发现LSTM-DCNN模型的信号识别准确率明显高于DCNN，LSTM和BP模型.DCNN和LSTM模型的总识别准确率分别达到95.16% 和88.77%，对岩石破裂信号的识别性能在95% 以上.这表明DCNN模型有很好地从时频图像中提取空间特征的能力，LSTM模型有很好地从时间序列数据提取时域特征的能力.通过比较网络模型的识别性能，LSTM-DCNN模型可以更好地融合LSTM和DCNN模型的优势.
对于岩石破裂信号识别，LSTM-DCNN，LSTM，DCNN准确率都在95% 以上，且都较为稳定，其中LSTM-DCNN的效果最好.BP模型在岩石破裂信号的识别中波动性较大，准确率也低于前3类模型.
4种模型识别的混淆矩阵如图 9所示.3种信号中用于测试的信号数量均为800条.从混淆矩阵也可以看出，LSTM-DCNN模型对岩石破裂信号有着较高的识别性能.对于爆破信号，800条信号中有23条信号会识别错误，对于机械振动信号，800条信号中有16条信号会识别错误，即识别错误的概率分别为2.875% 和2.000%.但与其他模型相比，LSTM-DCNN对于爆破信号和机械振动信号识别准确率依旧最高.
图 9(Fig. 9)

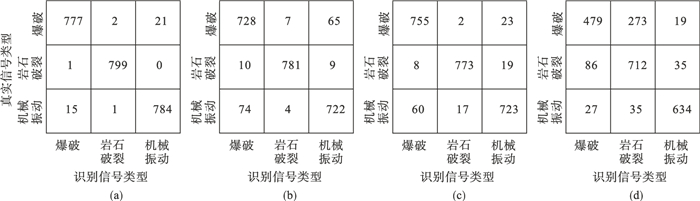图 9 4种识别模型混淆矩阵Fig.9 Confusion matrix of 4 recognition models (a)—LSTM-DCNN; (b)—LSTM; (c)—DCNN; (d)—BP.

对相同数据使用4种常规识别方法：支持向量机(support vector machine，SVM)、邻近算法(K-nearestneighbor，KNN)、决策树(decision tree，DT)和线性判别分析(linear discriminant analysis，LDA)进行比较，结果见表 3.其中SVM识别准确率最高，为85.03%，相比之下，本文提出的LSTM-DCNN模型准确率提高了12.85%.
表 3(Table 3)

表 3 4种传统方法的信号识别准确率(每种信号4 000个)Table 3 Signal recognition accuracy of four conventional methods(4 000 signals of each type)? % 模型 信号类型 测试1 测试2 测试3 测试4 测试5 平均值 SVM 岩石破裂 92.1 91.6 92.2 93.4 92.4 92.34 爆破 88.2 89.2 89.3 90.6 88.5 89.16 机械振动 72. 77.4 73.2 75.0 72.6 73.6 总计 84.37 85.07 84.90 86.33 84.50 85.03 KNN 岩石破裂 90.1 89.1 91.2 90.4 89.7 90.1 爆破 85.2 86.3 87.1 85.1 86.6 86.06 机械振动 74.8 74.6 73.1 73.2 74.1 73.96 总计 83.37 83.33 83.80 82.90 83.47 83.37 DT 岩石破裂 89.1 89.4 91.0 89.5 91.6 90.12 爆破 88.7 87.6 88.1 90.1 87.5 88.4 机械振动 71.5 74.25 70.6 71.1 72.3 71.94 总计 83.10 83.73 83.23 83.57 83.80 83.49 LDA 岩石破裂 89.6 90.2 88.4 90.6 89.9 89.74 爆破 80.5 78.9 81.1 79.6 79.4 79.9 机械振动 69.5 70.6 71.4 71.8 70.2 70.7 总计 79.87 79.90 80.30 80.67 79.83 80.11

表 3 4种传统方法的信号识别准确率(每种信号4 000个) Table 3 Signal recognition accuracy of four conventional methods(4 000 signals of each type)?

当各类信号总量减小到2 000条(其中80% 用于训练，20% 用于测试)时，由表 4可以看出，4种模型对于信号识别的准确率均有下降，可以说明模型识别的准确率与样本数量有着密不可分的关系.其中对爆破信号识别的准确率下降最为明显.但即使样本数量减少一半，本文提出的LSTM-DCNN模型对于岩石破裂信号识别的准确率依旧能够达到99% 以上，对所有信号识别的整体准确率能够达到94% 以上.
表 4(Table 4)

表 4 4种神经网络的信号识别准确率(每种信号2 000个)Table 4 Signal recognition accuracy of four neural network methods(2000 signals of each type)? % 模型 信号类型 测试1 测试2 测试3 测试4 测试5 平均值 LSTM-DCNN 岩石破裂 99.5 99.0 99.5 99.5 99.2 99.34 爆破 89.5 89.0 91.0 88.2 90.5 89.64 机械振动 96.2 94.8 96.0 96.2 95.2 95.68 总计 95.08 94.25 95.50 94.67 95.00 94.94 LSTM 岩石破裂 97.7 98.0 95.5 97.2 97.7 97.22 爆破 87.8 79.8 87.8 75.5 87.0 83.58 机械振动 87.5 91.0 82.8 89.0 84.0 86.86 总计 91.00 89.58 88.67 87.25 89.58 89.22 DCNN 岩石破裂 98.5 93.2 92.8 99.75 98.2 96.49 爆破 95.7 91.0 89.0 92.2 79.5 89.48 机械振动 85.25 96.5 94.5 95.0 99.2 94.09 总计 93.17 93.58 92.08 95.67 92.33 93.37 BP 岩石破裂 91.7 97.0 90.5 92.6 95.1 93.38 爆破 66.9 71.8 76.9 68.8 72.7 71.42 机械振动 78.5 77.3 72.7 81.4 73.6 76.70 总计 78.63 81.56 80.48 80.33 79.58 80.12

表 4 4种神经网络的信号识别准确率(每种信号2 000个) Table 4 Signal recognition accuracy of four neural network methods(2000 signals of each type)?

4 结论1) 本文提出了一种基于Mel频谱LSTM以及DCNN混合的微震监测信号识别模型.将监测信号映射到Mel频谱降低干扰频段的权重，使用LSTM对信号时间特征进行提取，DCNN对信号的空间特征进行提取，以提高微震信号识别精度.
2) 经测试，LSTM-DCNN模型对矿山岩石破裂信号识别的准确率达到99.66%，在岩石破裂信号识别方面表现优异.且LSTM-DCNN模型训练时间短，具有一定的优越性.在样本数量相同的情况下，LSTM-DCNN模型对岩石破裂信号的识别准确率高于LSTM，DCNN及BP模型.即使样本数量下降一半，LSTM-DCNN模型对于岩石破裂信号识别准确率仍能保持99% 以上.
3) LSTM-DCNN混合模型对训练样本有很强的依赖性.如果没有足够的样本，就无法涵盖分类对象的一般特征，很容易发生模型过度拟合和无效训练.在样本数量下降的情况下，识别的准确率有所降低.同时，由于矿山环境的复杂性，本文中的网络结构在应用于其他矿山数据时需要进行调整.
参考文献

[1]	Zhang C, Jin G H, Liu C, et al. Prediction of rockbursts in a typical island working face of a coal mine through microseismic monitoring technology[J]. Tunnelling and Underground Space Technology, 2021, 113: 103972. DOI:10.1016/j.tust.2021.103972
[2]	Xue R X, Liang Z Z, Xu N W. Rockburst prediction and analysis of activity characteristics within surrounding rock based on microseismic monitoring and numerical simulation[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 142: 104750. DOI:10.1016/j.ijrmms.2021.104750
[3]	刘建坡, 武峰, 王人, 等. 基于模糊综合评价的深部巷道破坏定量风险评估[J]. 东北大学学报(自然科学版), 2022, 43(5): 733-739. (Liu Jian-po, Wu Feng, Wang Ren, et al. Quantitative risk assessment for deep tunnel failure based on fuzzy comprehensive evaluation[J]. Journal of Northeastern University(Natural Science), 2022, 43(5): 733-739.)
[4]	Wang J C, Chen G Q, Xiao Y X, et al. Effect of structural planes on rock burst distribution: case study of a deep tunnel in Southwest China[J]. Engineering Geology, 2021, 292(4): 106250.
[5]	Dong L L, Yang Y, Qian B, et al. Deformation analysis of large-scale rock slopes considering the effect of microseismic events[J]. Applied Sciences, 2019, 9(16): 3409. DOI:10.3390/app9163409
[6]	Gu J X, Wang Z H, Kuen J, et al. Recent advances in convolutional neural networks[J]. Pattern Recognition, 2018, 77: 354-377. DOI:10.1016/j.patcog.2017.10.013
[7]	Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386
[8]	郭峰. 基于CNN+LSTM的运动想象脑电四分类研究[D]. 广州: 广东工业大学, 2022. (Guo Feng. Study on four classification of motor imagery EEG based on CNN+LSTM[D]. Guangzhou: Guangdong University of Technology, 2022. )
[9]	Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult[J]. IEEE Transactions on Neural Networks, 1994, 5(2): 157-166. DOI:10.1109/72.279181
[10]	Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735
[11]	Hsueh Y L, Yang Y R. A short-term traffic speed prediction model based on LSTM networks[J]. International Journal of Intelligent Transportation Systems Research, 2021, 19(3): 510-524. DOI:10.1007/s13177-021-00260-7
[12]	Dudek G, Pe?ka P, Smyl S. A hybrid residual dilated LSTM and exponential smoothing model for mid-term electric load forecasting[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 33(7): 2879-2891.
[13]	Abduh Z, Nehary E A, Wahed M A, et al. Classification of heart sounds using fractional Fourier transform based Mel-frequency spectral coefficients and traditional classifiers[J]. Biomedical Signal Processing and Control, 2020, 57: 101788. DOI:10.1016/j.bspc.2019.101788
[14]	刘云鹏, 罗世豪, 王博闻, 等. 基于Mel时频谱-卷积神经网络的变压器铁芯夹件松动故障声纹模式识别[J]. 华北电力大学学报(自然科学版), 2020, 47(6): 52-60, 67. (Liu Yun-peng, Luo Shi-hao, Wang Bo-wen, et al. Voiceprint recognition of transformer core clamp looseness fault by Mel-spectrum and convolutional neural network[J]. Journal of North China Electric Power University(Natural Science Edition), 2020, 47(6): 52-60, 67.)
[15]	Mei Q P, Gül M, Boay M. Indirect health monitoring of bridges using Mel-frequency cepstral coefficients and principal component analysis[J]. Mechanical Systems and Signal Processing, 2019, 119: 523-546. DOI:10.1016/j.ymssp.2018.10.006
[16]	周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229-1251. (Zhou Fei-yan, Jin Lin-peng, Dong Jun. Review of convolutional neural network[J]. Journal of Computer Science, 2017, 40(6): 1229-1251.)