
 , 王鑫
, 王鑫 东北大学 资源与土木工程学院,辽宁 沈阳 110819
收稿日期:2022-06-04
基金项目:国家自然科学基金资助项目(51878127)。
作者简介:赵文(1962-), 男, 内蒙古乌兰察布人, 东北大学教授, 博士生导师。
摘要:在传统管幕工法的钢管两侧分别焊接上下两条钢板(称为翼缘板),并将相邻钢管翼缘板焊接形成新型管幕结构.由于翼缘板的存在,顶进过程土体变形规律与圆形钢管不同.本文应用Midas GTS有限元分析软件,对不同钢管直径、翼缘板位置的带翼缘板圆钢管顶进过程进行模拟.结果表明,随上下翼缘板间距增大或管径的不断增加,管顶土体沉降、管底土体隆起、翼缘板处土体竖向位移不断增大;当顶管开挖面距离监测断面一节管长时,监测断面位置土体隆起;顶至监测断面位置时,土体变形变为沉降;当顶管位置超过监测断面一节管长后,土体变形趋于稳定;同时通过拟合曲线,得到了土体变形与上下翼缘板间距、管径的函数关系.
关键词:带翼缘板圆钢管顶管数值模拟土体变形Midas GTS
Numerical Simulation of Soil Deformation During Jacking of Circular Steel Pipes with Flange Plates
ZHAO Wen, WANG Zhi-guo, WANG Zhao-peng

 , WANG Xin
, WANG Xin School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Zhao-peng, E-mail: wzpneu@163.com.
Abstract: In the traditional pipe curtain construction, two steel plates, known as flange plates, are welded on both sides of the original circular steel pipe, creating a circular steel pipe with flange plates. Adjacent steel pipe with flange plates are welded together to form a new pipe curtain structure. The presentence of the flange plate cause the soil deformation law during jacking process to differ from that of circular steel pipes. In this study, Midas GTS finite element analysis software was used to simulate the jacking process of circular steel pipes with flange plates of different pipe diameters and flange plate positions. The results show that the soil settlement at the pipe top, the soil uplift at the bottom of the pipe, and the vertical displacement of the soil at the flange plate increase continuously with an increase in the spacing between the upper and lower flange plates or an increase in pipe diameter. When the top excavation surface is one section length away from the monitoring section, soil uplift occurs at the monitoring section position. When the top reaches the monitoring section position, the soil deformation becomes settlement. When the top position exceeds one section length of the monitoring section, the soil deformation tends to stablize. Meanwhile, the functional relationship between soil deformation and spacing between upper and lower flange plates, as well as pipe diameter, is obtained by fitting the curve.
Key words: circular steel pipe with flange platespipe jackingnumerical simulationsoil deformationMidas GTS
管幕法是一种新型暗挖法施工技术,由于传统管幕工法存在横向刚度较弱的问题,因此钢管-翼缘板(steel tube slab, STS)管幕工法被提出.STS管幕工法施工时,先逐根顶进带翼缘板圆形钢管,相邻钢管内应用螺栓进行横向连接,并焊接相邻翼缘板形成新型管幕结构,国内****对STS管幕工法进行了深入研究.文献[1-2]应用数值模拟、现场监测以及现场实验等多种方式对STS管幕工法不同横向连接下抗弯性能、顶管顶力、掌子面受力、盾构顶管开挖面土压力[3]等多方面进行探究及分析,得出了管间距、横向连接方式、横向连接间距对STS结构承载力的影响,并得出相对应的极限承载力.
国内外****应用理论分析、数值模拟、现场监测等方法,对顶管顶力、土体变形进行了大量的研究.Chapman等[4]应用日本顶管实际工程顶力数据,提出了用于预测顶力的计算方法.Zhen等[5]采用有限条法(finite strip method, FSM)得到了顶进钢管在轴压作用下的弹性屈曲变化下界.同时,国内外****[6-8]对顶管纠偏、润滑减阻、停机等多种情况进行了研究,分析了各因素对顶管工程的影响.文献[9-13]对顶管顶进过程中的土体变形情况进行了分析,得出了顶管顶进过程中土体变形的计算方法及影响因素.王志国等[14]通过数值模拟及理论推导,得出异形界面钢管顶进过程土体变形计算方法.刘波等[15]对南京某顶管工程进行了数值模拟,得到了顶管周围土体变形变化规律.宋建学等[16]结合某顶管工程实例,分析了超挖量和地面超载对地表沉降的影响.
综上所述,国内外的研究主要针对圆形或矩形顶管,对不同参数的带翼缘板圆形钢管顶进过程中的土体变形研究较少.基于此,本文应用Midas GTS有限元分析软件,以沈阳地铁九号线奥体中心站顶管工程为依托,对不同钢管直径、翼缘板位置的带翼缘板圆钢管顶进过程进行了模拟,对顶进过程中管周土体变形进行了分析.
1 工程概况沈阳地铁九号线奥体中心站暗挖段顶管施工中,带翼缘板钢管管顶覆土深度3.5 m.地表以下地层地质勘测结果如表 1所示.
表 1(Table 1)
| 表 1 土体力学性质 Table 1 Mechanical properties of soil |
在工程实际中顶管采用直径为900 mm、材料为Q235的钢管,管壁厚度及翼缘板厚度均为16 mm,共顶进28根顶管,顶管施工现场如图 1所示.采用德国ABS水平定向螺旋钻机顶进并开挖管内土体.为保证其水平精度,顶管采用长导向支架定位.
图 1(Fig. 1)
 | 图 1 管幕结构Fig.1 Pipe curtain structure |
根据顶管顶进的实际位置,布设地表变形监测点.如图 2所示,选取其中6个断面,分别为A,B,C,D,E,F,断面A,B,D,E,F分别布设6个监测点;断面C布设4个监测点.监测点从北往南分别编号为1,2,3,4,5,6.
图 2(Fig. 2)
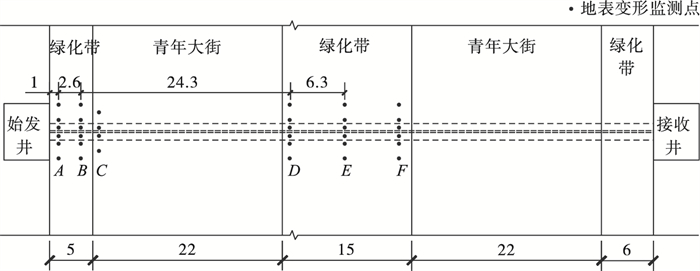 | 图 2 监测点布置图(单位:m)Fig.2 Monitoring point layout(unit: m) |
在正式顶进之前,先进行试验管的顶进.顶管每根长72 m(12段6 m定长顶管,各管段之间采用焊接连接),试验管尺寸如图 3所示.
图 3(Fig. 3)
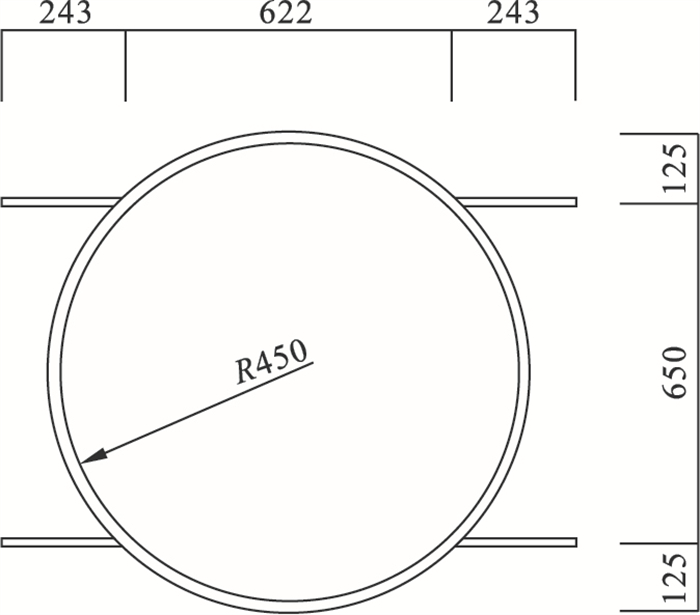 | 图 3 试验管尺寸图(单位:mm)Fig.3 Test steel pipe size chart(unit: mm) |
2 钢管顶进模拟2.1 计算假定1) 土体计算过程中采用摩尔-库仑模型,假定模型中土体符合摩尔-库仑破坏准则,将所有实体视为均匀各向同性体,土体视为理想的弹塑性体;
2) 模拟顶管过程中不考虑水对顶管工程的影响;
3) 模型中钢材视为各向同性的弹性体,模拟过程中只考虑弹性变形,引起周围土体变形及地表沉降的原因主要是上覆土体土压力造成的管土之间的摩擦阻力.
2.2 模型参数选取模型土体参数选取与奥体中心地铁站工程地质勘测结果一致,如表 1所示,因模型中涉及到钢管及翼缘板材料选取,以及管土接触截面参数设置,钢的弹性模量为210 GPa,重度为78.5 kN·m-3,泊松比为0.3,管土接触界面法向刚度模量为54 600 kN·m-3,剪切刚度模量为5 460 kN·m-3.
2.3 模型建立模型尺寸为长45 m,宽72 m,高45 m,如图 4所示.
图 4(Fig. 4)
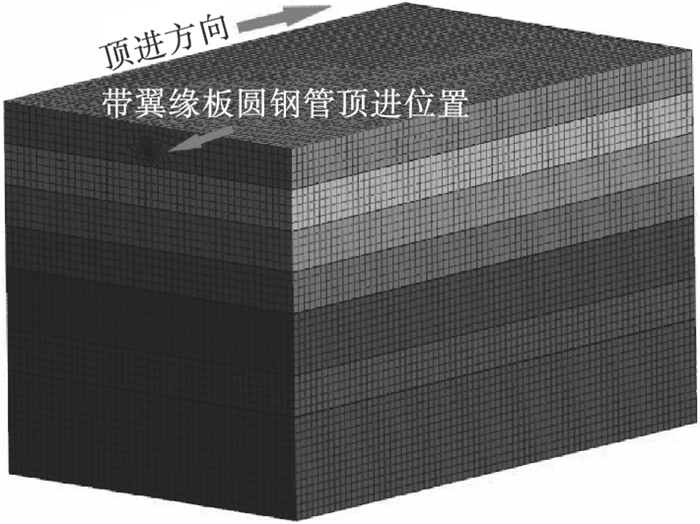 | 图 4 整体模型图Fig.4 Overall model |
模型边界采用MIDAS中的自动约束设置,在带翼缘板钢管与土体接触面上设置界面属性,通过确定法向刚度模量以及剪切刚度模量确定管土接触性质,模型界面单元图如图 5所示.
图 5(Fig. 5)
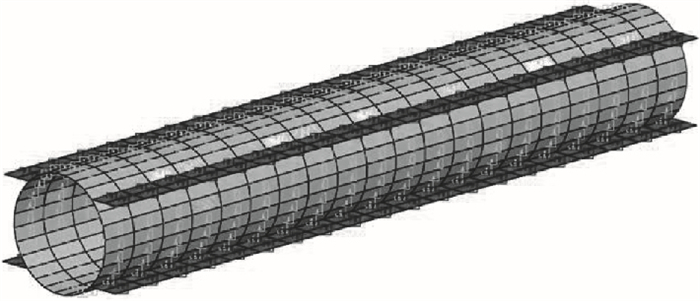 | 图 5 单节带翼缘板钢管界面单元图Fig.5 Interface element of steel pipe with flange plates |
2.4 模拟结果对比取监测断面D和E,对比数值模拟结果与试验顶管实际监测地表沉降结果.
2.4.1 断面D地表沉降值对比由图 6可以看出,实际监测和数值模拟的地表沉降均符合土体沉降槽理论.对比实测值与模拟值发现,由于实际顶进过程中管头前端的超挖现象,顶进轴线上方的监测点地表沉降值大于数值模拟沉降值,但整体拟合曲线趋势相同.
图 6(Fig. 6)
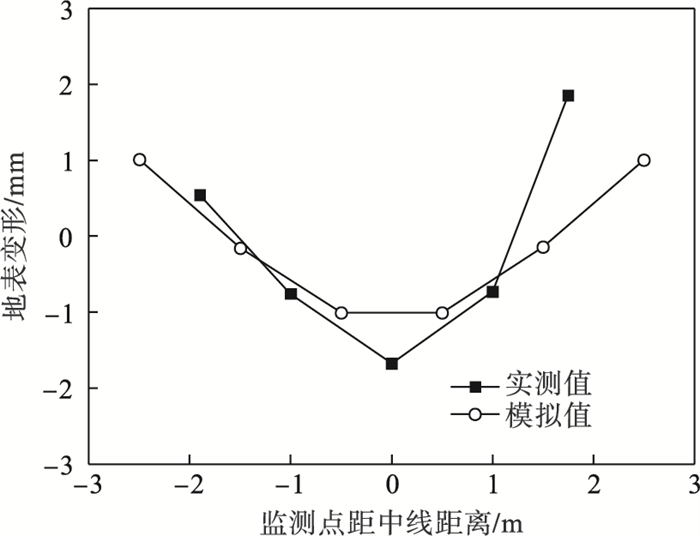 | 图 6 顶进54 m时断面D监测点地表沉降Fig.6 Surface settlement of section D monitoring point when jacking 54 m |
2.4.2 断面E地表沉降值对比由图 7可知,由于实际工程中超挖现象的存在,当开挖面距离断面E较近时,开挖面土体损失较大,实际工程中地表沉降发生突变,当开挖面未到断面E时,实际监测地表沉降值大于数值模拟沉降值,当开挖面超过监测断面E时,实际监测值仍大于模拟值,但整体变化趋势相同.
图 7(Fig. 7)
 | 图 7 监测点地表变形情况Fig.7 Surface deformation of monitoring sites (a)—监测点E2;(b)—监测点E3. |
综上所述,虽然实际工程中的超挖现象导致部分监测点地表沉降产生突变,但整体模拟结果与实际监测相似度较高,可以通过数值模拟结果分析带翼缘板钢管顶进过程中周围土体变形情况,得出变形规律及结论.
在带翼缘板圆钢管顶进过程中,由于翼缘板的存在,导致钢管周围土压力分布不均,因此顶管顶力与土体变形与常规圆钢管顶进过程不同.因此,针对带翼缘板圆钢管这种异形截面形式,翼缘板位置与钢管参数是影响顶进过程土体变形的主要因素.针对不同的土层参数,在顶力及土体变形计算中,可代入相应的土体参数得到计算结果.
根据实际工程施工及模拟可知,对土体变形影响最大的因素是钢管的直径与翼缘板的位置,因此本文选择不同钢管直径和翼缘板位置的情况来进行分析.
3 翼缘板位置对土体变形影响分析3.1 模型建立应用Midas GTS有限元分析软件,建立900 m钢管直径下,翼缘板分别位于30°,45°,60°位置的有限元模型,三组参数条件下带翼缘板钢管如图 8所示.
图 8(Fig. 8)
 | 图 8 不同翼缘板位置的钢管模型Fig.8 Steel pipe model with different flange positions |
3.2 土体变形模拟结果分析3.2.1 管顶土体竖向变形由管顶土体沉降规律可以看出,翼缘板形成的悬臂结构产生的变形,会增加管顶土体沉降,因受到各区域摩擦阻力的整体作用,管顶土体竖向变形依次增大.由图 9可以看出,随着带翼缘板钢管的逐渐顶进,后方已完成顶进和管内土体开挖区域土体变形逐步趋于稳定,基本不发生变化.每节钢管顶进过程中,从管两端至管中心土体变形成抛物线分布,即管中心土体沉降最大.三种翼缘板位置情况下,管顶最大沉降分别为0.995,1.05,1.14 mm,相比于翼缘板位于30°位置时依次增长5.53 % 和8.57 %.
图 9(Fig. 9)
 | 图 9 900 mm钢管直径下管顶土体变形Fig.9 Deformation of pipe top soil at 900 mm pipe diameter (a)—钢管顶进60 m;(b)—钢管顶进72 m. |
提取顶进30,60 m两种工况下管顶土体竖向变形的最大值,分别拟合曲线,如图 10所示.可以看出,随着顶进距离的不断增加,不同翼缘板位置下新顶入带翼缘板钢管管顶的最大土体竖向变形增长速度上升,曲线拟合结果近似为线性,随着上下翼缘板间距增加,管顶土体竖向变形最大值逐渐增大.该拟合线适用于管径为900 mm,上覆土层厚度为3.5 m的浅埋顶管工况条件下,顶管顶进地层为杂填土地层时,用于描述翼缘板不同位置的圆钢管在顶进30 m和顶进60 m管顶土体竖向变形的变化趋势.
图 10(Fig. 10)
 | 图 10 管顶土体竖向变形拟合线Fig.10 Vertical deformation fitting lines of pipe top soil |
3.2.2 管底土体竖向变形因为下翼缘板的存在,管底区域受到地基反力以及管内掏土产生的土体损失影响较大,导致土体竖向变形逐渐增大.由图 11可以看出,已完成顶管的区域,随着新的管节顶进,管底土体变形基本不受影响,最后一节顶进过程中,对应管底土体竖向变形最大值分别为1.04,1.08,1.24 mm,依次增长3.85 % 和14.8 %.
图 11(Fig. 11)
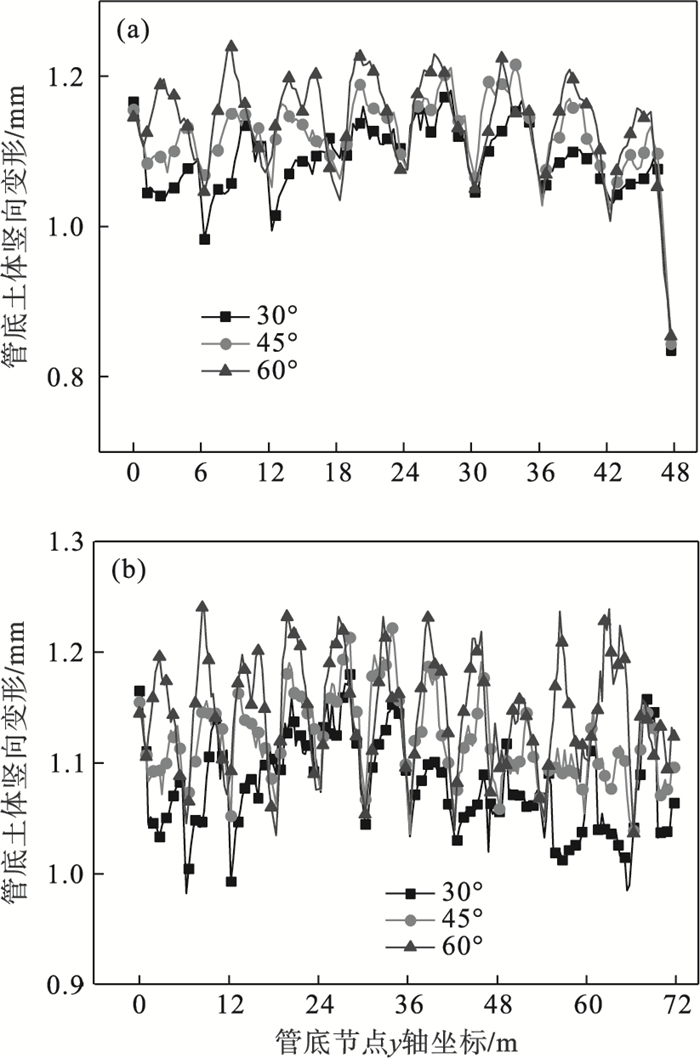 | 图 11 900 mm钢管直径下管底土体竖向变形Fig.11 Vertical deformation of the soil at the bottom of the pipe at 900 mm pipe diameter (a)—钢管顶进48 m;(b)—钢管顶进72 m. |
在顶进48,72 m两种工况下,取数值模拟结果中管底土体竖向变形最大值,拟合曲线如图 12所示.可以看出,随着顶进距离的增加,不同翼缘板位置下新顶入带翼缘板钢管管底的最大土体竖向变形增加,随着上下翼缘板间距逐渐增大,管底土体竖向变形最大值逐渐增大,该拟合线的适用条件与3.2.1节中相同.
图 12(Fig. 12)
 | 图 12 管底土体竖向变形拟合线Fig.12 Vertical deformation fitting line of soil at the bottom of the pipe |
3.2.3 翼缘板周围土体变形研究带翼缘板钢管顶进过程中翼缘板周围土体竖向变形,选定位于顶进方向距离始发井24 m处截面S,各点设置如图 13所示.
图 13(Fig. 13)
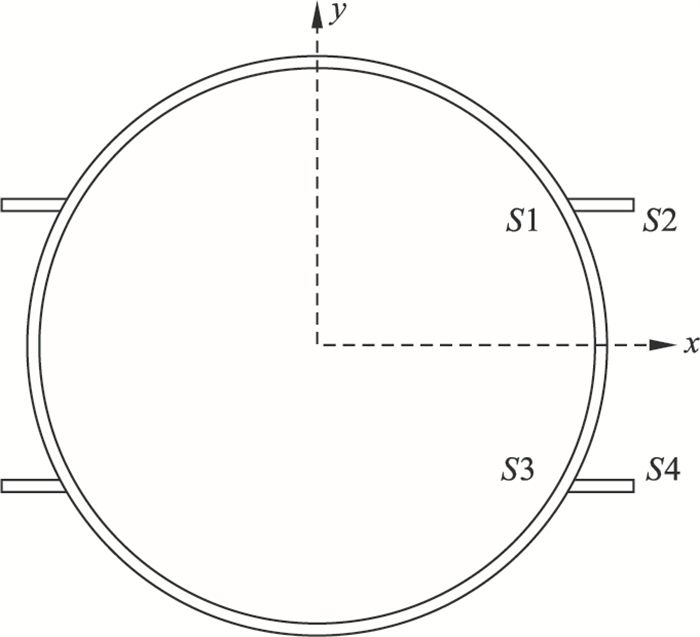 | 图 13 24 m处截面S示意图Fig.13 Schematic diagram of section S at 24 m |
如图 14所示,由距离始发井24 m处截面S上S1,S2,S3,S4点周围土体变形可以看出,当开挖面顶进过程中与截面距离超过一节管长时,对截面土体基本没有扰动;当开挖面距离截面距离仅为一节管长并继续顶进时,翼缘板周围土体开始产生显著的土体变形;当开挖面超过截面一节管长后,截面位置土体竖向变形趋于稳定,翼缘板与钢管连接点周围土体变形量较大,远离钢管端的翼缘板周围土体变形量较小.
图 14(Fig. 14)
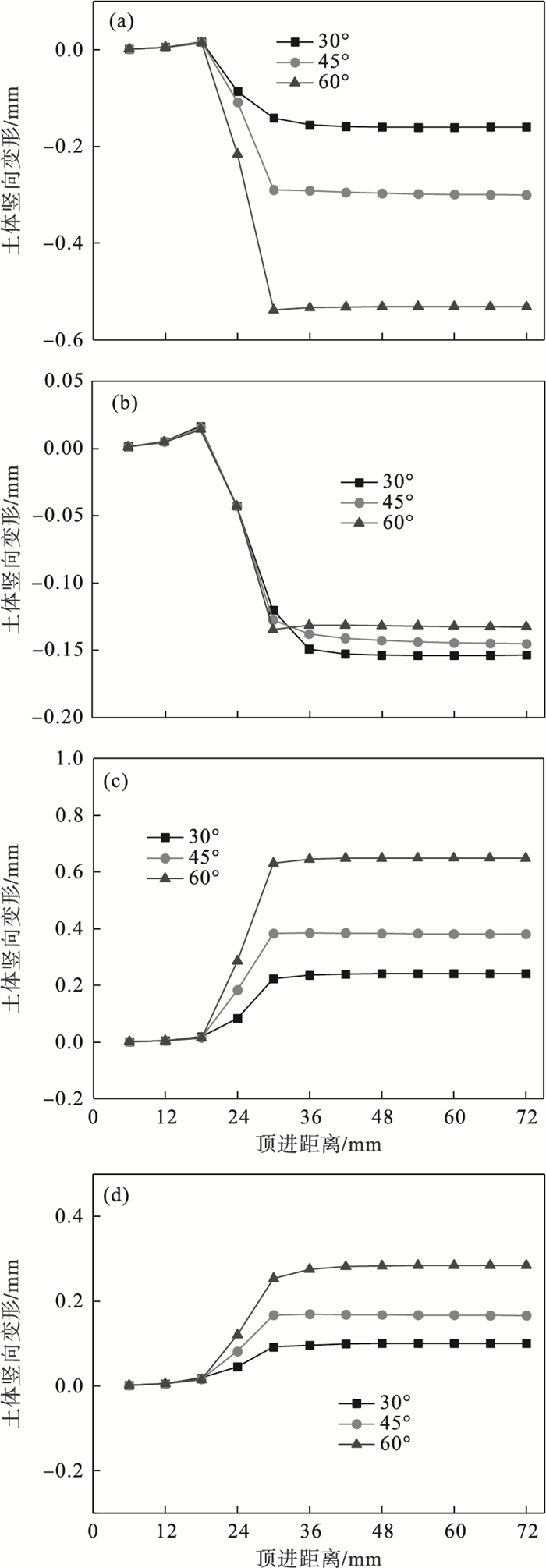 | 图 14 900 mm钢管直径下截面S各点土体竖向变形Fig.14 Vertical deformation of soil at section S at 900 mm pipe diameter (a)—S1点;(b)—S2点;(c)—S3点;(d)—S4点. |
随着上下翼缘板间距的增大,上翼缘板上部承担的土重增大,上翼缘板S1点周边土体沉降逐渐增大,当上翼缘板位置由45°变为30°和由60°变为45°时,土体最大竖向变形分别增大86.9 % 和77.3 %,S2点翼缘板不同位置下土体沉降基本不变甚至出现下降;当下翼缘板位置由45°变为30°和由60°变为45°时,下翼缘板S3点土体隆起的最大竖向变形分别增大58.1 % 和70.1 %,S4点土体隆起同样变大,但增长量较小.
综上所述,随着翼缘板间距的增大,钢管受到地基反力以及管内掏土产生的土体损失影响较大,导致管顶区域沉降、管底土体竖向隆起逐渐增大,上翼缘板上部承担的土重增加,下翼缘板承受的地基反力同样逐渐增大,导致翼缘板处位移不断增加.
4 钢管直径对土体变形影响分析4.1 模型建立建立翼缘板位置相同、管径不同的有限元模型,钢管管径分别为900,1 200,1 500 mm,翼缘板位于与水平夹角30°的位置,如图 15所示.
图 15(Fig. 15)
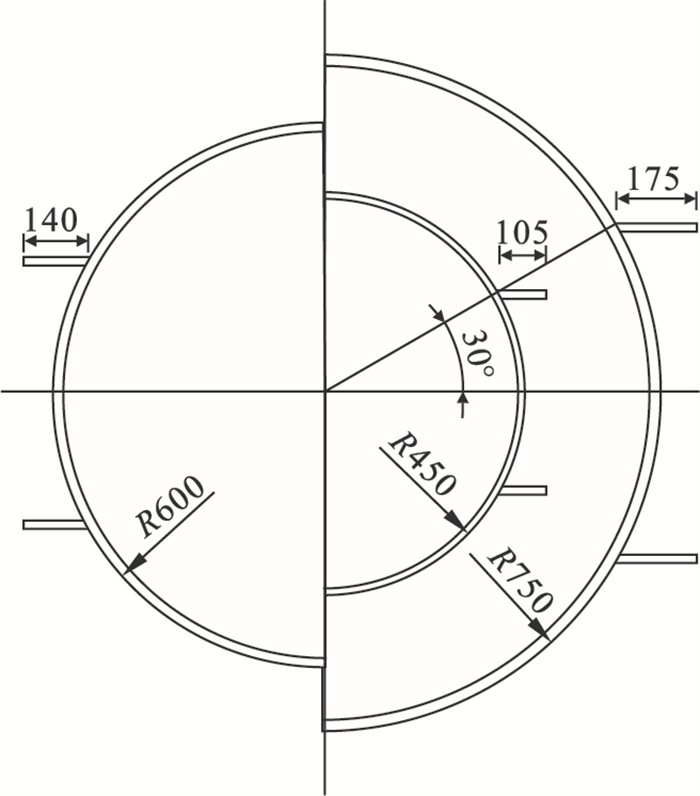 | 图 15 不同管径的带翼缘板钢管模型(单位:mm)Fig.15 Steel pipe model with flange plates for different pipe diameters(unit: mm) |
4.2 土体变形模拟结果分析4.2.1 管顶土体竖向变形由图 16可以看出,随着管径的不断增大,钢管顶进并完成掏土后,管内土体损失逐渐增多,导致管顶土体竖向变形增加.顶进最后一节带翼缘板钢管后,3种管径条件下管顶土体最大竖向沉降分别为0.995,1.311,1.46 mm,依次增长31.76 %,11.4 %.管径900~1 200 mm管内土体损失增长率高于管径1 200~1 500 mm管内土体损失增长率.
图 16(Fig. 16)
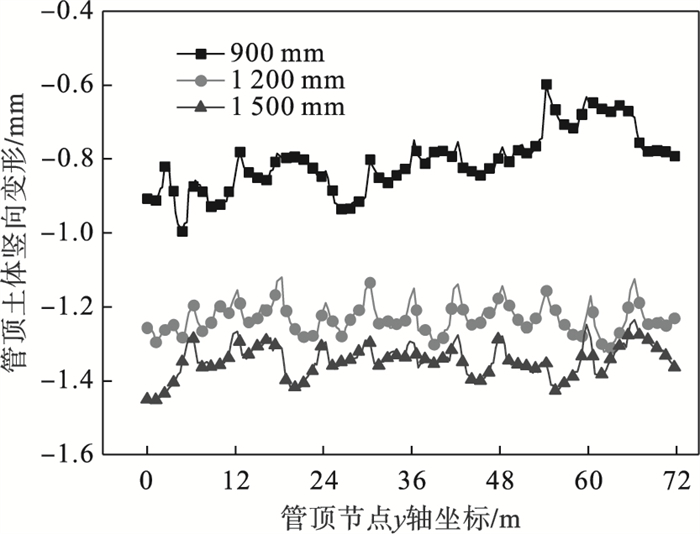 | 图 16 顶进72 m时不同管径管顶土体竖向变形Fig.16 Vertical deformation of pipe top soil under different tube diameters when jacking 72 m |
选取不同管径条件下,顶进30,60 m两种工况下带翼缘板钢管管顶最大土体竖向变形值进行拟合,结果如图 17所示.可以看出,顶进过程中管顶土体竖向变形随管径增大而增大,且土体变形增长率随顶进距离增大而增长.
图 17(Fig. 17)
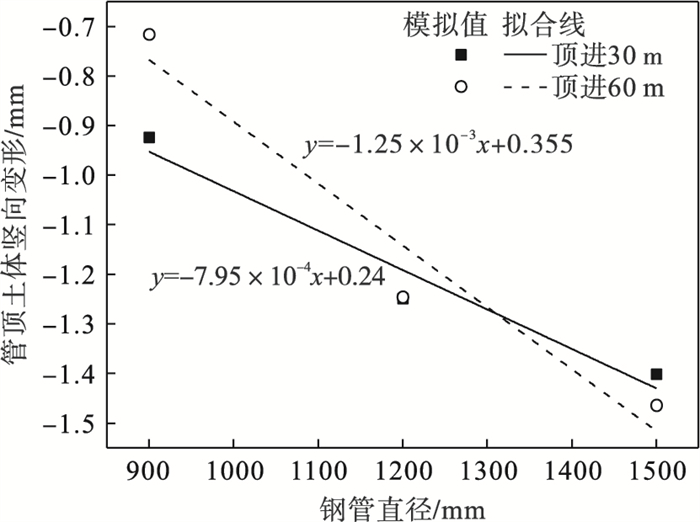 | 图 17 不同管径下管顶土体变形拟合线Fig.17 Fitting line of soil deformation at pipe top under different pipe diameters |
4.2.2 管底土体竖向变形由图 18可以看出,随着管径的逐渐增大,由于管内土体损失逐渐增多,管底土体应力值及应力作用范围变大,管底土体隆起量逐渐增大.每节管管底竖向隆起变化不大,说明带翼缘板钢管顶进过程中管底土体变形基本不变.最后一节顶进完成后,在900,1 200,1 500 mm的3种管径条件下管底土体最大竖向变形为1.171,1.736,2.18 mm,随管径增加依次增长48.2 %,25.6 %.
图 18(Fig. 18)
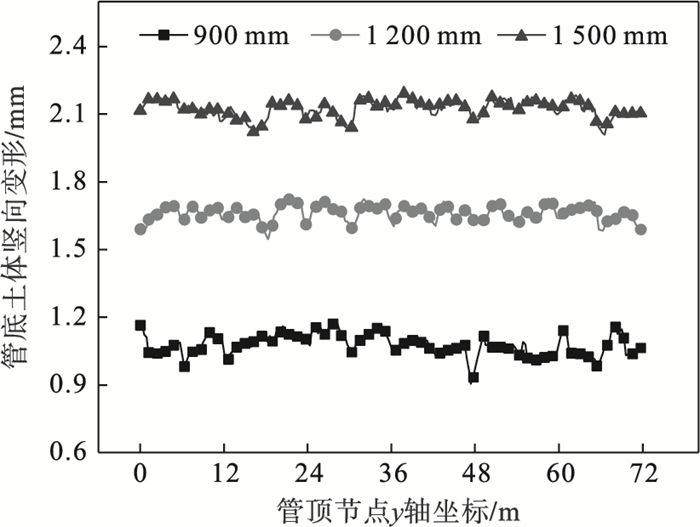 | 图 18 顶进72 m时不同管径管底土体变形Fig.18 Vertical deformation of the soil at pipe bottom under different pipe diameters when jacking 72 m |
选取不同管径条件下,顶进48, 72 m工况下带翼缘板钢管管底最大土体竖向变形进行拟合,结果如图 19所示.可以看出,不同管径条件下管底土体竖向变形变化率基本保持不变,且随着管径的增大管底土体隆起值逐渐增大.顶进72 m时隆起值大于顶进48 m时隆起值,模拟结果与拟合线相关性较好,均大于0.9.
图 19(Fig. 19)
 | 图 19 不同管径下管底土体竖向变形拟合线Fig.19 Fitting line of soil vertical deformation at pipe bottom under different pipe diameters |
4.2.3 翼缘板周围土体变形与3.2.3节相同,选取顶进方向距离始发井24 m的截面S,提取不同参数下截面上下翼缘板周围土体竖向变形结果,如图 20所示.
图 20(Fig. 20)
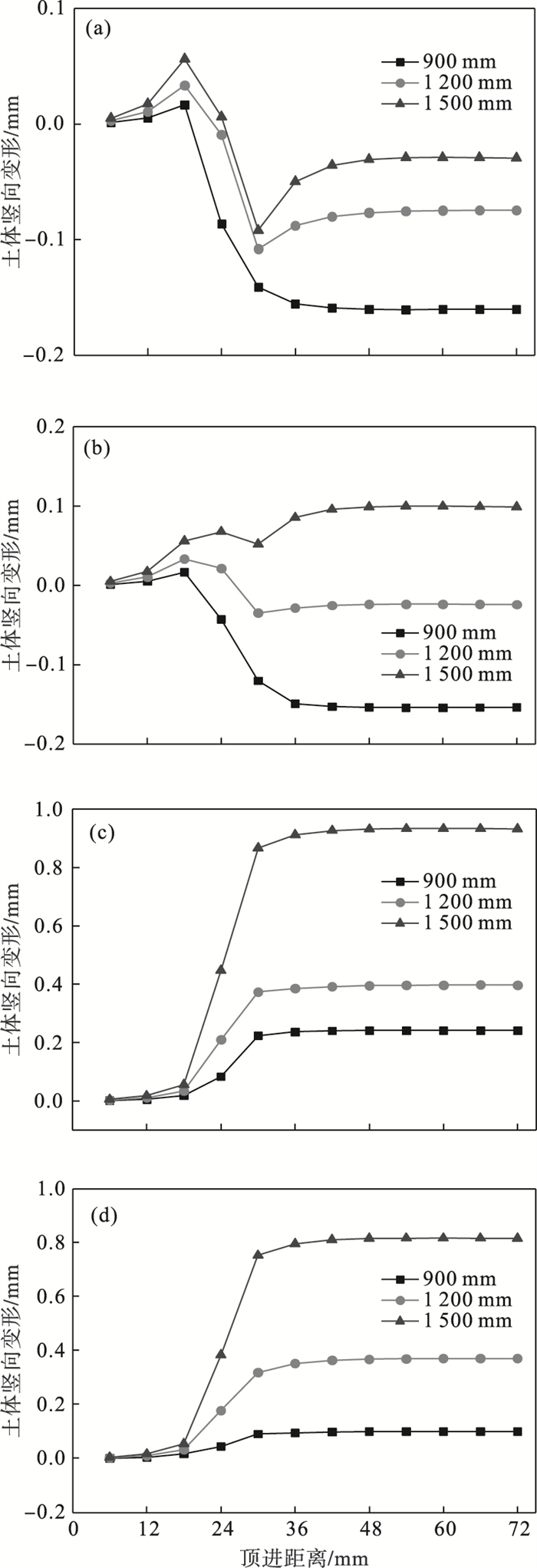 | 图 20 不同管径的截面S土体竖向变形Fig.20 Vertical deformation of soil at section S under different pipe diameters (a)—S1点;(b)—S2点;(c)—S3点;(d)—S4点. |
上翼缘板S1点,在开挖面未到截面并与截面相距一节管长时,截面周围土体开始因受到扰动产生一定隆起;开挖面到达截面S并逐渐顶进至超过截面一节管长时,土体沉降明显;当开挖面顶进距离超过截面一节管长后,土体产生一定的回弹,沉降量减小0.05 mm后趋于稳定.上翼缘板S2点变化趋势与S1点基本相同,但在1 500 mm管径条件下,S2点产生隆起现象,这是由于1 500 mm管径带翼缘板钢管管内土体损失较大,导致管底隆起增长量较大,使得翼缘板边缘土体向上隆起.
下翼缘板S3,S4点,随着管径的不断增大,管底隆起量逐渐增大,翼缘板与钢管接触位置的土体变形大于远离钢管处翼缘板的土体变形.下翼缘板S3点在900,1 200,1 500 mm三种管径下土体隆起最大值分别为0.241,0.397,0.933 mm,依次增长64.7 % 和135 %.
综上所述,随着管径的不断增大,钢管顶进并完成掏土后,管内土体损失逐渐增多,导致各位置应力增大,同时管径的增大导致管顶卸荷拱曲线更高,钢管和翼缘板承担的卸荷拱内土量增多,导致管顶区域沉降、管底土体竖向隆起、翼缘板处竖向位移不断增大.
5 结论1) 基于奥体中心试验管顶进实际工程,建立同样参数的有限元模型,将模拟的沉降结果与实际工程地表沉降结果进行对比,证实了数值模拟的准确性.
2) 随着上下翼缘板间距或管径逐渐增大,管顶区域沉降、管底土体竖向隆起、翼缘板处竖向位移不断增大.
3) 在开挖面未到截面并与截面相距一节管长时,截面周围土体开始因受到扰动产生一定隆起;随着带翼缘板钢管的顶进,开挖面到达截面并逐渐顶进至超过截面一节管长时,土体沉降明显;当开挖面顶进距离超过截面一节管长后,管底土体产生一定的回弹,沉降量减小后趋于稳定.
4) 当管径不变而上下翼缘板间距逐渐增大时,土体竖向变形最大值增长率上升,最大值也逐渐增大;当翼缘板位置不变而管径逐渐增大时,管顶土体竖向变形增长率逐渐增大,管底土体变化率基本保持不变,土体变形最大值逐渐增大.
参考文献
| [1] | 贾鹏蛟, 赵文, 关永平, 等. STS新管幕构件抗弯性能试验研究及数值模拟[J]. 中南大学学报(自然科学版), 2016, 47(8): 2738-2746. (Jia Peng-jiao, Zhao Wen, Guan Yong-ping, et al. Numerical simulation and experimental study on flexural behavior of steel tube slab members[J]. Journal of Central South University(Science and Technology), 2016, 47(8): 2738-2746.) |
| [2] | 赵文, 贾鹏蛟, 王连广, 等. 地铁车站STS新管幕构件抗弯承载力试验研究[J]. 工程力学, 2016, 33(8): 167-176. (Zhao Wen, Jia Peng-jiao, Wang Lian-guang, et al. Experimental study on the flexural capacity of steel tube slab members of subway station[J]. Engineering Mechanics, 2016, 33(8): 167-176.) |
| [3] | Ji X B, Ni P P, Barla M, et al. Earth pressure on shield excavation face for pipe jacking considering arching effect[J]. Tunnelling and Underground Space Technology, 2018, 72: 17-27. DOI:10.1016/j.tust.2017.11.010 |
| [4] | Chapman D N, Ichioka Y. Prediction of jacking forces for microtunnelling operations[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 1999, 14(1): 31-41. |
| [5] | Zhen L, Qiao P Z, Zhong J B, et al. Design of steel pipe-jacking based on buckling analysis by finite strip method[J]. Engineering Structures, 2017, 132: 139-151. DOI:10.1016/j.engstruct.2016.11.016 |
| [6] | Pellet-Beaucour A L, Kastner R. Experimental and analytical study of friction forces during microtunneling operations[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2002, 17(1): 83-97. |
| [7] | Sofianos A I, Loukas P, Chantzakos C. Pipe jacking a sewer under Athens[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2004, 19(2): 193-203. |
| [8] | Barla M, Camusso M, Aiassa S. Analysis of jacking forces during microtunnelling in limestone[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2006, 21(6): 668-683. |
| [9] | Zhang H F, Zhang P, Zhou W, et al. A new model to predict soil pressure acting on deep burial jacked pipes[J]. Tunnelling and Underground Space Technology, 2016, 60: 183-196. DOI:10.1016/j.tust.2016.09.005 |
| [10] | Zhang P, Behbahani S S, Ma B S, et al. A jacking force study of curved steel pipe roof in Gongbei tunnel: calculation review and monitoring data analysis[J]. Tunnelling and Underground Space Technology, 2018, 72: 305-322. DOI:10.1016/j.tust.2017.12.016 |
| [11] | Sun Y, Shen S L, Xu Z L, et al. Prediction of lateral displacement of soil behind the reaction wall caused by pipe jacking operation[J]. Tunnelling and Underground Space Technology, 2014, 40: 210-217. DOI:10.1016/j.tust.2013.10.010 |
| [12] | Ren D J, Xu Y S, Shen J S, et al. Prediction of ground deformation during pipe-jacking considering multiple factors[J]. Applied Sciences, 2018, 8(7): 1051. DOI:10.3390/app8071051 |
| [13] | Cheng L Y, Ariaratnam S T, Chen S X. Analytical solution for predicting ground deformation associated with pipe jacking[J]. Journal of Pipeline Systems Engineering and Practice, 2017, 8(3): 4017008. DOI:10.1061/(ASCE)PS.1949-1204.0000267 |
| [14] | 王志国, 赵文, 董驾潮, 等. 带翼缘板圆钢管顶进过程地表变形研究[J]. 东北大学学报(自然科学版), 2021, 42(6): 849-856. (Wang Zhi-guo, Zhao Wen, Dong Jia-chao, et al. Study on ground surface settlement due to pipe jacking of circular steel pipes with flange plates[J]. Journal of Northeastern University(Natural Science), 2021, 42(6): 849-856.) |
| [15] | 刘波, 章定文, 刘松玉, 等. 大断面顶管通道近接穿越下覆既有地铁隧道数值模拟与现场试验[J]. 岩石力学与工程学报, 2017, 36(11): 2850-2860. (Liu Bo, Zhang Ding-wen, Liu Song-yu, et al. Numerical simulation and field monitoring on a large cross-section pipe-jacking underpass traversing existing metro tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(11): 2850-2860.) |
| [16] | 宋建学, 张瑞鑫, 孙宇赫. 机械顶管施工中超挖和地面超载引起的地表沉降规律研究[J]. 建筑科学, 2018, 34(11): 134-139. (Song Jian-xue, Zhang Rui-xin, Sun Yu-he. Research on surface settlement regularity caused by over excavation and ground overloading in mechanical pipe jacking[J]. Building Science, 2018, 34(11): 134-139.) |
