周娟, 伯丽萍
东北大学 理学院，辽宁 沈阳 110819
收稿日期：2022-05-09
作者简介：周娟(1981-)，女，辽宁沈阳人，东北大学副教授。

摘要：研究了具有不确定转移速率的广义马尔可夫跳变系统的耗散模糊控制问题.首先，建立了一个新的李雅普诺夫函数，进而得到了能够保证系统随机可容许并且具有给定耗散性能指标α的有界实引理.利用时滞分割方法和新的不等式去处理函数，从而在一定程度上减少了结论的保守性.其次，基于这些因素，得到了可以利用严格的线性矩阵不等式求解的期望控制器的显式表达式.在设计控制器的过程中，将不确定转移速率分为两种情况，进而得到了两种不同情况下的线性矩阵不等式.最后，一些数值算例反映出本文方法具有较小的保守性和有效性.
关键词：广义系统马尔可夫跳变系统耗散性模糊控制不确定转移速率
Dissipative Fuzzy Control for Singular Markovian Jump Systems with Generally Uncertain Transition Rates
ZHOU Juan, BAI Li-ping
School of Sciences, Northeastern University, Shenyang 110819, China
Corresponding author: BAI Li-ping, E-mail: 2000098@stu.neu.edu.cn.

Abstract: The problem of dissipative fuzzy control for singular Markovian jump systems is studied with generally uncertain transition rates. Firstly, a new Lyapunov-Krasovskii functional is established to develop the new bounded real lemma (BRL) which guarantee the system to be stochastically admissible with given dissipative performance α. Delay decomposition approach and new inequality to deal with functional are used, which can reduce the conservatism to a certain extent. Secondly, based on these ingredients, the explicit expression of the desired controller is obtained by solving a set of strict linear matrix inequalities (LMIs). In the design process of the controller, the generally uncertain transition rates are divided into two cases, and then obtain the LMIs in two different cases. Finally, some numerical examples reflect the less conservatism and effectiveness of the method in this article.
Key words: singular systemsMarkovian jump systemsdissipativityfuzzy controlgenerally uncertain transition rates
广义系统，也称为隐式系统、半状态系统，在生物系统和其他实际系统中都有着广泛的应用^[1].在实际的工业生产过程中，系统的状态在一定程度上会发生突变，在这种情况下很难利用一般系统进行描述.因此，马尔可夫跳变系统近些年受到越来越多的关注.
作为一种特殊的混合系统，马尔可夫跳变系统常常应用于网络控制系统^[2]、经济系统^[3]等实际系统中.但是在解决实际问题时，获取转移速率可能需要花费大量的精力，那么不确定转移速率就有了研究的意义.文献[4]研究了具有不确定转移速率的广义马尔可夫跳变系统的耗散滤波器设计的相关问题.同时，时滞是在建模时不可忽略的因素.通常情况下，时滞是系统不稳定和性能下降的根源，尤其是考虑了时变时滞，会在分析稳定性、设计控制器、设计滤波器等方面增加一定的难度.文献[5]考虑具有时变时滞和参数不确定的广义马尔可夫跳变系统，通过构造一个更全面的李雅普诺夫泛函，建立了新的时滞相关条件，然后通过求解一组严格的线性矩阵不等式，得到所需的滤波器参数.
近年来，由于T-S模糊模型能够代表一类广泛的非线性系统，因此涌现了大量的研究.尤其对于广义T-S模糊模型，得到很多有价值的稳定性分析和控制综合结果.文献[6]研究了具有执行器饱和的马尔可夫跳变系统的非脆弱模糊耗散静态输出反馈控制问题，基于李雅普诺夫理论和凸组合引理，得到了闭环系统随机稳定和耗散的充分条件，最后设计出非脆弱模糊静态输出反馈控制器.文献[7]研究了具有时变时滞和随机增益变化的不确定T-S模糊系统的非脆弱动态输出反馈控制.考虑到T-S模糊模型和模糊控制器不具有相同的隶属度函数这一前提，通过调整扩展耗散概念中的自由权矩阵，进而在一个统一的框架内求解.
耗散性作为无源性和H_∞的推广，具有重要意义.文献[8]研究了一类在T-S模糊规则下的连续时间非线性广义Markov跳变系统的严格异步耗散控制问题.文献[6]考虑了执行器饱和损坏和部分未知转移速率的影响，研究了广义T-S模糊马尔可夫跳变系统的静态输出反馈控制问题.得到了闭环系统不仅是有限时间有界的，而且是耗散的充分条件.控制器增益和吸引域的估计可以通过求解基于线性矩阵不等式的优化问题来解决.基于上述讨论，本文研究具有参数不确定、且转移速率不确定的广义马尔可夫跳变系统的模糊耗散控制问题.
本文主要通过时滞分割法建立了一个新的李雅普诺夫函数，不同于詹森不等式，用保守性较小的新的不等式去处理函数，得到了使系统随机可容许并且具有给定的耗散性能指标α的有界实引理，与文献[9]相比，本文方法能够得到更大的时滞上界.在此基础上，基于两种不同情况下不确定转移速率设计了模糊控制器，此时本文方法同样适用于转移速率完全已知的情况.还考虑了控制器的弹性，并以严格线性矩阵不等式的形式给出.最后，一些例子验证了本文方法较小的保守性和有效性.
1 问题描述符号表示：Rⁿ为n维欧几里得空间；A^T为矩阵A的转置；A^-1为矩阵A的逆；rank(A)为矩阵A的秩；det A为矩阵A的行列式；A>0表示A是正定矩阵；diag{·}表示对角矩阵；||·||表示向量的欧几里得范数；E{·}表示向量或随机过程的数学期望；L₂[0, ∞)表示n维平方可积的函数空间；I是适当维数的单位矩阵；λ_max(A)表示矩阵的最大特征值；*代表对称矩阵中的对称项；定义
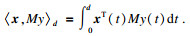
考虑一个由T-S模糊模型描述的不确定时滞广义Markovian跳变系统，模型的第i条规则为: R_i: If ε₁(t) is M_i1 and ε₂(t) is M_i2, …, and ε_p (t) is M_ip, then

(1)

其中：x(t)∈Rⁿ是系统的状态变量u(t)∈R^m是控制输入变量; ω(t)∈R^q是属于L₂[0, ∞)的外部扰动; z(t)∈R^p是受控输出变量; φ(t)是满足相容性条件的初始函数.r是IF-THEN规则数.M_ij(i∈R, j=1, 2, …, l)是模糊集, ε(t)=[ε₁(t), ε₂(t), …, ε_p(t)]^T是前件变量.E是奇异矩阵，且满足rank E=r < n.d(t)是时变连续函数且满足是右连续的Markov过程且在S={1, 2, …, N} 内取值，其模态转移速率矩阵满足
其中并且π_pq≥0(q≠p)是从模态p到模态q的转移速率，并满足
为了方便，对于r_t=p∈S，矩阵A_i(r_t)简写为A_pi，A_di(r_t)简写为A_pdi, 以此类推.
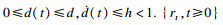
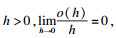
其中：
A_i(r_t), A_di(r_t), B_i(r_t), B_ωi(r_t), C_i(r_t), C_di(r_t), D_i(r_t), D_ωi(r_t)是适当维数的已知矩阵；ΔA_i(r_t), ΔA_di(r_t)ΔB_i(r_t), ΔB_ωi(r_t), ΔC_i(r_t), ΔC_di(r_t), ΔD_i(r_t), ΔD_ωi(r_t)是表示范数有界参数不确定性的未知矩阵，假设其形式为

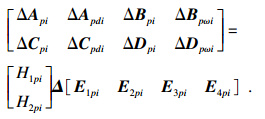(2)

其中：H_1pi, H_2pi, E_1pi, E_2pi, E_3pi, E_4pi是适当维数的已知实矩阵; Δ是未知时变实矩阵, 满足Δ^TΔ≤I.
考虑不确定转移速率问题，系统(1)的转移速率矩阵可以表示为

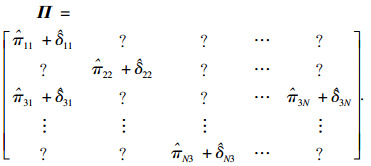(3)

其中：表示已知估值; 表示不确定转移速率的误差; ？表示未知转移速率.
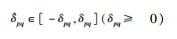
方便起见，对于集合其中:
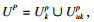
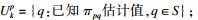
U_uk^p={q: 未知π_pq估计值, q∈S}.
设U_k^p={l₁^p, l₂^p, …, l^p_sp}, s_p∈{1, 2, …, N}, 1≤l_q^p≤N·q=1, 2, …, s_p是转移速率矩阵中第p行的第q个已知元素.另外，如果p∈U_uk^p，设其下界为π_p^d.
对系统(1)采用单点模糊化，乘机推理和中心加权平均解模糊方法, 则全局模糊模型可表示为

(4)

其中，β_i(ε(t))=∏_j=1^pM_ij(ε_j(t)) 是系统关于第i条模糊规则的隶属度函数, 令 接下来，用h_i代替h_i(ε(t)).
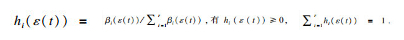
设计模糊控制器：

(5)

令为待确定的常数控制器增益, ΔK_pi摄动矩阵并满足

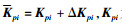
(6)

其中E_5pi是已知实矩阵，Δ_c未知并满足Δ_c^TΔ_c≤I.
根据式(4), 式(5), 得到闭环系统(7).

(7)

定义1^[4]?? 对于任意给定标量d>0, 时滞广义Markov跳变系统

(8)

对于满足d(t)∈[0, d], 如果矩阵(E, A(r_t))和(E, A(r_t)+A_d(r_t))是正则和无脉冲的，则该系统是正则和无脉冲的.
定义2^[4]?? 系统(8)是随机稳定的，如果存在有限值使得下面的不等式成立:
定义3^[4]?? 系统(8)是随机可容许的，如果它是正则的、无脉冲的和随机稳定的.
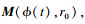
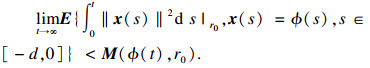定义4^[4]?? 系统(1)是严格(Q, S, R_ω)-耗散, 如果对T≥0和α>0, 在零初始条件下, 满足：
其中是适当维数的实矩阵，且Q，R_ω对称.
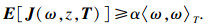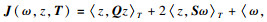
引理1^[6]?? 给定矩阵E, X>0, Y, 如果E^TX+YΛ^T可逆, 则存在矩阵S>0, L, 使得
其中：X, S∈R^n×n, Y, L∈R^n×(n-r), Λ, Θ∈R^n×(n-r)是列满秩矩阵且满足E^TΛ=0, EΘ=0.
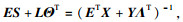
引理2^[6]?? 对于矩阵N₁, N₂∈R^n×n, L∈R^n×p, 正定矩阵Z∈R^n×n时滞d(t)，有
其中：
引理3^[10]?? 对于不确定转移速率矩阵(3), 不等式 成立当且仅当下列不等式成立:
其中
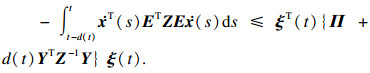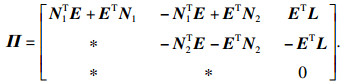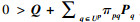
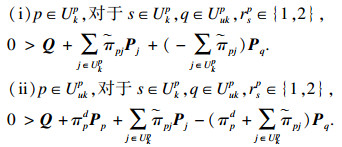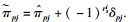
引理4^[6]?? 对于适当维数矩阵Q, H, E, 其中Q是对称的, Q+HFE+E^TF^TH^T < 0成立对于F^TF≤I, 当且仅当Q+εHH^T+ε^-1E^TE < 0成立.
2 主要结论定理1 ??对于给定α>0, d, 系统(7)随机可容许并且严格(Q, S, R_ω)-耗散, 如果存在对称矩阵P_p>0, P₀>0, Q₁>0, Q₂>0, Q₃>0, Q₄>0和S_p使得对任意的p∈S, i∈R，

(9)

其中：

(10)

其中：
证明??首先证明系统(4)是正则无脉冲的.
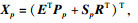
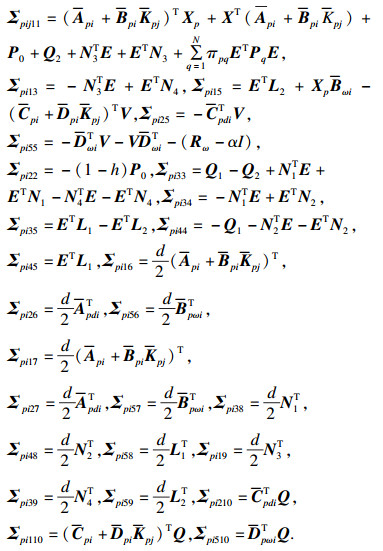方便起见, 令
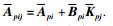
因为rankE=r < n，则一定存在非奇异矩阵G和H使得
且R能重新写成其中Φ∈R^(n-r)×(n-r)是非奇异矩阵.分别用H^T和H去乘Σ_pij11的左右两侧得到对于每 这说明A_p4是非奇异的.
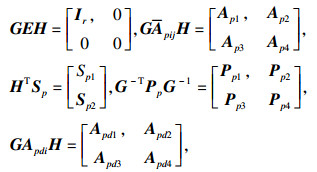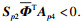
因此对于每个p∈S，矩阵对(E, A_pij)是正则和无脉冲的.再分别用[I I I I 0]和[I I I I 0]^T去乘式(10)的左右两侧，可得到
同理对每个p∈S, 矩阵对(E, A_pij+A_pdi)是正则和无脉冲的.
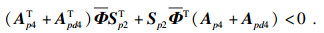接下来考虑随机稳定性.选择Lyapunov-Krasovakii泛函：
设L是随机过程的弱无穷小算子，则对于每个p∈S, 有
令
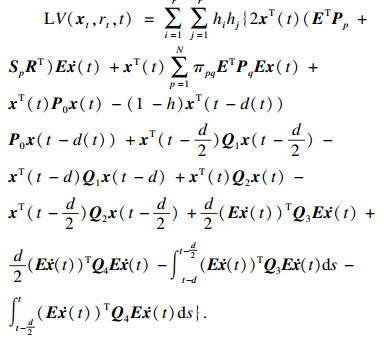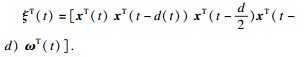
利用引理2, 有如下不等式成立：
其中：
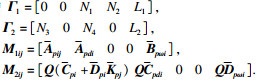
根据Schur补引理, 可以得到
根据不等式(9)可得
因此, 令那么有
利用Dynkin引理可得
进而得到
利用与文献[9]相同的想法可知，存在标量n₂使得
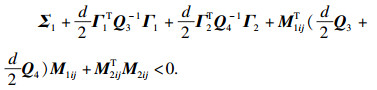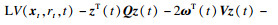
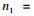
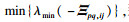
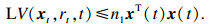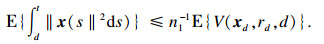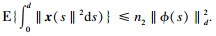
因此，根据V(x_t, r_t, t)}和x(t)的定义可知总存在一个标量ρ使得
然后就有
因此，根据定义1, 系统(6)是随机可容许的.证毕.
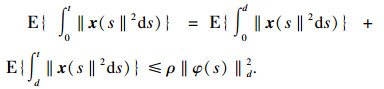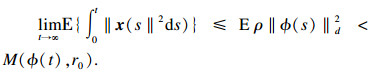基于定理1设计控制器.
定理2 ??对于给定的α>0, d，存在形如式(5)的状态反馈控制器使得系统(6)随机可容许并且严格耗散的，如果存在和S_p使得对任意的p∈S, i∈R,

(11)

(12)

其中:
在这种情况下，控制器增益为
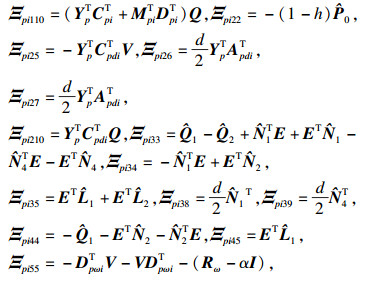证明??根据定理1, 可以得到
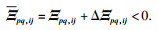
其中：
然后根据式(2)和式(6)，以及引理4得
其中：
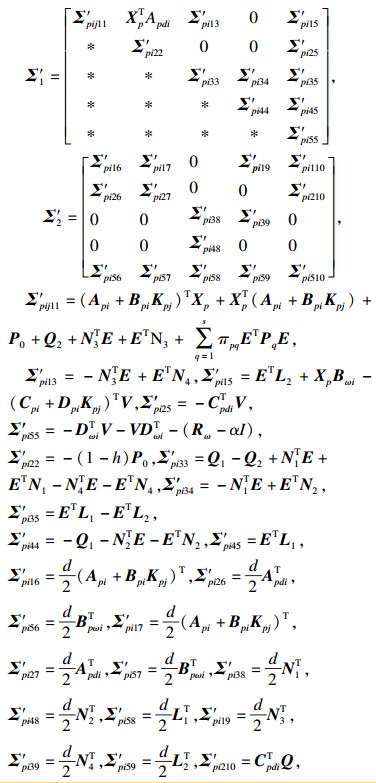利用Schur补引理, 有式(13)成立：

(13)

根据式(11), Y_p是非奇异的, 并且所以令可得到Y_p12=0, 并且Y_p12是对称的, 故可简写为那么Y_p11和Y_p22是非奇异的.故可得到并且是非奇异的.根据引理3, 存在其中P_p>0, 且R是满足E^TR=0的列满秩矩阵，进而得到
用及其转置去乘式(13)左右两侧，并令
并且这表明利用Schur补引理以及引理3得到式(11)和式(12), 证毕.
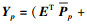
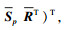
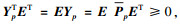
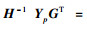
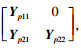
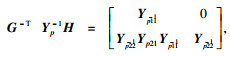
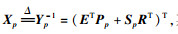
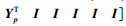
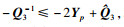
3 数值仿真例1 ??考虑一个文献[11]中的T-S马尔可夫时滞系统，其中E=I, S={1, 2}, T={1}和下列参数:
通过不同的方法得到了对于不同π₁₁的时滞上界，从表 1中可以看出本文的方法能够容纳更大的时滞，从而具有较小的保守性.
表 1(Table 1)

表 1 对于不同π11的时滞上界Table 1 The upper bound of time-delay for different π11 π11 -0.1 -0.3 -0.5 -0.7 -0.9 文献[12] 0.425 2 0.425 0 0.424 8 0.424 6 0.434 4 文献[9] 0.764 9 0.690 4 0.620 8 0.574 0 0.536 8 定理1 0.874 2 0.872 4 0.869 5 0.865 6 0.860 9

表 1 对于不同π11的时滞上界 Table 1 The upper bound of time-delay for different π11

例2 ??考虑如下不确定广义模糊马尔可夫跳变系统，模糊规则：IF ε_p(t) is M_ip THEN
其中：
不确定转移速率矩阵为
其中: 对于
利用MATLAB中的LMI工具箱，能够得到如下的控制器增益：
图 1是马尔可夫跳变模式，利用上面参数计算得到的控制器增益，开环和闭环系统的状态反馈仿真结果如图 2和图 3所示.能够清楚地看到，开环系统的状态是不稳定的，最后闭环系统的状态趋于稳定，由此说明，本文的方法对于不确定转移速率的系统是有效的.
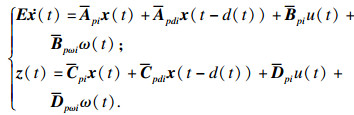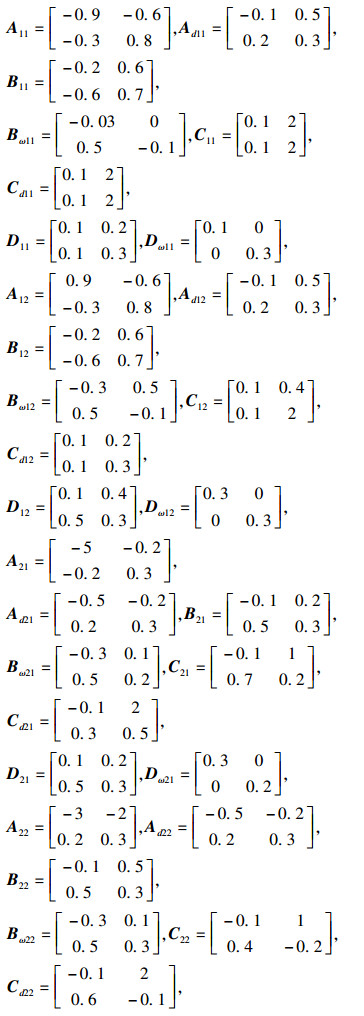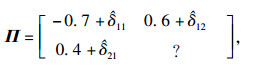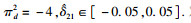
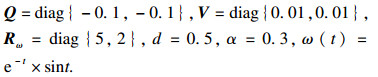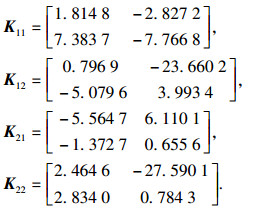图 1(Fig. 1)

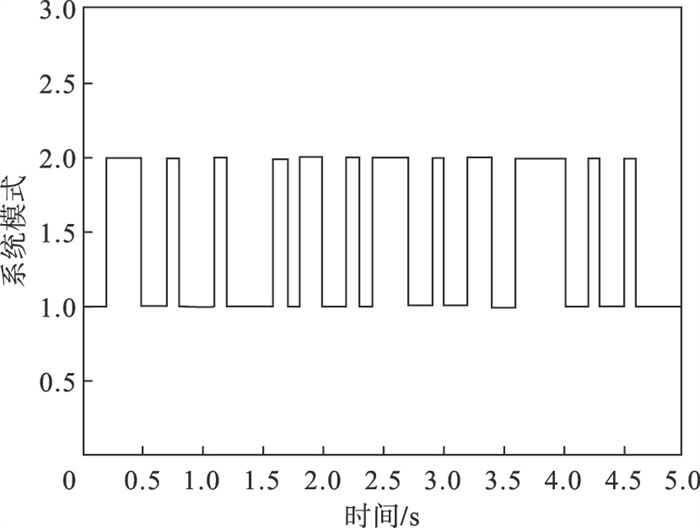图 1 马尔可夫跳变模式Fig.1 Markovian jump modes

图 2(Fig. 2)

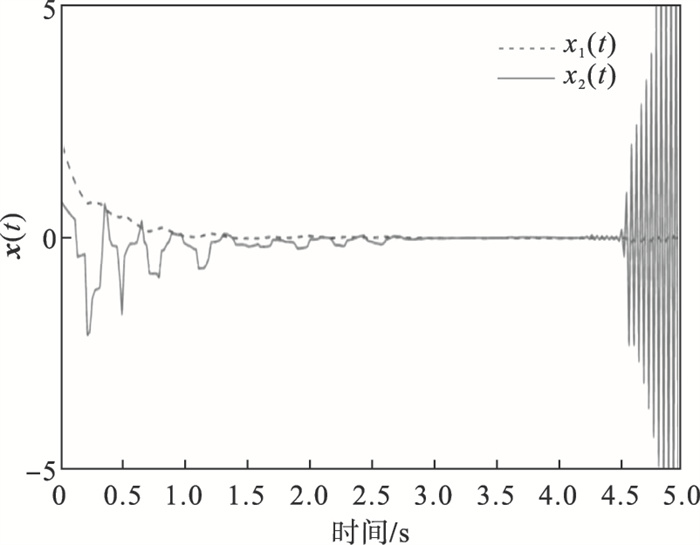图 2 开环系统状态响应Fig.2 State response of open-loop system

图 3(Fig. 3)

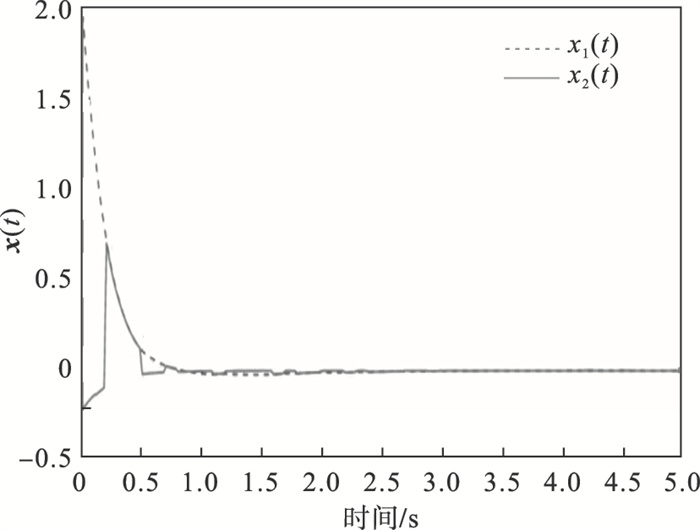图 3 闭环系统状态响应Fig.3 State response of close-loop system

4 结语本文提出了新的具有不确定转移速率的广义不确定马尔可夫跳变系统的模糊耗散控制的充分条件.其中通过时滞分割方法以及新的积分不等式处理函数，在一定程度上减小了保守性.然后在此基础上，得到了两种不同的不确定转移速率情形下的满足给定指标α耗散控制器，同时考虑了控制器的不确定性，且以严格的线性矩阵不等式的形式给出.数值仿真验证了本文的结果具有较小的保守性和有效性.未来，作者将尝试广义模糊系统的非脆弱输出反馈、记忆反馈控制等方面的研究.
参考文献

[1]	Shen A Y, Li L, Li C Y. H∞ filtering for discrete time singular Markovian jump systems with generally uncertain transition rates[J]. Circuits, Systems, and Signal Processing, 2021, 40(7): 3204-3226. DOI:10.1007/s00034-020-01626-0
[2]	Cao Y, Samidurai R, Sriraman R. Stability and dissipativity analysis for neutral type stochastic Markovian jump static neural networks with time delays[J]. Journal of Artificial Intelligence and Soft Computing Research, 2019, 9(3): 189-204. DOI:10.2478/jaiscr-2019-0003
[3]	Song Y, Zhang Y, Yang S, et al. Investigation on stability and controller design for singular bio-economic systems with stochastic fluctuations[J]. Mathematical Biosciences and Engineering, 2021, 18(3): 2991-3005. DOI:10.3934/mbe.2021150
[4]	Fu L, Ma Y C. Dissipative filtering for singular Markov jump systems with generally uncertain transition rates via newintegral inequality approach[J]. Journal of the Franklin Institute, 2018, 355(15): 7354-7383. DOI:10.1016/j.jfranklin.2018.07.023
[5]	Zhuang G M, Xu S Y, Zhang B Y, et al. Robust H∞deconvolution filtering for uncertain singular Markovian jump systems with time-varying delays[J]. International Journal of Robust and Nonlinear Control, 2016, 26(12): 2564-2585. DOI:10.1002/rnc.3461
[6]	管巍. 饱和受限T-S模糊Makov跳变系统的稳定性分析与控制器设计[D]. 秦皇岛: 燕山大学, 2018. (Guan Wei. Analysis and controller design for T-S fuzzy Markovian jump systems with saturation constraints[D]. Qinhuangdao: Yanshan University, 2018. )
[7]	Yu H, Ma Y C, Liu J W. Extended dissipative analysis for uncertain T-S fuzzy system with time-varying delay and randomly occurring gain variations[J]. Journal of the Franklin Institute, 2019, 356: 8542-8568. DOI:10.1016/j.jfranklin.2019.08.025
[8]	杨冬梅, 李达. 非线性广义Markov跳变系统的异步耗散控制[J]. 东北大学学报(自然科学版), 2021, 42(9): 1226-1230. (Yang Dong-mei, Li Da. Asynchronous dissipative control for nonlinear generalized Markov jump systems[J]. Journal of Northeastern University (Natural Science, 2021, 42(9): 1226-1230.)
[9]	Ma Y C, Chen M H. Non-fragile H∞ state feedback control for singular Markovian jump fuzzy systems with interval time-delay[J]. International Journal of Machine Learning and Cybernetics, 2017, 8: 1223-1233. DOI:10.1007/s13042-016-0495-1
[10]	Park I S, Park C, Park P G. Output-feedback stabilization for descriptor Markovian jump systems with generally uncertain transition rates[C]//21st IFAC World Congress on Automatic Control-Meeting Societal Challenges. Berlin, 2020: 2045-2050.
[11]	李丽. 广义Markovian跳变系统的控制问题研究[D]. 沈阳: 东北大学, 2015. (Li Li. Study of control problems for singular Markovian jump systems[D]. Shenyang: Northeastern University, 2015. )
[12]	Wu Z G, Su H Y, Chu J. Delay-dependent filtering for singular Markovian jump time-delay systems[J]. Signal Processing, 2010, 90: 1815-1824. DOI:10.1016/j.sigpro.2009.11.029