
 , 郝元卿1, 唐忠1, 汪锐2
, 郝元卿1, 唐忠1, 汪锐2 1. 东北大学 计算机科学与工程学院,辽宁 沈阳 110819;
2. 中国科学院 沈阳自动化研究所,辽宁 沈阳 110169
收稿日期:2022-05-17
基金项目:国家重点研发计划项目(2019YFB1405302);国家自然科学基金资助项目(61872072)。
作者简介:乔百友(1970-), 男, 甘肃礼县人, 东北大学副教授。
摘要:现有非线性相关分析方法准确性低、计算代价大,因而不适合大规模、高维度台风轨迹数据相关分析.针对这一问题,首次将希尔伯特-施密特独立准则经验估计(Hilbert-Schmidt independent criterion empirical estimation, HSIC0)引入到台风移动轨迹相关研究中,提出了一种基于标准化互信息(normalized mutual information, NMI)结合HSIC0的多因素相关分析方法.该方法首先利用NMI来过滤掉台风数据中相关性低的冗余因素,然后采用XGBoost机器学习模型来剔除掉无效因素,从而降低后续计算代价.在此基础上,采用基于HSIC0的多因素相关分析方法对台风数据进行了分析,挖掘出了相关性较强的台风移动轨迹影响因素组合,从而提高了台风移动轨迹的预测精度.真实台风数据集上的一系列实验结果表明,提出的方法在MSE,MAE,R2指标上均优于NMI、Pearson相关系数、距离相关系数等分析方法.
关键词:台风移动轨迹相关分析多因素HSIC0XGBoost
A Multi-factor Correlation Analysis Method for Typhoon Moving Track Based on NMI and HSIC0
QIAO Bai-you1

 , HAO Yuan-qing1, TANG Zhong1, WANG Rui2
, HAO Yuan-qing1, TANG Zhong1, WANG Rui2 1. School of Computer Science & Engineering, Northeastern University, Shenyang 110819, China;
2. Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110169, China
Corresponding author: QIAO Bai-you, E-mail: qiaobaiyou@mail.neu.edu.cn.
Abstract: The existing nonlinear correlation analysis methods have low accuracy and high computational cost, making them unsuitable for the correlation analysis of large-scale and high-dimensional typhoon track data.To solve this problem, the Hilbert-Schmidt independent criterion empirical estimation (HSIC0) is introduced into typhoon track correlation study for the first time, and a multi-factor correlation analysis method based on normalized mutual information (NMI) and HSIC0 is proposed. The method first uses NMI to filter out redundant factors with low correlation in typhoon data, and then uses XGBoost to eliminate invalid factors, thus reducing the subsequent computational costs.On this basis, a multi-factor correlation analysis method based on HSIC0 is used to analyze typhoon data, and a combination of factors affecting typhoon moving track with strong correlation is mined, thereby improving the prediction accuracy of typhoon moving track.A series of experimental results on real typhoon data sets show that the proposed method outperforms the correlation analysis methods such as NMI, Pearson correlation coefficient, and distance correlation coefficient in indicators such as MSE, MAE, R2.
Key words: typhoon moving trackcorrelation analysismulti-factorHSIC0XGBoost
台风是一种极具威胁的灾害性热带天气系统,产生的强风暴雨和风暴潮会导致大量的直接灾害和次生灾害,是影响我国的主要自然灾害之一[1].准确及时地预测台风移动轨迹,已成为抗风防灾和进行辅助决策的重要手段之一.台风移动轨迹的分析涉及到大气、海洋、地理等诸多环境因素,这些因素之间具有复杂的时空关联关系,呈现出高维非线性特征.因此,设计有效的相关性分析方法对台风轨迹影响因素进行分析,筛选对台风轨迹预测有较大影响的因素组合,就成为进行快速精准台风轨迹预测的关键,也一直是台风相关研究领域的热点之一.
早期对台风影响因素的分析主要利用热力学和动力学知识[2]、复杂地形和海岸线特征,并结合常规天气图和卫星云图等进行分析,这种方法主要依赖于人工经验,需要先验知识积累.随着大数据和基于数据驱动预测方法的快速发展,人们发现相关分析可以更高效地发现事物间的内在关联,对之的关注愈发广泛[3-4],逐渐应用到台风移动轨迹的分析预测中.黄奕武等[5]利用相关系数方法分析了西北太平洋和南海台风的环境场预报变量与路径预报误差的相关性,并采用线性回归分析方法建立了预测模型,在24 h预报中取得了较好效果.但该方法主要用于分析数据之间的线性相关性,不适合分析各因素间的非线性相关性.为此,研究者提出了一系列非线性相关分析方法,主要包括互信息方法[6]、距离相关(distance correlation, DC)分析方法[7]和基于希尔伯特-施密特独立准则经验估计(Hilbert-Schmidt independent criterion empirical estimation, HSIC0)[8]的相关分析方法.
互信息方法定义了两个变量之间的最大信息系数,用它可以衡量两个变量之间的非线性相关性,应用领域比较广泛.Chen等[9]通过最大化隐变量和生成图片之前的互信息,可以学习到数据的局部特征,从而调控生成图片的样式.胡兵兵等[10]在CatGAN的基础上增加了互信息约束,提出一种生成对抗网络分类模型,该模型可以通过隐变量控制生成图片的类别,对数据增强具有一定意义.Vinh等[11]提出了标准化互信息(normalized mutual information, NMI)的概念,来更好地刻画变量之间的非线性关系,并提出了基于NMI的特征选择算法.
距离相关分析方法主要用特征函数的距离来刻画两个随机变量之间的非线性关系,通过距离协方差和距离相关系数来度量非线性关系,并被广泛应用到了相关分析领域.王黎明等[12]基于距离相关系数和SVR提出一种PM2.5浓度分析预报方法,主要利用距离相关系数来筛选出重要因素,并借助SVR实现了精准预测.Wen等[13]提出一种加权距离相关系数方法wdCor,用于评估遗传标记与影像数据之间的相关性,解决了高维度数据的相关性分析问题.然而,距离相关系数方法的时间复杂度较高,对于大规模数据,其计算效率较低[14].
HSIC0在理论上已经被证明具有收敛速度快、计算简单的优点,能够刻画类之间的非线性关系,目前受到了越来越多的关注.宋成宝等[15]利用HSIC分析了传感器之间的相对独立性,并依据信息最大化原则提出了传感器配置优先级排序算法,建立了日光温室传感器优化配置策略.李柏松等[16]提出了基于HSIC的格兰杰因果分析方法,并应用于空气质量指数和气象时间序列的非线性因果关系分析中.张晓琴等[17]在HSIC0的基础上通过增加标准化处理实现了类之间相关性度量,并验证了HSIC0求解非线性相关性的有效性.
从上面的分析可以得出,现有的各种基于线性相关分析的方法不能很好地刻画台风轨迹数据因素之间的非线性关系.而基于互信息、距离相关系数等分析方法虽然可以分析变量间的非线性相关关系,但存在计算效率不高、精度有限,且不能很好地支持多因素组合分析的问题,因而无法完全满足台风轨迹这种大规模、高维度数据的多因素相关分析.HSIC0方法虽然在计算效率上具有一定的优势,但目前鲜有在台风相关领域的应用.
针对现有方法存在的问题,本文将HSIC0引入到台风轨迹影响因素的分析中,提出了一种NMI结合HSIC0的台风移动轨迹多因素相关分析方法.该方法综合采用多种技术手段,实现了对台风轨迹数据的多因素组合分析.首先,采用基于NMI的过滤方法过滤掉台风轨迹数据中相关性低的冗余因素,然后采用基于XGBoost机器学习模型的包裹技术来剔除掉无效因素,从而降低整个数据维度,减轻后续分析计算代价.在此基础上,基于HSIC0多因素相关分析结果,通过分层聚簇方式挖掘出相关性较强的台风移动轨迹影响因素组合,从而实现了多因素的组合分析与特征选择,提高了模型的预测精度.真实台风轨迹数据集上的一系列实验结果表明,本文提出的方法在MSE, MAE, R2等评价指标上均优于NMI, Pearson相关系数[18]、距离相关系数等相关分析方法.
1 相关技术1.1 标准化互信息标准化互信息(NMI)主要用于度量两个类之间的相似程度,其取值范围为[0, 1],值越大表示类之间越相似.下面首先介绍信息熵、互信息的计算方法,然后给出NMI的计算公式.
信息熵是一种有效刻画变量中所包含信息含量的度量工具,对于包含n个变量的数据序列X=(x1, x2, …, xi, …, xn)而言,假设其概率分布为P(X=xi)=pi,i=1, 2, …, n.则H(X)的计算见式(1).
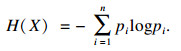 | (1) |
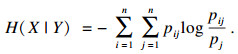 | (2) |
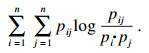 | (3) |
 | (4) |
1.2 XGBoost模型XGBoost[19]是基于梯度提升决策树(gradient boosting decision tree, GBDT)而改进的一种机器学习算法.它通过将多个弱学习器的预测结果进行求和来得到样本的最终预测值,具有计算效率高和防止过拟合的特性.本文采用由k棵分类回归树(classification and regression tree, CART)作为弱学习器的XGBoost模型来进行台风路径的预测,其预测值?i的计算见式(5).
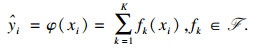 | (5) |
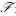
XGBoost算法的目标函数L(φ)由两个部分组成,其计算方法见式(6).其中,l(yi, ?i)是损失函数,用来描述预测值?i与实际值yi之间的拟合程度;Ω(fk)为模型的惩罚项,用来防止模型过拟合.惩罚项Ω(fk)的计算见式(7).
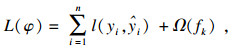 | (6) |
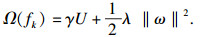 | (7) |
2 基于NMI结合HSIC0的多因素相关分析方法本文着眼于台风移动路径影响因素分析与特征选择问题,致力于通过多因素相关分析来得到相关度最大的因素组合.基于NMI结合HSIC0的多因素相关分析方法总体框架如图 1所示.
图 1(Fig. 1)
 | 图 1 基于NMI和HSIC0的多因素相关分析方法总体框架Fig.1 Overall framework of multi-factor correlation analysis method based on NMI and HSIC0 |
首先对台风相关数据进行标准化,利用NMI进行初步过滤,去除相关性较低的冗余因素;然后利用XGBoost机器学习预测模型,采用前向排除和递归删除的策略,剔除对预测起反向作用的无效因素,从而实现特征降维.在此基础上,基于HSIC0对剩余因素进行聚簇分析,从而得到相关性最大的因素组合,并作为预测模型的最终特征,下面详细介绍各组成部分.
2.1 数据标准化为了消除不同量纲的数据特征对分析和预测的影响,本文采用小数定标标准化方法对台风相关数据进行预处理.若F为包含m个特征(因素)的台风数据集,则F={(f1j, f2j, …, fmj)|j=1, 2, …, n},n为样本数,fij表示第i个因素的第j个样本值.当对因素fi(i=1, 2, …, m)进行标准化处理时,首先需要确定该因素样本数据小数点移动的位数ki,其计算方法见式(8).确定ki后,便可通过式(9)将因素集合中的样本元素fij标准化处理成fij′.
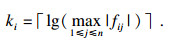 | (8) |
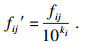 | (9) |
图 2(Fig. 2)
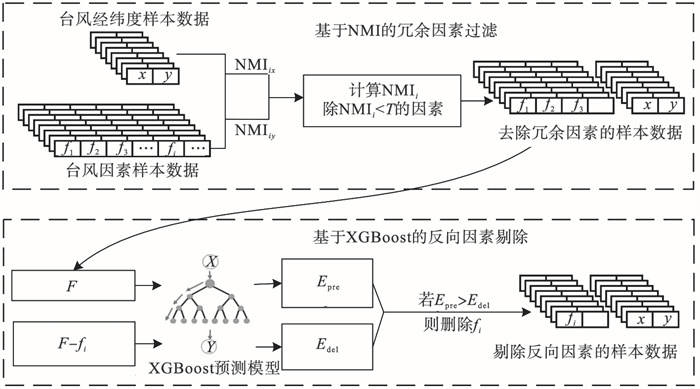 | 图 2 基于NMI和XGBoost的因素降维处理流程Fig.2 Factor dimension reduction process based on NMI and XGBoost |
2.2.1 基于NMI的冗余因素过滤不同于传统相关系数,NMI值能够有效刻画两个变量之间的线性和非线性关系,因此能够较好地刻画台风数据集中因素之间的相关性,这也是本文选择利用NMI来过滤台风数据中冗余因素的原因.
设集合L={(xj, yj)|j=1, 2, …, n}为台风经纬度样本数据集,其中,n为样本数,xj和yj分别代表经度和纬度的第j个样本.则对于每个因素fi(i=1, 2, …, m)因素,使用式(4)可以计算出每个台风因素fi与经度x和纬度y之间的标准化互信息值NMI(fi; x)和NMI(fi; y),分别记作NMIix和NMIiy.这样可以得到因素fi与台风轨迹间的NMI值NMIi,来表征该因素fi与经/纬度的相关程度:
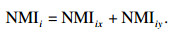 | (10) |
2.2.2 基于XGBoost的反向因素剔除虽然过滤阶段利用NMI方法过滤掉了低于给定阈值T的因素,但剩余因素中可能还存在对台风路径预测没有贡献或者起反向作用的因素,为此本文利用XGBoost模型来进行无效因素的剔除,从而进一步降低特征维度.
经第一阶段处理得到的台风轨迹特征集合F,按照NMI值从小到大进行排序,然后利用给出的XGBoost学习模型,根据预测误差变化来评估每个特征对预测结果的影响,并根据评估结果删除对预测贡献较小甚至起反作用的特征.这样能够在有效减小特征数量的同时确保预测模型的准确度,具体步骤如下:
1) 采用滑动窗口方法对F集合中特征所对应的台风样本数据进行划分,将前k个时刻的特征样本数据作为输入,k+t时刻的台风移动位置(经纬度)数据作为标签,利用XGBoost模型进行训练和预测,采用欧氏距离作为预测效果的衡量指标,计算出相应的预测误差Epre;
2) 按照顺序从F中去掉一个因素(特征)fi,按照步骤1)的方式重新划分数据,并训练XGBoost模型进行台风移动位置(经纬度)的预测,同理得出删除该特征因素后的预测误差Edel;
3) 如果Edel < Epre,则将因素fi从F中删除,赋值Epre=Edel,回到步骤2)继续执行下一次筛选,逐次缩减集合F中的特征数量,直到每个特征都被筛选过一次为止.
算法1为基于NMI和XGBoost的因素降维算法描述.其中,1~8行是计算每个因素与经纬度之间的NMI值,9~12行过滤NMI值低于阈值的冗余因素;13~19行则对NMI排序后的特征因素集进行第二阶段的筛选,利用XGBoost模型剔除对预测起反向作用的无效因素;最终返回降维后的因素集合.
与传统特征选择方法不同,本算法在第一阶段先基于NMI过滤冗余因素,在第二阶段将排除某个因素前后XGBoost模型预测误差作为评价指标,递归去除起反向作用的因素,保证了降维后的因素集合冗余小,且具有较强的相关性.两阶段的因素降维能够有效降低下一阶段多因素分析的计算代价.
算法1基于NMI和XGBoost的因素降维
输入:F(全体因素数据集),L(当前时刻台风经/纬度数据集), T(NMI阈值)
输出:F′(经过降维处理后的数据集)
begin
1. for each fi in F do
2.???? H(fi); //计算因素fi信息熵
3.???? H(x); H(y); //计算经/纬度信息熵
4.???? H(fi|x); H(fi|y); //计算fi与经/纬度的条件熵
5.???? I(fi; x); I(fi; y); //计算fi与经/纬度的互信息值
6.???? NMIix←NMI(fi; x); NMIiy←NMI(fi; y);
????????//计算因素fi与经/纬度的标准化互信息值
7.???? NMI_ll[]←NMIi=NMIix+NMIiy;
????????//记录因素fi与经/纬度的标准化互信息值
8. end for
9. for each NMIi in NMI_ll[] do
10.???? if NMIi < T then
11.???? delete NMIi; //过滤低于阈值的因素
12. end for
13. NMI_ll[].sort(); //对NMI值升序排序
14. for each fi in F do
15.????Epre←XGB_error(F); //删除fi前的预测误差
16.????Edel←XGB_error(F-fi); //删除fi后的预测误差
17.???? if Epre>Edel then
18.?????? delete fi; //筛选剔除反向因素
19. end for
20. F′←F;
21. return F′;
end
2.3 基于HSIC0的多因素相关分析分析台风路径影响因素时,现有工作往往着眼于各因素对台风路径的单一影响,从中选出前k个因素作为预测模型的特征,并未考虑多个因素组合在一起后对台风路径预测的影响.实际上,考虑多个因素组合整体对台风移动路径预测的影响,更有助于台风特征的筛选,也更有利于提高台风移动路径的预测精度.本文利用聚类思想,提出了一种基于HSIC0的多因素相关分析方法,利用核函数将元素映射到再生希尔伯特空间,通过分析类间的非线性相关性,挖掘出对台风轨迹影响较大的因素组合.
设台风数据集Z=(F, L),L=(x, y)为台风位置信息.定义两个非线性映射:?: F→P, φ: L→Q,P和Q分别为F和L的再生希尔伯特空间,相应的核函数分别为k(fi, fj)和s(li, lj).Γ和Λ分别为F和L的博雷尔集,Pfl是(F×L, Γ×Λ)上的联合分布,观测值{(f1, l1), (f2, l2), …, (fn, ln)}独立同分布于Pfl,样本数量为n.由文献[20]可知,HSIC0计算方法见式(11),其中,K, S, H∈Rn×n.
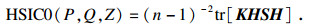 | (11) |
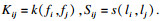
HSIC0的值代表了类F和类L之间的非线性相关性,HSIC0等于0时说明两个类相互独立,值越大表示关联性越强.显然,通过求取HSIC0值可以度量不同特征组合F与台风轨迹L的相关性,从而找到对台风轨迹影响较大的因素组合.考虑台风因素之间的非线性关系,采用高斯径向基函数(radial basis function, RBF)来计算核矩阵.RBF核函数如式(12)所示.
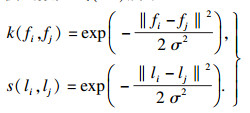 | (12) |
虽然利用HSIC0可以计算出台风因素组合与台风移动轨迹之间的相关度,但由于台风因素维度高,如果计算每种因素组合,计算复杂度较高,影响算法效率.本文结合层次聚类思想,提出基于HSIC0的多因素相关分析算法(HSIC0_CLU),该算法在相关性和计算复杂度之间取折中,放弃计算所有可能的因素组合,而是采用迭代计算的方式,每次仅对相关性最大的组合进行扩增,直到达到给定因素数量要求,算法处理流程如图 3所示.从图中可以看出,该算法采用类似层次聚类的迭代求解过程.第一次迭代中,计算每个因素与台风经纬度集合之间的HSIC0值,并选择HSIC0值最大的因素f3(假设f3的HSIC0值最大)作为结果集中的第1个元素;第二次迭代中,将剩余的每个因素分别加入到结果集中形成多个因素组合,并求解每个因素组合与台风经纬度组合之间的HSIC0,将HSIC0值最大的因素组合(f3, f25) 作为结果集;依此方式继续迭代,每次迭代都使得结果集增加1个因素,直到满足相应的阈值为止.最终结果集中的因素组合即为相关性最强的因素集合.
图 3(Fig. 3)
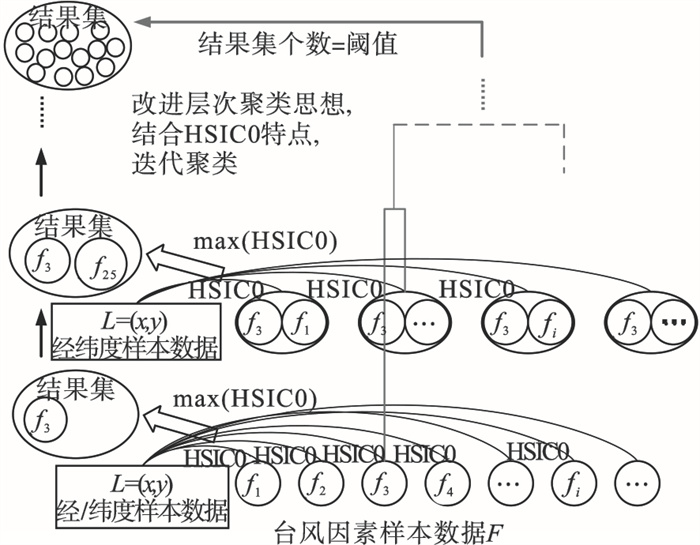 | 图 3 基于HSIC0的多因素相关分析流程Fig.3 Multi-factor correlation analysis based on HSIC0 |
迭代过程中,可以设置迭代次数阈值来降低迭代次数,减少计算时间.假设迭代次数阈值为n,则一共需要迭代n次,每次迭代因素组合中会增加一个新的因素,因此,当迭代n次后,该算法会将n个因素聚到一个组合当中,完成聚类过程.阈值选取可以采用文献[12]中方法进行计算,见式(13).
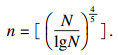 | (13) |
算法2为基于HSIC0的多因素相关分析算法的具体描述.算法2的1~2行计算阈值和进行计数器初始化,3~19行外层循环负责控制聚类结果集中的因素个数,6~16行内层循环负责分析出相关性最强的因素组合,20行返回聚类结果.其中,8,9行根据RBF核函数计算公式计算因素对应的核矩阵,第10行利用式(11)计算组合因素(候选结果集)与经纬度之间的HSIC0.
算法2 ??基于HSIC0的多因素相关分析算法
输入:F(联合因素降维后的因素数据集),L(当前时刻台风经纬度数据)
输出:Res(基于HSIC0的多因素聚类分析结果集)
begin
1. ??N←F.length; n←(N/logN)4/5; //聚类组合阈值
2. ??count←n; //计数器
3. ??while count!=0 do
4.???? hsic0_max←0 //最大HSIC0值
5.???? hsic0_max_f; //最大HSIC0值对应因素
6.???? for each f in F do
7.?????? Res←f; //将因素f放入拟结果集
8.?????? K←RBF(Res); //计算拟结果集的高斯核矩阵
9.?????? S←RBF(L); //计算经纬度集合的高斯核矩阵
10.?????? hsic0_temp←HSIC0(K, S);
//计算拟结果集与L的HSIC0值
11.?????? if hsic0_temp>hsic0_max do
12.???????? hsic0_max←hsic0_temp;
13.???????? hsic0_max_f←f;
14.?????? end if
15.?????? delete f from Res; //从拟结果集中删除因素f
16.???? end for
17.???? Res←hsic0_max_f; //本轮最优因素放入结果集
18.???? count--;
19.?? end while
20.?? return Res;
end
3 性能评价为了验证本文提出的基于NMI和HSIC0的台风移动轨迹多因素相关分析方法的有效性,在真实数据集上进行了一系列实验,并和现有的Pearson相关系数、非线性相关系数NMI和距离相关系数DC等相关分析方法进行了对比,下面就具体实验环境及对比结果展开详细分析.
3.1 实验数据本文实验使用的数据来自中国气象局(China Meteorological Administration, CMA)提供的台风最佳路径数据集[21-22](https://tcdata.typhoon.org.cn/zjljsjj_zlhq.html)和美国国家环境预报中心(National Centers for Environmental Prediction, NCEP)提供的每6小时再分析资料[23-24](http://poles.tpdc.ac.cn/zh-hans/data/2793ba69-7122-4a62-876b-647a1a50a121/).
台风轨迹数据集所覆盖的时间范围是1990—2018年每年的7~10月,内容包含西北太平洋和中国南海区域所产生的台风移动轨迹数据、大气环境数据、海洋环境场数据三部分,共计302个因素,数据样本数量3 428,部分台风移动轨迹数据如图 4所示.
图 4(Fig. 4)
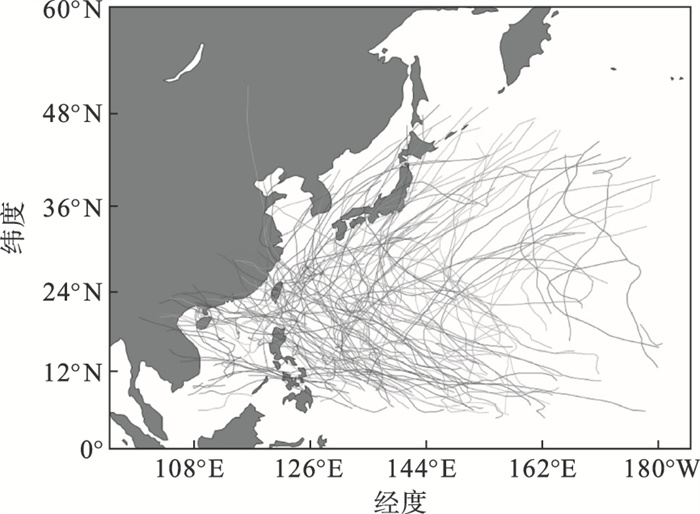 | 图 4 部分台风移动轨迹数据展示Fig.4 Demonstration of some typhoon moving track data |
3.2 实验环境及评价指标实验环境由5台IBM PC机架式服务器组成的Spark集群构成,其中1台为管理节点,其余为计算节点.每台服务器的配置为E5-2620 CPU(6核,2.0 GHz), 32 GB内存和6TB的硬盘,每台服务器都安装了CentOS 7.0操作系统、Python 3.6运行环境和相应的算法模块.
本文使用常用评价指标来评价几种方法的预测误差,主要包括MSE(均方误差)、RMSE(均方根误差)、MAE(平均绝对误差)、MAPE(平均绝对百分比误差)、SMAPE(对称平均绝对百分比误差)和R2(确定系数),具体计算公式为
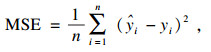 | (14) |
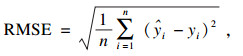 | (15) |
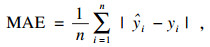 | (16) |
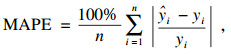 | (17) |
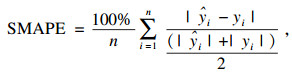 | (18) |
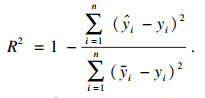 | (19) |
3.3 实验方法和结果分析本文采用上述真实数据集,对提出的方法进行了实验研究,并与现有的Pearson,NMI和距离相关系数(DC)等方法进行了对比,分别采用XGBoost和SVR机器学习模型进行了验证.下面将具体描述所用模型的参数设置和实验结果分析.
3.3.1 模型参数设置及数据划分方式针对模型的参数设定,本文依据已有经验知识设定了多组参数,并设计了系列实验对比模型在不同参数下的降维效果与拟合情况,最后选取具有最好降维效果和拟合能力的一组,具体如下:
1) 因素降维阶段XGBoost模型参数:迭代训练次数设置为30,最大深度为5,γ值取默认值0,随机采样比例设置为0.8,正则化项参数分别设置为1和0.8,学习率为0.3.
2) 实验验证阶段XGBoost模型参数:除模型学习率调整为0.1外,其他与因素降维阶段一致.
3) 实验验证阶段SVR模型参数:惩罚项函数设置为1,指定核函数为高斯核径向基函数,其系数γ设置为“auto”,其他参数使用默认值.
预测模型采用样本数据集划分如下:
1) 因素降维阶段XGBoost模型:样本的80%作为训练数据,其余20%作为测试数据.
2) 预测验证阶段XGBoost和SVR模型:样本的70%作为训练数据,其余30%作为测试数据.
3.3.2 实验结果分析1) 消融实验.本文提出的方法分为因素降维和多因素相关分析两部分,本文设计消融实验对各阶段方法进行测试,共设计了4种方法:HSIC0(基于HSIC0的单因素分析)、NX_HSIC0(因素降维+基于HSIC0的单因素分析)、HSIC0_CLU(多因素聚类分析)和NX_HSIC0_CLU(因素降维+多因素聚类分析).4种方法分别从包含300个因素的数据集中分析筛选35个因素,利用XGBoost模型和SVR模型分别进行台风移动路径的预测,根据预测结果得到各项指标上的得分.
图 5为XGBoost预测模型下的结果对比,对于单因素分析方法HSIC0,单独增加因素降维阶段后(NX_ HSIC0),在MAE指标上表现最好,误差降低了17%;单独增加多因素聚类分析阶段(HSIC0_CLU)后,MAPE和SMAPE误差均降低了26%.而同时增加两个阶段的处理后,即本文提出的结合两阶段的方法NX_HSIC0_CLU,在4种方法中表现最好,除R2指标得分基本持平外,MSE, RMSE, MAE, MAPE, SMAPE各项指标均明显降低,预测误差最多可降低50%,这充分证明了本文算法的有效性.
图 5(Fig. 5)
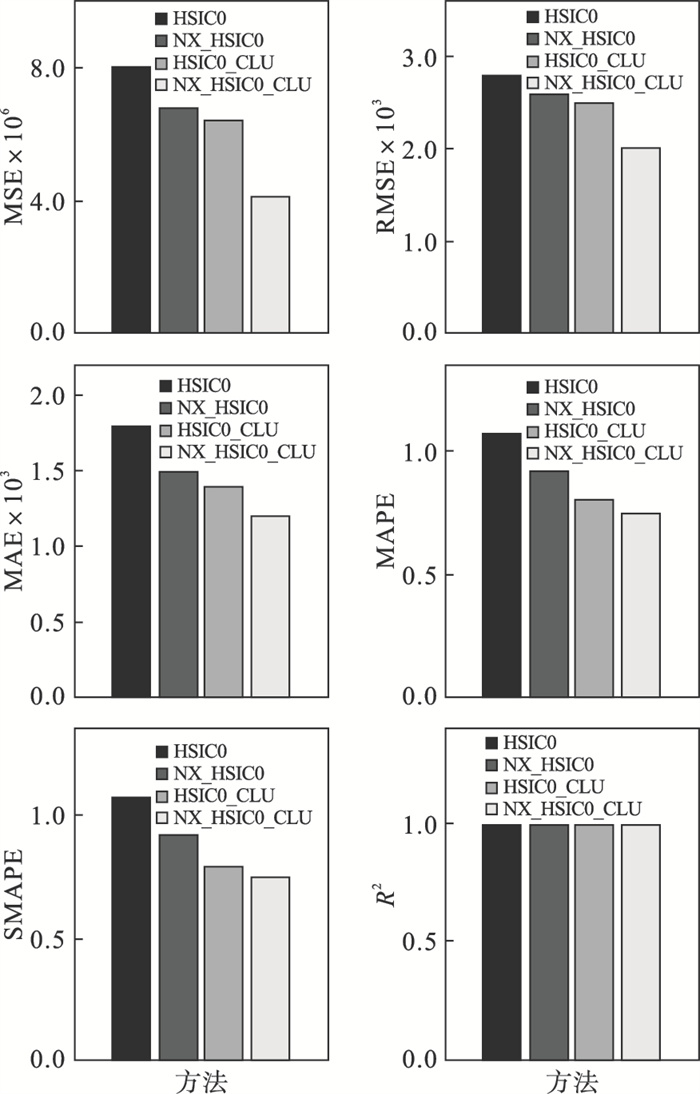 | 图 5 XGBoost预测模型下4种方法的对比Fig.5 Comparison of four methods under XGBoost |
图 6是在和图 5相同条件下,基于SVR机器学习模型预测的结果,从图中可以看出,分别添加因素降维和聚类分析后,NX_HSIC0方法和HSIC0_CLU在各指标上的表现比HSIC0方法略有提升但基本持平.结合两阶段的NX_HSIC0_CLU方法在R2上的得分提高至1.56倍,同样证明了本文提出的方法是有效的,但在MSE等其他指标上的提升效果不明显,误差最多能减少7%.因此,综合来看,本文提出的多因素相关分析方法在SVR模型上的预测效果总体不如XGBoost模型.
图 6(Fig. 6)
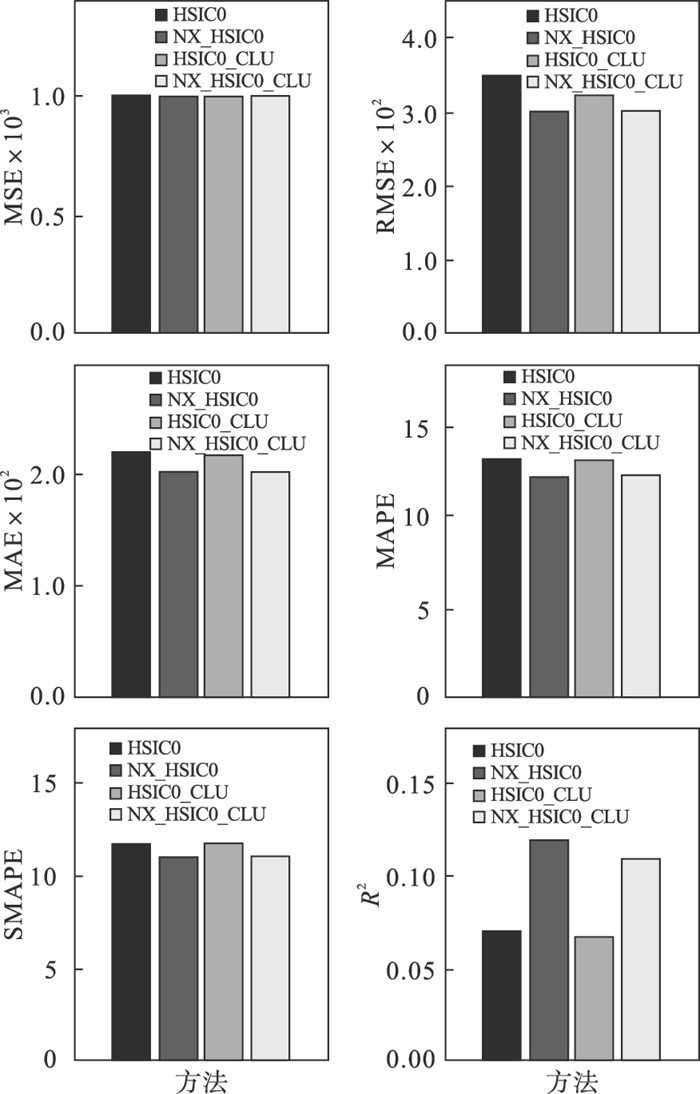 | 图 6 SVR预测模型下4种方法的对比Fig.6 Comparison of four methods under SVR |
2) NX_HSIC0_CLU算法效果分析.为了进一步对比分析本文提出方法的效果,在前述数据集上,分别采用NX_HSIC0_CLU(本文方法)、Pearson(Pearson相关系数)、NMI(基于互信息的相关分析方法)、DC(距离相关系数)和HSIC0(基于HSIC0的单因素分析)共5种方法进行台风路径因素的挖掘分析.每种方法均从300个台风因素中挖掘出35个特征,进行台风移动路径的预测测试.表 1为采用XGBoost预测模型时5种方法在6个指标上的得分情况.可以看出,NX_HSIC0_CLU方法在MSE, RMSE, MAE, MAPE和SMAPE指标上的得分都是最好的,R2值略小于Pearson方法.与其他4种方法中指标得分最好的方法相比,NMI_HSIC0_CLU方法分别降低MSE约50%,RMSE约26%,MAE约20%,MAPE和SMAPE约10%;R2值接近最佳值.整体上来看,本文的NX_HSIC0_CLU方法明显好于其他方法.
表 1(Table 1)
| 表 1 XGBoost预测模型下5种方法对比 Table 1 Comparison of five methods under XGBoost |
为了不失一般性,本实验将上述5种分析方法筛选的35个因素分别作为特征输入,用SVR机器学习模型进行了台风轨迹预测,5种分析方法在不同指标上的得分情况如表 2所示.
表 2(Table 2)
| 表 2 SVR预测模型下5种方法的效果对比 Table 2 Comparison of five methods under SVR |
从表 2中可以观察到,在使用SVR作为预测工具时,5种算法在6个指标上的得分都是最好的.与其他4种方法中指标得分最好的方法相比,NMI_HSIC0_CLU方法的MSE得分基本一致,RMSE,MAE,MAPE和SMAPE均降低了3%~5%,R2值则增长了20%.整体来看,NMI_HSIC0_CLU方法的表现依然是最好的,这说明本文提出的相关分析方法具有良好的准确度,明显优于其他4种方法.
综合表 1和表 2可以看出,NMI_HSIC0_CLU方法在XGBoost模型上的各项指标得分,相较于在SVR模型上的得分,下降幅度均达到90%以上,R2得分也是SVR模型的9倍,这说明XGBoost模型更适合于大数据量下的预测.
3) 因素降维阶段对相关分析方法的影响.为了进一步验证因素降维对相关分析的影响,对5种相关分析方法采用联合因素降维处理前后的预测效果进行了比较,预测模型采用XGBoost,具体结果如表 3所示.表中NMI,Pearson,DC,HSIC0和HSIC0_CLU使用未经因素降维处理的数据集,即需要从300个因素中分析35个因素;表中NX_NMI, NX_Pearson, NX_DC, NX_HSIC0和NX_HSIC0_CLU则增加因素降维处理,即需要从降维后的200个因素中分析挖掘出35个因素.
表 3(Table 3)
| 表 3 XGBoost预测模型下因素降维效果对比 Table 3 Comparison of factor dimension reduction under XGBoost |
从表 3可以看出,NX_HSIC0_CLU,NX_HSIC0和NX_DC由于使用了经过因素降维处理的数据集,在MSE, RMSE, MAE, MAPESMAPE指标上的得分降低,表现最好的为NX_DC方法,在MSE上的得分降低至DC方法的37%,RMSE, MAE, MAPE和SMAPE值也都降低至50%左右;而R2得分则都有所提升,表示处理后的因素集预测效果更优.同时,NX_HSIC0_CLU的MSE,RMSE,MAE,MAPE和SMAPE指标得分都是最好的,只有R2值排在第二位,再次说明NX_HSIC0_CLU方法可以提高台风路径预测精度.
此外,通过上述对比可以看出,NMI和Pearson两个方法在联合因素降维处理前后数据集上的表现基本一致,各指标值变化幅度在5%左右,说明本文提出的因素降维方法对NMI和Pearson效果并不明显,但对DC, HSIC0和HSIC0_CLU三种方法起到了很好的辅助作用.同时证明,无论是否使用经联合因素降维处理的数据,本文提出的NX_HSIC0_CLU方法效果均优于其他方法.
将SVR作为预测模型时,几种方法在各项指标上的得分如表 4所示.5种方法的效果变化并不明显,各指标上的得分基本持平,DC, HSIC0, HSIC0_CLU的预测效果略有提升,其中,因素降维对HSIC0方法的提升效果最为明显,R2得分可提升至1.7倍.整体来看,NX_HSIC0_CLU方法的各项指标得分最佳.这也证明了本文提出的因素降维方法对于DC, HSIC0_CLU和HSIC0方法具有良好效果.
表 4(Table 4)
| 表 4 SVR预测模型下因素降维效果对比 Table 4 Comparison of factor dimension reduction under SVR |
4 结语本文将HSIC0引入到台风移动轨迹相关因素分析中,提出了一种NMI结合HSIC0的台风移动轨迹多因素相关分析方法.该方法首先基于NMI对预处理后的原始因素集进行初步过滤,然后利用XGBoost模型剔除反向因素,从而实现因素降维;在此基础上,基于HSIC0实现了多因素相关分析.真实台风相关数据集上的实验结果表明,本文提出的多因素相关分析方法在MSE,MAE等各预测精度评价指标上优于NMI,Pearson,DC等传统相关分析方法.这是由于该方法充分结合了过滤与筛选两阶段降维,剔除了相关性弱和起反向作用的因素,并采用基于相关性的聚类分析技术,因而选出了相关性较大的组合,取得较优的效果.
考虑到执行时间因素,本文提出的聚类分析方法并没有逐一计算所有可能的因素组合,同时整个算法相对来说还是比较复杂,还存在着一定的优化空间.后续将考虑增加对因素内部相关性的分析,并继续对算法进行优化和完善,以进一步提高算法的性能.
参考文献
| [1] | Zhang L, Zhu H, Liu J. Characteristics of tropical cyclones formed in the Eastern Pacific Northwest[J]. Natural Hazards, 2021, 106(3): 2619-2633. DOI:10.1007/s11069-021-04557-4 |
| [2] | Huang X Y, Jin L. An artificial intelligence prediction model based on principal component analysis for typhoon tracks[J]. Chinese Journal of Atmospheric Sciences, 2013, 37(5): 1154-1164. |
| [3] | Vazirani V V. Approximation algorithms[M]. Berlin: Springer-Verlag, 2001. |
| [4] | Mayer-Schonberger V, Cukier K. Big data: a revolution that will transform how we live, work, and think[M]. New York: Eamon Dolan/Houghton Mifflin Harcourt, 2013. |
| [5] | 黄奕武, 高拴柱, 钱奇峰. T639台风预报误差与环境场变量的相关分析和回归分析[J]. 气象, 2016, 42(12): 1506-1512. (Huang Yi-wu, Gao Shuan-zhu, Qian Qi-feng. Correlation and regression analysis of typhoon forecast errors and ambient variables by T639[J]. Meteorological Monthly, 2016, 42(12): 1506-1512. DOI:10.7519/j.issn.1000-0526.2016.12.008) |
| [6] | Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334(6062): 1518-1524. DOI:10.1126/science.1205438 |
| [7] | Székely G J, Rizzo M L, Bakirov N K. Measuring and testing dependence by correlation of distances[J]. The Annals of Statistics, 2007, 35(6): 2769-2794. |
| [8] | Gretton A, Bousquet O, Smola A, et al. Measuring statistical dependence with Hilbert-Schmidt norms[C]// Proceedings of the 16th International Conference on Algorithmic Learning Theory. Singapore: Sanjay Jain, 2005: 63-77. |
| [9] | Chen X, Duan Y, Houthooft R, et al. InfoGAN: interpretable representation learning by information maximizing generative adversarial nets[C]//The 30th Annual Conference on Neural Information Processing Systems. Barcelona, 2016: 2172-2180. |
| [10] | 胡兵兵, 唐华, 吴幼龙. 基于互信息约束的生成对抗网络分类模型[J]. 中国科学院大学学报, 2022, 39(4): 551-560. (Hu Bing-bing, Tang Hua, Wu You-long. Classification models based on generative adversarial networks with mutual information regularization[J]. Journal of University of Chinese Academy of Sciences, 2022, 39(4): 551-560.) |
| [11] | Vinh L T, Lee S, Park Y T, et al. A novel feature selection method based on normalized mutual information[J]. Applied Intelligence, 2012, 37(1): 100-120. DOI:10.1007/s10489-011-0315-y |
| [12] | 王黎明, 吴香华, 赵天良, 等. 基于距离相关系数和支持向量机回归的PM2.5浓度滚动统计预报方案[J]. 环境科学学报, 2017, 37(4): 1268-1276. (Wang Li-ming, Wu Xiang-hua, Zhao Tian-liang, et al. A scheme for rolling statistical forecasting of PM2.5 concentrations based on distance correlation coefficient and support vector regression[J]. Acta Scientiae Circumstantiae, 2017, 37(4): 1268-1276.) |
| [13] | Wen C, Yang Y, Xiao Q, et al. Genome-wide association studies of brain imaging data via weighted distance correlation[J]. Bioinformatics, 2020, 36(19): 4942-4950. DOI:10.1093/bioinformatics/btaa612 |
| [14] | 梁吉业, 冯晨娇, 宋鹏. 大数据相关分析综述[J]. 计算机学报, 2016, 39(1): 1-18. (Liang Ji-ye, Feng Chen-jiao, Song Peng. A survey on correlation analysis of big data[J]. Chinese Journal of Computers, 2016, 39(1): 1-18.) |
| [15] | 宋成宝, 柳平增, 刘兴华, 等. 基于HSIC的日光温室温度传感器优化配置策略[J]. 农业工程学报, 2022, 38(8): 200-208. (Song Cheng-bao, Liu Ping-zeng, Liu Xing-hua, et al. Optimal configuration strategy for temperature sensors in solar greenhouse based on HSIC[J]. Transactions of the Chinese Society of Agricultural Engineering, 2022, 38(8): 200-208.) |
| [16] | 李柏松, 任伟杰, 韩敏. 基于HSIC-GL的多元时间序列非线性Granger因果关系分析[J]. 信息与控制, 2021, 50(3): 356-365. (Li Bai-song, Ren Wei-jie, Han Min. Nonlinear Granger causality analysis for multivariate time series using HSIC-GL model[J]. Information and Control, 2021, 50(3): 356-365.) |
| [17] | 张晓琴, 刘玲, 郭鑫垚. 基于HSIC0的类间非线性相关系数度量[J]. 计算机工程与应用, 2019, 55(3): 46-49. (Zhang Xiao-qin, Liu Ling, Guo Xin-yao. Measurement of nonlinear correlation coefficient among classes based on HSIC0[J]. Computer Engineering and Applications, 2019, 55(3): 46-49.) |
| [18] | Pearson K. Contributions to the mathematical theory of evolution(Ⅲ): regression, heredity, and panmixia[J]. Proceedings of the Royal Society of London, 1895, 59(1): 69-71. |
| [19] | Chen T Q, Guestrin C. XGBoost: a scalable tree boosting system[C]// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, 2016: 785-794. |
| [20] | Song L, Smola A J, Gretton A, et al. Feature selection via dependence maximization[J]. Journal of Machine Learning Research, 2012, 13: 1393-1434. |
| [21] | Ying M, Zhang W, Yu H, et al. An overview of the China Meteorological Administration tropical cyclone database[J]. Journal of Atmospheric and Oceanic Technology, 2014, 31(2): 287-301. |
| [22] | Lu X, Yu H, Ying M., et al. Western north pacific tropical cyclone database created by the China Meteorological Administration[J]. Advances in Atmospheric Sciences, 2021, 38(4): 690-699. |
| [23] | Kalnay E, Kanamitsu M, Kistler R, et al. The NCEP/NCAR 40-year reanalysis project[J]. Bulletin of the American Meteorological Society, 1996, 77(3): 437-470. |
| [24] | National Oceanic and Atmospheric Administration, National Center for Atmospheric Research. NCEP reanalysis datasets (1948-2018). A big earth data platform for three poles[EB/OL]. [2022-03-20]. https://doi.org/10.11888/Meteoro.tpdc.270922. |
