

1. 新疆大学 电气工程学院,乌鲁木齐 830046;
2. 清华大学 能源与动力工程系,北京 100084
收稿日期:2022-05-09
基金项目:国家自然科学基金资助项目(52176011, 52236003)。
作者简介:库尔班江·乌丝曼(1985-),男,新疆喀什人, 新疆大学讲师, 清华大学博士研究生;
史琳(1964-),女,河南洛阳人,清华大学教授, 博士生导师。
摘要:相变材料(PCMs)是潜热储热系统的核心媒介,而相变温度、导热系数及储能密度是选择PCMs的最关键三大因素.通过热阻模型相对热阻变化,对PCMs以上三个因素分别对储热系统换热速率的影响进行了分析.结果表明, PCMs的导热系数提高到2倍时对系统的换热效果提升显著,提高到5倍以后继续提高导热系数增强系统换热速率效果几乎已失效;在蓄热过程中PCMs相变温度越低,换热速率越快,在释热过程中恰好相反;提高储能密度对系统的换热速率并没有影响,只是相应倍数地延长了蓄/释热功率的时间.
关键词:PCMs换热速率导热系数相变温度储能密度
Effects of Phase Change Materials on the Heat Transfer Rate of Thermal Energy Storage System
WUSIMAN Kuerbanjiang1,2, DAI Xiao-ye2, SHI Lin2


1. School of Electrical Engineering, Xinjiang University, Urumqi 830046, China;
2. Department of Energy and Power Engineering, Tsinghua University, Beijing 100084, China
Corresponding author: SHI Lin, E-mail: rnxsl@mail.tsinghua.edu.cn.
Abstract: Phase change materials (PCMs) are the core media in latent heat thermal energy storage system, and phase change temperature, thermal conductivity and energy storage density of PCMs are the three most critical factors for selecting PCMs. These effects of three key factors of PCMs on heat transfer rate of thermal energy storage system are analyzed by means of relative thermal resistance variation according to thermal resistance modeling, respectively. The results indicate that when the thermal conductivity of PCMs is increased to about 2 folds, the heat transfer improvement of the system is significantly effective. After increasing to 5 folds, the effect of increasing the thermal conductivity to enhance the heat transfer rate of the system is almost invalid. During the charging process, the lower of PCMs' phase change temperature is, the higher heat transfer rate becomes, and it's just on the contrary during the discharging process. The increase of energy storage density has no effect on the heat transfer rate of the system, but the time of heat charging/discharging power is extended by corresponding multiple.
Key words: PCMsheat transfer ratethermal conductivityphase change temperatureenergy storage density
在“双碳”目标驱动下,随着可再生能源利用比列不断地提高以及节能减排增效政策的进一步引领下储能技术越来越受到重视,而储热技术因其技术相对成熟、经济性好且储热的能源利用方式更加灵活多效的特点被广泛应用.储热技术可分为显热储热、潜热储热、热化学储能三大类,而潜热储热具有比显热储热更高的储能密度(5倍左右)及较小温度波动范围[1],技术突破难度又远低于热化学储能,因此成为当前关注度最高的子储热技术[2-4].相变材料(PCMs)是相变储热系统的核心储热媒介,在综合衡量其安全性、环保性、实用性和经济性因素之外,PCMs的热物性(相变潜热、密度、导热系数、膨胀系数等)、动力学性质(过冷度、相分离)、化学性质(稳定性、无毒、阻燃性、与材料的兼容性等)是决定PCMs应用的主要因素,尤其是相变温度(熔化温度和结晶温度)、储能密度和导热系数是选择PCMs材料的最关键因素[5].在这三大关键因素中,相变温度是衡量PCMs适用性的前提,在此基础上优先考虑相变潜热较高的PCMs作为候选材料[6-7],比如糖醇类材料的熔化潜热普遍在200 kJ/kg以上, 正在被考虑作为中低温相变材料而广泛研究[8-9].对于选定的PCMs候选材料需进一步提升导热系数来增强其换热速率,目前通常做法是通过添加导热剂、微纳米封装、浸注等[10-12]物理或化学手段改性得到较高导热系数的PCMs,而碳基微纳米材料因其具有高导热系数的固有特性常被用于改善PCMs的导热性能且效果明显.Zeng等在赤藓糖醇材料中加入质量分数10 % 的片状石墨使其导热系数增大了408 % [13].Karthik等制造出以赤藓糖醇为PCMs的三维互联结构的石墨泡沫复合材料,当石墨泡沫为25 % 时复合材料的导热系数提高了5倍以上[14].Yuan等利用10 % 的膨胀石墨为基体封装的赤藓糖醇复合相变材料使得赤藓糖醇导热系数提高了17.38倍[15]. 而Guo等指出虽然通过碳基纳米材料改性的手段可以有效改善PCMs导热系数,但是随着碳基纳米材料的质量百分比的增加,不仅会使PCMs原有储能密度会有不同程度的降低,而且随着导热剂的增加还会提高PCMs实际应用的经济成本[16].
以上****对导热系数提高性能的研究都基于PCMs本身进行了综合分析优化,而本文提出以储热系统为基础,结合PCMs的三大关键性因素对储热系统换热速率的影响效果进行综合分析,从而在工程应用上对这三大因素进行综合衡量选取给予指引和帮助.
本文通过常用的管壳式结构的储热系统作为研究对象,引入常用的热阻模型[17]简化进行分析比较,说明导热系数、相变温度及储能密度对管壳式储热系统的换热功率的影响.
1 导热系数对系统蓄/释热功率的影响显热在潜热系统中储能占比小,为简化问题分析, 可忽略PCMs显热影响,只考虑PCMs系统相变潜热过程.引入换热器的换热效能[18-19],它表示换热器实际换热功率与理想换热功率的比值, 对于相变储热系统的换热效能可表示为
 | (1) |
 | (2) |
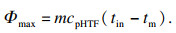 | (3) |
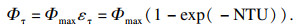 | (4) |
 | (5) |
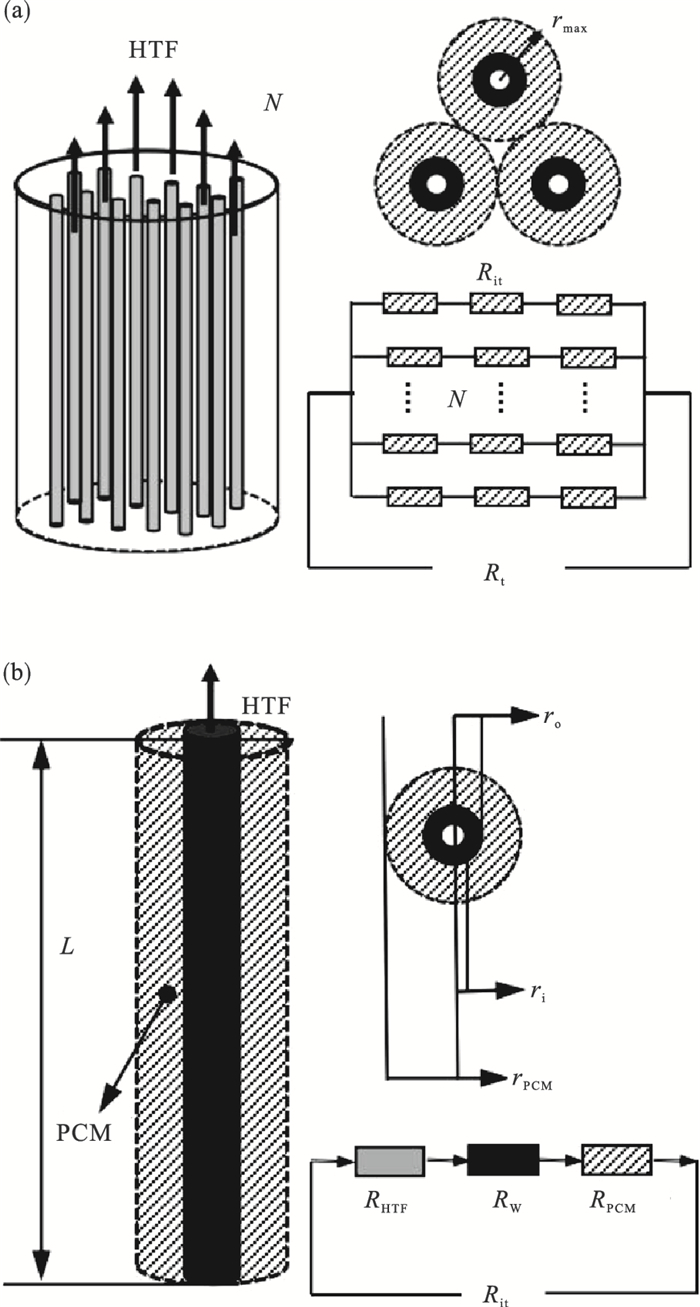 | 图 1 管壳式蓄能系统及蓄能单元总热阻示意图Fig.1 Schematic diagram of thermal resistance of shell and tube energy storage system and storage unit (a)—系统;(b)—单元. |
如图 1b所示,系统蓄能单元总热阻Rit由三部分组成:换热流体的对流换热热阻RHTF,管壁导热热阻RW和管外PCMs的导热热阻RPCM, 系统蓄热单元总数为N个(图 1a),由此可得系统单元总热阻Rit:
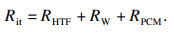 | (6) |
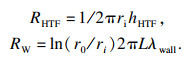 |
 | (7) |
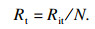 | (8) |
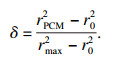 | (9) |
 | (10) |
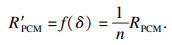 | (11) |
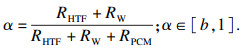 | (12) |
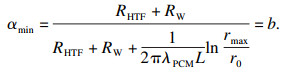 | (13) |
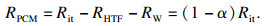 | (14) |
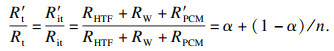 | (15) |
图 2(Fig. 2)
 | 图 2 系统相对总热阻随PCMs导热系数提高倍数变化Fig.2 Variation of relative total thermal resistance vs. thermal conductivity enhancement times of PCMs |
1.2 系统热阻Rs随n的变化系统热阻Rs与总热阻R′t之比随PCMs导热系数提高的倍数n的变化曲线如图 3所示.随着导热系数不断提高,Rs占系统总热阻R′t比例不断提高,说明随着PCMs导热系数的不断提升系统热阻Rs逐渐上升为储热系统换热的主要热阻,当PCMs导热系数提高到5倍时,α=0.2时系统热阻Rs占比已上升为56 %,说明此时系统热阻Rs已成为影响换热的主要热阻,PCMs热阻通过导热系数不断提升此时已降为次要热阻,而继续通过提高PCMs导热系数降低换热总热阻的效果变得不明显,由此可以说明图 2中当PCMs导热系数提高到5倍后系统总热阻之比进入了“平台区”的原因.
图 3(Fig. 3)
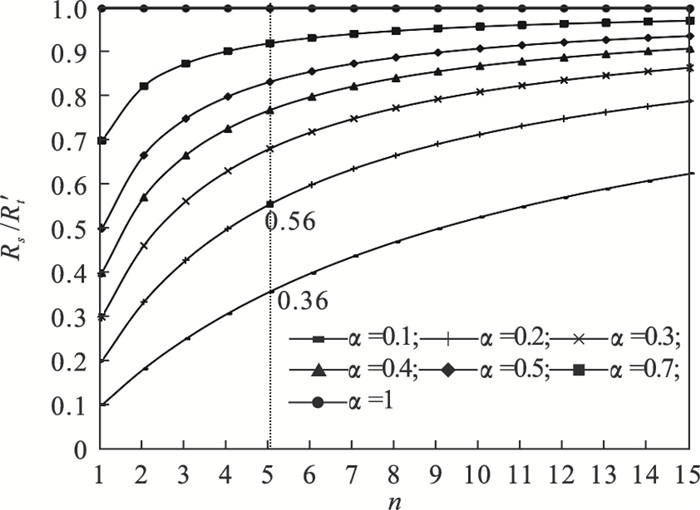 | 图 3 系统热阻与总热阻之比随PCMs导热系数提高倍数的变化Fig.3 Variation of the ratio of system thermal resistance to total thermal resistance vs. thermal conductivity enhancement times of PCMs |
1.3 系统相对平均总热阻R′t/Rt随n的变化在相变过程α∈[b, 1]中,随导热系数提高的倍数n的瞬时相对热阻如式(15)所示.则在此过程中的相对平均总热阻为
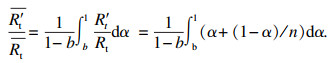 | (16) |
 | (17) |

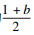
平均热阻的下降率ΔR/R (ΔR = Rt-R′t)随导热系数增强的倍数n的曲线如图 4所示,由图可知平均总热阻下降率在n=2范围下降最明显,且最小系统热阻占比b越小时下降率越明显,比如在PCMs导热系数提高2倍(n=2), b=0.1时,总热阻降低了23 %,而b=0.7时,总热阻只下降了8 %;在导热系数提高2倍后随着导热系数进一步的提高,总热阻下降率趋于缓慢,例如在b=0.1时,导热系数由2倍值提升到3倍时其总热阻只下降了7 %,因此当导热系数提高到2倍后继续增大导热系数对系统换热功率的提升效果越有限,且进一步提升PCMs导热系数所付出的综合代价也越高[17],因此对于给定储热系统,PCMs导热系数提高到2倍范围为适当的选择.
图 4(Fig. 4)
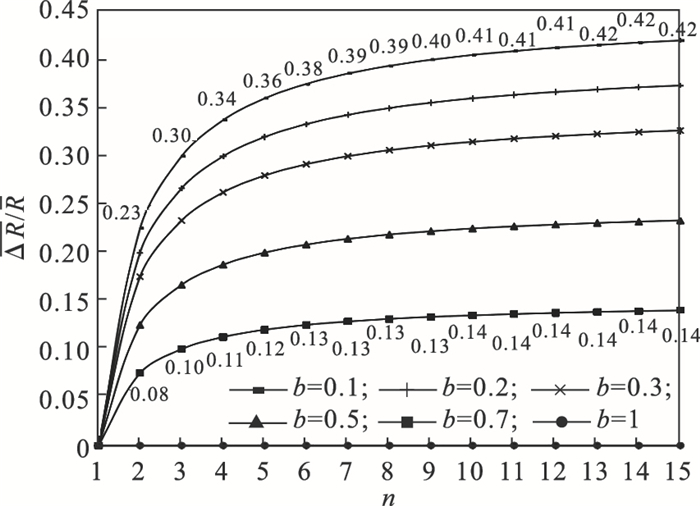 | 图 4 平均热阻下降率比随PCMs导热系数提高倍数的变化Fig.4 Variation of the mean thermal resistance decline rate vs. thermal conductivity enhancement times of PCMs |
综上所述, 当PCMs导热系数提高到2倍范围内时对系统的换热功率提升最明显,而提升到5倍以后,系统热阻上升为主要热阻,继续通过提高导热系数增强换热效果几乎失效,此时应考虑优化储热系统本身,减小系统热阻来增强换热效果.
2 相变温度对系统蓄/释热功率的影响对于导热系数和储能密度不变,相变温度由tm变为t′m的PCMs候选材料,在相分数为δ(δ∈[0, 1])时系统的相对蓄释热功率可由式(1), (3), (4)得出:
 | (18) |
 | (19) |
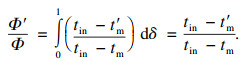 | (20) |
 | (21) |
图 5(Fig. 5)
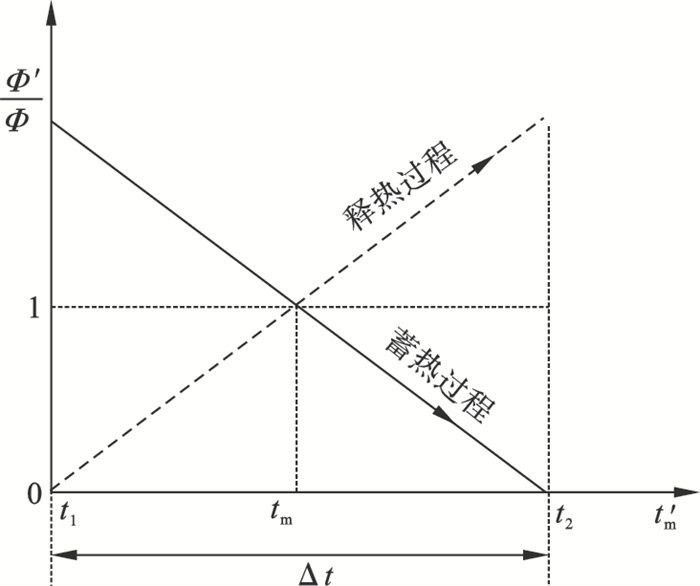 | 图 5 相对功率随PCMs相变温度变化示意图Fig.5 Schematic diagram of relative power changing vs. phase change temperature of PCMs |
3 储能密度对系统蓄/释热功率的影响对比导热系数和相变温度相当,储能密度Edens(kJ/m3)不同的PCMs候选材料,对于给定结构的储热系统容纳PCMs的体积VTES(m3)也相同,在给定工作进口温度tin和换热流体流量m工况下,同理由热阻模型可知在相变过程中相分数δ为[0, 1]时,两种PCMs系统的瞬时换热效能ε也相同,因此在任意相分数δ∈[0, 1]时两种PCMs瞬时蓄释热功率比值由式(3), 式(4)可得
 | (22) |
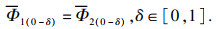 | (23) |
 | (24) |
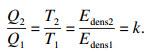 | (25) |
4 结论1) 通过提高PCMs的导热系数可提高储热系统的蓄/释热功率,因为随着PCMs导热系数的提高使得系统在相变过程中换热总热阻下降;当导热系数提高到2倍范围时储热系统蓄释热功率提升效果最明显,随着导热系数的不断提高,储热系统换热功率提升的效果越来越缓慢,而提高到5倍后继续通过提高导热系数来增强系统换热功率的方法几乎已失效,因为此时系统热阻上升为储热系统换热的主要热阻.因此在工程应用时可以首选考虑储热系统本身的优化设计,使得系统热阻尽量小,再考虑提高PCMs导热系数提升换热功率,而PCMs导热系数越高,往往付出代价也越高,因此导热系数提高到2倍是恰当的选择.
2) 对于在系统设定工况范围内的几种候选PCMs,在储能密度和导热系数相当的情况下,相变温度越低,使得系统蓄热功率越高,释热功率越低,而在释热过程结果正好相反.因此权衡储热系统蓄/释功率相当及考虑蓄能品质的因素,相变温度接近设定工作温度范围中间值的PCMs较优.
3) 在相变温度和导热系数相当而储能密度不同的PCMs系统,在相同相分数时的蓄/释瞬时功率和相变过程中的平均功率都相等,因此提高储能密度对系统蓄/释热功率没有影响,而在相同相分数时储能密度大的PCMs系统蓄/释热量是储能密度小的系统的k倍(k=Edensmax/Edensmin),因此提高储能密度会相应倍数的延长系统蓄释热有效功率功率的时间.
参考文献
| [1] | 姜竹, 邹博杨, 丛琳, 等. 储热技术研究进展与展望[J]. 储能科学与技术, 2022, 11(9): 2746-2771. (Jiang Zhu, Zou Bo-yang, Cong Lin, et al. Recent progress and outlook of thermal energy storage technologies[J]. Energy Storage Science and Technology, 2022, 11(9): 2746-2771. DOI:10.19799/j.cnki.2095-4239.2021.0538) |
| [2] | 李拴魁, 林原, 潘锋. 热能存储及转化技术进展与展望[J]. 储能科学与技术, 2022, 11(5): 1551-1562. (Li Shuan-kui, Lin Yuan, Pan Feng. Research progress in thermal energy storage and conversion technology[J]. Energy Storage Science and Technology, 2022, 11(5): 1551-1562.) |
| [3] | 汪翔, 陈海生, 徐玉杰, 等. 储热技术研究进展与趋势[J]. 科学通报, 2017, 62(15): 1602-1610. (Wang Xiang, Chen Hai-sheng, Xu Yu-jie, et al. Advances and prospects in thermal energy storage: a critical review[J]. Chinese Science Bulletin, 2017, 62(15): 1602-1610.) |
| [4] | 陈海生, 凌浩恕, 徐玉杰. 能源革命中的物理储能技术[J]. 中国科学院院刊, 2019, 34(4): 450-459. (Chen Hai-sheng, Ling Hao-shu, Xu Yu-jie. Physical energy storage technology in energy revolution[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(4): 450-459.) |
| [5] | Nazir H, Batool M, Osorio F, et al. Recent developments in phase change materials for energy storage applications: a review[J]. International Journal of Heat and Mass Transfer, 2019, 129: 491-523. DOI:10.1016/j.ijheatmasstransfer.2018.09.126 |
| [6] | Ge H, Li H, Mei S, et al. Low melting point liquid metal as a new class of phase change material: an emerging frontier in energy area[J]. Renewable & Sustainable Energy Reviews, 2013, 21: 331-346. |
| [7] | Nomura T, Akiyama T. High-temperature latent heat storage technology to utilize exergy of solar heat and industrial exhaust heat[J]. International Journal of Energy Research, 2017, 41(2): 240-251. DOI:10.1002/er.3611 |
| [8] | Barrio E, Godin A, Duquesne M, et al. Characterization of different sugar alcohols as phase change materials for thermal energy storage applications[J]. Solar Energy Materials and Solar Cells, 2017, 159: 560-569. DOI:10.1016/j.solmat.2016.10.009 |
| [9] | Yuan M, Xu C, Wang T, et al. Supercooling suppression and crystallization behaviour of erythritol/expanded graphite as form-stable phase change material[J]. Chemical Engineering Journal, 2020, 413: 127394. |
| [10] | Mamunya Y P, Davydenko V V, Pissis P, et al. Electrical and thermal conductivity of polymers filled with metal powders[J]. European Polymer Journal, 2002, 38(9): 1887-1897. |
| [11] | Yu A, Ramesh P, Itkis M E, et al. Graphite nanoplatelet epoxy composite thermal interface materials[J]. The Journal of Physical Chemistry C, 2007, 111(21): 7565-7569. |
| [12] | Li W, Zhang D, Jing T, et al. Nano-encapsulated phase change material slurry (Nano-PCMsS) saturated in metal foam: a new stable and efficient strategy for passive thermal management[J]. Energy, 2018, 165: 743-751. |
| [13] | Zeng J, Chen Y, Shu L, et al. Preparation and thermal properties of exfoliated graphite/erythritol/mannitol eutectic composite as form-stable phase change material for thermal energy storage[J]. Solar Energy Materials & Solar Cells, 2018, 178: 84-90. |
| [14] | Karthik M, Faik A, Blanco-Rodríguez P, et al. Preparation of erythritol-graphite foam phase change composite with enhanced thermal conductivity for thermal energy storage applications[J]. Carbon, 2015, 94: 266-276. |
| [15] | Yuan M, Ren Y, Xu C, et al. Characterization and stability study of a form-stable erythritol/expanded graphite composite phase change material for thermal energy storage[J]. Renewable Energy, 2019, 136: 211-222. |
| [16] | Guo S, Liu Q, Zhao J, et al. Evaluation and comparison of erythritol-based composites with addition of expanded graphite and carbon nanotubes[J]. Applied Energy, 2017, 205: 703-709. |
| [17] | 陈则韶. 求解凝固相变热传导问题的简便方法—热阻法[J]. 中国科学技术大学学报, 1991, 21(3): 69-76. (Chen Ze-shao. A simple heat-resistance method for the solution to heat conduction undergoing solidification[J]. Journal of University of Science and Technology of China, 1991, 21(3): 69-76.) |
| [18] | Barone G, Martelli D, Forgione N. Implementation of lead-lithium as working fluid in RELAP5/Mod3.3[J]. Fusion Engineering and Design, 2019, 146: 1308-1312. |
| [19] | Khare S, Dell'Amico M, Knight C, et al. Selection of materials for high temperature latent heat energy storage[J]. Solar Energy Materials & Solar Cells, 2012, 107: 20-27. |
| [20] | Tay N, Belusko M, Bruno F. An effectiveness-NTU technique for characterising tube-in-tank phase change thermal energy storage systems[J]. Applied Energy, 2012, 91(1): 309-319. |
| [21] | 陈静. CCHP系统中管壳式潜热蓄能装置蓄/释能特性研究[D]. 北京: 清华大学, 2018: 50-59. (Chen Jing. Study on the Storage/release characteristics of tube-shell latent energy storage device in CCHP system[D]. Beijing: Tsinghua University, 2018: 50-59. ) |
