
 , 包芮, 黄玮强
, 包芮, 黄玮强 东北大学 工商管理学院,辽宁 沈阳 110169
收稿日期:2022-05-13
基金项目:国家自然科学基金资助项目(72171039,71771042); 教育部人文社会科学研究项目(18YJCZH224); 中央高校基本科研业务费专项资金资助项目(N2206008); 辽宁省社会科学规划基金重点项目(L22AGL011)。
作者简介:郑红(1972-),女,辽宁沈阳人,东北大学副教授;
黄玮强(1982-),男,福建长汀人,东北大学教授,博士生导师。
摘要:基于我国各商业银行的银行间资产和银行间负债总体数据,利用最大熵法间接推断得到银行间借贷关联网络.在此基础上,利用DebtRank算法研究了单一冲击和共同冲击情形下我国商业银行损失困境的传染过程,进而衡量银行的系统重要性和系统脆弱性及其影响因素.研究结果表明,在特定情形下,银行损失困境给系统内其他银行造成的权益损失反而比银行违约造成的损失更大.我国商业银行没有位于“高脆弱性/强重要性”区域,表明我国银行体系较为安全.在影响因素方面,平均资产回报率对银行的系统重要性具有显著的负向影响,贷款拨备率、一级资本充足率和同业拆借率均对银行的系统重要性具有显著的正向影响;一级资本充足率和资产规模对银行的系统脆弱性均具有显著负向影响,同业拆借率对银行的系统脆弱性具有显著的正向影响.研究结果不仅有助于各银行了解自身处境,而且为金融监管提供依据.
关键词:困境传染借贷关联网络DebtRank系统重要性系统脆弱性
Inter-bank Distress Propagation and Identification of Systemic Impactand Vulnerability: Based on DebtRank Algorithm
ZHENG Hong

 , BAO Rui, HUANG Wei-qiang
, BAO Rui, HUANG Wei-qiang School of Business Administration, Northeastern University, Shenyang 110169, China
Corresponding author: ZHENG Hong, E-mail: hzheng@mail.neu.edu.cn.
Abstract: Based on the overall data of inter-bank assets and inter-bank liabilities of China's commercial banks, the inter-bank borrowing-lending correlation network is inferred indirectly by the maximum entropy method, and the distress propagation process under a single shock or common shocks is investigated based on the DebtRank algorithm. The systemic impact and vulnerability of banks and their influencing factors are also investigated. The empirical results show that under certain circumstances, the negative results brought by bank distress are more severe than those brought by bank default. China's commercial banks are not located in the area of "high vulnerability/strong impact", indicating that China's banking system is relatively safe. In terms of influencing factors, the average return on assets has a significant negative effect on banks' systemic impact, while the loan reserve ratio, the tier-one leverage capital ratio and the inter-bank lending volume have significant positive effect on banks' systemic impact. The tier-one leverage capital ratio and asset size have significant negative effect on the systemic vulnerability and the inter-bank lending volume has significant positive effect on the systemic vulnerability. The results not only help banks to understand their own situations, but also provide a basis for financial regulation.
Key words: distress propagationborrowing-lending correlation networkDebtRanksystemic impactsystemic vulnerability
银行间借贷市场在为银行提供短期的资金借贷以调剂资金余缺的同时,也放大了银行困境或违约[1],成为银行间风险传染的重要渠道.虽然通过更高水平的相互关联而实现的多样化降低了个体风险,但也可以增加系统性风险[2].自2008年金融危机以来,监管层意识到金融机构间相互关联的重要性,因此提出将监管重点从微观审慎转变为宏观审慎,以维护整个银行体系的稳健性[3].近年来越来越多的研究将银行间复杂借贷关联关系抽象成借贷关联网络,即用网络节点表示银行,节点之间的有向连边表示银行间的资金借贷关系,在此基础上设计传染算法刻画银行间风险传染机制,研究银行间市场风险的传染演化过程[4-5].
两个公认的量化研究金融风险损失传染的算法是Furfine算法[6]和DebtRank算法[7].前者本质上是一个门槛模型,银行只有在违约后才向其债权人传播风险,其对没有违约的冲击传播不敏感,可能低估风险传染效应和潜在的系统性风险[8].DebtRank的引入是为了解释在没有违约的情况下借款人权益的相对损失转化为相应债权人银行资产相对贬值所发生的冲击传播.事实上,即使没有违约,冲击会从借款人转移到贷款人,进而导致其他银行的权益受损, 即当一家银行遭受损失时,困境传播到其债权人,而债权人反过来遭受损失,而且困境可以传播并导致放大现象,最终导致系统风险.根据巴塞尔银行监管委员会的报告,2008年金融危机期间,约2/3的银行损失源于银行间的困境传染,约1/3是源于实际的违约传染.可见,银行的权益部分损失也会导致银行间的风险传染,银行困境的级联效应最终会使整个银行体系的权益受到严重损失,因此,分析银行间的困境传染过程,在此基础上准确识别具有系统重要性和脆弱性的银行,对于防范化解银行系统性风险具有重要意义.
系统重要性银行和系统脆弱性银行都是金融系统的关键性机构,它们的稳定与否决定着系统性风险是否发生,是宏观审慎监管的重要对象[9].《巴塞尔协议Ⅲ》对系统重要性银行界定为:如果一家银行陷入财务困境或破产清算,金融系统稳定性因此受到严重损害,金融功能不能得到正常发挥,金融提供服务的成本也大幅度上升,说明该银行在系统中常发挥“稳定器”作用,这样的银行即为系统重要性银行.反之,系统脆弱性银行是受到无差别冲击后可能最先倒闭的银行.系统重要性是反映机构对整个系统造成的影响,评估一家金融机构陷入损失困境时对金融系统造成的威胁;系统脆弱性是反映系统对机构的影响,评估危机发生时哪些机构面临的风险最高、对金融危机的敞口最大[10].对金融机构的宏观审慎监管应综合考虑两个方面的结果,缺一不可.
国内外已有文献主要是利用破产传染算法,对2008年美国金融危机、2010年欧债危机,以及2013年中国银行业“钱荒”问题进行了研究.胡可为等[11]基于2008年、2015年、2018年的三次股灾及2020年新冠肺炎疫情时期的子样本,分析了我国各金融部门(证券、银行和保险)的系统重要性与脆弱性.我国银行业资产占整体金融资产的比例已逾80 %,有效测度并防范银行系统性风险对于维护金融系统稳定运行具有深远意义,而聚焦于银行系统,基于DebtRank算法对我国银行间困境传染的研究还不多见.2016年我国提出供给侧结构改革,随着供给侧结构改革的不断推进,落后产能逐步出清,行业整合不断推进,部分中小企业在此过程中被淘汰、破产.与之对应,一些银行在实体企业洗牌的过程中,信贷资产演变为不良资产,资产质量压力急剧增加.特别是2016年下半年,严监管大幕开启,金融去杠杆下银行资产端开始收缩.那么,面对内外环境的冲击我国银行间困境传染的演化过程具有什么特点?各家银行在风险传染过程中表现出来的系统重要性和系统脆弱性差异如何?这些差异受什么特征因素影响?这些问题的解答将为政府宏微观审慎监管提供有益参考.
本文主要是通过收集我国150家商业银行(包括国家开发银行、邮政储蓄银行、大型国有商业银行、股份制商业银行、城市商业银行、农村商业银行以及外资银行)的银行间资产和银行间负债总体数据,利用最大熵法间接推断得到银行间借贷关联网络.在此基础上,利用DebtRank算法分别研究了单一冲击和共同冲击情形下我国银行损失困境的传染过程,识别出系统重要性和系统脆弱性银行,并实证分析各自的影响因素.研究结果对于我国银行系统性风险监管具有重要意义.
1 文献综述系统重要性和系统脆弱性银行的识别与评估是制定和执行宏观审慎监管政策、防范系统性风险的关键.识别方法主要有指标法、市场模型法和网络分析法.指标法主要是采用财务方面的历史数据分析系统性风险发生前后各机构指标变动对金融体系的影响程度,其数据可得性较强但在指标选取上存在主观性.市场模型法是在金融市场完全有效的潜在假设下,基于股票价格、信用违约互换(credit default swap,CDS)等市场数据建立风险计量模型进行实证分析,主要包括条件在险价值法、边际期望损失法和灾难保险法.Adrian等[12]在在险价值(VaR)模型基础上,利用条件在险价值(CoVaR)模型度量一家银行的倒闭对其他银行乃至整个银行体系造成的风险溢出效应,并识别出系统重要性银行.该方法的缺点在于不同机构的系统性风险贡献不具有可加性,无法考察金融体系整体的系统性风险水平[13].边际期望损失法:Acharya等[14]提出了系统期望损失(systemic expected shortfall, SES)和边际期望损失(marginal expected shortfall,MES).SES基于危机发生的事后数据进行测度,MES则基于危机发生前的数据进行测度.鉴于SES无法进行事前测度,Brownlees等[15]提出测度金融机构系统性风险的实证方法SRISK.灾害保险费法(disaster insurance premium,DIP)主要是利用保险费用理论来衡量银行体系的系统性风险.MES定义为金融系统处于极端损失(收益率最低的5 % 交易日)时机构的平均权益收益率.与此对照,DIP定义为未来一段时间系统的总负债损失超过临界值时(如15 %)机构的保险(CDS)溢价.两者思路类似,但区别在于前者的计算基于股票收益率数据,后者融合了股票收益率和CDS数据[16].此外,DIP基于事前的CDS违约概率和股票收益相关性数据,是一种“事前”的系统性风险衡量指标.
指标法和市场模型法虽然有各自的优势和不同应用场景,但很难立足于全局捕捉风险动态传染过程,相比之下,网络分析法通过借助资产负债表的数据构建银行的同业拆借网络,模拟评估系统性风险的发生机制和传染效应,为解决上述问题提供新思路.DebtRank算法克服了传统违约级联方法的局限性,近年来受到广泛关注,许多****基于DebtRank算法对金融机构的系统性风险进行识别[17-18].DebtRank算法能够在银行不完全破产、仅出现损失困境的情况下,计算损失在银行间市场的传染效应,该算法的思想类似于反馈中心性和万维网网页排名算法PageRank,其递归地计算银行破产或出现困境时对整个银行网络中的交易对手造成的损失,而传统的“仅破产传染”机制是DebtRank算法的下界.Bardoscia等[1]针对DebtRank算法只能向其债权银行传播一次冲击的假设,对其进行了改进.Bardoscia等[8]放松了原DebtRank算法中损失在银行间是线性传播的假设,引入了一个单参数非线性传播函数.在应用方面,Thurner等[19]建议央行定期计算各银行的DebtRank值,将其提供给所有银行,并规定借款银行尽量避免从DebtRank值较高的银行借款,从而降低系统性风险发生的可能性.
DebtRank算法相对于其他方法的优势在于,DebtRank算法是对“仅破产算法”的有益补充.仅破产传染算法对风险的微小变化不敏感,也意味着只有对银行资产造成足够大的冲击或者是银行的核心资本足够低,才会使银行破产,银行间风险传染效应才会显现.但更为普遍且更接近现实的情况是银行不发生破产,仅仅出现一些经营困境但仍具有清偿能力时,也会造成银行间风险传染效应的发生.即使当初始冲击不足以引发银行破产时,对银行资产负债表银行间资产的冲击也会沿着银行间网络传播.同时DebtRank算法能够产生一个准确识别最有影响力节点的排名,并量化它们之间的具体差异,这是其他方法无法做到的.目前国内少有****利用该算法研究我国银行间损失困境风险传染造成的影响,因此有必要运用DebtRank算法来分析银行间风险传染演化过程,识别系统重要性和系统脆弱性银行,从而更有利于我国银行系统性风险监管.
2 银行间借贷关联网络构建银行间借贷关联网络是一个有向加权网络,其中节点表示银行,节点之间的连边方向和权重表示银行之间的资金借贷方向和数额.该网络可用加权邻接矩阵A=[Aij]n×n表示,其中n为银行数量,元素Aij表示银行i借给银行j的资金数额,即i是债权人,j是债务人.最大熵法是常用的网络间接推断算法[20].具体地,已知加权邻接矩阵A为
 | (1) |
在银行间借贷交易中,银行不可能给自己贷款或者向自己借款,因此当i=j时,Aij=0,即主对角线元素为0.通过使交叉熵最小化来对初始矩阵A进行修正,得到新矩阵A*:
 | (2) |
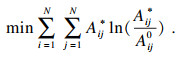 | (3) |
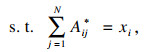 | (4) |
 | (5) |
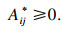 | (6) |
3 DebtRank算法与银行损失困境传染DebtRank算法是赋予复杂网络中部分节点初始风险值,依照设定的拒绝重复路径的传播算法,通过债务连线,经过N轮传播,最终传播停止,所有受波及的节点都有相应的最终风险值,再经过标准化处理后,形成整个网络的风险值,即DebtRank值[7].Bardoscia等[1]改进了DebtRank算法,克服了银行只将困境转嫁给债权人一次的限制,认为在某些情况下,会导致对系统中困境程度的严重低估,在此基础上提出一种允许进一步冲击传播直到违约的动力学设计.
令Aij(t)表示t时期银行i对银行j的贷款额,Lij(t)表示t时期银行i向银行j的借款额,银行i在t时期的外部资产(除银行间资产外的其他资产)和外部负债(除银行间负债外的其他负债)分别用AiE(t)和LiE(t)表示.银行i在t时期的资产和负债之间的差额即为权益Ei(t),它是银行i用来吸收损失的资本缓冲.将权益为负作为银行违约的代理变量.一般来说,只要权益为正,银行就被认为具有偿付能力;一旦权益为负(资不抵债),即使其清算了全部资产也不够偿还债务.银行i在t时期的资产负债恒等式为
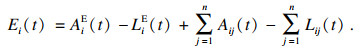 | (7) |
 | (8) |
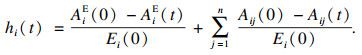 | (9) |
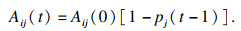 | (10) |
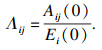 | (11) |
 | (12) |
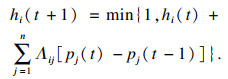 | (13) |
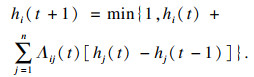 | (14) |
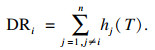 | (15) |
另一方面,当银行j(j=1, 2, …, n,j≠i)分别受到初始冲击后,经过损失困境传染机制给银行i带来的平均权益损失率VULi衡量了银行i的系统脆弱性:
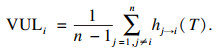 | (16) |
4 实证研究4.1 样本数据选取150家商业银行作为样本,包括国家开发银行、邮政储蓄银行、5家大型国有商业银行、11家股份制商业银行、76家城市商业银行、32家农村商业银行以及24家外资银行.为估计银行间借贷关联网络,收集各银行的相关财务指标,其中, 银行间资产指标由存放同业和其他金融机构款项以及拆出资金两项数据构成;银行间负债指标由同业和其他金融机构存放款项以及拆入资金两项数据构成;权益指标由一级资本净额来衡量,它是抵御冲击的缓冲资本.考虑到DebtRank算法主要适用于银行之间借贷风险传导,2016年的供给侧结构改革提供了一次难得的自然实验,更有助于反映企业结构调整这一冲击对银行间损失困境传染的影响,有鉴于此,相关数据来源于各商业银行2017年财务年报.截至2017年底, 我国银行业金融机构总资产规模达到2 524 040亿元,样本银行总资产规模约2 062 195亿元,占整个银行业金融机构总资产规模的82 %,表明所选样本具有良好的代表性.
4.2 银行困境传染过程分析根据已知的每家银行的银行间资产和银行间负债数据,利用最大熵法估计出银行间的借贷关系矩阵,然后基于DebtRank算法,对银行损失困境传染过程进行分析.
4.2.1 单一冲击情形单一冲击是指在初始时期银行i出现一定程度的权益损失(hi(1)∈[0, 1]),导致其陷入损失困境.根据困境传染过程分析,本文用DR刻画银行的损失困境给系统内其他银行带来的不利影响,反映了银行的系统重要性.VUL则刻画银行受到其他银行经营困境的影响程度,反映了银行的系统脆弱性.
1) 银行的系统重要性.在初始时期t=1时,对每家银行i分别施加相同的初始冲击,hi(1)=1 %,5 %,…,100 %,进而计算每家银行在相同初始冲击下的系统重要性指标DRi.篇幅所限,仅列出每种初始冲击下系统重要性排序前十位银行的DR值(图 1).从图中可以看出,不同初始冲击会影响银行系统重要性指标值的具体大小,但排序结果的相关性均达到99.997 % 以上,说明初始冲击大小对银行系统重要性排序的影响较小.系统重要性排序前十位的银行没有变化,且集中于国家开发银行、大型国有商业银行以及重要的股份制商业银行.还可发现,并非所有银行的DR值都随着初始冲击的增加而增大,例如当初始冲击由1 % 逐渐增大到80 % 时,国家开发银行的系统重要性(DR值)逐渐增大,但初始冲击由80 % 继续增大至100 % 时,该银行的系统重要性逐渐减弱.这说明在特定情形下,银行陷入损失困境(部分权益损失)给银行体系带来的负面影响比银行违约(全部权益损失)带来的负面影响反而更大.一方面,应该加强对那些出现较严重损失但尚未违约银行的监管,另一方面也凸显了DebtRank算法相对于传统违约级联传染算法的优势.
图 1(Fig. 1)
 | 图 1 不同初始冲击情形下系统重要性排序前十位的银行及其DR值Fig.1 Top 10 banks and their DR values under different initial shocks |
进一步比较分析不同性质商业银行的系统重要性差异.图 2是面临不同初始冲击情形下,不同性质商业银行的平均系统重要性DR值,该值越大说明系统重要性越强.从图中可以看出,不同性质商业银行的系统重要性程度由强到弱排序依次为:国家开发银行、国有商业银行、股份制商业银行、邮政储蓄银行、城市商业银行、外资银行、农村商业银行(除5 %,10 % 和15 % 的初始冲击下,农村商业银行的平均DR值大于外资银行).国家开发银行的平均DR值在初始冲击为80 % 时达到最大,邮政储蓄银行、国有商业银行、股份制商业银行的平均DR值在初始冲击为95 % 时达到最大,城市商业银行、农村商业银行和外资银行的平均DR值在初始冲击为100 % 时达到最大.
图 2(Fig. 2)
 | 图 2 不同初始冲击情形下不同性质商业银行的平均DR值Fig.2 Average DR values of different commercial banks under different initial shocks |
将样本银行划分为4类:资产规模大于10万亿元的定义为大型银行、处于1万亿~10万亿元之间的定义为中型银行、处于1 000亿~1万亿元之间的定义为小型银行、小于1 000亿元的定义为微型银行,进而比较分析不同资产规模商业银行的系统重要性差异,结果如图 3所示.从图中可以看出,在不同初始冲击水平下,不同资产规模商业银行的系统重要性程度由强到弱排序依次为:大型银行、中型银行、小型银行、微型银行.大型银行和中型银行的平均DR值在初始冲击为95 % 时达到最大,小型银行和微型银行的平均DR值在初始冲击为100 % 时达到最大.
图 3(Fig. 3)
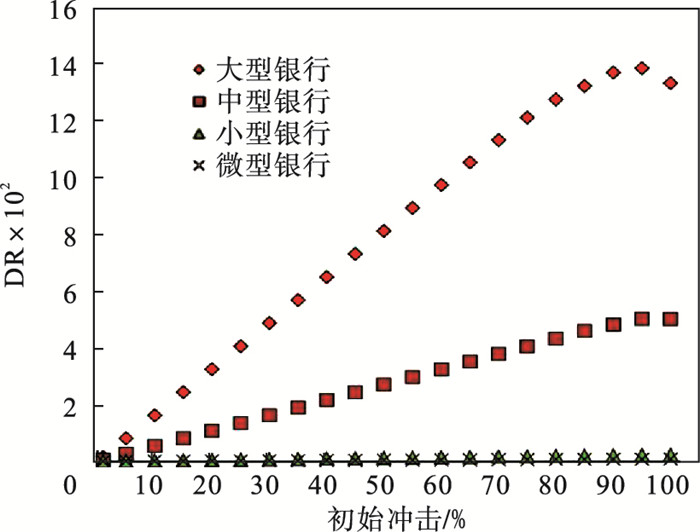 | 图 3 不同初始冲击情形下不同资产规模商业银行的平均DR值Fig.3 Average DR values of commercial banks in different asset sizes under different initial shocks |
2) 银行的系统脆弱性.图 4为不同初始冲击情形下,系统脆弱性由高到低排序前十位的银行及其VUL值.从图中可看出,随着初始冲击增大,各银行的脆弱性程度提高.不同初始冲击水平下,系统脆弱性排序前十位的银行没有变化,具体地,系统脆弱性程度高的银行大多是外资银行、城市商业银行和农村商业银行.
图 4(Fig. 4)
 | 图 4 不同初始冲击情形下系统脆弱性排序前十位的银行及其VUL值Fig.4 Top 10 banks in systemic vulnerability ranking and their VUL values under different initial shocks |
同样地,进一步比较分析不同性质商业银行的系统脆弱性差异.图 5是不同初始冲击情形下,不同性质商业银行的平均系统脆弱性VUL值,该值越大说明越脆弱.从图中可以看出,系统脆弱性程度由高到低依次为:外资银行、邮储银行、国家开发银行、农村商业银行、城市商业银行、国有商业银行、股份制商业银行.
图 5(Fig. 5)
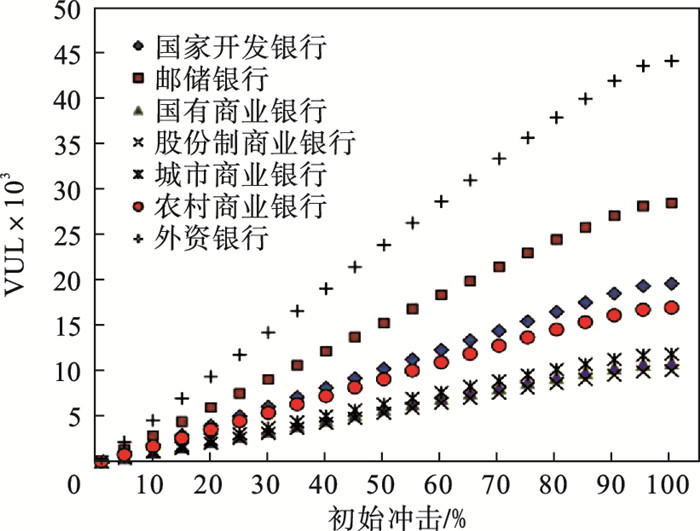 | 图 5 不同初始冲击情形下不同性质商业银行的平均VUL值Fig.5 Average VUL values of different commercial banks under different initial shocks |
进一步比较分析不同资产规模商业银行的系统脆弱性差异,结果如图 6所示.从图中可看出,当初始冲击水平为1 % 时,银行的系统脆弱性程度由高到低依次是:中型银行、微型银行、小型银行、大型银行;其余初始冲击水平下的银行系统脆弱性程度从高到低依次为微型银行、小型银行、中型银行、大型银行.
图 6(Fig. 6)
 | 图 6 不同初始冲击情形下不同资产规模商业银行的平均VUL值Fig.6 Average VUL values of commercial banks in different asset sizes under different initial shocks |
3) 银行的系统重要性和系统脆弱性综合分析.DR和VUL指标分别刻画了银行的系统重要性和系统脆弱性程度.当系统重要性强的银行其系统脆弱性也高的时候,系统性风险极易发生.因此有必要将2个指标进行综合分析.
图 7为样本银行的系统重要性与系统脆弱性指标值,气泡大小与银行资产规模成比例,气泡颜色反映了银行间杠杆(银行间资产/核心一级资本净额)的大小,红色表示高杠杆,蓝色表示低杠杆.将散点图分为4个象限,分别对应以下4类银行:高脆弱性/强重要性、高脆弱性/弱重要性、低脆弱性/弱重要性、低脆弱性/强重要性.一般来说,高脆弱性/强重要性银行应是重点关注和监管的银行.从图中可看出目前没有商业银行位于“高脆弱性/强重要性”区域,这说明我国银行体系较为安全.但是,一家可能导致整个银行体系产生10 % 以上权益损失的银行仍然是不可忽视的系统性风险来源,例如国家开发银行(b1)、建设银行(b4)、兴业银行(b8)、工商银行(b3)、中国银行(b6)、交通银行(b7)、浦发银行(b10)、民生银行(b11).
图 7(Fig. 7)
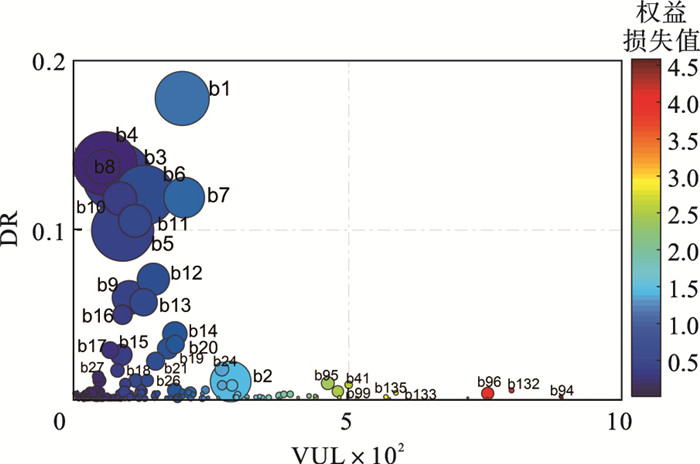 | 图 7 样本银行的系统重要性与系统脆弱性指标值Fig.7 Systemic impact and vulnerability index values of the sample banks |
总体来说,高脆弱性/弱重要性(如b96,b32和b94等)和低脆弱性/强重要性(如b1,b4,b3等)的银行个数较少,低脆弱性/弱重要性(如b18,b15,b26等)的银行个数较多.对于自贡银行(b94)来说,它虽容易受到其他银行的影响而出现损失困境,但一旦该银行违约,对整个银行体系造成的影响极低.对于国开行(b1)来说,它不易受到其他银行的影响而出现损失困境或违约,然而一旦该银行违约,将对整个银行体系产生巨大影响,造成接近20 % 的权益损失.对于渤海银行(b18)来说,其抗风险能力较强,既不易受到其他银行影响,也不会给银行体系带来较大权益损失.此外还发现,系统脆弱性较高的银行,其银行间杠杆也较高.
4.2.2 共同冲击情形共同冲击情形是指在初始时期所有商业银行同时处于相同的损失困境.初始共同冲击下,经由借贷关联网络,引起银行间损失困境的传染.整个银行体系的最终总权益损失率H(t)=∑iHi(t),它由初始共同冲击带来的权益损失率H(1)和传染带来的权益损失率DR组成.DR值可通过DebtRank算法运行至稳态时得到.
H(1)设定在0~70 % 之间,图 8给出了随着初始共同冲击的变化,体系总权益损失率H(t)、传染带来的权益损失率DR的动态变化情况.从图中可看出,H(t)随着初始共同冲击的增加而增加,当H(1)为70 % 时,H(t)达到100 %,此时银行体系完全崩溃.DR随着初始共同冲击的增加呈先增大后减小的变化趋势.
图 8(Fig. 8)
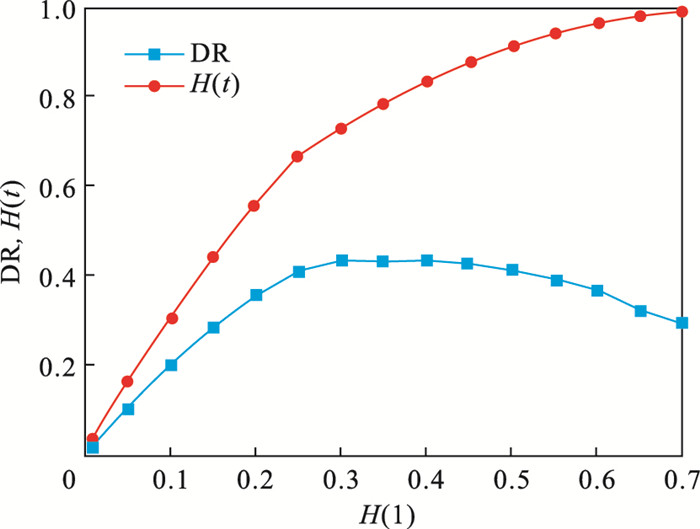 | 图 8 共同冲击情形下H(t)和DR动态变化情况Fig.8 Dynamic variation of H(t) and DR in the case of co-shocks |
进一步研究共同冲击情形下,由于传染效应给银行体系带来的权益损失率及违约银行(100 % 权益损失率)数量的变化情况,如图 9所示,图中圆圈颜色代表由于传染效应而导致的违约银行数量,红色越深,违约银行数量越多.从图中可以看出,随着初始共同冲击增强,由于传染效应带来的银行权益损失率DR先增加后减小,违约银行数量则不断增加.当初始冲击达到38 % 时,DR达到最大值,银行间的传染效应最严重.当初始冲击小于43 % 时,传染效应造成的权益损失率DR大于初始冲击造成的损失;当初始冲击大于43 % 时,传染效应造成的权益损失率DR小于初始冲击造成的损失.
图 9(Fig. 9)
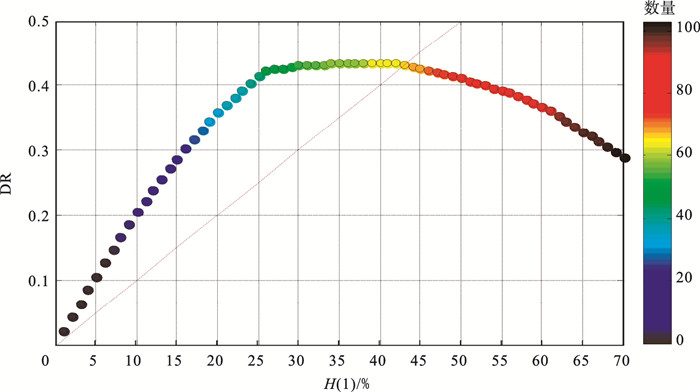 | 图 9 初始共同冲击与传染效应带来的权益损失率DR、违约银行数量的关系图Fig.9 Relationship between the equity loss ratio of DR and the number of defaulted banks resulting from initial co-shocks and propagation effects |
4.3 银行的系统重要性及系统脆弱性影响因素分析从银行个体特征出发,分析银行的系统重要性及系统脆弱性的影响因素.根据文献[21]并结合数据可得性,从银行盈利能力、资产质量、资本充足性、规模大小、风险暴露程度等方面,选取了平均资产回报率、贷款拨备率、一级资本充足率、资产规模、同业拆借率等具体指标(表 1).DR和VUL指标的计算依据单一初始冲击100 % 情形下的经营困境传染结果.建立影响因素回归方程,如式(17)和式(18)所示.
表 1(Table 1)
| 表 1 银行的系统重要性和系统脆弱性影响因素指标 Table 1 Index of influencing factors of banks'systemic impact and vulnerability |
 | (17) |
 | (18) |
表 2(Table 2)
| 表 2 回归估计结果(被解释变量为DR) Table 2 Regression estimation results(explained variable DR) | ||||||||||||||||||||||||||||
表 3(Table 3)
| 表 3 回归估计结果(被解释变量为VUL) Table 3 Regression estimation results(explained variable VUL) |
从表 2的结果可以看出,平均资产回报率(ROAA)、贷款拨备率(LPR)、一级资本充足率(CAP)、资产规模(lnTA)、同业拆借率(IR)均在1 % 置信水平下显著,表明这些影响因素均对银行的系统重要性有显著影响.具体地,平均资产回报率对银行的系统重要性具有显著负向影响,即盈利能力越强,系统重要性越弱,这是因为盈利能力较强的银行具有较好的抵御风险的能力.当经营困境发生时,它自身能够吸收足够的损失并依然保持稳定经营,因此对系统中其他银行造成的经营困境传染影响是非常有限的.贷款拨备率对银行的系统重要性具有显著正向影响,贷款拨备率越高说明银行贷款损失准备越充足,进而占用更多的资金,致使银行增加银行间借贷头寸,增强了风险传染的联结度及影响力.一级资本充足率对银行的系统重要性具有显著正向影响.一级资本充足率越高说明银行抵御风险能力越强,这类银行是不易出现问题的.一旦这类银行出现经营困境,必将对整个银行系统造成非常大的损失.资产规模对银行的系统重要性具有显著正向影响,可能是因为资产规模越大的银行,其同业业务关联性也更紧密,一旦出现经营困境,越容易对系统中的其他银行造成不良影响.同业拆借率对银行的系统重要性具有显著正向影响,同业拆借率越高说明银行在同业拆借市场中资金借贷参与度较高,因此容易对系统中的其他银行造成影响.
从表 3的结果可看出,一级资本充足率(CAP)、资产规模(lnTA)、同业拆借率(IR)在1 % 置信水平下显著,表明这3个指标均对银行的系统脆弱性有显著影响.具体地,一级资本充足率和资产规模对银行的系统脆弱性均具有显著负向影响.一级资本充足率越高,银行利用自有资本抵御风险冲击的能力越强,系统脆弱性越低;资产规模越大的银行越容易获得流动性支持,抵御外部冲击的能力越强,系统脆弱性也越低;同业拆借率对银行的系统脆弱性具有显著的正向影响,同业拆借率越高说明银行在同业拆借市场中的风险暴露程度越大,越容易受到其他银行经营困境的影响.
5 结论与建议1) 银行间损失困境传染给银行体系带来的负面影响,并不一定随着初始冲击的增大而增大.在特定情形下,银行损失困境(部分权益损失)带来的负面影响反而要比银行违约(全部权益损失)带来的负面影响更大.这说明应该加强对那些出现严重损失困境但尚未违约银行的监管,也说明DebtRank算法相对于传统违约级联传染算法具有优势.
2) 初始冲击大小对银行系统重要性排序的影响较小.不同性质商业银行的系统重要性程度由强到弱排序依次为:国家开发银行、国有商业银行、股份制商业银行、邮政储蓄银行、城市商业银行、外资银行、农村商业银行.不同资产规模商业银行的系统重要性程度由强到弱排序依次为:大型银行、中型银行、小型银行、微型银行.
3) 初始冲击大小对银行系统脆弱性排序的影响较小.从银行性质看,系统脆弱性程度由高到低依次为:外资银行、邮储银行、国家开发银行、农村商业银行、城市商业银行、国有商业银行、股份制商业银行.从资产规模看,银行系统脆弱性程度从高到低依次为微型银行、小型银行、中型银行、大型银行.
4) 综合分析各银行的系统重要性和系统脆弱性发现,我国商业银行没有位于“高脆弱性/强重要性”区域,这说明我国银行体系较为安全.表现为高脆弱性/弱重要性和低脆弱性/强重要性的银行个数较少,低脆弱性/弱重要性的银行个数较多.研究表明,随着初始共同冲击增强,由于传染效应带来的银行权益损失率先增加后减小,违约银行数量则是不断增加.当初始共同冲击达到38 % 时,银行间的传染效应最严重.
5) 平均资产回报率对银行的系统重要性具有显著负向影响,贷款拨备率、一级资本充足率和同业拆借率均对银行的系统重要性具有显著正向影响;一级资本充足率和资产规模对银行的系统脆弱性均具有显著负向影响,同业拆借率对银行的系统脆弱性具有显著正向影响.
根据研究结论,为防范系统性风险可以从以下几个方面入手:一是控制风险源头.重点关注出现严重损失困境的银行,防止后期风险的大规模蔓延,减小系统性风险发生的可能性;二是控制银行间风险传染程度.定期计算并对外公布每个银行的DebtRank值,让所有银行都及时了解各家银行的风险情况,制定一个避免或较少从DebtRank值较大的银行(系统重要性银行)借款的规则;三是要同时监测银行的系统重要性和系统脆弱性.当系统重要性银行也变得脆弱时,系统风险就会出现,所以要警惕“高脆弱性/强重要性”银行的出现,特别要对系统重要性银行和系统脆弱性银行分类监管,提高监管的针对性.
参考文献
| [1] | Bardoscia M, Battiston S, Caccioli F, et al. DebtRank: a microscopic foundation for shock propagation[J]. PloS One, 2015, 10(6): 1-13. |
| [2] | 范小云, 荣宇浩, 段月姣. 系统性风险传染机制中的级联故障研究——兼论"多而不能倒"与"大而不能倒"[J]. 经济学动态, 2021(9): 48-60. (Fan Xiao-yun, Rong Yu-hao, Duan Yue-jiao. Cascading failures and systemic risk in China's banking system: with discussion "too many to fail"and "too big to fail"[J]. Economic Dynamics, 2021(9): 48-60.) |
| [3] | Acemoglu D, Ozdaglar A, Tahbaz-Salehi A. Systemic risk and stability in financial networks[J]. American Economic Review, 2015, 105(2): 564-608. DOI:10.1257/aer.20130456 |
| [4] | 黄玮强, 范铭杰, 庄新田. 基于借贷关联网络的我国银行间市场风险传染[J]. 系统管理学报, 2019, 29(5): 899-906. (Huang Wei-qiang, Fan Ming-jie, Zhuang Xin-tian. Risk contagion in China's inter-bank market based on inter-bank lending networks[J]. Journal of Systems Management, 2019, 29(5): 899-906.) |
| [5] | 于剑男, 赵金楼, 王世波. 基于网络动态模拟的银行间市场系统性风险研究[J]. 统计与决策, 2019, 35(526): 157-161. (Yu Jian-nan, Zhao Jin-lou, Wang Shi-bo. Research on systemic risk of inter-bank market based on network dynamic simulation[J]. Statistics and Decision Making, 2019, 35(526): 157-161. DOI:10.13546/j.cnki.tjyjc.2019.10.038) |
| [6] | Furfine C H. Interbank exposures: quantifying the risk of contagion[J]. Journal of Money, Credit & Banking, 2003, 35(1): 111-129. |
| [7] | Battiston S, Puliga M, Kaushik R, et al. DebtRank: too central to fail? Financial networks, the fed and systemic risk[J]. Scientific Reports, 2012, 2: 541-547. DOI:10.1038/srep00541 |
| [8] | Bardoscia M, Caccioli F, Perotti J I, et al. DistRess propagation in complex networks: the case of non-linear DebtRank[J]. PloS One, 2016, 11(10): 1-12. |
| [9] | 黄岩渠, 胡宗义, 喻采平. 改进的DebtRank算法与系统重要性系统脆弱性研究[J]. 系统工程理论与实践, 2019, 39(2): 311-318. (Huang Yan-qu, Hu Zong-yi, Yu Cai-ping. DebtRank algorithm and vulnerability study of system importance system[J]. Systems Engineering—Theory & Practice, 2019, 39(2): 311-318.) |
| [10] | 李政, 涂晓枫, 卜林. 金融机构系统性风险: 重要性与脆弱性[J]. 财经研究, 2019, 45(2): 100-112, 152. (Li Zheng, Tu Xiao-feng, Bu Lin. Systemic risks of financial institutions: importance and vulnerability[J]. Journal of Finance and Economics, 2019, 45(2): 100-112, 152.) |
| [11] | 胡可为, 安毅, 刘文超. 我国金融部门的系统性风险: 系统重要性与脆弱性[J]. 中国证券期货, 2022(1): 10-22. (Hu Ke-wei, An Yi, Liu Wen-chao. Systemic risk of financial sector in China: systemic importance and vulnerability[J]. Securities & Futures of China, 2022(1): 10-22.) |
| [12] | Adrian T, Brunnermeier M K. CoVaR[J]. American Economic Review, 2016, 106(7): 1705-1741. |
| [13] | 邹辉文, 王佳玲. 基于复杂网络模型的银行间极端风险传染研究[J]. 福建金融, 2021(2): 41-50. (Zou Hui-wen, Wang Jia-ling. Extreme risk contagion among banks based on complex network model[J]. Fujian Finance, 2021(2): 41-50.) |
| [14] | Acharya V V, Pedersen L H, Philippon T, et al. Measuring systemic risk[J]. The Review of Financial Studies, 2017, 30(1): 2-47. |
| [15] | Brownlees C, Engle R F. SRISK: a conditional capital shortfall measure of systemic risk[J]. The Review of Financial Studies, 2017, 30(1): 48-79. |
| [16] | Huang X, Zhou H, Zhu H B. Systemic risk contributions[J]. Journal of Financial Services Research, 2012, 42(1/2): 55-83. |
| [17] | Bardoscia M, Battiston S, Caccioli F, et al. Pathways towards instability in financial networks[J]. Nature Communications, 2017, 8(1): 1-7. |
| [18] | Battiston S, Caldarelli G, D'Errico M, et al. Leveraging the network: a stress-test framework based on DebtRank[J]. Statistics and Risk Modeling, 2016, 33(3/4): 117-138. |
| [19] | Thurner S, Poledna S. DebtRank-transparency: controlling systemic risk in financial networks[J]. Scientific Reports, 2013, 3: 1-7. |
| [20] | Upper C, Worms A. Estimating bilateral exposures in the German interbank market: is there a danger of contation[J]. European Economic Review, 2004, 48: 827-849. |
| [21] | Kanno M. Assessing systemic risk using interbank exposures in the global banking system[J]. Journal of Financial Stability, 2015, 20(10): 105-130. |
