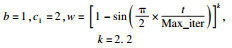赵俊涛¹, 罗小川¹, 刘俊秘²
1. 东北大学 信息科学与工程学院，辽宁 沈阳 110819;
2. 河南城建学院 电气与控制工程学院，河南 平顶山 467000
收稿日期：2022-04-22
基金项目：国家重点研发计划项目(2019YFB1705002)；辽宁省“兴辽英才计划”项目(XLYC2002041)。
作者简介：赵俊涛(1990-)，男，河北沧州人，东北大学博士研究生;
罗小川(1974-)，男，四川西充人，东北大学教授，博士生导师。

摘要：针对使用标准鲸鱼优化算法求解机器人路径规划问题时，存在收敛速度慢且容易陷入局部最优值的问题，提出混合粒子群优化算法与自适应权重策略的改进鲸鱼优化算法(PSO-AWOA).通过在标准PSO和WOA算法中引入非线性惯性权重因子，使种群进化过程中自适应更新权重，提高了算法的全局探索能力和收敛速度，同时通过将寻优能力较强的PSO算法引入WOA算法的开发阶段，保证迭代的新解优于原始解，增强了算法跳出局部最优的能力.最后，将PSO-AWOA算法应用到的栅格地图仿真环境中进行机器人最佳路径求解.通过对比给定算法的耗时、规划路径长度以及拐点数，结果表明，提出的PSO-AWOA算法在优化精度和收敛速度上优于文中给定的其他算法，验证了改进算法的有效性.
关键词：混合优化算法粒子群优化鲸鱼优化算法自适应权重路径规划
Application of Improved Whale Optimization Algorithm in Robot Path Planning
ZHAO ZHAO Jun-tao¹, LUO Xiao-chuan¹, LIU Jun-mi²
1. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
2. School of Electrical and Control Engineering, Henan University of Urban Construction, Pingdingshan 467000, China
Corresponding author: LUO Xiao-chuan, E-mail: luoxch@mail.neu.edu.cn.

Abstract: To solve the problem of slow convergence and susceptibility to local optima in solving robot path planning problems using the standard whale optimization algorithm (WOA), an improved whale optimization algorithm (PSO-AWOA) with hybrid particle swarm algorithm and adaptive weights strategy is proposed. By introducing nonlinear inertia weight factors into the standard PSO and WOA algorithms and adaptively updating the weights during the population evolution, the global exploration ability and convergence speed are improved. Meanwhile, by introducing the PSO algorithm with strong optimization-seeking ability into the exploitation stage of the WOA algorithm, the new solution of iteration is guaranteed to be better than the original solution, which enhances the ability to jump out of the local optima. Finally, the PSO-AWOA algorithm is applied to generate the optimal path for the robot in the grid map simulation environment. The results show that the proposed PSO-AWOA algorithm outperforms in terms of optimization accuracy and convergence speed by comparing the time consumption, planning path length, and the number of turning points of the algorithms given, which verifies the effectiveness of the improved algorithm.
Key words: hybrid optimization algorithmparticle swarm optimization (PSO)whale optimization algorithm (WOA)adaptive weightpath planning
目前，随着移动机器人的智能化和自主化程度越来越高，移动机器人已经被广泛应用于家庭、医院、酒店、工业以及军事领域.路径规划是移动机器人应用过程中需要解决的基本问题，其目的是为机器人在复杂场景中寻求从起始点到目标点的最优无碰撞可行路径^[1].评判路径最优的标准包括规划路径的长度、耗时、转弯角度以及拐点数等.目前使用的路径规划方法可以分为两类：传统算法和启发式算法^[2].传统的路径规划算法包括单元分解法(cell decomposition, DE)、人工势场法(artificial potential field, APF)以及快速扩展随机树(rapidly exploring random tree)等，该类方法可以规划出近最优路径，但是随着网络节点的增加，存在规划效率低和耗时长的不足.启发式算法由于具有良好的空间搜索能力被广泛应用于机器人路径规划中.启发式算法包括神经网络法(neural networks, NNs)、模糊推理法(fuzzy logic, FL)以及自然启发式算法(nature-inspired algorithms, NIAs).其中自然启发式算法是研究者受自然界生物行为方式的启发而提出的，如蚁群优化(ant colony optimization, ACO)、粒子群优化(particle swarm optimization，PSO)、萤火虫算法(firefly algorithm, FA)、布谷鸟搜索(cuckoo search, CS)和鲸鱼优化算法(whale optimization algorithm, WOA)等，这些算法为解决机器人在复杂环境中的路径规划问题提供了新思路.
鲸鱼优化算法是由澳大利亚****Mirjalili等受座头鲸气泡网捕食行为启发提出的群体智能优化算法^[3].该算法具有实现原理简单、调整参数少和寻优性能强等优点，因此众多研究者将其应用于神经网络、自动控制以及机器人路径规划中.标准WOA寻优后期由于种群多样性减少，造成算法存在收敛速度慢、寻优精度低和容易陷入局部最优等缺点.针对以上不足，许多****在原有算法基础上进行改进：文献[4]提出一种基于遗传算法和改进鲸鱼优化算法相结合的路径规划方法，解决了机器人在复杂动态环境中的路径规划和智能避障问题；文献[5]提出一种基于鲸鱼优化算法和模糊逻辑控制器的混合算法，可以用于工业场景下机器人规划平滑路径和实现避障功能，提高了机器人的自主性，降低了算法的计算复杂度；文献[6]提出一种基于和声二次优化和动态平衡策略的鲸鱼优化算法，通过将和声搜索策略、动态平衡策略与鲸鱼优化算法相融合，提高了算法的寻优能力，并将其用于解决地面无人车的全局路径规划问题；文献[7]提出一种时变独立搜索概率和免疫记忆改进的鲸鱼优化算法(IWTWOA)，通过采用非线性收敛因子、时变独立搜索概率以及免疫记忆机制，提高了算法的计算精度和收敛速度，将该算法应用在机器人路径规划中，验证了算法的有效性和稳定性.
为了克服WOA解决复杂优化问题时早熟收敛、搜索能力差以及求解精度低等不足，进一步提高算法性能，本文提出了一种混合粒子群优化算法和自适应权重策略的改进鲸鱼优化算法(PSO-AWOA)，首先，通过在PSO算法和WOA中引入非线性权重因子，平衡算法的局部寻优能力和全局寻优能力，算法开始初期，由于种群个体较为分散，权重值较大，可以加快算法的全局探索能力；随着算法迭代次数的增加，权重值逐渐减小，加快算法的收敛速度，对局部进行精细化搜索.同时通过将PSO算法引入WOA算法的开发阶段，保证迭代后新解优于原始解，增强了算法的寻优能力.最后将改进的PSO-AWOA应用于模拟环境下机器人路径规划问题的求解.
1 机器人路径规划问题数学模型1.1 环境建模机器人路径规划的目的是在包含障碍物和自由运行空间的未知环境中求得最优无碰撞路径，因此可以将机器人的运行环境使用栅格地图进行表示，其中白色栅格代表机器人的可运行区域，黑色栅格代表环境中的静态障碍物，如图 1所示.
图 1(Fig. 1)

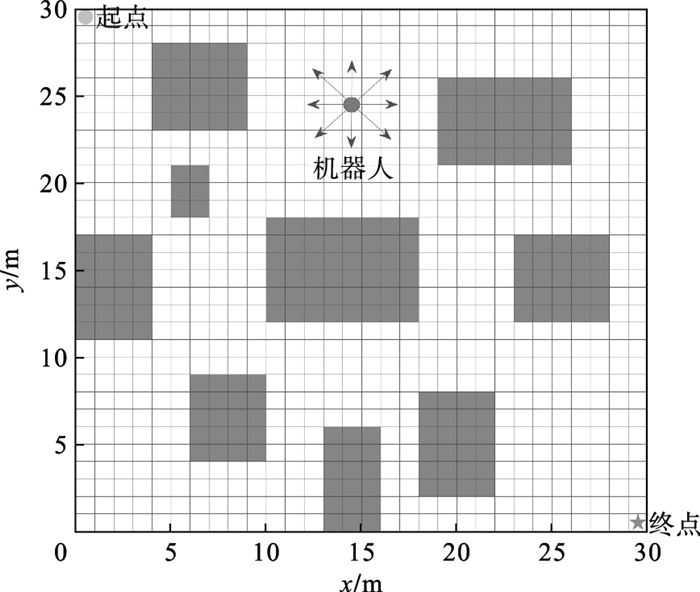图 1 机器人运行环境栅格地图Fig.1 Grid map of robot movement environment

机器人可以在中心坐标的八邻域白色栅格方向运动，从图中圆圈表示的起始位置移动至五角星表示的目标点位置.环境地图的数学表示为G=N×N的二值矩阵^[8]，地图中的栅格按从左至右，从上至下依次编号为(1, 2, …, N×N)，其中任意栅格n的坐标(x, y)可通过公式(1)计算求得

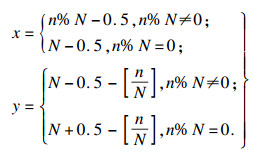(1)

式中：% 表示取余运算；[]表示取整运算.
1.2 适应度函数机器人路径规划过程中需要满足如下约束条件：①运动路径必须局限于地图的栅格空间内，且不能超出地图边界；②规划路径长度最短，以保证获取路径为最优路径；③机器人运动路径不能穿越障碍物栅格区域，避免发生碰撞.根据以上约束可以将机器人路径规划问题抽象为求解适应度最小的单目标优化问题，定义路径规划问题的适应度函数：

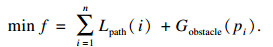(2)

式中：i为算法的迭代次数；L_path(i)为第i次迭代时机器人的路径规划长度，其具体定义为

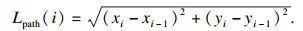(3)

式中：(x_i, y_i)为第i次迭代时机器人位置坐标；(x_i-1, y_i-1)为第i-1次迭代时机器人位置坐标；求得的L_path(i)为两点之间的欧氏距离.
G_obstacle(p_i)用于判断第i次迭代时路径点p_i是否发生越界或与上一路径点连线是否穿越障碍物，当路径点可行时，返回值为0，反之，返回较大的常数N×N，具体定义如下：

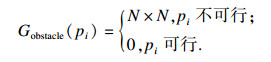(4)

2 混合粒子群和自适应权重鲸鱼优化算法2.1 鲸鱼优化算法(WOA)鲸鱼优化算法是根据座头鲸群体捕食小型鱼虾的行为提出的仿生元启发式算法，种群中每条鲸鱼相当于问题的一个解，通过收缩包围、气泡网攻击和随机搜索完成捕食猎物过程，最终猎物的位置相当于问题的全局最优解^[8].假设初始鲸鱼种群规模为M，搜索空间的维度为d，则第i条鲸鱼位置可以通过X_i=(X_i1, X_i2, …, X_id)表示, 其中i=1, 2, …, M.
1) 收缩包围.座头鲸在发现猎物后，会逐步对其进行包围，算法假设猎物位置或最接近猎物的位置为问题的最优解，定义最优位置以后，其他鲸鱼将通过不断更新自身位置来靠近最优位置，位置更新公式为

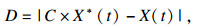(5)

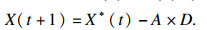(6)

式中：t为当前的迭代次数；X为当前的鲸鱼位置；X^*为当前为止最优的鲸鱼位置；X^*的值会随着迭代次数的增加而不断更新；A和C为系数，计算公式为

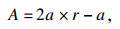(7)

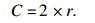(8)

式中：，其值将随着迭代次数的增加从2减小至0，a不断减小的过程即鲸鱼收缩包围猎物的过程；Max_iter为最大迭代次数；r为取值范围在[0, 1]之间的随机数.
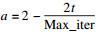
2) 气泡网攻击.座头鲸捕食包括收缩包围和螺旋位置更新两个过程，在收缩包围阶段，由公式(7)可以看出A的取值范围为[-a, a]，随着a的改变A的值也随之改变.当A的取值为[-1, 1]时，算法处于开发阶段，鲸鱼通过螺旋游动的方式不断向最优位置靠近，该过程中螺旋位置更新通过公式(9)计算求得

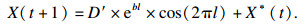(9)

式中：D′=|X^*(t)-X(t)|表示当前鲸鱼位置与最优位置之间的距离；b为对数螺旋形状常数；l为取值[-1, 1]的随机值.
鲸鱼在螺旋游向猎物的同时，伴随着收缩包围的过程，鲸鱼以收缩包围机制进行位置更新和以螺旋游动进行位置更新的概率均为50%，具体可以表示为

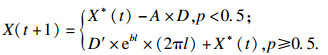(10)

式中：p为取值范围在[0, 1]之间的随机数.
3) 随机搜索.为了增强算法的全局搜索能力，当A的取值在[-1, 1]之外时，算法处于探索阶段，将在鲸鱼种群中随机选择鲸鱼个体进行位置更新，计算公式：

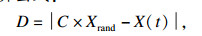(11)

(12)

式中：X_rand为种群中随机选择的鲸鱼个体；D表示当前鲸鱼位置与随机选择的鲸鱼个体之间的距离；系数A和C与式(7)和式(8)的取值相同.
2.2 粒子群优化算法(PSO)粒子群优化算法是由Kennedy等受鸟群觅食行为启发而提出的一种群体智能优化算法^[9]，算法模型中将群体中的每只鸟看作优化问题的一个解，并称之为“粒子”，这些粒子将以一定的速度在搜索空间飞行，飞行过程中该速度会根据自身与其他粒子的经验进行动态更新.假设初始种群中有M个粒子，这些粒子在d维搜索空间进行搜索，则第i个粒子的位置可以表示为X_i=(X_i1, X_i2, …, X_id)，i=1, 2, …, M，飞行速度为V_i=(V_i1, V_i2, …, V_id).在飞行过程中粒子i的个体最优位置为P_i=(P_i1, P_i2, …, P_id)，目前为止种群中所有粒子的全局最优位置为P_g=(P_g1, P_g2, …, P_gd).粒子i的飞行速度和位置更新可以通过如下公式求得

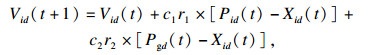(13)

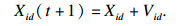(14)

式中：t为算法当前的迭代次数；c₁, c₂为加速因子；r₁, r₂为介于[0, 1]之间的随机数.
2.3 混合粒子群和自适应权重鲸鱼优化算法(PSO-AWOA)通常，使用群体智能算法解决NLP(nonlinear programming)问题时，算法的性能主要受收敛早熟和收敛速度的影响，平衡算法在搜索空间中的探索和开发能力颇为重要.PSO算法收敛速度快但全局探索的能力较弱，WOA具有良好的探索能力，但开发能力主要受公式(6)和公式(9)中当前位置与最优位置之间的距离制约.在PSO算法中，如果种群的全局最优解陷入局部最优时，其他粒子也将停止继续搜索而跟随全局最优解陷入局部最优.总结来说，PSO算法寻优能力强但搜索空间能力较弱，WOA探索空间能力强，但寻优能力受收敛速度制约.因此，可以将PSO算法应用于WOA的开发阶段，以提高算法得到全局最优解的能力.
混合PSO-AWOA是粒子群算法和鲸鱼优化算法的结合体，通过在PSO算法和WOA中同时引入非线性权重因子，克服了PSO算法由于受恒定惯性权重的限制造成搜索空间范围小的缺点，同时在WOA中，通过引入非线性惯性权重进行收缩包围和螺旋游走位置更新，可以加快算法的收敛速度，提升算法的寻优能力.混合PSO-AWOA吸收了二者各自的优点，因此寻优性能更为突出.
惯性权重因子是平衡算法全局探索和局部开发能力的主要因素，本文使用了自适应惯性权重策略，引入非线性权重w，随着迭代次数的增加，w的值将随之动态改变.在迭代初期，较大的权重可以提高算法的全局探索能力，迭代后期较小的权重有利于算法进行精细化的局部寻优.w的更新公式为

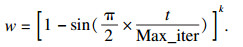(15)

式中：k为调节系数，当k取不同值时，权重w随之改变，如图 2所示.
图 2(Fig. 2)

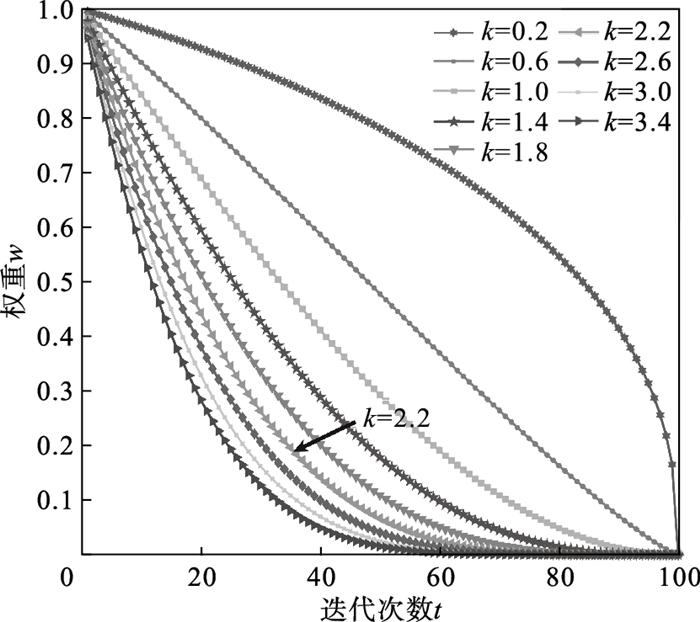图 2 不同k值下的权重曲线Fig.2 Weight curves under different k values

从图中可以看出，k取不同值时，权重w的变化速率不同，PSO-AWOA期望迭代前期权重取值较大，算法具有较强的全局搜索能力和收敛速度，随着迭代次数的增加，迭代中期权重大幅减小，直至后期缓慢趋近于0，提高算法的收敛速度和求解精度，经过多次实验，本文选取k=2.2.
混合算法中引入非线性权重以后，WOA算法的位置更新公式为

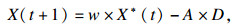(16)

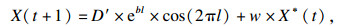(17)

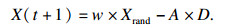(18)

PSO算法粒子移动速度和位置更新公式为

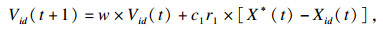(19)

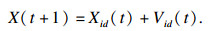(20)

2.4 混合PSO-AWOA实现步骤及流程混合PSO-AWOA的具体实现步骤描述如下：
步骤1??种群及算法参数初始化.随机初始化鲸鱼种群和粒子群的位置为X_i=(X_i1, X_i2, …, X_id)，初始化移动速度为V_i=(V_i1, V_i2, …, V_id)，i=1, 2, …, M.同时需要对种群规模M，最大迭代次数Max_iter，搜索空间维度d，迭代次数初始值t等参数进行初始化；
步骤2??计算种群中每个个体适应度值，通过比较找出最优个体位置X^*；
步骤3??根据公式(7)与公式(8)更新系数A和C的值，更新b，l，c₁以及r₁的值，生成取值为[0, 1]区间的随机数p；
步骤4??根据p和|A|的取值进行位置更新.如果p＜0.5且|A|≥1，则在种群中随机选择鲸鱼个体X_rand，并根据公式(11)和公式(18)进行位置更新；如果p＜0.5且|A|＜1，则根据公式(5)和公式(16)进行位置更新；如果p≥0.5，则根据公式(17)进行位置更新;
步骤5??根据公式(19)更新粒子群个体的移动速度，根据公式(20)更新粒子群位置X；
步骤6??返回步骤3进行迭代更新，判断是否达到最大迭代次数，如果算法迭代完成，则终止算法执行;
步骤7??算法迭代完成，返回最终计算得到的最优位置X^*，以及求解最优值时的种群个体位置，求解完成.
PSO-AWOA的流程图如图 3所示.
图 3(Fig. 3)

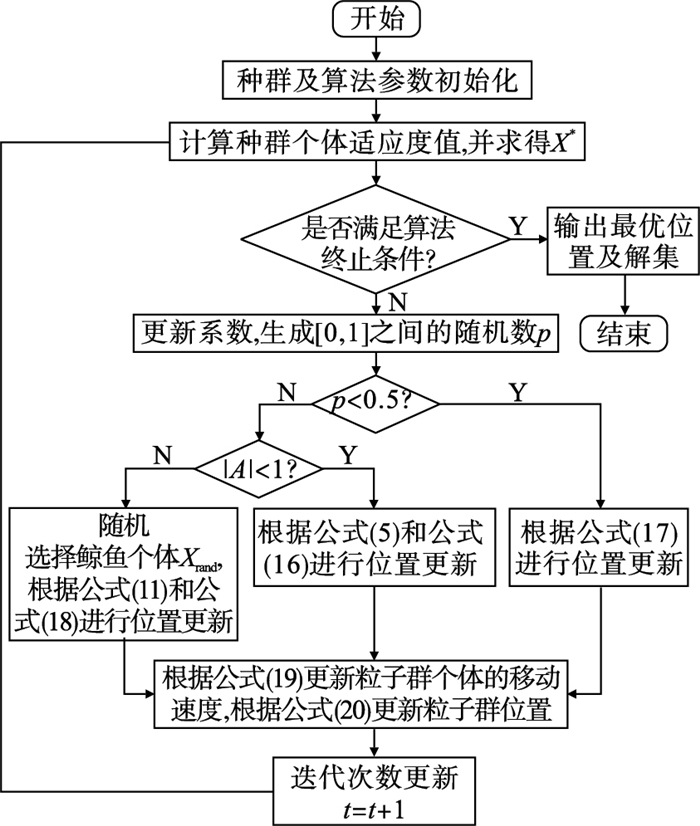图 3 PSO-AWOA流程图Fig.3 Flow chart of PSO-AWOA

3 PSO-AWOA在机器人路径规划中的应用为了验证混合PSO-AWOA在求解机器人路径规划问题上的有效性，本文分别在简单少障碍物场景和复杂多障碍物场景两种仿真实验环境中选择文献[12]中的灰狼优化算法GWO、文献[14]中的蚁群优化算法ACO、标准鲸鱼优化算法WOA、以及本文的混合PSO-AWOA 4种算法进行对比仿真实验.
3.1 硬件环境及参数配置实验运行硬件平台主机操作系统为Windows 10 64bit，处理器为Intel(R) Core(TM) i7-8550U，主频1.8 GHz，内存16 GB，软件平台使用的是Matlab R2020a.各对比算法相关参数设置如表 1所示.
表 1(Table 1)

表 1 各算法参数设置Table 1 Parameter settings of each algorithm 算法 参数 GWO a=2-2×t/Max_iter ACO α=10, β=1, ρ=0.1 WOA b=1 PSO-AWOA

表 1 各算法参数设置 Table 1 Parameter settings of each algorithm

3.2 路径规划仿真实验实验环境选择为30 m×30 m的栅格地图，机器人从起始点移动至目标点，地图中黑色区域为障碍物.仿真实验中4种算法采用相同的参数，如初始种群规模均为30，最大迭代次数为500次，搜索空间范围为[-30, 30]，适应度函数如公式(2)所示.为了保证生成路径的最优性，在路径生成阶段对路径的生成方向做了进一步限定，即路径不会出现“折返”或“回环”的现象，生成路径点无障碍区选择使用插值或直连方式进行简单优化处理，保证了路径的最优性.最后通过对算法生成的规划路径长度、耗时及拐点数量进行统计分析，进而对算法的性能进行评估.仿真实验得到的规划路径以及适应度曲线分别如图 4~图 7所示，各算法规划路径的耗时、路径长度及拐点数对比数据如表 2，表 3所示.
图 4(Fig. 4)

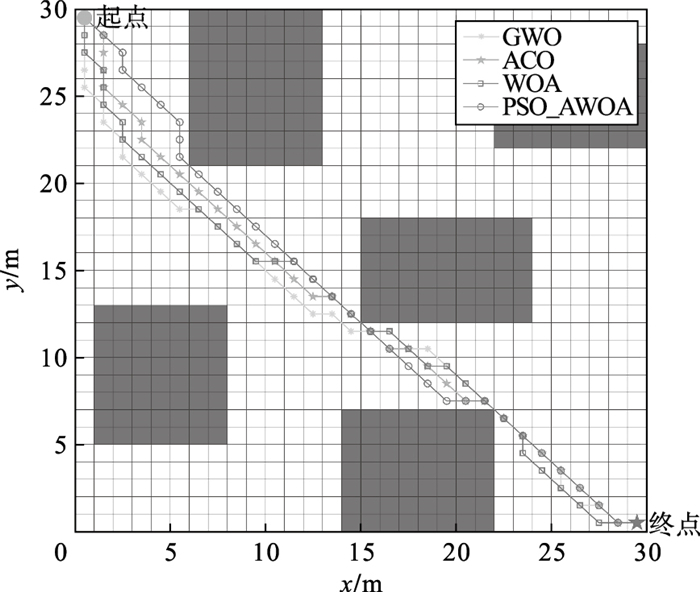图 4 简单场景路径规划仿真结果Fig.4 Path planning results in the simple scene

图 5(Fig. 5)

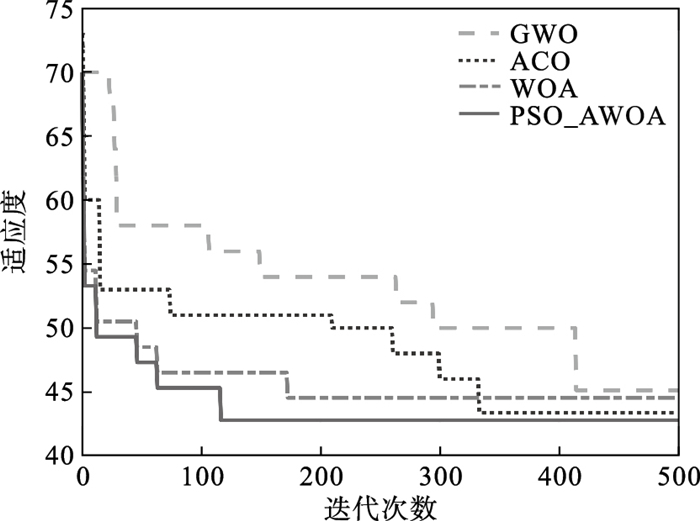图 5 简单场景适应度函数变化曲线Fig.5 Fitness function change curves in the simple scene

图 6(Fig. 6)

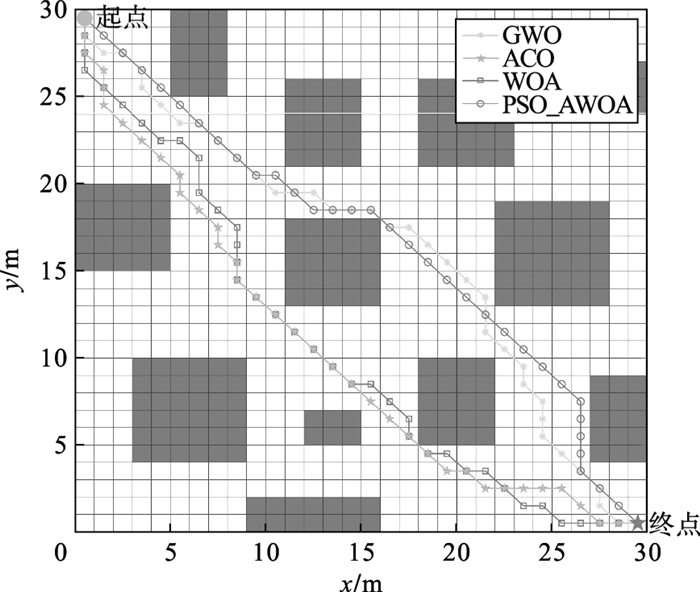图 6 复杂场景路径规划仿真结果Fig.6 Path planning results in the complex scene

图 7(Fig. 7)

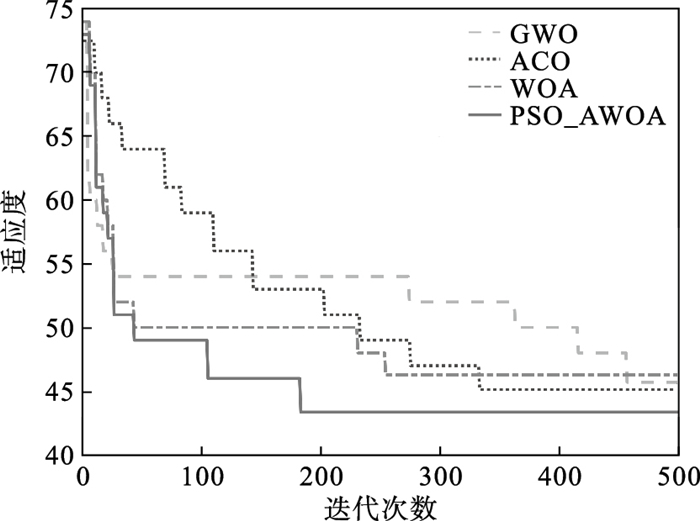图 7 复杂场景适应度函数变化曲线Fig.7 Fitness function change curves in the complex scene

表 2(Table 2)

表 2 简单场景仿真实验结果Table 2 Simulation experiment results in the simple scene 算法 耗时/s 路径长度/m 拐点数 GWO 0.34 45.11 18 ACO 1.84 43.35 11 WOA 0.26 44.53 14 PSO-AWOA 0.19 42.77 7

表 2 简单场景仿真实验结果 Table 2 Simulation experiment results in the simple scene

表 3(Table 3)

表 3 复杂场景仿真实验结果Table 3 Simulation experiment results in the complex scene 算法 耗时/s 路径长度/m 拐点数 GWO 0.45 45.70 21 ACO 2.47 45.13 14 WOA 0.33 46.28 17 PSO-AWOA 0.25 43.36 6

表 3 复杂场景仿真实验结果 Table 3 Simulation experiment results in the complex scene

3.3 实验结果与分析由图 4和图 5可以看出，在障碍物较少的简单环境中GWO，ACO，WOA和改进的PSO-AWOA均可以规划出较优的路径：GWO算法在迭代414次后获得最优路径，长度为45.11 m; ACO算法在迭代332次后获得最优路径，长度为43.35 m; WOA在迭代172次以后获得最优路径，长度为44.53 m; 而改进的PSO-AWOA在迭代117次后获得最优路径，长度为42.77 m.可以看出，ACO算法耗时最长，GWO算法迭代次数最多，改进的混合PSO-AWOA迭代次数最少，与WOA相比提高了32%，路径长度与ACO算法相比缩短了1.08 m，在收敛精度和收敛速度上都得到了提升.通过表 2对比4种算法的耗时和路径拐点数来看，改进后的算法耗时最短为0.19 s，相对于对比算法中规划耗时最短的WOA提高27%，路径拐点数为7，路径优于其他3种算法.
由图 6和图 7可以看出，在障碍物较多的复杂环境中GWO算法在迭代458次后获得最优路径，长度为45.70 m; ACO算法在迭代335次后获得最优路径，长度为45.13 m; WOA在迭代256次后获得最优路径，长度为46.28 m; 改进后的PSO-AWOA在迭代184次后获得了最优路径，长度为43.36 m.虽然GWO，ACO算法的路径长度优于WOA，但三者在收敛精度和收敛速度方面都不及改进后的PSO-AWOA，改进后的算法在迭代次数方面与对比算法中迭代次数最少的WOA相比效率提高了28%，路径长度方面与ACO算法相比缩短了1.77 m.在耗时和路径拐点数上来看，改进后的算法耗时最短为0.25 s，相对于对比算法中耗时最短的WOA提高了24%，路径拐点数为6，算法的性能在4种算法中为最优.
综合以上数据和分析说明，改进后的PSO-AWOA能够成功应用于机器人的路径规划问题，无论在简单场景还是复杂场景中，算法的收敛精度和收敛速度等性能均得到了提升.
4 结语本文针对机器人路径规划问题，提出一种基于混合粒子群和自适应惯性权重的改进鲸鱼优化算法.将寻优能力较强的粒子群算法引入鲸鱼优化算法的开发阶段，平衡算法的探索和开发能力.同时，通过引入自适应权重因子，使改进的算法在迭代初期具有较大的权重，充分探索未知空间，算法迭代后期权重呈非线性减小，算法可以在局部范围进行精细化搜索.最后，将改进后的算法应用于求解栅格地图环境机器人路径规划的问题，验证了算法可以更快地求解机器人的最佳无碰撞运动路径.后续的研究工作将在真实环境和动态障碍物环境中进一步探索算法性能的提升空间.
参考文献

[1]	Zhang H Y, Lin W M, Chen A X. Path planning for the mobile robot: a review[J]. Symmetry, 2018, 10(10): 450. DOI:10.3390/sym10100450
[2]	Chen Z, Wu H, Chen Y, et al. Patrol robot path planning in nuclear power plant using an interval multi-objective particle swarm optimization algorithm[J]. Applied Soft Computing, 2022, 116: 108192. DOI:10.1016/j.asoc.2021.108192
[3]	Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008
[4]	Zan J. Research on robot path perception and optimization technology based on whale optimization algorithm[J]. Journal of Computational and Cognitive Engineering, 2022, 1(4): 201-208.
[5]	Raiesdana S. A hybrid method for industrial robot navigation[J]. Journal of Optimization in Industrial Engineering, 2021, 14(1): 133-148.
[6]	蔡雨岑, 杜鹏桢. 基于平衡鲸鱼优化算法的无人车路径规划[J]. 控制与决策, 2021, 36(11): 2647-2655. (Cai Yu-cen, Du Peng-zhen. Path planning of unmanned ground vehicle based on balanced whale optimization algorithm[J]. Control and Decision, 2021, 36(11): 2647-2655.)
[7]	杨博, 李昌华, 李智杰, 等. 改进鲸鱼算法及其在路径规划的应用[J]. 计算机测量与控制, 2021, 29(2): 187-193. (Yang Bo, Li Chang-hua, Li Zhi-jie, et al. Improved whale optimization algorithm and application in path planning[J]. Computer Measurement & Control, 2021, 29(2): 187-193.)
[8]	Hou W, Xiong Z, Wang C, et al. Enhanced ant colony algorithm with communication mechanism for mobile robot path planning[J]. Robotics and Autonomous Systems, 2022, 148: 103949. DOI:10.1016/j.robot.2021.103949
[9]	Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Perth, 1995: 1942-1948.
[10]	Laskar N M, Guha K, Chatterjee I, et al. HWPSO: a new hybrid whale-particle swarm optimization algorithm and its application in electronic design optimization problems[J]. Applied Intelligence, 2019, 49(1): 265-291. DOI:10.1007/s10489-018-1247-6
[11]	Cheng X, Li J, Zheng C, et al. An improved PSO-GWO algorithm with chaos and adaptive inertial weight for robot path planning[J]. Frontiers in Neurorobotics, 2021, 15: 770361. DOI:10.3389/fnbot.2021.770361
[12]	Do?an L, Yüzge? U. Robot path planning using gray wolf optimizer[C]//Proceedings of the International Conference on Advanced Technologies, Computer Engineering and Science(ICATCES'18). Safranbolu, 2018: 11-13.
[13]	孔芝, 杨青峰, 赵杰, 等. 基于自适应调整权重和搜索策略的鲸鱼优化算法[J]. 东北大学学报(自然科学版), 2020, 41(1): 35-43. (Kong Zhi, Yang Qing-feng, Zhao Jie, et al. Adaptive adjustment of weights and search strategies-based whale optimization algorithm[J]. Journal of Northeastern University(Nature Science), 2020, 41(1): 35-43.)
[14]	Brand M, Masuda M, Wehner N, et al. Ant colony optimization algorithm for robot path planning[C]//2010 International Conference on Computer Design and Applications. Qinhuangdao, 2010: 436-440.
[15]	Zhang Z, He R, Yang K. A bioinspired path planning approach for mobile robots based on improved sparrow search algorithm[J]. Advances in Manufacturing, 2022, 10(1): 114-130. DOI:10.1007/s40436-021-00366-x
[16]	Liu M, Yao X, Li Y. Hybrid whale optimization algorithm enhanced with Lévy flight and differential evolution for job shop scheduling problems[J]. Applied Soft Computing, 2020, 87: 105954. DOI:10.1016/j.asoc.2019.105954
[17]	赵志刚, 林玉娇, 尹兆远. 基于自适应惯性权重的均值粒子群优化算法[J]. 计算机工程与科学, 2016, 38(3): 501-506. (Zhao Zhi-gang, Lin Yu-jiao, Yin Zhao-yuan. A mean particle swarm optimization algorithm based on adaptive inertia weight[J]. Computer Engineering & Science, 2016, 38(3): 501-506.)
[18]	Pattnaik S K, Mishra D, Panda S. A comparative study of meta-heuristics for local path planning of a mobile robot[J]. Engineering Optimization, 2022, 54(1): 134-152.