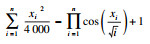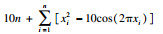西安交通大学 机械工程学院, 陕西 西安 710049
收稿日期:2022-04-26
作者简介:康岩松(1998-), 男, 河北保定人, 西安交通大学硕士研究生。
摘要:针对粒子群优化算法收敛速度慢、难以跳出局部最优解的问题, 使用多种策略对标准粒子群优化算法进行改进, 提出了混合动态粒子群优化(hybrid dynamic particle swarm optimization, HDPSO)算法.该算法按比例将粒子分为优势粒子和劣势粒子, 使用不同公式分别计算每个粒子的惯性权重;为每个粒子单独设置变异系数, 记录粒子相邻两次适应度变化较小的持续次数, 若大于阈值则开始累加变异系数, 变异系数达到上限值后重新设为初始值;在位置更新公式中引入加速系数提高算法的收敛速度.采用标准测试函数对HDPSO算法和其他粒子群优化算法进行了测试.结果表明HDPSO算法在收敛速度、寻优精度和稳定性方面具有明显的优势, 进而证明所提方法的有效性.
关键词:粒子群优化算法自适应惯性权重变异加速系数局部最优解
Improved Particle Swarm Optimization Algorithm Based on Multiple Strategies
KANG Yan-song, ZANG Shun-lai


School of Mechanical Engineering, Xi'an Jiaotong University, Xi'an 710049, China
Corresponding author: ZANG Shun-lai, E-mail: shawn@mail.xjtu.edu.cn.
Abstract: Aiming the problem of slow convergence speed and difficulty in jumping out of the local optimal solution of particle swarm optimization (PSO) algorithm, the standard PSO algorithm is improved with various strategies, and the hybrid dynamic PSO (HDPSO) algorithm is proposed. The algorithm divides particles into dominant particles and inferior particles according to a proportion, and uses different formulas to calculate the inertia weights of each particle respectively. Each particle is assigned a variation coefficient, and the duration of small fitness changes between adjacent particles is recorded. If this duration exceeds a threshold value, the variation coefficient is accumulated and reset to the initial value after reaching the upper limit. The acceleration coefficient is introduced into the position update formula to improve the convergence speed of the algorithm. The standard test functions are used to test the HDPSO algorithm and other PSO algorithms. The results show that HDPSO algorithm has obvious advantages in terms of convergence speed, optimization accuracy and stability, which further proves the effectiveness of the proposed method.
Key words: particle swarm optimization (PSO) algorithmadaptive inertia weightmutationacceleration coefficientlocal optimal solution
粒子群优化(particle swarm optimization, PSO)算法在1995年首次由Kennedy和Eberhart提出, 是一种简单有效的群智能优化算法[1].与其他智能算法相比, 参数少、容易实现是PSO算法的优势.但是在解决复杂问题时, PSO算法则暴露出收敛过早和跳出局部最优解比较困难等问题.
全局搜索和局部搜索之间的平衡是PSO算法成功求解优化问题的关键[2].Shi等[3]研究发现惯性权重是控制算法搜寻能力的核心参数, 惯性权重较大时粒子的搜寻步长也较大, 有助于对解空间进行全局搜索, 反之有助于对解空间进行局部搜索.PSO算法的惯性权重是常数, 粒子搜索能力单一, 无法适应复杂的非线性优化问题.因此对于惯性权重的改进受到****的关注.经典的调整方法有惯性权重随迭代次数线性递减(linear decrease inertia weight, LDIW)[4]和非线性递减[5-8], 使粒子群从全局搜索逐步过渡到局部搜索, 这在一定程度上提升了算法的寻优能力.虽然非线性策略比线性策略有更好的表现, 但两者都只是逐渐减小惯性权重[9], 不考虑全局最优是否朝着更好的方向改变.Farooq等[10]将迭代过程分为相等的两部分, 在每一部分重复LDIW的过程, 这种调整方法并没有改变惯性权重是随迭代次数递减的本质.Ozcan等[11]指出由于粒子群的搜索过程是不确定的, 难以预测接下来的搜索状态, 因此通过构造某个确定的函数来调整惯性权重使之符合不确定的搜索过程是比较困难的.也就是说,当需要较小的惯性权重时, 可能根据函数计算得到的惯性权重是较大的, 反之亦然.对此有****尝试利用迭代过程中的适应度等信息更新惯性权重.张选平等[12]提出使用进化速度因子h和粒子聚集度因子s计算惯性权重, 所有粒子使用一个惯性权重, 将其表示成h和s的函数, 随着粒子的分散或聚集实时更新惯性权重.Liu等[13]提出了新的惯性权重计算方法, 将其表示成适应度的函数, 为每个粒子单独赋予不同的惯性权重, 给粒子提供了与之相适应的搜索能力.张天泽等[14]结合RMSprop (root mean square propagation)算法与自适应惯性权重策略, 为粒子的每个维度单独计算惯性权重, 考虑了不同维度之间搜索的差异, 使得算法在面对多维复杂问题时有更优的表现.
融合其他算法是增强PSO算法寻优能力的常用手段.遗传算法的变异策略可以丰富种群的多样性, 从而使算法跳出局部最优解, 将其与PSO算法结合起来可以有效提高PSO算法跳出局部最优解的能力[15-17].混沌粒子群优化算法基于混沌理论增加了粒子的遍历性, 使算法能够更好地进行全局搜索[18-20].
Clerc[21]通过引入压缩因子对粒子的飞行速度进行约束, 既平衡了算法的全局和局部搜索能力, 又对算法的收敛速度有一定的提升.任子晖等[22]提出一种加速收敛的ACPSO算法, 并给出了加速因子的最佳组合形式.
本文提出了一种基于多种策略的改进粒子群优化算法,即混合动态粒子群优化(hybrid dynamic particle swarm optimization, HDPSO)算法, 该算法根据粒子适应度大小递增排列,按比例将粒子分为优势和劣势两种, 迭代过程中采用不同的公式分别计算每个粒子的惯性权重, 并引入了变异系数和加速系数, 以增强算法的寻优能力和提高算法的收敛速度.最后使用标准测试函数测试现有的粒子群优化算法和HDPSO算法, 结果表明HDPSO算法在收敛速度方面是最优的, 在寻优精度和稳定性方面也有明显优势.
1 粒子群优化算法PSO算法是模仿鸟类在觅食过程中个体之间的行为而开发的算法.初始化PSO算法时会随机生成一群粒子, 给定问题的潜在解用这些粒子表示.粒子相互之间会交换信息, 并根据这些信息计算下一次迭代时自己的飞行速度和位置, 经过多次迭代后就会得到问题的最优解.
对于一个D维的优化问题, 使用一个种群规模为N的PSO算法对其求解.在第t轮迭代时, 第i个粒子的位置表示为Xit=(x1i, x2i, …, xDi), 第i个粒子的飞行速度表示为Vit=(v1i, v2i, …, vDi)x, 第i个粒子搜寻到的历史最优位置称为个体最优解, 即pbestit=(p1i, p2i, …, pDi), 整个粒子群搜寻到的历史最优位置称为群体最优解, 即gbestt=(g1, g2, …, gD).每一轮迭代会根据当前的飞行速度、个体最优解和群体最优解计算下一次迭代时的飞行速度和位置, 公式为
 | (1) |
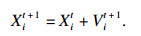 | (2) |
 | (3) |
2 改进粒子群优化算法2.1 自适应惯性权重公式(3)将劣势粒子的惯性权重统一设置成最大值, 忽略了劣势粒子之间的差异, 而且以群体适应度的平均值作为粒子分类标准也有待商榷.当样本的直方图是对称图形时,平均数才能反映样本的真实平均水平[23].众所周知, 在迭代过程中难以避免有少数粒子陷入局部最优解而一直保持在适应度较高的区域, 而且在迭代中后期大部分粒子出现聚集现象, 此时群体适应度的直方图是偏态的, 这会导致群体的适应度平均值高于大部分粒子.此时按照公式(3)计算, 会降低大部分粒子的惯性权重, 使得大部分粒子进行局部搜索,增大了算法跳出局部最优解的难度.
因此群体适应度的平均值不适合代表群体当前的状态, 应该按比例设置劣势粒子的数量.本文对公式(3)进行修改, 按比例选择适应度较大的粒子作为劣势粒子, 记为DCIW(dynamic calculation inertia weight)方法.这样可以保证每次迭代都有部分粒子的惯性权重取较大值, 进行大范围搜索, 而优势粒子也不会都取较小值, 既有利于局部搜索又可以增加跳出局部最优解的可能.此外劣势粒子的惯性权重不再是固定值, 具体计算公式为
 | (4) |
 | (5) |
公式(5)中没有出现的ωs与ωa和ωe有关, 而一般是给定ωs和ωe的值, 因此需要推导参数ωa的表达式.
为了保持连续性, 公式(5)应该在分段点取相同值, 此时b=1, 分别代入得
 | (6) |
 | (7) |
 | (8) |
 | (9) |
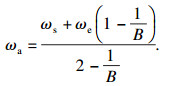 | (10) |
图 1(Fig. 1)
 | 图 1 两种惯性权重计算方法测试结果对比Fig.1 Comparison of test results of two inertia weight calculation methods |
为进一步比较两种方法的不同, 设粒子数量为100个,DCIW方法劣势粒子的占比为15%, 惯性权重取值的上下限分别为1.2和0.2.图 2a为两种方法随机初始化惯性权重的分布情况, 可以看出在AIWF方法中得到的惯性权重分布较为集中, 大约有半数粒子的惯性权重取上限值, 而DICW方法分布则更加均匀一些.在迭代后期经常出现的情况是部分粒子陷入适应度较高的局部最优解而大部分粒子相对聚集, 此时各个粒子惯性权重的分布情况如图 2b所示.设置10个粒子的适应度在(100, 110)之间, 90个粒子适应度在(0, 3)之间.群体适应度的平均值为11.85, DICW方法的分界点为2.55, 两者相差4.65倍.从图 2b中可以明显看出, 采用AIWF策略会让大部分粒子的惯性权重上限下降到0.4左右, 使这些粒子局限在小范围搜索, 若粒子群已陷入局部最优解将难以摆脱.而DICW方法使粒子的惯性权重仍然可以保持一个良好的分布, 惯性权重上限下降到0.7左右.因此即使当前群体陷入了局部最优解, 这些粒子当中仍然有部分粒子具有较高的惯性权重.如此兼顾了全局搜索和局部搜索, 也提高了算法摆脱局部最优解的能力.
图 2(Fig. 2)
 | 图 2 两种方法惯性权重初始与后期分布Fig.2 The initial and later distributions of the two weight methods (a)—初始期;(b)—后期. |
图 3是惯性权重关于适应度的函数图, 可以看出在AIWF方法中优势粒子的惯性权重的取值范围是ωe~ωs, 这对于优势粒子来说偏大.DICW方法克服了上述缺点, 优势粒子惯性权重的取值范围是ωe~ωa, 降低了优势粒子惯性权重的上限, 保证了优势粒子的局部搜索能力.
图 3(Fig. 3)
 | 图 3 两种自适应权重函数曲线Fig.3 Function curves of two adaptive weight methods |
2.2 变异系数遗传算法中的变异策略可以产生原有种群中不存在的基因模板, 这会极大地丰富种群多样性, 有助于个体摆脱局部最优解.PSO算法容易陷入局部最优解而导致求解问题失败, 在算法中加入变异策略是目前常用的改进方法.
适应度的变化量体现了粒子搜索区域的性质.适应度函数图如图 4所示, 包含了搜索过程中可能遇到的大部分情况.
图 4(Fig. 4)
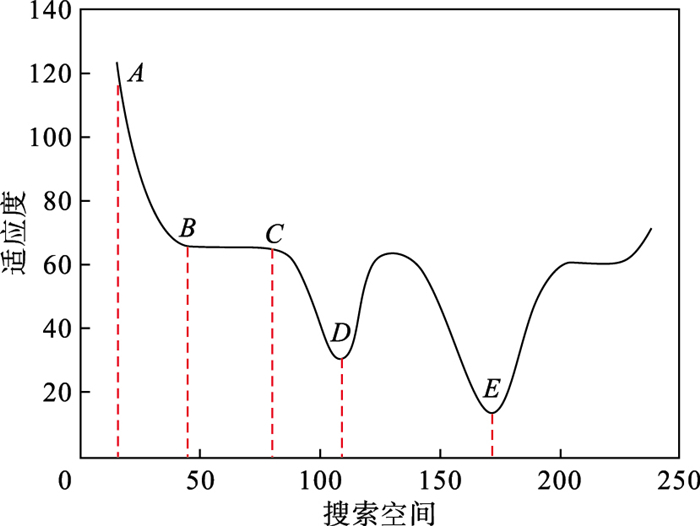 | 图 4 适应度函数曲线Fig.4 Curve of fitness function |
AB段函数斜率较大, 自变量有微小变化能够引起函数值较大变化.粒子在AB段搜索时能够顺利地向适应度减小的方向移动, 不需要提高变异系数.
BC段函数的斜率较小, 自变量有较大变化时函数值不会有明显变化, 该情况被定义为适应度变化较小.粒子可能会花费较长时间(迭代次数)才能摆脱BC段, 所以需要增加粒子变异概率, 期望通过变异使粒子快速摆脱该区域.
D点为局部最优解, 即在其邻域内的所有可行解里使目标函数取值最小的那个解,但是不保证优于不在此邻域内的其他可行解.当粒子进入D点附近时有较大概率在D点附近震荡, 粒子的适应度将保持在某个数值左右, 该情况也被定义为适应度变化较小, 需要通过变异使粒子摆脱该区域.
E点为全局最优解, 当粒子进入该区域时表现出的行为与进入D点附近时相同, 也会被算法判定为适应度变化较小从而使粒子变异, 这不是期望的.但是粒子群优化算法会单独保存全局最优解, 因此这并不影响最终的寻优结果.
综上所述, 粒子搜索过程中有三种情况被定义为适应度变化较小, 其中有两种情况希望通过变异摆脱.基于此本文提出一种新的变异策略, 在迭代过程中计算当前适应度与上一代适应度比值的绝对值R, 用R值作为判定标准: 当粒子在AB段时, R小于1, 说明粒子的适应度在变小, 搜索方向是正确的; 当粒子在BC段时, R小于1且接近1;当粒子在D点附近时, R在1左右变化, 且变化范围较小.因此选用0.9作为阈值, 将R大于0.9的粒子记为可能需要变异的粒子.
当粒子被记为可能需要变异的粒子时.不能说明粒子一定不能摆脱不利的搜索区域.需要给粒子一定的自主性.若连续一定次数后R仍大于0.9, 说明粒子无法依靠常规搜索摆脱不利的搜索区域, 此时可通过变异策略帮助粒子摆脱.
具体的变异策略为: 为每个粒子单独设置变异系数.所有粒子的初始变异系数是相同的, 且设置为一个较小的数值.当R值连续5次大于0.9时开始累加变异系数.每次迭代遍历每个粒子的全部维度, 同时产生一个(0, 1)之间的随机数, 若该数小于粒子的变异系数, 则按式(11)对该维度的参数进行变异.
群体的变异概率不会太高, 以此作为选用累计次数的标准.在使用标准测试函数进行测试时, 初始变异系数设为0.000 5, 变异系数累加量设为0.001, 累计次数设定为5次时群体变异概率在0.3%左右, 这样能够取得较高的求解成功率和较短的搜索时间[24].群体变异概率=变异次数/(迭代次数×粒子数×维度).针对不同问题可设置不同的次数, 一般来说5次是较为通用的值.
粒子会因变异系数增大而增加变异概率, 为控制变异概率上限, 需要限制变异系数的累积上限.当粒子变异5次后将变异系数设为初始值.
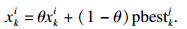 | (11) |
2.3 加速系数迭代算法的收敛趋势一般可分为三类: 收敛速度快、收敛速度慢和收敛过早, 如图 5所示.收敛速度快和收敛速度慢是指算法能够找到较为满意的解, 但是后者需要的迭代次数较多.收敛过早是指算法无法找到较为满意的解, 在迭代初期就陷入局部最优解, 直到算法结束也没有摆脱.
图 5(Fig. 5)
 | 图 5 迭代算法收敛趋势Fig.5 Convergence trend of iterative algorithm |
公式(2)中Xit的系数是1.0, 也就是说先前的搜索历史在迭代过程中会一直影响后续位置的更新.而粒子在迭代初期是大范围的全局搜索, 难免会经过一些适应度较高的位置.若这些较差的位置信息一直保留在迭代过程中, 可能会对后续位置更新产生较坏的影响, 导致粒子在搜索过程中多走许多弯路.因此本文引入加速系数, 按公式(12)更新位置.由于Xit的系数η小于1, 迭代若干次后初始阶段的位置信息会减小到非常小, 降低了前期大范围搜索对后期局部搜索的影响.
 | (12) |
公式(11)关注的是粒子短时搜索状态, 公式(12)关注的是粒子长期搜索状态.通过公式(12)可提高算法的收敛速度.
2.4 HDPSO算法伪代码HDPSO算法在PSO算法的基础上增加了自适应惯性权重策略、遗传算法的变异策略和加速系数, 其算法伪代码如表 1所示.
表 1(Table 1)
| 表 1 HDPSO算法伪代码 Table 1 Pseudo code of HDPSO |
3 数值仿真和对比分析为了验证HDPSO算法的寻优能力, 本文选取6个标准测试函数进行测试, 并与PSO算法、LDIWPSO算法、CFMPSO算法[21]、RMSPSO算法和CPSO算法的测试结果进行对比分析.
3.1 仿真条件及结果表 2给出了测试函数的定义, 其中F1~F2是单峰函数, 只存在一个极值点.F3是典型的病态函数, 虽然只有一个极值点, 但是很难收敛到该点.F4~F6是多峰函数, 存在大量的局部极值点.测试函数的维度均设为30, 最优值均为0.为了保证公平, 各个粒子群优化算法的参数设置基本一致, 粒子个数设为30, 迭代次数设为500, 其余参数设置如表 3和表 4所示.为了降低算法的随机性对测试结果的影响, 各个算法对每个测试函数独立运行50次, 表 5给出了测试结果的平均值、标准差、最优值、最差值、中位数等信息.
表 2(Table 2)
| 表 2 测试函数 Table 2 Benchmark functions |
表 3(Table 3)
| 表 3 粒子群优化算法基本参数 Table 3 Basic parameters of PSO algorithm | ||||||||||||||||||||||||||||||||||||||||
表 4(Table 4)
| 表 4 改进粒子群优化算法额外参数 Table 4 Additional parameters for improved PSO algorithm | ||||||||||||||||||||||||||||||||
表 5(Table 5)
| 表 5 6种粒子群优化算法的测试结果 Table 5 Test results of six kinds of PSO algorithms |
3.2 仿真结果分析分析表 5数据可知, HDPSO算法在平均值这一项全部是最优的, RMSPSO算法次之, 这2种算法相比其他算法寻优结果精度均至少提升了两个数量级, 而CPSO算法在6个测试函数中均是最差的.在标准差中, HDPSO算法除了在F6上比RMSPSO算法略低, 在其他测试函数上均是最小的, CPSO算法仅在F4上的标准差比CFMPSO算法低, 在其他测试函数中的表现均较差, 说明本算法对于单峰函数和多峰函数的寻优能力都有较高的稳定性.在最优值这一项中, HDPSO算法明显优于其他算法, 仅有F2和F3的寻优结果比RMSPSO算法略高.在最差值这一项中, HDPSO对所有测试函数均是最优的.分析最优值和最差值可知,HDPSO的寻优精度具有较高的上下限.在中位数这一项中, HDPSO算法和RMSPSO算法均明显优于其他算法.RMSPSO算法只有F2的寻优结果明显优于HDPSO算法, F6的优化结果与HDPSO相差不大.综合分析各项统计数据, 可以发现CPSO算法在30维度时的测试结果与其他粒子群优化算法有较大差距.
为方便对比各个算法的收敛情况, 图 6给出了各个算法求解6个测试函数时适应度的曲线图.从图 6中可以明显发现, 对于全部的测试函数, HDPSO算法均收敛到一个较为满意的解, 而CPSO算法在所有测试函数上均有过早收敛的现象.以F4的测试过程为例, 只有RMSPSO算法和HDPSO算法收敛到了最优解附近, 其他算法均被困在了局部最优解.在收敛速度方面, HDPSO算法是最快的, RMSPSO算法和CFMPSO算法在迭代初期的收敛速度基本一致,但是CFMPSO算法收敛过早, 与LDIWPSO算法收敛到相同结果, 没有求解成功.PSO算法的收敛速度在迭代前期与RMSPSO算法接近, 中后期便显露出收敛缓慢的不足.CPSO算法的迭代曲线呈现阶梯状, 说明在搜索过程中多次陷入局部最优解, 并且花费较多的迭代次数才摆脱局部最优解, 但最终仍没有得到一个较为满意的解.RMSPSO算法和HDPSO算法迭代500次平均用时分别为0.33 s和0.25 s.RMSPSO算法迭代400次左右得到最优解, 而HDPSO算法迭代120次左右得到最优解.假设每次迭代的用时相等, 则RMSPSO算法得到最优解用时0.264 s, 而HDPSO算法仅用时0.06 s, 说明加速系数能够提高算法的收敛速度, 节省算法寻优的时间.硬件配置为Intel(R) Core(TM) i5-10400F CPU @ 2.90 GHz, 内存16GB, 软件版本为MATLAB R2019b.
图 6(Fig. 6)
 | 图 6 6种粒子群优化算法迭代过程Fig.6 Iterative process of the six kinds of PSO algorithms (a)—F1;(b)—F2;(c)—F3;(d)—F4;(e)—F5;(f)—F6. |
此外, 本文进行测试时发现是否使用加速系数(加速系数设为1.0即为不使用)对不同测试函数的测试结果具有不同的影响.表 6给出了加速系数为1.0时的测试结果.对比表 5和表 6数据, 可以发现加速系数仅对测试函数F2有负面影响, 而对其他5个测试函数的寻优结果均有明显的提升作用.这说明在解决实际问题时需要视情况决定加速系数的取值.
表 6(Table 6)
| 表 6 加速系数为1.0时HDPSO测试结果 Table 6 Results of HDPSO when acceleration factor is 1.0 |
4 结论1) 结合3种策略对粒子群优化算法进行改进,自适应惯性权重能够使每个粒子搜索能力差异化;变异系数能够提高算法跳出局部最优解的能力;加速系数能够提高算法的收敛速度.
2) 使用标准测试函数对改进算法进行测试, 结果表明HDPSO算法在收敛速度方面是最优的, 在寻优精度和稳定性方面也有明显优势.
3) 加速系数对于某些问题有负面影响, 需要根据实际情况合理取值.
4) 若B值较大, 说明有较多的粒子陷入局部最优解, 是否将其忽略而仅用剩余粒子来计算B值, 这在未来工作中需要进一步研究分析.
参考文献
| [1] | Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceeding of IEEE International Conference on Neural Networks. Piscataway: IEEE, 1995: 1492-1498. |
| [2] | Shi Y H, Eberhart R. Fuzzy adaptive particle swarm optimization[C]//Proceedings of the 2000 Congress on Evolutionary Computation. Seoul, 2000: 101-106. |
| [3] | Shi Y H, Eberhart R. Parameter selection in particle swarm optimization[C]//Evolutionary Programming Ⅶ. 7th International Conference, EP98. San Diego, 1998: 591-600. |
| [4] | Shi Y H, Eberhart R. A modified particle swarm optimizer[C]// 1998 IEEE International Conference on Evolutionary Computation. Anchorage, 1998: 69-73. |
| [5] | Chatterjee A, Siarry P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J]. Computers & Operations Research, 2006, 33(3): 859-871. |
| [6] | Tang Y, Wang Z D, Fang J A. Feedback learning particle swarm optimization[J]. Applied Soft Computing, 2011, 11(8): 4713-4725. DOI:10.1016/j.asoc.2011.07.012 |
| [7] | Jiang C W, Etorre B. A self-adaptive chaotic particle swarm algorithm for short term hydroelectric system scheduling in deregulated environment[J]. Energy Conversion and Management, 2005, 46(17): 2689-2696. DOI:10.1016/j.enconman.2005.01.002 |
| [8] | Amoshahy M J, Shamsi M, Sedaaghi M H. A novel flexible inertia weight particle swarm optimization algorithm[J]. PLoS One, 2016, 11(8): e161558. |
| [9] | Houssein E, Gad A, H K, et al. Major advances in particle swarm optimization: theory, analysis, and application[J]. Swarm and Evolutionary Computation, 2021, 63: 100868. DOI:10.1016/j.swevo.2021.100868 |
| [10] | Farooq M, Ahmad A, Hameed A. Opposition-based initialization and a modified pattern for Inertia Weight(IW)in PSO[C]//2017 IEEE International Conference on Inovations in Intelligent Systems and Applications. Gdynia, 2017: 96-101. |
| [11] | Ozcan E, Mohan C K. Particle swarm optimization: surfing the waves[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington D C, 1999: 1939-1944. |
| [12] | 张选平, 杜玉平, 秦国强, 等. 一种动态改变惯性权的自适应粒子群算法[J]. 西安交通大学学报, 2005, 39(10): 1039-1042. (Zhang Xuan-ping, Du Yu-ping, Qin guo-qiang, et al. Adaptive particle swarm algorithm with dynamically changing inertia weight[J]. Journal of Xi'an Jiaotong University, 2005, 39(10): 1039-1042.) |
| [13] | Liu B, Wang L, Jin Y H, et al. Improved particle swarm optimization combined with chaos[J]. Chaos, Solitons & Fractals, 2005, 25(5): 1261-1271. |
| [14] | 张天泽, 李元香, 项正龙, 等. 基于RMSprop的粒子群优化算法[J]. 计算机工程与设计, 2021, 42(3): 642-648. (vZhang Tian-ze, Li Yuan-xiang, Xiang Zheng-long, et al. Paritcle swarm optimization algorithm based on RMSprop method[J]. Computer Engineering and Design, 2021, 42(3): 642-648.) |
| [15] | 陈璐璐, 邱建林, 陈燕云, 等. 改进的遗传粒子群混合优化算法[J]. 计算机工程与设计, 2017, 38(2): 395-399. (Chen Lu-lu, Qiu Jian-lin, Chen Yan-yun, et al. Improved hybrid optimization algorithms based on genetic algorithm and particle swarm optimization[J]. Computer Engineering and Design, 2017, 38(2): 395-399.) |
| [16] | Chen Y G, Li L X, Peng H P, et al. Particle swarm optimizer with two differential mutation[J]. Applied Soft Computing, 2017, 61: 314-330. DOI:10.1016/j.asoc.2017.07.020 |
| [17] | Zhou X J, Yang C H G. A particle swarm optimization algorithm with variable random functions and mutation[J]. Acta Automatica Sinica, 2014, 40(7): 1339-1347. DOI:10.1016/S1874-1029(14)60015-X |
| [18] | Ren W Z, Cao J. A chaos particle swarm optimization ranging correction location in complex environment[J]. Journal of China Universities of Posts and Telecommunications, 2012, 19: 1-5. |
| [19] | Gandomi A, Yun G J, Yang X S, et al. Chaos-enhanced accelerated particle swarm optimization[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(2): 327-340. DOI:10.1016/j.cnsns.2012.07.017 |
| [20] | Pluhacek M, Senkerik R, Davendra D. Chaos particle swarm optimization with ensemble of chaotic systems[J]. Swarm and Evolutionary Computation, 2015, 25: 29-35. |
| [21] | Clerc M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization[C]//Proceedings of the 1999 Congress on Evolutionary Computation. Washington D C, 1999: 1951-1957. |
| [22] | 任子晖, 王坚. 加速收敛的粒子群优化算法[J]. 控制与决策, 2011, 26(2): 201-206. (Ren Zi-hui, Wang Jian. Accelerate convergence particle swarm optimization algorithm[J]. Control and Decision, 2011, 26(2): 201-206.) |
| [23] | Freedman D, Pisani R, Purves R. Statistics[M]. New York: William Warder Norton & Company, 2007. |
| [24] | 李宁, 刘飞, 孙德宝. 基于带变异算子粒子群优化算法的约束布局优化研究[J]. 计算机学报, 2004, 27(7): 897-903. (Li Ning, Liu Fei, Sun De-bao. A study on the particle swarm optimization with mutation operator constrained layout optimization[J]. Chinese Journal of Computers, 2004, 27(7): 897-903.) |