
 , 杜姗珊3
, 杜姗珊3 1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室,辽宁 沈阳 110819;
3. 瓦房店轴承集团有限责任公司 风电轴承事业部,辽宁 瓦房店 116300
收稿日期:2022-04-24
基金项目:国家自然科学基金资助项目(51975511, 51975110, U22B2087)。
作者简介:胡兵(1997-), 男, 山东菏泽人, 东北大学硕士研究生;
黄贤振(1982-), 男, 山东定陶人, 东北大学教授, 博士生导师。
摘要:以某2 MW风电轴承为例,给出四自由度载荷作用下圆柱滚子轴承疲劳寿命的数学模型,通过Romax软件分析结果验证所建模型的准确性.按轴承最小额定寿命建立极限状态方程,采用自适应克里金与蒙特卡罗模拟相结合(adaptive Kriging-Monte Carlo simulation, AK-MCS)进行轴承疲劳寿命可靠性灵敏度分析.结果表明: 轴承游隙、弹性模量、密度增大,轴承失效概率增大;轴承节圆、滚子有限长度增大,轴承失效概率减小;游隙对可靠性的影响最为明显,弹性模量、密度、滚子有限长度次之,节圆影响最小.
关键词:圆柱滚子轴承轴承疲劳寿命自适应克里金与蒙特卡罗模拟可靠性灵敏度分析风力发电机
Reliability Sensitivity Analysis of the Fatigue Life of Wind Turbine Bearings
HU Bing1, HUANG Xian-zhen1,2

 , DU Shan-shan3
, DU Shan-shan3 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems, Ministry of Education, Northeastern University, Shenyang 110819, China;
3. Wind Power Bearing Division, Wafangdian Bearing Group Co., Ltd., Wafangdian 116300, China
Corresponding author: HUANG Xian-zhen, E-mail: xzhhuang@mail.neu.edu.cn.
Abstract: A 2MW wind turbine bearing is taken as an example, and the mathematical model of the fatigue life of cylindrical roller bearings under four degrees of freedom load is given. The accuracy of the model is verified by Romax software analysis results. The limit state equation is established according to the minimum rated life of the bearing, and the adaptive Kriging-Monte Carlo simulation (AK-MCS) method is used to analyze the reliability sensitivity of the bearing′s fatigue life. The results show that the bearing failure probability increases with the increase of bearing clearance, elastic modulus and density. With the increase of bearing pitch and roller finite length, the failure probability of bearings decreases. The influence of clearance on reliability is the most obvious, followed by elastic modulus, density and roller finite length, and the influence of pitch is the least.
Key words: cylindrical roller bearingbearing fatigue lifeAK-MCSreliability sensitivity analysiswind turbine
在我国,由于国家政策使得以风力发电为主的清洁能源行业迅速发展[1].同时,风力发电机故障频发.根据调查显示,在风力发电机故障原因中,约50%是由轴承失效因素引起的[2],对轴承疲劳寿命进行分析显得尤为重要.
针对轴承的疲劳寿命问题,许多研究人员提供了大量理论依据.Kabus等[3]采用弹性半空间理论计算滚子接触应力,计算了滚动轴承疲劳寿命.Warda等[4]利用三维弹性体接触方法计算滚子接触应力,对轴承疲劳寿命进行预测.Tong等[5]分析了误差源对轴承疲劳寿命的影响,但未对误差源进行可靠性分析.Cretu[6]研究了滚子几何形状、游隙、偏转角和工作载荷对滚子接触应力的影响, 通过切片技术计算了轴承疲劳寿命.Li等[7]基于损伤演化方程研究了接触载荷对轴承疲劳寿命的影响.Duan等[8]建立了轴承疲劳寿命耦合模型,探究了高速圆柱滚子轴承偏心角对轴承性能的影响.Zhao等[9]考虑了径向力、轴向力和弯矩的耦合效应,给出了多自由度载荷下轴承疲劳寿命的预测方法.虽然轴承疲劳寿命的研究趋于成熟,但传统轴承疲劳寿命分析方法认为轴承结构参数是确定的.实际上,受加工、制造和装配工艺的影响,轴承结构参数具有随机性[10],使得理论分析与实际情况不符;此外,将轴承疲劳寿命模型与AK-MCS可靠性分析方法相结合的研究鲜有报道.
针对上述问题,本文以某2MW风电轴承为研究对象,建立圆柱滚子轴承疲劳寿命模型——四自由度拟静力学模型,按风电行业标准,给出轴承疲劳寿命的极限状态方程,通过AK-MCS方法计算轴承疲劳寿命的可靠度及灵敏度,从而确定轴承结构参数对轴承疲劳寿命的影响程度,为提高风机轴承可靠度提供理论依据.
1 圆柱滚子轴承疲劳寿命模型1.1 轴承接触载荷模型为了得到计算轴承疲劳寿命所需要的各滚子接触载荷,建立了图 1所示的圆柱滚子轴承全局坐标系和图 2所示的滚子局部坐标系.在图 1和图 2中,FT= [Fx, Fy, Mx, My]和ΔT= [Δx, Δy, γx, γy] 分别为轴承外载荷和轴承内圈位移,UT= [Δu, γu]和VT= [Δv, γv] 分别为轴承内圈在滚子处的位移和滚子位移.
图 1(Fig. 1)
 | 图 1 全局坐标系Fig.1 Global coordinate system |
图 2(Fig. 2)
 | 图 2 局部坐标系Fig.2 Local coordinate system (a)—滚子方位角;(b)—滚子变形. |
轴承内圈位移在全局坐标系与局部坐标系下的映射关系为
 | (1) |
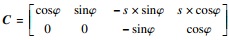
如图 3所示,为了对滚子运用切片技术,需对滚子受力分析和构建滚子薄片变形协调关系.其中,lk为第k个薄片到h轴的距离(k=1, 2, …, ns),hk为第k个薄片凸度量,ns为薄片总数,w为单个薄片的厚度.在外载荷作用下,滚子承受离心力为Fc、滚子与内(外)滚道之间的接触力为Qi(Qe)以及滚子与内(外)滚道之间的接触力矩为Mi(Me).
图 3(Fig. 3)
 | 图 3 滚子切片技术Fig.3 Roller slicing technique |
为了获得滚子各薄片的接触力,需在实际接触区域内对滚子进行切片处理,第k个薄片上的接触力qk为
 | (2) |
 | (3) |
滚子与滚道之间的初始变形量Δ0、相对角位移β以及接触变形量Δk分别为
 | (4) |
 | (5) |
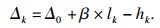 | (6) |
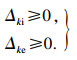 | (7) |
 | (8) |
 | (9) |
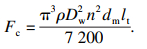 | (10) |
联立式(1)~式(10),可得到轴承内圈的平衡方程为
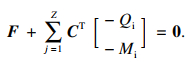 | (11) |
图 4(Fig. 4)
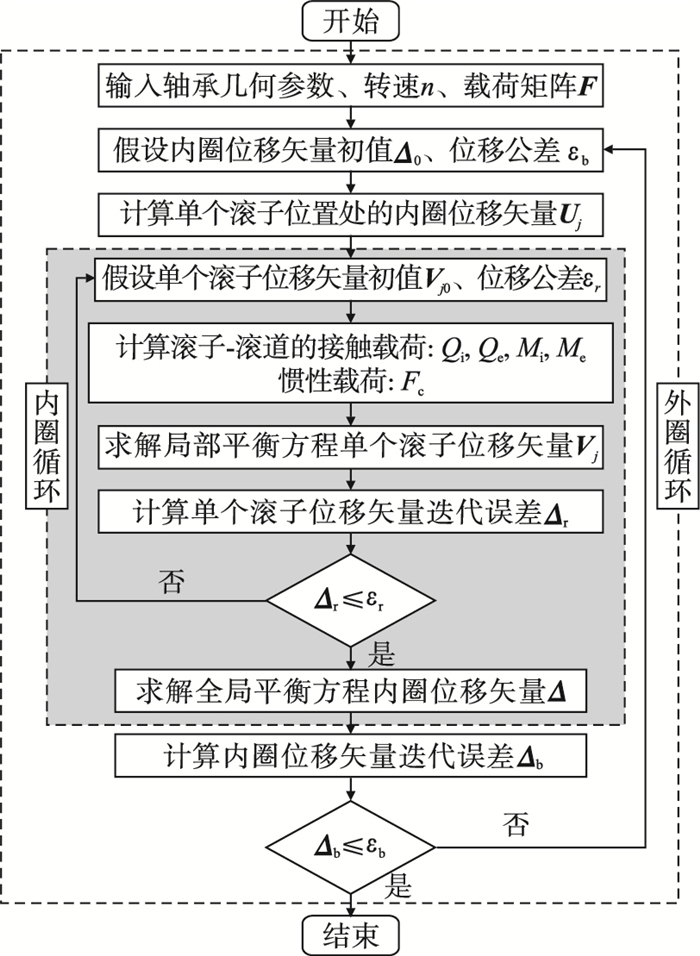 | 图 4 求解流程图Fig.4 Solution flow chart |
1.2 疲劳寿命计算轴承内、外滚道额定动载荷分别为
 | (12) |
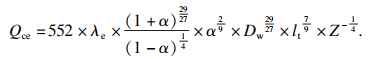 | (13) |
 | (14) |
 | (15) |
 | (16) |
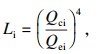 | (17) |
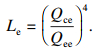 | (18) |
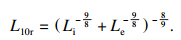 | (19) |
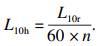 | (20) |
 | (21) |
当函数G>0时,安全域S={x: g(x)>0},则轴承疲劳寿命大于30 000 h,风力发电机正常工作;当函数G < 0时,故障域F={x: g(x) < 0},则轴承疲劳寿命小于30 000 h,导致风力发电机故障.
轴承疲劳寿命的失效概率Pf为
 | (22) |
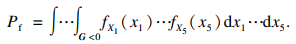 | (23) |
2.2 Kriging代理模型在实际工程问题中,Monte Carlo模拟方法通常用于可靠性分析,但运算量大.为提高计算效率,通过Kriging代理模型对轴承疲劳寿命模型进行可靠性分析.Kriging代理模型为
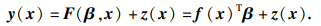 | (24) |
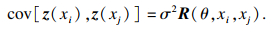 | (25) |
Kriging代理模型的预测值为
 | (26) |
 | (27) |
 | (28) |
 | (29) |
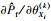
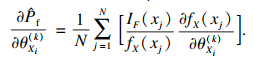 | (30) |
对等式(30)两边计算数学期望,则
 | (31) |
 | (32) |
 | (33) |
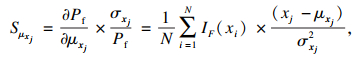 | (34) |
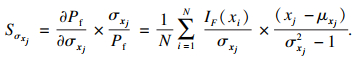 | (35) |
图 5为AK-MCS方法分析灵敏度流程,其步骤:
图 5(Fig. 5)
 | 图 5 AK-MCS方法流程图Fig.5 AK-MCS method flow chart |
1) 由联合概率密度函数fX(x)生成随机变量X的Monte Carlo样本池Smc,样本池Smc包括Nmc组随机变量;
2) 从样本池Smc中选取N1样本点,代入轴承疲劳寿命模型中得到基本额定寿命,形成初始训练集Tmc;
3) 根据初始训练集Tmc的数据,通过Matlab中DACE工具箱构建初始Kriging代理模型Gk;
4) 当满足U学习函数收敛准则时,即
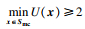
 | (36) |
6) 利用式(29)~式(33)计算可靠性局部灵敏度和变异系数;
7) 当满足AK-MCS方法收敛准则时,即
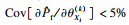
3 数值计算3.1 轴承疲劳寿命模型验证本文所研究的2MW风力发电机安装在嘉峪关市,轴承型号为NU2232,轴承结构如图 6所示,相关参数见表 1.
图 6(Fig. 6)
 | 图 6 NU2232结构图Fig.6 NU2232 structure diagram |
表 1(Table 1)
| 表 1 轴承参数 Table 1 Bearing parameters |
在额定工况下,轴承的工作载荷为105 kN,转速为1 530 r/min,嘉峪关极限阵风达到52.5 m/s,轴承转速可达5 000 r/min.将轴承承受的载荷从90 kN增加到130 kN,转速从500 r/min增加到5 000 r/min,用于验证模型准确性.通过Romax软件建立风机主轴轴系简化模型,进行网格划分,连接相关节点,如图 7所示.
图 7(Fig. 7)
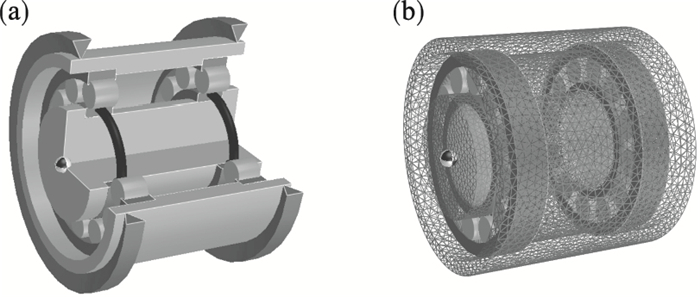 | 图 7 轴系示意图Fig.7 Schematic diagram of the shaft system (a)—轴系简化模型;(b)—网格划分. |
将轴承疲劳寿命模型的数值计算结果与Romax软件分析结果进行对比.结果表明:①在额定工况下,即Fx=105 kN,n=1 530 r/min,计算最大误差不超过1 %;内滚道承载区为180°,最大接触载荷为25.26 kN;由于惯性载荷的作用,导致外滚道承载区为360°,最大接触载荷为25.46 kN;如图 8所示.②径向力Fx从90 kN增加到130 kN,轴承承载区接触载荷显著增加,轴承承载区未发生变化,其中内滚道最大接触载荷从21.76 kN增加到31.09 kN, 如图 9所示.③游隙Pd从0增加到30 μm,轴承承载区接触载荷显著增加;其中内滚道最大接触载荷从25.26 kN增加到27.77 kN,承载区从180°减少到140°;如图 10所示.④转速n从500 r/min增加到5 000 r/min,未导致轴承承载区发生变化;由于惯性载荷作用,外滚道接触载荷从25.24 kN增加到27.69 kN, 如图 11所示.⑤转速n从500 r/min增加到5 000 r/min、游隙Pd从0增加到30 μm,轴承基本额定寿命L10h从1.11×105 h减少到7.53×103 h;如图 12所示.
图 8(Fig. 8)
 | 图 8 接触载荷雷达图Fig.8 Radar chart of contact load (a)—内滚道接触载荷;(b)—外滚道接触载荷. |
图 9(Fig. 9)
 | 图 9 力对内滚道接触载荷影响Fig.9 Influence of force on the inner raceway contact load |
图 10(Fig. 10)
 | 图 10 游隙对内滚道接触载荷影响Fig.10 Influence of clearance on the contact load of inner race |
图 11(Fig. 11)
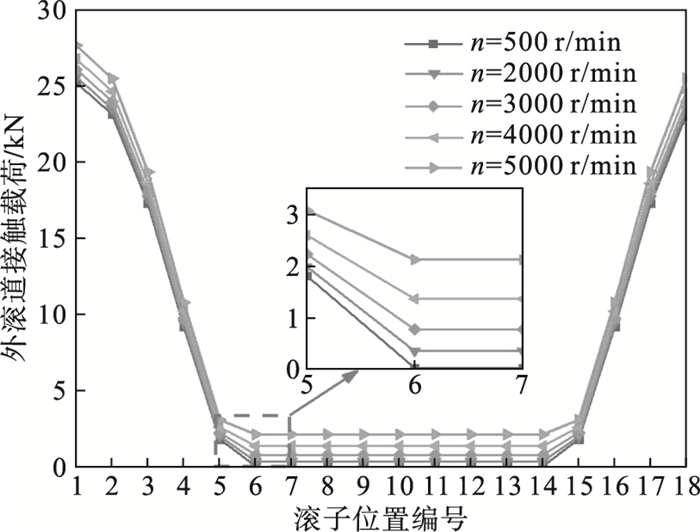 | 图 11 转速对外滚道接触载荷影响Fig.11 Influence of rotational speed on the outer raceway contact load |
图 12(Fig. 12)
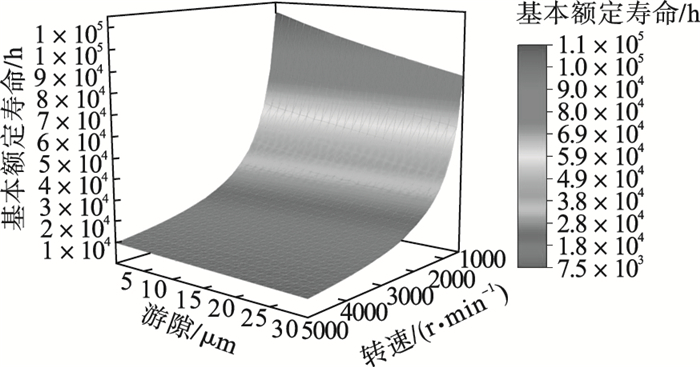 | 图 12 游隙及转速对轴承疲劳寿命影响Fig.12 Influence of clearance and rotational speed on the bearing′s fatigue life |
3.2 轴承疲劳寿命可靠性灵敏度分析轴承结构参数X=[dm, Pd, lt, E, ρ]T具有随机性,且符合正态分布, 各参数对应的均值和标准差如表 2所示.在Fx=105 kN,n=1 530 r/min的额定工况下,通过拉丁超立方抽样方法,抽取50组随机变量样本,作为自适应Kriging代理模型的输入量;通过轴承疲劳寿命模型得到轴承疲劳寿命L10h,作为自适应Kriging代理模型的输出量;构建自适应Kriging代理模型.抽取100组随机变量作为测试样本,分别代入轴承疲劳寿命模型和自适应Kriging代理模型中计算,得到100组L10h的对比情况,如图 13所示.图 14显示了自适应Kriging代理模型的预测误差,最大误差为0.058%,验证了构建的自适应Kriging代理模型的有效性.
表 2(Table 2)
| 表 2 随机变量表 Table 2 Table of random variables |
图 13(Fig. 13)
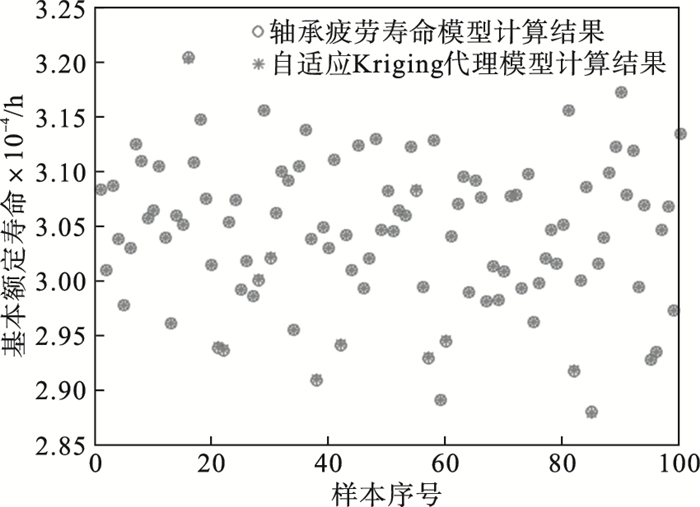 | 图 13 两种模型计算结果对比Fig.13 Comparison of the calculation results of the two models |
图 14(Fig. 14)
 | 图 14 自适应Kriging代理模型的预测误差Fig.14 Prediction errors of adaptive Kriging surrogate models |
为探究转速n对轴承疲劳寿命可靠度的影响,在径向力Fx=105 kN、游隙Pd=0条件下,用AK-MCS方法进行可靠性分析,得到了轴承疲劳寿命可靠度随转速n的变化规律.当转速n=1 530 r/min时,可靠度为1,即轴承疲劳寿命大于30 000 h,风力发电机正常工作;当转速n=1 600 r/min时,可靠度为0.999 8,轴承开始失效,发生疲劳失效概率较低;随着转速的增加,可靠度降低,当转速n=1 900 r/min时,可靠度为0,轴承完全失效,风力发电机停机,如图 15所示.
图 15(Fig. 15)
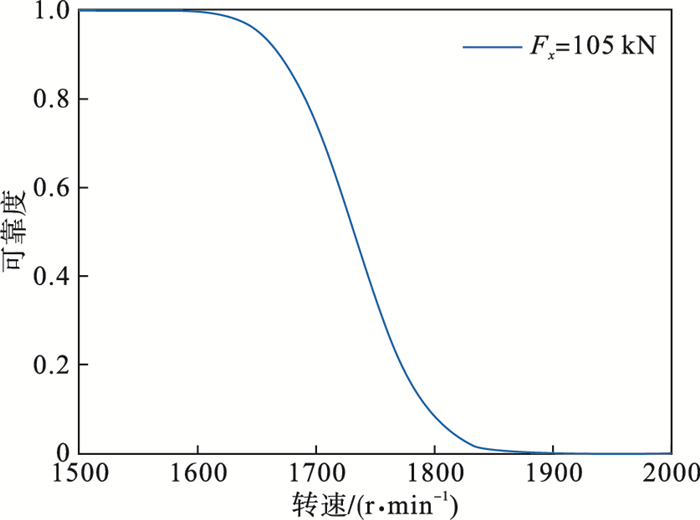 | 图 15 转速对轴承疲劳寿命可靠度影响Fig.15 Influence of rotational speed on the reliability of the bearing′s fatigue life |
为探究径向力Fx对轴承疲劳寿命可靠度的影响,在转速n=1 530 r/min、游隙Pd=0条件下,用AK-MCS方法进行可靠性分析,得到了轴承疲劳寿命可靠度随径向力Fx的变化规律.当径向力Fx=105 kN时,可靠度为1,即轴承疲劳寿命大于30 000 h,风机正常工作;当径向力Fx=106.5 kN时,可靠度为0.999 5,轴承开始失效,发生疲劳失效概率较低;随着径向力的增加,可靠度降低,当径向力Fx=111 kN时,可靠度为0,轴承完全失效,风力发电机停机, 如图 16所示.
图 16(Fig. 16)
 | 图 16 径向力对轴承疲劳寿命可靠度影响Fig.16 Influence of radial force on the reliability of the bearing′s fatigue life |
为探究轴承随机变量对轴承疲劳寿命影响程度,用AK-MCS方法进行可靠性灵敏度分析.随着游隙Pd、弹性模量E、密度ρ的增大,轴承疲劳失效概率也随之增大;随着节圆dm、滚子有限长度lt的增大,轴承疲劳失效概率随之减小,其中轴承疲劳失效概率受游隙的影响最大,占所有随机变量的89.49%, 如图 17~图 18所示.因此,在加工轴承的过程中,应严格控制轴承内、外滚道沟底直径及滚子直径的加工误差,保证加工精度.
图 17(Fig. 17)
 | 图 17 均值可靠性灵敏度Fig.17 Mean reliability sensitivity |
图 18(Fig. 18)
 | 图 18 随机变量占比图Fig.18 Proportion of random variables |
4 结论1) 本文以某2MW风电轴承为例,建立了圆柱滚子轴承疲劳寿命的数学模型,通过与Romax软件计算结果对比,验证轴承疲劳寿命模型的有效性,且误差控制在1%以内.
2) 考虑了圆柱滚子轴承在制造中存在的随机因素: 内(外)滚道沟底直径、滚子直径、滚子长度、密度、弹性模量,建立轴承疲劳寿命极限状态方程,通过AK-MCS方法对轴承疲劳寿命进行可靠性分析.
3) 随转速及载荷的增大,轴承疲劳失效概率随之增大;轴承游隙、弹性模量、密度增大,轴承疲劳失效概率增大;轴承节圆、滚子有限长度增大,轴承疲劳失效概率减小,游隙对轴承疲劳寿命可靠性的影响最为明显,占所有随机变量的89.49%,弹性模量、密度、滚子有限长度次之,节圆影响最小.
参考文献
| [1] | 李俊峰, 施鹏飞, 高虎. 中国风电发展报告2010[M]. 海口: 海南出版社, 2010. (Li Jun-feng, Shi Peng-fei, Gao Hu. China wind power development report 2010[M]. Haikou: Hainan Press, 2010.) |
| [2] | Keller J, Sheng S, Cotrell J, et al. Wind turbine drivetrain reliability collaborative workshop: a recap[R]. National Renewable Energy Lab(NREL), Golden, 2016. |
| [3] | Kabus S, Hansen M R, Mouritsen O. A new quasistatic multi-degree of freedom tapered roller bearing model to accurately consider non-Hertzian contact pressures in time-domain simulations[J]. Multi-body Dynamics, 2014, 228: 111-125. |
| [4] | Warda B, Chudzik A. Fatigue life prediction of the radial roller bearing with the correction of roller generators[J]. International Joural of Mechanical Sciences, 2014, 89: 299-231. DOI:10.1016/j.ijmecsci.2014.09.015 |
| [5] | Tong V C, Kwon S W, Hong S W. Fatigue life of cylindrical roller bearings[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part J: Journal of Engineering Tribology, 2016, 231(5): 623-636. |
| [6] | Cretu S S. The effect of primary loading on fatigue life of cylindrical roller bearings[C]//IOP Conference Series: Materials Science and Engineering. Pennsylvania: IOP Publishing, 2016, 147(1): 012011. |
| [7] | Li F, Hu W, Meng Q, et al. A new damage-mechanics-based model for rolling contact fatigue analysis of cylindrical roller bearing[J]. Tribology International, 2018, 120: 105-114. DOI:10.1016/j.triboint.2017.12.001 |
| [8] | Duan H, Song J, Wang Z. Lubrication and fatigue life evaluation of high-speed cylindrical roller bearing under misalignment[J]. Mathematical Problems in Engineering, 2020, 2020: 1-11. |
| [9] | Zhao L H, Li Q C, Feng J Z, et al. Service life prediction method for wheel-hub-bearing under random multi-axial wheel loading[J]. Engineering Failure Analysis, 2021, 122: 105211. DOI:10.1016/j.engfailanal.2020.105211 |
| [10] | 黄贤振, 朱会彬, 姜智元, 等. 角接触球轴承打滑可靠性灵敏度分析[J]. 东北大学学报(自然科学版), 2021, 42(12): 1731-1738. (Huang Xian-zhen, Zhu Hui-bin, Jiang Zhi-yuan, et al. Sensitivity analysis of slip reliability of angular contact ball bearings[J]. Journal of Northeastern University (Natural Science), 2021, 42(12): 1731-1738. DOI:10.12068/j.issn.1005-3026.2021.12.009) |
| [11] | Biswanath N, Douglas L. Positioning bearings for high-speed shafts and high-speed intermediate shafts of wind turbine gearboxes[J]. Electrical Manufacturing, 2009(9): 76-78. |
| [12] | Huang X Z, Li Y X, Zhang Y M, et al. A new direct second-order reliability analysis method[J]. Applied Mathematical Modelling, 2018, 55: 68-80. DOI:10.1016/j.apm.2017.10.026 |
| [13] | 杨周, 朴银成, 权哲优. 盘式制动器热-机耦合渐变可靠性灵敏度分析[J]. 东北大学学报(自然科学版), 2022, 43(1): 48-55, 64. (Yang Zhou, Pu Yin-cheng, Quan Zhe-you. Sensitivity analysis of thermal-mechanical coupling reliability of disc brake[J]. Journal of Northeastern University(Natural Science), 2022, 43(1): 48-55, 64.) |
