
 , 陶磊1
, 陶磊1 1. 太原理工大学 机械与运载工程学院,山西 太原 030024;
2. 吉林大学 汽车仿真与控制国家 重点实验室,吉林 长春 130025;
3. 清华大学 车辆与运载学院,北京 100084
收稿日期:2022-05-01
基金项目:国家重点研发计划项目(2020YFB1314001);汽车仿真与控制国家重点实验室开放基金资助项目(20210218);山西省基础研究计划(自由探索类)项目(20210302124119);山西省高等学校科技创新计划项目(2021L085)。
作者简介:陈龙(1990-),男,山西朔州人,太原理工大学讲师。
摘要:准确、高效的车辆状态估计是智能汽车实现精准控制的前提,因此迫切需要开展又快又准的状态估计算法研究.为此,提出一种分级串联型扩展卡尔曼滤波(graded series extended Kalman filter,GS-EKF)车辆状态参数估计方法,旨在保证估计精度的同时,提升算法的计算效率和鲁棒性.首先,基于分级串联思想,将初级扩展卡尔曼滤波估计的结果,作为次级状态估计的可量测控制输入信号,实现分级串联状态估计;然后,建立3自由度非线性动力学车辆状态参数估计模型,以方向盘转角及纵向、侧向加速度为输入变量和观测变量;最后,搭建联合仿真验证平台,对比分析4种不同算法的精度、鲁棒性以及效率.结果表明所提出的算法在精度和鲁棒性方面可达到粒子滤波的效果,而效率比粒子滤波提升了41.2%.
关键词:智能汽车状态估计分级串联扩展卡尔曼鲁棒性
Vehicle State Parameter Estimation Based on Graded Series Extended Kalman Filter Method
CHEN Long1,2, LIU Qiao-bin3

 , TAO Lei1
, TAO Lei1 1. College of Mechanical and Vehicle Engineering, Taiyuan University of Technology, Taiyuan 030024, China;
2. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China;
3. School of Vehicle and Mobility, Tsinghua University, Beijing 100084, China
Corresponding author: LIU Qiao-bin, E-mail: liuqiaobin@tsinghua.edu.cn.
Abstract: Accurate and efficient vehicle state estimation is the prerequisite for intelligent vehicles to achieve precise control, thus there is an urgent need to carry out research on fast and accurate state estimation algorithms. To this end, a graded series extended Kalman filter (GS-EKF) method of vehicle state parameter estimation is proposed, which aims to improve the computational efficiency and robustness of the algorithm while ensuring the estimation accuracy. Firstly, based on the graded series idea, the result of the primary extended Kalman filter estimation is used as the measurable control input signal of the secondary state estimation to realize the hierarchical cascading state estimation. Then, a 3-degree-of-freedom nonlinear dynamic vehicle state parameter estimation is established which takes the steering wheel angle and longitudinal/lateral acceleration as input variables and observation variables. Finally, a joint simulation verification platform is built to compare and analyze the accuracy, robustness and efficiency of four different algorithms. The results show that the proposed algorithm can achieve the effect of particle filter in terms of accuracy and robustness, and the efficiency is 41.2% higher than that of particle filter.
Key words: intelligent vehiclestate estimationgraded seriesextended Kalmanrobustness
汽车智能化在提高行驶安全性、减少交通事故、提升交通效率以及促进节能减排等方面都具有很大优势,已成为全球汽车产业发展的热点方向[1-2].智能汽车运动行驶过程可分为:环境感知、决策规划和运动控制[3],其中环境感知是智能车辆决策规划和运动控制的基础环节,主要包括车辆周围环境感知和车辆自身状态感知.因此,车辆自身状态感知的准确性直接影响车辆智能决策规划的准确性以及运动控制稳定性,开展车辆运行状态参数感知对提升车辆智能控制运行稳定性具有重要的意义[4-6].然而受限于传感测量技术和成本,一些车辆关键状态变量无法通过现有传感器直接测量获取或者测量成本太高[7-8].为克服该问题,采用低成本传感器测量易获取信息,利用车辆模型结合状态估计算法来实现对车辆行驶状态的估计,已成为车辆行驶状态参数获取的重要手段,也是当前的研究热点.
车辆行驶状态参数估计的优劣,核心是估计算法的设计.针对车辆行驶状态参数估计算法的研究,国内外****目前主要集中在卡尔曼(Kalman filter, KF)、扩展卡尔曼滤波(extended Kalman filter, EKF)[9]、容积卡尔曼滤波[10]、无迹卡尔曼滤波(unscented Kalman filter, UKF)[11]和粒子滤波(particle filter, PF)[12]等算法的研究.文献[9]采用EKF状态估计算法,通过采集方向盘转角、纵向加速度、侧向加速度等信息,实现车辆行驶状态最小方差估计,但是估计精度以及抗噪鲁棒性较差.文献[11, 13]采用UKF算法对车辆行驶状态参数进行估计,仿真与实车试验结果表明其性能优于传统EKF算法.文献[14]提出采用PF算法进行车辆状态估计,仿真与实车试验结果表明该方法具有良好的估计精度,但是PF算法存在计算量较大的不足.文献[15-17]则是针对现有EKF算法的不足,提出多种改进型EKF状态估计算法.文献[18]针对状态估计过程噪声和量测噪声统计特性不确定的问题,采用遗传优化算法对UKF算法进行优化,从而提升状态估计性能.文献[19]采用一种改进的粒子滤波算法——无味粒子滤波算法,对轮毂电机电动汽车进行状态估计,结果表明在高度非线性状态下,无味粒子滤波算法性能优于UKF和EKF算法,但是依然存在计算量大的问题.
本文在现有研究基础上,旨在不影响状态估计精度的前提下,采用分级串联估计的思想,提出了一种分级串联扩展卡尔曼(graded series extended Kalman filter, GS-EKF)状态估计算法,使其能够兼具EKF算法计算量少和UKF,PF算法精度高、鲁棒性好的优点.建立了3自由度车辆非线性动力学模型和分级串联扩展卡尔曼状态估计算法,利用Matlab/Simulink与Carsim搭建了车辆行驶状态估计算法联合仿真试验验证平台,并将本文所提算法与EKF, UKF和PF状态估计算法进行了对比,以验证所提算法的优越性.
1 车辆动力学模型车辆动力学建模是汽车行驶状态估计的基础,本文模型综合考虑了实际车辆纵向车速的变化对横摆、侧偏引入的非线性动力学特性,以及车辆转向时横摆、侧偏也会向纵向运动引入的非线性特性,建立包括车辆纵向、侧向以及横摆3个方向自由度的车辆非线性动力学模型,如图 1所示[12].
图 1(Fig. 1)
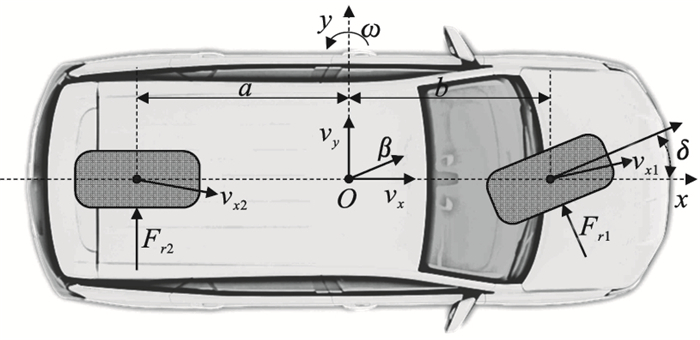 | 图 1 车辆动力学模型Fig.1 Vehicle dynamics model |
根据车辆动力学模型建立的动力学方程为
 | (1) |
 | (2) |
 | (3) |
 | (4) |
根据车辆模型,定义状态变量为
 | (5) |
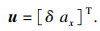 | (6) |
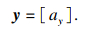 | (7) |
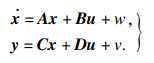 | (8) |
 |
由于计算机系统只能处理离散信号,需要对连续系统方程进行离散化,采用差分变换法,车辆动力学离散化方程为
 | (9) |
2 GS-EKF状态估计算法2.1 扩展卡尔曼滤波算法扩展卡尔曼滤波算法是在经典卡尔曼滤波算法基础上,为解决KF仅适用于线性系统状态估计而提出的改进算法[9].EKF的基本思想是将非线性系统动力学方程在参考点附近进行Taylor展开,舍弃二阶及其以上的高阶项,保留非线性系统的近似线性项,从而得到系统的线性化近似.利用一阶线性化近似的状态方程和测量方程进行状态估计,具体步骤如下.
1) 时间更新.状态一步预测方程为
 | (10) |
 | (11) |
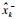
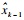
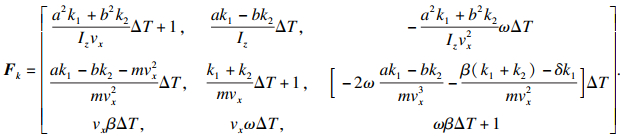 |
卡尔曼滤波增益矩阵为
 | (12) |
 |
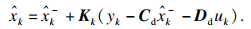 | (13) |
 | (14) |
2.2 GS-EKF状态估计算法EKF算法相较于UKF和PF状态估计算法而言,具有计算量小的优点,但是在状态估计精度和鲁棒性方面存在不足.本文在对EKF状态估计算法的动态性能及鲁棒性研究中发现,在车辆行驶状态估计过程中,不同的状态变量对噪声的敏感程度不同.在状态变量横摆角速度ω、质心侧偏角β和车辆纵向车速vx中,横摆角速度的估计结果准确性和鲁棒性最好,传感器噪声对其估计精度影响较小,而质心侧偏角和车辆纵向车速vx的估计则不具备上述优点.基于此,本文提出GS-EKF状态估计算法,其具体的实现步骤如图 2所示.
图 2(Fig. 2)
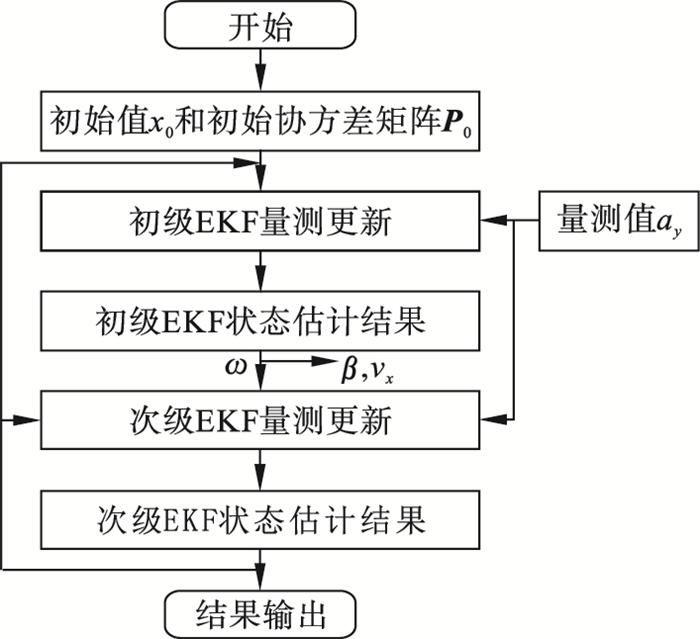 | 图 2 GS-EKF状态估计算法Fig.2 GS-EKF state estimation algorithm |
基于分级串联估计策略,利用状态变量横摆角速度ω估计精度高、鲁棒性好的优点,将初级EKF估计结果中的ω作为次级EKF状态估计的可量测控制输入信号,从而提高次级EKF状态估计的精度.而且次级EKF估计模型由原来3个状态变量减少为2个状态变量,降低了次级EKF状态估计的计算量.次级EKF的状态变量变为x′=[βvx]T,控制输入为u′=[ω δ ax]T,则其状态方程和观测方程增益矩阵变为
 |
 |
 |
图 3(Fig. 3)
 | 图 3 状态估计算法对比仿真结构原理图Fig.3 Schematic diagram of state estimation algorithm comparison simulation structure |
表 1(Table 1)
| 表 1 车辆参数 Table 1 Parameters of vehicle |
图 4(Fig. 4)
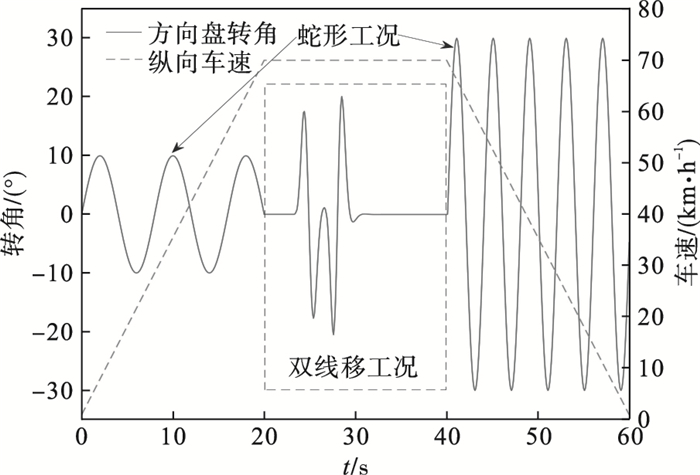 | 图 4 组合工况方向盘转角和车速Fig.4 Steering angle and speed under combined conditions |
为定量评价状态估计算法间的性能差异,分别采用状态估计结果与仿真实际值的峰值相对误差(peak of relative error, PRE)、平均绝对误差(mean absolute error, MAE)和均方根误差(root-mean-square error, RMSE)来表征算法的估计误差大小,计算公式分别为[15]
 | (15) |
 | (16) |
 | (17) |
3.2 仿真结果分析状态估计算法参数选取x0=[0, 0, 0]T,误差协方差矩阵初始值P0=eye(3),过程噪声协方差矩阵初始值Q=diag(0.1,0.1,0.1);测量噪声协方差矩阵初始值为R=0.001,PF算法的粒子数量取100.不考虑传感器噪声影响,组合工况下4种状态估计算法仿真结果如图 5所示.
图 5(Fig. 5)
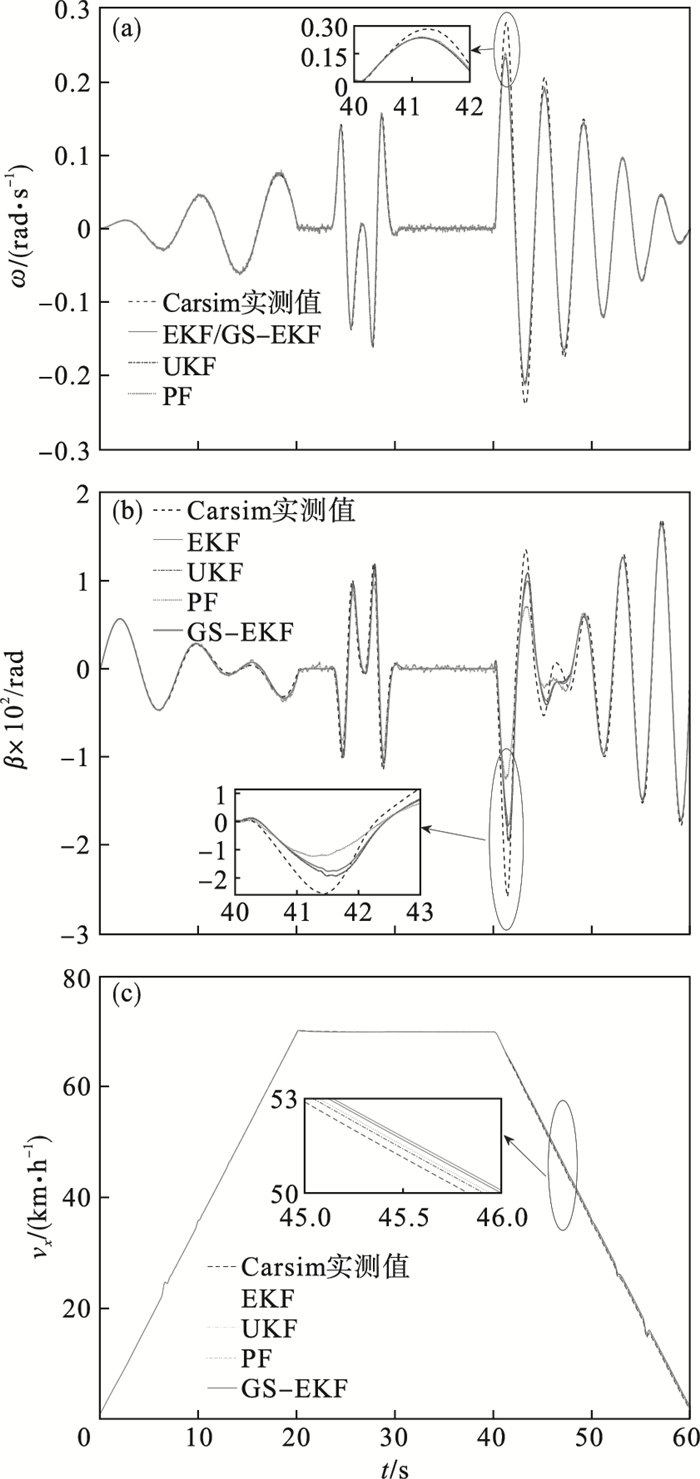 | 图 5 组合工况状态估计结果Fig.5 State estimation results under combined conditions (a)—横摆角速度;(b)—质心侧偏角;(c)—纵向车速. |
由图 5可知,不考虑传感器噪声干扰的情况下,4种状态估计算法计算结果与真实值一致性较好,但是在40~50 s仿真区间内,此时车速为减速初期,车速较高,同时蛇形工况转向角增大,导致横摆角速度ω和质心侧偏角β估计结果峰值误差增大.需说明图 5a横摆角速度没有绘制GS-EKF的状态估计曲线,这是因为分级串联中初级EKF对横摆角速度的估计结果即为GS-EKF的最终估计结果,因而GS-EKF对横摆角速度的估计结果与传统EKF结果一样,本文没有单独绘制曲线.定量对比4种状态估计算法的误差,结果如图 6所示.
图 6(Fig. 6)
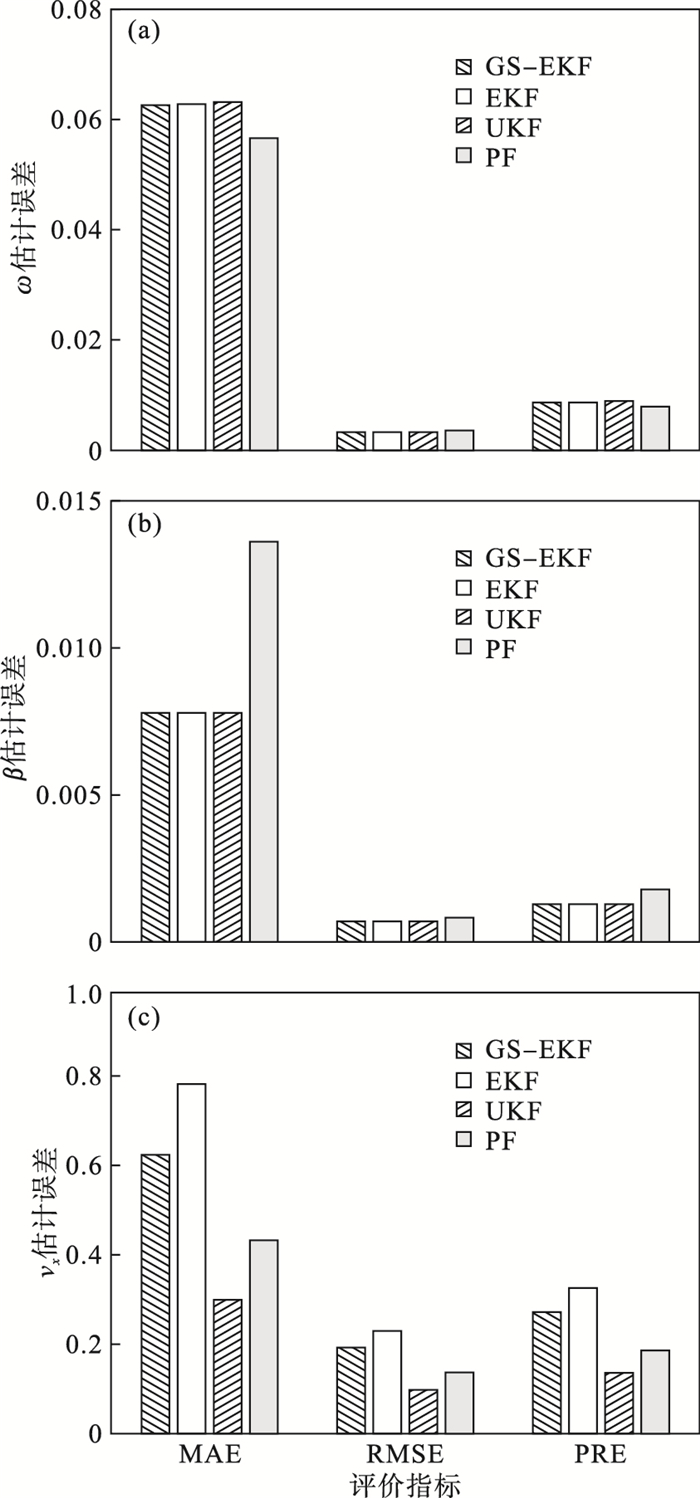 | 图 6 组合工况状态估计误差Fig.6 State estimation errors under combined conditions (a)—横摆角速度误差;(b)—质心侧偏角误差;(c)—纵向车速误差. |
由图 6可知,在不考虑传感器噪声的前提下,4种状态估计算法的估计误差总体相差不大,都非常接近实际值;由图 6b质心侧偏角β的估计结果可知,GS-EKF算法的估计误差最小;而由图 6c纵向车速vx的估计结果可知,GS-EKF算法的估计误差优于EKF算法,但是不如UKF算法和PF算法.
进一步分析状态估计算法的计算效率,采用仿真耗时来表征算法的计算效率.本文仿真所使用的计算机CPU为AMD R7 5800H主频为3.2 GHz,内存16 GB,模型仿真时长设置为60 s,仿真步长为0.001 s.计算得到4种状态估计算法仿真耗时如图 7所示.
图 7(Fig. 7)
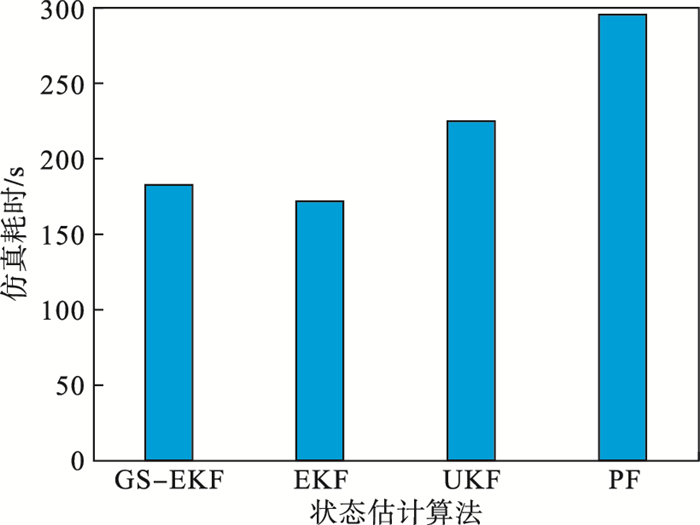 | 图 7 组合工况仿真耗时Fig.7 Simulation time of combined conditions |
由图 7可知GS-EKF算法相比传统EKF耗时增加11 s,但是相比UKF和PF算法,仿真耗时分别缩短42和113 s,计算效率分别提升18.7%和41.2%.基于对仿真精度产生较小影响前提下,GS-EKF算法有效提升了状态估计算法计算效率,降低算法计算量,有助于降低车辆控制芯片计算量.
3.3 状态估计算法鲁棒性分析实际工程应用中,传感器信号噪声干扰可造成算法的不稳定、不收敛.因此针对状态估计算法的鲁棒性开展研究具有重要的工程实际意义.本文对传感器量测信号叠加不同信噪比的高斯白噪声,分别设定信噪比SNR为80和40 dB,来模拟传感器信号处于中等噪声干扰和强干扰状态,并且在信号中添加野值来模拟实际数据中可能存在的野值信号干扰,最终可获得本文鲁棒性分析的4组仿真如表 2所示.
表 2(Table 2)
| 表 2 仿真工况类型 Table 2 Simulation condition types |
信噪比SNR计算公式为
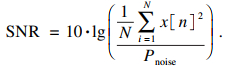 | (18) |
图 8(Fig. 8)
 | 图 8 信噪比40 dB+野值仿真结果Fig.8 Simulation results of SNR 40 dB+outlier (a)—横摆角速度;(b)—质心侧偏角;(c)—纵向车速. |
由图 8可知,传感器量测信息噪声的存在,4种算法的估计精度都存在一定程度下降,其中对横摆角速度ω估计准确性的影响较小;而质心侧偏角β的估计则出现较为明显的噪声干扰波动,尤其EKF算法受噪声的影响最为显著.同时传感器野值也对估计精度有影响,分析质心侧偏角和纵向车速的估计结果,在野值出现时刻EKF,UKF算法受野值影响估计结果发生异常,而GS-EKF算法和PF算法有效抑制了野值对估计结果的干扰,说明其抗干扰的鲁棒性要优于EKF和UKF算法.
进一步计算不同信噪比下的估计误差,结果如表 3所示.
表 3(Table 3)
| 表 3 不同信噪比干扰下状态估计算法误差 Table 3 State estimation algorithm errors under different SNR interference | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 3可知,信噪比的减小对横摆角速度的估计精度影响很小,而且4种状态估计算法间的估计误差相差不大,进一步证明该状态稳定且不易受干扰,可用来做次级EKF的量测输入.而质心侧偏角β和纵向车速vx的估计误差受信噪比的影响较为明显.
图 9为不同信噪比下的状态估计误差对比图.由图 9可知,信噪比减小对横摆角速度ω的估计影响较小,而对质心侧偏角β和纵向车速vx的估计误差影响较大, 尤其是对EKF算法,其次为UKF算法,本文所提出的GS-EKF和PF算法的抗噪声鲁棒性最优.
图 9(Fig. 9)
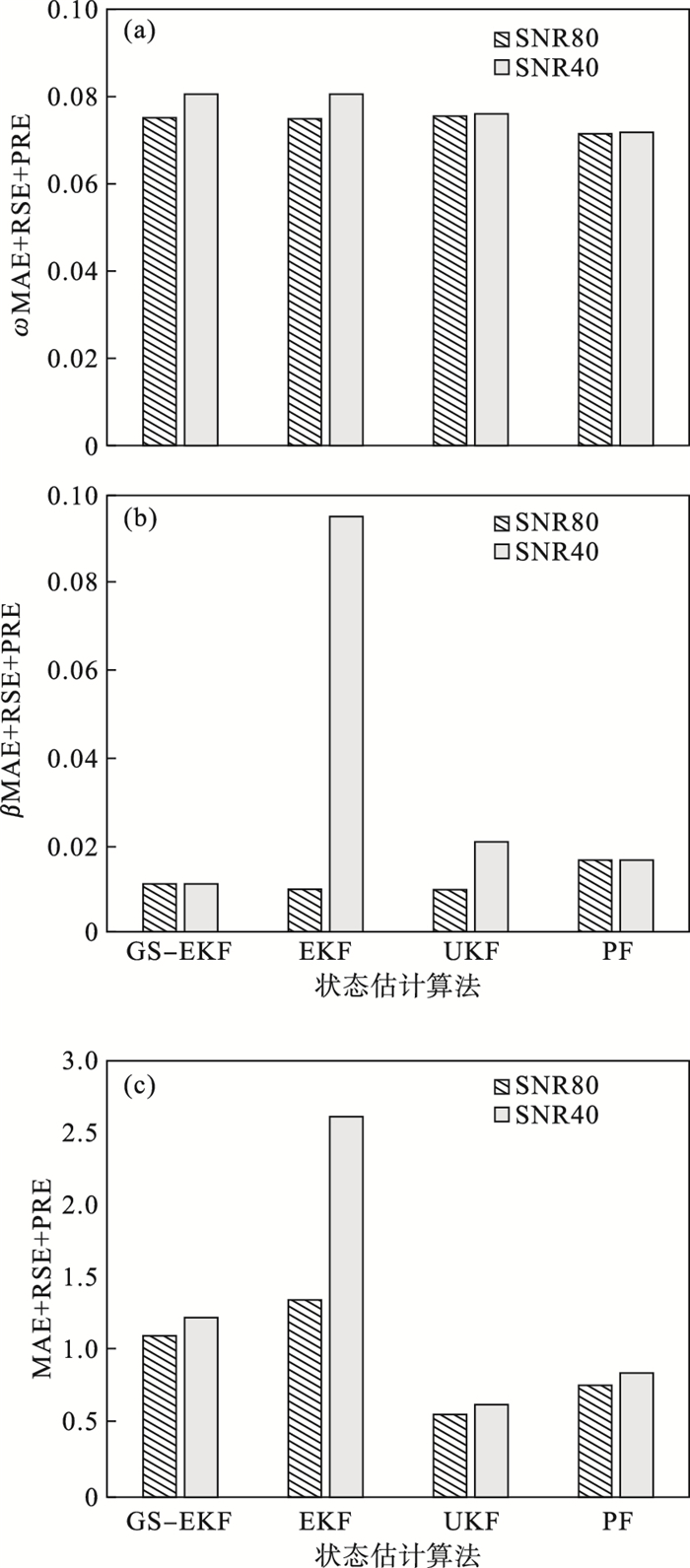 | 图 9 不同信噪比下的状态估计误差Fig.9 State estimation errors under different SNR (a)—横摆角速度;(b)—质心侧偏角;(c)—纵向车速误差. |
随着信噪比的减小,4种估计算法的估计误差都呈现增大趋势.不同信噪比下,GS-EKF算法对质心侧偏角β的估计误差最小;UKF算法对纵向车速vx的估计误差最小.本文所提出的GS-EKF算法有效地克服了传统EKF算法估计精度和鲁棒性不足的缺点,同时保持了其计算量小的优点.因此在综合考虑状态估计精度、计算效率以及抗量测信号噪声鲁棒性的条件下,GS-EKF算法具有优势.
4 结论1) 通过与EKF, UKF和PF算法的仿真对比,GS-EKF状态估计精度和抗噪鲁棒性与PF算法相当,其中对质心侧偏角的估计精度优于其他算法,且计算效率比UKF和PF算法分别提升18.7%和41.2%.
2) 本文提出的GS-EKF算法在继承传统EKF算法的基础上,有效地克服了传统EKF算法估计精度和抗噪鲁棒性不足的缺点.
3) GS-EKF算法兼具EKF算法计算量少和PF算法精度高、鲁棒性好的优点,因此该算法具有较好的实际工程应用前景.
参考文献
| [1] | Yang D G, Jiang K, Zhao D, et al. Intelligent and connected vehicles: current status and future perspectives[J]. Science China (Technological Sciences), 2018, 61(10): 1446-1471. DOI:10.1007/s11431-017-9338-1 |
| [2] | 梁忠超, 张欢, 赵晶, 等. 基于自适应MPC的无人驾驶车辆轨迹跟踪控制[J]. 东北大学学报(自然科学版), 2020, 41(6): 835-840. (Liang Zhong-chao, Zhang Huan, Zhao Jing, et al. Trajectory tracking control of unmanned vehicles based on adaptive MPC[J]. Journal of Northeastern University(Natural Science), 2020, 41(6): 835-840.) |
| [3] | 翟强, 程洪, 黄瑞, 等. 智能汽车中人工智能算法应用及其安全综述[J]. 电子科技大学学报, 2020, 49(4): 490-498, 510. (Zhai Qiang, Cheng Hong, Huang Rui, et al. A survey: artificial intelligence and its security in intelligent vehicle[J]. Journal of University of Electronic Science and Technology of China, 2020, 49(4): 490-498, 510.) |
| [4] | Viehweger M, Vaseur C, van Aalst S, et al. Vehicle state and tyre force estimation: demonstrations and guidelines[J]. Vehicle System Dynamics, 2021, 59(5): 675-702. DOI:10.1080/00423114.2020.1714672 |
| [5] | 张志达, 郑玲, 李以农, 等. 基于鲁棒自适应SCKF的智能汽车目标状态跟踪研究[J]. 机械工程学报, 2021, 57(20): 181-193. (Zhang Zhi-da, Zheng Ling, Li Yi-nong, et al. State estimation of distributed electric vehicle based on robust adaptive UKF[J]. Journal of Mechanical Engineering, 2020, 50: 1461-1473.) |
| [6] | 陈特, 徐兴, 蔡英凤, 等. 基于状态估计的无人车前轮转角与横摆稳定协调控制[J]. 北京理工大学学报, 2021, 41(10): 1050-1057. (Chen Te, Xu Xing, Cai Ying-feng, et al. Coordinated control of front-wheel steering angle and yaw stability for unmanned ground vehicle based on state estimation[J]. Transactions of Beijing Institute of Technology, 2021, 41(10): 1050-1057.) |
| [7] | Song R, Fang Y. Vehicle state estimation for INS/GPS aided by sensors fusion and SCKF-based algorithm[J]. Mechanical Systems and Signal Processing, 2021, 150: 107315. DOI:10.1016/j.ymssp.2020.107315 |
| [8] | Liao Y W, Borrelli F. An adaptive approach to real-time estimation of vehicle sideslip, road bank angles, and sensor bias[J]. IEEE Transactions on Vehicular Technology, 2019, 68(8): 7443-7454. DOI:10.1109/TVT.2019.2919129 |
| [9] | 宗长富, 潘钊, 胡丹, 等. 基于扩展卡尔曼滤波的信息融合技术在车辆状态估计中的应用[J]. 机械工程学报, 2009, 45(10): 272-277. (Zong Chang-fu, Pan Zhao, Hu Dan, et al. Information fusion algorithm for vehicle state estimation based on extended Kalman filtering[J]. Journal of Mechanical Engineering, 2009, 45(10): 272-277.) |
| [10] | 王凡勋, 殷国栋, 沈童, 等. 四轮驱动电动汽车质心侧偏角与轮胎侧向力非线性鲁棒融合估计[J]. 中国机械工程, 2022, 33(22): 2673-2683. (Wang Fan-xun, Yin Guo-dong, Shen Tong, et al. Nonlinear robust fusion estimation of sideslip angle and tire lateral forces for four-wheel-drive vehicles[J]. China Mechanical Engineering, 2022, 33(22): 2673-2673.) |
| [11] | Antonov S, Fehn A, Kugi A. Unscented Kalman filter for vehicle state estimation[J]. Vehicle System Dynamics, 2011, 49(9): 1497-1520. |
| [12] | Wang F S, Lu M Y, Zhao Q J. Particle filtering algorithm[J]. Chinese Journal of Computers, 2016, 37(8): 1679-1694. |
| [13] | 宋义彤, 舒红宇, 陈仙宝, 等. 分布式电动汽车状态与参数无迹卡尔曼滤波估计[J]. 机械工程学报, 2020, 56(16): 204-213. (Song Yi-tong, Shu Hong-yu, Chen Xian-bao, et al. State and parameters estimation for distributed drive electric vehicle based on unscented Kalman filter[J]. Journal of Mechanical Engineering, 2020, 56(16): 204-213.) |
| [14] | 林棻, 赵又群, 徐朔南. 基于粒子滤波算法的汽车状态估计技术[J]. 农业机械学报, 2011, 42(2): 23-27. (Lin Fen, Zhao You-qun, Xu Shuo-nan. Vehicle states estimation technology based on particle filter algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(2): 23-27.) |
| [15] | 汪 䶮, 魏民祥, 赵万忠, 等. 基于递推最小二乘法与模糊自适应扩展卡尔曼滤波相结合的车辆状态估计[J]. 中国机械工程, 2017, 28(6): 750-755. (Wang Yan, Wei Min-xiang, Zhao Wan-zhong, et al. Vehicle state estimation based on combined RLS and FAEKF[J]. China Mechanical Engineering, 2017, 28(6): 750-755.) |
| [16] | Katriniok A, Abel D. Adaptive EKF-based vehicle state estimation with online assessment of local observability[J]. IEEE Transactions on Control Systems Technology A Publication of the IEEE Control Systems Society, 2016, 24(4): 1368-1381. |
| [17] | 张志勇, 张淑芝, 黄彩霞, 等. 基于自适应扩展卡尔曼滤波的分布式驱动电动汽车状态估计[J]. 机械工程学报, 2019, 55(6): 156-165. (Zhang Zhi-yong, Zhang Shu-zhi, Huang Cai-xia, et al. State estimation of distributed drive electric vehicle based on adaptive extended Kalman filter[J]. Journal of Mechanical Engineering, 2019, 55(6): 156-165.) |
| [18] | 周卫琪, 齐翔, 陈龙, 等. 基于无迹卡尔曼滤波与遗传算法相结合的车辆状态估计[J]. 汽车工程, 2019, 41(2): 198-205. (Zhou Wei-qi, Qi Xiang, Chen Long, et al. Vehicle state estimation based on the combination of unscented Kalman filtering and genetic algorithm[J]. Automotive Engineering, 2019, 41(2): 198-205.) |
| [19] | Chu W, Luo Y, Dai Y, et al. In-wheel motor electric vehicle state estimation by using unscented particle filter[J]. International Journal of Vehicle Design, 2015, 67(2): 115-136. |
