
 , 周世康, 刘士乙, 梁力
, 周世康, 刘士乙, 梁力 东北大学 资源与土木工程学院,辽宁 沈阳 110819
收稿日期:2022-04-16
基金项目:中央高校基本科研业务费专项资金资助项目(N2001015, N2101009);国家留学基金资助项目(201906085065)。
作者简介:李明(1980-),男,辽宁沈阳人,东北大学副教授;
梁力(1955-),男,辽宁丹东人,东北大学教授,博士生导师。
摘要:在基于渗透率修正的水力压裂(permeability-based hydraulic fracture,PHF)模型基础上引入概率破坏模型(statistical fracture model, SFM),采用Weibull概率模型描述岩石材料微观的非均匀分布对宏观水力裂缝特征离散性的影响.PHF-SFM模型假设岩石材料的渗透率是平均有效应力的函数,基于Biot固结理论,采用摩尔-库伦弹塑性本构模型和达西定律分别描述岩石材料固体骨架和孔隙流体开裂前后的力学特征.通过与KGD模型对比验证该模型的可行性,并通过数值模拟分析了模型中Weibull模量和尺度参数以及岩石材料性质对起裂压力、裂缝高度和裂缝宽度等的影响.结果表明,概率破坏模型的引入不会影响起裂压力,但会影响裂缝的几何特征.当Weibull模量降低或尺度参数增加时,裂缝的几何特征离散性呈增大趋势.
关键词:水力压裂非均匀岩石PHF-SFM概率破坏韦伯分布
Study on Numerical Calculation Model of Hydraulic Fracture for Heterogeneous Rock Materials Based on PHF-SFM
LI Ming

 , ZHOU Shi-kang, LIU Shi-yi, LIANG Li
, ZHOU Shi-kang, LIU Shi-yi, LIANG Li School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: LI Ming, E-mail: liming@mail.neu.edu.cn.
Abstract: Based on the permeability-based hydraulic fracture (PHF) model, a statistical fracture model (SFM) is introduced to capture the influence of the micro non-uniform distribution of rock materials on the macroscale characteristics of hydraulic fracture. The Weibull probability model is adopted to account for the discreteness of characteristics of these characteristics. By assuming that the permeability of rock material is a function of the mean effective stress, the PHF-SFM model is proposed based on the Biot consolidation theory. The model incorporates the Mohr-Coulomb elastoplastic constitutive model and Darcy's law to represent mechanical behaviors for the solid and liquid phase of rock material in pre- and post-failure part. The verification is carried out by comparing the simulated results with those of the KGD model. Breakdown pressure, equivalent fracture height and fracture width were studied by varying the Weibull modulus and scale parameters in the SFM model and material properties of rock. The simulation results indicate that including the SFM model does not affect the breakdown pressure, but does vary the fracture geometry. When the Weibull modulus decreases or the scale parameter increases, the discreteness of fracture geometry features increases.
Key words: hydraulic fractureheterogeneous rockPHF-SFMstatistical fractureWeibull distribution
水力压裂技术通过提高储层的渗透率达到增加产量的目的,是油气开采和低渗透储层改造的主要方法[1].水力压裂过程的研究可采用如KGD(Khristianovich-Zheltov-Geertsma-De Klerk)模型[2-3]、PKN(Perkins-Kern-Nordgren)模型[4]以及P3D(Pseudo three-dimensional)模型[5]等的理论方法,也可采用能够综合考虑岩石非均质特征以及复杂边界条件等因素的数值计算方法,如:有限单元法、离散元法[6]和相场法[7]等.
岩石材料微观特征的非均匀性对水力裂缝发展特征有很大影响[8],均匀连续性的假设并不能完全反映实际情况[9],因此建立能够有效反映实际岩石损伤模型的研究十分重要.
以有限元法为基础的弥散裂缝模型是通过改变破坏区域材料的力学参数来模拟结构中裂缝的发展过程,因其在计算过程中具有无需重构网格且易于实现的优势已被广泛用于损伤研究[10].已有的PHF(permeability-based hydraulic fracture)水力压裂模型就是弥散裂缝模型的一种.该模型通过假定渗透率是平均有效应力的函数来模拟水力裂缝发展过程[11].但是在该模型中未能考虑岩石材料微观特征对宏观裂缝发展过程的影响.因此本文在已有的PHF模型基础上,通过引入基于Weibull分布的概率破坏模型(statistical fracture model, SFM),建立适用于考虑岩石材料微观非均匀破坏特征的PHF-SFM水力压裂数值计算模型,同时探讨概率破坏模型中的参数以及岩石材料性质等因素对宏观裂缝特征的影响.
1 PHF-SFM模型的基本方程1.1 PHF水力压裂模型基于Biot固结理论的PHF水力压裂数值计算模型中的多孔岩石材料的固体骨架和孔隙流体的平衡方程分别如式(1)和式(2);有效应力原理和应变与位移关系分别如式(3)和式(4);岩石材料开裂前采用线弹性本构模型如式(5),开裂后采用摩尔-库仑塑性模型描述[11-13].
 | (1) |
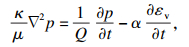 | (2) |
 | (3) |
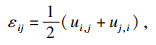 | (4) |
 | (5) |
渗透系数K与平均有效应力σm′的关系,以及压裂液引起的修正后的渗透系数Kf采用式(6)和式(7)计算.
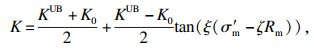 | (6) |
 | (7) |
 | (8) |
 | (9) |
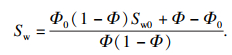 | (10) |
在本文的数值计算中ζ=0.45,μinj/μ0=100,KUB=0.01 m/s,kr0=0.5,Swi=Sorw=0.15,ξ=artanh(1-10-12)/Rm[13].
1.2 SFM概率破坏模式本文引入描述岩石材料损伤的Weibull概率破坏模型来表征由岩石材料强度非均匀性引起的概率破坏特征.Weibull分布在其他学科中已多次成功运用,并解决了许多实际工程问题[14].本文水力压裂过程引起的岩石材料产生开裂的概率Phf可表示为
 | (11) |
2 PHF-SFM模型实现2.1 PHF-SFM的ABAQUS实现本文以有限元分析软件ABAQUS为依托,应用其提供的二次开发功能实现PHF-SFM水力压裂数值计算模型.为建立岩石材料参数杨氏模量E,泊松比ν,抗拉强度Rm和渗透系数K与材料点所处的空间位置关系,输入文件中的场变量的设置共涉及关键字有*Elastic,*Mohr Coulomb Hardening和*Permeability,并设置参数DEPENDENCIES分别为2,3和4,分别表示弹性参数为前2个场变量,摩尔-库仑强化准则中抗拉强度为第3个场变量,渗透系数为第4个场变量.当为均质材料时,各参数为常量,当为非均质材料时,各参数是空间位置的函数.各变量的初值和当前值分别存储于状态变量STATEV(10)和场变量FIELD(10)中,两者为对应关系.模型的实现共涉及3个用户子程序,即:UEXTERNALDB,SDVINI和USDFLD.程序流程图如图 1所示.
图 1(Fig. 1)
 | 图 1 PHF-SFM模型流程图Fig.1 Flowchart of the PHF-SFM model |
2.2 模型验证图 2a为使用力学模型建立的有限元模型,其网格划分如图 2b所示.
图 2(Fig. 2)
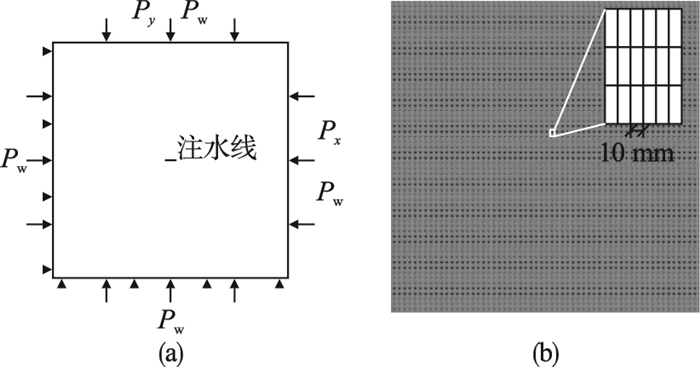 | 图 2 力学模型与有限元网格图Fig.2 Mechanical model and finite element grid diagram (a)—力学模型;(b)—网格划分. |
模型几何尺寸为5 000 mm×5 000 mm,有限元网格中每个单元宽度为10 mm,高度为30 mm.假设该模型位于地下约3 000 m位置,受到垂直方向的压应力Py=70 MPa,水平方向受到的压应力Px=60 MPa,初始孔隙水压力Pw=49 MPa.模型中心位置设置注水面,宽度为10 mm,并施加持续时间为3 600 s的注水荷载qinj=0.005 62 mm/s. 模型对应的材料参数如表 1所示.破坏概率Token的引入考虑了材料的非均匀破坏特征,同时由于概率模型的加入,每个位置的岩石破坏情况亦不同.本节算例选取图 3所示的其中一种破坏概率Token分布情况进行计算.
表 1(Table 1)
| 表 1 材料特性 Table 1 Material properties |
图 3(Fig. 3)
 | 图 3 破坏概率Token分布Fig.3 Token distribution of fracture probability |
对于具有相同宏观材料性质的岩石材料其微观分布不一定相同,因此对表 1所列参数的岩石材料进行5次随机算例计算,即每次计算中的初始破坏概率Token分布不同.计算得到等效裂缝宽度Wf,等效裂缝高度Hf和注水点水压力Pw随注水时间t的变化与KGD理论模型结果的对比分别如图 4和图 5所示.其中KGD模型的水力裂缝高度Hf,裂缝宽度Wf和注水压力Pw与注水时间t的关系分别采用式(12)~式(14)计算[13].
 | (12) |
 | (13) |
 | (14) |
 | 图 4 裂缝等效几何特征随时间的变化曲线Fig.4 Equivalent fracture width and height versus injection duration |
图 5(Fig. 5)
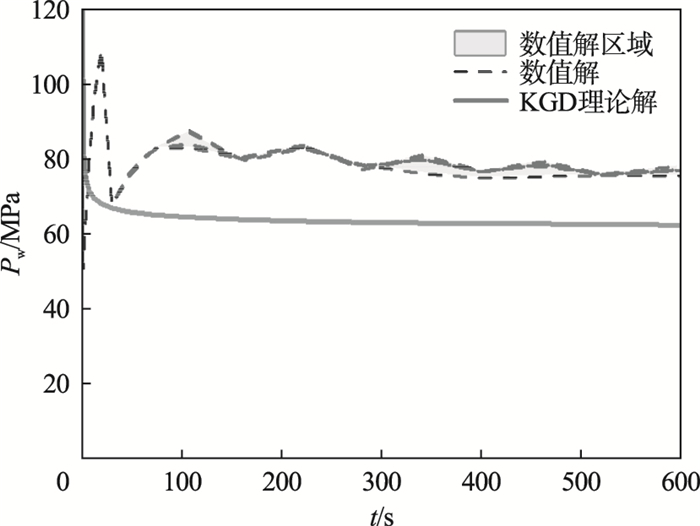 | 图 5 注水点孔隙水压力随时间的变化曲线Fig.5 Pore pressure development of injection point versus injection duration |
式中: G为剪切模量;当水力裂缝双向扩展时,系数取值为a=0.48,b=1.32,c=1.9[18].
由计算结果可以看出,不同随机算例中等效裂缝高度与等效裂缝宽度的发展过程受概率破坏模型的影响,在发展过程中有一定的波动,并且在KGD模型的理论附近,而裂缝传播阶段的水压力值(传播压力)大于由式(14)计算得到的理论解.
由式(14)可以看出,当注水时间t越短,计算的水压力越大,因此该式不适合计算起裂压力.采用基于多孔弹性理论且考虑压裂液可渗透岩石时起裂压力的理论解[19]:
 | (15) |
5个随机算例中注水点位置的应力路径发展过程如图 6所示.可以看出初始状态下注水点位置的岩石材料处于受压状态.随着注水时间增加,平均有效应力逐渐减小,当其达到负值时,岩石材料由受压状态转为受拉状态,即裂缝开始发展.随着注水时间的进一步增加,平均有效应力进一步降低,裂缝持续保持开裂状态.整个注水过程中,等效剪应力在受压阶段呈下降趋势,并沿屈服面降低至零点附近.
图 6(Fig. 6)
 | 图 6 注水位置的应力路径发展Fig.6 Stress path development at injection position |
3 参数σ0与m对裂缝特征影响3.1 材料参数空间分布为常量对于材料参数的分布不随位置改变的均质岩石材料,引入概率破坏模型后,分别考虑当尺度参数σ0=7 MPa,Weibull模量m取值0.5~6时和当m=2,σ0取值1~13 MPa时两种情况,其中每组(σ0,m)参数计算4个不同的随机算例,即每个算例的破坏概率Token不同,反映不同的微观分布.
当尺度参数σ0和Weibull模量m分别保持不变时,水力裂缝的等效宽度Wf,等效高度Hf,起裂压力Pb和传播压力Pp随参数m和σ0的变化规律分别如图 7和图 8所示.
图 7(Fig. 7)
 | 图 7 Weibull模量m对裂缝特征的影响(σ0=7 MPa)Fig.7 Influences of Weibull modulus m on fracture characteristics (σ0=7 MPa) (a)—裂缝宽度和裂缝高度;(b)—起裂压力和传播压力. |
图 8(Fig. 8)
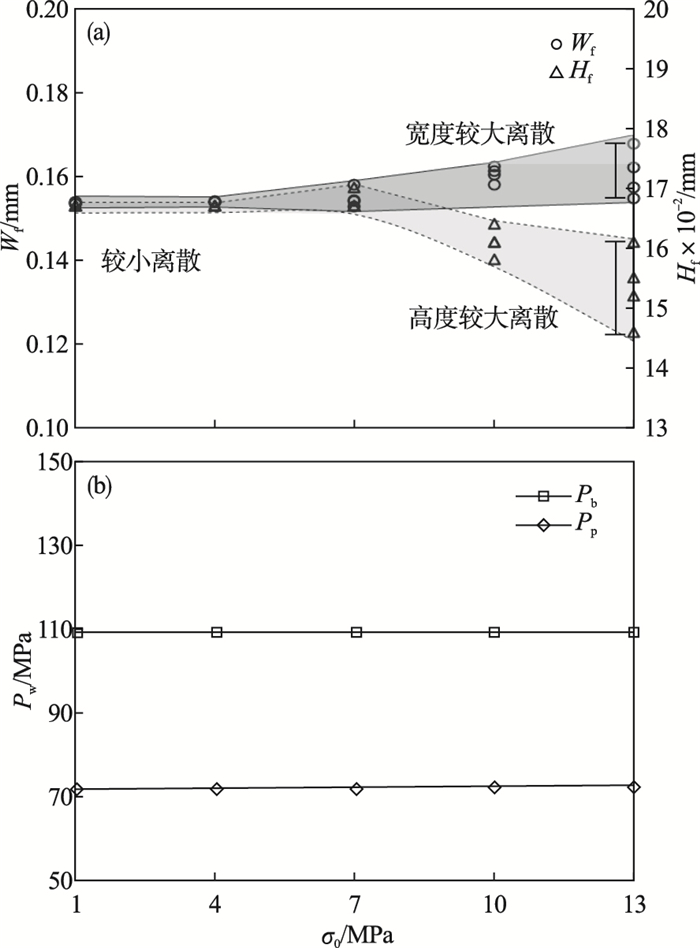 | 图 8 尺度参数σ0对裂缝特征的影响(m=2)Fig.8 Influence of scale parameter σ0 on fracture characteristics(m=2) (a)—裂缝宽度和裂缝高度;(b)—起裂压力和传播压力. |
数值计算结果表明,当尺度参数不变,Weibull模量增加时,裂缝几何特征的离散性降低,见图 7a;当Weibull模量不变,尺度参数增加时,裂缝几何特征的离散性增加,见图 8a.
由图 7b和图 8b可以看出,岩石材料参数为常量时,m和σ0的变化对应Pb和Pp的幅值变化均为零.该结果表明概率模型未改变岩石材料的起裂压力和传播压力.这是由于SFM模型是用于计算破坏概率,即用于判断模型对应位置发生破坏的可能性,而并未真实改变此处的材料性质,因而起裂压力和传播压力不受尺度参数σ0和Weibull模量m的影响.
3.2 抗拉强度空间分布非均匀当岩石材料的抗拉强度Rm=3~11 MPa在计算区域为非均匀分布时,分别考虑5种不同的尺度参数σ0和Weibull模量m取值,每组参数进行4次随机算例计算.尺度参数和Weibull模量分别改变时对水力裂缝特征影响分别如图 9和图 10所示.
图 9(Fig. 9)
 | 图 9 非均质岩石中参数m对裂缝特征的影响(σ0=7 MPa)Fig.9 Influences of parameter m on fracture characteristics in heterogeneous rocks (σ0=7 MPa) (a)—裂缝等效宽度和高度;(b)—起裂压力和传播压力. |
图 10(Fig. 10)
 | 图 10 非均质岩石中尺度参数σ0对裂缝的影响(m=2)Fig.10 Effect of scale parameters σ0 on fracture characteristics in heterogeneous rocks (m=2) (a)—裂缝等效宽度和高度;(b)—起裂压力和传播压力. |
计算结果表明,当保持σ0不变,m增加时,裂缝几何特征的离散性呈降低趋势,见图 9a;当保持m不变,σ0增加时,裂缝几何特征的离散性增加,见图 10a.
与材料参数分布为常数的计算工况相比(图 7,图 8),岩石材料抗拉强度Rm的非均匀分布加大了几何特征的幅值变化,即增加了离散程度;同时,由于Rm在计算区域内的空间分布为随机变化的,因此各算例中的起裂压力和传播压力也表现为一定程度的离散性,如图 9b和图 10b所示.
3.3 不同抗拉强度上限当抗拉强度空间分布为非均匀且Weibull模量和尺度参数分别为2和7 MPa时,保持抗拉强度最小值不变,通过改变抗拉强度的上限值,调整抗拉强度在模型中空间分布的变化幅值.在本文的计算中共考虑Rm幅值的变化为5种情况,取值范围为11~15 MPa.计算得到的抗拉强度幅值改变时对等效裂缝高度、等效裂缝宽度、起裂压力和传播压力的影响如图 11所示.
图 11(Fig. 11)
 | 图 11 抗拉强度上限值Rm对裂缝特征的影响Fig.11 Effect of upper limit of tensile strength (Rm) on fracture characteristics (a)—裂缝等效宽度和高度;(b)—起裂压力和传播压力. |
计算结果表明,随着Rm幅值的增大,等效裂缝宽度Wf和等效裂缝高度Hf在一定范围内随机变化,如图 11a所示;当Rm幅值增加,即抗拉强度最大值增加时,提高了注水点周围岩石材料抗拉强度增加的概率,从而引起起裂压力Pb和传播压力Pp的增加,表现为随着抗拉强度上限增加Pb和Pp呈增加趋势,如图 11b所示.
4 岩石材料性质对裂缝特征影响本节探讨当考虑概率破坏模式中Weibull模量和尺度参数为定值时,岩石材料性质,即杨氏模量、泊松比、抗拉强度和渗透系数分别对水力裂缝特征的影响.计算中各个模型的Weibull模量和尺度参数分别为2和7 MPa,各材料参数的取值如表 2所示.
表 2(Table 2)
| 表 2 材料参数影响计算工况 Table 2 Cases for the influences of material properties | ||||||||||||||||||||||||||||||
当杨氏模量、泊松比、抗拉强度和渗透系数变化时,裂缝几何特征和水压力特征的变化规律分别如图 12~图 15所示.图 12、图 13计算结果表明:随着杨氏模量的增大,等效裂缝高度逐渐增大,注水点位置的等效裂缝宽度逐渐降低;起裂压力和传播压力在一定范围内波动;随着岩石材料泊松比的增加,裂缝的等效高度增加,等效宽度改变较小;起裂压力和传播压力呈降低趋势.
图 12(Fig. 12)
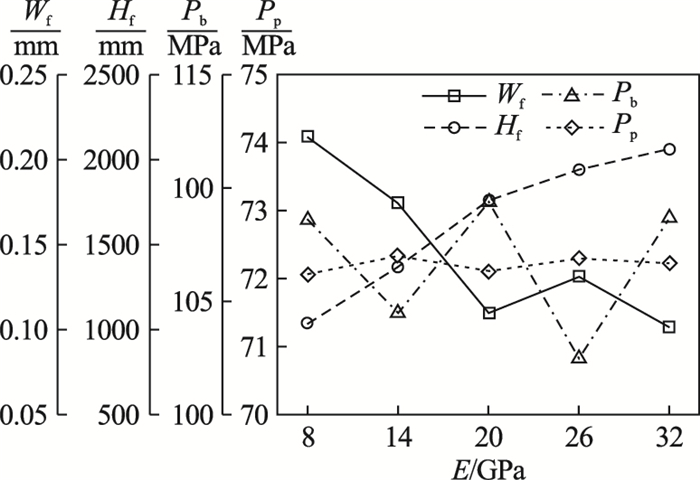 | 图 12 杨氏模量对裂缝特征的影响Fig.12 Influence of Young's modulus on fracture characteristics |
图 13(Fig. 13)
 | 图 13 泊松比对裂缝特征的影响Fig.13 Influence of Poisson's ratio on fracture characteristics |
图 14(Fig. 14)
 | 图 14 抗拉强度对裂缝特征的影响Fig.14 Effect of tensile strength on fracture characteristics |
图 15(Fig. 15)
 | 图 15 渗透系数对裂缝特征的影响Fig.15 Effect of hydraulic conductivity on fracture characteristics |
图 14、图 15结果表明: 随着岩石材料抗拉强度的增大,等效裂缝高度和等效裂缝宽度总体呈增加趋势;起裂压力和传播压力随抗拉强度增加而增加;裂缝高度随渗透系数增加而降低,等效裂缝宽度随渗透系数增加而增加;起裂压力和传播压力与受渗透系数影响较小.
5 结论1) 通过与理论解计算的对比,证明PHF-SFM模型能够用来模拟水力压裂过程中的水力裂缝特征.
2) 当岩石材料参数的空间分布为常量时,分别增加SFM模型中的Weibull模量和尺度参数,裂缝几何特征的离散程度分别呈降低和增加趋势.起裂压力和传播压力不受概率破坏模型参数的影响.
3) 当抗拉强度空间分布非均匀时,Weibull模量和尺度参数改变使裂缝几何特征的变化幅值增加,同时影响了起裂压力和传播压力的变化幅值.
4) 当杨氏模量或泊松比增大,渗透系数减小时,裂缝等效高度增大,等效宽度减小;当泊松比降低,抗拉强度增大时,起裂压力和传播压力均呈上升趋势.
参考文献
| [1] | Zou C, Zhao Q, Cong L, et al. Development progress, potential and prospect of shale gas in China[J]. Natural Gas Industry, 2021, 41(1): 1-14. |
| [2] | Yew C H, Weng X. Fracturing of a wellbore and 2D fracture models[D]. Waltham: Gulf Professional Publishing, 2015: 1-22. |
| [3] | Zhao Y, He P. Numerical simulation of KGD hydraulic fracture based on PPCZ model[J]. Journal of the China Coal Society, 2018, 43(10): 2866-2875. |
| [4] | Nordgren R P. Propagation of a vertical hydraulic fracture[J]. Society of Petroleum Engineers Journal, 1972, 12(4): 306-314. DOI:10.2118/3009-PA |
| [5] | Zhang X, Wu B, Jeffrey R G, et al. A Pseudo-3D model for hydraulic fracture growth in a layered rock[J]. International Journal of Solids and Structures, 2017, 115/116: 208-223. DOI:10.1016/j.ijsolstr.2017.03.022 |
| [6] | Huang L, Liu J, Zhang F, et al. Exploring the influence of rock inherent heterogeneity and grain size on hydraulic fracturing using discrete element modeling[J]. International Journal of Solids and Structures, 2019, 176/177: 207-220. DOI:10.1016/j.ijsolstr.2019.06.018 |
| [7] | Mikeli? A, Wheeler M F, Wick T. A phase-field method for propagating fluid-filled fractures coupled to a surrounding porous medium[J]. Multiscale Modeling & Simulation, 2015, 13(1): 367-398. |
| [8] | Ma G, Zhang Y, Zhou W, et al. The effect of different fracture mechanisms on impact fragmentation of brittle heterogeneous solid[J]. International Journal of Impact Engineering, 2018, 113: 132-143. DOI:10.1016/j.ijimpeng.2017.11.016 |
| [9] | Wang Y L, Zhuang Z, Liu Z L, et al. Finite element analysis of transversely isotropic rock with mechanical-chemical-damage coupling[J]. Engineering Mechanics, 2017, 34(9): 102-109. |
| [10] | Hu Y, Chen G, Cheng W, et al. Simulation of hydraulic fracturing in rock mass using a smeared crack model[J]. Computers and Structures, 2014, 137: 72-77. DOI:10.1016/j.compstruc.2013.04.011 |
| [11] | Li M, Guo P, Stolle D, et al. Development of hydraulic fracture zone in heterogeneous material based on smeared crack method[J]. Journal of Natural Gas Science and Engineering, 2016, 35: 761-774. DOI:10.1016/j.jngse.2016.09.018 |
| [12] | Li M, Guo P, Stolle D, et al. Modeling method and hydraulic fracture propagation for jointed rock mass using PHF-LSM method[J]. Journal of Natural Gas Science and Engineering, 2019, 68: 104657. |
| [13] | Li M, Guo P, Stolle D, et al. Modeling hydraulic fracture propagation in a saturated porous rock media based on EPHF method[J]. Journal of Natural Gas Science and Engineering, 2021, 89: 103887. DOI:10.1016/j.jngse.2021.103887 |
| [14] | Xiong J, Wang S, Li X, et al. Mechanical behavior and Weibull statistics based failure analysis of vanadium flow battery stacks[J]. Journal of Power Sources, 2019, 412: 272-281. DOI:10.1016/j.jpowsour.2018.11.060 |
| [15] | 高峰, 谢和平, 赵鹏. Weibull模量和岩石强度的分形性质[J]. 科学通报, 1993, 38(15): 1435-1438. (Gao Feng, Xie He-ping, Zhao Peng. Fractal properties of Weibull modulus and rock strength[J]. Chinese Science Bulletin, 1993, 38(15): 1435-1438. DOI:10.3321/j.issn:0023-074X.1993.15.016) |
| [16] | Deng B, Jiang D, Gong J. Is a three-parameter Weibull function really necessary for the characterization of the statistical variation of the strength of brittle ceramics?[J]. Journal of the European Ceramic Society, 2018, 38(4): 2234-2242. DOI:10.1016/j.jeurceramsoc.2017.10.017 |
| [17] | Shin K, Sugawara K, Okubo S. Application of Weibull's theory to estimating in situ maximum stress σH hydrofracturing[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 413-420. DOI:10.1016/S1365-1609(01)00009-0 |
| [18] | Wasantha P L P, Konietzky H, Xu C. Effect of in-situ stress contrast on fracture containment during single- and multi-stage hydraulic fracturing[J]. Engineering Fracture Mechanics, 2019, 205: 175-189. DOI:10.1016/j.engfracmech.2018.11.016 |
| [19] | 李明, 张砚琨, 赵岐, 等. 基于EPHF模型均质多孔岩石材料水力压裂特性[J]. 东北大学学报(自然科学版), 2021, 42(7): 996-1004. (Li Ming, Zhang Yan-kun, Zhao Qi, et al. Characteristics of hydraulic fracture in homogeneous porous rock material based on EPHF model[J]. Journal of Northeastern University(Natural Science), 2021, 42(7): 996-1004.) |
| [20] | Krief M, Garat J, Stellingwerff J, et al. A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic)[J]. The Log Analyst, 1990, 31: 355-369. |

