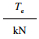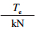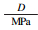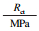, 牛鹏, 李友 东北大学 资源与土木工程学院，辽宁 沈阳 110819
收稿日期：2022-05-01
基金项目：国家自然科学基金联合基金资助项目(U21A20106)；国家自然科学基金资助项目(52074060)；中央高校基本科研业务费专项资金资助项目(N2101036)。
作者简介：王宇恒(1996-)，男，河北邯郸人，东北大学硕士研究生;
于庆磊(1981-), 男，山东泰安人，东北大学教授，博士生导师。
摘要：凿岩过程中钻机工作参数的变化响应与岩石单轴抗压强度密切相关，为利用随钻响应快速表征岩石力学性质，使用自主搭建的随钻获取试验平台，选取了4种岩石，开展了一系列不同推力条件下的钻进试验，研究岩石单轴抗压强度与钻机工作参数之间的相关性.研究结果发现，推力随切削深度的变化率Fe、扭矩随切削深度的变化率Te、钻头单位尺寸上法向力与切向力之比ζ与岩石单轴抗压强度正相关，且不受试验条件影响.在此基础上，基于随钻参数Fe和Te是可以表征可钻性和机械比能的物理量，结合量纲分析，建立了以Fe和Te为参数的岩石单轴抗压强度表征模型，并通过其他种类岩石的钻进数据初步验证了该模型的可靠性.为利用凿岩过程快速表征岩石单轴抗压强度提供了一种新方法.
关键词：随钻获取岩石可钻性机械比能岩石强度钻进参数
Uniaxial Compressive Strength Model of Rock Using Measurement While Drilling (MWD) Data
WANG Yu-heng, YU Qing-lei
, NIU Peng, LI You School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: YU Qing-lei, E-mail: yuqinglei@mail.neu.edu.cn.
Abstract: The uniaxial compressive strength (UCS) of rock is an important factor in drilling and blasting operations, and it is closely related to measurement while drilling (MWD) data. A series of rock drilling tests were carried out under different thrusts using a self-built MWD test platform to investigate the correlation between UCS and MWD data. The results show that slope of thrust and cutting depth (Fe), the slope of torque and cutting depth (Te), and the ratio of normal force to tangential force per unit size of bit (ζ) are positively correlated with rock UCS and not affected by test conditions. Based on the fact that Fe and Te can characterize rock drillability and mechanical specific energy, respectively, a model was developed to estimate rock UCS by Fe and Te. Additionally, the validity of the model was preliminarily verified using a different type of rock. The research provids a new method for estimating rock UCS during drilling process.
Key words: measurement while drilling (MWD)rock drillabilitymechanical specific energyrock strengthdrilling parameters
岩体作为一种天然地质体，结构复杂，空间多变，及时掌握围岩结构特征与力学性质变化，对优化工程设计、提高施工效率和安全性具有重要意义.传统的岩石力学参数一般通过现场取芯和室内试验获取，其测试过程周期长且不连续，难以及时对工程施工形成指导.金属矿山的开采活动依赖于大量钻孔作业，大量工程实践表明，钻头在遇到不同岩层或岩体结构面时，钻机工作参数会发生相应的响应特征[1-3]，钻头动力学响应特征与岩石的力学性质存在内在联系.通过随钻获取(measurement while drilling，MWD)技术，可以捕捉钻机的推力、扭矩、转速、钻速等随钻参数.因此，探寻随钻参数变化与岩石力学性质之间的内部联系，建立可靠的随钻响应的解译方法，能够借助凿岩过程快速了解岩石力学性质和结构特征，对优化金属矿山爆破设计具有重要的工程应用价值.
国内外****在利用MWD技术表征岩石力学性质方面开展了许多研究工作.Teale[4]最早提出机械比能的概念，定义为破碎单位岩石所需要的能量；谭卓英等[5-6]利用机械比能对花岗岩风化程度进行划分；Karasawa等[7-8]发现了可钻性指标与岩石单轴抗压强度具有较好的相关性.以上研究表明可钻性指标、机械比能等与岩石力学性质具有较好的相关性.
岩石切割试验从细观力学角度解释了刀岩相互作用机理，部分****基于切割试验的结论建立了随钻参数与岩石强度的数学关系.Detournay等[9-10]进一步将机械比能细化，提出固有比能的概念；Richard等[11]通过刮擦试验发现岩石固有比能与岩石单轴抗压强度成正比，验证了能量与岩石单轴抗压强度的定量关系；Yahiaoui等[12]发现切削力倾角与岩石种类无关；王琦等[13-15]考虑岩石韧性破坏模式，通过细观力学分析，建立了随钻参数与岩石力学参数的定量关系; Kalantari等[16]基于极限平衡理论，推导了随钻参数与岩石单轴抗压强度的理论模型，并使用微钻进行了验证.这些研究成果，多是从细观力学角度开展研究工作，结论在实验室得到了很好的验证.
通过室内细观力学的研究工作，建立的岩石单轴抗压强度定量模型，大多是针对岩石的韧性破坏模式，但金属矿山多以硬岩为主，钻进过程中，岩石的脆性破坏模式占主导地位[17]，基于韧性破坏提出的强度模型在实际应用中偏差较大.鉴于此，本文借助矿山工程凿岩机，在室内搭建了随钻获取的试验平台，模拟现场凿岩钻进过程；考虑岩石脆性破坏模式，针对不同类型岩石进行了大量的钻进试验，基于凿岩切割与贯入的实际物理过程，分析随钻参数与岩石力学性质之间的内在关系，并在此基础上，建立了基于随钻参数表征的岩石单轴抗压强度模型，并进行初步验证.
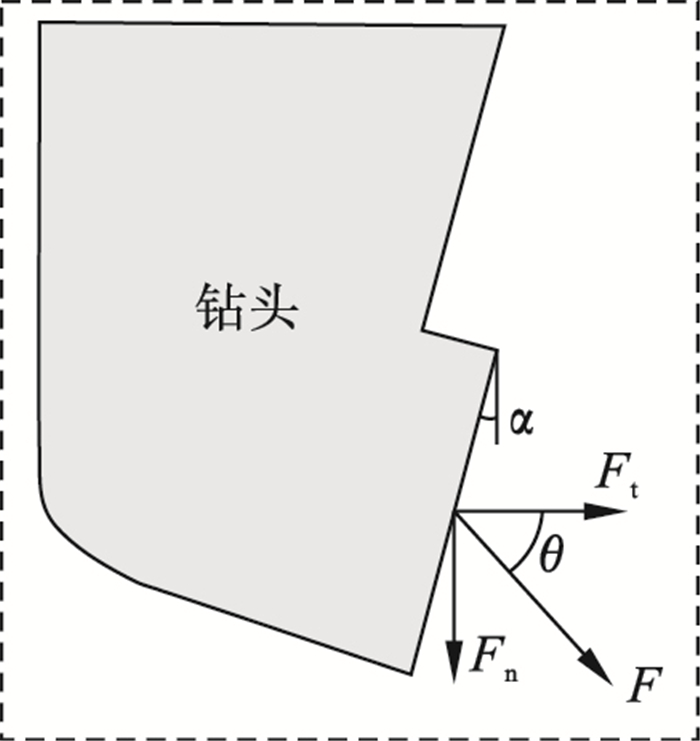
1 随钻表征的理论基础1.1 钻头力学特征考虑完全锋利钻头，不考虑摩擦作用，钻头与岩石的相互作用可以简化成单刀模型进行分析[10]，如图 1所示.假设推力在钻头半径上均匀分布，钻头单位尺寸上的法向力表示为
 | (1) |
 | 图 1 锋利钻头力学分析Fig.1 Sharp cutter mechanical analysis |
式中：Fn为钻头单位尺寸上的法向力，N·mm-1；F为推力，N；r为钻头半径，mm.
假设扭矩在钻头半径上均匀分布，钻头单位尺寸上的切向力表示为
 | (2) |
不考虑摩擦作用，切向力与法向力完全作用于切削岩石，则二者合力为切削力，切削力与水平面夹角的正切值可以表示为
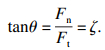 | (3) |
钻进过程中，切向力Ft作用于切割岩石，法向力Fn作用于贯入岩石，系数ζ反映了钻头切削力作用于贯入和切割岩石的比例.ζ增大代表着法向力Fn占比升高，说明贯入岩石的难度占比增大，ζ减小则代表着切割岩石的难度占比增大.
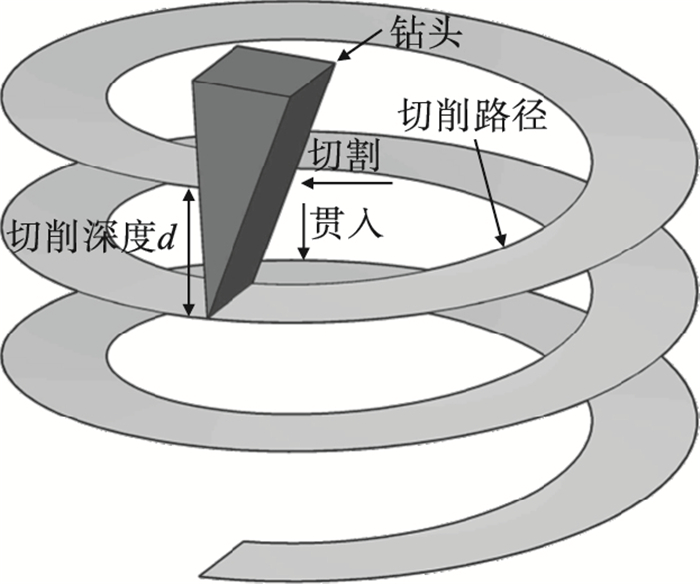
1.2 岩石破坏模式切削深度是表征钻头与岩石接触长度的参数，如图 2所示.在相同推力条件下，切削深度不受转速影响[18]，切削深度d可表示为
 | (4) |
 | 图 2 钻头三维运动轨迹Fig.2 Drill bit trajectory in three-dimensional |
式中：d为切削深度，mm；v为钻速，m·min-1；N为转速，r·min-1.
随切削深度的增大，岩石由韧性破坏向脆性破坏转变，控制破坏模式转变的深度称为临界切削深度，与岩石力学性质有关，通常小于1 mm[19]. 由于能量耗散机制不同，机械比能可作为区分岩石破坏模式的指标[20]，机械比能是破碎单位体积岩石所消耗的能量，表达式为[4]
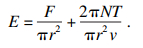 | (5) |
切削深度小于临界切削深度时，机械比能较高，当大于临界切削深度时，机械比能迅速降低.金属矿山钻进过程中，岩石硬度较大，脆性破坏模式占主导地位[17].因此，从岩石脆性破坏模式出发，研究随钻参数与岩石力学性质之间关系，更符合实际工程中的钻进物理过程.
1.3 工程钻进指标可钻性指标和机械比能分别从生产和能量的角度对钻进行为进行定量化描述，是重要的工程钻进指标.
机械比能包括推力做功和扭矩做功两部分，试验表明，扭矩是破碎岩石的主要因素，推力做功可以忽略不计[7].忽略推力部分做功，并结合式(4)，可得到扭矩与切削深度的关系：
 | (6) |
可钻性指标最早以钻速表示，然而钻速同时受转速和推力的影响，冯上鑫等[18]研究表明，推力一定的条件下，转速不影响扭矩和切削深度的大小，据此提出以推力随切削深度的增长速率作为岩石可钻性的评价指标Dp, kN/mm：
 | (7) |
 | (8) |
进一步将式(8)转换成推力与切削深度的关系：
 | (9) |
钻头实际运动过程包括持续切割和持续贯入，如图 2所示，机械比能定量描述了切割岩石的难易程度，可钻性指标定量描述了钻头贯入岩石的难易程度，综合二者对钻进行为进行描述，更符合实际过程.通过获取钻机的推力F、扭矩T、切削深度d，建立三者的变化特征，可得到机械比能E、可钻性指标D以及表征切削力倾角的系数ζ.
2 随钻获取试验平台与试验方案2.1 试验平台搭建为了获取与现场凿岩一致的随钻数据，采用工程中常用液压凿岩装备，在室内搭建了随钻获取的试验平台.钻头类型为矿用三翼金刚石钻头，直径为56 mm，钻头上共镶嵌有4个切削齿，每个切削齿直径13 mm，倾角α=15°，材料为复合金刚石，如图 3所示.液压回转式钻机型号为KY-150A，给进油缸最大压力为14 MPa，最大提供60 kN的推力，旋转油缸最大压力为12 MPa，最大提供1 200 N·m的扭矩.试验平台最大可进行850 mm深度的钻进试验，示意图如图 4所示.
图 3(Fig. 3)
 | 图 3 钻进试验所用复合金刚石钻头Fig.3 PDC bit used for drilling test |
图 4(Fig. 4)
 | 图 4 随钻获取试验平台示意图Fig.4 Schematic diagram of MWD test platform a—岩石搭载平台；b—进给压力测量；c—旋转压力测量；d—转速测量；e—位移测量；f—数据采集仪；g—岩石试件；h—钻头. |
2.2 随钻参数获取为获取随钻参数，随钻获取试验平台安装了精密的数据采集传感器.试验平台的数据采集系统由压力传感器、光电式接近开关、位移传感器、数据采集仪、PC机等组成.钻进时，各传感器以时间序列分别记录钻机的工作参数，数据采集频率为10 Hz.本节以岩石钻进试验数据为例，介绍随钻参数的获取方式.
通过4个压力传感器，获取给进油缸液压油进口、给进油缸液压油出口、旋转油缸液压油进口、旋转油缸液压油出口处的压力，分别记为TPin，TPout，RPin，RPout，压力传感器采集的原始数据如图 5a所示.试验表明，钻机输出的推力与扭矩作用在两方面：①克服钻机自身机械摩擦；②作用在岩石上.钻机通过空载运行，排除抵抗机械摩擦消耗的推力与扭矩，可以得到实际作用在岩石上的推力与扭矩.根据压力与推力、扭矩的线性关系，推力与扭矩获取方法如式(10)、式(11)所示，换算后的结果如图 5b所示.
 | (10) |
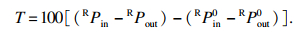 | (11) |
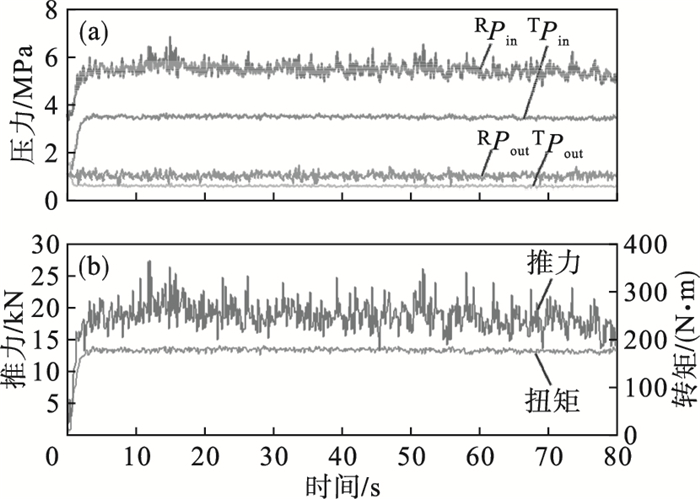 | 图 5 钻机推力与扭矩测量Fig.5 Drilling rig thrust and torque measurement (a)—4个压力传感器原始数据；(b)—处理后的推力与扭矩数据. |
式中：30/7为推力与液压力换算系数；F为推力，kN；(TPin0-TPout0)为空载运行时，给进油缸液压油进出口处的压力差，用于抵抗机械摩擦，经现场测试，取0.173 6 MPa；100为扭矩与液压力换算系数；T为扭矩，N·m；(RPin0-RPout0)为空载运行时旋转油缸液压油进出口处的压力差，经测试，取2.026 5 MPa.
钻杆的转速通过安装的光电式接近开关采集获取.钻杆表面共粘有16对均匀分布的黑白条纹，钻杆每旋转一周，接近开关记录16次，以0.1 s为间隔，向PC端发送0.1 s内记录的次数，通过计算单位时间内光电式接近开关记录的次数，可以得到钻头的转速，计算公式为
 | (12) |
图 6(Fig. 6)
 | 图 6 钻头转速测量Fig.6 Drill rotation speed measurement (a)—光电式接近开关原始数据；(b)—处理后的转速数据. |
钻头的钻速是通过计算单位时间内位移传感器记录的位移变化量得到，计算公式为
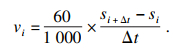 | (13) |
图 7(Fig. 7)
 | 图 7 钻头钻速测量Fig.7 Drill rate of penetration measurement (a)—位移传感器原始数据；(b)—处理后的钻速数据. |
由处理后的随钻数据可以看出，各项随钻参数在钻进过程中均维持在稳定值附近波动，满足试验要求.
2.3 试验方案考虑岩石种类的影响，选取4种不同种类的岩石进行钻进试验，试验岩样的长度为300 mm，其中2种砂岩产地为四川，闪长岩、花岗岩产地为辽宁，通过国际岩石力学学会(ISRM)建议的方法，测定了岩石单轴抗压强度与抗拉强度，如表 1所示.
表 1(Table 1)
 表 1 岩石的力学参数Table 1 Mechanical parameters of rock samples?
| 表 1 岩石的力学参数 Table 1 Mechanical parameters of rock samples? | |||||||||||||||||||||||||||||||||||||||||||||
对每种岩石，进行不同推力条件下的钻进试验，钻进深度均为300 mm，每次钻进试验推力增加约2 kN，直到钻进试验推力达到设定的30 kN，钻机的推力通过手动调节液压阀门开度进行设定.通过改变推力，获得推力-切削深度关系曲线、扭矩-切削深度关系曲线.
钻进试验中未对试件加载，因此各钻孔之间无影响，钻进后的部分岩石试件如图 8所示.
图 8(Fig. 8)
 | 图 8 部分钻进后的岩石试件Fig.8 Partial rock specimens after drilling |
3 结果与分析钻进岩石过程中，随钻参数在平均值附近平稳波动，因此以钻进阶段各随钻参数的平均值作为试验结果.根据试验方案开展岩石钻进试验，数据处理后得到每次钻进试验的推力、扭矩、钻速、转速、切削深度等随钻参数.
3.1 随钻参数变化特征根据试验结果，分别建立钻头推力与切削深度、扭矩与切削深度、单位尺寸上法向力与切向力关系曲线，如图 9~图 11所示.
图 9(Fig. 9)
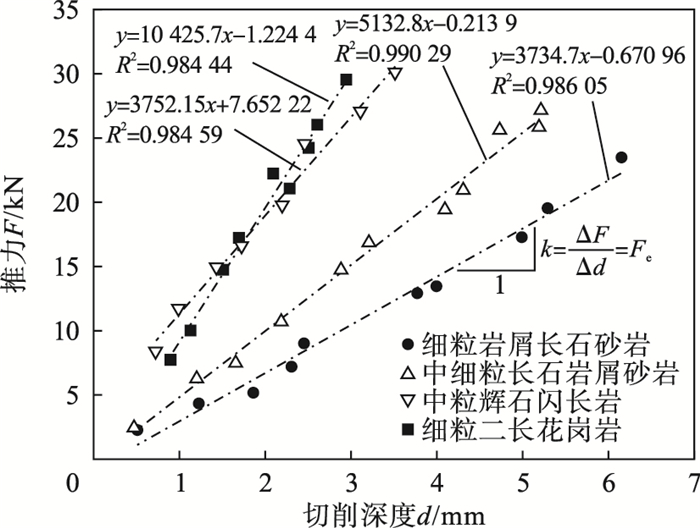 | 图 9 切削深度与推力关系曲线Fig.9 Relationship between cutting depth and thrust |
图 10(Fig. 10)
 | 图 10 切削深度与扭矩关系曲线Fig.10 Relationship between cutting depth and torque |
图 11(Fig. 11)
 | 图 11 钻头单位尺寸上的切向力与法向力关系曲线Fig.11 Relationship between tangential force and normal force on unit size of bit |
从图 9与图 10可知，推力-切削深度、扭矩-切削深度曲线表现出显著的线性拟合关系，与式(9)和式(6)提出的模型相符，二者的变化特征分别用最佳拟合曲线的斜率Fe，Te表示，即增加单位切削深度所需要的推力增量与扭矩增量.对于同一种岩石，即使在不同推力的钻进试验中，Fe，Te均保持不变，与工况无关，但在不同岩石中Fe，Te有明显差异，表现出与岩石力学性质有明显的相关性.
图 11为钻头单位尺寸上法向力与切向力的关系曲线，二者的比值ζ是关于切削力倾角的系数，表示了切削力作用在贯入和切割岩石的比例.从图可知，在相同岩石钻进过程中，切削力倾角保持恒定，并且不受工况条件影响，同样表现出与岩石力学性质的相关性.
3.2 岩石单轴抗压强度对钻进指标的影响通过以上分析，进一步定义岩石可钻性指标D，机械比能E为
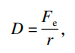 | (14) |
 | (15) |
表 2(Table 2)
表 2 岩石的随钻参数变化特征Fe，Te，ζTable 2 Drilling parameter variation characteristics Fe, Te, ζ of rocks
| 表 2 岩石的随钻参数变化特征Fe，Te，ζ Table 2 Drilling parameter variation characteristics Fe, Te, ζ of rocks |
图 12显示了岩石可钻性指标D、机械比能E、法向力与切向力比值ζ与岩石单轴抗压强度之间的关系.由图可以看出，本文定义的岩石可钻性指标D、机械比能E与岩石单轴抗压强度具有较好的线性关系，验证了采用这两个参数表征岩石强度的可行性.ζ与岩石单轴抗压强度呈正相关，说明随岩石单轴抗压强度的增大，和切割岩石相比，贯入岩石的难度越来越大.
图 12(Fig. 12)
 | 图 12 D，E，ζ与岩石单轴抗压强度的关系Fig.12 Relationship between D, E and ζ UCS of rock |
4 岩石单轴抗压强度表征模型4.1 模型提出以上分析表明，本文定义的岩石可钻性指标D与机械比能E这两个随钻获取的参数与岩石单轴抗压强度密切相关，并且与岩石单轴抗压强度量纲相同.可钻性指标和机械比能分别描述了钻头贯入和切割岩石的难易程度，图 13显示了D2/E与岩石单轴抗压强度的关系.从图中可以看出，D2/E与岩石单轴抗压强度存在显著的正比例关系.同时考虑钻头差异的影响，引入与钻头特征有关的修正系数γ，最终建立的基于随钻参数变化特征的岩石单轴抗压强度表征模型为
 | (16) |
 | 图 13 D2/E与岩石单轴抗压强度关系Fig.13 Relationship between D2/E and UCS of rock |
式中：Rc为岩石单轴抗压强度表征值，MPa；γ为钻头特征修正系数，根据图 13最优拟合曲线的斜率取0.924 02.
公式(16)的物理含义可以理解为岩石单轴抗压强度与岩石可钻性指标(D)有关，也与切削力用于贯入和切割岩石的比例(D2/E)有关.岩石可钻性指标(D)与岩石自身力学性质有关，切削力作用于贯入和切割岩石的比例(D2/E)正比于钻头法向力(w)与切向力(t)的比值ζ.Richard等[11]和Huang等[19]分别从室内试验和数值模拟的角度证明了ζ与钻头切削齿的倾角α有关，本文提出的强度指标表征模型可能还受钻头特征的影响，因此引入与钻头有关的修正系数γ描述不同几何特征钻头的影响，钻头特征和系数γ的关系需要进一步深入探究.
为评价表征值与试验值Rct的差异，定义差异率指标δ：
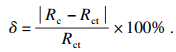 | (17) |
图 14(Fig. 14)
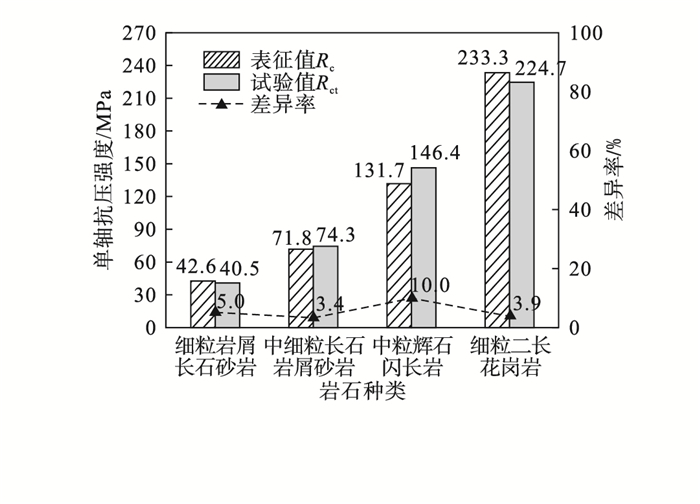 | 图 14 岩石单轴抗压强度表征值与试验值对比Fig.14 Comparison of presented and tested value of UCS of rock |
4.2 模型对比基于本文试验数据，利用已有模型表征不同工况下的岩石强度，结果如图 15所示.从图可知，相同岩石在不同工况下的强度表征结果存在多解性，已有模型受工况影响较大，而岩石的UCS作为岩石的客观属性不应随钻进工况发生变化.本文所提出的模型考虑了钻进工况对随钻参数的影响，通过一系列不同工况下的随钻数据，每种岩石只得到唯一的强度表征结果(图 13)，并且显示出与试验值较高的相关性.
图 15(Fig. 15)
 | 图 15 不同工况下岩石强度表征值与岩石单轴抗压强度试验值的关系散点图Fig.15 Scatter diagrams of the relationship between estimation value and UCS test value (a)—机械比能MSE[4]；(b)—单位体积切削能ηc[15]；(c)—可钻性强度Ds[7]；(d)—可钻性指数Id[21]. |
4.3 初步验证为验证提出的强度表征模型的可靠性，选取另一种类的岩石进行了验证.所用试验岩样为泥质细粒长石岩屑砂岩，通过开展不同推力条件下的钻孔试验，建立推力、扭矩与切削深度的关系，如图 16所示.根据曲线斜率，得到岩样的随钻参数变化特征Fe，Te.试验采用同样的钻头，因此γ可取值为0.924 02.泥质细粒长石岩屑砂岩的具体计算结果及随钻参数见表 3.
图 16(Fig. 16)
 | 图 16 钻头推力、扭矩随切削深度关系Fig.16 Relationship between thrust, torque, and cutting depth |
表 3(Table 3)
表 3 泥质细粒长石岩屑砂岩的试验结果和计算结果Table 3 Drilling test result and computation result of fine feldspathic detritus sandstone
| 表 3 泥质细粒长石岩屑砂岩的试验结果和计算结果 Table 3 Drilling test result and computation result of fine feldspathic detritus sandstone |
由表 3可知，泥质细粒长石岩屑砂岩的单轴抗压强度试验值为148.8 MPa，基于随钻参数的单轴抗压强度表征值为142.2 MPa，差异率为5.07%，初步验证了模型的可靠性.
另外，本文所用的泥质细粒长石岩屑砂岩与中粒辉石闪长岩的单轴抗压强度十分接近，但通过随钻获取试验得到的两种岩石的可钻性指标D与机械比能E却差别很大，如表 4所示.泥质细粒长石岩屑砂岩的可钻性指标D与机械比能E比中粒辉石闪长岩分别高出18.74%，30.60%，这表明单一指标无法较好地表征岩石的单轴抗压强度，也进一步验证了本文采用可钻性指标和机械比能作为岩石单轴抗压强度表征指标的可行性.
表 4(Table 4)
表 4 泥质细粒长石岩屑砂岩与中粒辉石闪长岩试验结果Table 4 Test results of fine feldspathic detritus sandstone and medium-grained pyroxene diorite ?
| 表 4 泥质细粒长石岩屑砂岩与中粒辉石闪长岩试验结果 Table 4 Test results of fine feldspathic detritus sandstone and medium-grained pyroxene diorite ? | |||||||||||||||||||||||||||||||||||||||||||||
5 结论1) 推力随切削深度的变化率Fe、扭矩随切削深度的变化率Te、钻头单位尺寸上法向力与切向力之比ζ，均表现出相对同种岩石不变性，并且不受试验条件影响.
2) 随钻参数变化特征Fe, Te, ζ均与岩石单轴抗压强度呈线性相关.
3) 基于本文定义的机械比能和可钻性指标，建立了岩石单轴抗压强度表征模型，表征结果与试验值比较接近，为利用凿岩过程快速表征岩石力学参数提供了一种新方法.
参考文献
| [1] | Scoble M J, Peck J. A technique for ground characterization using automated production drill monitoring[J]. International Journal of Surface Mining, Reclamation and Environment, 1987, 1(1): 41-54. DOI:10.1080/09208118708944101 |
| [2] | Peck J, Scoble M J, Carter M. Interpretation of drilling parameters for ground characterization in exploration and development of quarries[J]. Transactions of the Institution of Mining and Metallurgy (Section B Applied Earch Science), 1987, 96(2): 141-148. |
| [3] | Scoble M J, Peck J, Hendricks C. Correlation between rotary drill performance parameters and borehole geophysical logging[J]. Mining Science and Technology, 1989, 8(3): 301-312. DOI:10.1016/S0167-9031(89)90448-9 |
| [4] | Teale R. The concept of specific energy in rock drilling[J]. International Journal of Rock Mechanics and Mining Sciences, 1965, 2(1): 57-73. DOI:10.1016/0148-9062(65)90022-7 |
| [5] | 谭卓英, 岳中琦, 蔡美峰. 风化花岗岩地层旋转钻进中的能量分析[J]. 岩石力学与工程学报, 2007, 26(3): 478-483. (Tan Zhuo-ying, Yue Zhong-qi, Cai Mei-feng. Analysis of energy for rotary drilling in weathered granite formation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 478-483. DOI:10.3321/j.issn:1000-6915.2007.03.006) |
| [6] | 谭卓英, 李文, 岳鹏君, 等. 基于钻进参数的岩土地层结构识别技术与方法[J]. 岩土工程学报, 2015, 37(7): 1328-1333. (Tan Zhuo-ying, Li Wen, Yue Peng-jun, et al. Techniques and approaches for identification of geo-formation structure based on diamond drilling parameters[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1328-1333.) |
| [7] | Karasawa H, Ohno T, Kosugi M, et al. Methods to estimate the rock strength and tooth wear while drilling with roller-bits part 1:milled-tooth bits[J]. Journal of Energy Resources Technology, 2002, 124(3): 125-132. DOI:10.1115/1.1482405 |
| [8] | Karasawa H, Ohno T, Kosugi M, et al. Methods to estimate the rock strength and tooth wear while drilling with roller-bits part 2:insert bits[J]. Journal of Energy Resources Technology, 2002, 124(3): 133-140. DOI:10.1115/1.1482406 |
| [9] | Detournay E, Defourny P. A phenomenological model for the drilling action of drag bits[J]. International Journal of Rock Mechanics and Mining Sciences, 1992, 29(1): 13-23. DOI:10.1016/0148-9062(92)91041-3 |
| [10] | Detournay E, Richard T, Shepherd M. Drilling response of drag bits: theory and experiment[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(8): 1347-1360. DOI:10.1016/j.ijrmms.2008.01.010 |
| [11] | Richard T, Dagrain F, Poyol E, et al. Rock strength determination from scratch tests[J]. Engineering Geology, 2012, 147: 91-100. |
| [12] | Yahiaoui M, Paris J Y, Delbé K, et al. Independent analyses of cutting and friction forces applied on a single polycrystalline diamond compact cutter[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 85: 20-26. DOI:10.1016/j.ijrmms.2016.03.002 |
| [13] | 王琦, 秦乾, 高红科, 等. 基于数字钻探的岩石c-φ参数测试方法[J]. 煤炭学报, 2019, 44(3): 915-922. (Wang Qi, Qin Qian, Gao Hong-ke, et al. A testing method for rock c-φ parameter based on digital drilling test technology[J]. Journal of China Coal Society, 2019, 44(3): 915.) |
| [14] | 王琦, 高红科, 蒋振华, 等. 地下工程围岩数字钻探测试系统研发与应用[J]. 岩石力学与工程学报, 2020, 39(2): 301-310. (Wang Qi, Gao Hong-ke, Jiang Zhen-hua, et al. Development and application of a surrounding rock digital drilling test system of underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(2): 301-310.) |
| [15] | 王琦, 秦乾, 高松, 等. 数字钻探随钻参数与岩石单轴抗压强度关系[J]. 煤炭学报, 2018, 43(5): 1289-1295. (Wang Qi, Qin qian, Gao Song, et al. Relationship between rock drilling parameters and rock uniaxial compressive strength based on energy analysis[J]. Journal of China Coal Society, 2018, 43(5): 1289-1295.) |
| [16] | Kalantari S, Hashemolhosseini H, Baghbanan A. Estimating rock strength parameters using drilling data[J]. International Journal of Rock Mechanics and Mining Science, 2018, 104: 45-52. DOI:10.1016/j.ijrmms.2018.02.013 |
| [17] | 周琴, 张在兴, 张凯, 等. 钻头切削齿破碎岩石的温度变化试验及机理分析[J]. 天然气工业, 2020, 40(10): 102-110. (Zhou Qin, Zhang Zai-xing, Zhang Kai, et al. Temperature variation tests and mechanism analysis of rock breaking by bit cutters[J]. Natural Gas Industry, 2020, 40(10): 102-110.) |
| [18] | 冯上鑫, 王善勇. 旋切作用下岩石破碎机理及岩石可钻性的试验研究[J]. 煤炭学报, 2022, 47(3): 1395-1404. (Feng Shang-xin, Wang Shan-yong. Experimental study of rock-bit interaction mechanism for rock drillability assessment in rotary drilling[J]. Journal of China Coal Society, 2022, 47(3): 1395-1404.) |
| [19] | Huang H, Lecampion B, Detournay E. Discrete element modeling of tool-rock interaction I: rock cutting[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(13): 1303-1336. |
| [20] | He X, Xu C. Specific energy as an index to identify the critical failure mode transition depth in rock cutting[J]. Rock Mechanics and Rock Engineering, 2016, 49(4): 1461-1478. |
| [21] | Zhang K, Hou R, Zhang G, et al. Rock drillability assessment and lithology classification based on the operating parameters of a drifter: case study in a coal mine in China[J]. Rock Mechanics and Rock Engineering, 2016, 49(1): 329-334. |
