, 骆敏 东北大学 软件学院, 辽宁 沈阳 110169
收稿日期：2022-07-13
基金项目：辽宁省自然科学基金资助项目(2021-YGJC-07)。
作者简介：刘晓熙(1995-), 女, 辽宁鞍山人, 东北大学硕士研究生;
姜慧研(1963-), 女, 辽宁鞍山人, 东北大学教授。
摘要：针对经典穿刺路径规划算法在量化路径情况时没有考虑路径周围区域的问题, 提出新的约束条件来弥补对路径周围信息量化的不足.基于血管位置信息提出一个严格约束条件(周围区域避开血管), 并基于骨骼密度、血管密度和直径信息提出3个软约束条件(骨骼密集度、血管密集度、血管风险度), 将周围信息添加到路径的量化中, 提高穿刺路径的安全性.为了适应患者的特异性, 提出软约束优化度评分算法, 根据软约束的优化度设置权重, 并将最大优化度对应的穿刺路径作为最优穿刺路径.为了验证算法的有效性, 在公开数据集3D-IRCADb上进行实验, 结果表明, 本文提出的算法可以快速计算出符合临床需求的最优穿刺路径.
关键词：肝癌消融术穿刺约束条件穿刺路径规划多目标优化手术导航
Multi-constraint Optimal Puncture Path Planning Algorithm for Liver Cancer Ablation
LIU Xiao-xi, JIANG Hui-yan
, LUO Min School of Software, Northeastern University, Shenyang 110169, China
Corresponding author: JIANG Hui-yan, E-mail: hyjiang@mail.neu.edu.cn.
Abstract: Aiming at the problem that the classic puncture path planning algorithm does not consider the area around the path when quantifying the path, new constraints condition are proposed to make up for the lack of quantification of the information around the path. A strict constraint condition was proposed based on the blood vessel position information (the surrounding area avoids the blood vessel), and based on bone density, blood vessel density, and diameter information, three soft constraints (bone density, blood vessel density, and blood vessel risk) were proposed, and the surrounding information was added to the quantification of the path to improve the safety of the puncture path. In order to adapt to the specificity of patients, a soft constraint optimization degree scoring algorithm is proposed, and the weight is set according to the optimization degree of soft constraints, and the puncture path corresponding to the maximum optimization degree is taken as the optimal puncture path. In order to verify the effectiveness of the algorithm, experiments were carried out on the public dataset 3D-IRCADb. The experimental results show that the algorithm proposed in this paper can quickly calculate the optimal puncture path that meets the clinical needs.
Key words: liver cancer ablationpuncture constraintspuncture path planningmulti-objective optimizationsurgical navigation
原发性肝癌是最常见的恶性肿瘤之一.肝细胞癌是原发性肝癌主要的病理学类型, 占原发性肝癌的85 % ~90 % [1].目前肝癌的根治性治疗主要包括3种方式：肝移植、手术切除和消融治疗.对于直径小于3 cm的肝脏恶性肿瘤, 广泛采用的根治性治疗是肝肿瘤消融术[2].肝肿瘤消融术包括术前、术中和术后3个部分, 其中术前的穿刺路径规划是消融术成功的重要前提.在术前阶段, 首先采用腹部增强CT、MRI等影像设备获得患者的病灶周围影像, 然后根据影像信息诊断出肿瘤位置、肿瘤数量、肿瘤体积等, 最后依据肿瘤及肿瘤周围的血管、骨骼、器官位置进行穿刺路径规划.由于不能从医学影像获得实际物理位置信息, 医生很难综合考虑多项穿刺临床约束条件获得最优穿刺路径.
在手术路径规划研究中, 国内外****取得了一定成果.Liu等[3]针对机器人辅助下大肿瘤治疗困难的问题, 将多个约束条件转化为数学模型并得到可进针区域(collision-free reachable workspace, CFRW), 然后在CFRW中选择最优穿刺路径；Villard等[4]将射频消融的烧蚀区模拟成理想的椭球型, 采用Nelder-Mead单纯形算法[5]覆盖肝肿瘤, 在避开腹腔重要组织结构的情况下, 计算穿刺路径与重要组织结构之间的距离；Villard等[6]首先计算出可进针区域, 然后将能够消融整个病灶且烧蚀区体积最小的穿刺路径作为最优穿刺路径；Villard等[7]考虑了直径大于3 mm的局部血管的冷却效果, 使坏死的形状更加逼真, 通过计算包含肿瘤及安全边界[8]的最小椭球体的中心和轴向, 得到穿刺针的最优位置.Baegert等[9]采用准穷举算法优化可行穿刺路径, 并将穿刺针轨迹与肿瘤长轴之间的夹角纳入软约束条件中；Baegert等[10]将穿刺针路径的深度、角度及经肝距离纳入硬约束条件；Baegert等[11]采用软约束与加权求和算法相结合优化可行穿刺路径, 并将穿刺针的深度和穿刺路径到重要结构的实际距离纳入软约束条件中；张睿等[12]采用改进的立方体映射算法, 对患者的CT图像包围盒表面进行二值化分类, 根据各自的软约束条件灰度图得到最优穿刺路径.
基于血管位置信息提出了一个严格约束条件, 使周围区域避开血管；然后基于骨骼密度、血管密度和直径信息提出了3个软约束条件, 即骨骼密集度、血管密集度及血管风险度, 以有效量化路径周围情况, 使穿刺路径最大程度地远离风险组织.本文提出软约束优化度评分算法进行多目标优化, 并计算得到优化度最高的路径.
1 多约束最优穿刺路径规划算法本文提出一种针对单针肝癌消融手术的多约束最优穿刺路径规划算法, 腹腔三维模型如图 1所示.
图 1(Fig. 1)
 | 图 1 腹腔三维模型Fig.1 3D abdominal cavity model |
整个算法的流程如图 2所示, 算法1给出了伪代码.具体步骤如下：
图 2(Fig. 2)
 | 图 2 多约束最优穿刺路径规划算法的流程Fig.2 Flow chart of multi-constraint optimal puncture path planning algorithm |
步骤?1?? 输入腹腔三维模型；
步骤?2?? 对皮肤进针点进行采样；
步骤?3?? 选择一个皮肤进针点生成穿刺路径后进入严格约束部分, 过滤不满足5个严格约束的皮肤进针点.其中, 前4个严格约束出自文献[11], 本文提出了第5个严格约束, 即周围区域避开血管；
步骤?4?? 如果满足5个严格约束条件, 则计算5个软约束指标.其中, 本文在文献[11]的2个软约束基础上又提出了3个软约束, 分别为基于骨骼密集度避开骨骼密集区域、基于血管密集度避开血管密集区域、基于血管风险度避开大直径血管区域, 即5个软约束指标为骨骼密集度、血管密集度、血管风险度、穿刺距离和穿刺角度；
步骤?5?? 遍历全部皮肤进针点, 计算出软约束指标值及其最大值；
步骤?6?? 基于本文提出的软约束优化度评分算法对皮肤进针点评分；
步骤?7?? 基于最优解确定最优进针点与穿刺路径.
| 算法?1:多约束最优穿刺路径规划算法 |
| 输入: 腹腔三维模型 |
| 输出: 最优皮肤进针点和最优穿刺路径 |
| 1.?? 设置皮肤点采样数量N; |
| 2. ?? 对皮肤进行采样得到皮肤进针点p1, p2, …, pN; |
| 3. ?? for j∈{1, 2, …, N} do |
| 4. ?????? if pj不满足严格约束then |
| ????????continue; |
| 5.?????? else |
| 6. ????????pj为可行进针点; |
| 7.????????计算pj的骨骼密集度Nbonej: Nbonej= ∑i=14nij; |
| 8.????????计算pj的血管密集度Nvesselj: Nvesselj= ∑i=14mij; |
| 9. ????????计算pj的血管风险度Rvesselj: Rvesselj= ∑i=14rij; |
| 10.????????计算pj的穿刺距离dj; |
| 11.????????计算pj的穿刺角度aj; |
| 12.????????更新骨骼密集度最大值Nbonemax; |
| 13.????????更新血管密集度最大值Nvesselmax; |
| 14.????????更新血管风险度最大值Rvesselmax; |
| 15.????????更新穿刺距离最大值dmax; |
| 16.????????更新穿刺角度最大值amax; |
| 17. ????end if |
| 18. ?? end for |
| 19. ?? for j∈{1, 2, …, N} do |
| 20.???? if pj是可行进针点then |
21.????????根据F(pj)式(8)计算pj的评分:   |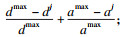
| 22.????????更新评分最大值Fmax; |
| 23. ??????end if |
| 24. ??end for |
| 25.?? Result Fmax皮肤进针点p和p对应的穿刺路径 |
1.1 基于蒙特卡洛法的皮肤进针点采样在穿刺路径规划中, 首先要设计皮肤进针点的位置, 然后根据约束条件对皮肤进针点进行筛选, 最后选出最优皮肤进针点.由于皮肤是连续曲面, 为了减少计算数量, 提高计算效率, 需要对皮肤采样得到离散的皮肤进针点.
马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)是一种近似的贝叶斯概率模型算法.MCMC利用从马尔科夫链中采集样本去模拟复杂的概率分布.当采集的样本数量足够大时, 样本能够为概率模型提供接近无偏估计.为此, 本文采用蒙特卡洛法按照均匀分布进行皮肤进针点采样.
皮肤进针点的采样步骤如下：
步骤?1?? 设置1个合理的样本容量值作为循环次数, 设样本容量值N=80 000；
步骤?2?? 确定皮肤在三维空间的坐标范围；
步骤?3?? 在坐标范围内采用随机函数rand()生成随机值, 得到随机的三维坐标, 将该坐标作为皮肤进针点.
1.2 约束条件在计算机辅助手术导航中, 需要对穿刺消融术约束量化成多个条件.Baegert等[11]将其量化为严格约束(strict constraints)和软约束(soft constraints).严格约束是必须遵循的条件, 软约束是可选条件, 软约束表示穿刺路径的安全性程度.
在实际手术中, 由于术中穿刺的路径与术前规划的路径会存在一定偏差, 为此在自动规划路径时还要考虑路径周围的骨骼和血管情况, 使路径避开重要组织结构, 以保证手术的安全性.本文提出基于周围区域避开血管的严格约束条件和基于骨骼密集度、血管密集度及血管风险度的软约束条件, 并设置风险组织包括肝静脉、门静脉、动脉和骨骼, 以更好地量化路径周围信息, 使穿刺路径更安全.肝癌穿刺路径规划包括严格约束和软约束, 如表 1所示.由于穿刺手术导致软组织变形的问题是目前临床上无法解决的问题, 因此本文暂时没有考虑软组织的变形问题.
表 1(Table 1)
 表 1 肝癌穿刺路径规划的约束Table 1 Constraints of liver cancer puncture path planning
| 表 1 肝癌穿刺路径规划的约束 Table 1 Constraints of liver cancer puncture path planning | |||||||||||||||||||||
1.3 周围区域避开血管的严格约束为了保证穿刺路径远离血管, 本文提出将周围区域避开血管作为一个严格约束条件.该约束条件将周围区域抽象为当前穿刺路径附近的4条穿刺路径, 如果4条边界穿刺路径碰撞到血管, 则当前穿刺路径被舍弃, 对应的皮肤进针点为不可进针点.
周围4条穿刺路径的位置如图 3所示.其中, 进针点均为皮肤上的点.以当前皮肤进针点为中心画出正方形.周围4个穿刺路径对应的皮肤进针点为正方形的4个顶点.
图 3(Fig. 3)
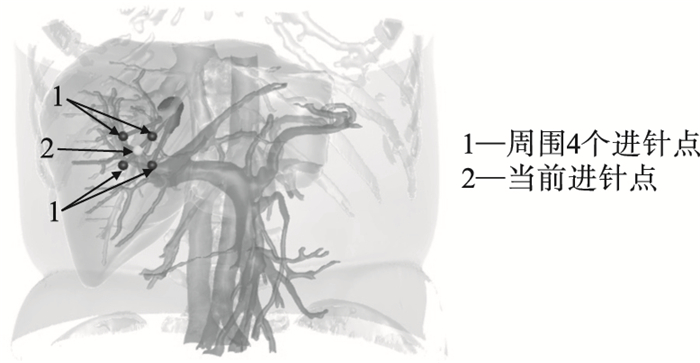 | 图 3 当前进针点的周围4条穿刺路径的可视化结果Fig.3 Visualization result of location of four puncture paths around the current injection point |
不同约束条件下，对d值设置如表 2所示.其中, d表示中心点与正方形边界的距离参数, d的单位为mm.
表 2(Table 2)
表 2 距离参数d的设置Table 2 Setting of distance parameter d
| 表 2 距离参数d的设置 Table 2 Setting of distance parameter d |
在全部5个严格约束条件下, 得到的可行进针区域三维可视化结果如图 4所示.可以看出, 周围区域避开血管的严格约束优化了可行进针区域.软约束条件a, b, c的计算是基于避开血管的进针点进行的.
图 4(Fig. 4)
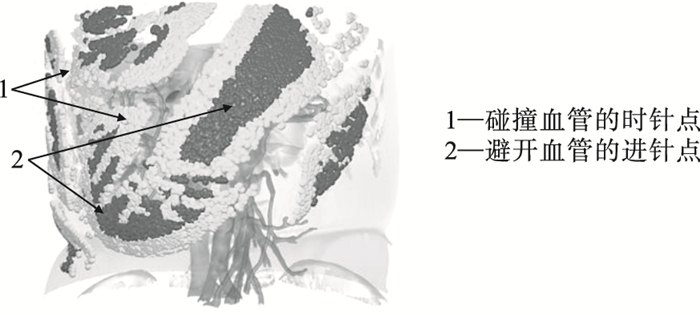 | 图 4 避开血管的进针点可选范围的可视化结果Fig.4 Visualization result of optional range of needle entry point avoiding blood vessels |
1.4 基于骨骼密集度避开骨骼密集区域的软约束为了保证穿刺路径周围的骨骼数量较少, 降低穿刺风险, 本文基于当前穿刺路径附近的骨骼密集度提出了第1个软约束条件, 计算式为
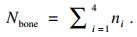 | (1) |
骨骼密集度的三维可视化结果如图 5a所示.骨骼密集度越大的皮肤进针点被标记的颜色越深.在患者腹腔三维模型中, 位于肋骨表面的皮肤进针点的骨骼密度大, 如矩形框内的皮肤区域贴近肋骨, 该区域的皮肤进针点的骨骼密集度大, 被标记的颜色深.如圆形框内的皮肤区域位于腹部, 没有骨骼, 该区域的皮肤进针点的骨骼密集度为0, 标记为白色.可知骨骼密集度有效评估了当前穿刺路径附近的骨骼密集度.
图 5(Fig. 5)
 | 图 5 骨骼/血管密集度的可视化结果Fig.5 Visualization results of the degree of bone / vessel density |
1.5 基于血管密集度避开血管密集区域的软约束为了保证穿刺路径周围的血管数量较少, 降低穿刺风险, 本文基于当前穿刺路径附近的血管密集度提出了第2个软约束条件, 计算式为
 | (2) |
在此约束中, 设置距离参数d=12 mm, 为手术提供更多的容错空间.血管密集度的三维可视化结果如图 5b所示, 血管密集度越大的皮肤进针点被标记的颜色越深, 如矩形框内的皮肤区域与肿瘤之间的三角形框内存在密集血管, 为此, 该区域的皮肤进针点的血管密集度大, 被标记的颜色深.圆形框内的皮肤区域与肿瘤之间无血管, 该区域的皮肤进针点的血管密集度为0, 标记为白色, 可知血管密集度有效评估了当前穿刺路径附近的血管密度.
1.6 基于血管风险度避开大直径血管区域的软约束在临床穿刺过程中, 如果待消融肿瘤位于血管密集区域, 穿刺路径不可避免地要碰撞到血管.为了防止穿刺碰撞到大血管造成大出血的手术事故, 穿刺路径尽可能向血管小分支偏移.为此, 自动计算血管直径十分必要.
本文提出一种自动计算血管直径的算法, 步骤如下：
步骤?1??如果穿刺路径可能碰撞到血管, 则将碰撞点标记为球体, 并计算碰撞点坐标, 如图 6所示；
图 6(Fig. 6)
 | 图 6 基于碰撞点检测的血管直径的可视化结果Fig.6 Visualization result of blood vessel diameter based on collision point detection |
步骤?2?? 如果碰撞点沿血管法线方向的路径碰撞到血管壁的另一侧, 则将碰撞点标记为另一个球体, 并计算碰撞点坐标, 线段表示当前血管直径；
步骤?3?? 基于2个碰撞点的距离计算当前血管直径, 计算式为
 | (3) |
为了保证穿刺路径周围的血管直径小, 降低穿刺风险, 基于血管风险度提出了第3个软约束条件, 评估当前穿刺路径附近血管的直径, 计算式为
 | (4) |
血管风险度的三维可视化结果如图 7所示.血管风险度越大皮肤进针点被标记的颜色越深, 如矩形框内的皮肤区域与肿瘤之间的三角形框内存在大直径血管, 该区域的皮肤进针点的血管风险度大, 被标记的颜色深.如圆形框内的皮肤域与肿瘤之间无血管, 血管直径为0, 该区域的皮肤进针点的血管风险度为0, 被标记为白色.可知, 血管风险度有效评估了当前穿刺路径附近的血管密度.
图 7(Fig. 7)
 | 图 7 血管风险度的可视化结果Fig.7 Visualization result of the degree of blood vessel risk. |
2 最优穿刺路径的计算医生规划的穿刺路径应该保证各项软约束条件均达到最优, 但在穿刺路径规划中各项软约束条件之间存在相互制约的关系, 不会存在软约束值全部最优的皮肤进针点.穿刺路径规划算法需要全局考虑各个软约束条件之间的平衡关系, 从而将穿刺路径规划问题转化为多目标优化问题.
传统加权求和算法将多目标整合为单目标, 是最简单的最优解决策方式.由于加权求和算法的权重无法适应患者特异性, 受主观因素影响严重.为了解决上述问题, 提出一种软约束优化度评分算法对皮肤进针点进行评分, 算法可以自适应设置权重, 评分最高的路径为最优穿刺路径.
软约束优化度评分算法如下：
步骤?1?? 为了量化不同软约束的可优化性, 本文提出了一种软约束权重的定义方法, 即根据软约束的可优化度定义软约束权重, 计算式为
 | (5) |
步骤?2?? 计算皮肤进针点在软约束上优化度的归一化值Hi, 计算式为
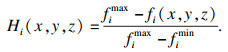 | (6) |
步骤?3?? 计算皮肤进针点的软约束优化度评分F, 计算式如式(7)所示.将式(5), 式(6)代入式(7), 将式(7)简化为式(8).简化后的软约束权重评分仅需计算第i个软约束的最大值fimax, 而无需计算fimin：
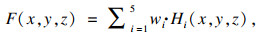 | (7) |
 | (8) |
综上, 根据不同软约束的可优化性, 计算得到适合患者的权重, 解决了权重的设置受主观因素影响的问题.基于软约束优化度评分算法获得优化度最高的穿刺路径, 以达到优化穿刺路径的目的.
3 实验与分析本文编程语言为C#, 基于Unity3D进行计算及可视化.实验数据采用3D-IRCADb-01数据集, 由数据集直接获得肿瘤的二维标签, 根据二维标签位置获得肿瘤位置；再根据数据集给出的肿瘤标签的连通区域数量计算肿瘤数量；最后根据肿瘤三维连通区域的立方体包围盒的体积估算肿瘤体积.从数据集中选择2位患者作为研究对象, 每位患者各选择3例满足半径 < 3 cm, 且无血管、胆管侵犯[2]要求, 并适合进行单针穿刺手术的肿瘤进行穿刺路径规划实验, 并将6例肿瘤分别编号为1#, 2#, 3#, 4#, 5#, 6#.
3.1 最优穿刺路径的计算结果为了分析最优穿刺路径的指标, 表 3列出了皮肤进针点坐标, 以及骨骼密集度、血管密集度、血管风险度、穿刺距离和穿刺角度5项软约束指标.软约束取值情况如下：骨骼密集度、血管密集度和血管风险度全为最优值0, 则表示最优穿刺路径全部远离骨骼和血管；穿刺距离 < 99 mm, 表示穿刺距离小于消融针长度150 mm, 消融针可以到达肿瘤；穿刺角度 < 5°, 表示消融针接近垂直角度穿刺进入肝脏, 不会发生滑针现象.综上, 最优穿刺路径的计算结果符合临床要求且安全性高.
表 3(Table 3)
表 3 最优穿刺路径计算结果Table 3 Computed results of optimal puncture paths
| 表 3 最优穿刺路径计算结果 Table 3 Computed results of optimal puncture paths |
3.2 基于新的约束条件的皮肤进针点筛选为了分析新的约束条件筛选皮肤进针点的正确性, 皮肤进针点筛选可视化结果如图 8所示.
图 8(Fig. 8)
 | 图 8 皮肤进针点筛选的可视化结果Fig.8 Visualization results of skin needle entry point screening (a)—在腹部三维模型上采样的皮肤进针点；(b)—基于严格约束a ~ d筛选的皮肤进针点；(c)—基于新的严格约束e筛选的皮肤进针点；(d)—基于所有软约束选出的最优皮肤进针点. |
具体步骤如下：
步骤?1 ??输入患者腹腔三维模型, 采样得到全部皮肤进针点, 如图 8a所示；
步骤?2?? 基于严格约束条件a, b, c, d, 筛选皮肤进针点, 如图 8b所示；
步骤?3?? 基于新的严格约束条件e, 筛选皮肤进针点, 除去周围区域存在血管的皮肤进针点, 如图 8c所示；
步骤?4?? 基于各项软约束选出最优皮肤进针点, 如图 8d所示.在最优穿刺路径的各项软约束值中, 新的软约束条件a, b, c的值全部为最优值0, 因此新的软约束条件保证了最优穿刺路径远离骨骼和血管.
随约束条件的逐渐增加, 满足穿刺手术基本要求的皮肤进针点越来越少.大部分皮肤区域无效, 只有少数标记点符合要求.综上, 新的约束条件保证了最优穿刺路径符合临床要求, 同时增加了最优穿刺路径安全性.
3.3 多约束最优穿刺路径规划算法的计算时间为了分析多约束最优穿刺路径规划算法的计算时间, 表 4列出了本文算法的计算时间, 平均时间为11.44 s.最优穿刺路径规划时间远小于临床医生人工规划时间.
表 4(Table 4)
表 4 多约束最优穿刺路径规划算法的计算时间Table 4 Calculation time of multi-constraint optimal puncture path planning algorithm
| 表 4 多约束最优穿刺路径规划算法的计算时间 Table 4 Calculation time of multi-constraint optimal puncture path planning algorithm |
3.4 实验与分析为了对比软约束优化度评分算法与加权求和算法的最优穿刺路径结果, 总结了在6例肿瘤实验中软约束的最优值、两种算法的最优解和优化度, 以及软约束优化度评分算法的软约束权重.实验设置加权求和算法的权重全部为1.
软约束的最优值与权重如表 5所示.骨骼密集度、血管密集度和血管风险度的最优值全为0, 表示存在远离骨骼和血管的可行进针点.穿刺距离的最优值取决于肿瘤相对于皮肤的位置, 穿刺角度的最优值接近0, 表示存在位置接近垂直肝包膜的可行进针点.对于软约束权重, 由于骨骼密集度、血管密集度、血管风险度和穿刺角度的最优值接近于0或等于0, 其软约束权重接近于1或等于1.由于肿瘤与皮肤存在距离, 最优值无法接近0, 为此穿刺距离的软约束权重较小.软约束优化度评分算法会优先优化权重大的骨骼密集度、血管密集度、血管风险度和穿刺角度, 最后优化权重小的穿刺距离.
表 5(Table 5)
表 5 软约束的最优值与权重Table 5 Optimal values and weights of soft constraints
| 表 5 软约束的最优值与权重 Table 5 Optimal values and weights of soft constraints | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 6总结了软约束优化度评分算法和加权求和算法计算结果在软约束上的优化度.在骨骼密集度、血管密集度和血管风险度的优化度上, 两种算法相同；在穿刺角度的优化度上, 软约束优化度评分算法较大；在穿刺距离的优化上, 软约束优化度评分算法较小.由于实验设置加权求和算法的权重全部为1, 因此加权求和算法将各个软约束的相同优先级进行优化.对比加权求和算法的优化度结果, 证明了软约束优化度评分算法遵循了设计目标, 将可优化度大的骨骼密集度、血管密集度、血管风险度和穿刺角度进行优化, 且基本优化到最优数值；将可优化度小的穿刺距离小程度优化, 优化结果>0.88.软约束优化度评分算法先优化可优化度高的软约束, 计算出了优化度最高的穿刺路径作为最优穿刺路径.
表 6(Table 6)
表 6 软约束优化度评分算法和加权求和算法的软约束优化度Table 6 Soft constraints optimization degree of soft constraint optimization scoring algorithm and weighted summation algorithm
| 表 6 软约束优化度评分算法和加权求和算法的软约束优化度 Table 6 Soft constraints optimization degree of soft constraint optimization scoring algorithm and weighted summation algorithm | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
软约束优化度评分算法与加权求和算法的三维可视化结果如图 9所示. 图 9a~图 9c分别表示肿瘤1#，2#，3#在两种算法的结果不同，肿瘤1#，2#在软约束优化度评分算法规划的最优穿刺路径更加远离血管，肿瘤3#的两种算法结果基本一致. 图 9d~图 9f分别表示肿瘤4#，5#，6#的两种算法结果一致. 可知，软约束优化度评分算法规划的最优穿刺路径优于加权求和算法.
图 9(Fig. 9)
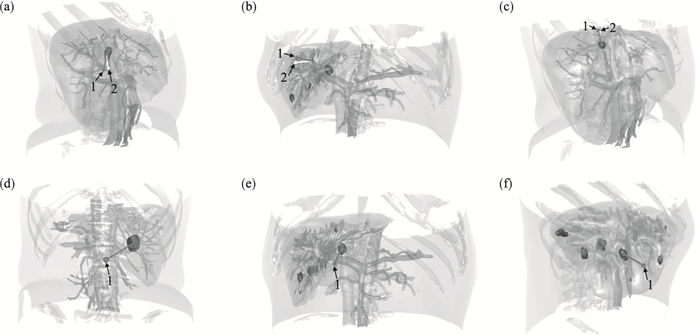 | 图 9 软约束优化度评分算法与加权求和算法的可视化结果Fig.9 Visualization results of soft constraint optimization scoring algorithm and weighted summation algorithm (a)—肿瘤1#；(b)—肿瘤2#；(c)—肿瘤3#；(d)—肿瘤4#；(d)—肿瘤5#；(e)—肿瘤6#. |
4 结论本文基于临床穿刺需求, 额外考虑了路径周围区域信息对穿刺的影响, 提出了一种多约束穿刺路径规划算法, 增加了周围区域避开血管、骨骼密集度、血管密集度及血管风险度多个约束条件, 在量化路径时引入了路径周围区域信息.通过软约束优化度评分算法获得优化度最高的穿刺路径, 并通过实验验证了本文算法可以快速优化皮肤进针点以获得安全的穿刺路径.
参考文献
| [1] | 陈敏山. 肝癌局部消融治疗规范的专家共识[J]. 中华肝脏病杂志, 2011, 19(4): 257-259. (Chen Min-shan. Expert consensus on the norms of local ablation therapy for hepatocellular carcinoma[J]. Chinese Journal of Hepatology, 2011, 19(4): 257-259.) |
| [2] | 高嵩, 朱旭, 邹英华, 等. 冷热多模态消融治疗肝脏恶性肿瘤操作规范专家共识[J]. 中国介入影像与治疗学, 2021, 18(1): 23-27. (Gao Song, Zhu Xu, Zou Ying-hua, et al. Expert consensus on clinical practice of multi-model ablation for treatment of liver malignant tumors[J]. Chinese Journal of Interventional Imaging and Therapy, 2021, 18(1): 23-27.) |
| [3] | Liu S, Xia Z, Liu J, et al. Automatic multiple-needle surgical planning of robotic-assisted microwave coagulation in large liver tumor therapy[J]. Plos One, 2016, 11(3): e0149482. DOI:10.1371/journal.pone.0149482 |
| [4] | Villard C, Soler L, Papier N, et al. RF-Sim: a treatment planning tool for radiofrequency ablation of hepatic tumors[C]//Proceedings of the Seventh International Conference on Information Visualization. Canterbury, 2003: 561-566. |
| [5] | Nel De R J A, Mead R. A simplex method for function minimization[J]. The Computer Journal, 1965, 7: 308-313. DOI:10.1093/comjnl/7.4.308 |
| [6] | Villard C, Baegert C, Schreck P, et al. Optimal trajectories computation within regions of interest for hepatic RFA planning[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Heidelberg, 2015: 49-56. |
| [7] | Villard C, Soler L, Gangi A. Radiofrequency ablation of hepatic tumors: simulation, planning, and contribution of virtual reality and haptics[J]. Computer Methods in Biomechanics and Biomedical Engineering, 2005, 8(4): 215-227. DOI:10.1080/10255840500289988 |
| [8] | Cady B, Jenkins R L, Steele G D, et al. Surgical margin in hepatic resection for colorectal metastasis: a critical and improvable determinant of outcome[J]. Annals of Surgery, 1998, 227(4): 566-571. DOI:10.1097/00000658-199804000-00019 |
| [9] | Baegert C, Villard C, Schreck P, et al. Trajectory optimization for the planning of percutaneous radiofrequency ablation of hepatic tumors[J]. Computer Aided Surgery, 2007, 12(2): 82-90. DOI:10.3109/10929080701312000 |
| [10] | Baegert C, Villard C, Schreck P, et al. Precise determination of regions of interest for hepatic RFA planning[J]. Studies in Health Technology and Informatics, 2007, 125: 31-36. |
| [11] | Baegert C, Villard C, Schreck P, et al. Multi-criteria trajectory planning for hepatic radio-frequency ablation[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Brisbane, 2007: 676-684. |
| [12] | 张睿, 周著黄, 吴薇薇, 等. CT引导肝肿瘤热消融治疗穿刺路径规划算法研究[J]. 医疗卫生装备, 2020, 41(4): 27-34. (Zhang Rui, Zhou Zhu-huang, Wu Wei-wei, et al. CT-guided puncture trajectory planning algorithm for thermal ablation of liver tumors[J]. Chinese Medical Equipment Journal, 2020, 41(4): 27-34.) |
