杨丹^1,2, 王雨佳¹, 辛采凝¹, 徐彬³
1. 东北大学 信息科学与工程学院, 辽宁 沈阳 110819;
2. 东北大学 智能工业数据解析与优化教育部重点实验室, 辽宁 沈阳 110819;
3. 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期：2022-06-26
基金项目：国家自然科学基金资助项目(U22A20221); 辽宁省自然科学基金资助项目(2021-MS093); 辽宁省教育厅基础科学研究项目(LJKZ0014)。
作者简介：杨丹(1979-), 女, 辽宁营口人, 东北大学副教授。

摘要：针对电磁血管断层图像重建中存在的欠定性、病态性, 提出一种基于Fractal-DenseNet的电磁血管断层图像重建算法.基于血流磁电耦合效应的血管断层图像重建原理, 将FractalNet的分形思想与DenseNet的密集紧密连接思想相结合, 构建了一种适用于反演血液流速分布的Fractal-DenseNet网络模型, 用于血管断层图像重建.通过人体前臂尺动脉血流磁电耦合测量模型, 建立血管断层剖面流速和血流磁电效应引起的电压信号的对应数据对, 分别作为网络模型输入和输出；通过监督学习, 实现基于血管断层流速分布的血管断层图像重建.结果表明：Fractal-DenseNet重建结果的均方根误差和相关系数分别为0.007 8, 99.28 %；本文算法具有良好的抗噪性, 可在复杂边界条件下实现血管断层图像重建.
关键词：血管断层图像重建Fractal-DenseNet血流磁电耦合效应人体前臂尺动脉监督学习
A Reconstruction Algorithm for Electromagnetic Vascular Tomography Image Based on Fractal-DenseNet
YANG Dan^1,2, WANG Yu-jia¹, XIN Cai-ning¹, XU Bin³
1. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Data Analytics & Optimization for Smart Industry, Northeastern University, Shenyang 110819, China;
3. School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: XU Bin, E-mail: xubin@mail.neu.edu.cn.

Abstract: In view of the lack of underdetermination and pathology in electromagnetic vascular tomography image reconstruction, a Fractal-DenseNet based vascular tomography image reconstruction algorithm is proposed. With the principle of vascular tomography image reconstruction based on the magneto-electric coupling effect of blood flow, combining FractalNet's fractal idea with DenseNet's dense connection idea, a Fractal-DenseNet network model suitable for the inversion of blood flow velocity distribution was built for the reconstruction of vascular tomography image. Based on the magneto-electric coupling measurement model of human forearm ulnar artery flow, the corresponding data pairs of vessel section velocity and voltage signal caused by magneto-electric effect of blood flow were established, which were respectively used as the input and the output of the network model. Through supervised learning, the image reconstruction based on the flow velocity distribution of the vessel is realized. The results show that the root mean square error and correlation coefficients of Fractal-DenseNet reconstruction are 0.007 8 and 99.28 %, respectively. The proposed model has good anti-noise performance and can be used to reconstruct vascular tomography images under complex boundary conditions.
Key words: vascular tomography image reconstructionFractal-DenseNetmagneto-electric coupling effect of blood flowulnar artery of human forearmsupervised learning
基于电磁生物信息成像方法多采用激励-检测线圈或电极来获得待测目标区域的电磁场信号的变化, 通过重建算法重建目标区域的生物信息分布图像^[1].由于其无创、无辐射等特点, 受到广泛关注.
基于血流磁电效应的血管断层成像是近年来出现的一种血管狭窄病变监测方法^[2], 该方法利用紧贴在目标体表面的电极检测到血流磁电效应引起的电压信号, 电压信号携带了目标体内血管血流位置和速度等信息, 可以用于探测血管血流分布情况.图像重建是电磁血管断层成像的关键问题之一, 它是一个典型的欠定、病态逆问题.经典图像重建算法是利用线性方程对非线性软场进行近似求解, 目前进展主要是对Landweber迭代^[3]、Gauss-Newton^[4]、Tikhonov正则化^[5]等算法进行改进.这些方法具有简单、快速的特点, 但容易获得局部最优解, 导致重建图像质量差, 难以满足实际临床医学的诊断需求.
近年来, 机器学习等智能算法被应用到逆问题求解中^[6].Wu等提出一种基于自编码器神经网络的电磁层析成像重建算法, 与传统的Landweber算法相比, 重建误差较小且相关系数较大, 但重建图像的边缘不清晰^[7].Huang等利用人工神经网络算法有效消除图像伪影, 但当目标较小、噪声较高时, 重建结果较差^[8].Yoo等提出一种基于深度学习方法与漫射光学断层扫描系统相结合的乳腺癌图像监测算法, 能够准确获得组织异常的三维分布, 但其性能受系统局部限制^[9].上述工作说明, 机器学习算法可用于病态图像重建问题的求解, 而如何更有效改善问题病态性、欠定性仍有待进一步研究.
基于此, 本文提出了一种基于分形-密集卷积神经网络的电磁血管断层图像重建算法.所设计的Fractal-DenseNet网络模型是在密集块基础上引入分形块结构, 其中不同卷积层根据分形的自相似性思想进行排布, 而每一个分形块与其后续的每个分形块的输入在通道层面上进行密集连接.通过血管仿真模型, 获得其在不同狭窄程度和流速下的电压信号数据, 用于训练所用的神经网络.将所提算法用于血管断层图像重建, 并与BP神经网络、CNN和DenseNet密集卷积网络等进行比较及定量分析.实验结果表明, Fractal-DenseNet具有更高的准确性和更好的鲁棒性, 本文算法重建的结果伪影更少, 边缘更清晰.
1 电磁血管断层图像重建原理血流磁电耦合效应^[10]如图 1所示.根据电流连续性定理, 假设血流的导电性是均匀的, 可得标量电势、血流矢量流速和矢量磁场之间满足泊松方程：

(1)

图 1(Fig. 1)

图 1 血流磁电耦合效应原理Fig.1 The principle of magneto-electric coupling effect of blood flow

利用M+1电极测量时, 根据互易定理, 可知体表电压信号与血液流速之间满足：

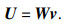(2)

式中：U为包含M个电压值的列向量；W是M×N的权重矩阵, 其矩阵元素w_ij表示第j个重建单元上的流速对第i个测量电极电压信号的贡献；v为包含N个流速值的列向量.因此, 匀强磁场激励下的血管断层流速分布重建方程为

(3)

当电压数据U和权重矩阵W已知时, 即可通过上述方程直接求解出流速分布列向量v.由于测量电极的数量限制, 电压数据U的数量远小于重建目标单元的数量, 所以式(3)为欠定方程组, 其中W为欠定矩阵, 无法通过计算W的逆来求解v.
本文设计Fractal-DenseNet卷积神经网络提取血流磁电信号中的特征信息, 按照非线性回归思想重建血管内血液流速分布, 改善重建方程固有的欠定性和病态性, 实现血管断层图像重建.
2 Fractal-DenseNet网络模型2.1 模型结构本文提出的Fractal-DenseNet网络模型, 将FractalNet^[11]中的分形思想与DenseNet^[12]中的紧密连接思想相结合, 在增加网络深度的同时, 扩大网络宽度.网络总体上由2个Dense Block与2个Transition Block交替排布而成.其中第一个Dense Block内设置2个Fractal Block作紧密连接, 第二个Dense Block中设置4个Fractal Block.每个Fractal Block均包含3条路径, 每条路径中不同数量的Conv Block进行不同层次的特征提取, 最后由连接层进行均值处理操作.所设计网络的整体结构如图 2所示.
图 2(Fig. 2)

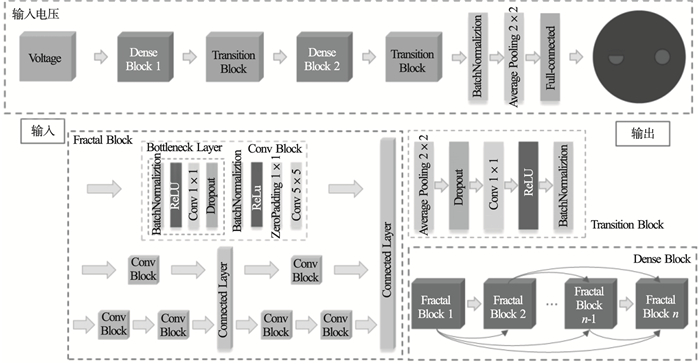图 2 网络结构Fig.2 The network structure

2.2 Conv Block模块Conv Block作为本模型中的基础模块, 由批次归一化层、激活函数层、零填充层和卷积层组成以提取输入数据特征.Dropout层按照设定概率随机选取特征进行丢弃.批次归一化层对输入数据进行批次归一化处理, 以加快训练速度；激活函数选取ReLU函数；零填充层对每一个输入特征进行处理, 保证其大小一致, 便于后续连接操作.由卷积层进行卷积操作提取输入特征^[13]：

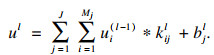(4)

式中：J为卷积核数量；M_j为第j个卷积核的通道数；k_ij^l表示第l层第j个卷积核第i个通道的权重；b_j^l表示第l层第j个卷积核的偏置.
在每个Conv Block模块前部, 引入瓶颈层.瓶颈层的主要作用是通过引入1×1大小的卷积核, 在保证输入数据大小不变的同时, 扩充输入数据的通道数.在搭建后续卷积层中, 通过设置尺寸较大、通道数同瓶颈层的卷积核进行卷积操作.这种结构可以减少权重训练参数, 提高计算效率.
2.3 Fractal Block模块设计中将分形思想引入神经网络结构中, 将Conv Block作为分形连接的基础模块, 按照自相似性思想进行排列, 进行宽度与深度的同步扩展, 构造Fractal Block模块, 其递归算法为

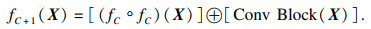(5)

式中：X为分形结构的输入；为组合单元；⊕为连接运算；C为设定的分形结构的列数；f_C为内部具有C列的一个分形结构；f_C+1为2个f_C按照分形思想进行扩展得到的具有C+1列的分形结构.f_C称作f_C+1的分形子结构, 分形结构的扩展规则如图 3所示.
图 3(Fig. 3)

图 3 分形扩展规则Fig.3 Fractal expansion rules

不同路径的Conv Block由连接层进行特征连接, 连接层将所有路径输入的卷积结果取元素级平均值再输出.设连接层的输入路径有m个, 每个输入元素个数为n个, 第i个路径的第j个输入特征为u′_ij, 则连接层的输出为

(6)

Fractal Block内部的多路径结构加宽了网络的整体结构, 由于不同子路径深度不同, 提取特征不同.浅层路径提供更快速的特征提取结果, 而深层路径可以提取更准确的特征结果, 可学习到更全面、更重要的特征, 有利于提升算法性能.
2.4 Dense Block模块Dense Block由多个Fractal Block模块共同组成.在Fractal Block模块之间采用的是密集连接模式, 即第l个Fractal Block接收前面所有Fractal Block(第0, 1, …, l-1块)的特征输入信息流, 并在通道层面对输入进行拼接, 其数学表达为

(7)

式中：H_l为紧密连接操作；f_l为第l个Fractal Block的输出.
在一个Dense Block模块中, 若第l个分形块有k₀个直接输入通道, 经过紧密连接操作后, 将获得k′个特征要素：

(8)

式中：k为网络增长率.通过设定合适的k值确定访问已提取的特征图的特征数量, 从而控制每个Fractal Block的新信息量.这种连接方式在使用较少的网络参数的同时, 加强特征和梯度的传递, 减弱梯度消失问题对网络训练的影响.
2.5 Transition Block模块在完成密集连接操作后, 在Dense Block后加入Transition Block对输入特征图进行尺寸大小的改变, 以实现下采样.每个Transition Block由池化层、Dropout层、卷积层、激活函数层和批次归一化层组成.池化层选取平均池化操作：

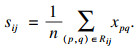(9)

式中：s_ij为在矩形区域R_ij的平均池化输出；x_pq为矩形区域R_ij中位于(p, q)处的元素；n为矩形区域R_ij内的元素个数.激活函数层同Conv Block中的激活函数层为ReLU激活函数.
为了提高网络模型的紧致性, 选取压缩因子减少Transition Block上特征通道的数量, 对冗余特征进行舍弃.如果一个Dense Block包含m个特征通道, 其后面的Transition Block将生成θm个输出特征图, 其中θ称为压缩因子, 设定其范围在0~1之间, 将输出特征按比例缩减.在提取出所有的电压特征后, 通过全连接层将特征信息映射到流速域, 得到单位流速预测序列.
3 信号建模及数据生成3.1 人体前臂血管COMSOL仿真模型将人体前臂尺动脉作为研究对象, 构建人体前臂血管断层COMSOL仿真模型, 如图 4a所示.模型中匀强磁场沿空间Z轴方向, 大小为0.1 mT, e₀, e₁, …, e₁₅表示16个按顺时针方向均匀分布电极, 血管部分的电导率为0.9 S/m, 人体组织部分的电导率设置为0.2 S/m.模型有限元网格设置包含164 393个域单元、18 770个边界单元和1 376个边缘单元, 如图 4b所示.
图 4(Fig. 4)

图 4 COMSOL仿真模型Fig.4 Simulation model of COMSOL (a)—人体前臂血管断层仿真测量模型；(b)—三维有限元网格模型.

3.2 数据集生成实验中通过改变血液流速、动脉血管狭窄率来获取足够多的网络训练数据.整个待测截面剖分为2 821个单元.设置血液流速范围在0.05~0.90 m/s, 以0.05 m/s的步长变化；动脉血管狭窄率在6.25 % ~93.75 % 范围内, 以6.25 % 的步长变化.共生成了1 027组电压-流速数据.按照4∶ 1的比例, 随机划分为训练集与验证集, 对网络模型进行训练与测试.
4 实验与结果分析4.1 网络训练及环境配置在所有卷积层中, 卷积核的大小均为3×3, 步长为1, 选择ReLU作为激活函数.在Transition Block中, 使用大小为2×2, 步长为1的池化核, 进行平均池化操作.密集连接操作中的增长率k被设定为64, 整个训练过程共进行200次迭代.根据模型和需要学习的数据的复杂程度, 学习率设置为0.001.模型内其他超参数设置如下：批次为32, Dropout为0.5, 压缩因子选取0.8.
实验在云服务器Google Colab的GPU平台上完成训练和测试.代码在Python 3.6和Keras 2.2.4的环境下实现.重建结果的可视化操作在MATLAB R2018a中进行.
4.2 评价指标利用均方根误差RMSE和相关系数CC两个评价指标来评价重建算法的性能, RMSE定义为

(10)

式中：v_i为第i个真实的流速；为第i个预测流速；n是流速单元的总数量.
相关系数描述了预测值与真实值的相似性, 其定义为

(11)

式中：为预测流速的均值；v为真实流速的均值.
4.3 重建结果与分析为了验证所提模型算法的有效性, 选取5个有代表性的信号测量模型, 对其网络预测结果, 即血管断层流速分布, 进行可视化重建, 将Fractal-DenseNet与其他BP, CNN和DenseNet三种网络模型的重建结果进行比较, 结果如图 5所示.Fractal-DenseNet在血液流速监测和狭窄位置监测方面与真实标签最为接近, 并且重建的伪影也大大减少.
图 5(Fig. 5)

图 5 本文算法与其他算法的图像重建结果对比Fig.5 The comparison of reconstruction results between proposed method and others

用均方根误差和相关系数两个评价指标对重建图像结果进行定量分析, 如表 1所示.结果表明, Fractal-DenseNet重建图像的RMSE平均值低于0.007 8, 较其他3种算法的0.048 9, 0.015 7和0.020 7更为精确.DenseNet算法在模型3的表现优于Fractal-DenseNet, 但其RMSE均值表现较Fractal-DenseNet差.表 2所示结果表明, 在所有5个模型中, Fractal-DenseNet的CC评价指标均值超过98.5 %, 且大部分模型的CC评价结果超过99 %, 与其他3种算法相比, 分别提升了10.86 %, 1.04 %, 2.11 %.
表 1(Table 1)

表 1 RMSE评价指标Table 1 RMSE evaluation indicators ? % 算法 模型1 模型2 模型3 模型4 模型5 BP 4.05 0.43 3.68 7.03 5.28 CNN 1.17 1.27 0.98 2.56 1.85 DenseNet 0.65 0.66 0.82 4.54 3.69 Fractal-DenseNet 0.34 0.51 0.96 0.77 1.30

表 1 RMSE评价指标 Table 1 RMSE evaluation indicators ?

表 2(Table 2)

表 2 CC评价指标Table 2 CC evaluation indicators ? % 算法 模型1 模型2 模型3 模型4 模型5 BP 89.8 87.6 89.0 86.3 89.4 CNN 97.4 98.5 98.4 98.4 98.5 DenseNet 99.2 97.7 96.0 97.2 95.7 Fractal-DenseNet 99.9 99.1 99.3 98.6 99.5

表 2 CC评价指标 Table 2 CC evaluation indicators ?

4.4 模型算法的性能分析4.4.1 抗噪性分析为了评价算法的鲁棒性, 设置对比实验, 分别在无噪声和信噪比为20, 30, 40, 50 dB进行图像重建.信噪比为20 dB时, Fractal-DenseNet及其他3种算法的重建结果如图 6所示.由图可知, 其他3种算法受噪声影响较大, 狭窄边缘重建方面存在较多伪影, 导致边缘不清晰, 无法观测狭窄的具体位置与形状.而Fractal-DenseNet对血液流速分布的狭窄情况重建形状与标签真实形状最为相似, 伪影最少, 同时流速检测较其他3种算法更为准确.
图 6(Fig. 6)

图 6 噪声为20 dB时重建结果对比Fig.6 The comparative reconstruction results when SNR=20 dB

不同信噪比条件下, 量化评价指标变化直方图如图 7所示.当噪声增加时, RMSE整体呈上升趋势, 如图 7a所示.当信噪比达到20 dB时, Fractal-DenseNet算法的RMSE最小, 较其他3种算法分别提高了52.1 %, 12.1 %, 19.2 %.所有重建方法的预测结果都与真实标签呈正相关关系, 如图 7b所示.Fractal-DenseNet算法的重建结果的CC值变化范围在0.953 7~0.989 7之间.当噪声最大时, 本文算法的CC指标为95.37 %, 优于其他3种算法.
图 7(Fig. 7)

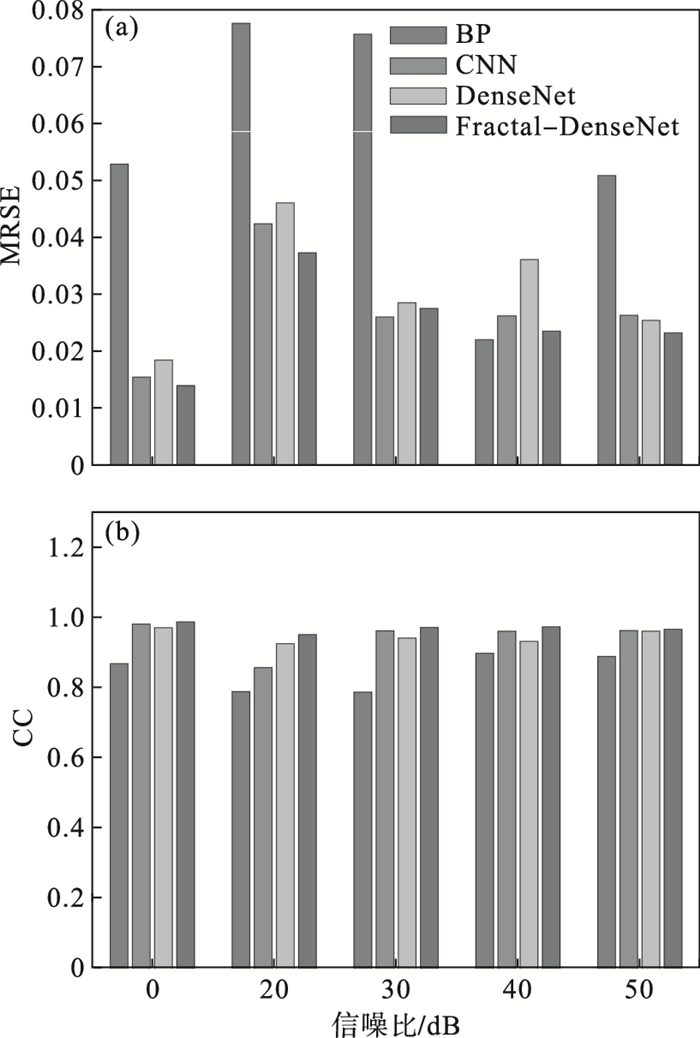图 7 不同噪声条件下评价指标的变化情况Fig.7 The evaluation metrics under different noise conditions (a)—RMSE；(b)—CC.

4.4.2 真实血管模型的血液流速分布重建为了评估Fractal-DenseNet在复杂边界条件下重建的可行性, 选择从冠状动脉CT血管造影图像中分割出动脉血管和动脉分叉血管作为研究对象, 建立人体真实动脉血管断层模型.选择模型中5个截面进行重建, 其Y轴坐标分别为3.0, 3.5, 4.0, 4.5, 5.0 mm.由于动脉血管占比较小, 所以选择进行局部成像, 如图 8所示.
图 8(Fig. 8)

图 8 真实分叉血管模型的局部重建示意图Fig.8 Schematic diagram of the local reconstruction of the real bifurcation vessel model

每个横截面对应16个电极, 去除接地的零电极后, 得到输入数据的维度为15×5, 输出的维度增加至20 245×1.除了改变网络的输入和输出外, 网络结构和参数不变, 重建结果如图 9所示.由图可知, 本文方法可较为准确地分辨出不同截面的狭窄位置, 但由于输出维度大幅增加, 部分重建结果边缘处出现伪影, 预测的流速在小范围内出现偏差.具体的评价指标结果如表 3所示, 表中最后一列表示所有测试模型的平均指标, 基于Fractal-DenseNet算法模型的RMSE和CC的均值分别为0.056 8，0.991 4, 在这2个指标上保持了良好的水平, 验证了本文方法的有效性.
图 9(Fig. 9)

图 9 Fractal-DenseNet的真实血管模型重建结果Fig.9 Results of realistic vascular model reconstruction by Fractal-DenseNet

表 3(Table 3)

表 3 真实血管模型重建结果的RMSE和CC评价指标Table 3 The RMSE and CC of realistic human vessel model reconstruction results 指标 模型1 模型2 模型3 模型4 平均 RMSE 0.032 8 0.055 8 0.048 0 0.018 7 0.056 8 CC 0.993 4 0.996 2 0.989 9 0.992 9 0.991 4

表 3 真实血管模型重建结果的RMSE和CC评价指标 Table 3 The RMSE and CC of realistic human vessel model reconstruction results

5 结论本文提出了一种基于深度学习模型的血管断层图像重建算法, 用于预测血管内流速分布.Fractal-DenseNet模型通过密集连接操作, 在纵向信息流上实现信息的重复利用.结合分形思想, 增加单元的子路径, 拓宽横向信息流, 使得信息特征得以充分学习和提取.结果表明, Fractal-DenseNet模型的RMSE和CC指标分别达到0.007 8和99.28 %, 其性能优于BP, CNN和DenseNet等传统算法.实验证明了该模型的鲁棒性和泛化性.未来研究工作将进一步考虑复杂的血管病变条件以及流速和狭窄率之间的相应关系.
参考文献

[1]	Ali M. Development of an electromagnetic induction method for non-invasive blood flow measurement[D]. Huddersfield: University of Huddersfield, 2016.
[2]	Yang D, Liu Y, Xu B, et al. A blood flow volume linear inversion model based on electromagnetic sensor for predicting the rate of arterial stenosis[J]. Sensors, 2019, 19(13): 3006. DOI:10.3390/s19133006
[3]	Wang J, Han B. Application of a class of iterative algorithms and their accelerations to Jacobian-based linearized EIT image reconstruction[J]. Inverse Problems in Science and Engineering, 2021, 29(8): 1108-1126. DOI:10.1080/17415977.2020.1826473
[4]	Harikumar R, Prabu R, Raghavan S. Electrical impedance tomography (EIT) and its medical applications: a review[J]. The International Journal of Soft Computing and Engineering, 2013, 3(4): 193-198.
[5]	Wei H Y, Soleimani M. Four dimensional reconstruction using magnetic induction tomography: experimental study[J]. Progress in Electromagnetics Research, 2012, 129: 17-32. DOI:10.2528/PIER12032403
[6]	Chen D, Davies M E. Deep decomposition learning for inverse imaging problems[C]//European Conference on Computer Vision. Glasgow, 2020: 510-526.
[7]	Wu X J, Xu M D, Li C D, et al. Research on image reconstruction algorithms based on autoencoder neural network of restricted boltzmann machine (RBM)[J]. Flow Measurement and Instrumentation, 2021, 80: 102009. DOI:10.1016/j.flowmeasinst.2021.102009
[8]	Huang S W, Cheng H M, Lin S F. Improved imaging resolution of electrical impedance tomography using artificial neural networks for image reconstruction[C]//2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Berlin, 2019: 1551-1554.
[9]	Yoo J, Sabir S, Heo D, et al. Deep learning diffuse optical tomography[J]. IEEE Transactions on Medical Imagin, 2019, 39(4): 877-887.
[10]	Liu Y, Yang D, Duo Y, et al. Numerical model and finite element simulation of arterial blood flow profile reconstruction in a uniform magnetic field[J]. Journal of Physics D: Applied Physics, 2020, 53(19): 195402.
[11]	Li J Y, Wen H B, Zhang K H, et al. Research progress in electromagnetic interference suppression of magnetically coupled radio energy transmission systems[J]. Proceedings of the CSEE, 2022, 42(20): 7387-7403.
[12]	Larsson G, Maire M, Shakhnarovich G. FractalNet: ultra-deep neural networks without residuals[J]. arXiv preprint arXiv: 1605.07648, 2016.
[13]	Huang G, Liu Z, van Der Maaten L, et al. Densely connected convolutional networks[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, 2017: 4700-4708.