
 , 柳泽阳, 武梦如
, 柳泽阳, 武梦如 东北大学 轧制技术及连轧自动化国家重点实验室, 辽宁 沈阳 110819
收稿日期:2022-07-14
基金项目:国家自然科学基金面上资助项目(51774082)。
作者简介:蓝慧芳(1981-),女,山东烟台人,东北大学副教授。
摘要:基于混合模型及吉布斯能量平衡模型思想,建立了一种简单的吉布斯能量平衡模型,应用于Fe-C-Mn低碳钢在780 ℃两相区等温过程中的铁素体向奥氏体相变模拟,并分析了三种吉布斯自由能、有效晶粒尺寸、元素分布等对相变的影响.结果表明,有效晶粒尺寸及界面迁移率影响相变速率,但对最终奥氏体体积分数无影响;相变过程中相界面处锰元素的富集导致的能量耗散同时降低了相变速率及最终奥氏体体积分数.对模拟结果进行实验验证,表明模拟结果与实验结果吻合良好.
关键词:相变动力学吉布斯能量平衡铁素体-奥氏体相变溶质拖曳效应
A Kinetic Model for Ferrite-Austenite Transformation
LAN Hui-fang

 , LIU Ze-yang, WU Meng-ru
, LIU Ze-yang, WU Meng-ru State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LAN Hui-fang, E-mail: lanhf@ral.neu.edu.cn.
Abstract: In this paper, based on the concepts of mixed model and Gibbs energy balance model, a simple Gibbs energy balance model was established to simulate the ferrite-austenite transformation of Fe-C-Mn low carbon steel during the intercritical annealing at 780℃. The effects of Gibbs free energy, effective grain size and alloying distribution on the transformation were studied. The results show that the initial effective grain size and interfacial mobility greatly affected the kinetics of phase transformation, while they had little effect on the final volume fraction of the austenite. The dissipation energy caused by the Mn enrichment at the interface during phase transformation slowed down the transformation kinetics and reduced the final volume fraction of the austenite. It is found that the modelling results above are in good accordance with the experimental ones.
Key words: phase transformation kineticsGibbs energy balanceferrite-austenite transformationsolute drag effect
铁素体-奥氏体相变在钢铁行业的研究中具有非常重要的意义,工业钢的组织和性能依附于奥氏体冷却之后形成的各种相[1].关于奥氏体向铁素体相变的冷却过程已得到广泛研究[2];相反的,对铁素体向奥氏体相变的加热过程研究相对较少.在加热过程中,奥氏体相变形核和长大受到诸多因素的影响.对于相变发生前的初始组织,如再结晶状态、第二相分布等,由于缺陷密度及空间碳分布差异,将在很大程度上影响奥氏体相变动力学[3-4],导致奥氏体冷却后所形成的组织(例如铁素体晶粒尺寸、马氏体相变分数与分布等)出现差异.对于加热过程的晶粒长大来说,相变过程中组织难以实时观测,加之再结晶与奥氏体相变的相互作用[5-6],使双相钢加热过程中对于相变及组织演变规律的研究具有挑战性.
除了上述影响因素外,研究奥氏体的形成存在诸多挑战:加热时形成的奥氏体在冷却时又转化为不同的产物相,因此很难直接观察加热时形成的奥氏体;升温使奥氏体形成动力学的研究变得困难,初始组织的相分布和形态会影响奥氏体的形成过程,因此必须从不同的初始组织开始研究,这增加了所需的实验数量[7].这也是多年以来奥氏体逆相相对较少的原因.
鉴于实验研究高温奥氏体化带来的不便,运用相关相变模型模拟相变过程成为可行之路.近些年来,人们已经提出了不同的生长模型来描述铁素体-奥氏体相变,其中运用较多的为:扩散控制模型[8]、界面控制模型[9]及混合模型[10].混合生长模型同时考虑了溶质扩散和界面迁移率的影响,与实验结果吻合较好[11].研究表明扩散控制模型与界面控制模型均为混合模型的一种极端情况[12-13],因而在最近的研究中,混合生长模型被广泛使用[14].但是传统的混合模型主要考虑的是Fe-C二元体系,将其他合金元素的影响整合到了比例因子中,较难对其进行深入讨论.
Mecozzi等[7]提出了基于Fe-C-Mn三元体系的等温铁素体向奥氏体转变的半解析混合模型,并对铁素体到奥氏体转变的扩散控制、界面控制和混合模型进行了比较研究.然而,他们没有对模型模拟结果进行实验验证.陈浩等提出了一个基于混合模型和溶质拖曳效应的吉布斯能量平衡(Gibbs energy balance,GEB)模型[15],该模型考虑了碳和其他替代元素的扩散,可以解释奥氏体→贝氏体、奥氏体→铁素体出现的停滞现象,但尚未应用于反向转变.安栋等基于混合模型的概念,建立了铁素体向奥氏体转变的吉布斯能量平衡模型[16],并应用于Fe-C-Mn和Fe-C-Mn-Si合金在760 ℃下的铁素体向奥氏体转变.模型预测的相变动力学与膨胀测量的结果比较接近,但未给出合金元素扩散对于相变过程影响的相关解释.
本文基于半解析混合模型与吉布斯能量平衡模型,建立了一种简单的吉布斯能量平衡模型,模拟了Fe-0.1C-2Mn在加热过程中的相变动力学.将不同影响因素对奥氏体化相变过程的影响进行了讨论,并将模拟结果与实验进行了比较.
1 GEB模型的建立吉布斯能量平衡模型的基本原理为[15]:相变过程的化学驱动力ΔGchem等于置换原子在相界面内再分配而引起的吉布斯自由能耗散ΔGdiff和界面移动带来的摩擦引起的吉布斯自由能耗散ΔGfric,即
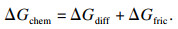 | (1) |
图 1(Fig. 1)
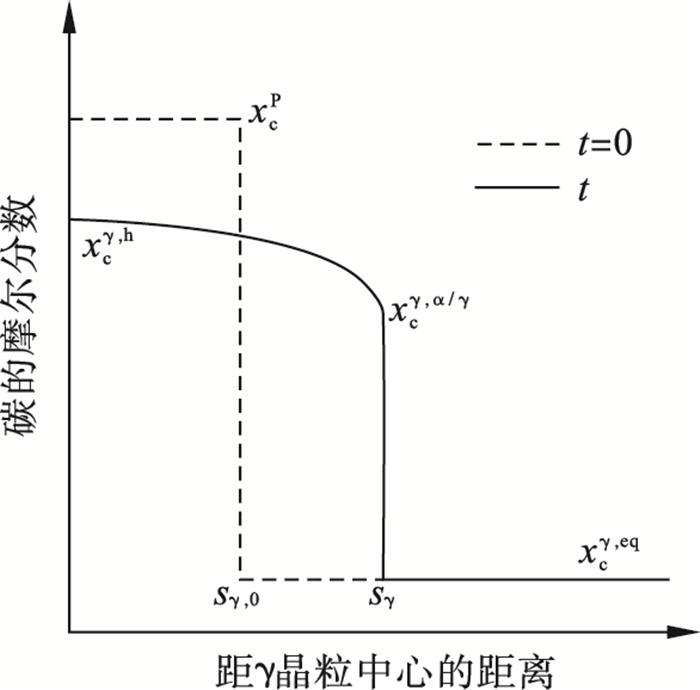 | 图 1 碳的摩尔分数分布示意图Fig.1 Schematic of the molar fraction distribution of the carbon |
根据半解析模型的假设,在奥氏体中存在与扩散距离z呈指数关系碳的摩尔分数为
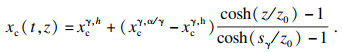 | (2) |
铁素体向奥氏体相变的化学驱动力ΔGchem可由式(3)计算[7]:
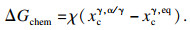 | (3) |
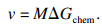 | (4) |
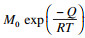
相变过程中界面处碳扩散通量守恒,即
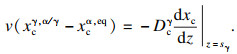 | (5) |
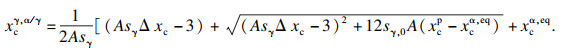 | (6) |
化学驱动力为
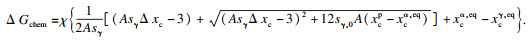 | (7) |
图 2(Fig. 2)
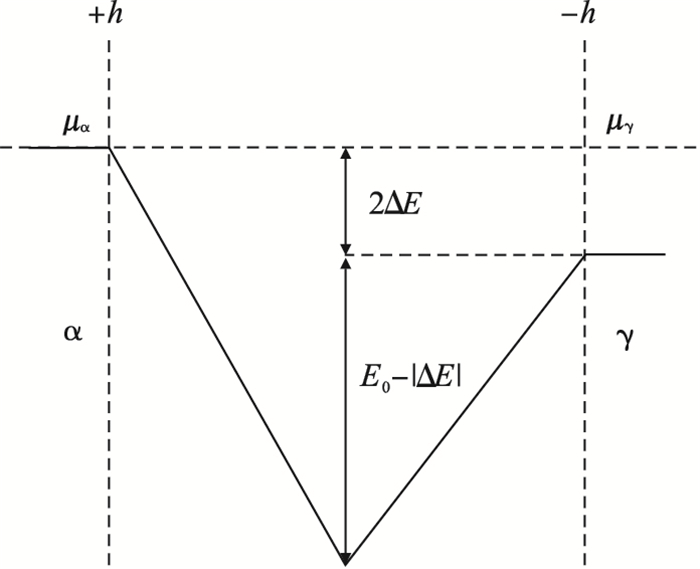 | 图 2 α/γ界面处Mn化学势阱示意图Fig.2 Schematic diagram of the chemic potential well of the Mn element at the α/γ interface |
根据上述假设,溶质原子耗散能ΔGdiff可由式(8)计算:
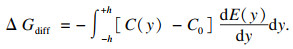 | (8) |
界面处置换元素的分布应满足菲克第二定律公式:
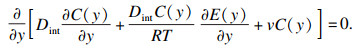 | (9) |
综合式(8)、式(9)可得到ΔGdiff的解析表达式:
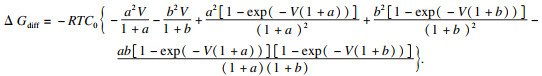 | (10) |
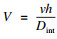
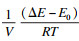
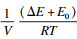
界面迁移造成的自由能耗散ΔGfric计算式为
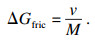 | (11) |
1.3 模拟条件模拟选取质量分数为0.1 % C-2 % Mn的低碳钢.模拟工艺为:780 ℃下铁素体向奥氏体的等温转变.碳在奥氏体中的扩散系数为1.5×10-5×exp (-142 100/RT)/(m2·s-1)[18].界面厚度2 h为0.5 nm[19].锰的结合能E0为9.9(kJ·mol-1)[20].锰在界面的扩散系数DMn取Mn在奥氏体、铁素体内以及铁素体晶界处的锰元素扩散系数的几何平均值[20],可由DICTRA[21]计算得到.碳平衡的摩尔分数xcp,xcα, eq,xcγ, eq,Mn的化学势差的一半ΔE、热力学比例因子χ均可由Thermo-calc计算[22].激活能Q为140(kJ·mol-1)[23],气体常数R= 8.314 J/(mol·K).M0为0.5~0.005 mol·mJ-1·s-1,在文献报道的取值范围内[24].计算区域长度L的大小由不同的奥氏体初始尺寸决定[7],计算可知:
 | (12) |
2 实验材料及方法实验材料选取质量分数为0.1 % C-2 % Mn、初始组织为铁素体+渗碳体的冷轧钢板.实验工艺如图 3所示.分别以5 ℃/s和80 ℃/s的速度升至780 ℃,等温300 s,随后加热至900 ℃,保温30 s,以确定等温阶段奥氏体体积分数,随后以80 ℃/s的速度冷却至室温,如图 3a所示;以5 ℃/s的速度升至660 ℃,保温100 s,使其发生再结晶,随后以5 ℃/s的速度升至780 ℃,等温300 s,再升温至900 ℃,保温30 s,最后以80 ℃/s的速度冷却至室温,如图 3b所示.
图 3(Fig. 3)
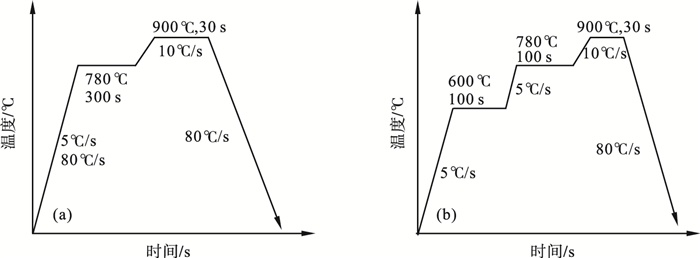 | 图 3 奥氏体化工艺示意图Fig.3 Schematic diagram of austenitization process (a)—加热等温;(b)—再结晶处理. |
3 结果与讨论3.1 模拟结果与实验结果对比80 ℃/s加热等温工艺下模拟得到能量变化情况及模拟与实验得到不同时间下的新相奥氏体如图 4所示.采用吉布斯自由能平衡模型及混合模型获得的80 ℃/s加热至780 ℃等温250 s的模拟结果及实验结果如图 4a所示.可知,GEB模型的计算结果与实验结果吻合较好,而混合模型所计算的最终奥氏体体积分数偏高,可见GEB模型预测结果更加准确.对GEB模型的模拟结果进行分析发现,在0~25 s阶段,相变进行迅速,奥氏体体积分数达到50 % 左右;25~100 s阶段,相变速率较慢,奥氏体体积分数逐渐增大至60 %;超过100 s后,相变基本停止,奥氏体体积分数基本不再发生改变.而混合模型不论是相变速率还是奥氏体体积分数都要高于GEB模型.由于GEB模型是在混合模型的基础上加入溶质拖曳效应,导致合金元素在界面处扩散而引起的耗散能ΔGdiff成为相变过程的阻力,因此ΔGdiff不仅降低了相变速率,还导致最终奥氏体体积分数的降低.
图 4(Fig. 4)
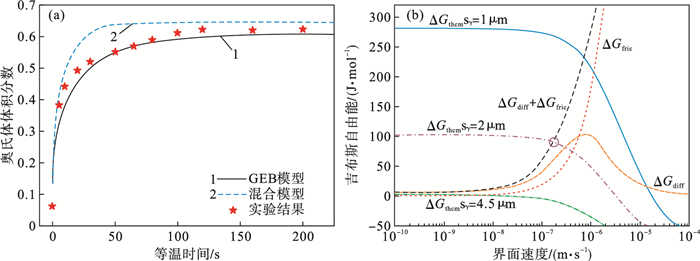 | 图 4 奥氏体体积分数随时间变化及能量耗散随速度的变化Fig.4 Austenite volume fraction with time and energy dissipation with velocity (a)—GEB模型、混合模型与实验结果;(b)—不同吉布斯自由能与界面速率的关系. |
在GEB模型预测的等温转变过程中,化学驱动力ΔGchem(实线)、合金元素扩散引起的吉布斯自由能耗散ΔGdiff(点划线)、界面造成的自由能耗散ΔGfric(点线)与自由能耗散之和ΔGdiff+ΔGfric(虚线)随界面速率的变化,两曲线的交点即为发生相变时的驱动力及界面移动的临界速率,如图 4b所示.可知,当奥氏体尺寸增大后,ΔGchem曲线向低能量、低界面迁移速率方向改变,即随相变的进行,奥氏体不断长大,相变的驱动力降低.对于ΔGdiff曲线,在低界面迁移速率(v < 10-8 m/s)下,ΔGdiff基本无变化(~10 J· mol-1);随界面速率增大,ΔGdiff逐渐增大至3×10-6 m/s处的峰值,此后随界面速率增大ΔGdiff逐渐降低.对于ΔGfric曲线,在低界面迁移速率阶段约为0,随界面速率的增加,ΔGfric不断增加,呈上升趋势.对于总耗散能ΔGdiff+ΔGfric曲线,在低界面速率阶段,耗散能主要由ΔGdiff控制;在中界面迁移速率(10-6 m/s < v < 10-8 m/s)阶段,总耗散能由两者共同控制;在高界面速率阶段(v>10-6 m/s),总耗散能主要由ΔGfric控制.分析ΔGchem曲线与ΔGdiff+ΔGfric曲线的交点可以发现,随奥氏体尺寸增加,交点处的界面迁移速率降低,这可以解释图 4a中随相变的进行,相变速率越来越慢.
3.2 有效晶粒尺寸的影响有效晶粒尺寸对相变的影响如图 5所示.GEB模型计算的有效晶粒尺寸L不同时奥氏体体积分数随时间的变化如图 5a所示,并与实验数据进行了对比.可知,随有效晶粒尺寸L的减小,相变速率加快,但其最终的稳定奥氏体体积分数基本不变.以80 ℃/s的速度加热时,在加热阶段基本不发生或很少发生再结晶,有效晶粒尺寸最小,相变速率最快;经过660 ℃等温100 s后,再结晶比较充分,晶粒尺寸最大,等温阶段的相变速率最慢;5 ℃/s的速率加热时,部分发生了再结晶,晶粒尺寸介于两者之间,因而相变速率介于两者之间.不同有效晶粒尺寸L对应的化学驱动力ΔGchem、耗散能之和ΔGdiff+ΔGfric随界面迁移速率的变化如图 5b所示.分析不同L化学驱动力曲线与耗散能之和曲线的交点,可知,L较小的奥氏体具有更高的化学驱动力及更快的界面迁移速率,这是因为随晶粒尺寸的减小,元素扩散距离减小;晶粒尺寸的减小会使单位面积内的晶粒数量增多,晶界面积更大,增加了形核的位置及数量,使得相变速率加快,这解释了有效晶粒尺寸较小的奥氏体相变速率相对更快的现象.
图 5(Fig. 5)
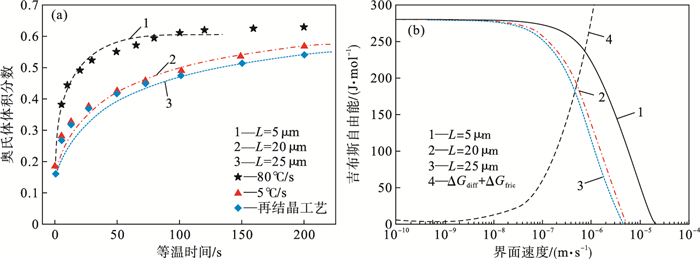 | 图 5 有效晶粒尺寸对相变的影响Fig.5 Effect of the effective grain size on phase transformation (a)—奥氏体体积分数与等温时间的关系;(b)—吉布斯自由能与界面速度的关系. |
3.3 界面处合金元素的分布GEB模型同样可以预测相变过程中界面处合金元素(本文为锰)的分布,图 6为GEB模型预测的780 ℃等温相变过程中界面处Mn的质量分数随界面位置的变化.由图可知,在高界面迁移速率(v=10-5 m/s)下,相变速率较快,相变主要由碳元素扩散控制,锰元素基本不发生扩散,界面处Mn的质量分数基本保持不变;在中界面迁移速率(v=4×10-7 m/s)下,Mn开始发生扩散,对相变有所影响,界面处出现了Mn的富集,从而导致Mn尖峰的形成;随相变继续进行,界面迁移速率进一步降低(v=10-9 m/s),此时相变已处于末期,主要由Mn扩散控制,Mn的尖峰也随之继续增高.这种相变过程中界面处出现的Mn元素富集导致产生较大的耗散能,从而抑制相变的进行.观察奥氏体侧Mn的质量分数可以发现,在高界面迁移速率情况下,奥氏体侧与基体Mn的质量分数接近;随相变速率进一步降低,相变接近停止时,奥氏体侧高于基体Mn的质量分数,即相变过程中出现了Mn的分配.
图 6(Fig. 6)
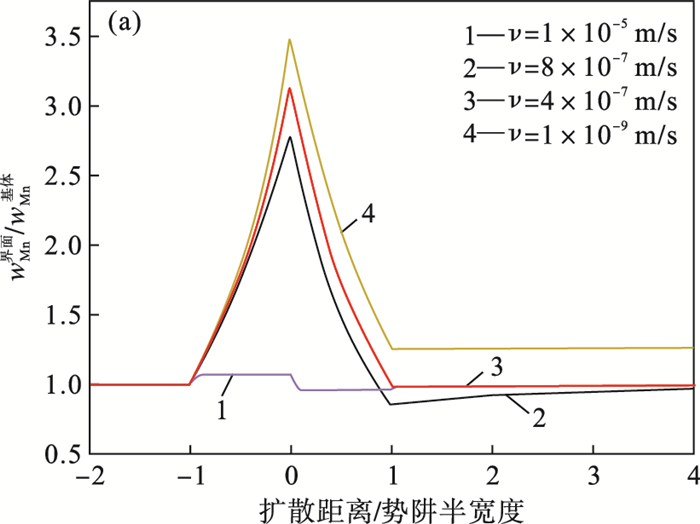 | 图 6 Mn元素在界面处分布情况Fig.6 Distribution of the Mn element at the interface |
4 结论1) 通过将混合模型与GEB模型相结合,建立了一个简单的GEB模型,并与实验进行了对比,模拟结果与实验结果吻合较好.
2) 合金元素扩散引起的自由能耗散不仅降低了相变速率,还导致最终奥氏体体积分数减少.
3) 不同的有效晶粒尺寸只影响了相变速率,对于最终的相变结果几乎没有影响.
4) 在相变过程中,锰在界面处出现了分布尖峰,离界面距离越远Mn的质量分数越低,最终趋近于一个稳定值.
参考文献
| [1] | Gouné M, Danoix F, ?gren J, et al. Overview of the current issues in austenite to ferrite transformation and the role of migrating interfaces therein for low alloyed steels[J]. Materials Science and Engineerings, 2015, 92: 1-38. |
| [2] | van Bohemen S M C, Sietsma J. The kinetics of bainite and martensite formation in steels during cooling[J]. Materials Science and Engineering: A, 2010, 527(24/25): 6672-6676. |
| [3] | Etesami S A, Enayati M H. Microstructural evolution and recrystallization kinetics of a cold-rolled, ferrite-martensite structure during intercritical annealing[J]. Metallurgical and Materials Transactions A, 2016, 47: 3271-3276. DOI:10.1007/s11661-016-3528-1 |
| [4] | Kulakov M, Poole W J, Militzer M. The effect of the initial microstructure on recrystallization and austenite formation in a DP600 steel[J]. Metallurgical and Materials Transactions A, 2013, 44: 3564-3576. DOI:10.1007/s11661-013-1721-z |
| [5] | Zheng C W, Raabe D. Interaction between recrystallization and phase transformation during intercritical annealing in a cold-rolled dual-phase steel: a cellular automaton model[J]. Acta Materialia, 2013, 61(19): 5504-5517. |
| [6] | Chbihi A, Barbier D, Germain L, et al. Interactions between ferrite recrystallization and austenite formation in high-strength steels[J]. Journal of Materials Science, 2014, 49: 3608-3621. DOI:10.1007/s10853-014-8029-2 |
| [7] | Mecozzi M G, Bos C, Sietsma J. A mixed-mode model for the ferrite-to-austenite transformation in a ferrite/pearlite microstructure[J]. Acta Materialia, 2015, 88: 302-313. DOI:10.1016/j.actamat.2015.01.058 |
| [8] | Zener C. Theory of growth of spherical precipitates from solid solution[J]. Journal of Applied Physics, 1949, 20(10): 950-953. DOI:10.1063/1.1698258 |
| [9] | Hillert M. Diffusion and interface control of reactions in alloys[J]. Metallurgical Transactions A, 1975, 6: 5-19. |
| [10] | Sietsma J, van der Zwaag S. A concise model for mixed-mode phase transformations in the solid state[J]. Acta Materialia, 2004, 52(14): 4143-4152. DOI:10.1016/j.actamat.2004.05.027 |
| [11] | Krielaart G P, Sietsma J, van der Zwaag S. Ferrite formation in Fe-C alloys during austenite decomposition under non-equilibrium interface conditions[J]. Materials Science and Engineering: A, 1997, 237(2): 216-223. DOI:10.1016/S0921-5093(97)00365-1 |
| [12] | Chen H, van der Zwaag S. Modeling of soft impingement effect during solid-state partitioning phase transformations in binary alloys[J]. Journal of Materials Science, 2011, 46(5): 1328-1336. DOI:10.1007/s10853-010-4922-5 |
| [13] | 陈浩, 张璁雨, 朱加宁, 等. 奥氏体/铁素体界面迁移与元素配分的研究进展[J]. 金属学报, 2018, 54(2): 217-227. (Chen Hao, Zhang Cong-yu, Zhu Jia-ning, et al. Austenite/ferrite interface migration and alloying elements partitioning: an overview[J]. Acta Metallurgica Sinica, 2018, 54(2): 217-227.) |
| [14] | Huizenga R M, Bos C, Sietsma J. Interface conditions during mixed-mode phase transformations in metals[J]. Journal of Materials Science, 2008, 43(11): 3744-3749. DOI:10.1007/s10853-007-2219-0 |
| [15] | Chen H, van der Zwaag S. A general mixed-mode model for the austenite-to-ferrite transformation kinetics in Fe-C-M alloys[J]. Acta Materialia, 2014, 72: 1-12. DOI:10.1016/j.actamat.2014.03.034 |
| [16] | An D, Pan S, Ren Q, et al. A Gibbs energy balance model for the isothermal ferrite-to-austenite transformation[J]. Scripta Materialia, 2020, 178: 207-210. DOI:10.1016/j.scriptamat.2019.11.027 |
| [17] | Purdy G R, Brechet Y. A solute drag treatment of the effects of alloying elements on the rate of the proeutectoid ferrite transformation in steels[J]. Acta Metallurgica et Materialia, 1995, 43(10): 3763-3774. DOI:10.1016/0956-7151(95)90160-4 |
| [18] | Militzer M, Meczzi M, Sietsma J, et al. Three-dimensional phase field modelling of the austenite-to-ferrite transformation[J]. Acta Materialia, 2006, 54(15): 3961-3972. DOI:10.1016/j.actamat.2006.04.029 |
| [19] | Chen H, Borgenstam A, Odqvist J, et al. Application of interrupted cooling experiments to study the mechanism of bainitic ferrite formation in steels[J]. Acta Materialia, 2013, 61(12): 4512-4523. DOI:10.1016/j.actamat.2013.04.020 |
| [20] | Chen H, Zhu K, Zhao L, et al. Analysis of transformation stasis during the isothermal bainitic ferrite formation in Fe-C-Mn and Fe-C-Mn-Si alloys[J]. Acta Materialia, 2013, 61(14): 5458-5468. DOI:10.1016/j.actamat.2013.05.034 |
| [21] | Borgenstam A, H?glund L, ?gren J, et al. DICTRA, a tool for simulation of diffusional transformations in alloys[J]. Journal of Phase Equilibria, 2000, 21(3): 269-280. DOI:10.1361/105497100770340057 |
| [22] | Andersson J, Helander T, H?glund L, et al. Thermo-Calc & DICTRA, computational tools for materials science[J]. Calphad, 2002, 26(2): 273-312. DOI:10.1016/S0364-5916(02)00037-8 |
| [23] | Fazeli F, Militzer M. Application of solute drag theory to model ferrite formation in multiphase steels[J]. Metallurgical and Materials Transactions A, 2005, 36(6): 1395-1405. DOI:10.1007/s11661-005-0232-y |
| [24] | An D, Baik S, Pan S, et al. Evolution of microstructure and carbon distribution during heat treatments of a dual-phase steel: modeling and atom-probe tomography experiments[J]. Metallurgical and Materials Transactions A, 2019, 50(1): 436-450. DOI:10.1007/s11661-018-4975-7 |
