闫玉涛, 姜程, 高连琪
东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期：2022-04-12
基金项目：国家自然科学基金资助项目(51875095)。
作者简介：闫玉涛(1970-), 男, 吉林磐石人, 东北大学副教授, 博士。

摘要：针对线接触滑动磨损与接触疲劳耦合损伤荷载摩擦副系统, 结合改进Archard磨损模型、临界平面法和虚拟裂纹扩展法, 建立了一种滑动磨损与接触疲劳耦合损伤分析模型.基于Morris灵敏度分析方法, 提出了耦合损伤接触疲劳灵敏度贡献比, 建立了一种基于灵敏度贡献比滑动磨损与接触疲劳耦合损伤寿命预测方法.结果表明：耦合损伤寿命明显小于单一损伤寿命；接触压力、接触宽度和曲率半径对耦合灵敏度具有显著影响, 接触疲劳损伤贡献比与显著影响参数基本呈线性关系；耦合损伤寿命预测结果与计算结果基本一致, 验证了耦合寿命预测模型的可用性.
关键词：耦合损伤滑动磨损接触疲劳灵敏度预测方法
Life Analysis of Coupling Damage Between Sliding Wear and Contact Fatigue Based on Morris Method
YAN Yu-tao, JIANG Cheng, GAO Lian-qi
School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: YAN Yu-tao, E-mail: ytyan@mail.neu.edu.cn.

Abstract: Aimed at a secondary system on the coupling damage of sliding wear and contact fatigue in linear contact, combining the modified Archard's wear model, the critical plane method and the virtual crack extension method, an analysis model of the coupling damage between sliding wear and contact fatigue is developed. Based on the Morris sensitivity method, the contribution ratio of contact fatigue sensitivity is established. Furthermore, a life prediction method of the coupling damage of both sliding wear and contact fatigue is proposed based on the sensitivity contribution ratio. The results show that the coupling damage life is obviously less than the single damage life. The sensitivity of coupling damage is significantly affected by contact pressure, contact width and curvature radius, and the contribution ratio of contact fatigue damage is basically linear with key parameters. The coupling damage life prediction result is in good agreement with the calculation result, which verifies the usability of the prediction model for coupling damage life.
Key words: coupling damagesliding wearcontact fatiguesensitivityprediction method
工作中产生和传递交变负荷的同时, 还进行某种形式摩擦磨损过程的系统被称为荷载摩擦副系统, 如齿轮副、钢丝绳、轮/轨系统及键连接等^[1-3].磨损损伤与疲劳损伤是导致荷载摩擦系统失效的主要形式, 二者之间存在复杂的相互作用关系^[1].Zeng等^[4]在考虑微动磨损导致应力重新分布对微动疲劳影响的基础上, 利用有限元方法, 通过铁路车辆压装轴微动疲劳分析, 提出了一种全尺寸压装轴微动疲劳裂纹萌生预测模型.Xue等^[5]基于Archard磨损模型, 利用有限元法研究了航空发动机渐开线花键联轴器微动磨损, 给出了一种花键联轴器磨损与疲劳耦合寿命评估方法.O'Halloran等^[6]将表面损伤参数和多轴疲劳损伤参数相结合, 对柔性立管压力保护层进行磨损疲劳耦合有限元分析, 提出了一种考虑表面损伤效应的裂纹萌生寿命预测方法.灵敏度用于表征系统输入发生变化时系统输出对其变化响应的程度.Morris方法是一种以较小计算量高效定性描述各个输入参数对系统输出作用效果大小的全局灵敏度分析方法^[7].Meghoe等^[8]运用Morris方法分析了参数与钢轨磨耗之间关系, 综合考虑轨道几何尺寸和使用轮廓等参数, 提出了一种铁路轨道剩余使用寿命估算方法.Velarde等^[9]利用Morris方法和蒙特卡洛模拟相结合的方式, 建立了海上风力涡轮机的安全性能和各参数的回归模型, 选出了关键影响参数.
综上所述, ****主要针对具体损伤系统开展强针对性研究, 对具有通用性典型荷载摩擦副系统的研究还鲜见报道.本文针对典型线接触滑动磨损与接触疲劳耦合损伤开展研究, 利用改进Archard磨损模型、基于临界平面法的多轴疲劳理论及虚拟裂纹扩展法, 建立典型线接触滑动磨损与接触疲劳耦合损伤分析模型, 应用Morris方法探究对两种损伤都具有影响的参数作用特性, 确定影响耦合损伤的关键参数, 提出接触疲劳损伤灵敏度贡献比, 明确疲劳损伤和磨损损伤对耦合损伤的贡献, 进而提出一种基于灵敏度贡献比的滑动磨损与接触疲劳耦合损伤寿命预测模型, 为线接触滑动磨损与接触疲劳耦合损伤设计分析方法及控制策略的完善奠定基础.
1 耦合损伤分析模型图 1为线接触滑动磨损与接触疲劳荷载摩擦副系统模型.两个圆柱体在接触压力F_N作用下相互接触, 圆柱C1以线速度v₁转动, 圆柱C2静止不动, 接触面间产生摩擦力为F_T.此时, 两圆柱接触区域承受接触压力和摩擦力耦合作用效应, 即同时存在接触疲劳和滑动磨损耦合损伤.图 2为赫兹接触模型, 根据赫兹接触理论, 可得接触区域的接触宽度和接触应力分布^[10]：

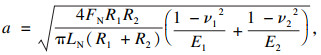(1)

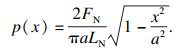(2)

图 1(Fig. 1)

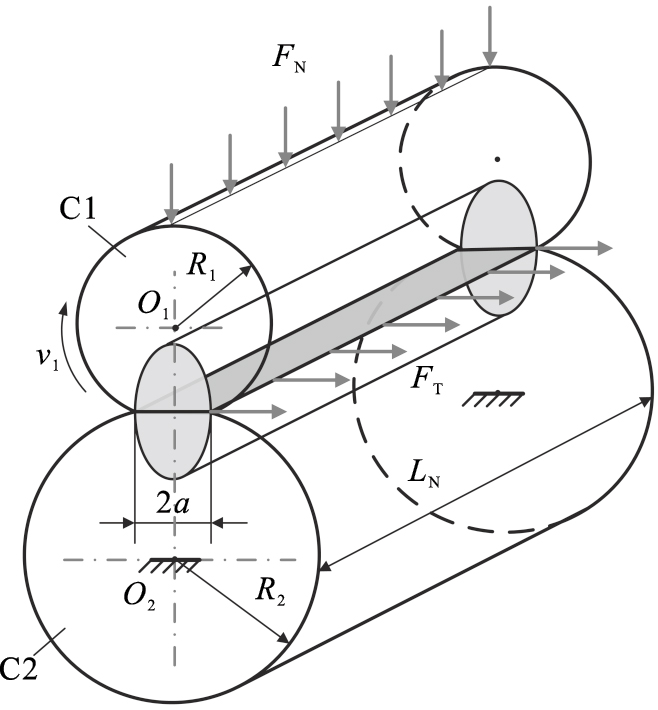图 1 滑动磨损与接触疲劳耦合模型Fig.1 Coupling model of sliding wear and contact fatigue

图 2(Fig. 2)

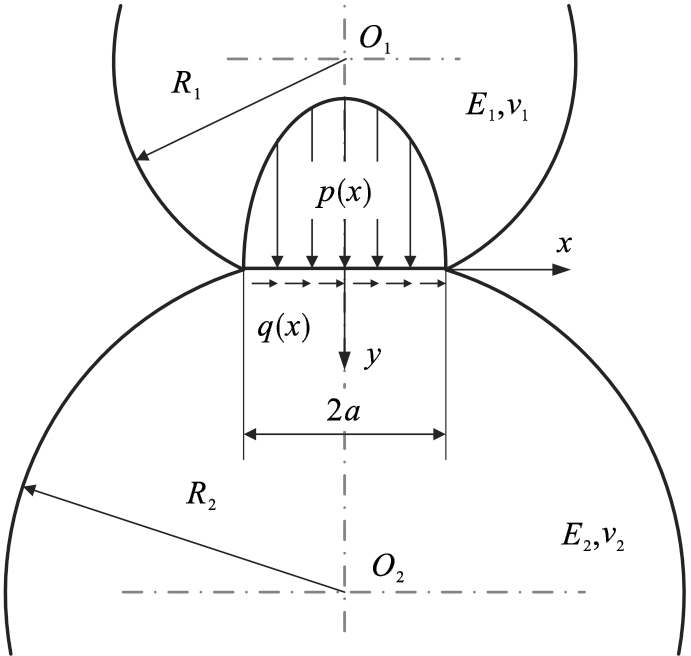图 2 赫兹接触模型Fig.2 Hertz contact model

式中：F_N为接触压力；L_N为接触宽度；R₁, R₂分别为两圆柱的曲率半径；ν₁, ν₂分别为两圆柱的泊松比；E₁, E₂分别为两圆柱的弹性模量.
根据库仑摩擦定律, 摩擦力分布为

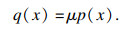(3)

式中：μ为摩擦因数.
滑动磨损和接触疲劳都是损伤连续累积过程.对于良好工作状态下单次磨损或单次疲劳作用导致损伤均较小.因此, 本文采用离散原理将分析过程划分为若干个离散阶段, 每个离散阶段循环载荷次数设定为n, 假定在每个离散阶段内模型的结构尺寸不变, 分析得到离散阶段累积损伤, 并判断失效状态.若未达到失效, 则以上一离散阶段损伤累积分析结果作为边界条件, 开展下一离散阶段损伤分析, 依次迭代, 直至达到损伤失效.
磨损损伤分析采用广泛应用的Archard磨损模型^{[3, 5, 11]}, 一般表达式为

(4)

式中：V为磨损体积；S为滑动距离；K_W为磨损系数；H_h为硬度.其中, dV, dS和dF_N可表示为dV=dhdA₀, dS=vdt, dF_N=pdA₀, h为磨损深度, A₀为接触面积, v为滑动速度, t为滑动时间, p为接触应力.改进的Archard磨损模型为

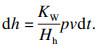(5)

转化为每循环的磨损深度为

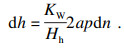(6)

离散阶段磨损深度为

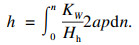(7)

接触疲劳损伤包括疲劳裂纹萌生和扩展两部分, 疲劳寿命N为裂纹萌生寿命N_I和裂纹扩展寿命N_P的总和.通过临界面方法和修正Basquin方程得到每个离散阶段应力水平下裂纹萌生寿命N_Ii为^[12]

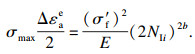(8)

式中：σ_f^'为疲劳强度系数, 取值为σ_f^'=1.5σ_b, σ_b为抗拉强度；b为疲劳强度指数；σ_max和Δε_a^e分别为一个离散加载阶段中临界面上正应力和正应变幅值.
根据Palmgren-Miner线性损伤累积准则^[13], 当循环载荷作用足够多, 裂纹萌生累积损伤D_I达到损伤极限时, 即D_I=1, 疲劳裂纹萌生.因此, 裂纹萌生寿命N_I为损伤达到极限之前各个阶段加载次数之和, 即

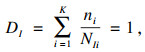(9)

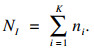(10)

式中, n_i为第i个阶段的循环载荷次数.
根据文献[14]确定裂纹萌生位置H、初始裂纹长度c₀和初始裂纹扩展角θ₀.疲劳裂纹萌生后, 在循环载荷连续作用下扩展, 根据虚拟裂纹扩展法, 裂纹可能将沿着几个不同的方向扩展, 如图 3所示.当在每个可能扩展方向上扩展一定增量时, 会产生一定的能量释放.根据最大能量释放率准则, 裂纹沿最大能量释放率方向扩展, 即最大等效应力强度因子方向扩展, 且裂纹扩向接触表面^{[3, 10]}.根据最大等效应力强度因子方向可确定裂纹扩展方向θ^[10].对于Ⅰ型和Ⅱ型复合裂纹, 等效应力强度因子可表示为

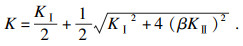(11)

图 3(Fig. 3)

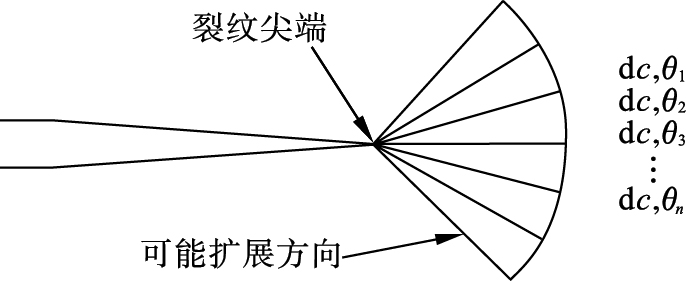图 3 虚拟裂纹扩展Fig.3 Virtual crack extension

式中：K为等效应力强度因子；K_Ⅰ和K_Ⅱ分别为Ⅰ型和Ⅱ型应力强度因子；β为材料常数, 取值为β=1.155^[15].
利用Forman公式计算裂纹扩展速率为

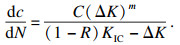(12)

式中：C, m为材料参数；R为应力比；ΔK为裂纹所在位置的应力强度因子幅值, ΔK=K_max-K_min；K_IC为断裂韧性.
图 4为滑动磨损与接触疲劳耦合下疲劳裂纹扩展过程示意图.在滑动磨损和接触疲劳耦合作用下, 接触表面材料因磨损被去除和裂纹扩展的耦合损伤不断累积, 当裂纹扩展到接触表面时, 判定为滑动磨损与接触疲劳耦合损伤失效.每阶段裂纹扩展长度和剩余距离可表示为

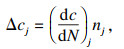(13)

(14)

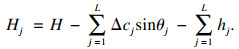图 4(Fig. 4)

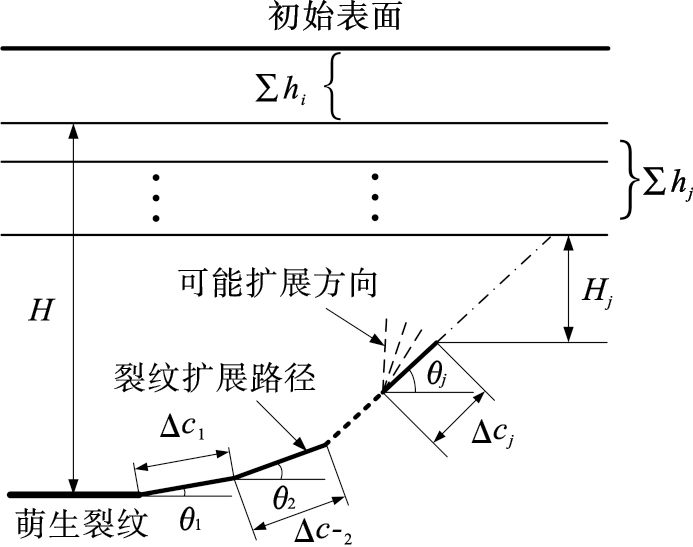图 4 裂纹扩展过程示意图Fig.4 Schematic diagram of crack propagation process

式中：n_j, Δc_j, (dc/dN)_j和θ_j分别为第j个阶段的循环载荷次数、裂纹扩展长度、裂纹扩展速率和裂纹扩展角度；H_j为裂纹扩展j个阶段后的剩余距离；h_j为第j个阶段磨损深度.
当裂纹尖端与接触表面间的距离为0时, 即H_j=0, 表明裂纹已扩展至接触表面, 发生耦合损伤失效, 则疲劳裂纹的扩展寿命为

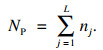(15)

若将滑动磨损与接触疲劳耦合损伤下的寿命记为N_C, 则有N_C=N_I+N_P.
滑动磨损与接触疲劳耦合损伤分析流程如图 5所示.以单一滑动磨损损伤为失效判定时, 即累计磨损损伤达到许用磨损量H_max, 失效寿命记为N_W, 以单一接触疲劳损伤为失效判定时, 即裂纹扩展到接触表面, 失效寿命记为N_F.
图 5(Fig. 5)

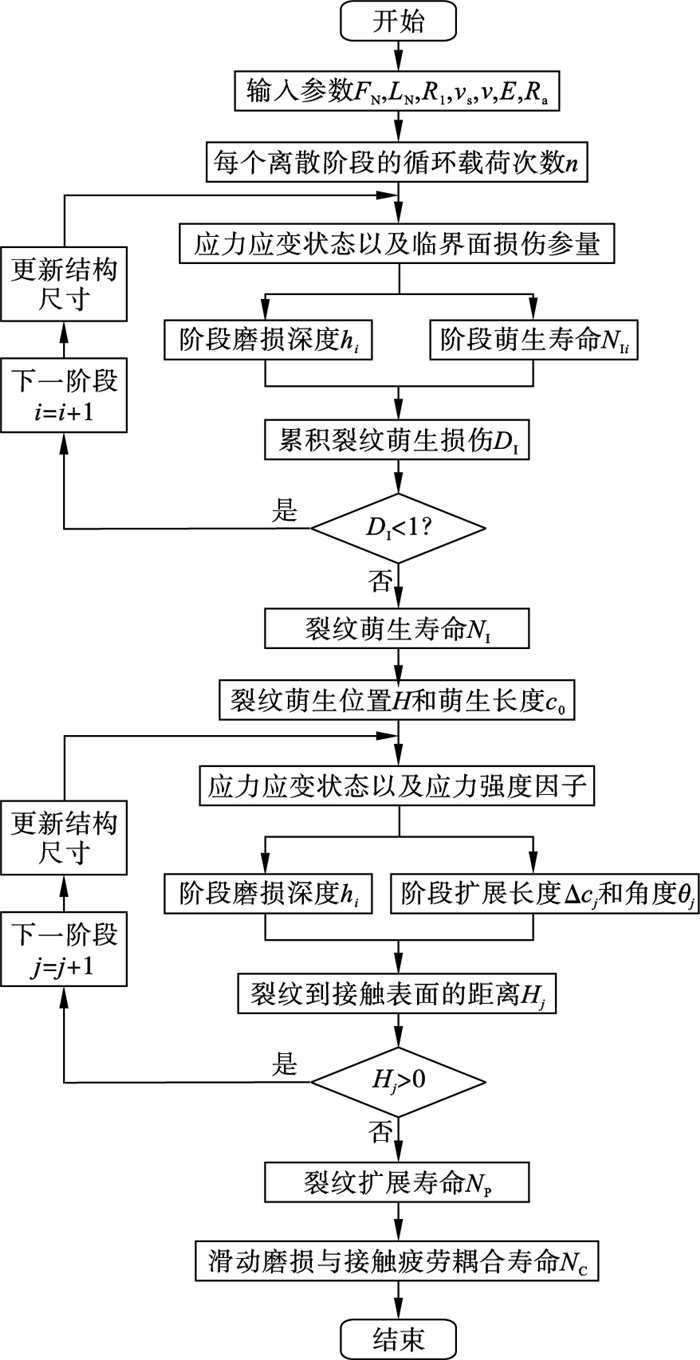图 5 滑动磨损与接触疲劳耦合分析流程图Fig.5 Flow chart of coupling analysis of sliding wear and contact fatigue

2 耦合损伤Morris灵敏度2.1 Morris方法Morris灵敏度方法以离散搜索方式对整个参数空间的灵敏度进行评估, 通过对参数空间内不同离散点增长率计算得到各参数对系统输出影响的统计规律^[7].假设系统的输出目标函数Y(X)含有q个输入参数x₁, …, x_i, …, x_q, 在耦合损伤分析中取为接触压力F_N, 接触宽度L_N, 曲率半径R₁, 滑动速度v_s, 泊松比ν, 弹性模量E和表面粗糙度R_a共7个参数.将各个参数取值范围映射到[0, 1]区间内, 使各输入参数随机从[0, 1]区间内p个相等的间隔取值, 计算得到输出目标Y(x₁, …, x_i, …, x_q).当系统中某个变量x_i发生变动, 其余参数值不变时, 由x_i参数变化对输出的影响程度为^[14-16]

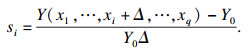(16)

式中, Δ=1/p-1，为映射后参数变化量.
依次计算所有参数对输出的影响程度, 并记为灵敏度因子S=(s₁, s₂, …, s_q).s_i越大, 则该参数对模型输出值影响越大, s_i为正数表示该参数与模型输出值呈正相关, 反之则为负相关.
2.2 灵敏度贡献比全寿命周期内, 假定每工作循环导致的损伤是相同的.若发生失效时的寿命为N, 则单次工作循环作用的损伤率为D=1/N.分别以耦合损伤率D_C、单一滑动磨损损伤率D_W和单一接触疲劳损伤率D_F为输出目标, 通过式(16)得到耦合灵敏度因子S_C、单一磨损损伤灵敏度因子S_W和单一疲劳损伤灵敏度因子S_F.根据叠加原理, 耦合灵敏度因子中滑动磨损损伤和接触疲劳损伤的叠加关系S_C, S_W和S_F的线性回归方程为

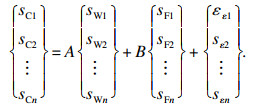(17)

式中：A, B为回归系数, 分别为滑动磨损损伤灵敏度贡献和接触疲劳损伤灵敏度贡献；ε_i为随机误差项.
对于滑动磨损与接触疲劳荷载摩擦副系统, 灵敏度贡献体现了滑动磨损损伤与接触疲劳损伤对总损伤的贡献, 如果某种损伤的灵敏度贡献大, 说明该损伤在总损伤中占比大.定义接触疲劳损伤贡献比r为

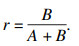(18)

基于单一滑动磨损损伤率、单一接触疲劳损伤率及耦合损伤中接触疲劳损伤贡献比, 滑动磨损与接触疲劳耦合预测寿命N_A为

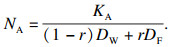(19)

式中, K_A为滑动磨损与接触疲劳耦合系数, 可以根据接触疲劳损伤贡献比确定K_A=2(r-0.5)²+0.5.
3 损伤特性分析通过算例对比分析耦合损伤寿命与单一滑动磨损/单一接触疲劳的损伤寿命, 分析采用图 1所示模型.材料为18Cr合金钢^[17], 泊松比和弹性模量分别为ν=0.3, E=210 GPa；断裂韧性K_IC=50 MPa·m^1/2, 抗拉强度σ_b=624 MPa；疲劳参数分别为b=-0.087, C=2.67×10^-9, m=3.77, Y=1.2.曲率半径R₁=4 mm, R₂=40 mm；接触压力F_N=150 N, 接触宽度L_N=4 mm, 滑动速度v_s=100 m/s, 表面粗糙度R_a=0.8 μm, 摩擦因数μ=0.05^[3].设定许用磨损量H_max=0.05 mm, 裂纹萌生长度c₀=0.05 mm^{[3, 14]}.
图 6为单一滑动磨损损伤、单一接触疲劳损伤和滑动磨损与接触疲劳耦合损伤寿命分析结果.由图 6a可知, 随加载次数增加, 磨损深度累积不断增大, 萌生裂纹不断向接触表面扩展, Q点为滑动磨损和接触疲劳耦合损伤导致的失效点.在滑动磨损与接触疲劳耦合损伤下, 疲劳裂纹萌生后, 不断向接触表面扩展, 裂纹距离接触表面越近, 其扩展角度越大, 扩展速率越快, 损伤越迅速^{[3, 10]}.滑动磨损与接触疲劳耦合损伤下, 裂纹萌生寿命为183 029次, 总寿命为388 307次.当单一滑动磨损损伤累积导致失效时, 其寿命为756 331次, 如图 6b所示.当单一疲劳损伤累积导致失效时, 裂纹萌生寿命为184 493, 单一接触疲劳损伤总寿命为569 495次, 如图 6c所示.可以看出, 耦合损伤寿命分别为单一磨损损伤寿命和单一接触疲劳损伤寿命的51.34%和68.18%, 表明滑动磨损与接触疲劳的耦合效应对寿命具有显著影响.这个损伤特性规律与文献[3]分析结果具有很好的一致性, 验证了所提耦合损伤特性分析方法是正确的.随科技的发展及对机械零件性能要求的不断提高, 对具有高精度和高可靠性要求的荷载摩擦副系统中机械零件设计分析必须考虑这种耦合效应.
图 6(Fig. 6)

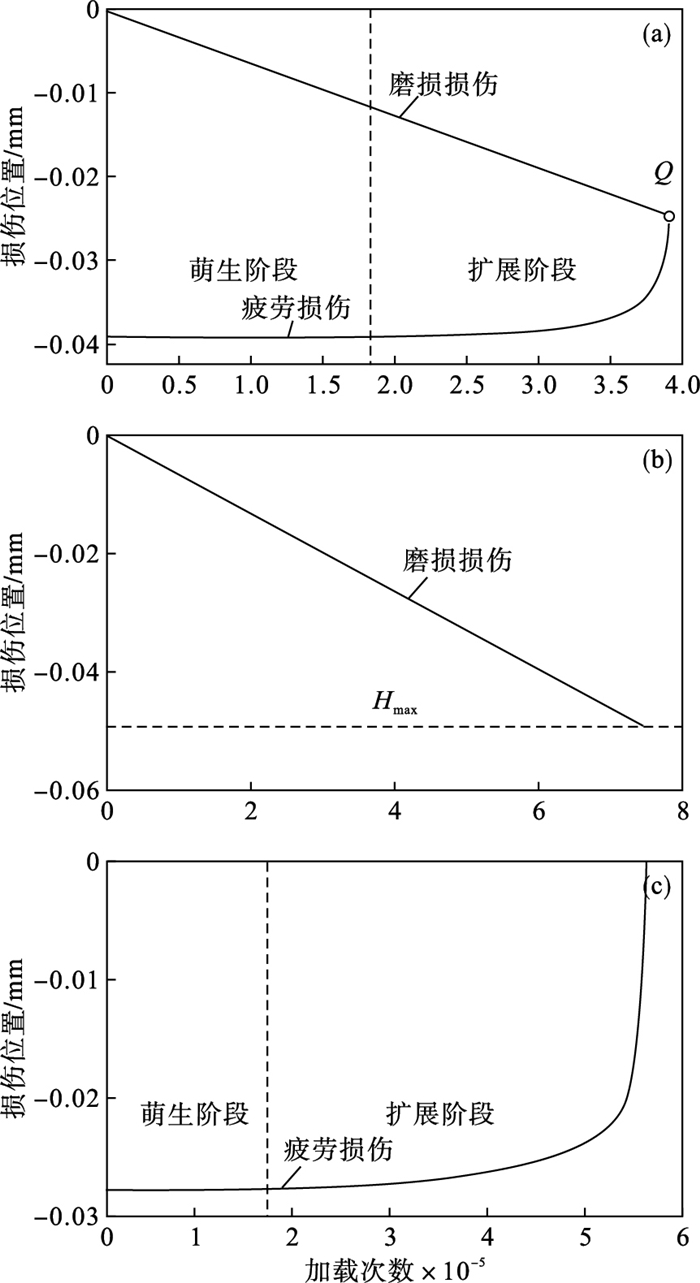图 6 损伤过程模拟Fig.6 Simulation of damage process (a)—耦合损伤；(b)—单一滑动磨损损伤；(c)—单一接触疲劳损伤.

4 耦合损伤结果分析依据第3部分算例, 选取接触压力F_N、接触宽度L_N、曲率半径R₁、相对滑动速度v_s、泊松比ν、弹性模量E和表面粗糙度R_a作为对滑动磨损和接触疲劳共同影响参数.根据第2部分Morris灵敏度分析, 以第3部分分析参数为均值, 设定各个影响参数取值范围, 具体如表 1所示.
表 1(Table 1)

表 1 参数取值范围Table 1 Range of parameters 参数 取值范围 FN/N [145, 155] LN/mm [3.9, 4.1] R1/mm [3.9, 4.1] vs/(mm·s-1) [97, 103] ν [0.29, 0.31] E/GPa [205, 215] Ra/μm [0.78, 0.82]

表 1 参数取值范围 Table 1 Range of parameters

4.1 Morris灵敏度单一滑动磨损损伤、单一接触疲劳损伤和滑动磨损与接触疲劳耦合损伤灵敏度因子S_W, S_F和S_C如图 7所示.可知, 对单一滑动磨损损伤, E影响最大, F_N, υ, L_N, v_s和R_a影响次之且程度逐渐递减, R₁影响甚微.其中, F_N, v_s和R_a与磨损损伤呈正相关, 而L_N, υ和E与磨损损伤呈负相关.对单一接触疲劳损伤, F_N, L_N和R₁影响较大, 其余参数影响相对较小, 而v_s和R_a几乎没有影响.其中, F_N, υ和E与单一接触疲劳损伤呈正相关, L_N和R₁与单一接触疲劳损伤呈负相关.在滑动磨损与接触疲劳耦合损伤下, F_N, L_N和R₁影响较为明显, 其余参数影响相对较小.其中, F_N, v_s, R_a和E与耦合损伤呈正相关, L_N, R₁和υ与耦合损伤呈负相关.分析发现, 有些参数对单一滑动磨损损伤和单一接触疲劳损伤的作用效应是同向的, 对耦合损伤作用表现为累加, 如F_N和L_N耦合损伤灵敏度是单一滑动磨损损伤灵敏度和单一接触疲劳损伤灵敏度的累加.有些参数对单一滑动磨损损伤和单一接触疲劳损伤的作用效应是反向的, 对耦合损伤的影响表现为中和, 如υ和E耦合损伤灵敏度是单一滑动磨损损伤灵敏度和单一接触疲劳损伤灵敏度正负相抵得到.有些参数仅对单一滑动磨损损伤或单一接触疲劳损伤影响, 对耦合损伤的影响效应表现为继承, 如v_s和R_a耦合损伤灵敏度继承了单一滑动磨损损伤灵敏度, R₁对损伤灵敏度的影响继承了单一接触疲劳损伤灵敏度.
图 7(Fig. 7)

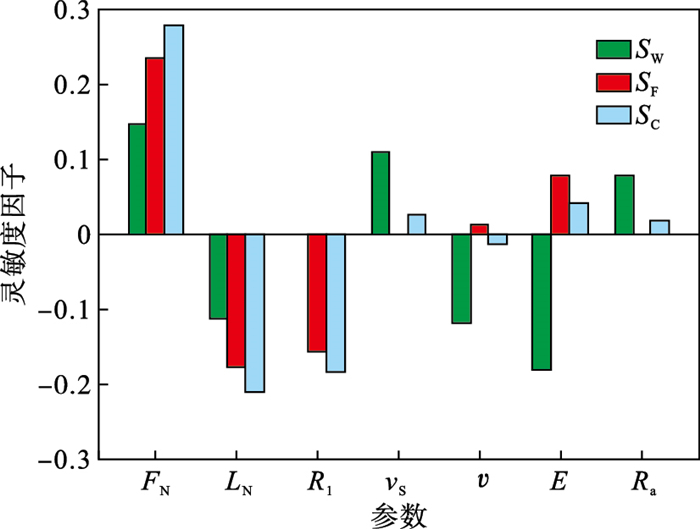图 7 参数对灵敏度因子的影响Fig.7 Effect of the parameters on the sensitivity factor

4.2 灵敏度贡献比各个参数的灵敏度因子S_W, S_F, S_C以式(17)的形式线性拟合得到滑动磨损损伤灵敏度贡献A和接触疲劳损伤灵敏度贡献B分别为0.232 3和1.086 5.拟合结果的决定系数R²为0.982 9, 说明拟合优度较好.分析条件下的疲劳损伤贡献比r为0.823 8, 参数变化对耦合损伤的影响规律与对接触疲劳损伤的影响规律更相近, 表明接触疲劳损伤在总损伤中的占比更大.
通过灵敏度分析可知, F_N, L_N和R₁对耦合损伤具有显著影响.接触疲劳贡献比r随显著影响参数F_N, L_N和R₁变化规律如图 8~图 10所示.可知, 接触疲劳损伤贡献比r随F_N, L_N和R₁近似呈线性变化规律.通过最小二乘法进行线性拟合, 得到的决定系数R²分别为0.990 3, 0.989 7和0.989 1, 说明具有很好拟合优度.由图 8可知, 接触疲劳损伤贡献比r随接触压力F_N增大而减小.这是由于接触压力较小时, 耦合损伤以接触疲劳损伤为主, 因此耦合损伤和单一接触疲劳损伤对于参数变化有着相近的变化趋势, 表现为相近的灵敏度因子, 接触疲劳损伤贡献比r较大.随接触压力的增加, 滑动磨损引起的表面损伤增加, 加快了耦合损伤失效进程, 导致滑动磨损损伤在耦合损伤中的贡献增加, 相应的接触疲劳损伤贡献减小.由图 9可知, 接触疲劳损伤贡献比r随接触宽度L_N增大而增大.这是由于接触宽度增大导致接触表面的磨损减轻, 对疲劳裂纹扩展至接触表面的作用减小, 发生以接触疲劳损伤为主的失效模式, 接触疲劳损伤贡献增大.由图 10可知, 接触疲劳损伤贡献比r随曲率半径R₁增大而增大, 这是由于曲率半径增大导致赫兹接触宽度增大, 一方面减小了赫兹接触应力, 接触表面的磨损减轻, 另一方面赫兹接触宽度增大导致裂纹萌生深度增大, 接触疲劳损伤加重, 二者共同作用导致接触疲劳损伤贡献增大^[17].
图 8(Fig. 8)

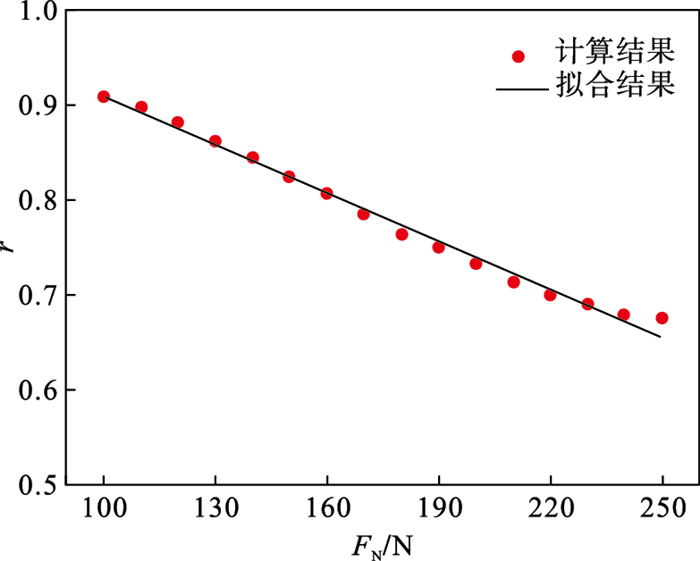图 8 r随FN的变化Fig.8 Variation of r with FN

图 9(Fig. 9)

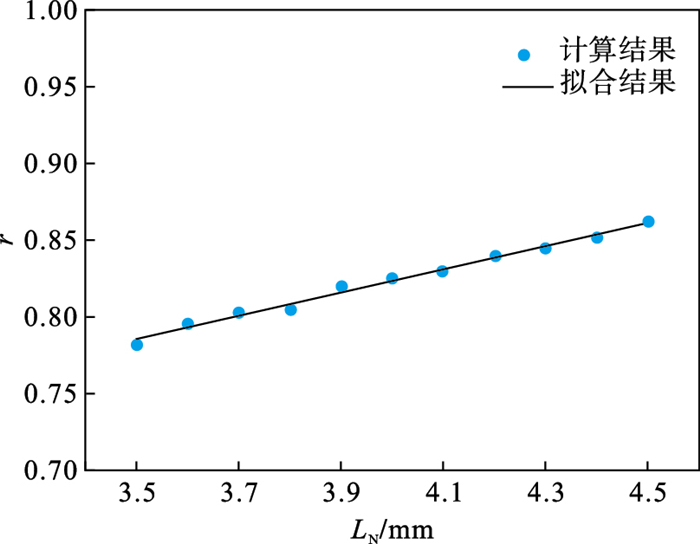图 9 r随LN的变化Fig.9 Variation of r with LN

图 10(Fig. 10)

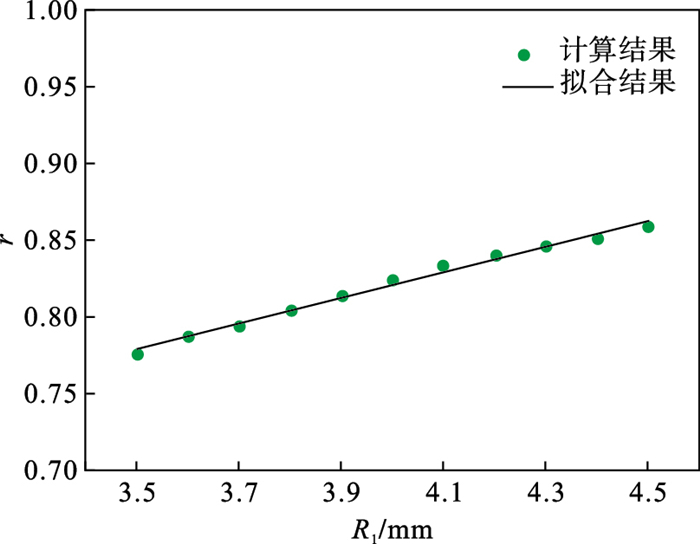图 10 r随R1的变化Fig.10 Variation of r with R1

4.3 耦合损伤寿命图 11~图 13为显著影响参数F_N, L_N和R₁作用耦合损伤预测寿命N_A与理论计算寿命N_C分析结果.由图 11可知, 耦合寿命随接触压力F_N增大而减小, 耦合损伤计算寿命和预测寿命的误差为1.17%~4.70%.耦合寿命随接触宽度L_N增大而增加, 耦合损伤的计算寿命和预测寿命的误差为1.96%~3.85%, 如图 12所示.
图 11(Fig. 11)

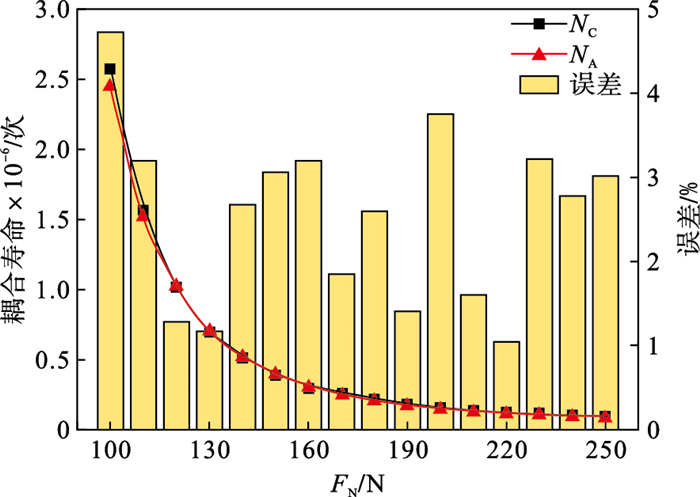图 11 接触压力下的耦合寿命对比分析Fig.11 Comparative analysis of coupling life under contact pressure

图 12(Fig. 12)

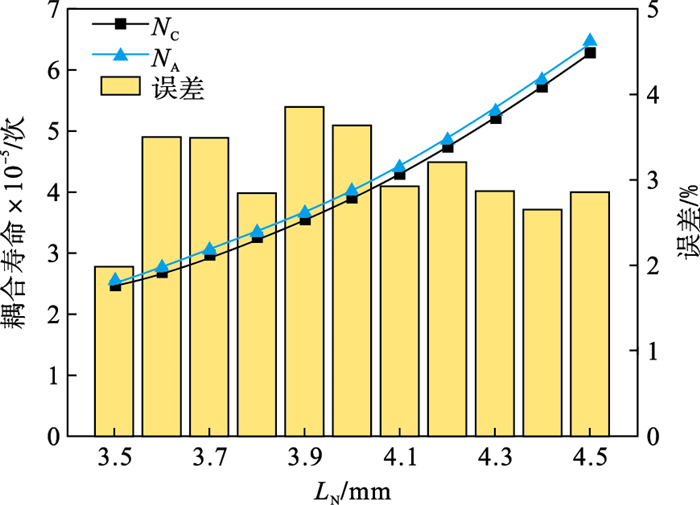图 12 接触宽度下的耦合寿命对比分析Fig.12 Comparative analysis of coupling life under contact width

图 13(Fig. 13)

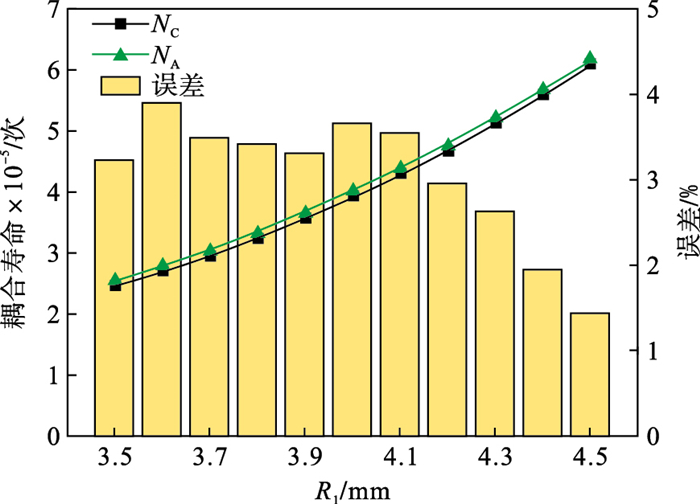图 13 曲率半径下的耦合寿命对比分析Fig.13 Comparative analysis of coupling life under curvature radius

耦合寿命随曲率半径R₁的增大而增加, 耦合损伤的计算寿命和预测寿命的误差为1.46%~3.91%, 如图 13所示.显著影响参数的预测寿命与计算寿命的最大误差均小于5%, 表明本文提出的基于灵敏度贡献比的滑动磨损与接触疲劳耦合损伤预测寿命模型可以对该种荷载摩擦副系统进行很好的寿命预测.
5 结论1) 建立了线接触滑动磨损与接触疲劳耦合损伤荷载摩擦副系统分析模型, 结合改进Archard磨损模型、临界平面法及虚拟裂纹扩展法, 实现了单一损伤和耦合损伤的寿命分析.
2) 基于Morris灵敏度方法, 结合耦合损伤分析模型, 建立了灵敏度贡献比模型, 提出了一种基于灵敏度贡献比的滑动磨损与接触疲劳耦合损伤的寿命预测方法.
3) 磨损损伤累积导致剩余距离减小, 同时增强了裂纹扩展, 导致耦合损伤寿命明显减小.灵敏度分析表明接触压力、接触宽度和曲率半径对耦合损伤具有显著影响.接触疲劳贡献比与接触压力、接触宽度和曲率半径近似呈线性关系, 但随接触压力增大而减小, 随接触宽度和曲率半径增大而增大.
参考文献

[1]	Sosnovskiy L A. Tribo-fatigue, wear-fatigue damage and its prediction[M]. Berlin: Springer-Verlag, 2005: 119-128.
[2]	Zhang J, Wang D G, Song D Z, et al. Tribo-fatigue behaviors of steel wire rope under bending fatigue with the variable tension[J]. Wear, 2019, 428/429: 154-161. DOI:10.1016/j.wear.2019.03.004
[3]	Yan Y T, Jiang C, Li W D. Simulation on coupling effects between surface wear and fatigue in spur gear[J]. Engineering Failure Analysis, 2022, 134: 106055. DOI:10.1016/j.engfailanal.2022.106055
[4]	Zeng D F, Zhang Y B, Lu L T, et al. Fretting wear and fatigue in press-fitted railway axle: a simulation study of the influence of stress relief groove[J]. International Journal of Fatigue, 2019, 118: 225-236. DOI:10.1016/j.ijfatigue.2018.09.008
[5]	Xue X Z, Huo Q X, Hong L. Fretting wear-fatigue life prediction for aero-engine's involute spline couplings based on abaqus[J]. Journal of Aerospace Engineering, 2019, 32(6): 04019081. DOI:10.1061/(ASCE)AS.1943-5525.0001058
[6]	O'Halloran S M, Shipway P H, Connaire A D, et al. A combined wear-fatigue design methodology for fretting in the pressure armour layer of flexible marine risers[J]. Tribology International, 2017, 108: 7-15. DOI:10.1016/j.triboint.2016.10.020
[7]	黄乐烽, 杜坤, 宋志刚, 等. 基于Morris法的供水管网全局灵敏度分析[J]. 工业安全与环保, 2021, 47(6): 103-106. (Huang Le-feng, Du Kun, Song Zhi-gang, et al. Global sensitivity analysis of water distribution network model based on Morris method[J]. Industrial Safety and Environmental Protection, 2021, 47(6): 103-106.)
[8]	Meghoe A, Loendersloot R, Tinga T. Rail wear and remaining life prediction using meta-models[J]. International Journal of Rail Transportation, 2020, 8(1): 1-26. DOI:10.1080/23248378.2019.1621780
[9]	Velarde J, Kramh?ft C, S?rensen J D. Global sensitivity analysis of offshore wind turbine foundation fatigue loads[J]. Renewable Energy, 2019, 140: 177-189. DOI:10.1016/j.renene.2019.03.055
[10]	Glode? S, Ren Z, Fla?ker J. Simulation of surface pitting due to contact loading[J]. International Journal for Numerical Methods in Engineering, 1998, 43(1): 33-50. DOI:10.1002/(SICI)1097-0207(19980915)43:1<33::AID-NME410>3.0.CO;2-Z
[11]	Brand?o J A, Martins R, Seabra J H O, et al. An approach to the simulation of concurrent gear micropitting and mild wear[J]. Wear, 2015, 324: 64-73.
[12]	Sum W S, Williams E J, Leen S B. Finite element, critical-plane, fatigue life prediction of simple and complex contact configurations[J]. International Journal of Fatigue, 2005, 27(4): 403-416. DOI:10.1016/j.ijfatigue.2004.08.001
[13]	Santecchia E, Hamouda A M S, Musharavati F, et al. A review on fatigue life prediction methods for metals[J]. Advances in Materials Science and Engineering, 2016, 2016: 9573524.
[14]	Osman T, Velex P. A model for the simulation of the interactions between dynamic tooth loads and contact fatigue in spur gears[J]. Tribology International, 2012, 46(1): 84-96. DOI:10.1016/j.triboint.2011.03.024
[15]	Richard H A, Fulland M, Sander M. Theoretical crack path prediction[J]. Fatigue & Fracture of Engineering Materials & Structure, 2005, 28(1/2): 3-12.
[16]	周兵, 黄晓婷, 耿元. 基于Morris法分析的液压参数对互联悬架的影响[J]. 湖南大学学报(自然科学版), 2016, 43(2): 70-76. (Zhou Bing, Huang Xiao-ting, Geng Yuan. Influence of hydraulic parameters on hydraulically interconnected suspension based on Morris[J]. Journal of Hunan University (Natural Sciences), 2016, 43(2): 70-76.)
[17]	Liu H L, Liu H J, Zhu C C, et al. Study on gear contact fatigue failure competition mechanism considering tooth wear evolution[J]. Tribology International, 2020, 147: 106277.