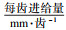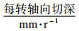, 武晔, 付麒麟, 周秩同
, 武晔, 付麒麟, 周秩同 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004
收稿日期:2022-05-17
基金项目:河北省自然科学基金资助项目(E2020501014)。
作者简介:王海艳(1973-), 女, 河北秦皇岛人, 东北大学副教授。
摘要:为了准确预测碳纤维增强复合材料(carbon fiber reinforced polymers, CFRP)螺旋铣孔过程中切削力的变化, 在切削力模型中着重考虑CFRP材料的各向异性和纤维方向角的影响, 根据不同损伤区域对CFRP细观单元体进行直角切削分析.在此基础上结合螺旋铣孔加工原理, 考虑侧刃及底刃的作用, 分析不同纤维方向角下切削力的变化情况, 建立螺旋铣孔切削力理论模型.开展CFRP螺旋铣孔实验, 以测量的三向切削力的周期波动值作为分析依据, 求解特定公转角度下的切削力理论值.结果表明切削力理论值与实验值拟合误差不超过16%, 验证了CFRP螺旋铣孔切削力理论模型的正确性.
关键词:CFRP细观切削纤维方向角螺旋铣孔切削力
Analysis of Micro Cutting Forces in the Helical Milling of CFRP
WANG Hai-yan

 , WU Ye, FU Qi-lin, ZHOU Zhi-tong
, WU Ye, FU Qi-lin, ZHOU Zhi-tong School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: WANG Hai-yan, E-mail: hywang16@126.com.
Abstract: In order to accurately predict the variation of cutting forces in the helical milling of CFRP, the effects of anisotropy of CFRP materials and fiber direction angle are emphatically considered in the modeling of cutting forces. The orthogonal cutting analysis of CFRP mesoscopic units is carried out according to different damage areas. On this basis, combining the machining principle of the helical milling and considering the cutting force generated by the periphery edges and bottom edges respectively, the change of cutting forces under different fiber direction angles is analyzed, and the theoretical model of cutting forces for helical milling is established. Through the helical milling experiment of CFRP, based on the measured periodic fluctuation values of the three-way cutting forces, the theoretical values of the cutting forces under the specific revolution angles are solved. The results show that the fitting error between the theoretical and experimental values of cutting forces is less than 16%, which verifies the correctness of the theoretical model of cutting forces in the helical milling of CFRP.
Key words: CFRPmicro cuttingfiber direction anglehelical millingcutting force
碳纤维增强复合材料CFRP具有比强度高、比模量高、耐疲劳性、耐腐蚀性及可设计性能强等优势[1], 已在航空航天领域得到广泛应用.由于CFRP的非均质性和各向异性, 其加工过程与传统金属相比有很大区别[2], 存在纤维断裂、纤维基体脱黏、基体破坏等失效形式[3].
Albert等[4]研究了单向复合材料的铣削过程.结果表明, 纤维方向角对材料去除和切屑形成机理有很大影响.张厚江[5]建立了单向CFRP直角切削力模型, 主要分析纤维方向角在0°~90°范围内切削力的变化.Zhang等[6]通过实验指出纤维方向角在0°~90°之间变化时, 会形成三个不同的变形区域:切屑形成区域、挤压区域及回弹区域.Jahromi等[7]利用能量法对单向复合材料的正交切削力进行预测, 其纤维方向角为90°~180°, 并发现切削力随刀具前角的增大而增大.
很多****已对CFRP的切削机理进行了分析, 但其加工时产生的损伤仍不可避免.相对于传统的钻孔加工, 螺旋铣孔具有加工质量好、切削力较小、刀具磨损少等优点[8].近些年, CFRP螺旋铣孔过程切削力建模的相关研究逐渐开展.Wang等[9]通过螺旋铣孔实验分析了不同切削参数对切削力的影响, 预测了CFRP螺旋铣孔的切削力.Li等[10]建立了螺旋铣孔的动态切削力模型, 分析了切削机理以及侧刃和底刃的切削力.万敏等[11]通过分析铣刀底刃和侧刃的动态切削, 对单向CFRP螺旋铣的切削力进行了建模, 并建立了纤维切削方向角与切削力系数之间的关联.上述模型多是在传统铣削力模型的基础上建立的, 但CFRP具有各向异性, 不同角度下的切削形式等问题需重点考虑.本文拟结合螺旋铣孔加工原理, 综合考虑CFRP材料的各向异性和纤维方向角对切削力的影响, 从细观角度对CFRP螺旋铣孔过程切削力进行研究.
1 CFRP直角切削细观分析在CFRP直角切削过程中, 定义碳纤维铺层方向与切削速度方向之间的角度为纤维方向角λ, 刀具前角γ导致实际切削时会出现以下两种状态:一种是纤维方向角λ≤90°+γ时, 切削时纤维在刀具前刀面上滑动, 刀具不断进给, 最终达到纤维的断裂准则;另一种情况是λ≤90°+γ, 刀具的进给作用使纤维发生弯曲退让, 最终使纤维达到其弯曲强度或最大拉应力.
如图 1所示, 在CFRP的细观直角切削过程中, 主要影响切削力的区域有3个:基体失效和纤维基体脱黏形成断裂区域;压缩部分回弹对后刀面产生压力区域;切屑滑移区域.在刀具切断纤维和其周围基体沿上刀面滑移并形成切屑的这一瞬时状态, 代表性体积单元体(representative volume element, RVE) RVE A, RVE a和RVE B, RVE b为已经被切削的部分, 与切削刃接触的单元体C还未出现损伤.可以看出, 直角切削分析是复杂切削过程分析的基础[12].
图 1(Fig. 1)
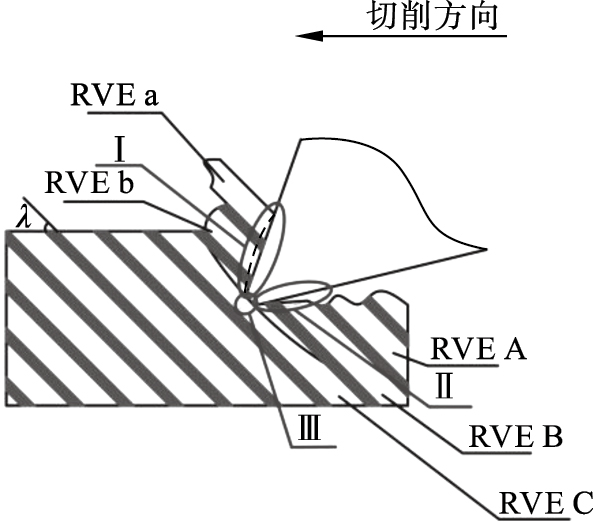 | 图 1 细观单元体切削状态Fig.1 Cutting state of RVE |
2 螺旋铣孔运动学螺旋铣孔运动是由刀具本身的自转运动和其以一定偏心距e围绕孔中心进行的公转运动及刀具自身的轴向进给运动复合而成, 加工原理如图 2所示.
图 2(Fig. 2)
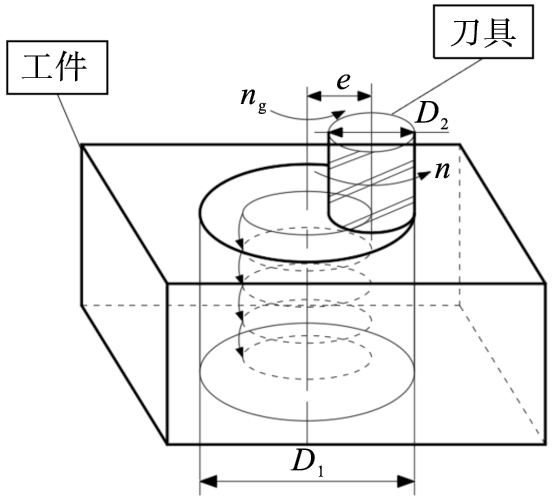 | 图 2 螺旋铣孔加工原理Fig.2 Machining principle of helical milling |
螺旋铣孔过程中, 与加工有关的参数为刀具的自转转速、公转转速、轴向和周向进给速度, 假设刀具轴向进给速度为fa, 自转转速为n, 公转速度为ng, 可以计算出每转轴向切削深度:
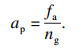 | (1) |
 | (2) |
在螺旋铣孔过程中, 确定了主轴自转转速, 每转轴向切削深度和切向每齿进给量这3个参数后, 可求解其他参数[9].
3 螺旋铣孔切削力分析3.1 坐标系建立与分析以加工孔中心和刀具中心为各自的坐标原点, 建立如图 3所示的坐标系XOY和xoy, 图中?为刀具自转角度, θ为刀具公转角度:
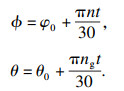 | (3) |
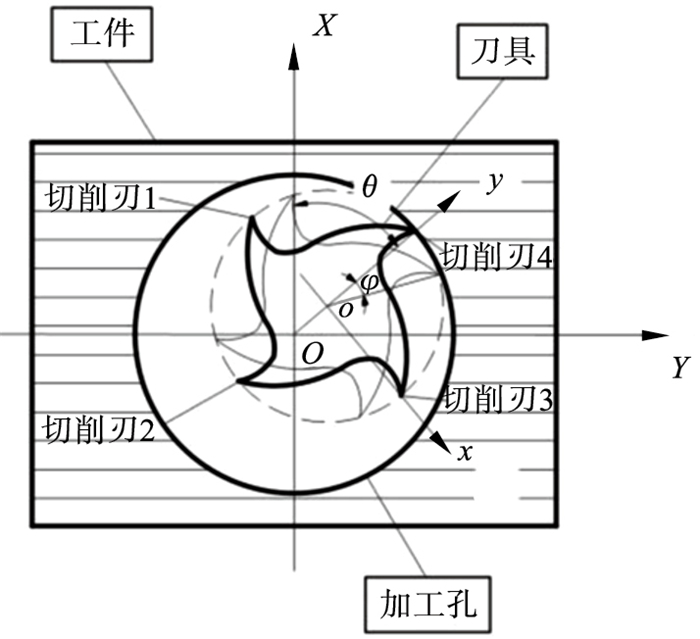 | 图 3 工件与刀具坐标系Fig.3 Coordinate systems of workpiece and tool |
式中:θ0为刀具公转初始位置角;φ0为刀具自转初始位置角;t为时间.
坐标系中X轴垂直于纤维方向, Y轴平行于纤维方向;x轴平行于切削速度方向, y轴沿切削刃方向.由于螺旋铣孔的特殊工作原理, 纤维方向角随自转和公转速度的变化而不断变化, 因此在螺旋铣孔切削过程中, 纤维方向角也可称为动态方向角.
3.2 侧刃切削力大多数情况下, 刀具的侧刃是具有一定螺旋角β的螺旋线.螺旋角的存在使切削方向和碳纤维方向之间的动态方向角发生变化, 同时使不同高度的侧刃与碳纤维之间的相对动态角也不同.
在螺旋铣孔切削过程中, 刀具侧刃对应的未发生变形的切屑为180°弧形切屑, 其展开图如图 4所示.侧刃1的切削长度不超过侧刃3底部从切削开始到完全切削结束的位移ΔL时, 由于螺旋角的原因, 将有3条侧刃同时参与切削, 如图 4a所示;若侧刃1的切削长度超过ΔL时, 侧刃3将完全脱离切削区域, 此时只有两个侧刃参与切削, 如图 4b所示[13].
图 4(Fig. 4)
 | 图 4 对应侧刃的未变形切屑展开图[13]Fig.4 Undeformed chip expansion of corresponding side edge (a)—3条侧刃;(b)—2条侧刃. |
切削过程中, 纤维方向和铣刀之间的夹角不断变化, 将导致两种不同的切削状态.
当0≤λ < 90°+γ时, 纤维的失效形式如图 5所示.图中x′为垂直于纤维方向, z′为平行于纤维方向, x为刀具进给方向, z为进给的垂直方向.在刀具的不断进给下, 加工平面产生变形, 碳纤维层与层之间发生分离并导致表面损伤, 左侧的纤维受到等效模量ka的推力作用, 而右侧的纤维受到纤维-基体黏结等效模量的拉力作用.在此切削状态下的侧刃微元切削力Fpli为[3]
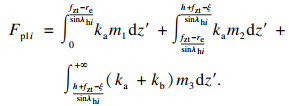 | (4) |
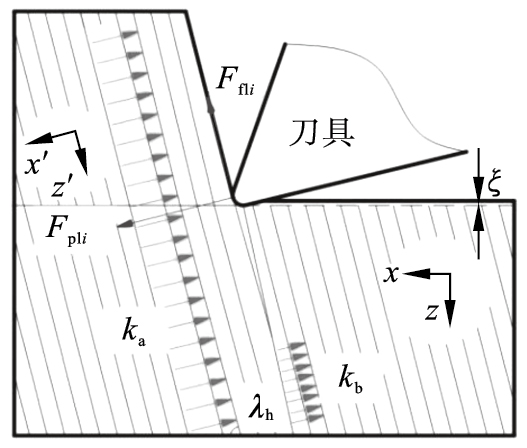 | 图 5 0≤λ < 90°+γ时CFRP的失效形式Fig.5 Failure mode of CFRP when 0≤λ < 90°+γ |
式中:re为刀尖半径;h为纤维-基体脱黏长度;mi(i=1, 2, 3)为各部分垂直于纤维铺层方向的纤维变形量;λhi为对应的侧刃与碳纤维之间的动态角[13].
在切削过程中, 由刀具侧刃或底刃进给引起的变形量ξ为[14]
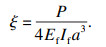 | (5) |
加工过程中平行于纤维方向会受到摩擦力作用, 如果摩擦系数为μ, 则Ffli=μFpli, 因此, 在此切削状态下总的微元切削力Fai为
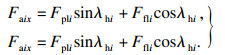 | (6) |
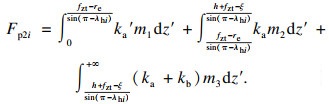 | (7) |
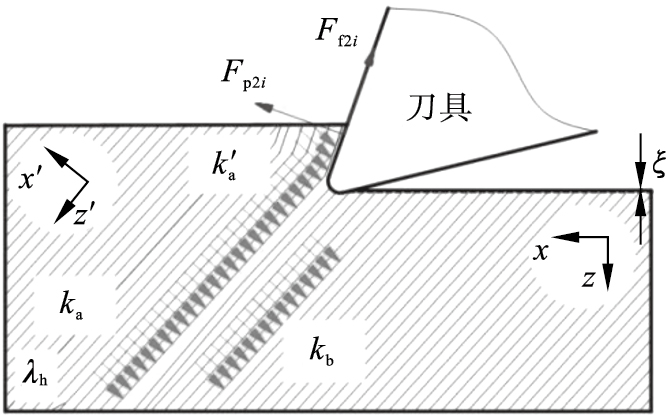 | 图 6 90°+γ≤λ < 180°时CFRP的失效形式Fig.6 Failure mode of CFRP when 90°+γ≤λ < 180° |
式中, ka'为纤维断裂区域的等效模量.
在此切削状态下的刀具前刀面受到摩擦力的作用, 即Ff2i=μFp2i, 此时总的微元切削力Fbi为
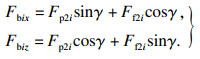 | (8) |
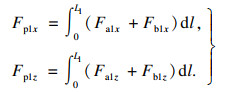 | (9) |
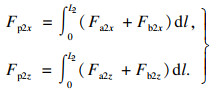 | (10) |
侧刃L3和侧刃L2进行交替切削, 所以需要讨论条到2条一下侧刃3的切削状态:当0≤θ≤90°时, 3条侧刃均参与切削;当90°≤θ≤180°时, 只有2条侧刃参与切削.因此, 侧刃3的切削力为
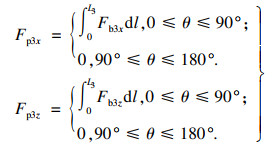 | (11) |
综上所述, 螺旋铣孔的侧刃总切削力可以表示为
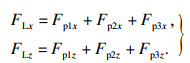 | (12) |
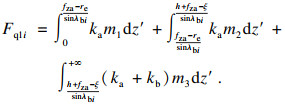 | (13) |
底刃总的微元切削力Fci为
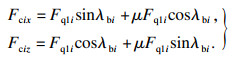 | (14) |
 | (15) |
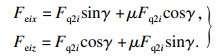 | (16) |
 | (17) |
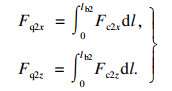 | (18) |
在切削过程中, CFRP受到刀具轴向进给的作用而发生弹性变形, 刀具受到沿z轴的力.由弹性变形引起的力为
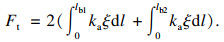 | (19) |
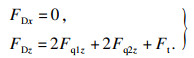 | (20) |
图 7(Fig. 7)
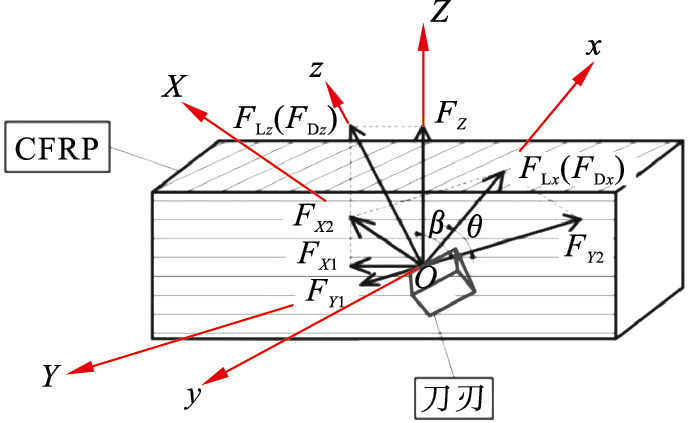 | 图 7 切削力在不同坐标系之间的关系Fig.7 Relationship between cutting forces in different coordinate systems |
轴向切削力由4个切削刃共同承担, 因此轴向切削力应乘上刀具切削刃刃数.CFRP螺旋铣孔过程中总体切削力为
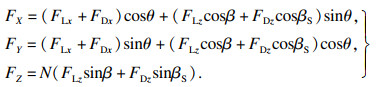 | (21) |
4 螺旋铣孔实验4.1 实验内容在DMC75V五轴联动加工中心上进行螺旋铣孔实验, 采用干切削方式进行加工, 实验工件为碳纤维增强复合材料板, 纤维铺层方向为0°, 板材长度和宽度分别为250,120 mm, 厚度为10 mm, 预加工的孔直径为10 mm.实验所用刀具为直径6 mm的TiAlN涂层四刃专用螺旋铣孔刀, 前角为螺旋角.使用Kistler 9257B三维测力仪测量切削力的大小, 采用单因素实验法, 切削参数如表 1所示, 实验平台如图 8所示.
表 1(Table 1)
| 表 1 切削参数 Table 1 Cutting parameters |
图 8(Fig. 8)
 | 图 8 螺旋铣孔实验Fig.8 Experiment setup for helical milling |
4.2 结果分析图 9a为主轴转速4 000 r/min, 进给量0.02 mm/齿, 轴向切深0.1 mm/r时测量的三向切削力;图 9b为100 Hz低通滤波后50~60 s内的切削力变化情况, 可以看出切削力呈周期性波动.螺旋铣孔在封闭区域切削, 不同角度下的切削很难实现.纤维铺层方向为0°, 可将螺旋铣孔过程中刀具旋转360°视为一个周期, 即切削力的一次波动.选取多个周期, 取平均值作为本文分析的依据, 从中选取30°, 45°, 60°, 90°公转角度进行对比.
图 9(Fig. 9)
 | 图 9 实测及滤波后的切削力Fig.9 Measured and filtered cutting forces (a)—主轴转速4 000 r/min;(b)—100 Hz低通滤波. |
图 10为不同切削参数下切削力的理论值与实验值的对比.图 10a为主轴转速4 000 r/min, 进给量为0.02 mm/齿, 轴向切深为0.10 mm/r, 由三向切削力的实验值与理论值进行对比, 可知, FX和FY远小于轴向力FZ, 且FX与FY相差不大.误差结果如表 2和表 3所示.
图 10(Fig. 10)
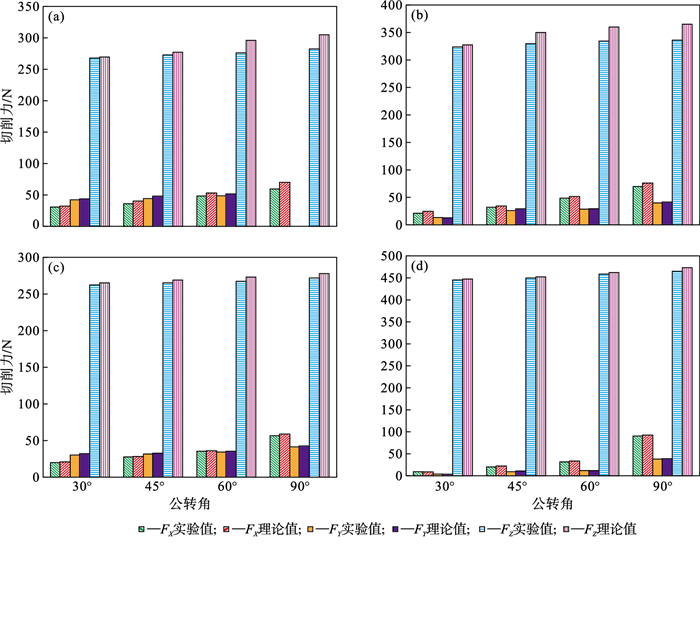 | 图 10 不同切削参数时切削力实验值与理论值的对比Fig.10 Comparison between experimental and theoretical cutting forces with different cutting parameters (a) —4 000 r·min-1, 0.02 mm·齿-1, 0.10 mm·r-1; (b) —4 000 r·min-1, 0.04 mm·齿-1, 0.15 mm·r-1; (c) —5 000 r·min-1, 0.02 mm·齿-1, 0.10 mm·r-1; (d) —5 000 r·min-1, 0.06 mm·齿-1, 0.20 mm·r-1. |
表 2(Table 2)
| 表 2 公转角为30°和45°切削力误差分析 Table 2 Error analysis of cutting forces when orbital revolution angles are 30° and 45° |
表 3(Table 3)
| 表 3 公转角为60°和90°切削力误差分析 Table 3 Error analysis of cutting forces when orbital revolution angles are 60° and 90° |
由图 10可知, 不同公转角度时切削力大小明显不同, 在30°~90°范围内, 三向切削力随公转角度的增大而不断增大, 且轴向切削力远大于其他两向切削力.出现这种现象的原因是切削过程中, X轴和Y轴方向上所有切削力都由侧刃提供.螺旋角的存在会使侧刃产生沿Z轴的分力, 而底刃只提供沿Z轴方向的切削力.此外, 工件在刀具轴向进给作用下产生的变形会导致较大轴向力的产生.
从上述数据及图表可以看出, 在不同切削参数条件下, 切削力理论值与实验值存在一定偏差, 但理论值能够较好地捕捉切削力在刀具公转一周0°~90°范围内的变化情况, 总体误差不超过16%, 通过多组实验数据验证了模型的正确性.分析造成误差的主要原因如下:在建立模型的过程中, 对CFRP的失效模式进行了简化, 实际切削要比理论模型中建立的切削问题更加复杂, 忽略其他的失效模式会对模型准确性造成一定影响;实际实验时由于操作问题造成一定偏差.
5 结论1) 考虑纤维方向角在不同范围内的变形方式, 分析了纤维基体脱黏区域、回弹区域以及切屑滑移区域这三种损伤区域对CFRP细观单元体直角切削力的影响.
2) 结合螺旋铣孔工作原理, 考虑侧刃和底刃的影响, 研究了不同纤维方向角下螺旋铣孔切削力的变化情况, 建立了CFRP螺旋铣孔切削力模型.
3) 开展了CFRP螺旋铣孔实验, 考虑了切削力的周期波动, 分析0°~90°公转角度下切削力的变化情况.结果显示, 切削力的变化与刀具的切削位置直接相关, 切削力理论值与实验值的总体误差不超过16%, 验证了模型的正确性.
参考文献
| [1] | 陈燕, 葛恩德, 傅玉灿, 等. 碳纤维增强树脂基复合材料制孔技术研究现状与展望[J]. 复合材料学报, 2015, 32(2): 301-316. (Chen Yan, Ge En-de, Fu Yu-can, et al. Review and prospect of drilling technologies for carbon fiber reinforced polymer[J]. Acta Materiae Compositae Sinica, 2015, 32(2): 301-316.) |
| [2] | Liu H T, Lin J, Sun Y Z, et al. Micro model of carbon fiber/cyanate ester composites and analysis of machining damage mechanism[J]. Chinese Journal of Mechanical Engineering, 2019, 32(1): 1-11. DOI:10.1186/s10033-018-0313-7 |
| [3] | Xu W X, Zhang L C. Mechanics of fibre deformation and fracture in vibration-assisted cutting of unidirectional fibre-reinforced polymer composites[J]. International Journal of Machine Tools & Manufacture, 2016, 103: 40-52. |
| [4] | Albert G, Laheurte R, Knevez J Y, et al. Experimental milling moment model in orthogonal cutting condition: to an accurate energy balance[J]. International Journal of Advanced Manufacturing Technology, 2011, 55(9/10/11/12): 843-854. |
| [5] | 张厚江. 单向碳纤维复合材料直角自由切削力的研究[J]. 航空学报, 2005(5): 604-609. (Zhang Hou-jiang. Study on cutting forces of unidirectional carbon fiber reinforced plastics under orthogonal cutting[J]. Acta Aeronautica et Astronautica Sinica, 2005(5): 604-609.) |
| [6] | Zhang L C, Zhang H J, Wang X M. A force prediction model for cutting unidirectional fiber-reinforced plastics[J]. Machining Science and Technology, 2001, 5(3): 293-305. DOI:10.1081/MST-100108616 |
| [7] | Jahromi A S, Bahr B. An analytical method for predicting cutting forces in orthogonal machining of unidirectional composites[J]. Composites Science & Technology, 2010, 70(16): 2290-2297. |
| [8] | Brinksmeier E, Fangmann S, Rentsch R. Drilling of composites and resulting surface integrity[J]. CIRP Annals-Manufacturing Technology, 2011, 60(1): 57-60. DOI:10.1016/j.cirp.2011.03.077 |
| [9] | Wang H Y, Qin X D, Li H, et al. Analysis of cutting forces in helical milling of carbon fiber-reinforced plastics[J]. Proceedings of the Institution of Mechanical Engineers.Part B: Journal of Engineering Manufacture, 2012, 227(1): 62-74. |
| [10] | Li Z Q, Liu Q, Ming X Z, et al. Cutting force prediction and analytical solution of regenerative chatter stability for helical milling operation[J]. International Journal of Advanced Manufacturing Technology, 2014, 73(1/2/3/4): 433-442. |
| [11] | 万敏, 杜宇轩, 张卫红, 等. 单向CFRP螺旋铣削力建模[J]. 航空学报, 2021, 42(10): 277-291. (Wan Min, Du Yu-xuan, Zhang Wei-hong, et al. Cutting force modeling in helical milling process of unidirectional CFRP[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(10): 277-291.) |
| [12] | 齐振超, 李丰辰, 王二化. 基于热力耦合仿真的CFRP直角切削机理研究[J]. 工具技术, 2019, 53(10): 36-41. (Qi Zhen-chao, Li Feng-chen, Wang Er-hua. Research on orthogonal cutting mechanism of CFRP based on thermos-mechanical couple simulation[J]. Tool Engineering, 2019, 53(10): 36-41.) |
| [13] | Zhang S, Jiao F, Wang X, et al. Modeling of cutting forces in helical milling of unidirectional CFRP considering carbon fiber fracture[J]. Journal of Manufacturing Processes, 2021, 68: 1495-1508. |
| [14] | Wang D, Jiao F, Mao X S. Mechanics of thrust force on chisel edge in carbon fiber reinforced polymer (CFRP) drilling based on bending failure theory[J]. International Journal of Mechanical Sciences, 2020, 169: 105336. |