
 , 习振华2, 刘坤1
, 习振华2, 刘坤1 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 兰州空间技术物理研究所 真空技术与物理重点实验室, 甘肃 兰州 730000
收稿日期:2022-07-21
基金项目:国家自然科学基金资助项目(62071209)。
作者简介:范栋(1992-), 男, 甘肃武威人, 东北大学博士研究生;
李得天(1966-), 男, 甘肃白银人, 兰州空间技术物理研究所研究员, 博士生导师, 中国工程院院士;
刘坤(1979-), 男, 湖北随州人, 东北大学教授, 博士生导师。
摘要:基于从头计算理论, 对氩气摩尔极化率、摩尔磁化率和维里系数等物理参数进行计算, 结合维里状态方程和Lorentz-Lorenz方程建立了气体压力关于折射率的理论参数模型.利用基于Fabry-Perot腔的光学真空测量装置, 通过精确测量Fabry-Perot腔内激光的谐振频率变化, 获得气体折射率和气体压力, 在105 Pa时, 折射率相对测量不确定度为1.8×10-11, 气体压力相对不确定度为4.4×10-6.对比分析基于Fabry-Perot腔的光学真空测量装置与电容薄膜真空计获得的测量压力, 结果表明基于Fabry-Perot腔的光学真空测量方法具有较高的稳定性和准确性.
关键词:真空测量量子化Fabry-Perot腔气体折射率不确定度
Research on Optical Vacuum Measurement Technology Based on Fabry-Perot Cavity
FAN Dong1,2, LI De-tian1

 , XI Zhen-hua2, LIU Kun1
, XI Zhen-hua2, LIU Kun1 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Science and Technology on Vacuum Technology and Physics Laboratory, Lanzhou Institute of Physics, Lanzhou 730000, China
Corresponding author: LI De-tian, E-mail: lidetian@sina.com.
Abstract: Based on the ab initio theory, the physical parameters such as molar polarization, molar susceptibility and Virial coefficient of argon gas were calculated, and the theoretical parameter model of gas pressure about refractive index was established by combining the Virial equation of state and Lorentz-Lorenz equation. The optical vacuum measuring device based on the Fabry-Perot cavity was used to accurately measure the resonant frequency change of the laser in the Fabry-Perot cavity to obtain the gas refractive index and gas pressure. At 105 Pa, the relative uncertainty of the refractive index is 1.8×10-11, and the relative uncertainty of the gas pressure is 4.4×10-6. The measured pressures obtained by the optical vacuum measuring device based on the Fabry-Perot cavity and the capacitance film vacuum gauge were compared and analyzed. The results showed that the Fabry-Perot cavity based optical vacuum measuring method has higher stability and accuracy.
Key words: vacuum measurementquantizationFabry-Perot cavitygas refractive indexuncertainty
在空间探测、工业生产、大气环境等领域, 真空测量技术已经成为一种不可或缺的技术, 为真空系统提供了大量的有效信息.真空计量的发展在着力解决原位及特殊环境下真空测量准确性问题的同时, 也对现有真空计量标准的测量范围和精度提出了更高要求[1].真空计量溯源及量传体系仍采用水银压力计(或活塞压力计)作为基/标准, 美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)建立的超声干涉水银压力计为世界最好水平[2], 但其含有水银, 不具便携性(重250 kg,高3 m), 正逐渐被世界各国弃用.虽然部分数字式活塞压力计已在应用中逐步取代了水银压力计, 但其仍需通过水银压力计进行溯源.众多****提出气体密度更适宜表征低于环境大气压的稀薄气体状态[3-4].采用Fabry-Perot腔(简称F-P腔)测量气体折射率, 结合Lorentz-Lorenz方程可获得气体密度, 利用维里状态方程可获得气体压力.
近年来, 国内外计量机构对基于F-P腔光学干涉测量折射率反演真空度的真空测量方法开展了深入研究.2014年, NIST提出利用固定长度光学腔(fixed length optical cavity, FLOC)及更高精度的可变长度光学腔(variable length optical cavity, VLOC)来实现腔内气体折射率的精确测量, 进而获得气体密度及真空度[5], 其灵敏度为1 mPa/kHz, 分辨力为10 mPa[6].2019年, 日本国家先进工业与技术研究所(National Institute of Advanced Industrial and Technology, AIST)利用基于腔外自准式宽调谐范围二极管激光器的F-P腔真空测量系统[7], 实现了从真空到高压范围的连续压力测量, 其重复性及非线性误差的标准方差分别为0.1, 0.5 Pa.2020年, 瑞典于默奥大学(Ume? University) 提出了一种基于因瓦合金材料的F-P腔的折射计[8], 该测量系统可提供小于1×10-7的测量精度.2020年, 法国国家计量和测试实验室(Laboratoire national de métrologie et d’essais, LNE)研建了一台基于F-P光学干涉腔的氦气绝对折射计[9], 该系统的压力测量短期稳定性为±2 mPa, 压力分辨率优于1 mPa.国内此类研究仍处于起步阶段[10-12].在该类研究中, 谐振腔腔体变形, 腔体材料对气体的吸附、渗透和脱附及温度不稳定等影响因素限制了气体折射率测量精度的提高[4].
2019年5月20日, 国际单位制(Système International d’Unités, SI)被重新修订, 消除了玻尔兹曼常数、阿伏伽德罗常数的不确定度[13], 故基于F-P腔的真空测量不确定度分量除直接测量物理量外, 仅受气体摩尔极化率、抗磁磁化率、维里系数等物理参数计算不确定度的限制.近年来, 通过对氩气压力的测量可得其极化率、磁化率和维里系数等气体参数.1985年, 加拿大西安大略大学(University of Western Ontario)构建偶极子微分振子强度分布(dipole oscillator strength distributions, DOSD)计算了氩气摩尔极化率的偶极子和[14].1992年, 加拿大新不伦瑞克大学(University of New Brunswick)利用从头计算(ab initio)法计算了氩气摩尔极化率的偶极子和, 其相对标准不确定度为2×10-6[15].2018年, 德国联邦物理技术研究院(Physikalisch-Technische Bundesanstalt, PTB)利用介电常数气体测温法(dielectric-constant gas thermometry, DCGT)测定了氩气的静态摩尔极化率, 其相对标准不确定度为2×10-6[16], 并用相同的方法测量了氩气的维里系数[17].随从头计算理论的迅速发展, 非极性气体分子关于电磁学和热力学性质的相关物理参数计算精度不断提高, 使建立基于光学方法的真空标准成为可能[11].
对基于F-P腔的光学真空测量方法开展研究, 基于从头计算理论计算氩气的摩尔极化率、摩尔磁化率、第二维里系数和第二介电维里系数等物理参数, 对气体压力不确定度进行分析.对比基于F-P腔的光学真空测量装置与电容薄膜真空计的测量结果, 分析影响相对偏差的主要因素.
1 气体压力理论计算光以电磁波的形式传播, 当一束单色光穿过气体介质时, 电磁波与气体分子相互作用, 电磁波波长会随气体折射率的变化而变化, 利用F-P腔可实现电磁波波长的测量.F-P腔是由两个高反射镜构成的光学腔, 当腔内往返光程长度等于波长整数倍时, 单色光会与腔体发生谐振.当F-P腔内充入气体导致折射率改变量为n-1时, 忽略腔体衍射相移和镜面反射相移, 光腔的纵模频率为
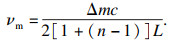 | (1) |
当对腔内抽气或充气时, 通过对式(1)求差后按折射率展开, 忽略折射率高阶项, 并考虑充气过程中激光纵模模数的变化, 可得到气体折射率关于频率的表达式为
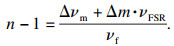 | (2) |
在充气过程中, 由于气体压力的影响, 腔体长度从真空状态下的长度L0变为充气状态下的长度Lf, 可知
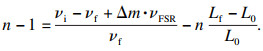 | (3) |
第二项长度变化因子可由气体压力改变量Δp近似表示为
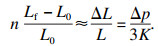 | (4) |
通过Lorentz-Lorenz方程, 结合气体折射率的测量值, 可得到气体摩尔密度:
 | (5) |
在稀薄气体状态下, 气体分子间存在范德瓦尔斯力, 导致气体显著偏离了理想状态, 利用第二维里系数可对该偏离行为进行修正.真实气体的维里状态方程为
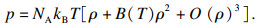 | (6) |
通过式(5)和式(6), 可建立10~105 Pa范围内的气体压力与折射率的理论参数模型, 如式(7)所示:
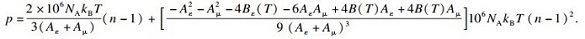 | (7) |
原子极化率包括静态极化率和动态极化率, 频率ω的函数展开为
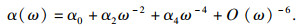 | (8) |
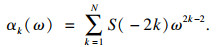 | (9) |
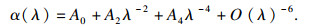 | (10) |
实验中, 所用激光波长λ=780 nm, 将其代入式(10)可以计算得到氩原子的极化率为α (780 nm)=1.604 417 472 9×10-24 cm3.
对于原子磁化率χ, 忽略其动态色散修正部分, 则静态磁化率为χ=-3.140 626 770 86×10-30 cm3.
由于采用气体的摩尔密度, 所以将原子极化率α和原子磁化率χ为摩尔极化率Aε和摩尔磁化率Aμ:
Aε=4πNAα/3=4.173 261 370 1 cm3/mol,
Aμ=4πNAχ/3=-0.000 019 5 cm3/mol[2].
除了摩尔极化率和摩尔磁化率, 气体压力的反演准确度在一定程度上还取决于维里系数(温度的函数).Vogel等利用从头计算理论对氩原子维里系数进行了精确计算[19], 根据该计算结果可得氩原子第二维里系数B(T)的表达式为
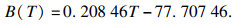 | (11) |
波长为780 nm时, 氩原子的第二介电维里系数Bε(T)可表示为
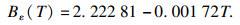 | (12) |
2 实验装置与方法实验装置如图 1所示, F-P腔腔体材料为超低膨胀(ultralow expansion, ULE)玻璃, 反射镜材料为熔融石英玻璃, 腔体和腔镜间采用无胶光学键和技术.采用ULE材料的首要原因是与其他低热膨胀材料相比, 其几何尺寸长期稳定性最理想, 但ULE腔体最显著的缺点是对氦气的吸附、渗透和脱附[11].反射镜基片双面镀膜, 工作面镀增反膜以保证腔镜基片的超高反射率, 在腔中心到腔外缘有一段凹槽以保证腔内气体与周围环境保持平衡.采用双腔结构, 参考腔长1 cm, 用于保持真空, 作为频率基准, 检测腔长10 cm, 用于充气, 改变腔内气体折射率.腔体采用双层控温, 温度由温度控制器设置, 控温后温度波动小于1 mK.采用中心波长为780 nm的外腔式半导体激光器(external-cavity diode laser, ECDL)作为探测光源, 激光通过90/10分束光纤分为两束, 一束用于拍频, 另一束用于探测.探测光透过透镜组进行模式匹配后进入电光调制器(electro-optic modulator, EOM)以产生边带用于频率锁定.探测光经过偏振分束镜(polarizing beam splitter, PBS)分为两束:一束进入腔内部分透射后被光电探测器探测;另一束被光电放大探测器探测, 两束光探测信号混频后产生误差信号.利用PDH(Pound-Drever-Hall)锁频装置分别对EOM和激光器进行调节, 即可实现频率锁定.利用机械泵对检测腔抽气, 并用电容薄膜真空计测量腔内气体压力.利用机械泵、分子泵和离子泵对参考腔抽气并维持高真空状态, 采用电离真空计测量腔内气体压力.
图 1(Fig. 1)
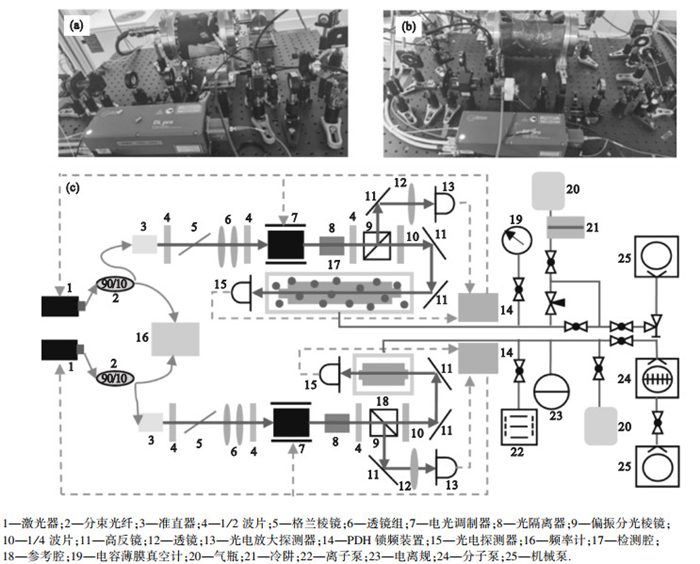 | 图 1 基于F-P腔的光学真空测量装置图Fig.1 Optical vacuum measuring device diagram based on F-P cavity (a)—参考光路实物图;(b)—检测光路实物图;(c)—测量装置示意图. |
在进行气体折射率测量时, 利用PDH锁频装置将激光频率锁定在双腔纵模, 并通过精密控温装置将腔内温度稳定在ULE材料的零膨胀点299.148 5 K.将双腔抽真空, 参考腔真空度维持在10-5 Pa, 利用波长计测量检测腔初始谐振频率, 利用频率计测量双腔初始拍频.给检测腔缓慢充入氩气, 在此过程中, 由于腔内气体折射率发生变化, 导致腔体谐振频率改变, 从而引起频率失锁.重新锁定后, 利用波长计测量检测腔最终谐振频率, 利用频率计测量双腔最终拍频, 将测量频率值代入式(13), 即可得到各压力点的折射率:
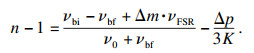 | (13) |
将Aε, Aμ, Bε(T), B(T)代入式(7), 可以获得气体压力的表达式:
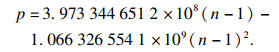 | (14) |
3 分析与讨论3.1 不确定度分析对基于F-P腔的光学真空测量装置的气体压力相对测量不确定度进行分析, 该不确定度来自于折射率测量不确定度和计算所用参数的测量不确定度.根据折射率测量结果, 利用式(13)分析折射率相对测量不确定度, 其中第二项-Δp/3K不确定度为10-15量级, 对折射率测量影响较小, 故忽略其对折射率测量不确定度的贡献, 则式(13)为
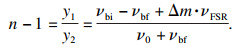 | (15) |
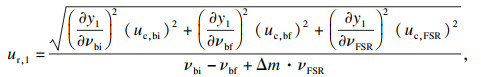 | (16) |
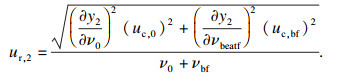 | (17) |
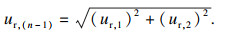 | (18) |
由式(7)对折射率至气体压力的计算不确定度进行分析.p=100 191 Pa时, 折射率二次项比一次项小5个数量级, 摩尔磁化率比摩尔极化率小5个数量级, 因此折射率二次项和摩尔磁化率对气体压力不确定度的贡献较小, 可以忽略不计.温度测量标准不确定度uc, T=5.0×10-4, 氩原子摩尔极化率标准不确定度uc, Aε=1.62×10-5, 重新修订的SI中, 取消了kB, NA的不确定度[20].式(7)中折射率一次项系数为
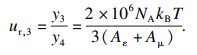 | (19) |
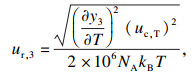 | (20) |
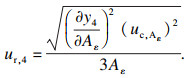 | (21) |
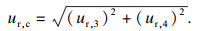 | (22) |
气体压力的相对不确定度为
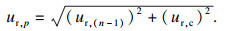 | (23) |
3.2 对比测试基于F-P腔的光学真空测量装置的测量压力pFP与电容薄膜真空计的测量压力pCDG进行对比分析, 将其相对偏差绘制成压力的函数, 如图 2所示.在103~104 Pa范围内, pFP与pCDG的相对偏差随压力的变化情况为pCDG大于pFP, 并随气体压力的增加, 其相对偏差从0.771%减小到0.398%, 并且在105 Pa量级内保持相对稳定.
图 2(Fig. 2)
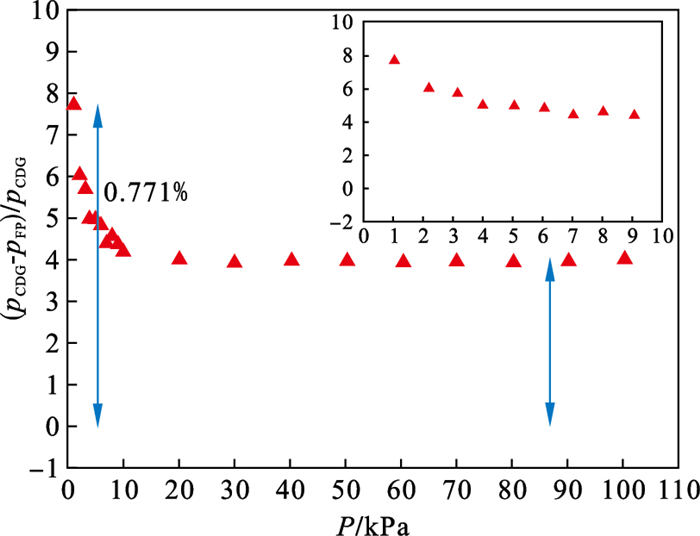 | 图 2 基于F-P腔的光学真空测量装置的测量压力(pFP)与电容薄膜真空计的测量压力(pCDG)对比结果.Fig.2 The measured pressure (pFP) of an optical vacuum measuring device based on an F-P cavity is compared with the measured pressure (pCDG) of a capacitive film vacuum gauge. |
存在偏差的主要原因为
1) pFP与pCDG之间数据不同步, 即基于F-P腔的光学真空测量装置的频率采集(频率计)相比电容薄膜真空计的数据采集时间延后大约0.4 s.
2) 基于F-P腔的光学真空测量装置与电容薄膜真空计的工作温度不同(工作温度分别为299.148 5, 296.15 K), 因此存在一个非线性压力修正, 在100 Pa时约为9 mPa.
3) pCDG受电容薄膜真空计测量精度的限制, 电容薄膜真空计的测量精度为0.025%.
4) pFP准确度受理论参数和仪器性能的限制, 具体不确定度分量来自于以下几项:
① 理论参数:采用从头计算法得出的摩尔极化率、摩尔磁化率、第二介电维里系数和第二维里系数的相对不确定度分别为4×10-6, 5×10-8, 3×10-7, 1×10-5, 其中摩尔极化率对pFP不确定度的贡献最大, 第二介电维里系数和第二维里系数的相对不确定度随温度升高而增大[2].
② 温度测量:实验中采用双层控温, 腔内温度仍然存在mK量级的波动, 1 mK的温度波动会引起0.6 mPa的压力漂移效应.同时由于腔内温度场分布不均匀, 测量温度与腔体中心实际温度存在10-4量级的相对偏差, 因此引入压力测量的不确定性.
③ 腔体稳定性:由于气体压力、振动、温度不稳定等引起的腔体形变, 约导致1.1 mPa的压力漂移[20].
④ 频率测量:检测腔中谐振频率在1 kHz范围内波动, 导致1×10-8的压力测量偏差.参考腔中谐振频率在300 kHz范围内波动, 导致3×10-6的压力测量偏差.
⑤ 系统漏气率:系统漏气导致0.1 Hz/s的频率变化, 此频率漂移会导致1×10-7 Pa/s的压力漂移.
⑥ 氩气纯度:实验中所用氩气含有0.001%的杂质, 由于材料放气腔内杂质含量逐渐增加, 导致高于5×10-6的压力偏差.
4 结论1) 利用F-P腔的光学真空测量装置测量了氩气折射率, 在105 Pa的气压下, 评定其相对测量不确定度为1.8×10-11.
2) 利用从头计算理论对氩气摩尔极化率、摩尔磁化率和维里系数等微观参量进行计算, 并依托气体维里状态方程和Lorentz-Lorenz方程建立了气体压力与折射率之间的理论关系, 评定氩气压力相对测量不确定度为4.4×10-6.
3) 对基于F-P腔的光学真空测量装置的测量压力与电容薄膜真空计的测量压力进行对比, 并对二者偏差原因进行分析.对比后发现其相对偏差从0.771%减小到0.398%, 并保持相对稳定, 结果表明在105 Pa量级内, 基于F-P腔的光学真空测量方法具有较高的稳定性和准确性.
参考文献
| [1] | Li D T, Wang Y J, Zhang H Z, et al. Applications of vacuum measurement technology in China's space programs[J]. Space: Science & Technology, 2021, 2021(7592858): 1-14. |
| [2] | 许玉蓉, 刘洋洋, 王进, 等. 基于气体折射率方法的真空计量[J]. 物理学报, 2020, 69(15): 150601. (Xu Yu-rong, Liu Yang-yang, Wang Jin, et al. Vacuum metrology based on refractive index of gas[J]. Acta Physica Sinica, 2020, 69(15): 150601.) |
| [3] | Jousten K, Hendricks J, Barker D, et al. Perspectives for a new realization of the pascal by optical methods[J]. Metrologia, 2017, 54(6): S146-S161. DOI:10.1088/1681-7575/aa8a4d |
| [4] | Forssen C, Silander I, Zakrisson J, et al. Anoptical pascal in Sweden[J]. Journal of Optics, 2022, 24(3): 1-15. |
| [5] | Ricker J, Hendricks J, Egan P, et al. Towards photonic based pascal realization as a primary pressure standard[C]// XXⅡ World Congress of the International Measurement Confederation. Belfast: IEEE, 2018: 316-323. |
| [6] | 李得天, 成永军, 习振华. 量子真空标准研究进展[J]. 宇航计测技术, 2018, 38(3): 131-139. (Li De-tian, Cheng Yong-jun, Xi Zhen-hua. Development of quantum vacuum standard[J]. Journal of Astronautic Metrology and Measurement, 2018, 38(3): 131-139.) |
| [7] | TaKei Y, Arai K, Yoshida H, et al. Development of an optical pressure measurement system using an external cavity diode laser with a wide tunable frequency range[J]. Measurement, 2020, 151: 107090. DOI:10.1016/j.measurement.2019.107090 |
| [8] | Silander I, Forssen C, Zakrisson J, et al. Aninvar-based Fabry-Perot cavity refractometer with a gallium fixed-point cell for assessment of pressure[J]. Acta IMEKO, 2020, 9(5): 293-298. DOI:10.21014/acta_imeko.v9i5.987 |
| [9] | Silvestri Z, Bentouati D, Otal P, et al. Towards an improved helium-based refractometer for pressure measurements[J]. Acta IMEKO, 2020, 9(5): 305-309. DOI:10.21014/acta_imeko.v9i5.989 |
| [10] | 贾文杰, 习振华, 范栋, 等. 基于Fabry-Perot激光谐振腔的量子真空计量技术研究[J]. 光学学报, 2020, 40(22): 2212005. (Jia Wen-jie, Xi Zhen-hua, Fan Dong, et al. Quantum vacuum measurement based on Fabry-Perot laser resonant cavity[J]. Acta Optica Sinica, 2020, 40(22): 2212005.) |
| [11] | 范栋, 习振华, 贾文杰, 等. 量子真空计量标准中的非极性稀薄气体折射率测量研究[J]. 物理学报, 2021, 70(4): 040602. (Fan Dong, Xi Zhen-hua, Jia Wen-jie, et al. Refractive index measurement of nonpolar rarefied gas in quantum vacuum metrology standard[J]. Acta Physica Sinica, 2021, 70(4): 040602.) |
| [12] | 范栋, 李得天, 习振华, 等. 量子真空计量中的气体折射率测量方法研究[J]. 中国激光, 2021, 48(23): 2304002. (Fan Dong, Li De-tian, Xi Zhen-hua, et al. Research on measurement method of gas refractive index in quantum vacuum metrology[J]. Chinese Journal of Lasers, 2021, 48(23): 2304002.) |
| [13] | Mohr P J, Newell D B, Taylor B N, et al. Data and analysis for the CODATA 2017 special fundamental constants adjustment[J]. Metrologia, 2018, 55(1): 125-146. |
| [14] | Kumar A, Meath W J. Integrated dipole oscillator strengths and dipole properties for Ne, Ar, Kr, Xe, HF, HCl, and HBr[J]. Canadian Journal of Chemistry, 1985, 63(7): 1616-1630. |
| [15] | Thakkar A J, Hettema H, Wormer P E S. Ab initio dispersion coefficients for interactions involving rare-gas atoms[J]. The Journal of Chemical Physics, 1992, 97(5): 3252-3257. |
| [16] | Gaiser C, Fellmuth B. Polarizability of helium, neon, and argon: new perspectives for gas metrology[J]. Physical Review Letters, 2018, 120(12): 123203. |
| [17] | Gaiser C, Fellmuth B. Highly-accurate density-virial-coefficient values for helium, neon, and argon at 0.01 ℃ determined by dielectric-constant gas thermometry[J]. The Journal of Chemical Physics, 2019, 150(13): 134303. |
| [18] | Puchalski M, Piszczatowski K, Komasa J, et al. Theoretical determination of the polarizability dispersion and the refractive index of helium[J]. Physical Review A, 2016, 93(3): 032515. |
| [19] | Vogel E, Jager B, Hellmann R, et al. Ab initio pair potential energy curve for the argon atom pair and thermophysical properties for the dilute argon gas.Ⅱ.thermophysical properties for low-density argon[J]. Molecular Physics, 2010, 108(24): 3335-3352. |
| [20] | Egan P F, Stone J A, Ricker J E, et al. Comparison measurements of low-pressure between a laser refractometer and ultrasonic manometer[J]. Review of Scientific Instruments, 2016, 87(5): 053113. |
