余俊, 张志中, 邓鹏兵, 和振
中南大学 土木工程学院, 湖南 长沙 410075
收稿日期：2022-04-11
基金项目：国家自然科学基金资助项目(52078496)。
作者简介：余俊(1978-), 男, 湖北新洲人, 中南大学副教授。

摘要：对地下水位周期性波动条件下的各向同性土层中基坑二维渗流场孔压响应进行了解析研究.将基坑周围土体划分为4个规则区域, 应用叠加原理和分离变量法得到各区域内孔压响应的级数解形式表达式, 结合各区域间连续条件求解基坑周围渗流场孔压的显式解析解.将解析解结果、数值结果及半解析解结果进行对比, 验证了该解析解方法的正确性.基于该解分析了基坑内、外侧水位等工程参数对孔压响应分布和相位滞后的影响, 结果表明基坑工程参数对孔压响应和相位滞后有较大影响, 对远场孔压响应和基坑内部相位滞后的影响更加明显.
关键词：分离变量法基坑渗流场解析解孔压响应相位滞后
Analytical Solution of Pore Pressure in Foundation Pit Seepage Field Under Groundwater Level Fluctuation
YU Jun, ZHANG Zhi-zhong, DENG Peng-bing, HE Zhen
School of Civil Engineering, Central South University, Changsha 410075, China
Corresponding author: YU Jun, E-mail: jjyy1017@163.com.

Abstract: The pore pressure response of a two-dimensional seepage field in an isotropic soil layer under the condition of periodic fluctuation of groundwater level is studied analytically. The soil around the pit is divided into four regular regions, and the expressions of the series solution form of the pore pressure response in each region are obtained by applying the superposition principle and the method of separation of variables, and the explicit analytical solution of the pore pressure of the seepage field around the pit is solved by combining the continuous conditions between the regions. The results of the analytical solution are compared with the results of numerical software and semi-analytical solutions to verify the correctness of the analytical solution method in this paper. Based on this solution, the influence of the variation of engineering parameters such as water level inside and outside the pit on the pore pressure response distribution and phase lag is analyzed. The results show that the pore pressure response and phase lag are influenced by the engineering parameters of the pit, and the influence on the far-field pore pressure response and the phase lag inside the pit is more obvious.
Key words: separation of variable methodfoundation pit seepage fieldanalytical solutionpore pressure responsephase lag
随着我国经济社会的快速发展, 广大临海临湖地区正在大量建设地下建筑及交通设施, 这些项目的基坑建设所面临的建设环境更加复杂.临海临湖地区的基坑工程与非沿海地区的基坑工程不同, 基坑周围的水文地质条件复杂, 受波浪、潮汐等周期性水位波动影响较大.
目前国内外对基坑渗流场的研究大多集中在基坑外侧水位恒定条件下的渗流场求解和基坑外侧水位波动条件下的半解析解.基坑渗流场孔压响应的求解方法主要包括试验方法^[1]、数值方法^[2-3]和解析方法.其中, 解析解及半解析解的求解方法主要有一维简化解法^[4]、保角变换方法^[5]、二维图解法^[6]、Fourier变换解法^[7-8]等.Javed等^[9]分析双层土条件下垂直于垫层平面的水流引起的渗透特性, 对比不同渗透性土层排列方式对渗透性的影响.Fontana^[10]评估了不同砂土厚度和板桩形式下水体渗流特性和水工结构的安全性.Bereslavski^[11]基于保角变换方法给出了Zhukovskii板桩墙下二维稳态渗流场的解析解.Lyu等^[12]分析了承压含水层中防水幕布对稳态渗流的阻挡机理, 采用解析方法求解设置防水幕布条件下承压含水层中基坑开挖时的地下水头分布.黄大中等^[8]将基坑周围土体划分为两个规则区域, 利用Fourier变换推导出各向异性土层中基坑二维渗流场的半解析解.应宏伟等^[13]采用Laplace, Fourier变换及其逆变换推导出基坑周围含水层内地下水位波动条件下地基土内部孔压响应分布的半解析解, 并分析了水位波动对基坑挡墙稳定性、孔压分布和相位滞后的影响.本文采用分离变量法求解渗流连续方程得到孔压响应的显式解, 而现有解析解多利用保角变换方法或积分变换方法求得, 保角变换方法在计算区域边界角点处存在不连续的奇异点, 采用积分变换法得到的解多是隐式解.
将基坑周围渗流场划分为4个规则区域, 对复杂边界条件进行简化, 使划分后的规则区域能够应用叠加原理和分离变量法将各区域内的孔压响应分布使用级数形式进行表达, 结合各区域边界条件和各区域之间连续条件可求解级数解的系数矩阵, 从而得到水位波动条件下各向同性土层中基坑二维渗流场孔压分布的显式解析解.解析解方法能够得到级数形式的显式精确解, 求解结果在计算区域内无奇异点.为验证该解析解方法的正确性, 将解析解结果与数值软件PLAXIS计算结果、半解析解计算结果进行对比.进一步分析了基坑内外侧水位、基坑开挖宽度、挡墙底部距不透水边界距离的变化对孔压响应幅值分布及相位滞后的影响.解析解方法为求解临海地区基坑的渗流场分布和未来进行水位波动条件下的基坑渗流数值模拟提供了一定的理论支持.
1 计算模型与基本假定1.1 计算模型以基坑挡墙所在竖直方向为Z轴, 挡墙底部水平方向为X轴, 选取基坑周围一定区域内土体建立基坑渗流场计算模型, 如图 1所示.记基坑宽度的一半为c, 挡墙外侧至计算边界处距离为b, 挡墙底部至不透水边界距离为a, 基坑外侧水位为h₁, 基坑内侧水位为h₂.
图 1(Fig. 1)

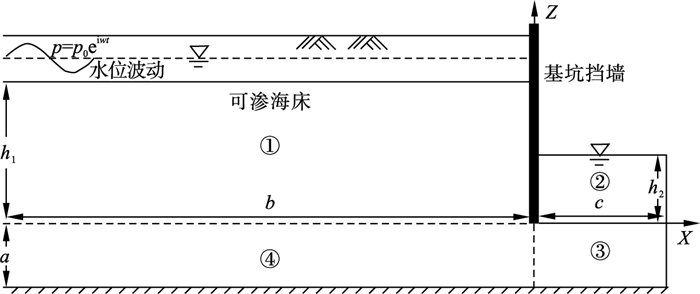图 1 基坑渗流分析模型示意图Fig.1 Schematic of seepage analysis model of waterfront pit

1.2 基本假定基坑纵向尺寸远大于横向尺寸时可视为平面渗流, 采用临海基坑的边界条件, 建立基坑横向截面的二维平面渗流模型.基坑截面为轴对称截面, 故只取对称轴左侧土体进行分析.基坑外侧土体为无穷远, 可近似取为不透水边界, 基坑内侧为对称形式也可视为不透水边界.
基坑工程位于沿江或沿海地区时, 基坑边界的水位波动主要由潮汐等水体波动引起, 因此在基坑周围海床土体渗透性较大时可认为基坑周围水位波动形式与潮汐波动形式相同, 均为简谐变化, 水位波动幅值、周期等也与潮汐变化相同可视为简谐变化^[14].
基本假定为：渗流场内土体土质均匀, 且为各向同性；地下水渗流符合达西定律；计算边界处可视为不透水边界.基坑内侧水位恒定, 基坑外侧水位变化处孔压视为简谐形式波动, 其波动形式为

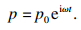(1)

式中：p为边界孔压；p₀为孔压波动幅值；t为波动时间；ω为波动频率.
2 渗流方程与求解2.1 方程建立与边界条件遵循以上假定前提下, 将基坑左侧土体划分为图 1所示的计算区域①、区域②、区域③、区域④, 各区域的渗流情况满足如下连续性方程：

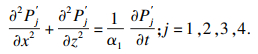(2)

式中：P_j^′为各区域内的孔压响应分布；α₁为饱和状态下土体的固结系数.
基坑周围土体孔压响应式为

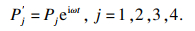(3)

渗流平衡方程为

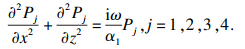(4)

为使叙述简洁，在后述过程中将孔压响应的简谐变化项e^iωt略去，求解P_j后代入式(3)即可得到各区域内的孔压响应P_j^′.
根据图 1划分的基坑计算区域及基坑边界条件, 分别给出各计算区域边界条件及各区域之间连续条件：
区域①边界条件为：上边界(z=h₁)：P₁=p₀；右边界(x=0)：?P₁/?x=0；左边界(x=-b)：?P₁/?x=0.
区域②边界条件为：上边界(z=h₂)：P₂=0；左边界(x=0)：?P₂/?x=0；右边界(x=c)：?P₂/?x=0.
区域③边界条件为：下边界(z=－a)：?P₃/?z=0；右边界(x=c)：?P₃/?x=0.
区域④边界条件为：下边界(z=－a)：?P₄/?z=0；左边界(x=－b)：?P₄/?x=0.
区域①与区域④之间连续条件为

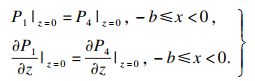(5)

区域②与区域③之间连续条件为

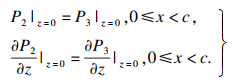(6)

区域③与区域④之间连续条件为

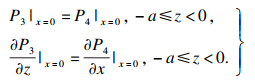(7)

2.2 方程求解应用叠加原理将区域①的边界条件改写为如下形式：

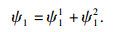(8)

式中：ψ₁¹为上边界孔压，P₁=p₀；下边界孔压P₁=0，左右两侧为不透水边界?P₁/?x=0；ψ₁²为上边界孔压，P₁=0，左右两侧为不透水边界?P₁/?x=0.
ψ₁¹所表示的边界条件可以应用分离变量法求出孔压分布解：

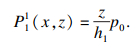(9)

ψ₁²所表示的边界条件可以应用分离变量法求出孔压分布的级数形式解：

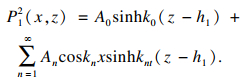(10)

式中：A₀，A_n为待求参数；；k_n=nπ/b, n=1, 2, 3, …, .
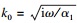
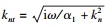
区域①中孔压的级数形式解可由式(9)与式(10)叠加得到：

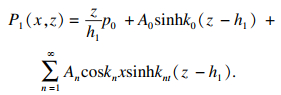(11)

区域②的边界条件与区域①的边界条件类似, 可利用叠加原理和分离变量法求出区域②内的孔压级数形式解：

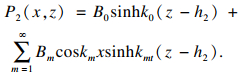(12)

式中：B₀, B_m为待求参数；; k_m=mπ/c, m=1, 2, 3, ….
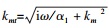
区域③的边界条件的可叠加原理为

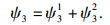(13)

式中：ψ₃¹为上边界孔压, P₃=0；下边界为不透水边界，?P₃/?z=0；右边界为不透水边界，?P₃/?x=0；ψ₃²为下边界不透水边界，?P₃/?z=0；左右两侧为不透水边界，?P₃/?x=0.
ψ₃¹所表示的边界条件可以应用分离变量法求出孔压的级数形式解：

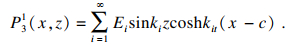(14)

式中：k_i=(2i－1)π/2a, i=1, 2, 3, …；E_i为待求参数；.
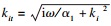
ψ₃²所表示的边界条件可以应用分离变量法求出孔压的级数形式解：

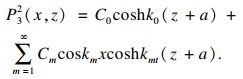(15)

式中，C₀，C_m为待求参数.
区域③中孔压的级数形式解可由式(14)与式(15)叠加得到：

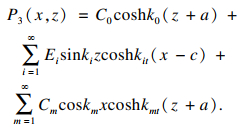(16)

区域④的边界条件与区域③的边界条件类似, 同样可利用叠加原理和分离变量法求出区域④内的孔压级数形式解：

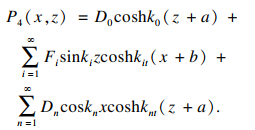(17)

式中，D₀，D_n，F_i为待求解参数.
由区域①与区域④之间的连续条件, 联立式(11)和式(17)可得：

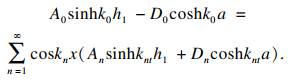(18)

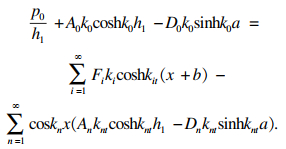(19)

由区域②与区域③之间的连续条件, 联立式(12)和式(16)可得:

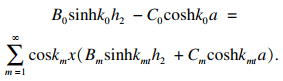(20)

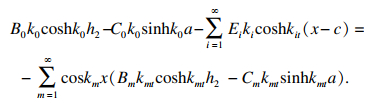(21)

由区域③与区域④之间的连续条件, 联立式(16)和式(17), 可得

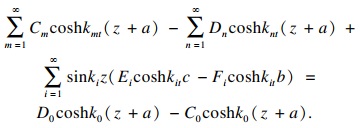(22)

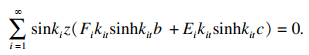(23)

由式(18)，式(20)，式(23)结合傅里叶级数的性质：

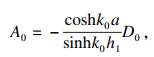(24)

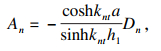(25)

(23)

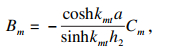(27)

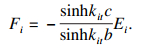(28)

将A₀，A_n，B₀，B_m，F_i代入式(19)，式(21)，式(22)得到：

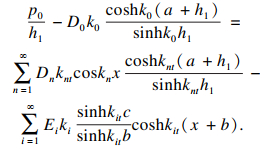(29)

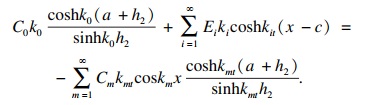(30)

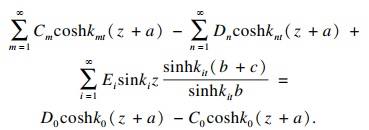(31)

将式(29)和式(30)分别在区间(-b, 0)和(0, c)内积分得到：

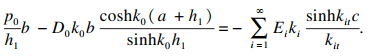(32)

(33)

联立式(32)和式(33)得到：

(34)

式(29)~式(31)分别在等式两侧乘以cosk_nx，cosk_mx，sink_iz，分别在区间(-b, 0)，(0, c)，(-a, 0)内积分，将式(34)代入得到：

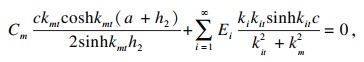(35)

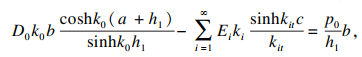(36)

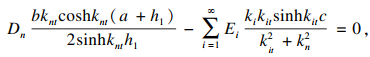(37)

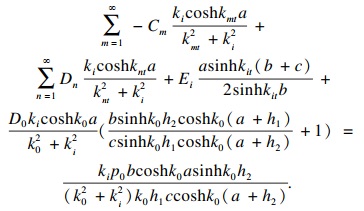(38)

联立式(35)~式(38)即可求出未知数C_m，D₀，D_n，E_i，采用MATLAB软件求解该无穷阶线性方程组系数矩阵，为方便计算，将所有待定系数在第N项处予以截断.将上述求解得到的参数代入式(11)、式(12)、式(16)及式(17)即可得到各区域内的孔压响应显式解析解.
按上述方法计算得到的孔压响应结果为式(39)所示的复数形式：

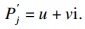(39)

式中：u为孔压响应实部；v为孔压响应虚部.
由该复数形式表达式可以给出相应位置的相位角计算式：

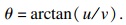(40)

式中，θ为相位角.
3 解析解验证与对比为验证水位波动条件下的基坑二维渗流场孔压解析解的正确性, 采用PLAXIS软件计算相同工程参数下基坑渗流模型的孔压响应, 将数值计算结果、解析解计算结果、现有半解析解计算结果进行对比.计算过程中使用文献[13]中的基坑参数, 如表 1所示.
表 1(Table 1)

表 1 基坑工程参数Table 1 Foundation pit engineering parameters a/m b/m c/m h1/m h2/m α1/(m2·d-1) 16 80 16 19 12 5 500

表 1 基坑工程参数 Table 1 Foundation pit engineering parameters

计算区域边界处孔压波动周期T=0.5d，选取t=0.25T时孔压响应幅值与边界孔压波动幅值之比p/p₀进行对比.为方便与数值软件计算结果、半解析解计算结果进行对比，截取基坑外侧b=35 m范围内的孔压响应分布进行对比验证.经试算，级数项在N=20时解析解计算结果已经收敛，后续分析均采用级数项N=20进行计算.
1) 孔压对比分析.解析解、现有半解析解和数值方法计算的基坑周围孔压响应结果对比如图 2所示.
图 2(Fig. 2)

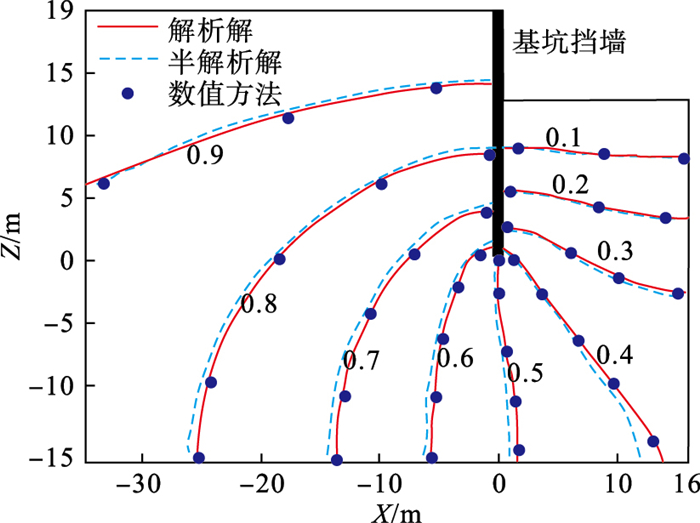图 2 基坑周围孔压响应分布对比Fig.2 Comparison of pore pressure response distribution around the foundation pit

从孔压响应对比结果来看, 解析解方法与数值结果误差最大为1.7 %, 半解析方法与数值结果误差最大为3.3 %.解析解方法计算结果与数值软件计算结果吻合较好且精度更高, 验证了解析解方法的正确性.
由解析解计算结果可知, 水位波动条件下沿海基坑周围土体孔压响应分布在距离挡墙越远处孔压变化越慢, 沿渗流最短路径变化最快, 挡墙底部孔压响应幅值约为0.5P₀.
2) 相位滞后分析：孔压响应滞后相位表示基坑周围土体中孔压响应与基坑边界处孔压波动的相位角差值.选取基坑挡墙两侧孔压响应相位滞后的解析解和数值解计算结果进行对比, 如图 3所示.由相位滞后对比结果可知, 解析解计算结果与数值软件计算结果吻合较好, 验证了解析解方法的正确性.
图 3(Fig. 3)

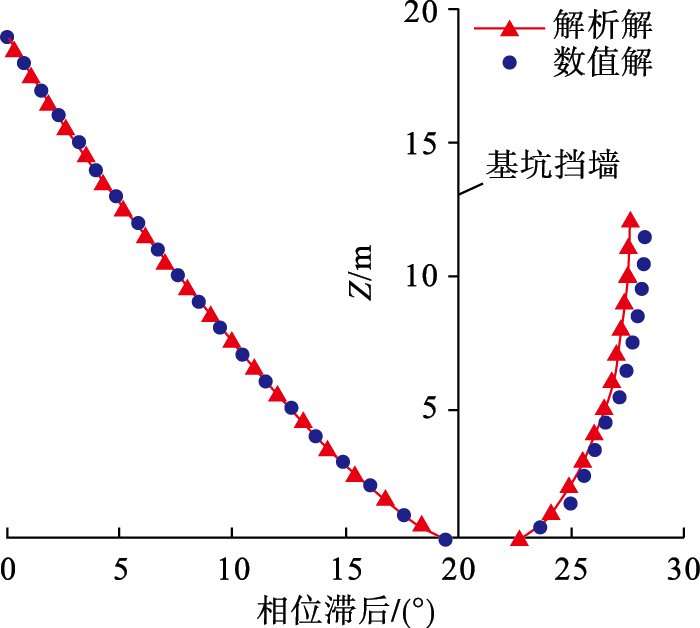图 3 孔压响应相位滞后对比Fig.3 Comparison of phase lag of pore pressure response

由图 3可知, 基坑周围土体的相位滞后现象十分明显, 在基坑挡墙底部外侧相位滞后约为20°, 内侧相位滞后约为23°, 挡墙内侧顶部相位滞后约为28°. 孔压响应的相位滞后沿渗流路径逐渐增大, 接近挡墙底部处相位滞后变化加快^[15].
4 孔压及相位滞后影响分析1) 基坑内部水位影响：基坑内部水位h₂为5, 7, 9 m时, 对基坑周围孔压响应幅值分布和相位滞后的变化情况进行对比, 其他基坑工程参数为a=5 m, b=15 m, h₁=15 m, c=9 m.使用t=0.25T时刻的孔压响应幅值与边界孔压波动幅值p₀的比值表示孔压响应的大小.对比结果如图 4、图 5所示.
图 4(Fig. 4)

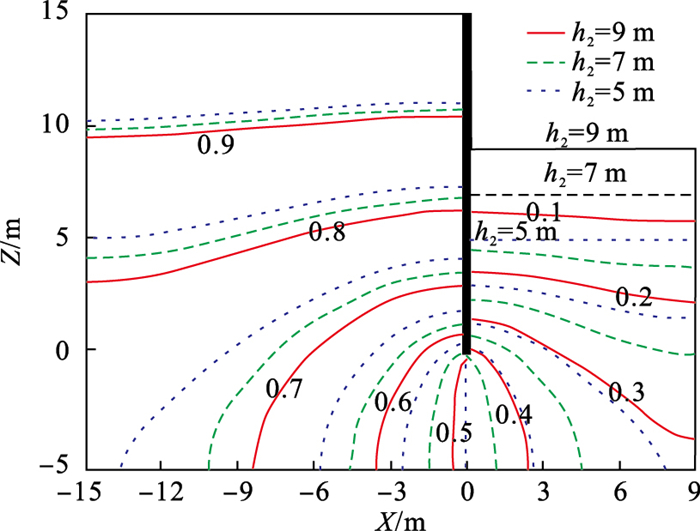图 4 基坑不同内侧水位下孔压响应分布Fig.4 Distribution of pore pressure response at different water levels in the pit

图 5(Fig. 5)

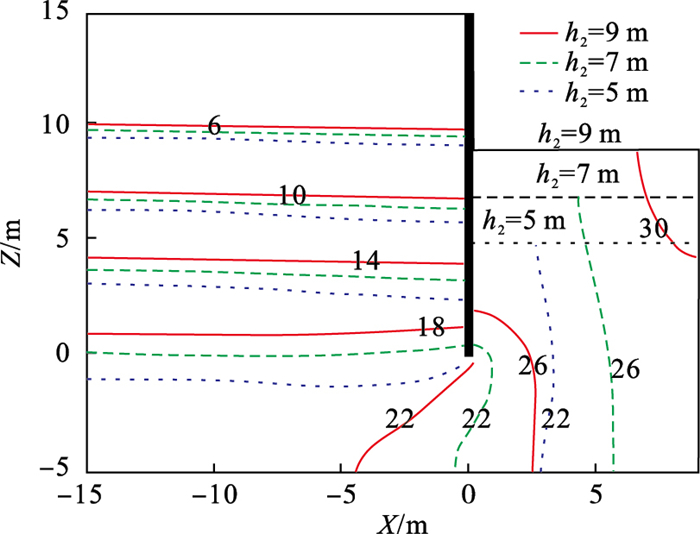图 5 基坑不同内侧水位下相位滞后/(°)Fig.5 Phase lag of different water levels of foundation pit

由对比结果可知, 随基坑内部水位增高, 挡墙外侧孔压响应幅值呈下移分布, 挡墙内侧孔压响应幅值呈上移分布, 即挡墙两侧孔压响应幅值均增大；挡墙底部的孔压响应幅值增大16.8 %, 距离挡墙越近的区域孔压响应幅值变化越快^[15].相位滞后随基坑内部水位上升而增加, 在挡墙底部增大3.2°, 在基坑底部紧邻挡墙处增大7.3°.
2) 基坑宽度影响：计算基坑半宽c为7, 9, 11 m时基坑周围孔压响应分布和相位滞后的变化情况, 其他基坑工程参数按照a=5 m, b=15 m, h₁=15 m, h₂=9 m取值.由对比结果可知, 随基坑宽度增大, 挡墙外侧孔压响应幅值呈上移分布, 挡墙内侧孔压响应幅值呈下移分布, 即挡墙两侧孔压响应幅值均减小；挡墙底部孔压响应幅值降低9.1 %, 距离挡墙越近的区域孔压响应幅值变化越快.对比结果如图 6、图 7所示.
图 6(Fig. 6)

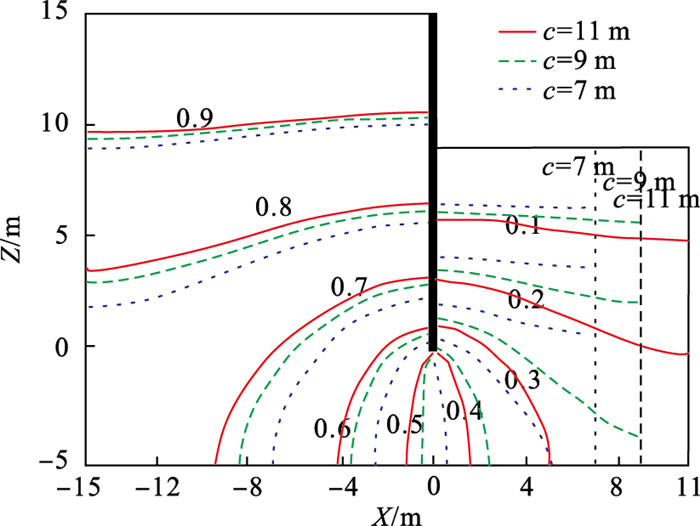图 6 基坑不同宽度下孔压响应分布Fig.6 Distribution of pore pressure response at different pit widths

图 7(Fig. 7)

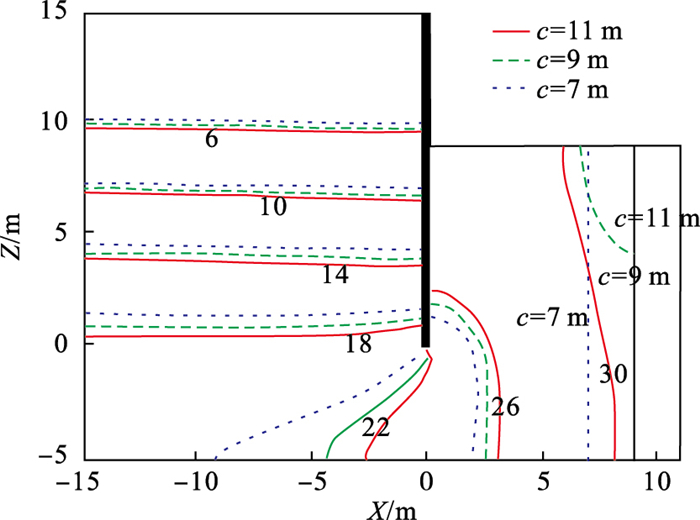图 7 基坑不同宽度下相位滞后/(°)Fig.7 Phase lag of different foundation pit widths

相位滞后在挡墙外侧及内侧靠近挡墙处随基坑宽度增加而减小, 在挡墙底部减小1.32°, 在基坑底部紧邻挡墙处减小0.57°；在基坑轴线处随基坑宽度增加而增大, c=7 m时, 基坑轴线处相位滞后低于30°.
3) 挡墙底部与不透水边界距离的影响：挡墙底部与不透水边界距离a为3, 5, 7 m时, 计算基坑周围孔压响应分布和相位滞后变化情况, 其他工程参数为c=9 m, b=15 m, h₁=15 m, h₂=9 m.对比结果如图 8、图 9所示.
图 8(Fig. 8)

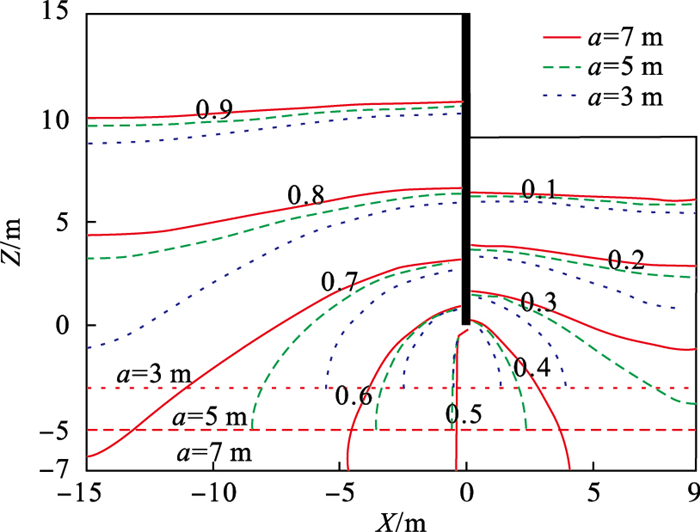图 8 不同挡墙底部与不透水边界距离下孔压响应分布Fig.8 Pore water pressure response distribution of different distance between the bottom of retaining wall and impervious boundary

图 9(Fig. 9)

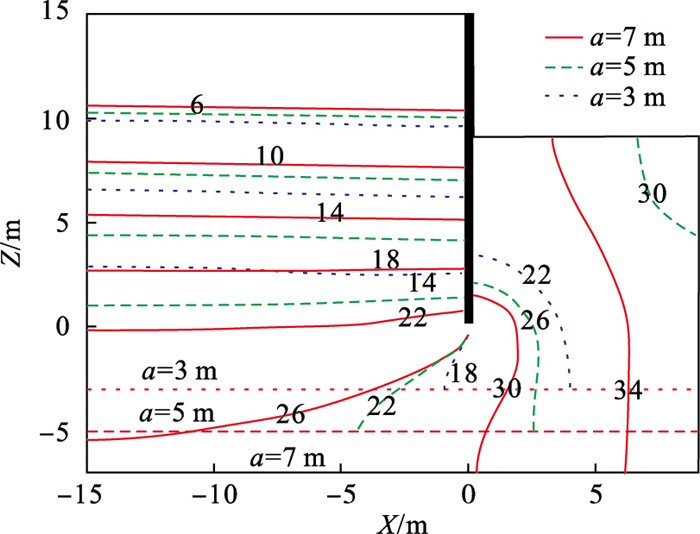图 9 不同挡墙底部与不透水边界距离下的相位滞后/(°)Fig.9 Phase lag of different distance between the bottom of retaining wall and impervious boundary

由对比结果可知, 随挡墙底部与不透水边界距离的增大, 挡墙两侧孔压响应幅值呈上移分布, 即挡墙外侧孔压响应幅值减小, 挡墙内侧孔压响应幅值增大；挡墙底部孔压响应幅值增大2.1 %, 距离挡墙越远的区域孔压响应幅值变化越大.
相位滞后随挡墙底部与不透水边界距离增加而增大, 在挡墙底部增加7.1°, 在基坑底部紧邻挡墙处增加9.8°, 基坑内侧及不透水边界处相位滞后变化较明显.
4) 基坑外侧水位影响：计算基坑外侧水位h₁为11, 15, 19 m时基坑周围孔压响应分布和相位滞后的变化情况, 其他工程参数按c=9 m, b=15 m, a=5 m, h₂=9 m取值.对比结果如图 10、图 11所示.
图 10(Fig. 10)

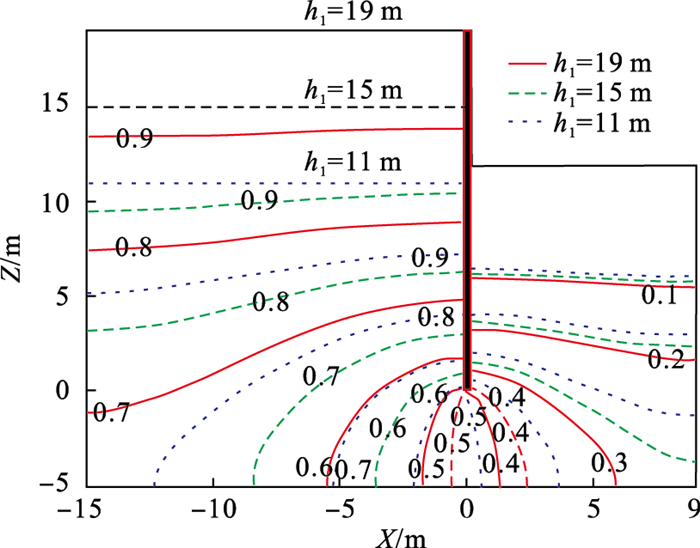图 10 基坑不同外侧水位下孔压响应分布Fig.10 Distribution of pore pressure response of different water levels outside the pit

图 11(Fig. 11)

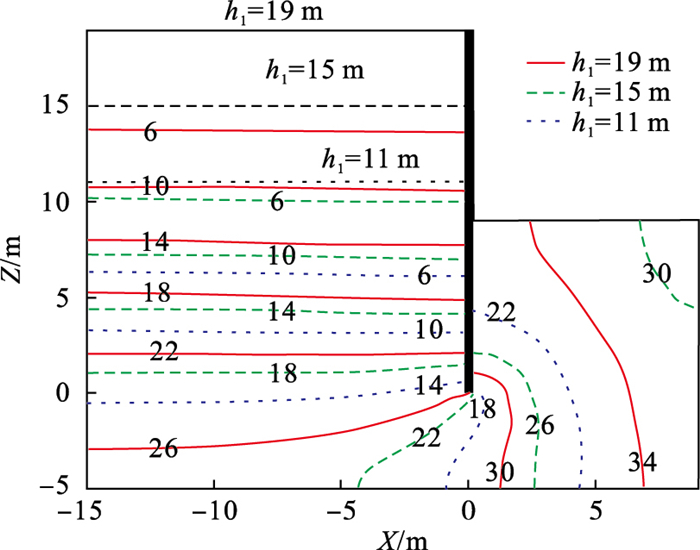图 11 基坑不同外侧水位下相位滞后/(°)Fig.11 Phase lag of different water levels outside the pit

由对比结果可知, 随基坑外侧水位升高, 挡墙外侧孔压响应幅值呈上移分布, 挡墙内侧孔压响应幅值呈下移分布, 即挡墙两侧孔压响应幅值均减小；挡墙底部孔压响应幅值降低15.1 %, 挡墙外侧区域孔压响应受影响更明显.
相位滞后随外侧水位升高而增大, 在挡墙底部增加10.6°, 在基坑底部紧邻挡墙处增加10.5°, 在基坑内侧及不透水边界处相位滞后变化更明显.
5 结论1) 解析解方法得到级数形式的显式解析解, 相对于保角变换法, 解析解方法能够求解出计算区域内任意位置的孔压响应, 不存在奇异点.
2) 基坑挡墙两侧孔压响应幅值随基坑宽度、基坑外部水位的增大而减小, 随基坑内部水位的升高而增大.挡墙底部与不透水边界距离的增大, 挡墙外侧孔压响应幅值减小, 挡墙内侧孔压响应幅值增大.基坑挡墙内、外侧水位变化会导致挡墙底部孔压分布发生明显变化, 最大变化量分别为16.8 % 和15.1 %.
3) 基坑周围孔压响应的相位滞后随基坑内外侧水位、挡墙底部与不透水边界距离的增大而增加；挡墙外侧及内侧靠近挡墙处随基坑宽度增加而减小.基坑参数变化量相同时, 挡墙底部与不透水边界距离对相位滞后的影响更加明显, 此时相位滞后在挡墙底部和基坑底部分别增加了7.1°和9.8°.
参考文献

[1]	Xu Y S, Yan X X, Shen S L, et al. Experimental investigation on the blocking of groundwater seepage from a waterproof curtain during pumped dewatering in an excavation[J]. Hydrogeology Journal, 2019, 27(7): 2659-2672. DOI:10.1007/s10040-019-01992-3
[2]	Sun Y, Zhou S, Luo Z. Basal-heave analysis of pit-in-pit braced excavations in soft clays[J]. Computers and Geotechnics, 2017, 81: 294-306. DOI:10.1016/j.compgeo.2016.09.003
[3]	Lai F, Chen F, Liu S, et al. Undrained stability of pit-in-pit braced excavations under hydraulic uplift[J]. Underground Space, 2022, 7(6): 1139-1155. DOI:10.1016/j.undsp.2022.04.003
[4]	Li H L, Jiao J J. Analytical studies of groundwater-head fluctuation in a coastal confined aquifer overlain by a semi-permeable layer with storage[J]. Advances in Water Resources, 2001, 24(5): 565-573. DOI:10.1016/S0309-1708(00)00074-9
[5]	Park K, Owatsiriwong A, Lee J. Analytical solution for steady-state groundwater inflow into a drained circular tunnel in a semi-infinite aquifer: a revisit[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 206-209. DOI:10.1016/j.tust.2007.02.004
[6]	王钊, 邹维列, 李广信. 挡土结构上的土压力和水压力[J]. 岩土力学, 2003(2): 146-150. (Wang Zhao, Zou Wei-lie, Li Guang-xin. Soil and water pressure on retaining structure[J]. Rock and Soil Mechanics, 2003(2): 146-150.)
[7]	Hu Z, Yang Z, Wilkinson S P. Active earth pressure acting on retaining wall considering anisotropic seepage effect[J]. Journal of Mountain Science, 2017, 14: 1202-1211. DOI:10.1007/s11629-016-4014-3
[8]	黄大中, 谢康和, 应宏伟. 渗透各向异性土层中基坑二维稳定渗流半解析解[J]. 浙江大学学报(工学版), 2014, 48(10): 1802-1808. (Huang Da-zhong, Xie Kang-he, Ying Hong-wei. Semi-analytical solutions for two-dimensional stable seepage in footings in permeably anisotropic soils[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(10): 1802-1808.)
[9]	Javed J, Muzzammil M, Singh H P, et al. Permeability of stratified soils for flow normal to bedding plane[J]. Aquatic Procedia, 2015, 4: 660-667. DOI:10.1016/j.aqpro.2015.02.085
[10]	Fontana N. Experimental analysis of heaving phenomena in sandy soils[J]. Journal of Hydraulic Engineering, 2008, 134(6): 794-799. DOI:10.1061/(ASCE)0733-9429(2008)134:6(794)
[11]	Bereslavskii E N. The flow of ground waters around a Zhukovskii sheet pile[J]. Journal of Applied Mathematics and Mechanics, 2011, 75(2): 210-217. DOI:10.1016/j.jappmathmech.2011.05.010
[12]	Lyu H M, Shen S L, Wu Y X, et al. Calculation of groundwater head distribution with a close barrier during excavation dewatering in confined aquifer[J]. Geoscience Frontiers, 2021, 12(2): 791-803. DOI:10.1016/j.gsf.2020.08.002
[13]	应宏伟, 聂文峰, 黄大中. 地下水位波动下基坑周围地基土的孔压响应半解析解[J]. 岩土工程学报, 2014, 36(6): 1012-1019. (Ying Hong-wei, Nie Wen-feng, Huang Da-zhong. Semi-analytical solution of pore pressure response of foundation soil around foundation pit under fluctuation of groundwater level[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1012-1019.)
[14]	Ying H, Zhu C, Gong X, et al. Analytical solutions for the steady-state seepage field in a finite seabed with a lined tunnel[J]. Marine Georesources & Geotechnology, 2019, 37(8): 972-978.
[15]	Zhang L, Ying H, Xie K, et al. Effect of groundwater fluctuations on pore pressures and earth pressures on coastal excavation retaining walls[J]. Marine Georesources & Geotechnology, 2016, 34(8): 770-781.