, 马海涛, 赵宇海
, 马海涛, 赵宇海 东北大学 计算机科学与工程学院,辽宁 沈阳 110169
收稿日期:2022-03-21
基金项目:国家自然科学基金资助项目(61772124)。
作者简介:于长永(1981-),男,辽宁海城人,东北大学副教授。
摘要:为了能够回答生物信息学中关于de Bruijn graph(DBG)的两个问题——①对于任意的k-mer,回答其是否为DBG的顶点,②对于DBG的任意顶点,回答其邻接信息(入边和出边),提出了一种针对大规模read mapping的高效DBG索引方法.本文将以上两个问题转化为非重复多路径上的k-mer和(k+1)-mer的确切查找问题,并利用FM-index进行解决.首先,对给定的参考序列进行压缩,即非重复多路径的发现,从而压缩了序列中大量存在的重复(k+1)-mer.其次,基于非重复多路径FM-index对DBG进行索引.查找k-mer是否出现在DBG上,若找到,给出该k-mer的直接前驱和直接后继结点,从而提高时空效率.最后,在62种大肠杆菌菌株的基因组上进行实验.实验结果表明,所提出的方法可以高效地对多参考序列的DBG进行索引.
关键词:de Bruijn graph索引read mapping(序列映射)FM-index参考序列
An Efficient DBG Indexing Method for Large-Scale Read Mapping
YU Chang-yong, LI Jun-jie

 , MA Hai-tao, ZHAO Yu-hai
, MA Hai-tao, ZHAO Yu-hai School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: LI Jun-jie, E-mail: tbaglee@163.com.
Abstract: In order to answer two questions about de Bruijn graph(DBG) in bioinformatics: ① For any k-mer, answer whether it is the vertex of DBG; ② For any vertex of DBG, answer its adjacency information(incoming edge and outgoing edge), an efficient DBG indexing method for large-scale read mapping is proposed. In this paper, the above two questions are transformed into the exact finding problem of k-mer and (k+1)-mer on non-repetitive multipath, and are solved by using FM-index. Firstly, a given reference sequence is compressed, which is the discovery of non-repetitive multipaths, thereby compressing the presence of large-scale repetitive (k+1)-mers in the sequence. Secondly, the DBG is indexed based on the non-repetitive multipath FM-index. The k-mer is searched whether it appears on the DBG, and if so, the direct predecessor and direct successor nodes of the k-mer are provided to improve the spatial-temporal efficiency. Finally, experiments are performed on the genomes of 62 E. coli strains. The experimental results show that the method proposed can efficiently index the DBG of multi-reference sequences.
Key words: de Bruijn graphindexread mappingFM-indexreference sequence
下一代测序(next generation sequencing, NGS)[1]技术能够快速有效地产生大规模reads,这给read mapping问题带来了新的挑战.de Bruijn graph(DBG)最近被广泛用来解决read mapping中参考基因组序列的索引问题,因为在解决参考基因组序列中子串重复问题方面,采用DBG方法是有显著成效的.
在生物信息学中,参考基因组序列的高效索引是解决read mapping问题的重要基础,它能够实现长度为k的碱基序列(k-mer)查找以及k-mer在序列上的位置查找.现有流行的索引算法主要是基于哈希表[2]和基于BWT(Burrows-Wheeler transform)[3]方法.其中,基于哈希索引算法的比对工具有Hobbes2[4],SOAP[5],SHRiMP[6]和BFAST[7]等.另外基于BWT的索引工具也很常见,比如经常提到的BWA[8],Bowtie2[9]和SOAP2[10]等比对工具,这些工具都使用FM-index[11](FM-index是基于Burrows-Wheeler变换的压缩全文子串索引),它是在BWT索引方法基础上作出的进一步改进.但由于基因组序列的重复基因组区域[12-13]是普遍存在的现象,而这恰恰是以上两种流行索引方法的主要瓶颈.目前,****已经努力将这两种方法从线性的参考基因组的索引扩展到不同类型序列图的索引,并在时间和空间效率方面进行了各种权衡.
近期DBG方法被应用到大规模的read mapping问题上,其优点是可以很好地处理基因组上的重复信息,因为重复的k-mer在DBG上作为结点仅出现一次.例如在deBGA[14]中,deBGA使用3个列表来存储参考序列的DBG的单路径信息,这些单个或者多个参考基因组信息被RDBG(reference de Bruijn graph)所构建和索引,从而能够快速地在单路径上进行k-mer的查询和定位.deBGA在保持类似或更高的灵敏度和准确性的同时,大大快于最流行的方法,然而对于DBG模型中的分支结点和分支结点组成的路径,是没有考虑全面的.类似仅考虑单路径信息的工具还有Pufferfish[15],该索引由6个部分(以及可选的第7个组成部分)组成,不仅能够确定k-mer是否存在于单路径上,还能很好地确定其在某条参考基因组序列上及其偏移位置,以及该k-mer所在的单路径的邻接信息.Pufferfish对于压缩的DBG和着色压缩的DBG都有很高的查找效率,但是它也只能处理DBG上的单路径信息.此外对于完整的DBG索引,BOSS模型[16]提出了一种新的简洁的DBG表示和索引方法,该表示形式的大小不受k-mer的影响,并且大小比现存的DBG表示方法小得多,还能在常数时间内计算出结点的出入边数量. VARI[17]在BOSS的基础上添加颜色信息,显著减少了存储和使用着色DBG所需的内存量.Rainbowfish[18]则利用了颜色集分布中存在的高偏斜度,在空间上比VARI提高了近20倍.但这些优化都是在表示和组装基因组集合(群体)方面的优化,是面向着色DBG和SNP发现等相关问题的.
除了在参考基因组序列索引方面的广泛应用,DBG在基因组序列和转录组序列的组装、装配[19-20]和基因变异的检测和发现,以及对变异结构的分析(来自多个基因组)方面也有重要作用.LDBG(linked de Bruijn graph)[21]中提出了一种新颖的装配图数据结构,它通过在DBG顶部添加注解来构建,并且通过图来存储远程连接信息,可以从LDBG中无损地存储和恢复序列,但该模型不能用于定位DBG在参考基因组序列上的路径.而GGMAP方法[22]是将read映射到DBG上,而不是映射到参考序列.另外,DBG经典结构的变体——着色de Bruijn图[23]——被广泛应用于个体或群体中检测简单和复杂的遗传变异,并对其进行基因分型.
在生物信息学中,虽然现有参考基因组的索引方法是丰富的,然而针对大规模read mapping的高效DBG索引方法是缺乏的.现存最流行的大规模read mapping的索引构建和比对方法如下:DynamicBOSS[24]支持无限数量的结点和边的添加或者删除操作,并且适用于非常大的样本(大于150亿的k-mers);deGSM[25]提出了一种轻量级并行DBG构造方法,用来解决内存不足的问题;CAS[26]为提高read mapping效率,使用上下文感知种子去降低种子频率.然而它们涉及的索引效率相对较低,且时空花费较大;另外一些现存的索引算法只针对图上的单路径进行处理,而忽略了图上非单路径结点和边的索引情况.因此本文针对参考基因组建立了一种高效的DBG索引,首先对于原参考序列进行压缩,即进行非重复多路径发现,然后基于非重复多路径FM的DBG索引进行k-mer查找.判断给定的k-mer是否存在于整个DBG的结点上,而不只是在图的单路径上查找.如果存在,同时给出该k-mer的直接前驱和直接后继结点,从而将索引问题转化为压缩后序列的子串确切查找问题.本文方法相比于现在最流行的索引方法,时间和空间花费更小,同时由于该方法是针对整个DBG构建索引,相比于仅面向单路径来构建索引的方法来说,考虑是更全面的.与目前最流行的针对大规模read mapping的DBG索引方法相比较而言,本文提出的算法是更有前景的.
1 符号及问题定义设g是给定字母表Σ={A,C,G,T}上的参考基因组序列,其长度用|g|来表示.g[i]表示序列g中的第i个字符,索引i是从1开始的.同时,本文定义g[i, j]作为序列g的子串,其中,子串的开始位置是i,结束位置是j.用g[*, d]和g[d, *]来表示长度为d的序列g的前缀和后缀.另外在DBG上,返回到结点vi的传入边数,称为入度,用符号indegree(vi)表示,通过入边和结点vi直接相连的结点称为直接前驱;同理,从结点vi传出来的边数,称为出度,用符号outdegree(vi)表示,通过出边和结点vi直接相连的结点称为直接后继.一个k-mer是字母表Σ上长度为k的字符串.本文用DBG(g, k)来表示具有长度为k的k-mer的序列g的DBG,并在定义1中定义DBG(g, k)如下.
定义1 DBG(de Bruijn graph) ??给定字母表Σ上的参考基因组序列g和一个整数k≥2, g的k阶de Bruijn图,DBGk(g)是一个有向图(V, A),其中V和A满足:V={d∈Σk | d是一个k-mer,同时d是g的子串}, A={(d, d′)|d[k-1, *]=d′[*, k-1]}.
定义2单路径(unipath)?? 如果DBG(g, k)上结点vi的入度和出度满足条件indegree(vi)=outdegree(vi)=1,则把这样的结点vi称作非分支结点.对于DBG(g, k)上的任意一条路径,p=vi, vi2, …, vik,如果这条路径上的每个结点都是非分支结点,那么就称这条路径为单路径.
为比较方便地说明和描述问题,本文给出DBG的具体示例.例如,设序列g:
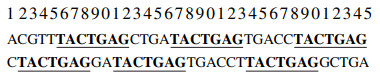 |
图 1(Fig. 1)
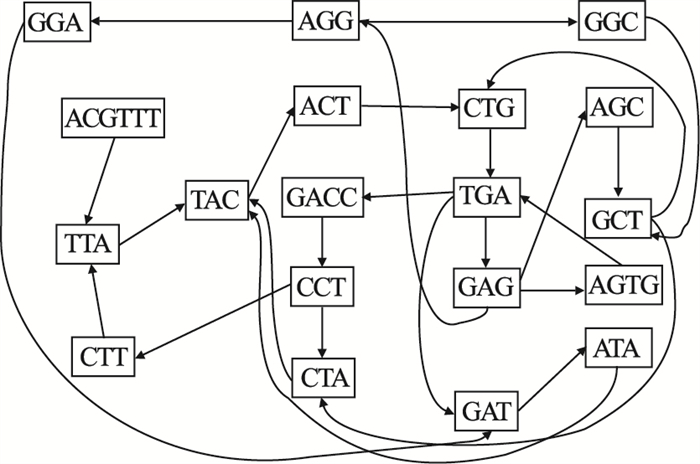 | 图 1 k=3,序列g的DBG(g, 3)Fig.1 The DBG(g, 3) of sequence g when k=3 |
很明显可以观察到,图 1中一共有19个结点(包含3条单路径)和26条有向边,图DBG(g, k)的详细信息见图 1.另外在参考基因组序列g上,k-mer的选取是按滑动窗口进行的,在k=6时,滑动窗口的示意图如图 2所示.
图 2(Fig. 2)
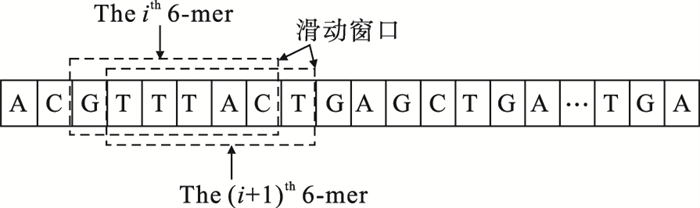 | 图 2 k=6时,序列g的滑动窗口Fig.2 The slide window of sequence g when k=6 |
给定一个参考基因组序列g及其DBG(g, k)=(V, E),DBG的索引问题主要包括以下两个方面:①对于任意k-mer d,判断d是否属于V?②如果d属于V,查找DBG中d的邻接信息,即d在图上的直接前驱和直接后继结点.
2 高效的DBG index算法2.1 FM-indexFM索引进行搜索主要通过两个关键功能进行执行:count和locate.Count用来计算序列g中有多少个文本匹配,而locate用来查找这些匹配的位置.在此过程中,需要OCC[][]数组、BWT字符串和C[]数组,但SA[]数组不是必需的.C[c]数组是指在序列g中,字典序小于字符c∈{A, C, G, T}的所有字符的个数,OCC[c][r]表示在gbw[0, r]中出现字符c的个数,其中字符串gbw是序列g的BWT.字符串cX的后缀数组区间可由式(1)~(2)[11]求得.
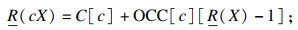 | (1) |
 | (2) |
序列g的FM索引可以处理问题定义中的两个问题.针对第一个问题,本文可以使用FM索引来精确查找序列g中的k-mer;而处理第二个问题,即查找DBG中k-mer的邻接信息,可以使用FM索引来精确搜索g中长度为k+1的8个字符串,这8个字符串分别是在k-mer的左端或者右端添加A,C,G,T字符来构造的.
2.2 非重复多路径发现序列g的FM索引是可以处理问题定义中的两个问题,然而序列g中存在大量的重复k-mer.设g′是压缩后的g,它仅存储g中重复(k+1)-mer一次,并且人为的添加符号$来连接多条路径,并规定$比字母表Σ={A, C, G, T}上的所有字符的字典序都小.通过g′的FM索引也可以解决问题定义中的问题,而g′的大小是远远小于序列g的.
在构建序列g′时,首先想到的数据结构就是B+树.它的查询性能更稳定,查询速度也更快.因为B+树上关键字的结点是唯一的,正好对应于序列g′上k-mer的不重复性要求.本文将k-mer转化成二进制整数存储到B+树上,同时叶结点之间用链表有序存储,利于范围查询.给定序列g和k-mer,按照图 2所示的滑动窗口迭代选取k-mer进行处理,对参考基因组序列进行压缩,从而构建非重复多路径,构建的具体过程如算法1所示.
算法1?非重复多路径生成算法
Input: R={r1, r2, …, rn}, 参考基因组序列; k, k-mer的长度;
Output: Y={y1, y2, …, ym}, 非重复多路径的集合;
1. ??bptree=?, Y=?//bptree是一棵B+树
2. 设str为一个空字符串, str="";
3. ??for i=1 to n do
4. ????for j=1 to |ri |-k do
5.??????m=hash(ri[j, j+k]);
6.??????if m
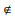
7.????????if str==""
8.???????????? str=cat(str, ri[j, j+k]);
9.???????? else
10.???????????? str=cat(str, ri[j+k]);
11.??????????将m插入bptree;
12.????????else if str≠"" then
????????????????????????将str插入集合Y; 重置str为一个空字符串, str="".
对于读入的参考序列R,按顺序循环处理R上的所有k-mer,首先按算法1中的第5行所示,把每个k-mer转化成哈希值m,然后判断m是否存在于B+树上,算法1中的bptree就定义成一棵用来存储(k+1)-mer的B+树.如果m之前并不存在于bptree上,则把m插入到bptree上,同时判断字符串str是否为空,若为空就把整个k-mer拼接到字符串str上,否则如算法1中第10行所示,直接把该k-mer的最后一个字符拼接到str上;另外一种情况,如果m之前出现在bptree里,同时字符串str非空,就把str插入到集合Y中,它是用来存放多条非重复路径的.另外把str置空,重新进入到下一次循环中,直至循环处理完序列R的最后一个k-mer结束.
由此,通过序列R生成的DBG(R, k)和压缩后的参考基因组序列Y所生成的DBG(Y, k)是等价的, 即DBG(R, k)=DBG(Y, k).所以通过压缩算法,很好地处理了序列R上的重复结点,提高索引效率的同时节省索引空间,为下一步非重复多路径FM的DBG索引创造了条件.
为了更清晰地说明算法1,这里给出示例.例如,符号定义部分给出的序列g,在k+1=4时,压缩后序列g′的集合为
 |
 |
2.3 基于非重复多路径FM的DBG索引由2.2节可知,查询k-mer是不是序列g相对应的DBG上的结点,该问题等价于验证k-mer是否是序列g′的子串.另外对于DBG上结点vi的邻接信息问题,等同于处理(k+1)-mers:A vi, C vi, G vi, T vi, vi A, vi C, vi G, vi T这8个字符串是否是序列g′的子串.因此,基于序列g′的BWT可以解决问题定义中的两个问题.
设g′=y1$y2$…ym是由算法1生成的多条非重复路径.其中,序列g′的长度表示为|g′|, |g′|=LACGT+L$,LACGT=Σi=1m|yi|是g′中字符A, C, G, T的数目,L$=(m-1)是g′中字符$的数目.为了计算k-mer或者(k+1)-mer的后缀数组区间,2.1节给出的式(1)和(2)需要满足
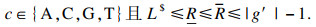 | (3) |
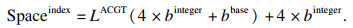 | (4) |
在处理FM索引时为减少索引空间的大小,OCC[c][r]的存储情况在理论上满足
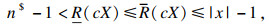 | (5) |
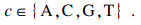 | (6) |
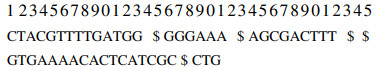 |
在OCC这个二维数组中,由于字符$所在的行和列是不会在实际的字符匹配中出现的,所以原本OCC数组的占用大小为54×5,实际存储的大小减小到49×4.另外,OCC数组在实际中是以压缩的形式进行存储的,所以在表 1中每10个后缀数组取1个进行存储,即OCC_gap=10.
表 1(Table 1)
| 表 1 OCC数组内部存储形式 Table 1 Internal storage format of OCC array |
由于原本OCC数组的占用大小为54×5,所以行代表按字母表顺序排列的后缀数组(SA),其中行数用i表示,从0开始到53结束,一共54行;列代表字符串中现存的字符类型,共5类,分别是{$, A, C, G, T},列数用j表示,从0开始到4结束,一共5列.在表 1中,表中的id即i每隔OCC_gap=10取值所得.
对于存在于表 1中的id的后缀数组,可以通过表 1直接查询.而对于检索那些不在id=0或者id=15等位置的后缀数组,以i=8为例,需要从i∈[0, 8]进行遍历查找.另外i∈[0, 4], j∈[0, 4]时和i∈[5, 53],j=0时,二维数组OCC[i][j]的空间范围内都用符号\来填充,表示在实际的OCC数组中并不进行存储,这里计算i∈[0, 4],j∈[0, 4]时,即以字符$开头的后缀数组中,字符A, C, G, T的个数分别是38, 30, 40, 42.而i∈[5, 53],j∈[1, 4]时,OCC[i][j]的空间范围,即表中的数值部分才是i取特定值时,不同id的后缀数组中字符A, C, G, T分别出现的数目.因此,当存储的数据量较大时,该数据结构节省空间的效果是很显著的.
3 实验与结果所有实验均在具有4个10核的Intel(R) Xeon(R) E5-2640 2.40 GHz CPU和160 GB内存的服务器上进行,操作系统为Ubuntu 16.04.DBG索引算法是使用C和C++编译器实现和编译的.
本文从NCBI RefSeq数据库[27](http://www.ncbi.nlm.nih.gov/refseq/)下载了所有可用的62种大肠杆菌菌株的基因组.这62种大肠杆菌的序列总长度为310 199 470 B.表 2中展示了不同k-mer序列压缩后的一些参数.
表 2(Table 2)
| 表 2 不同k-mer序列压缩后的大小 Table 2 Compressed sequence size in different k-mer |
表 2中的第1列是k-mer长度的取值,从10到20;第2列是在每个k-mer取值下,压缩后的文件中字符$的个数;第3列是压缩后文件的大小,单位是字节;第4列是压缩后DBG上边的数量,很明显,随着k-mer长度的增加,边数也在增加;而第5列是压缩后文件大小与压缩前文件大小的一个比值,结果为百分数.就62种大肠杆菌数据集而言,在k=13时,序列压缩后大小是压缩前的20.68%,在k-mer长度取其他值时,序列压缩后大小和压缩前的比值都小于它,所以总体上相对压缩前的文件来说,本文算法的空间压缩效果不错.
表 3记录了不同k-mer长度下序列压缩算法的时间花费情况.很明显可以看到,序列压缩算法在k=13时花费时间最长,需要10 min左右,而k-mer选取其余长度时,压缩时间都小于10 min,该算法的时间复杂度是较小的.因此结合表 2,本文的压缩算法在时空上是高效可行的.
表 3(Table 3)
| 表 3 压缩序列的时间花费 Table 3 Time consumption in compressing the sequence |
表 4是在不同k-mer长度下,OCC_gap分别取10和30时查找2 000 000个k-mer的时间花费情况.平均时间这一列是指查询每个k-mer所需要的时间,单位是ms;总时间这一列是查询2 000 000个k-mer所需的总时间,单位是s.很明显,在相同的k-mer长度下,OCC_gap取值越大,查找时间会越长;在同样的OCC_gap取值下,随着k-mer长度的增加,时间花费总体上是增加的.但最重要的是,时间花费都很小,查询k-mer的效率很高,这也说明本文提出的算法的可行性和高效性.
表 4(Table 4)
| 表 4 查找2 000 000个k-mer的时间花费 Table 4 Time consumption to find 2 000 000 k-mers | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 结语本文针对大规模read mapping的索引问题,提出了一种高效的DBG索引方法.方法主要思路是对给定的参考序列进行压缩,即非重复多路径的发现,然后利用FM-index对DBG进行索引,查找给定的k-mer是否存在,存在的话给出其直接前驱和直接后继结点,从而提高了时空效率. 因此,基于DBG索引方法不仅解决了先前算法的主要瓶颈——基因组上普遍存在的重复区域,还考虑在DBG的单路径上查找k-mer,它是一种全面高效的针对多参考序列的整个DBG索引方法.从实验结果中也可以看出,算法的压缩部分在时空上是高效的,在查找k-mer时的时间花费是很小的.另外,由于单路径是DBG上大量存在的结构,未来为进一步优化索引效率,可以针对DBG上的单路径进行细化研究.
参考文献
| [1] | El-Metwally S, Ouda O M, Helmy M. Next-generation sequencing platforms[J]. Springer New York, 2014, 7(4): 37-44. |
| [2] | Zhang H W, Chan Y D, Fan K C, et al. Fast and efficient short read mapping based on a succinct Hash index[J]. BMC Bioinformatics, 2018, 19(1): 92-105. DOI:10.1186/s12859-018-2094-5 |
| [3] | Burrows M, Wheeler D J. A block-sorting lossless data compression algorithm[J]. Technical Report Digital SRC Research Report, 1994, 124(1): 1-24. |
| [4] | Kim J, Chen L, Xie X. Improving read mapping using additional prefix grams[J]. BMC Bioinformatics, 2014, 15(1): 42-52. DOI:10.1186/1471-2105-15-42 |
| [5] | Li R Q, Li Y R, Kristiansen K, et al. SOAP: short oligonucleotide alignment program[J]. Bioinformatics, 2008, 24(5): 713-714. DOI:10.1093/bioinformatics/btn025 |
| [6] | Rumble S M, Lacroute P, Dalca A V, et al. SHRiMP: accurate mapping of short color-space reads[J]. Public Library of Science Computational Biology, 2009, 5(5): e1000386. |
| [7] | Homer N, Merriman B, Nelson S F. BFAST: an alignment tool for large scale genome resequencing[J]. Public Library of Science ONE, 2009, 4(11): e7767. |
| [8] | Li H, Richard D. Fast and accurate short read alignment with Burrows-Wheeler transform[J]. Bioinformatics, 2010, 25(14): 1754-1760. |
| [9] | Langmead B, Salzberg S L. Fast gapped-read alignment with Bowtie 2[J]. Nature Methods, 2012, 9(4): 357-359. DOI:10.1038/nmeth.1923 |
| [10] | Li R Q, Yu C, Li Y R, et al. SOAP2: an improved ultrafast tool for short read alignment[J]. Bioinformatics, 2009, 25(15): 1966-1972. DOI:10.1093/bioinformatics/btp336 |
| [11] | Ferragina P, Manzini G. Opportunistic data structures with applications[C]//Foundations of Computer Science. Redondo Beach: IEEE, 2000: 390-398. |
| [12] | Simon G. A de Bruijn graph approach to the quantification of closely-related genomes in a microbial community[J]. Journal of Computational Biology, 2012, 19(6): 814-825. DOI:10.1089/cmb.2012.0058 |
| [13] | Ye Y Z, Tang H X. Utilizing de Bruijn graph of metagenome assembly for metatranscriptome analysis[J]. Bioinformatics, 2016, 32(7): 1001-1008. DOI:10.1093/bioinformatics/btv510 |
| [14] | Liu B, Guo H Z, Michael B, et al. deBGA: read alignment with de Bruijn graph-based seed and extension[J]. Bioinformatics, 2016, 32(21): 3224-3232. DOI:10.1093/bioinformatics/btw371 |
| [15] | Fatemeh A, Hirak S, Avi S, et al. A space and time-efficient index for the compacted colored de Bruijn graph[J]. Bioinformatics, 2018, 34(13): 169-177. DOI:10.1093/bioinformatics/bty292 |
| [16] | Bowe A, Onodera T, Sadakane K, et al. Succinct de Bruijn graphs[C]//Workshop on Algorithms in Bioinformatics. Berlin: Springer, 2012: 225-235. |
| [17] | Muggli M D, Alexander B, Noyes N R, et al. Succinct colored de Bruijn graphs[J]. Bioinformatics, 2017, 33(20): 3181-3187. DOI:10.1093/bioinformatics/btx067 |
| [18] | Almodaresi F, Pandey P, Patro R. Rainbowfish: a succinct colored de Bruijn graph representation[C]//Workshop on Algorithms in Bioinformatics. Dagstuhl, 2017: 1-15. |
| [19] | Grabherr M G, Haas B J, Yassour M, et al. Full-length transcriptome assembly from RNA-Seq data without a reference genome[J]. Nature Biotechnology, 2011, 29(7): 644-652. DOI:10.1038/nbt.1883 |
| [20] | Haas B J, Papanicolaou A, Yassour M, et al. Transcript sequence reconstruction from RNA-seq using the Trinity platform for reference generation and analysis[J]. Nature Protocols, 2013, 8(8): 1494-1512. DOI:10.1038/nprot.2013.084 |
| [21] | Isaac T, Garimella K V, Zamin I, et al. Integrating long-range connectivity information into de Bruijn graphs[J]. Bioinformatics, 2018, 34(15): 2556-2565. DOI:10.1093/bioinformatics/bty157 |
| [22] | Limasset A, Cazaux B, Rivals E, et al. Read mapping on de Bruijn graphs[J]. BMC Bioinformatics, 2016, 17(1): 237-248. DOI:10.1186/s12859-016-1103-9 |
| [23] | Iqbal Z, Caccamo M, Turner I, et al. De novo assembly and genotyping of variants using colored de Bruijn graphs[J]. Nature Genetics, 2012, 44(2): 226-257. DOI:10.1038/ng.1028 |
| [24] | Alipanahi B, Kuhnle A, Puglisi S J, et al. Succinct dynamic de Bruijn graphs[J]. Bioinformatics, 2021, 37(14): 1946-1952. DOI:10.1093/bioinformatics/btaa546 |
| [25] | Guo H Z, Fu Y L, Gao Y, et al. deGSM: memory scalable construction of large scale de Bruijn graph[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2021, 18(6): 2157-2166. DOI:10.1109/TCBB.2019.2913932 |
| [26] | Xin H Y, Shao M F, Carl K. Context-aware seeds for read mapping[J]. Algorithms for Molecular Biology, 2020, 15(1): 10-21. DOI:10.1186/s13015-020-00172-3 |
| [27] | Pruitt K D, Brown G R, Hiatt S M, et al. RefSeq: an update on mammalian reference sequences[J]. Nucleic Acids Research, 2014, 42(D1): 756-763. |