
 , 姚红良, 曹焱博, 郭俞良
, 姚红良, 曹焱博, 郭俞良 东北大学 机械工程与自动化学院,辽宁 沈阳 110819
收稿日期:2022-03-14
基金项目:国家自然科学基金资助项目(52075084)。
作者简介:窦金鑫(1996-),男,辽宁朝阳人,东北大学博士研究生;
姚红良(1979-),男,河北唐县人,东北大学教授,博士生导师。
摘要:为了抑制转子系统的扭转振动,提出了一种双稳态非线性能量阱(bi-stable nonlinear energy sink, BNES).首先介绍了BNES的结构和工作原理,在此基础上建立了转子-BNES耦合系统的动力学方程.然后利用数值计算方法,对BNES在瞬态和稳态激励下的振动抑制能力进行了研究,并与相同转动惯量的线性动力吸振器(linear dynamic vibration absorber, LDVA)进行了对比.最后,搭建测试平台,试验验证了BNES对转子系统扭转振动抑制的能力.研究结果表明,该BNES对转子系统的瞬态响应以及稳态响应具有良好的振动抑制效果;在给定的参数下,BNES的振动抑制能力优于LDVA.
关键词:双稳态非线性能量阱转子系统扭转振动振动抑制
Theoretical and Experimental Research of BNES in Torsional Vibration Suppression of Rotor Systems
DOU Jin-xin

 , YAO Hong-liang, CAO Yan-bo, GUO Yu-liang
, YAO Hong-liang, CAO Yan-bo, GUO Yu-liang School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: DOU Jin-xin, E-mail: doujinxin96@163.com.
Abstract: A bi-stable nonlinear energy sink(BNES) is proposed to suppress the torsional vibration of rotor systems. Firstly, the structure and working principles of BNES are introduced, and the dynamic equation of the rotor-BNES system is established. Then, the vibration suppression performance of BNES under transient and steady-state excitation is studied by the numerical calculation method, and compared with the linear dynamic vibration absorber(LDVA) with the same moment of inertia. Finally, a test platform is built to verify the capacity of BNES to suppress the torsional vibration of the rotor system. It is shown that the proposed BNES has a good vibration suppression effect on the transient response and steady-state response of the rotor system, and under the given parameters, the vibration suppression performance of BNES is better than that of LDVA.
Key words: bi-stabilitynonlinear energy sink (NES)rotor systemtorsional vibrationvibration suppression
旋转机械在服役过程中,由于各种激励和扰动等原因会产生剧烈振动.过多的有害振动会对旋转机械造成灾难性的影响,因此对转子系统进行振动抑制的研究非常重要.
目前,****们已经提出了很多方法用来抑制振动,包括动平衡[1]、支撑刚度调节[2]以及主动控制[3].此外,被动控制方法由于结构简单且不需要复杂算法辅助而被广泛应用于振动抑制领域[4].在主体结构附加线性动力吸振器是一种常用的被动控制方法,但这种方法只有在反共振点附近具有较好的振动抑制效果[5-6].因此,阻尼优化方法[7]、半主动控制[8]以及将线性吸振器非线性化[9]等振动控制方法逐渐出现.
非线性能量阱(nonlinear energy sink, NES)是一种被动控制方法,主要由非线性刚度、阻尼元件和NES质量组成[10].非线性刚度可以提供非线性的恢复力[11],且NES可以通过靶能量传递(target energy transfer, TET)机制将主系统的振动能量单向传递给NES质量,从而提高振动抑制效率[12].
研究表明,多稳态NES比单稳态NES更具有优势,主要原因是系统在多个稳态之间的跳跃能够消耗更多的能量.因此,研究者提出了各种多稳态NES,例如文献[13]提出了一种双稳态能量阱,并将其应用于转子系统的弯曲振动抑制;文献[14]对比了三稳态吸振器和双稳态吸振器的振动抑制能力;文献[15]从非线性特性的角度研究了双稳态吸振器的动力学响应.
上述研究已经说明了利用多稳态能量阱实现振动抑制的有效性.但针对多稳态能量阱对扭转振动抑制的研究目前很少[16],试验研究仅有1例[17].因此,为了扩大NES在扭转振动抑制上的应用范围,本文提出了一种应用于转子系统扭转振动的双稳态非线性能量阱(bi-stable nonlinear energy sink, BNES),对其结构原理、振动特性和抑振效果进行了理论和试验研究,并与线性动力吸振器进行了对比分析.
1 BNES结构与系统动力学方程1.1 BNES的结构如图 1a所示,静磁座固定在轴上,动磁座含有内置轴承,即动磁座相当于NES的质量.非线性刚度通过正负刚度磁副并联单元(共4个)来实现.
图 1(Fig. 1)
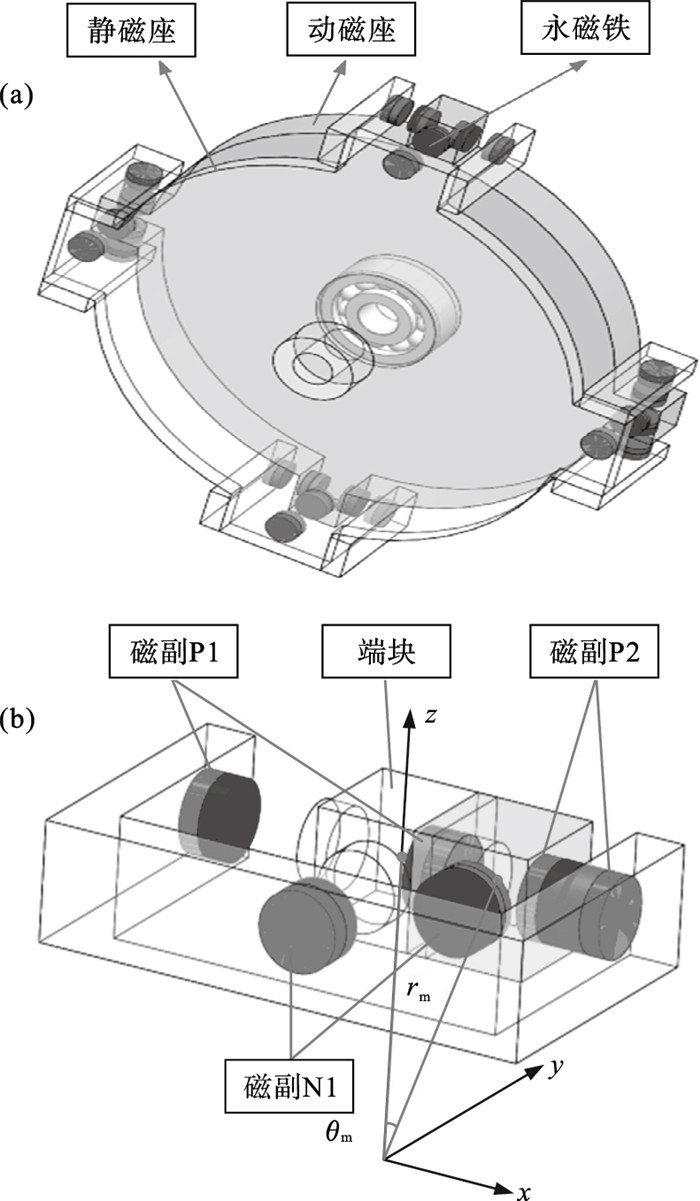 | 图 1 BNES的结构Fig.1 Structure of BNES (a)—整体结构;(b)—正负刚度磁副并联单元. |
正负刚度磁副并联单元的具体结构如图 1b所示.3对磁副中,磁副N1在x方向上的磁力用于提供负刚度,而磁副P1和P2在x方向上的磁力用来提供正刚度.结构中的永磁铁具有相同的尺寸和材料,并且磁化方向都沿其轴线方向.每对磁副中的磁铁都以互斥的方式配置.假设NES质量在扭转振动时,端块上的磁铁只在x方向上存在位移.当端块处于原点位置时(即黑色实线位置),NES质量为临界平衡状态.如果系统产生扭转振动使其偏离静态平衡位置,正负刚度磁副将共同产生所需要的非线性恢复扭矩.此外,可以通过在z方向上移动静磁座和动磁座来改变磁铁之间的距离.θm为扭转角,rm为磁铁的旋转半径.
1.2 BNES的双稳态刚度永磁铁的磁力计算模型如图 2所示.将左端磁铁的内外表面分别定义为面1和面2,右端磁铁的内外表面分别定义为面3和面4.磁铁的半径和厚度分别为Rm和cm,2个磁铁间的距离为hm,2个磁铁在x方向上的位移差为em.
图 2(Fig. 2)
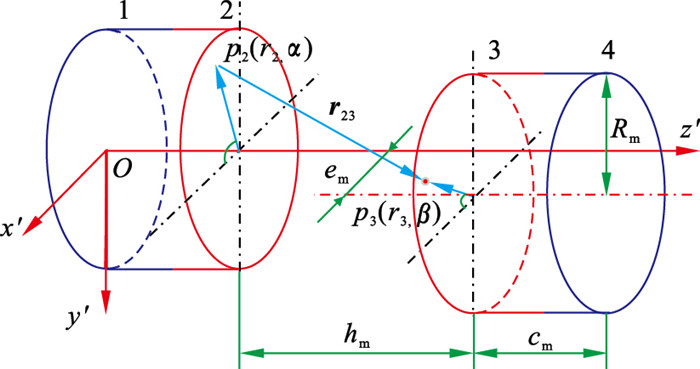 | 图 2 磁力计算模型Fig.2 Magnetic calculation model |
基于静磁学理论[18],磁铁的表面密度可以表示为
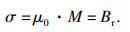 | (1) |
以面2和面3为例,计算永磁铁之间的力.面2上任意点p2处的磁荷为
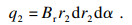 | (2) |
面2上点p2处的点磁荷在面3上任意点p3处产生的磁场强度为
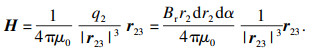 | (3) |
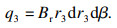 | (4) |
根据等效磁荷理论,可以得到点p3所受的磁场力为
 | (5) |
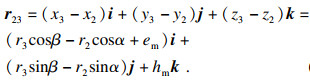 | (6) |
在面3上,点p3处x方向的磁力为
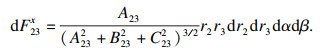 | (7) |
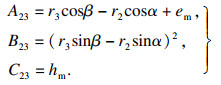 | (8) |
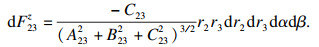 | (9) |
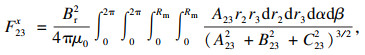 | (10) |
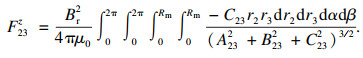 | (11) |
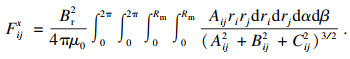 | (12) |
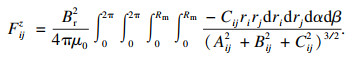 | (13) |
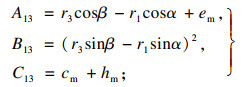 | (14) |
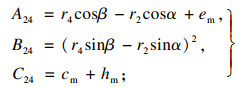 | (15) |
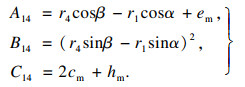 | (16) |
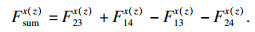 | (17) |
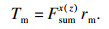 | (18) |
表 1(Table 1)
| 表 1 BNES参数 Table 1 BNES parameters |
根据以上参数,求得正刚度磁副P1和P2磁力Tp与位移的关系曲线如图 3a所示,负刚度磁副N1磁力Tn与位移的关系曲线如图 3b所示.将作用于NES质量上的磁力相加,可以得到正负刚度磁副并联结构磁力与位移的关系曲线如图 3c所示.图中A,B和C为平衡点.
图 3(Fig. 3)
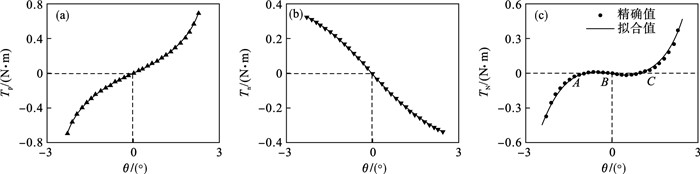 | 图 3 BNES的非线性力Fig.3 Nonlinear force of BNES (a)—Tp;(b)—Tn;(c)—TN. |
对图 3c中的精确值进行拟合,可以得到非线性扭矩TN的近似表达式如下:
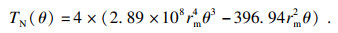 | (19) |
图 4(Fig. 4)
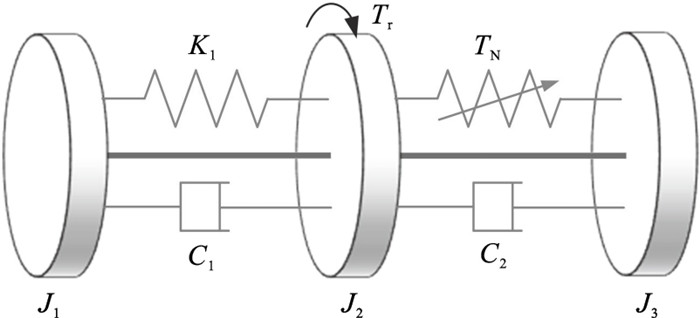 | 图 4 转子-BNES的动力学模型Fig.4 Dynamics model for the rotor-BNES system |
根据图 4所示的扭转振动动力学模型,该耦合系统的运动方程为
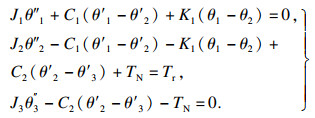 | (20) |
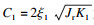
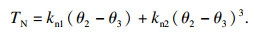 | (21) |
将φi=θi-θi+1(i=1, 2)代入式(20),消去转子刚体转动,将其转化为正定形式:
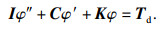 | (22) |
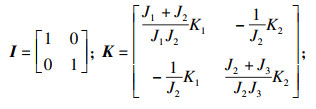 |
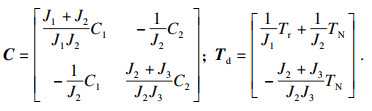 |
表 2(Table 2)
| 表 2 仿真参数 Table 2 Simulation parameters |
2.2 瞬态响应减振分析本节研究了BNES在瞬态激励作用下的扭转振动抑制性能.
1) 图 5a为θ2(t0)=1.5°时,未加吸振器、加LDVA(linear dynamic vibration absorber)与加BNES三种情况下转子系统的瞬态响应曲线.水平黑色虚线表示初始幅值的5%.可以看出,加入LDVA后,对转子系统的抑振效果并不明显,而加入BNES后,转子系统的振动幅值衰减较快.原因可以通过分析图 5b来解释,可以看到,在0~0.28 s的时间间隔内,BNES进行阱间运动,在其2个平衡点之间快速消耗初始能量.最后,BNES稳定在平衡点C.转子系统添加BNES后的小波谱图如图 6所示,可以看出,转子系统与BNES之间发生了1∶1共振.
图 5(Fig. 5)
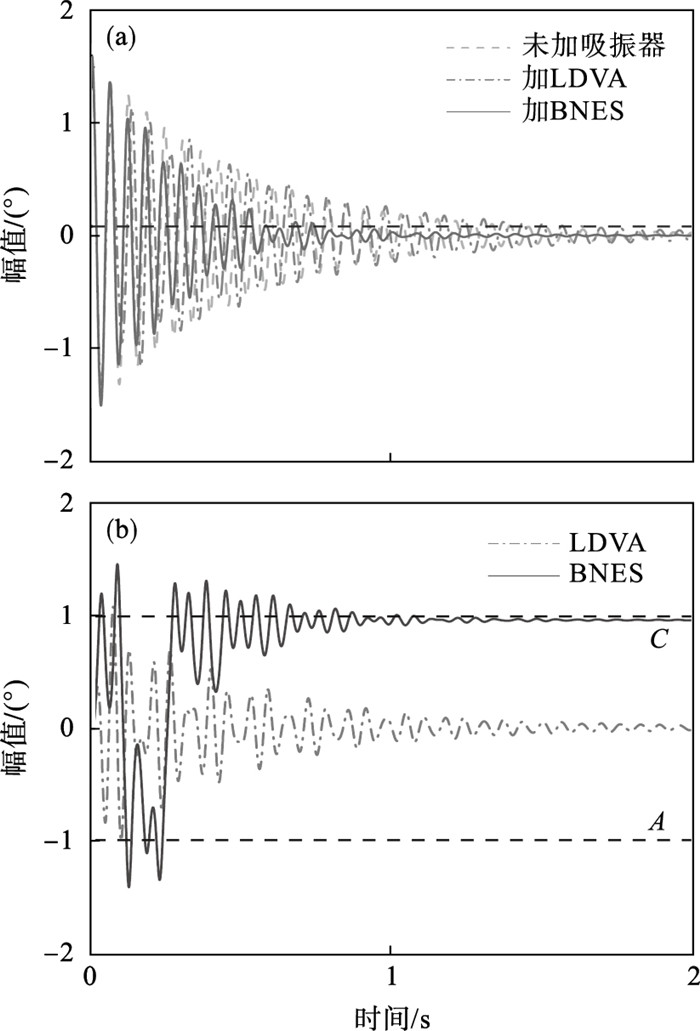 | 图 5 θ2(t0)=1.5°时耦合系统的瞬态响应曲线Fig.5 Transient response curves of the coupled system under θ2(t0)=1.5° (a)—转子系统;(b)—吸振器. |
图 6(Fig. 6)
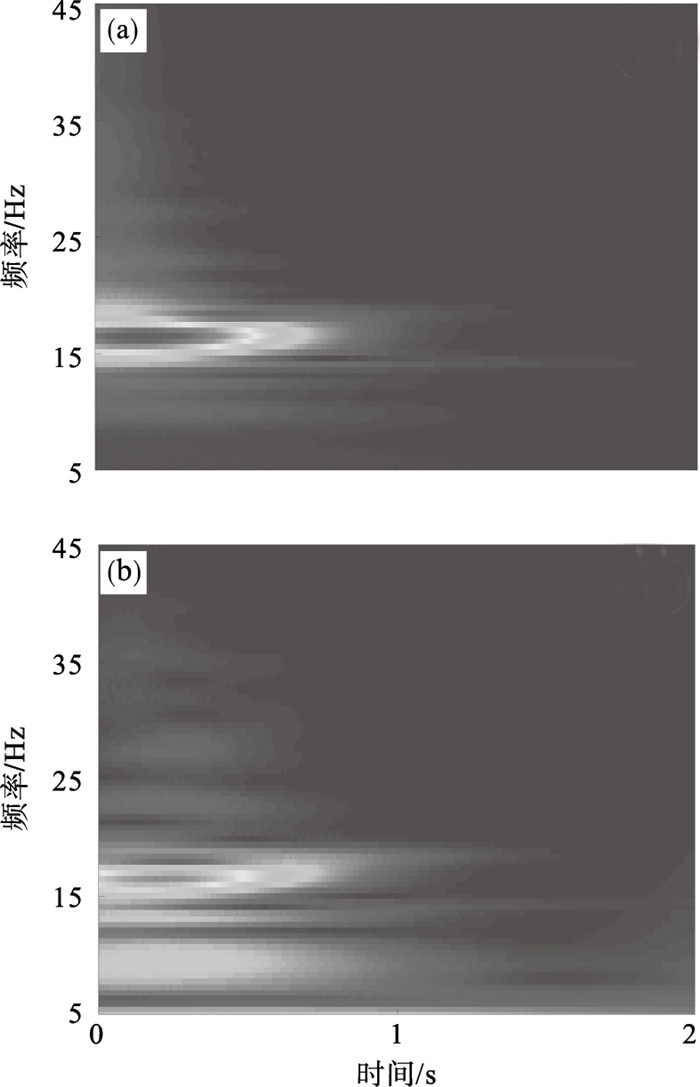 | 图 6 θ2(t0)=1.5°时耦合系统的小波谱图Fig.6 Wavelet spectra of the coupled system under θ2(t0)=1.5° (a)—转子系统;(b)—BNES. |
2) 将瞬态激励幅值增加到θ2(t0)=2.5°,从图 7a中可以看出,加入LDVA后,转子系统角位移幅值需要1.21 s下降到初始幅值的5%以下.加入BNES后,转子系统只需要0.59 s衰减到初始幅值的5%以下,耗能速度是加入LDVA的2.05倍.原因如图 7b所示,在0~0.25 s之间,BNES在其2个平衡点之间进行snap-through大幅值运动.穿过平衡点将导致更多的能量耗散,因此转子系统的振动抑制效率更高.最后,BNES稳定在平衡点A.转子系统添加BNES后的小波谱图如图 8所示,可以看出,转子系统与BNES之间在相同的频率范围内发生了能量传递,导致系统的初始输入能量被快速耗散.
图 7(Fig. 7)
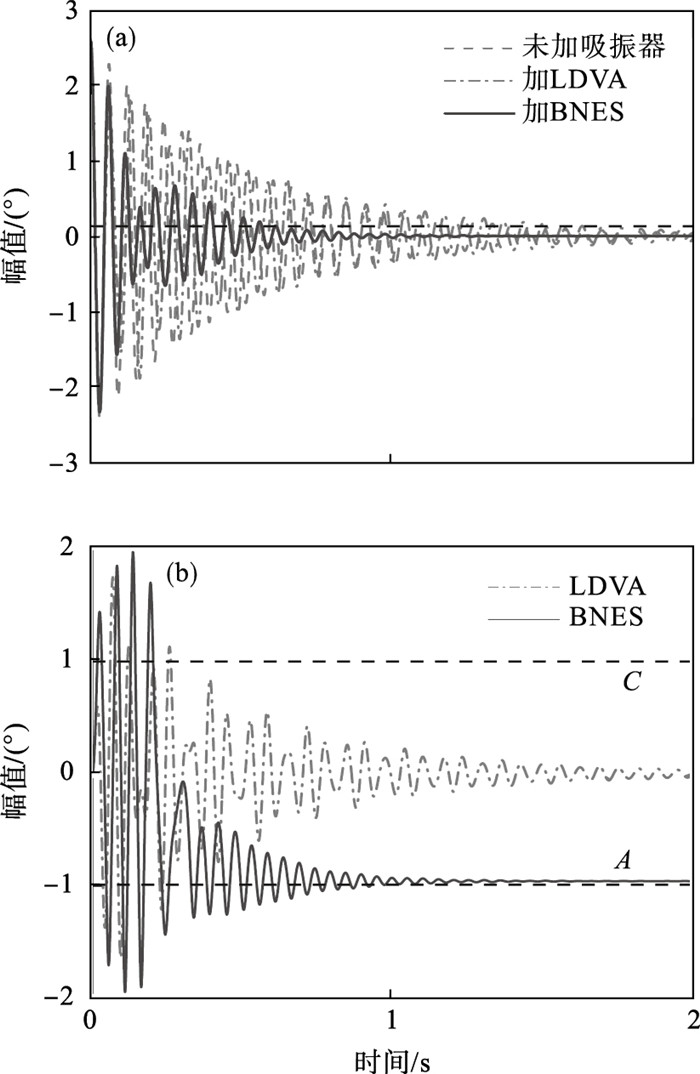 | 图 7 θ2(t0)=2.5°时耦合系统的瞬态响应曲线Fig.7 Transient response curves of the coupled system under θ2(t0)=2.5° (a)—转子系统;(b)—吸振器. |
图 8(Fig. 8)
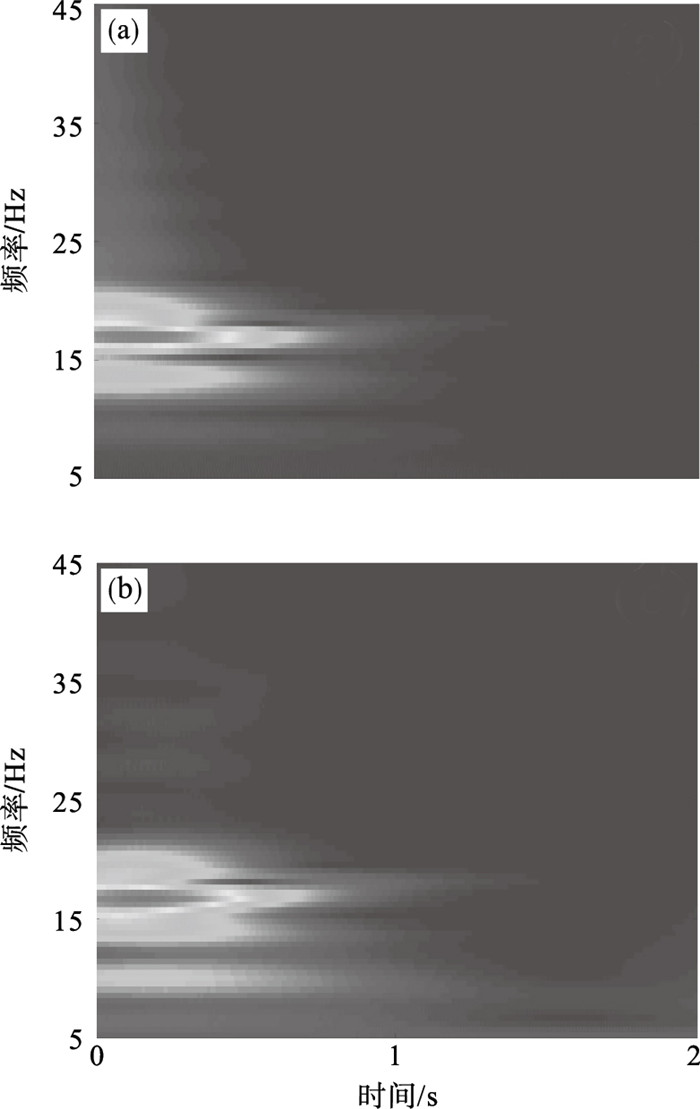 | 图 8 θ2(t0)=2.5°时耦合系统的小波谱图Fig.8 Wavelet spectra of the coupled system under θ2(t0)=2.5° (a)—转子系统;(b)—BNES. |
2.3 稳态响应减振分析本节中,将不同的周期激励应用于转子系统,来验证BNES的稳态振动抑制能力.
1) 首先令Tra=0.15 N·m.转子系统的幅频响应曲线如图 9a所示,未加吸振器的转子系统在16.5 Hz处的幅值为3.32°.加入LDVA后,转子系统最大幅值为2.34°,与未加吸振器相比,幅值降低了29.52%.加入BNES后,转子系统在14~20 Hz频率范围内出现SMR现象,表明BNES在共振点附近很好地抑制了转子系统的振动.转子系统最大幅值为1.7°,比未加吸振器时降低了48.80%.转子系统在16.5 Hz频率下的时域响应如图 9b所示,转子系统表现出非线性拍振现象.由图 9c可得,BNES进行混沌阱间运动,并在其2个平衡点之间振荡.
图 9(Fig. 9)
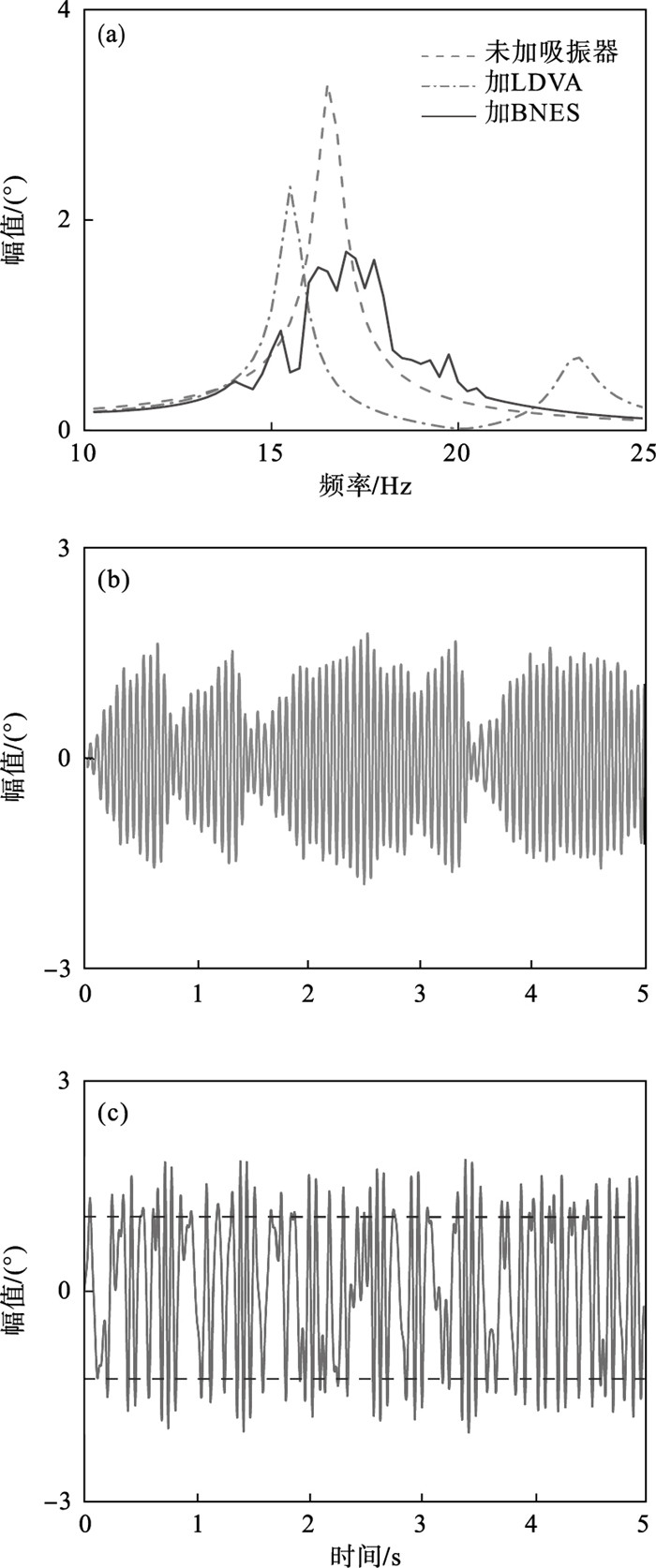 | 图 9 Tra=0.15 N·m时耦合系统的振动响应曲线Fig.9 Vibration response curves of the coupled system under Tra=0.15 N·m (a)—转子系统幅频响应;(b)—转子系统时域响应;(c)—BNES时域响应. |
2) 将周期激励幅值提高为Tra=0.25 N·m.如图 10a所示,未加吸振器的转子系统的共振频率仍为16.5 Hz,最大幅值为5.41°.添加LDVA和BNES对转子系统的扭转振动都有抑制能力,但BNES的抑振效果更加明显.BNES将响应幅值从5.41°降低到2.02°,振动抑制率为62.66%.此外,转子-BNES系统在14~23 Hz的频率范围内存在SMR现象.结果表明,适当增大激励幅值,BNES的抑振范围较图 9a变宽,抑振能力也增强.由图 10b可知,转子-BNES系统中发生了更加明显的拍振现象,这表明SMR行为发生在耦合系统的共振区域.从图 10c中可以看出,BNES在时间历程中穿过其平衡点并进行大振幅阱间振荡.
图 10(Fig. 10)
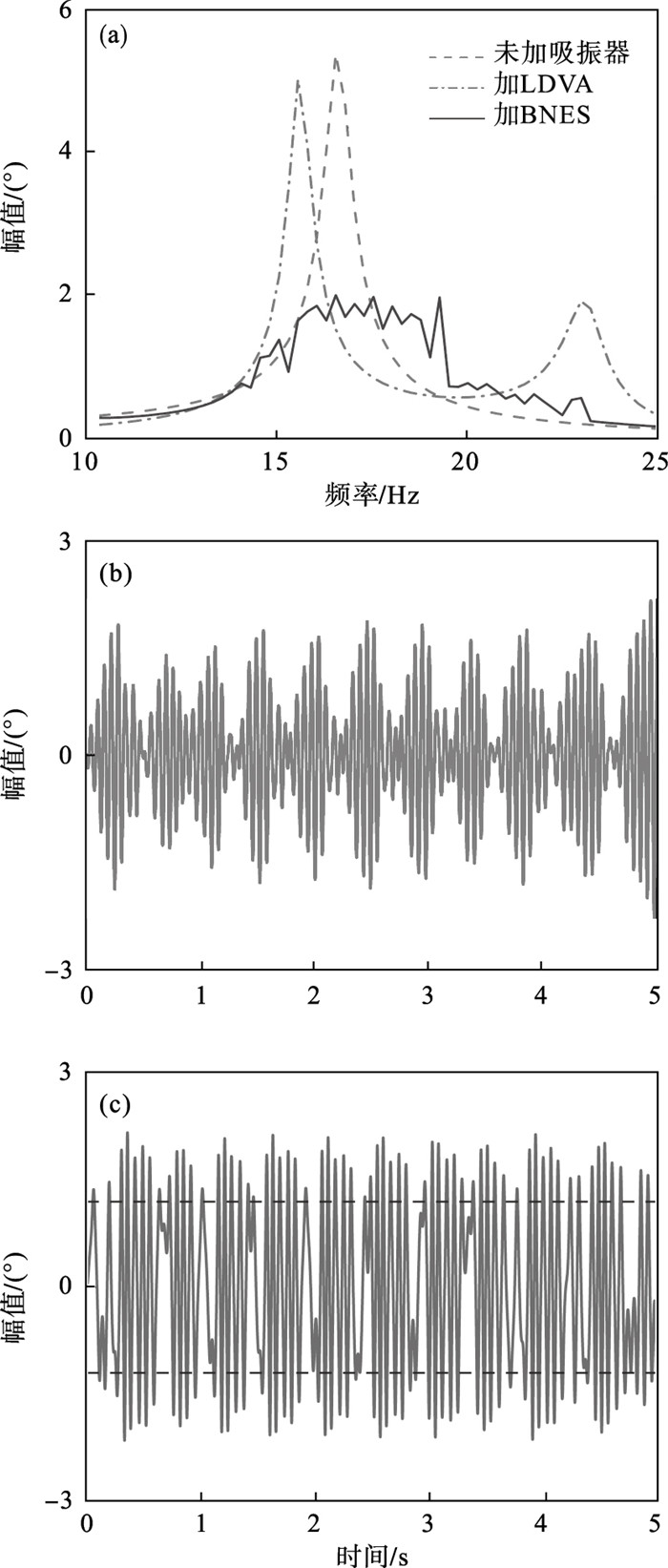 | 图 10 Tra=0.25 N·m时耦合系统的振动响应曲线Fig.10 Vibration response curves of the coupled system under Tra=0.25 N·m (a)—转子系统幅频响应;(b)—转子系统时域响应;(c)—BNES时域响应. |
3 试验研究3.1 试验建立为验证BNES的扭转振动抑制能力,建立了转子系统试验台如图 11所示,主要包括单盘转子系统、LMS SCADAS数据采集系统、Monarch激光转速传感器等.BNES安装在圆盘的附近,斑马带粘贴在圆盘以及PLA轻质圆盘的外表面,其旋转脉冲由激光传感器测量,并通过计算机的LMS Test.Lab工作站进行数据采集和分析.激光转速传感器安装在可调支撑座上,对应于斑马带分别设置在转轴的两端,并取两者的相对量来确定圆盘的扭转振动.
图 11(Fig. 11)
 | 图 11 试验装置Fig.11 Test device |
3.2 试验结果试验中,电机转速由60 r/min线性增加到1 500 r/min,得到转子系统的colormap图如图 12所示.由图 12a可以看出,不加BNES的转子系统出现了整数倍谐次(1谐次、2谐次、3谐次和4谐次)以及非整数倍谐次(0.5谐次和1.5谐次)的扭转振动激励.加入BNES后,如图 12b所示,0.5谐次和1.5谐次消失,同时整数倍谐波分量的强度明显减弱.此外,从两图中可以看到转子系统的一阶共振频率均出现在16.67 Hz左右,与仿真结果一致.
图 12(Fig. 12)
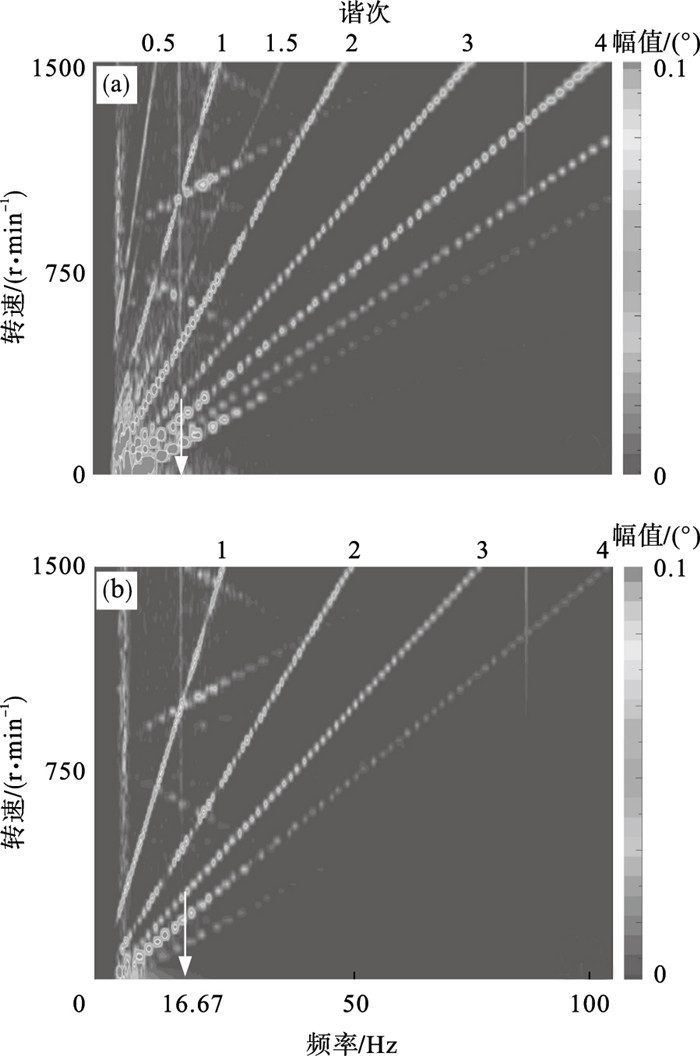 | 图 12 转子系统的colormap图Fig.12 Colormap of the rotor system (a)—未加BNES;(b)—加BNES. |
转子系统的角位移波动曲线如图 13所示.虚线为未加BNES的转子系统振动响应,可以看出转子系统存在较大的扭转波动幅值.当加入BNES后,响应幅值快速衰减,如实线所示.转速波动幅值(最大值与最小值的差值)由3.91°减小为1.07°,加入BNES前后角位移波动曲线的均方根由1.73°减小为0.41°,振动抑制率分别为72.63%和76.30%,说明了BNES具有良好的振动抑制能力.
图 13(Fig. 13)
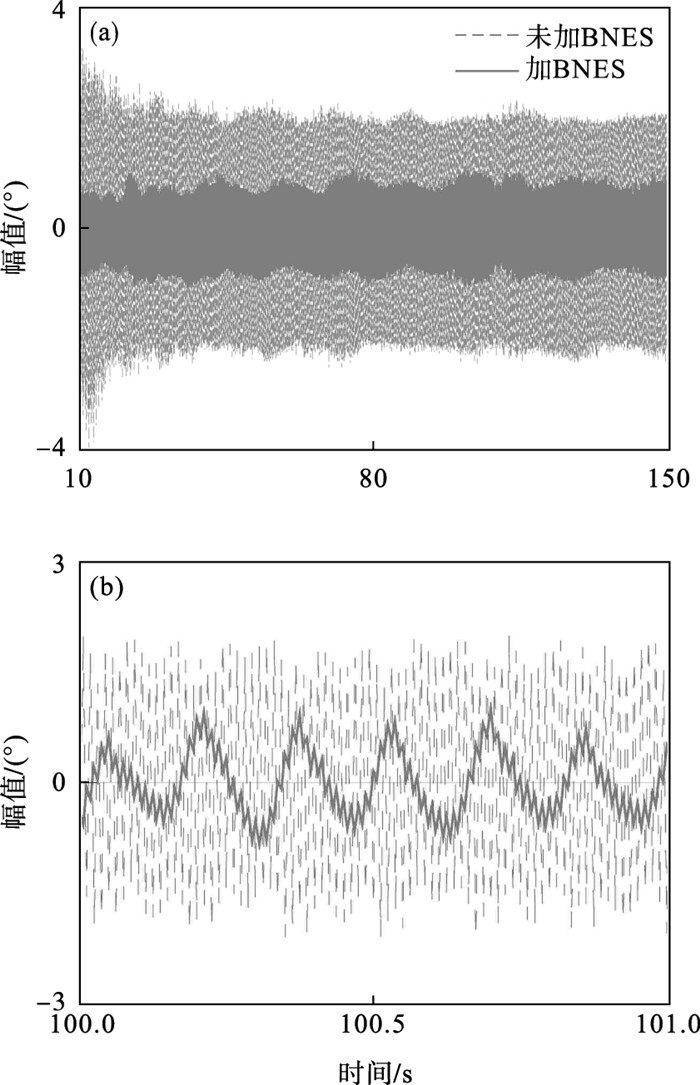 | 图 13 转子系统的时域响应曲线Fig.13 Time response curves of the rotor system (a)—整体;(b)—局部放大. |
转子系统在ω=996 r/min(16.6 Hz)时的振动响应如图 14所示.由图 14a可以看出,当转子系统添加BNES后,角位移波动幅值迅速衰减,幅值绝对值的算术平均值由0.63°衰减到0.29°,均方根值由0.75°衰减到0.35°,衰减率分别为53.97%和53.33%,说明所提出的BNES对定转速工况下的转子系统也具有良好的振动抑制能力.此外,由图 14b可以看出,转子系统在16.6 Hz时发生了明显的拍振现象.
图 14(Fig. 14)
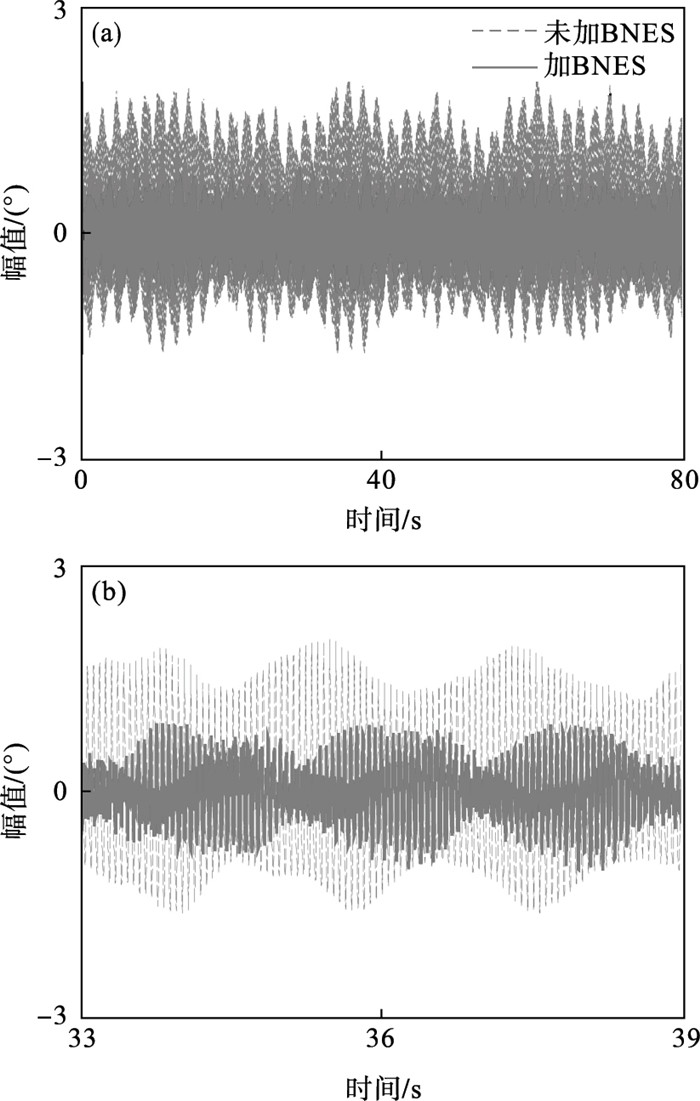 | 图 14 ω=996 r/min时转子系统的时域响应曲线Fig.14 Time response curves of the rotor system under ω=996 r/min (a)—整体;(b)—局部放大. |
4 结论1) 当采用相同转动惯量的BNES和LDVA对转子系统进行扭振振动抑制时,BNES的减振效果优于LDVA.
2) 转子系统在不同瞬态激励下的动力学响应表明,BNES能够快速耗散主体结构的能量.
3) BNES在仿真中对稳态响应的振动抑制率可以达到62.66%,而在试验中振动抑制率可以达到72.63%.
参考文献
| [1] | Haidar A M, Palacios J L. A general model for passive balancing of supercritical shafts with experimental validation of friction and collision effects[J]. Journal of Sound and Vibration, 2016, 384: 273-293. DOI:10.1016/j.jsv.2016.08.023 |
| [2] | Song Y S, Sun X T. Modeling and dynamics of a MDOF isolation system[J]. Applied Sciences, 2017, 7(4): 393. DOI:10.3390/app7040393 |
| [3] | Poplawski B, Miku?owski G, Wiszowaty R, et al. Mitigation of forced vibrations by semi-active control of local transfer of moments[J]. Mechanical Systems and Signal Processing, 2021, 157(2): 107733. |
| [4] | Ding H, Chen L Q. Designs, analysis, and applications of nonlinear energy sinks[J]. Nonlinear Dynamics, 2020, 100(1): 3061-3107. |
| [5] | Javad T, Morteza D, Hadi P M. Vibration mitigation of a nonlinear rotor system with linear and nonlinear vibration absorbers[J]. Mechanism and Machine Theory, 2018, 128: 586-615. DOI:10.1016/j.mechmachtheory.2018.07.001 |
| [6] | 鲁正, 王自欣, 吕西林. 非线性能量阱技术研究综述[J]. 振动与冲击, 2020, 39(4): 1-16, 26. (Lu Zheng, Wang Zi-xin, Lyu Xi-lin. A review on nonlinear energy sink technology[J]. Journal of Vibration and Shock, 2020, 39(4): 1-16, 26.) |
| [7] | Zhang X P, Kang Z. Vibration suppression using integrated topology optimization of host structures and damping layers[J]. Journal of Vibration and Control, 2014, 22: 60-76. |
| [8] | Arrigan J, Pakrashi V, Basu B, et al. Control of flapwise vibrations in wind turbine blades using semi-active tuned mass dampers[J]. Structural Control and Health Monitoring, 2011, 18(8): 840-851. DOI:10.1002/stc.404 |
| [9] | Li X, Zhang Y W, Ding H, et al. Dynamics and evaluation of a nonlinear energy sink integrated by a piezoelectric energy harvester under a harmonic excitation[J]. Journal of Vibration and Control, 2018, 25: 851-867. |
| [10] | 刘良坤, 潘兆东, 谭平, 等. 非线性能量阱系统受基底简谐激励的参数优化分析[J]. 振动与冲击, 2019, 38(22): 36-43. (Liu Liang-kun, Pan Zhao-dong, Tan Ping, et al. Parameter optimization analysis of a nonlinear energy sink system under base harmonic excitation[J]. Journal of Vibration and Shock, 2019, 38(22): 36-43.) |
| [11] | Bab S, Khadem S E, Shahgholi M, et al. Vibration attenuation of a continuous rotor-blisk-journal bearing system employing smooth nonlinear energy sinks[J]. Mechanical Systems and Signal Processing, 2017, 84: 128-157. DOI:10.1016/j.ymssp.2016.07.002 |
| [12] | 曹焱博, 李之傲, 韩金超, 等. 非光滑NES在转子-叶片系统振动抑制中的应用[J]. 东北大学学报(自然科学版), 2020, 41(8): 1103-1110. (Cao Yan-bo, Li Zhi-ao, Han Jin-chao, et al. Application of non-smooth NES in vibration suppression of rotor-blade systems[J]. Journal of Northeastern University(Natural Science), 2020, 41(8): 1103-1110.) |
| [13] | Yao H L, Wang Y W, Xie L Q, et al. Bi-stable buckled beam nonlinear energy sink applied to rotor system[J]. Mechanical Systems and Signal Processing, 2020, 138: 106546. DOI:10.1016/j.ymssp.2019.106546 |
| [14] | Huang X, Yang B. Investigation on the energy trapping and conversion performances of a multi-stable vibration absorber[J]. Mechanical Systems and Signal Processing, 2021, 160(4): 107938. |
| [15] | Rezaei M, Talebitooti R, Liao W H. Exploiting bi-stable magneto-piezoelastic absorber for simultaneous energy harvesting and vibration mitigation[J]. International Journal of Mechanical Sciences, 2021, 207: 107938. |
| [16] | Haris A, Motato E, Mohammadpour M, et al. On the effect of multiple parallel nonlinear absorbers in palliation of torsional response of automotive drivetrain[J]. International Journal of Non-linear Mechanics, 2017, 96: 22-35. |
| [17] | Haris A, Alevras P, Mohammadpour M, et al. Design and validation of a nonlinear vibration absorber to attenuate torsional oscillations of propulsion systems[J]. Nonlinear Dynamics, 2020, 100: 33-49. |
| [18] | Liu C, Zhao R, Yu K, et al. In-plane quasi-zero-stiffness vibration isolator using magnetic interaction and cables: theoretical and experimental study[J]. Applied Mathematical Modelling, 2021, 96: 497-522. |
