

1. 东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004;
2. 大连大学 机械工程学院,辽宁 大连 116622;
3. 燕山大学 国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004
收稿日期:2022-03-18
基金项目:河北省自然科学基金高端钢铁冶金联合基金项目(E2020501029);中央高校基本科研业务费专项资金资助项目(2022GFZD013)。
作者简介:赵玉倩(1977-),女,河北秦皇岛人,东北大学副教授;
韩毅(1982-),男,河北唐山人,燕山大学副教授,博士生导师。
摘要:风电齿轮体积庞大、结构较复杂且在感应加热时存在端部效应,导致难以实现齿廓及齿宽的均匀加热,影响最终强化质量.本文以平均温度、最大温差和相对温度浮动率作为加热效果判定指标,研究了风电齿轮在扫描感应加热过程中沿齿廓及沿齿宽方向的温度场,并对齿轮相变和淬硬情况进行分析.研究发现,一定范围内的温度均匀性在齿宽方向由齿顶至齿底逐渐提升,其原因在于齿形结构厚度的剧烈变化.在稳态位置经感应淬火强化的齿轮,齿廓方向淬硬层深度整体上几乎与宏观相变层深度保持一致,过渡区域相对较窄.阐明了齿轮扫描感应加热的效果以及强化结果,为高性能钢铁材料在风电领域广泛应用提供了研究基础.
关键词:齿轮风电感应加热温度均匀性淬硬层
Research on Temperature Uniformity of Gear Moving Induction Heating
ZHAO Yu-qian1, WANG Shan1, WEN Huai-yu2, HAN Yi3


1. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China;
2. School of Mechanical Engineering, Dalian University, Dalian 116622, China;
3. National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Yanshan University, Qinhuangdao 066004, China
Corresponding author: HAN Yi, E-mail: hanyi@ysu.edu.cn.
Abstract: Due to the huge volume, complex structure and end effect of wind power gear, it is difficult to realize the uniform heating of tooth profile and tooth width, which affects the final strengthening quality. In this paper, the average temperature, the maximum temperature difference and the relative temperature fluctuation rate are taken as the evaluation indexes of the heating effect. The temperature fields along the tooth profile and the tooth width direction of wind power gear in the scanning induction heating process are studied, and the phase transformation and hardening of the gear are analyzed. It is found that the temperature uniformity increases gradually in the direction of tooth width from top to bottom within a certain range, which is due to the drastic change of tooth structure thickness. To gears strengthened by induction hardening in steady-state positions, the depth of hardened layer in the direction of tooth profile is almost the same as the depth of macroscopic phase change layer, and the transition region is relatively narrow. The heating effect and strengthening result of gear scanning induction heating are expounded, which provides the research foundation for the wide application of high-performance steel materials in the field of wind power.
Key words: gearwind powerinduction heatingtemperature uniformityhardened layer
近些年,风电等清洁能源的快速发展对钢铁材料提出更高的要求.由于风电机组常服役于高山、低谷等风能资源丰富但环境恶劣的地区,维护成本高昂,因此,保证其关键部件的可靠性尤为重要.风电齿轮是风电机组正常运行的重要传动部件.感应淬火技术作为一种金属冶金加工有效的强化方式,凭借其清洁、高效的优势,对碳中和等产业发展产生积极影响.
良好的温度均匀性是获得沿齿廓均匀分布的硬化层以及全齿宽均匀淬硬的前提,也是保障齿轮表面强化质量的重要条件.然而,目前齿轮的感应淬火较难获得理想的硬化层,齿根位置以及端面位置是热处理的薄弱区域,容易产生软点和淬火软带,风电等重载齿轮更是如此,当齿轮发生偏载时,轮齿的两端未硬化区极易发生开裂失效.因此,实现全齿宽硬化是提高齿轮使用性能的重要途径[1].Lusgin等[2]在铸铁熔炼的多频加热中,改变现有低高频电流功率的调节方法,实现对熔池加热和金属运动的灵活控制.王宁等[3]发现感应加热能够明显提高加热速率,并有效解决在加热过程中温降的问题.Sung等[4]发现采用相邻方向相反的两种线圈均匀加热工具钢表面,可使表面具有更均匀的温度分布.Kierepka等[5]利用双频谐振逆变器改变形状不规则复杂元件的磁场穿透深度,从而达到控制加热过程的目的.Min等[6]研究发现不同的材料性能参数对感应加热过程有着不同的影响;感应焊管焊接生产中,受加热参数影响,焊缝表面沿壁厚形成沙漏状温度场[7];横向磁通感应加热可以有效加热连铸和热轧之间的板坯表面,选择合适的参数可使温度分布更加均匀[8].Barglik等[9]将连续双频淬火(consecutive dual frequency induct harding,CDFIH)工艺应用在齿轮的高频节能轮廓淬火中,并提出数学模型能够对硬化温度及硬度进行有效预测,获得齿轮的完全硬化区域的齿廓形状.Barglik等[10]认为短时高功率感应加热有利于提高齿面硬化层厚度均匀性.Su等[11]对一种新开发的两步感应加热(double induction quenching, DIQ)方法进行研究,发现进行过DIQ处理的硬化层中存在陡峭的压缩残余应变.
随着计算机技术的发展,计算机仿真技术越来越多被应用于制造领域,用以解决传统方式较难完成以及实验成本较高的工作与研究.感应加热的计算机仿真有助于明确工件内的磁场、温度场、功率分布等情况[12-13],进而明确加热区域温度相关影响[14],建立经验公式等[15].相较于实验方式,计算机仿真具有实施灵活、周期短的特点,并且可以探究实验较难发现的工件内部演变情况.周丹等[16]利用ABAQUS模拟软件,准确地预测球扁钢感应加热过程中截面温度场变化,并且预测结果可作为球扁钢感应加热工艺参数优化的参考;肖瑶等[17]利用有限元软件ANSYS以及专用焊接软件SYSWELD进行中频组织场模拟,得出加热后焊管焊缝附近的组织分布.将运动考虑在内的感应加热有限元模型可以得到更精确的数值结果[18-19],通过计算机模拟仿真的方式进行风电齿轮感应加热过程预测与研究,有利于提升研究效率,降低成本.
然而,目前专门针对感应加热过程中金属工件的温度分布和变化的研究相对较少.实现齿轮等材料感应加热的精确控制,明确其存在的温度分布形式及原因对生产精品钢铁具有积极意义.本文研究大模数风电齿轮扫描感应加热沿齿廓和齿宽方向的温度分布与温度场均匀性,为研究全齿宽硬化提供了有效手段,为适应未来风电产业的快速发展对高端齿轮的需求提供理论参考.
1 有限元模型本文以一风电机组齿轮箱齿圈为仿真对象,齿轮模数m=16,齿数z=95,齿宽b=200 mm.所用感应器为∏形感应器,图 1为∏形感应器电流走向和实体结构,其中hπ=10 mm,dmπ=20 mm,hπ0=40 mm.冷却采用在感应器端部增加喷淋孔的方式,根据感应器的实体结构可以得到该热处理过程的扫描速度为3.8 mm/s.扫描感应淬火的电参数均为用示波器测量感应线圈接线柱得到的,相关参数如表 1所示.所用电源为IGBT晶体管变频电源,额定输出功率为250 kW.
图 1(Fig. 1)
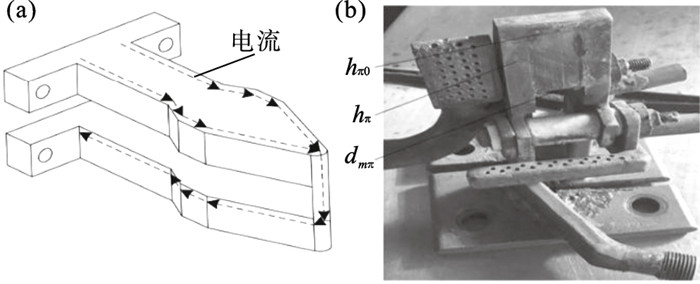 | 图 1 ∏形感应器Fig.1 ∏ shaped induction coil (a)—感应器中电流;(b)—感应器实体. |
表 1(Table 1)
| 表 1 扫描加热参数 Table 1 Parameters of scanning heating |
齿轮材料为42CrMo,加热时珠光体向奥氏体转变的温度AC1为718 ℃,铁素体向奥氏体转变的终了温度AC3为775 ℃.感应加热过程中,材料的磁导率、电阻率决定了涡流产生的过程,热导率、比热容则决定了传热过程.针对这4个与温度相关的重要物性参数,本模型采用查表法进行非线性变化的计算.
图 2为∏形感应器原理图与齿轮的有限元模型.在中频感应加热中,所用频率为6 000 Hz,计算得到波长为5×104 m,波长远大于所研究工件的几何尺寸.本文采用∏形感应器进行感应加热,其工作原理如图 2a所示.感应器的两侧形成一个完整的电流环,感应器放置于两齿之间,在齿轮上产生相应的涡流区.为了确保仿真结果的准确性同时节省计算成本,对齿轮进行如图 2b所示的网格划分.将渗透层中的网格进行精细划分,并在加热层与基体之间添加过渡层.由于加热时感应器靠近轮齿表面,在扫描加热过程中很难准确测量到加热表面温度,故采用感应淬火相变层深度测量实验来验证该动态仿真过程.
图 2(Fig. 2)
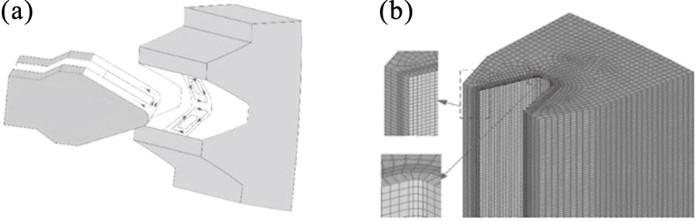 | 图 2 有限元模型Fig.2 Finite element model (a)—感应器原理;(b)—网格划分. |
在此工艺参数下,扫描至齿宽中部加热稳定状态的相变层宏观形貌如图 3所示,以感应器完全驶入齿轮开始计算,所截取齿轮截面位置为距离驶入端面100 mm处.其中,δm,δrl,δe,δrr分别表示侧向齿廓、左侧齿根圆角、齿根中部,以及右侧齿根圆角处的最小相变层深度.
图 3(Fig. 3)
 | 图 3 加热稳态相变层宏观形貌Fig.3 The macroscopic morphology of phase change layer at steady state |
位置不同,相变层深度也不同.侧向齿廓位置与齿根处相变层距离分别达到3 mm与2 mm,深度分别为δm=3.38 mm,δe=2.10 mm.而两侧齿根圆角位置,相变层深度则分别为δrl=1.65 mm,δrr=1.40 mm.左右两侧齿根圆角处相变层深度不一致,主要原因在于执行设备的运行偏差,导致感应器与两侧齿廓间隙存在误差从而使加热结果产生差异.同时,由于感应器喷淋孔的结构不能够保证完全对称导致冷却的不同,也会影响相变的结果.
在沿齿沟逐齿感应淬火中,端部淬火质量较薄弱.图 4所示为试件的不同位置截面,齿轮端面为起始位置,l1, l2, l3, l4分别表示相应截面与齿轮端面的距离,其中,l1=5 mm,l2=10 mm,l3=15 mm,l4=20 mm.运动参数引入后,将使加热过程发生改变,因而需再次对模型进行验证与修正.齿轮端部的冷却在整个齿宽处理中属于较佳区域,而加热结果较差.因此取l1处截面位置进行分析,该位置冷却充分使组织保存良好.
图 4(Fig. 4)
 | 图 4 取样位置说明Fig.4 Description of sampling location |
对试件打磨抛光后,使用4%硝酸酒精溶液腐蚀表面,获得如图 5a所示相变层形貌.对修正后模型的计算结果,截取相同位置的温度场,获取图 5b所示云图.结果显示,侧向齿廓位置相变层深度显著大于齿根及圆角处.齿轮材料42CrMo的相变起始温度为718 ℃,以此为判据测量仿真云图中的加热层深度.齿廓方向不同位置的加热层深度及相变层深度如表 2所示.
图 5(Fig. 5)
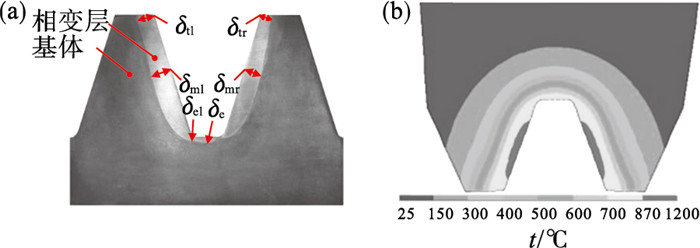 | 图 5 实验结果Fig.5 Experimental results (a)—相变层宏观形貌;(b)—截面温度场. |
表 2(Table 2)
| 表 2 相变层深度与加热深度 Table 2 Phase transformation layer depth and heating depth? | |||||||||||||||||||||||||||||||||||||||||||||||||||
图 5a及表 2均显示,实验获得的相变层具有显著的偏移现象,而仿真结果则具有良好的对称性.设备运行偏差在齿轮端部位置的影响尤其剧烈.因此将实验数据两侧对应位置的平均值,作为分析数据.在此,齿顶的相变层深度为4.65 mm,中部相变层深度为6.15 mm,左侧齿根圆角相变深度为1.60 mm,齿根相变层深度为2.50 mm.仿真结果与此相比,齿顶位置偏差5.38%,中部位置偏差7.30%,齿根圆角处偏差0%.而齿根处偏差较大,达到66.60%,这是由于感应器为图 1b所示结构,引发的冷却不足所导致的.综上认定,本文所建立的风电齿轮移动感应加热模型可以进行相关研究.
2 移动加热效果分析在齿轮的逐齿扫描感应加热中,齿轮两侧端部位置及中间部位的温度分布及演化过程存在较大差异.对齿轮端部及中间位置的齿廓方向温度分布,以及齿宽方向上的温度场进行研究,揭示移动加热的效果.为加热质量的预测以及工艺优化提供了参考依据.
2.1 相对温度浮动率分析在风电齿轮的移动感应加热过程中,由于感应器为上下两层线圈结构,导致同一位置先后经历了预热与加热两个过程.同时,在输入功率与频率一定的情况下,齿轮的表面温度可反映一定深度内的加热温度.因此,对于不同的分析截面,获取整个加热过程中表面上各位置的最高温度记为“综合温度”,以综合温度作为判定加热效果的基础数据.
对于齿廓方向,根据齿轮的特殊几何结构,建立由齿顶中点为起点,沿齿轮表面终止于齿根中点的路径.所建立的路径位于图 4所示的取样截面上.以平均温度与路径上的最大温度差Δtmax作为加热结果判定指标,其数据来源于节点上的综合温度.
对于齿宽方向,由于齿根位置加热状态相对稳定,因此对侧向齿廓的温度加热结果进行分析.建立如图 6所示的路径,因加热过程中的对称性,选取一侧齿廓作为研究对象.图 6所示的路径位于齿轮的一侧齿廓表面,LA-LA,LB-LB,LC-LC三条分析路径均与齿顶的棱边平行.路径完整地贯穿齿轮两侧,起于齿轮端面,经过侧向齿廓,终于另一端面.
图 6(Fig. 6)
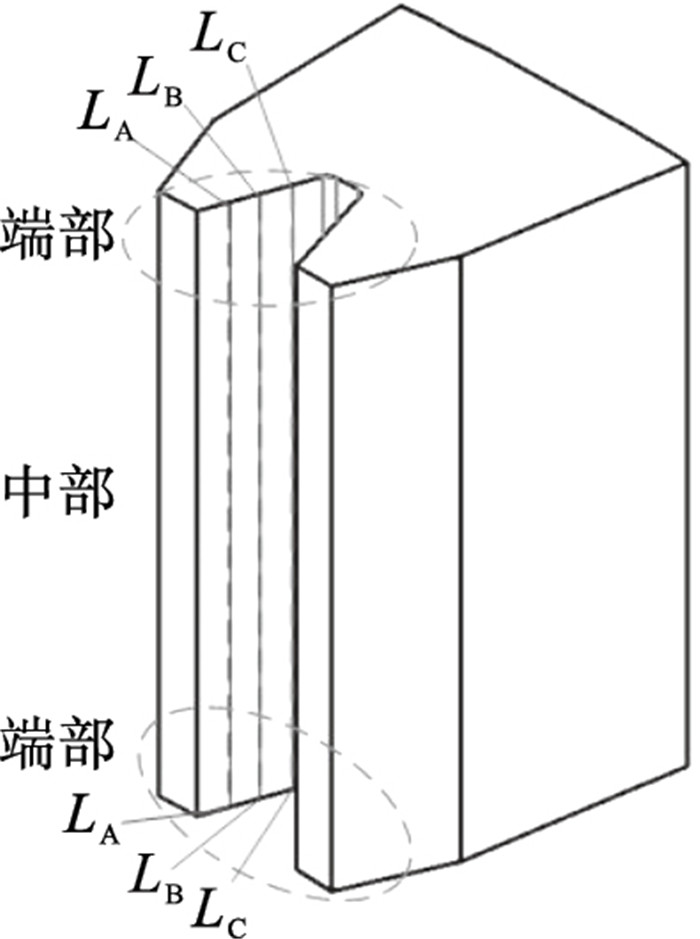 | 图 6 齿宽分析路径Fig.6 Analysis path of tooth width |
对于齿宽方向上的温度分布,除经综合温度计算的平均温度t及最大温度差Δtmax外,引入相对温度浮动率Ut作为另一判断指标.Ut的定义如式(1)所示.路径在齿宽中间部分的数据点选取数量,与两侧端部的数量相同.相对温度浮动率Ut的数值越大,则表示齿轮两端与中部的差距越大,温度在齿宽方向上的温度分布均匀性越差.
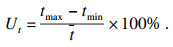 | (1) |
2.2 入口端加热效果分析图 7为截面齿廓方向温度变化.以图 4所示取样位置,获取完整加热过程中每个齿廓上节点的综合温度.齿轮入口端部位置的综合温度分布如图 7a所示.在l1=5 mm截面位置,齿廓侧边的综合温度显著高于其他截面,而齿根处温度则低于其他截面.原因在于齿轮端部具有的棱边结构,导致边部磁场集中,同时向外传热较小.而对于齿根及附近位置,由于l1=5 mm截面距离端面较近,使得此处磁力线逸散严重.在l2=10 mm截面到l4=20 mm截面位置,最高温度产生于齿根处,而齿根圆角位置温度则相对较低.原因则在于导磁体的驱磁作用使齿根磁力线集中,同时因导磁体的缺口,使得圆角附近的磁力线较少.
图 7(Fig. 7)
 | 图 7 截面齿廓方向温度变化Fig.7 Temperature in the direction of the cross-section tooth profile (a)—温度分布;(b)—平均温度与最大温度差. |
以图 7a中温度数据为基础,计算得到不同截面的平均温度与最大温度差Δtmax结果如图 7b所示.在l1=5 mm截面处的平均温度显著高于l2=10 mm至l4=20 mm截面处.由l2=10 mm向l4=20 mm截面位置靠近,平均温度有小幅度的升高.最大温度差Δtmax则先略有降低,而后显著升高.原因在于,齿轮的棱边使得靠近其位置截面的平均温度明显更高.随着位置由l2=10 mm截面继续深入,区域的保温效果较好,导致平均温度略有上升.
对于远离齿轮端面的l2=10 mm截面和l4=20 mm截面,不同位置的加热深度如表 3所示.其中,δt, δm, δr, δe分别表示齿顶、齿侧、齿根圆角以及齿根的加热深度.在不同截面中,齿根圆角处均为深度最小位置.在加热达到运动稳态之前,随着远离齿轮端面,加热深度逐渐降低.齿根圆角处不但是强化的薄弱区域,同时还是加热的薄弱区.
表 3(Table 3)
| 表 3 不同位置870 ℃加热深度 Table 3 Heating depth at 870 ℃ for different sections? | |||||||||||||||||||||||||||||||||||||||||||||
2.3 稳态齿廓加热效果分析感应器运动至齿轮中部达到加热稳态时,任一截面在一个完整的感应器扫描加热历程中,其加热过程皆相同.因此,对于加热稳态,只需选取一截面进行分析.截面上的综合温度分布如图 8所示.
图 8(Fig. 8)
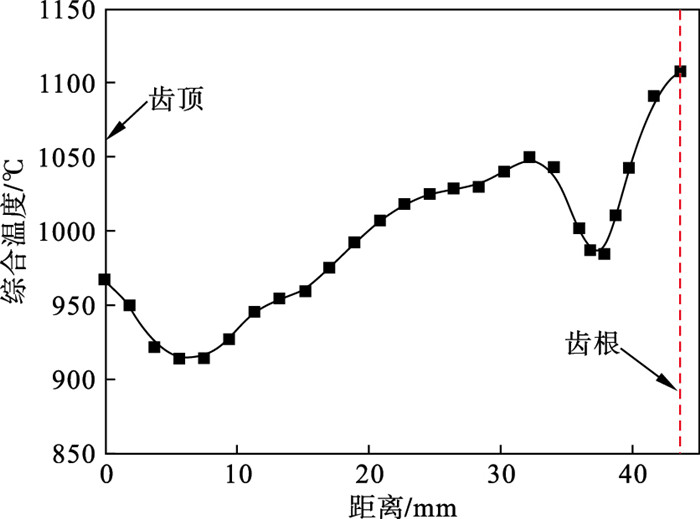 | 图 8 稳态位置齿面综合温度分布Fig.8 Comprehensive temperature distribution of tooth surface at steady state position |
在整个加热历程中,截面的温度最大值出现在齿根位置.整个截面上的平均温度t为995.9 ℃,最大温度差Δtmax达到194 ℃.稳态位置截面远离齿轮端面,最低温度由890 ℃上升为914 ℃,而最高温度几乎维持不变.914 ℃产生于第二层线圈扫描加热时,原因在于稳态位置时感应器运动的后方和前方温度整体较高,同时前方未加热区域热梯度降低.
当感应器运动达到加热稳态时,温度场三维等值面情况如图 9所示.齿根部分的高温区域覆盖范围显著高于齿侧位置.同时,虽然高温区域达到稳定的加热状态,但较低的温度范围仍存在明显的向齿端滞后的现象.滞后现象持续的时间随等温线下限的降低而不断延长.
图 9(Fig. 9)
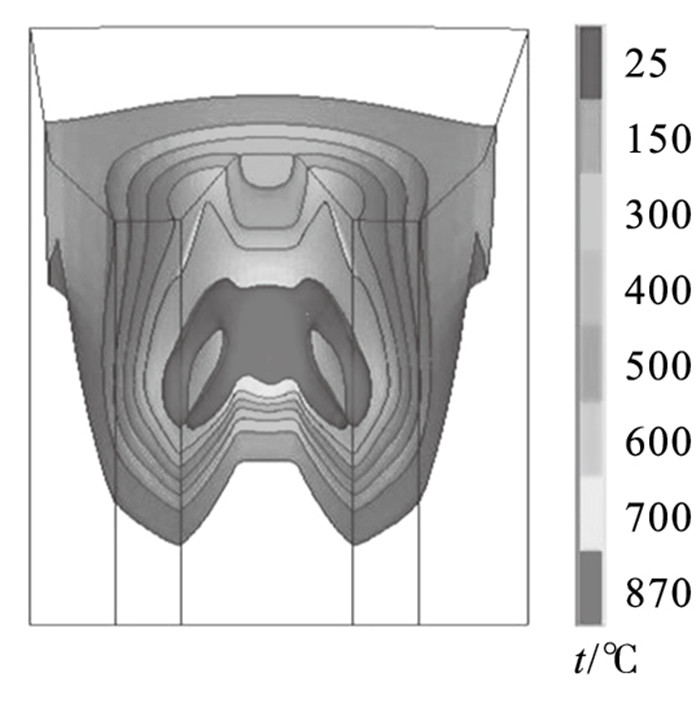 | 图 9 稳态位置温度等值面Fig.9 Temperature isosurface at steady state position |
在加热深度方向,生热情况将反向影响加热结果,齿轮内部对应位置与表面温度的差值是最直接的体现.图 10为深度方向温度图,如图 10a所示分别在齿顶、齿中、齿根以及齿底位置取分析节点,计算表面与内部温度差,取样深度为3 mm.D1-D1、D2-D2、D3-D3及D4-D4位置的温度差值随时间变化如图 10b所示.其中,起始时间为截面出现870 ℃高温区域时.
图 10(Fig. 10)
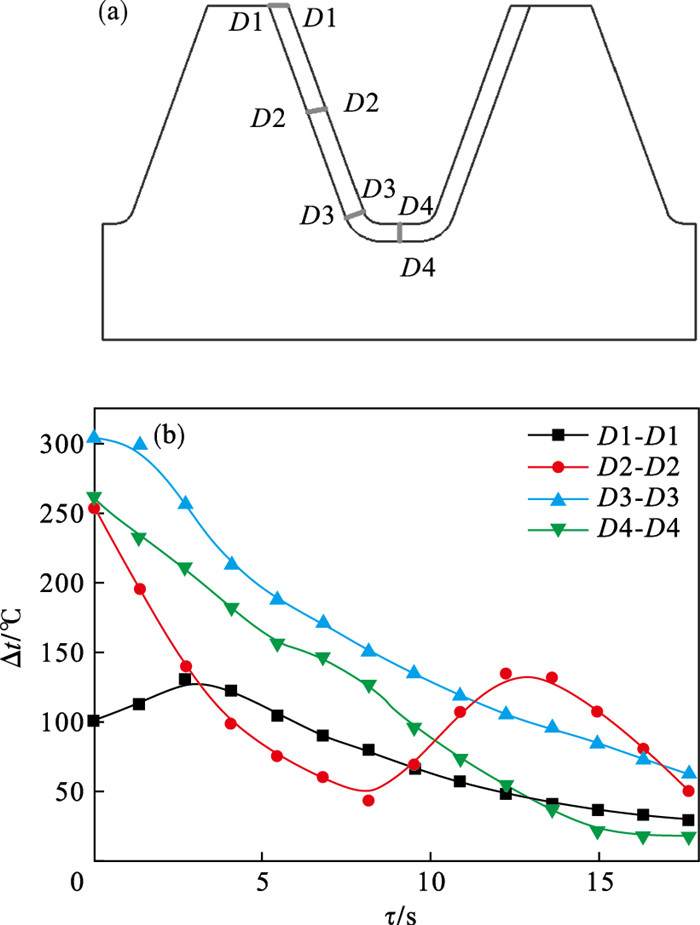 | 图 10 深度方向温度Fig.10 Temperature at depth direction (a)—取样位置;(b)—温度差值. |
如图 10b所示,齿根位置D4-D4,齿根圆角位置D3-D3的内外温度场Δt随着温度的升高而稳步降低.原因在于两处位置对应的感应器连续,加热始终连续稳定进行,持续的加热使温度越来越均匀.D3-D3处的温差波动幅度最大,达到79.5%.齿顶D1-D1的表面与内部温差首先升高,而后逐渐降低.原因则在于初始加热时能量在表面集中,而随着加热进行,剧烈的感应加热层不断向内移动.而侧向齿面中部的D2-D2位置,由于感应器在齿宽的不连续,导致温度差Δt发生起伏.同时,由于感应器侧边结构在齿宽方向上的不连续,导致扫描加热过程与静态产生差异.因此,侧向齿廓温度有所降低.
2.4 齿宽加热效果分析风电齿轮的扫描感应强化,全齿宽高质量淬硬始终是风电齿轮热处理的技术难题.优异的加热质量是获取高质量强化结果的前提,因此采用如图 6所示分析路径,以综合温度作为分析温度,对齿宽方向的加热效果进行分析,以期为齿宽方向加热质量的提升提供研究基础与依据.
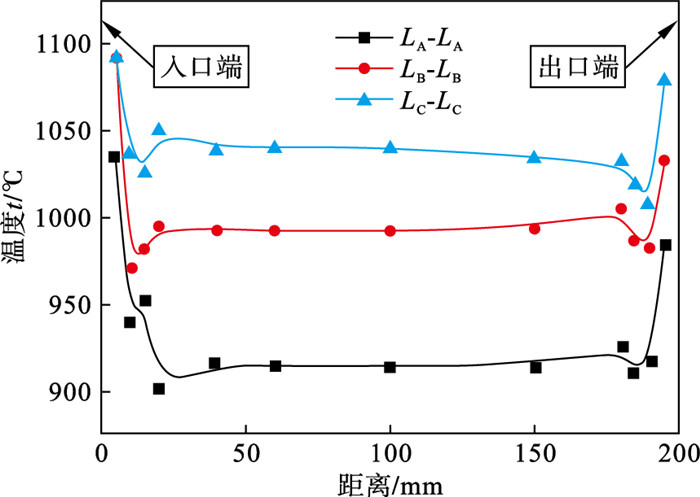
图 11为在齿宽方向上3条路径的综合温度分布.其中,入口端表示感应器驶入位置的齿轮端面,出口端表示感应器驶出位置齿轮的端面,图中横坐标表示与入口端之间的距离.3条分析路径在齿宽中部的温度分布较为平稳,而在两端面温度有显著变化.在距离两端面15 mm附近位置,温度有显著的降低,继续远离则稍有回升.齿轮端面的棱边结构,是其温度更高的直接原因.而热量的向内快速传递,则导致衔接处温度较低.并且由于感应器扫描加热过程中,齿轮中热量向其前方位置传递,导致端部温度更早到达居里点温度,因此3条路径上出口端的温度均低于入口端位置温度.
图 11(Fig. 11)
 | 图 11 齿宽方向表面温度分布Fig.11 Surface temperature distribution in the tooth width direction |
综合温度的最大温度差在LA-LA路径上达到133 ℃,LB-LB路径上为121.11 ℃,LC-LC路径上为86 ℃.由此可见,齿形几何结构在端面对加热结果的影响贯穿整个加热过程.LA-LA, LB-LB,LC-LC 3条路径上的温度浮动率分别为14.3%,12.1%以及8.3%.因此,齿宽方向上的加热温度结果,受齿形位置的影响较大.在齿侧位置沿着齿宽方向,由齿顶向齿根方向的温度均匀性不断提升,原因在于齿形结构厚度的剧烈变化.
3 感应强化实验研究经感应加热的齿轮,再经过急冷处理,将使其表层被强化,能够极大地提升现有性能.在冷速达到临界冷却速度且冷却充分的情况下,所获得的相变层与加热温度层能够较好地贴合.因此高温区域温度场边界,可表示理想冷却条件下的感应加热淬火强化层.而对于淬硬深度,则根据GB/T 5617—2005规定,淬硬深度处极限硬度为零件表面所要求的最低硬度的0.8倍.本节分别对齿轮相变情况,以及实际淬硬情况进行分析并观察组织成分,以明确最终强化结果.本实验中齿轮的表面硬度目标值为HRC58~62.
3.1 相变层深度分析不同截面位置的相变层变化如图 12所示.在各个截面位置,齿根圆角处的相变层深度均为最低.在靠近齿轮端部位置的l1=5 mm截面层,齿侧中部相变层深度变化平缓,这与加热结果及冷却过程相契合.而随着远离端面,相变层发生较快改变,中部位置相变层深度发生显著收缩.至l4=20 mm截面时,相变层达到稳定状态.而齿根及圆角处,随着远离端面,由于设备运行偏差导致的影响降低.
图 12(Fig. 12)
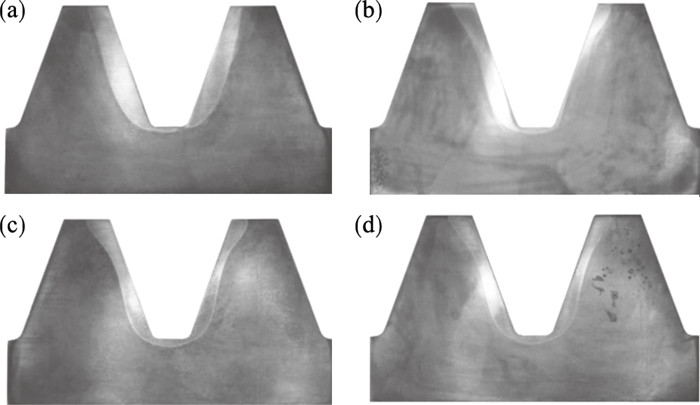 | 图 12 齿轮端部的相变层变化Fig.12 Phase transformation layer change on gear end face (a)—l1=5 mm;(b)—l2=10 mm;(c)—l3=15 mm;(d)—l4=20 mm. |
而远离端面位置的侧向齿廓中部,加热状态相对稳定,同时冷却状态相对稳定,因而产生相似的相变形貌.在齿侧中部位置,最高温度相对较低并且高温持续时间更短,因而深度下降.而齿顶的棱边结构,则会导致加热深度更大.同时结合感应器下方冷却结构,产生图 12所示的结果.
图 13为不同模数的齿轮逐齿感应淬火后的相变层形貌.图 13a中齿轮模数为14,图 13b中齿轮模数为20.两齿轮侧向齿廓靠近齿顶中上的位置,均如图 12中存在相似的相变层深度减小现象,图 13a中的减小现象相较于图 13b中的减小现象更为明显.同时随着模数增大,齿根及齿根圆角位置的相变层深度发生明显的降低.
图 13(Fig. 13)
 | 图 13 不同模数齿轮相变层Fig.13 Phase transformation layer of gear with different modulus (a)—模数14;(b)—模数20. |
将模数为16的齿轮侧向齿廓最小相变层深度δm继续细化为左侧最小相变层深度δml,以及右侧最小相变层深度δmr.l1至l4截面位置,其各处的相变层深度数值如表 4所示.左侧齿廓相变层深度在l1=5 mm时较大,达到了δml =5.80 mm.其余位置稳定在3.40 mm附近,变化率为43.1%.同样,右侧齿廓的相变层深度δmr由3.30 mm逐渐降低至2.90 mm.而齿根处以及两侧齿根圆角位置,相变层深度则不断增加.δrl由1.16 mm增加至1.83 mm,δe由1.50 mm增加至2.30 mm附近,δrr由0.51 mm增加至1.48 mm附近.然而,在此参数进行模数16齿轮的感应处理时,齿根及圆角位置硬化层与加热结果不完全匹配,原因在于感应器冷却结构导致齿轮对应位置的冷却不足.
表 4(Table 4)
| 表 4 不同截面位置相变层深度 Table 4 Depth of phase transformation layer at different section positions? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.2 金相组织图 14为实验齿轮的金相组织照片.图 14a显示42CrMo的原始组织为片状珠光体和铁素体组织.图 14b为经感应淬硬后的金相组织,经感应淬火后形成板条状马氏体组织.
图 14(Fig. 14)
 | 图 14 金相组织Fig.14 Optical microscopy image (a)—原始组织;(b)—顶端淬硬层组织. |
3.3 硬度分布硬度是判断齿轮淬火强化结果的一项重要指标,在硬化层内应获得相对均匀的硬度分布.测量硬度的硬度计为TMHV-30Z维氏硬度计,硬度计通过接口与计算机连接,测量得到的数据可以直接在计算机上转换成洛氏硬度并读取.为研究齿廓及深度方向的淬硬效果,建立图 15所示的5条分析路径进行显微硬度测定.其中路径HL1-HL1与齿廓平行,距离为0.5 mm.路径HL2-HL2与齿顶边界平行,距离为1.35 mm.路径HL3-HL3、HL4-HL4为与侧向齿廓垂直向内的路径,与齿顶距离分别为14.5 mm和29 mm.HL5-HL5为与齿根中心位置垂直向内的路径.
图 15(Fig. 15)
 | 图 15 硬度测量路径Fig.15 Hardness measuring path |
图 16为侧向齿廓HL1-HL1路径与齿顶HL2-HL2路径的硬度分布.齿廓HL1-HL1路径硬度几乎全部达到58HRC以上,符合硬度要求,并且硬度数值变化相对较小.HL2-HL2路径上,硬度在距离齿廓5 mm以内相对稳定,维持在较高数值.齿顶淬硬深度约为6.5 mm,小于相变层深度(7.45 mm).
图 16(Fig. 16)
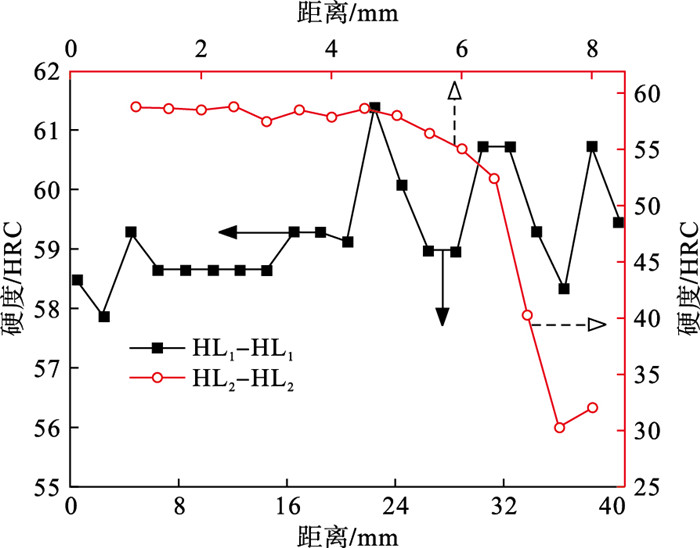 | 图 16 齿廓硬度Fig.16 Tooth profile hardness |
垂直于齿轮齿面的HL3-HL3至HL5-HL5路径上的硬度分布如图 17所示.在HL3-HL3路径上,硬化层内硬度较为稳定,在交界处硬度有显著降低.在HL4-HL4路径上的硬度从齿廓向内较均匀地降低,同样在齿根位置HL5-HL5路径上的硬度分布有相同的趋势.
图 17(Fig. 17)
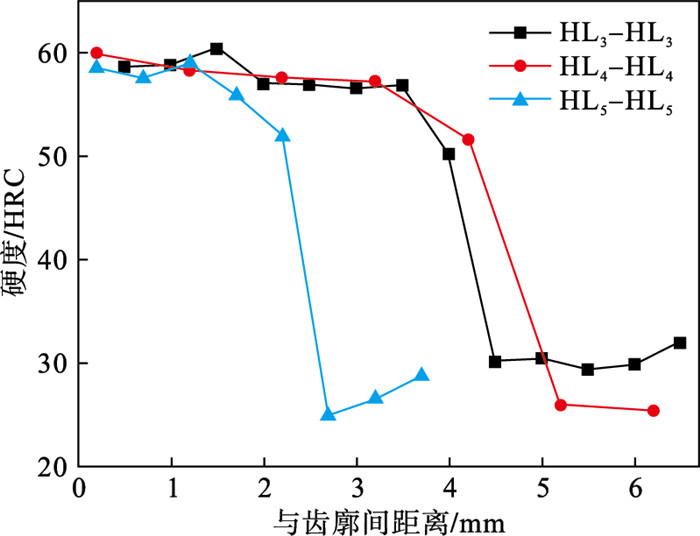 | 图 17 垂直于表面的硬度分布Fig.17 Hardness distribution perpendicular to the surface |
4 结论1) 在入口端距离齿轮端面不同位置,温度分布具有显著差异,平均温度与最大温度差同样具有明显的波动情况.
2) 在齿宽方向中间部位达到加热稳态,侧向齿面在整个齿宽方向由齿顶至齿底的温度均匀程度不断提升,温度偏差率最大可降低6%.
3) 在稳态位置经感应淬火强化齿轮的齿廓方向,淬硬层深度整体上几乎与宏观相变层深度保持一致,过渡区域相对较窄.淬硬区形成细小的马氏体组织,在相变交界区域存在明显的过渡性组织结构.
参考文献
| [1] | 汪正兵, 朱百智, 陈贺. 风电齿轮热处理技术现状和趋势[J]. 金属热处理, 2020, 45(1): 34-41. (Wang Zheng-bing, Zhu Bai-zhi, Chen He. Situation and trend of heat treatment technology in wind power gear[J]. Heat Treatment of Metals, 2020, 45(1): 34-41.) |
| [2] | Lusgin V I, Koptyakov A S, Petrov A U, et al. Power supplies for dual-frequency induction melting of metals[J]. IOP Conference Series: Materials Science and Engineering, 2018, 313(1): 1-7. |
| [3] | 王宁, 李宝宽, 齐凤升, 等. 蝶式感应加热中间包流场与升温特性[J]. 东北大学学报(自然科学版), 2021, 42(12): 1724-1730. (Wang Ning, Li Bao-kuan, Qi Feng-sheng, et al. Flow field and temperature rising characteristics of butterfly induction heating tundish[J]. Journal of Northeastern University (Natural Science), 2021, 42(12): 1724-1730. DOI:10.12068/j.issn.1005-3026.2021.12.008) |
| [4] | Sung Y T, Hwang S J, Lee H H, et al. Study on induction heating coil for uniform mold cavity surface heating[J]. Advances in Mechanical Engineering, 2014, 6: 349078. DOI:10.1155/2014/349078 |
| [5] | Kierepka K, Legutko P, Zimoch P, et al. Dual-frequency induction heating for gear hardening: converter, resonant circuit, and FEM modelling[J]. IET Power Electronics, 2018, 11(14): 2396-2402. DOI:10.1049/iet-pel.2018.5336 |
| [6] | Min C S, Young H M. Coupled electromagnetic and thermal analysis of induction heating for the forging of marine crank-shafts[J]. Applied Thermal Engineering, 2016, 98: 98-109. DOI:10.1016/j.applthermaleng.2015.11.129 |
| [7] | Han Y, Yu E L, Zhang H L, et al. Numerical analysis on the medium-frequency induction heat treatment of welded pipe[J]. Applied Thermal Engineering, 2013, 51(1/2): 212-217. |
| [8] | Yu C, Xiao H, Qi Z C, et al. Finite element analysis and experiment on induction heating process of slab continuous casting-direct rolling[J]. Metallurgical Research & Technology, 2019, 116(4): 403-502. |
| [9] | Barglik J, Smagor A, Smalcerz A, et al. Induction heating of gear wheels in consecutive contour hardening process[J]. Energies, 2021, 14(13): 3885-3899. DOI:10.3390/en14133885 |
| [10] | Barglik J, Ducki K, Kuc D, et al. Hardness and microstructure distributions in gear wheels made of steel AISI 4340 after consecutive dual frequency induction hardening[J]. International Journal of Applied Electromagnetics and Mechanics, 2020, 63(sup1): 131-140. |
| [11] | Su Y H, Oikawa K, Shinohara T, et al. Neutron bragg-edge transmission imaging for microstructure and residual strain in induction hardened gears[J]. Scientific Reports, 2021, 11(1): 4155-4169. DOI:10.1038/s41598-021-83555-9 |
| [12] | Bioul F, Dupret F. Application of asymptotic expansions to model two-dimensional induction heating systems. part I: calculation of electromagnetic field distribution[J]. IEEE Transactions on Magnetics, 2005, 41(9): 2496-2505. DOI:10.1109/TMAG.2005.854325 |
| [13] | Dughiero F, Forzan M. 3D solution of electromagnetic and thermal coupled field-problems in the continuous transverse flux heating of metal strips[J]. IEEE Transactions on Magnetics, 1997, 33(2): 2147-2150. |
| [14] | Luo J, Shih A J. Inverse heat transfer solution of the heat flux due to induction heating[J]. Journal of Manufacturing Science and Engineering, 2004, 127(3): 555-563. |
| [15] | Xu W, Ding W F, Zhu Y J, et al. Investigation on heating temperature characteristics during rotating induction brazing of monolayer CBN grinding wheels: numerical simulation and experimental verification[J]. International Journal of Applied Electromagnetics and Mechanics, 2017, 53(4): 697-713. |
| [16] | 周丹, 梁丰瑞, 王天琪, 等. 高强度球扁钢感应加热有限元模拟与工艺优化[J]. 中国冶金, 2019, 29(8): 45-51. (Zhou Dan, Liang Feng-rui, Wang Tian-qi, et al. Finite element simulation and process optimizing of induction heating for high strength bulb flat steel[J]. China Metallurgy, 2019, 29(8): 45-51.) |
| [17] | 肖瑶, 牛身身, 韩毅, 等. 高频直缝焊管中频热处理参数分析[J]. 钢铁, 2021, 56(5): 113-121. (Xiao Yao, Niu Shen-shen, Han Yi, et al. Analysis of intermediate frequency heat treatment parameters on high frequency straight welded pipe[J]. Iron and Steel, 2021, 56(5): 113-121.) |
| [18] | Cho K H. Coupled electro-magneto-thermal model for induction heating process of a moving billet[J]. International Journal of Thermal Sciences, 2012, 60: 195-204. |
| [19] | Yun J O, Yang Y S. Analysis of the induction heating for moving inductor coil[J]. Journal of Mechanical Science and Technology, 2006, 20(8): 1217-1223. |
