
 , 邹平, 曲圆辉, 方立廷
, 邹平, 曲圆辉, 方立廷 东北大学 机械工程与自动化学院,辽宁 沈阳 110819
收稿日期:2022-03-29
作者简介:刘晓寒(1997-), 男,安徽马鞍山人,东北大学硕士研究生;
邹平(1963-),男,辽宁沈阳人,东北大学教授,博士生导师。
摘要:为了解决传统成型加工过程中304不锈钢材料表面质量差、易产生毛刺等问题,设计了一种新型三维超声振动切削装置并进行了实验研究.首先通过对装置结构几何变形关系的分析,建立了刀尖的理论运动轨迹模型,通过Matlab对轨迹模型进行拟合并利用ANSYS对实际输出轨迹进行仿真分析,得到刀尖运动轨迹为空间中的三维抛物线.其次对装置进行有无超声振动切削实验,通过超景深系统和三维轮廓仪对已加工工件表面进行了测量和观察,发现超声振动切削下已加工表面粗糙度的算术平均高度明显小于普通车削的情况.结果表明:相较于普通车削,超声振动切削对于304不锈钢材料具有良好的加工性能.
关键词:超声振动切削装置结构设计轨迹建模有限元仿真超声振动加工
Design of a Single Excitation Three-Dimensional Vibration Cutting Device for Improving 304 Stainless Steel Machined Surface
LIU Xiao-han

 , ZOU Ping, QU Yuan-hui, FANG Li-ting
, ZOU Ping, QU Yuan-hui, FANG Li-ting School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: LIU Xiao-han, E-mail: 302793256@qq.com.
Abstract: In order to solve the problems of poor surface quality and easy to produce burrs in the traditional forming process of 304 stainless steel, a new type of three-dimensional ultrasonic vibration cutting device was designed and tested. Firstly, through the analysis of the geometric deformation relationship of the device structure, the theoretical motion trajectory model of the tool tip is established. The trajectory model is fitted by Matlab and the actual output trajectory is simulated by ANSYS. The tool tip motion trajectory is a three-dimensional parabola in space. Secondly, the cutting experiment with or without ultrasonic vibration was carried out on the device, and the machined workpiece surface was measured and observed by the super depth of field system and the three-dimensional profiler. It was found that the arithmetic average height of the machined surface roughness under ultrasonic vibration cutting is significantly lower than that of the ordinary turning. The results show that ultrasonic vibration cutting has better machinability for 304 stainless steel than conventional turning.
Key words: ultrasonic vibration cutting devicestructural designtrajectory modelingfinite element simulationultrasonic vibration machining
在过去的半个多世纪中,随着科学技术的迅猛发展,新的原创理论和工程技术层出不穷.作为工业生产和社会生活的支柱型行业,机械制造业在不断吸收新技术、开发新工艺的同时,也正在积极融合相关基础理论研究的新成果.在航空航天、半导体以及电子工程等领域内,业界对工件的加工精度和表面结构及质量的要求越来越高,同时也诞生了大量特殊材料和难加工结构的工件.对于这类工件的加工,使用传统的机械加工工艺,容易出现加工缺陷、加工精度难以保证等问题,难以满足切削加工要求,因此需要新式加工方法的出现[1].在各种新式精密加工研究中,超声振动切削技术是一种卓有成效的探索.超声振动切削是使刀具以20~40 kHz的频率、沿切削方向高速振动的一种特种切削技术,是目前制造领域中最为重要的切削方式之一.20世纪50年代,日本宇都宫大学的Kumabe最早提出一维振动辅助切削理论[2];90年代,在一维振动切削理论的基础上,日本名古屋大学的Shamoto与神户大学的Moriwaki提出椭圆振动辅助切削技术,即二维振动辅助切削理论[3];21世纪初,Shamoto等[4]在二维振动切削理论的基础上,又进一步提出了三维超声振动切削,从而逐步完善了超声加工的相关理论框架.其中,三维超声振动在具有二维超声振动原有优点的基础上,还可以大大降低切削过程中的摩擦力,具有很高的研究价值.但因其理论提出的时间最晚,目前发展还处于起步阶段,所以开展这方面的研究是很有意义的.目前关于三维超声装置的多种设计中,根据其输入源的数量,有单激励[5-6]、双激励[7-9]和三激励[10-12]等多种类型.本文拟设计一种单激励式三维振动切削装置,用于解决304不锈钢材料的高效率、高质量加工问题.
1 装置的构型设计和轨迹模型的建立1.1 装置的构型设计如图 1所示,装置主体由3条支链构成,其中支链1为压电陶瓷换能器,作为输入源提供输入;支链2为包含2个柔性铰链的双轴直圆柔性铰链支链;支链3为包含1个柔性铰链的双轴直圆柔性铰链支链.3条支链在空间中呈正三角形分布且每条支链均位于该正三角形的一个顶点上,刀具位于该正三角形的中心位置.3条支链的顶端与刀具所在平板相连,底端与机架固定.为便于后续分析,可按图 2所示结构对装置进行简化.AA′,BB′,CC′分别表示支链1、支链2、支链3.当支链1产生输入驱动装置时,刀具平面由原先的ABC变化至A3B3C3,如图 3所示.
图 1(Fig. 1)
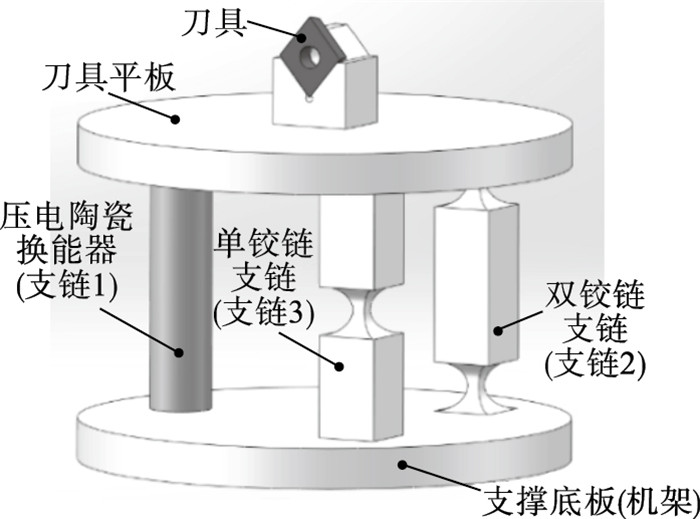 | 图 1 装置结构示意图Fig.1 Schematic diagram of device structure |
图 2(Fig. 2)
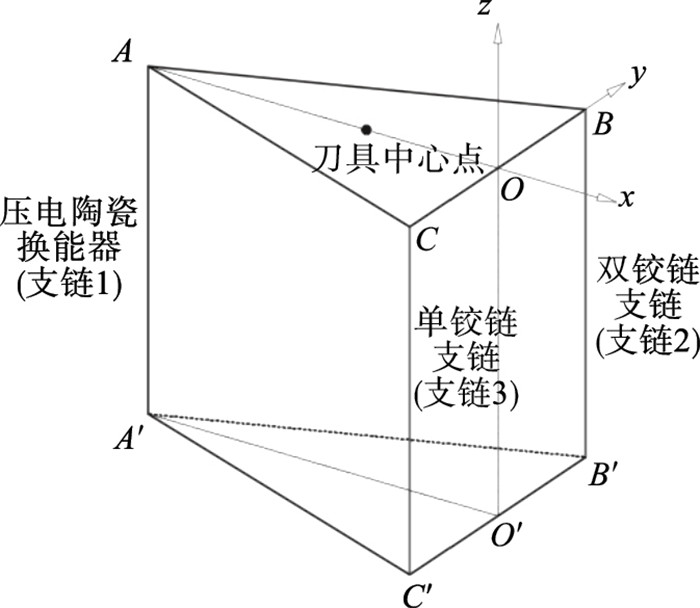 | 图 2 简化后的机构示意图Fig.2 Simplified mechanism diagram |
图 3(Fig. 3)
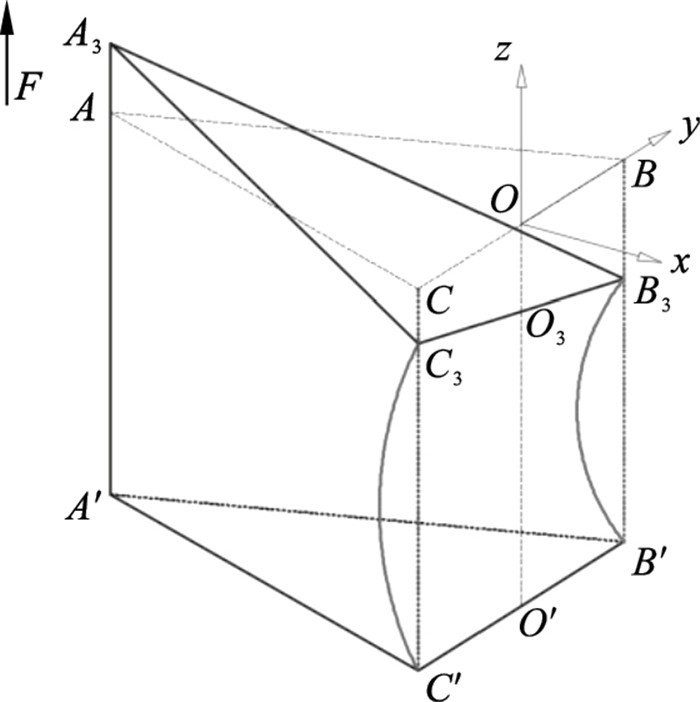 | 图 3 有输入时机构整体的变化情况Fig.3 Overall change of mechanism with input |
假设支链2,3的结构完全一致,则在xOz平面内,刀具会按图 4所示发生偏转,产生一个平面二维运动;但实际上,由于2条支链的结构并不完全一致,所以在发生弯曲时,两支链的弯曲量并不相同,从而在竖直方向上产生高度差,使得刀具在yOz平面内也发生偏转,如图 5所示,产生另一个平面二维运动.最终将这两个分别处在两相互垂直平面内的二维运动进行合成,使刀具产生空间中的三维轨迹.
图 4(Fig. 4)
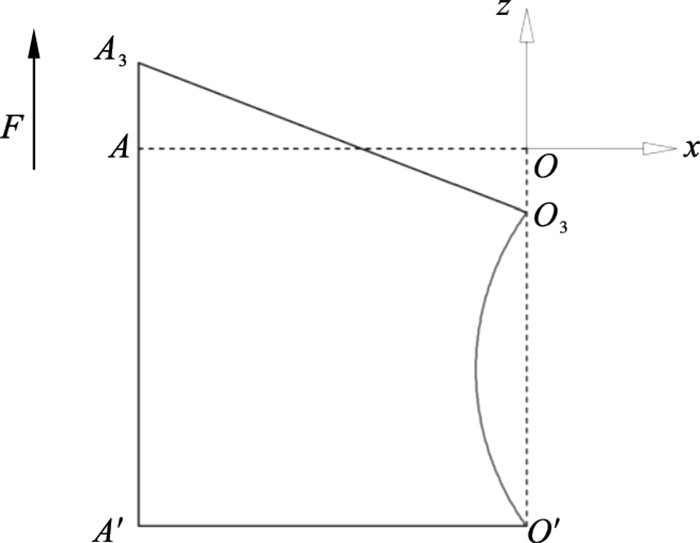 | 图 4 机构在xOz面内的变化情况Fig.4 Change of mechanism in the xOz plane |
图 5(Fig. 5)
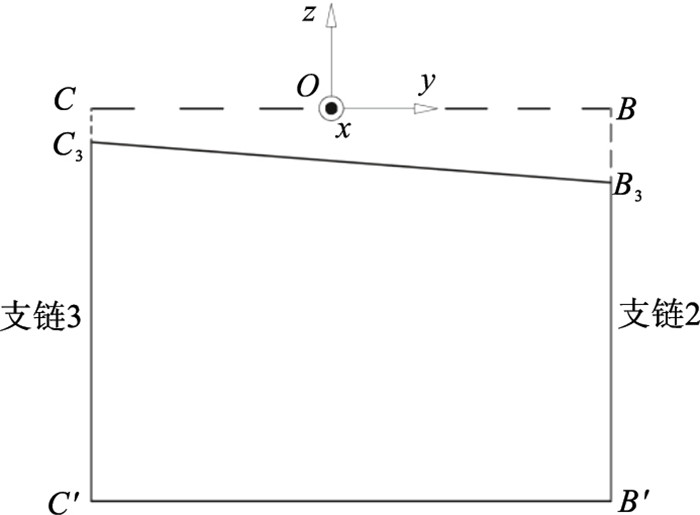 | 图 5 机构在yOz面内的变化情况Fig.5 Change of mechanism in the yOz plane |
1.2 刀尖运动轨迹模型的建立为了便于后续分析,建立轨迹模型时只考虑刀具在竖直方向上的运动情况,忽略由于铰链偏转等原因在水平方向上产生的位移变化.
图 3所示的机构变化情况可用图 6的简化示意图表示,ABC为初始时刻的刀具平面.当支链1产生输入y1时,设支链2,3的弯曲量分别为y2,y3;o,p分别表示初始时刻刀具底端和顶端;o3,p3分别表示产生运动后的刀具底端和顶端;以点p为原点建立空间直角坐标系.由于刀具固连在刀具平板上,所以对刀尖点p的轨迹分析可以转化为对刀具平面ABC的运动分析.图 6所示的运动简图可进一步按照图 7步骤进行分解,即刀具平面的变化情况如下:ABC—A1B1C1—A2B2C2—A3B3C3,根据上述分析过程,即可对刀尖输出轨迹进行建模,步骤如下:
图 6(Fig. 6)
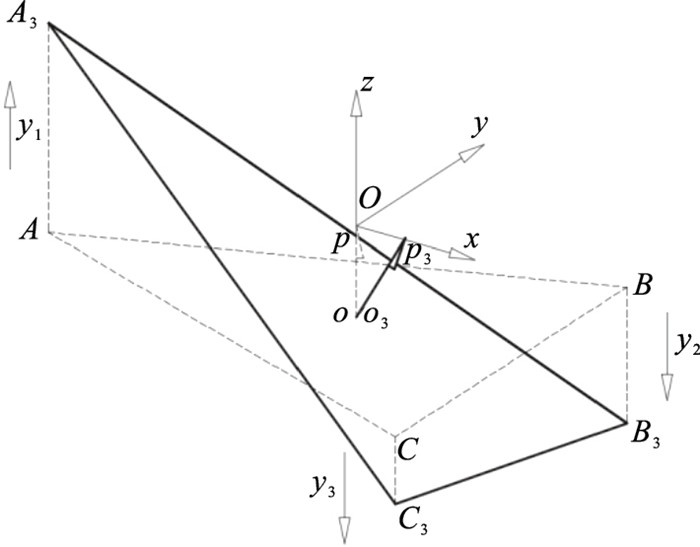 | 图 6 机构运动情况简图Fig.6 Schematic diagram of mechanism movement |
图 7(Fig. 7)
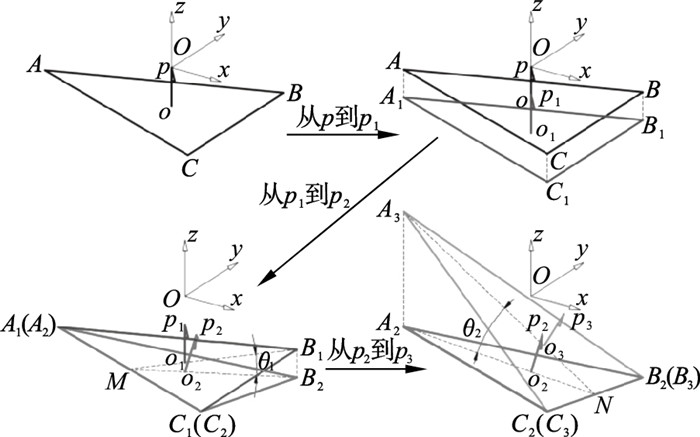 | 图 7 刀尖运动轨迹的分解Fig.7 Decomposition of tool tip trajectory |
① 支链1的位移y1属于输入位移,支链2,3的位移y2,y3属于输出位移,所以y1>y2,y1>y3,又因为支链2包含2个铰链,其弯曲能力强于只包含1个铰链的支链3,所以y2>y3.即3条支链位移的大小关系为y1>y2>y3.
② 设初始时刻刀尖点p坐标为(0, 0, 0),轨迹末端刀尖点p3坐标为(x, y, z),对点p到点p3的轨迹直接建模比较困难,可按照图 7所示步骤进行分解:初始时刻刀具平面为ABC,首先平面整体沿z轴负方向平移y3, 得到新平面A1B1C1;然后点B1向z轴负方向平移y2-y3到点B2,得到新平面A2B2C2;最后点A2向z轴正方向平移y1+y3到点A3,得到新平面A3B3C3,完成整个运动过程.
③ 设
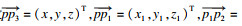
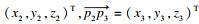
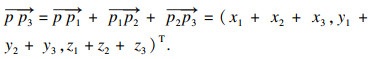 | (1) |
当刀具平面从ABC变化至A1B1C1时,将平面整体沿z轴负方向平移y3即可,有
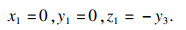 | (2) |
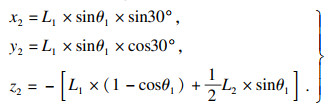 | (3) |
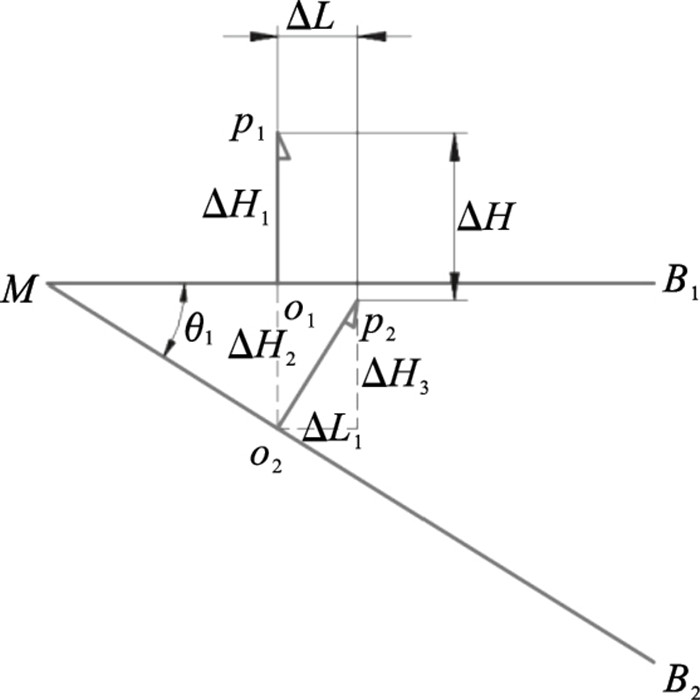 | 图 8 刀具平面第二次变化时的刀尖运动轨迹Fig.8 Tool tip trajectory when the tool plane changes for the second time |
当刀具平面从A2B2C2变化至A3B3C3时,设两平面的夹角为θ2,保持B2,C2两点不变,将点A2沿轴B2C2旋转角θ2即可, 相当于点A2沿z轴正方向平移y1+y3至点A3,如图 9所示,则有
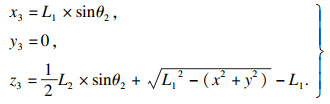 | (4) |
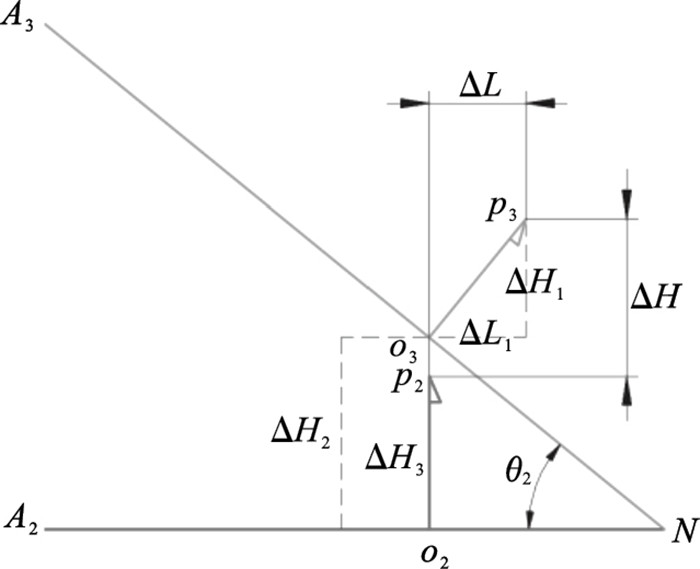 | 图 9 刀具平面第三次变化时的刀尖运动轨迹Fig.9 Tool tip trajectory when the tool plane changes for the third time |
⑤ 由式(1)可得,刀尖运动轨迹坐标为
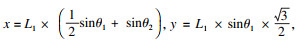
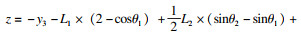
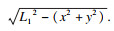
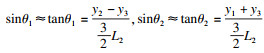
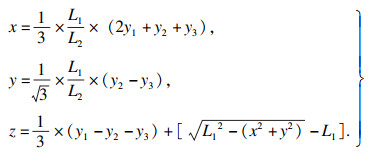 | (5) |
⑥ 设某时刻点A处的输入力大小为F1,支链2,3底端均与地相连,属于固定端约束,所受力系可简化为一个主矢和一个主矩.故设支链2底端B′所受力及力矩大小分别为F2x,F2z,M2,支链3底端C′所受力及力矩大小分别为F3x,F3z,M3,如图 10所示.对点O进行分析,可得力平衡:F1+F2z+F3z=0,F2x+F3x=0;力矩平衡:F1×AO=F2x×BB′+F3x×CC′+M2+M3,F2z×OB=F3z×OC,F2x×OB=F3x×OC, 联立解得F2x=F3x=0,F2z=F3z=-F1/2,即机构整体在水平方向上所受外力为零,在竖直方向上两支链所受力大小相等,方向与输入力方向相反.又因为3条支链的空间分布为正三角形,支链2,3的空间位置关于坐标轴Oz对称,且其所受轴向力大小及横截面积均相同,所以2条支链所受力矩也相同,即:M1=M2=(F1×AO)/2.
图 10(Fig. 10)
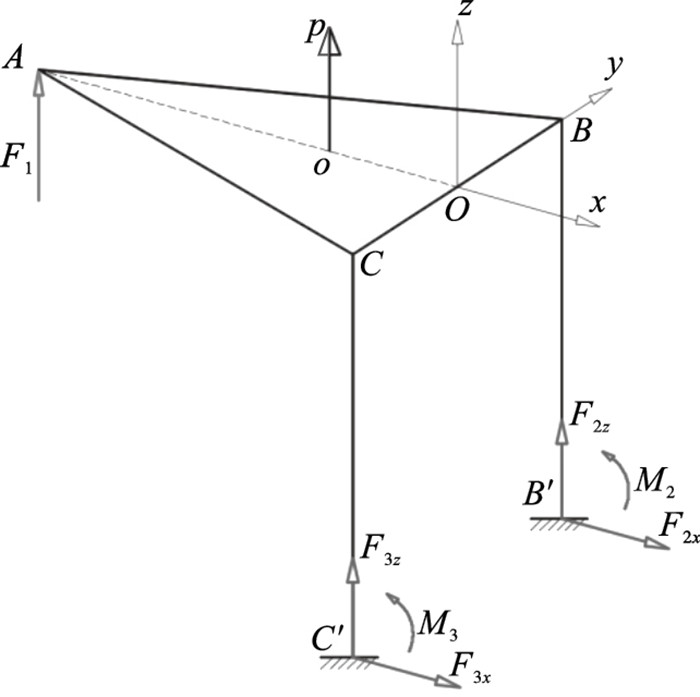 | 图 10 机构整体受力情况示意图Fig.10 Schematic diagram of overall stress of mechanism |
对柔性铰链支链进行受力分析,图 10的简化模型可进一步化简为图 11所示的L型钢架进行分析,将钢架OO′段任一处截开,运用截面法可知,其截面处所受力及力矩大小相等,方向相反,即支链2,3任一横截面处力矩大小均相等.
图 11(Fig. 11)
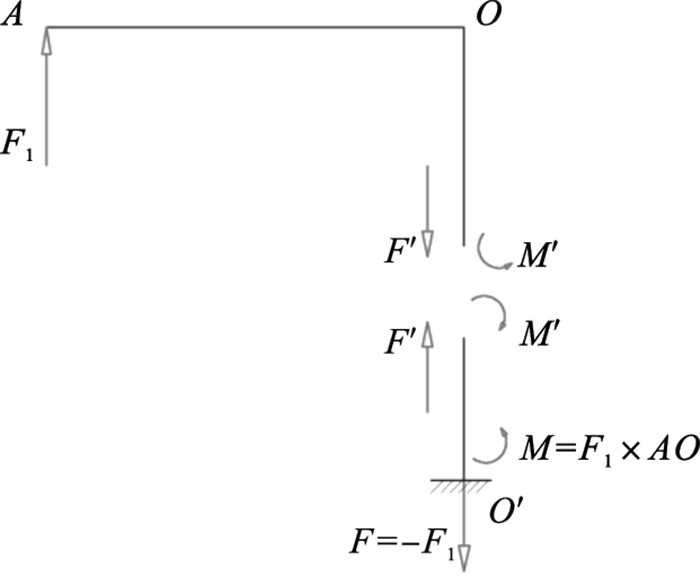 | 图 11 截面法分析机架的受力情况Fig.11 Stress analysis of frame by section method |
⑦ 对支链3进行模型简化, 将铰链处简化为转动副,铰链间的支链部分简化为连杆进行分析,如图 12所示.设直圆柔性铰链的半径为r3,两端连杆部分长分别为l31,l32,转角为α3,设支链顶端点A3在竖直方向上的下降距离为y3,A3与C3之间在竖直方向上的距离为y3′,由几何关系可得
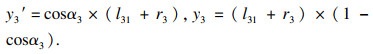 | (6) |
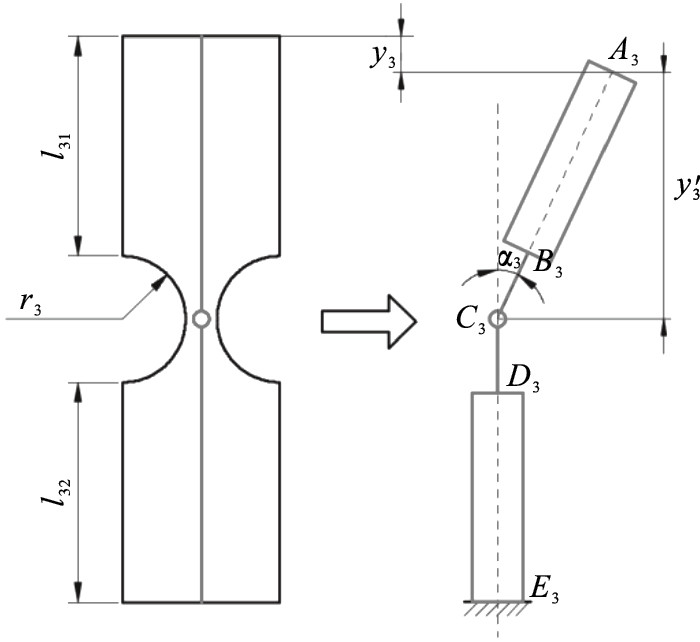 | 图 12 单铰链支链(支链3)变形分析图Fig.12 Deformation analysis diagram of single hinge branch chain (branch chain 3) |
对支链2进行相同的模型简化,支链各部分的标注如图 13所示,由几何关系可得
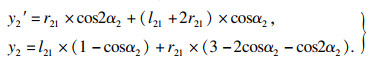 | (7) |
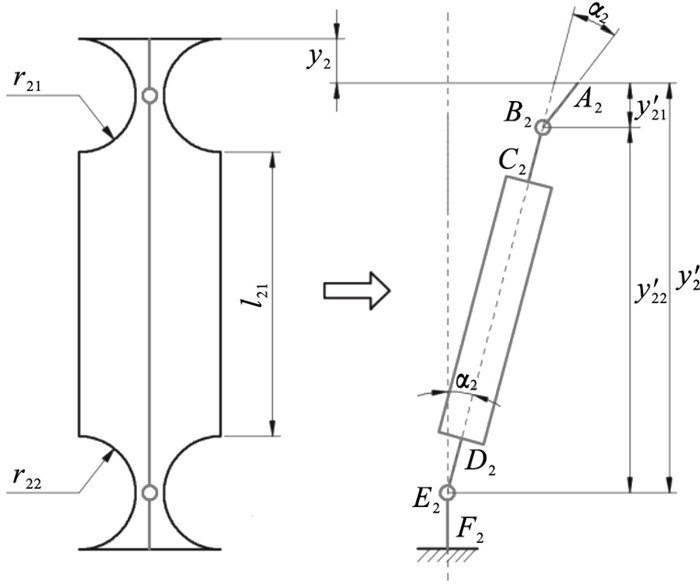 | 图 13 双铰链支链(支链2)变形分析图Fig.13 Deformation analysis diagram of double hinge branch chain (branch chain 2) |
⑧ 由式(6),式(7)可知通过建立柔铰的变形模型,将未知量y2,y3转化为了只包含2条支链转角的函数关系式.对于双轴直圆柔性铰链而言,其角变形量为[13]
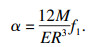 | (8) |
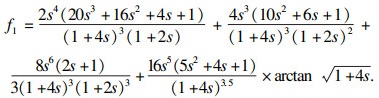 |
为确定装置的设计构想是否能产生空间的三维轨迹,同时验证刀尖理论轨迹模型的正确性,将表 1所示参数代入轨迹方程并用Matlab进行图像绘制,如图 14所示,结果为空间中的1条抛物线轨迹,满足设计要求.
表 1(Table 1)
| 表 1 刀尖运动轨迹的参数值 Table 1 Parameter values of tool tip trajectory |
图 14(Fig. 14)
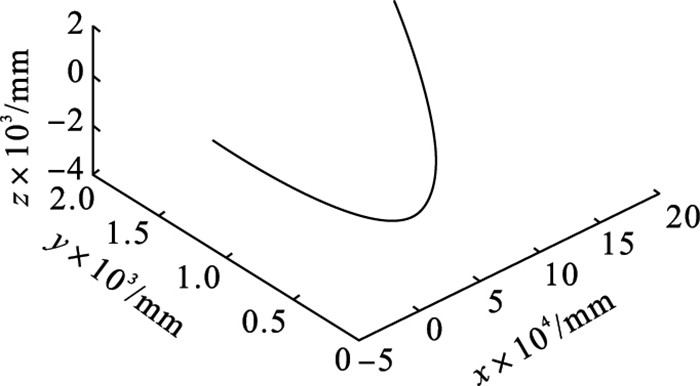 | 图 14 刀尖理论运动轨迹模型的仿真结果Fig.14 Simulation results of tool tip theoretical trajectory model |
将机构的Solidworks模型导入ANSYS中并进行瞬态动力学分析,以进一步确定刀尖的实际运动轨迹.如图 15所示,支链1处施加的力为100×sin(2π×20 000t) N,方向竖直向上.支链2,3底端均与地面固定,取刀尖在x,y,z三个方向上的位移量为输出量,将结果导入Matlab进行绘制,如图 16所示,依然为空间中的1条抛物线,但与图 14所示结果在细节上存在差异.这是因为建立理论模型时只将柔性铰链处作为柔性体分析,其余部分均当作刚体考虑,而实际上不存在理想刚体,刀具平板存在一定柔性,所以导致刀尖在每个振动周期内的轨迹都会产生一定的波动,并不能完全重合,但宏观轨迹是符合机构运动时的几何变形关系的,所以刀尖轨迹的有限元仿真结果在宏观上会呈现为和理论模型结果一致的空间三维抛物线.
图 15(Fig. 15)
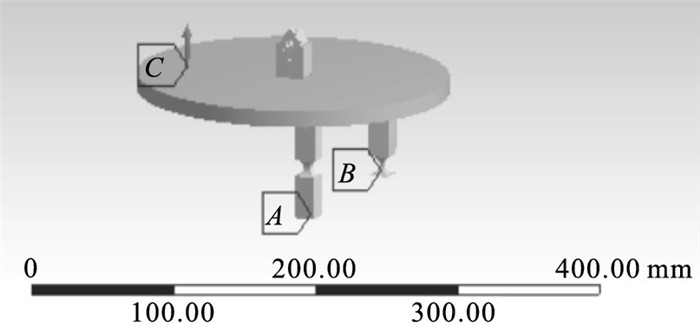 | 图 15 机构的有限元仿真模型Fig.15 Finite element simulation model of mechanism |
图 16(Fig. 16)
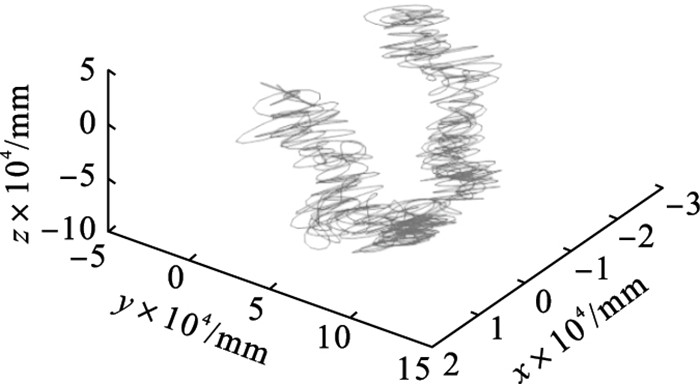 | 图 16 刀尖运动轨迹的有限元仿真结果Fig.16 Finite element simulation results of tool tip trajectory |
2 装置的切削实验验证2.1 装置实物的设计加工由前文的分析可知,3条支链运动变形时的主体结构为其空间分布所形成的正三角形,考虑到设备所占的实际空间大小,将原先为圆形的刀具平板缩减为三角形结构并减小半径,如图 17所示,以减小装置整体的尺寸和质量,便于装置的实际安装.同时考虑到铰链的不同圆半径对刀尖运动轨迹的影响各不相同,所以支链与刀具平板间做成可拆卸式结构,便于后续的实验,选择支链的固定方式为螺栓连接.支链2,3的铰链圆半径选为3 mm,修改后的模型如图 18所示,装置模型的整体示意图如图 19所示,实物图如图 20所示.
图 17(Fig. 17)
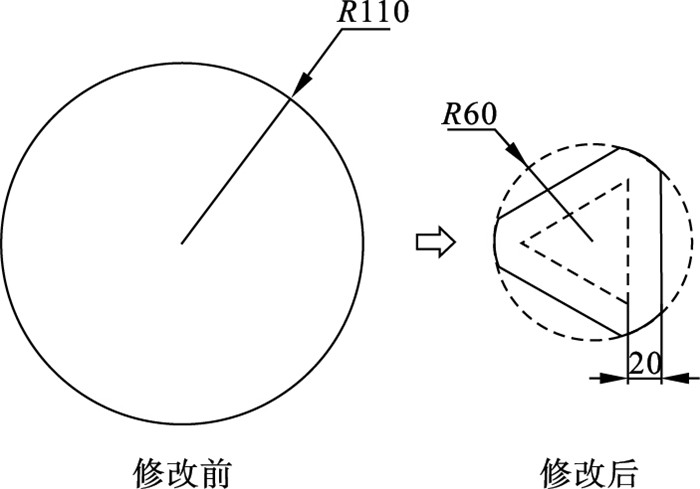 | 图 17 修改后的刀具平板示意图(单位:mm)Fig.17 Schematic diagram of modified tool plate(unit: mm) |
图 18(Fig. 18)
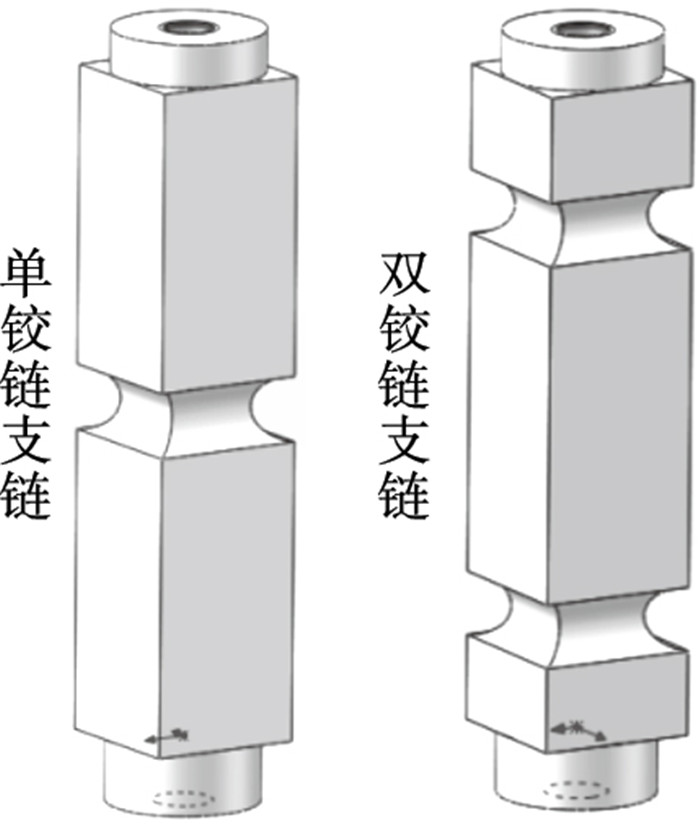 | 图 18 支链2,3的模型示意图Fig.18 Model diagram of branch chain 2 and 3 |
图 19(Fig. 19)
 | 图 19 装置模型整体示意图Fig.19 Overall schematic diagram of device model |
图 20(Fig. 20)
 | 图 20 装置实物示意图Fig.20 Physical schematic diagram of the device |
2.2 装置的实验验证实验材料选用304不锈钢,直径30 mm, 长度450 mm,其弹性模量、泊松比、密度分别为1.99×1011 Pa,0.3,7 930 kg/m3;实验刀具选用型号为CCMT120404的硬质合金刀片;实验所用车床型号为CA6140.实验时将振动切削装置、压电陶瓷换能器、超声波发生器相连接,并将振动切削装置固定在车床上,超声波发生器的工作与否分别对应了装置超声振动切削和普通切削两种工作状态,装置实际的安装示意图如图 21所示.实验方案为在有无超声振动的情况下,探究被加工工件表面粗糙度评定参数Sa和超声振幅的关系.
图 21(Fig. 21)
 | 图 21 装置实际的安装示意图Fig.21 Actual installation diagram of the device (a)—正面;(b)—侧后方. |
在固定进给量为0.08 mm、切深为0.1 mm、切削速度为503 mm/s(对应主轴转速为320 r/min)的情况下,超声振幅与粗糙度大小的关系如图 22所示.对比结果可以看出,随着振幅的不断增大,工件的表面粗糙度不断降低,且当振幅为0即普通车削时,粗糙度最大,此时Sa为4.807 μm;而在施加超声后,工件的表面粗糙度开始显著降低,当振幅为1.50,2.25,3.00,3.75 μm时,对应的Sa分别为3.901,2.663,2.246,2.175 μm.相较于普通车削,超声切削均具有良好地改善加工表面质量的效果.这是因为在普通车削时,工件表面的切削残余面积为条形波峰波谷的形式,而三维超声切削中,刀具在三个维度上都附加有振动,在普通车削形成的表面形貌的基础上,对切削残余面积会起到削减的作用,且随着振幅在一定范围内的增大,对残余面积的削减作用也越明显,当振幅过大时,虽然此时Sa的值仍不断减小,但由于残余高度去除率的不断降低,Sa的下降速率也会逐渐降低.
图 22(Fig. 22)
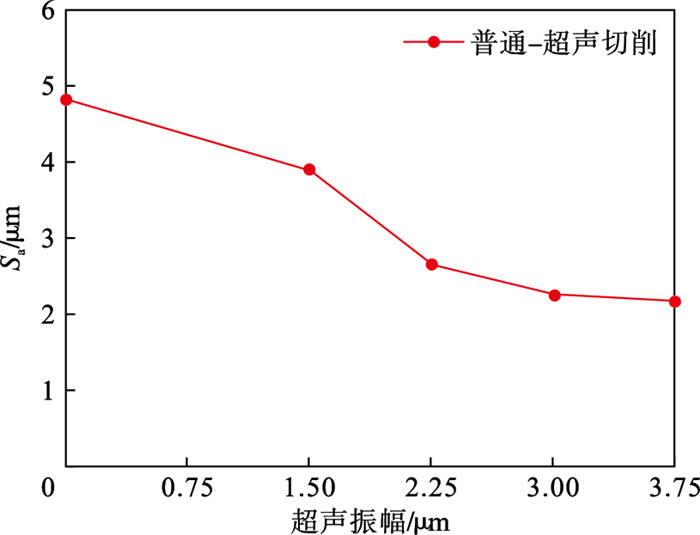 | 图 22 超声振幅与粗糙度评定参数Sa的关系示意图Fig.22 Schematic diagram of the relationship between ultrasonic amplitude and roughness evaluation parameter Sa |
图 23为使用超景深三维显示系统观察不同切削方式下的工件表面形貌:普通车削下的工件表面形貌为条形的沟壑状;超声切削下,由于刀具上附加有振动,所以会削去“沟壑”的波峰,形成条形的振纹状,从而提高工件的表面质量.
图 23(Fig. 23)
 | 图 23 不同切削方式下的工件表面形貌Fig.23 Workpiece surface morphology under different cutting modes (a)—普通车削;(b)—超声切削(振幅为3 μm). |
图 24为使用三维轮廓仪观察时两种切削方式对应工件的表面微观形貌,同样可以看到普通车削的工件微观表面呈现出明显的沟壑状凹槽,与前文的描述一致;而超声切削条件下,刀具在三个维度上的振动能有效切除普通车削情况下形成的沟壑的波峰,所以整个表面看起来较为规则,波峰与波谷之间的高度并不那么明显,像是被“削平”了一样,也从侧面反映出超声切削对改善工件表面加工质量的良好效果,超声振幅为1.50,2.25,3.00,3.75 μm的情况下,对应的Sa相较于普通车削分别下降了18.848%,44.602%,53.276%,54.753%.
图 24(Fig. 24)
 | 图 24 不同切削方式下的工件微观形貌Fig.24 Micro morphology of the workpieces under different cutting methods (a)—普通车削;(b)—超声切削(振幅为3 μm). |
3 结语本文研制了一种新型单激励式三维振动切削装置,通过对机构支链间的几何变形关系分析,建立了刀尖运动轨迹的理论模型,通过Matlab仿真和ANSYS瞬态动力学仿真,分别绘制了刀尖的理论和实际运动轨迹,结果均显示为空间三维抛物线,符合设计要求.
通过对比实验,对该装置的实际加工效果进行了检验,结果表明超声振动切削相对于普通车削,工件的表面加工质量具有明显的改善,且随着振幅的不断增大,已加工表面粗糙度Sa逐渐减小.因此,可采用该装置对304不锈钢材料进行高质量、高效率的加工.
参考文献
| [1] | 康仁科, 马付建, 董志刚, 等. 难加工材料超声辅助切削加工技术[J]. 航空制造技术, 2012, 412(16): 44-49. (Kang Ren-ke, Ma Fu-jian, Dong Zhi-gang, et al. Ultrasonic assisted cutting technology for difficult to machine materials[J]. Aviation Manufacturing Technology, 2012, 412(16): 44-49.) |
| [2] | Kumabe J. Precision machining vibration cutting[M]. Utsunomiya: Machinery Industry Press, 1985. |
| [3] | Shamoto E, Moriwaki T. Study on elliptical vibration cutting[J]. CIRP Annals, 1994, 43(1): 35-38. DOI:10.1016/S0007-8506(07)62158-1 |
| [4] | Shamoto E, Suzuki N. Ultraprecision cutting by applying elliptical vibration[J]. Journal of the Japan Society of Precision Engineering, 2006, 72(4): 440-443. |
| [5] | 张志坚. 三维曲面超声车削加工理论及仿真研究[D]. 沈阳: 东北大学, 2019. (Zhang Zhi-jian. Research on theory and simulation of ultrasonic turning of 3D curved surfaces[D]. Shenyang: Northeastern University, 2019. ) |
| [6] | 康仁科, 鲍岩, 殷森, 等. 一种单激励三维超声椭圆车削装置: ZL201911287547. 3[P]. 2020-04-17. (Kang Ren-ke, Bao Yan, Yin Sen, et al. A single excitation three-dimensional ultrasonic elliptical turning device: ZL201911287547. 3[P]. 2020-04-17. ) |
| [7] | Lu D, Wang Q, Wu Y, et al. Fundamental turning characteristics of inconel 718 by applying ultrasonic elliptical vibration on the base plane[J]. Advanced Manufacturing Processes, 2015, 30(8): 1010-1017. |
| [8] | Hamade A. BUEVA: a bi-directional ultrasonic elliptical vibration actuator for micromachining[J]. The International Journal of Advanced Manufacturing Technology, 2012, 58: 991-1001. DOI:10.1007/s00170-011-3463-7 |
| [9] | Kim G D, Loh B G. An ultrasonic elliptical vibration cutting device for micro V-groove machining: kinematical analysis and micro V-groove machining characteristics[J]. Journal of Materials Processing Technology, 2007, 190(1/2/3): 181-188. |
| [10] | 宋云. 三维椭圆振动辅助切削系统研究与开发[D]. 南京: 南京航空航天大学, 2017. (Song Yun. Research and development of three-dimensional elliptical vibration assisted cutting system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2017. ) |
| [11] | Wada T, Takahashi M, Moriwaki T, et al. Development of a three axis controlled fast tool servo for ultra precision machining (1st report)[J]. Journal of the Japan Society of Precision Engineering, 2007, 73(12): 1345-1349. |
| [12] | Kurniawan R, Ko T J. Surface topography analysis in three-dimensional elliptical vibration texturing (3D-EVT)[J]. The International Journal of Advanced Manufacturing Technology, 2019, 102: 1601-1621. DOI:10.1007/s00170-018-03253-1 |
| [13] | 李成, 何涛, 陈国瑜, 等. 结构参数对并联型双轴直圆柔性铰链刚度的影响[J]. 机械传动, 2020, 44(3): 34-38. (Li Cheng, He Tao, Chen Guo-yu, et al. Influence of structural parameters on stiffness of parallel double axis straight circular flexure hing[J]. Mechanical Transmission, 2020, 44(3): 34-38.) |
