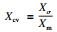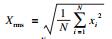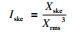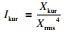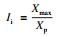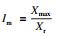, 孙良仕1, 高娓2, 李禹雄1
, 孙良仕1, 高娓2, 李禹雄1 1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 中国重汽集团济南卡车股份有限公司,山东 济南 250116
收稿日期:2022-03-07
基金项目:国家自然科学基金资助项目(51975110)。
作者简介:黄贤振(1982-),男,山东定陶人,东北大学教授,博士生导师。
通信作者:HUANG Xian-zhen, E-mail: xzhhuang@mail.neu.edu.cn。
摘要:在高速铣削加工中,为了判断更换刀具的最佳时间,迫切地需要对刀具的剩余使用寿命进行准确地预测,但预测中常常会存在历史数据不足的问题.因此,本文提出了一种解决小样本空间的刀具剩余使用寿命预测方法.该方法基于支持向量回归(SVR)方法,通过随机分形搜索(SFS)算法优化模型中的关键参数.相比于传统方法,本文所采用的方法可获得更优的模型参数和更快的收敛速度.最后,将所采用的方法与隐马尔可夫模型(HMM)方法进行比较,平均精确度由0.627 7提高至0.819 9,为刀具的更换提供了可靠的参考.
关键词:高速铣削刀具磨损剩余使用寿命随机分形搜索支持向量回归
Remaining Useful Life Prediction of Cutting Tools Based on SFS-SVR in High Speed Milling Operations
HUANG Xian-zhen1

 , SUN Liang-shi1, GAO Wei2, LI Yu-xiong1
, SUN Liang-shi1, GAO Wei2, LI Yu-xiong1 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. China National Heavy Duty Truck Group Jinan Truck Co., Ltd., Jinan 250116, China
Abstract: In high speed milling operations, it is urgent to accurately predict the remaining useful life of cutting tools to determine the best time to replace them, but there is often a problem of insufficient historical data in the prediction. Therefore, a method for remaining useful life prediction of cutting tools in small sample space is proposed, which is based on the support vector regression (SVR) method. And the stochastic fractal search (SFS) algorithm is used to optimize the key parameters of SVR. Compared with the traditional method, it obtains better model parameters and faster convergence speed. Finally, the as-adopted method is compared with the hidden Markov model (HMM) approach. The accuracy rate increases from 0.627 7 to 0.819 9, which provides a reliable reference for tool replacement.
Key words: high-speed millingtool wearremaining useful lifestochastic fractal searchsupport vector regression
高速铣削加工是一种极具发展前景的先进制造技术,相比于传统的铣削加工,其无论是在加工效率上,还是在加工质量上都具有明显的优势.因此,随着对产品要求的提高,高速铣削加工技术迅速发展起来,已经广泛应用于航空航天等众多前沿领域.但是,在高速铣削过程中,由于刀具磨损较快,很容易失效,何时更换刀具的问题就引起了人们的注意.在高速铣削系统中,刀具的更换十分重要.一方面,刀具失效后若未能及时更换,产品的加工质量会受到影响,严重时还会引发事故,甚至发生危险;另一方面,频繁地更换刀具会降低刀具的使用率,造成多余的停机和刀具的浪费,隐形地增加了加工成本.刀具的剩余使用寿命(remaining useful life,RUL)定义为刀具从当前的切削状态至失效状态所经历的时间.通过准确地预测RUL,能够避免刀具的过度使用或使用不足,实现加工质量、加工效率和生产成本之间的平衡.
传统上,刀具的RUL是操作人员根据自己多年的经验从主观上估算出来的,这很难被大众学习和推广[1],而且培养一名优秀的操作人员也绝非易事.多年来,国内外的很多研究人员对刀具以及其他机械装备的RUL预测进行了大量的研究,其目的是希望可以找到能够被大众广泛学习的有效方法.目前,相关的方法大致可分为三类,基于物理模型的方法、基于统计模型的方法和基于人工智能的方法.
基于物理模型的方法是在分析了装备系统以后,根据失效机制或损伤原理建立能够描述退化过程的数学模型,这个过程需要对装备系统的物理机制有着深入的理解.基于Taylor模型和Paris-Erdogan模型的RUL预测方法相继被提出[2-3],其中模型参数与装备的材料特性和力学特征等有关,可以通过特定的实验或有限元技术来确定.如果这些数学模型能够很好地描述装备退化的物理过程,那么就能够实现准确的RUL预测.然而,由于刀具磨损机理的复杂性,还不能完全掌握其中的机理知识,导致很难建立准确的数学模型.基于统计模型的方法是通过经验知识和统计理论的结合,建立统计模型来估计RUL,常见的方法有马尔可夫模型、维纳过程模型和逆高斯过程模型等.其中,Li等[4]考虑了切削时间和加工条件,提出了一种改进的隐马尔可夫模型,用于微铣削过程中的刀具RUL预测.Sun等[5]考虑了测量变异性,针对特定的刀具建立了基于维纳过程的非线性RUL预测模型,并实现了预测不确定性的置信区间量化.Huang等[6]采用随机效应逆高斯过程模型,以表面粗糙度作为失效判据进行了刀具RUL预测.基于统计模型的方法虽然不需要对装备的失效机理进行了解,但如果没有足够的寿命数据来建立分布模型,预测结果可能不太理想.随着人工智能技术和传感器技术的发展,基于人工智能的预测方法越来越被人们所关注.这类方法是通过运行过程中的传感器监测,挖掘性能退化的内在规律,从而估计装备的RUL.
在基于人工智能的方法中,神经网络和支持向量回归(support vector regression,SVR)是文献中报道最多的预测方法.Drouillet等[7]基于机床主轴功率,利用神经网络技术得到了较好的刀具RUL预测效果.Huang等[8]提出了一种长短期记忆递归神经网络模型,并结合边缘数据处理方法对刀具的RUL进行实时预测.Zhang等[9]将信号区分和神经网络技术相结合,使用Hurst指数和CNN-LSTM对切削刀具的RUL进行预测.然而,在某些情况下会存在刀具运行数据稀缺的问题,这给神经网络模型的训练带来了困难.SVR是一种应用广泛的方法,在样本数量少、预测准确等方面具有一定的优势[10].
为了解决小样本情况的刀具RUL预测,本文建立了SVR模型并引入了随机分形搜索(stochastic fractal search,SFS)算法优化模型中的关键参数,从而得到回归效果更好的刀具RUL预测模型.此外,还引入了隐马尔可夫模型(hidden Markov model,HMM)方法作为比较,并采用交叉验证对所提方法的预测性能进行测试.
1 高速铣削实验在复杂的加工系统中,刀具的退化过程往往不足以用某个单一信号来描述,采用单一的传感器难以准确地预测刀具RUL.因此,为了丰富刀具的退化信息以提高预测精度,在加工工件时,有必要同时采用多个传感器进行数据获取.考虑到传感器的成本和测量的难易程度,力传感器、加速度传感器和声发射传感器使用频率较高,更适合工业生产的现场环境.
本文使用了2010年PHM Society Data Challenge的高速铣削实验数据[11].该实验是在Roders Tech RFM760铣床上完成的,以直径6 mm的三刃碳化钨球头铣刀作为研究对象,对不锈钢(HRC52)工件进行铣削加工,实验参数如表 1所示.
表 1(Table 1)
| 表 1 高速铣削实验参数 Table 1 High-speed milling experiment parameters |
实验中分别使用了6把球头铣刀进行加工,其中,刀具C1, C4和C6每次在切削108 mm长度后,被置于LEICA MZ12显微镜下测量切削刃的磨损量,整个过程中一共切削了315次.在高速铣削时,采用Kistler三维测力仪、加速度传感器和声发射传感器获取整个切削过程中的传感器信号,所有原始信号均由NI DAQ PCI 1200以50 kHz的频率采集[5, 12].
3个切削刃的磨损量与切削次数的关系如图 1所示,VB为切削刃的最大磨损量.刀具磨损量随切削次数的变化呈现出了3个阶段.初始时,由于刀具切削刃锋利,刀具与工件的接触面积较小,磨损量迅速增加;之后进入了稳定磨损阶段,随着刀具渐渐磨钝,其与工件的接触面积变大,此时的磨损量较为稳定;在最后的磨损阶段,切削力以及切削温度迅速升高,因此,刀具磨损急剧增加.
图 1(Fig. 1)
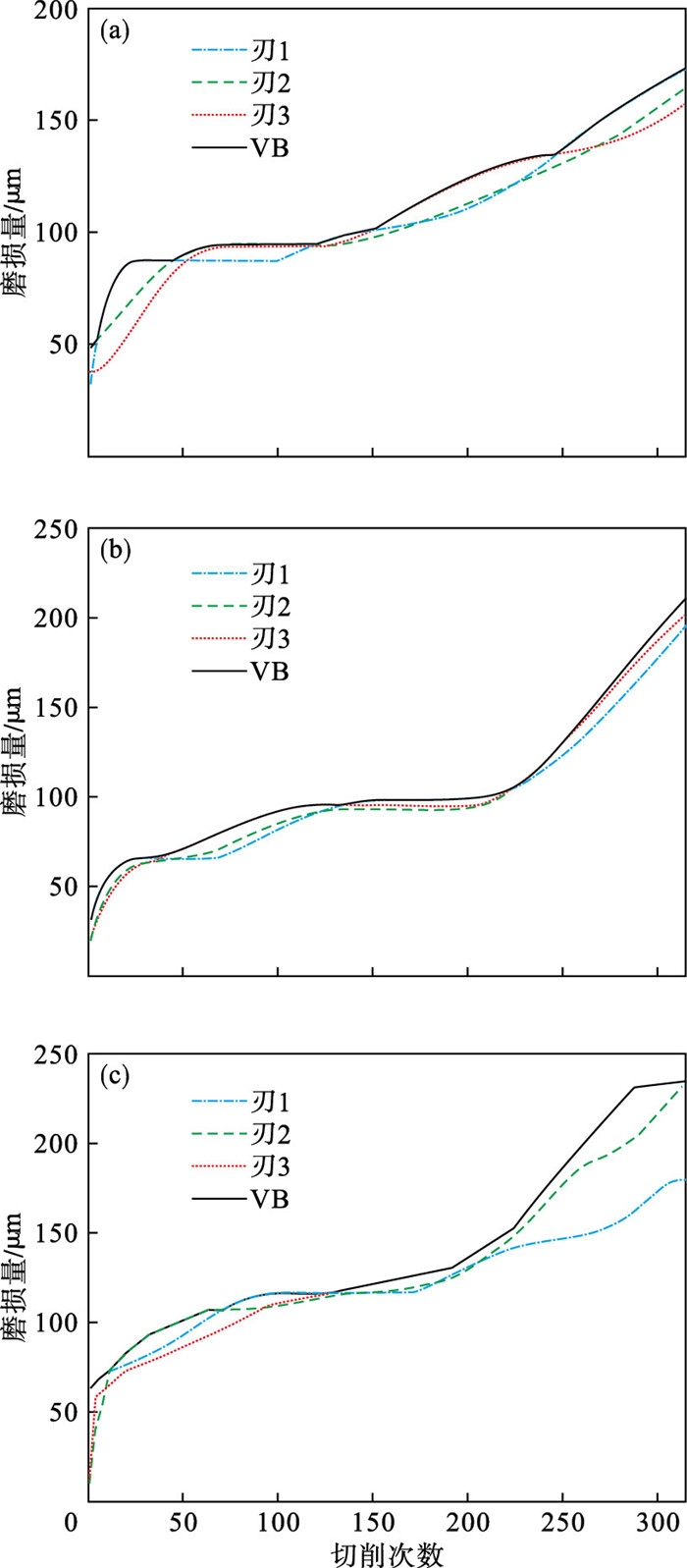 | 图 1 刀具C1, C4和C6的磨损量Fig.1 Wear of tool C1, C4 and C6 (a)—C1; (b)—C4; (c)—C6. |
2 SFS-SVR预测模型2.1 SVR模型SVR是在支持向量机(support vector machine,SVM)的基础上加入回归函数的一种扩展,由于其优越的泛化性能和结构风险最小化原则,常用于解决小样本回归问题,也是SVM最常见的应用形式. SVR的基本思想是通过一个非线性映射函数(核函数)将输入数据从原始空间映射到高维特征空间,然后构造超平面来拟合样本数据[13].
给定一个训练样本集
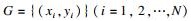
 | (1) |
 | (2) |
然后,引入拉格朗日乘子,可将上述优化问题转换到对偶空间中,优化问题重新表示为
 | (3) |
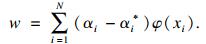 | (4) |
 | (5) |
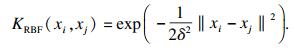 | (6) |
在扩散阶段,每个解是由初始位置随机游走产生新的解,如式(7)所示:
 | (7) |
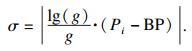 | (8) |
对于一个D维参数优化问题,在初始化时,按照规定的上下边界,在约束条件下随机初始化种群中的每一个解.第i个解的初始化方程为
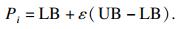 | (9) |
在更新阶段开始前,所有的解先根据适应度函数值进行排序,从而获得种群中的最优解BP.然后按照式(10)计算出每个解的性能能级Pai.
 | (10) |
更新阶段主要分为两个过程.第一次更新的目的是为了修改解向量中的某个分量.更新的程序是对Pai进行判别,若Pai≥ε,则解保持不变,否则,按照式(11)进行更新,
 | (1) |
第二次更新则是通过种群中其他解的位置信息来修改解的整体位置.首先,仍要按照式(10)对总体进行排序.然后,重新判别Pai,若Pai < ε,按照式(12)进行更新.
 | (12) |
由于在两个阶段中都采用了随机的思想,所以很大程度上避免了解落入局部最优.
2.3 基于SFS-SVR的预测方法为了合理确定SVR模型中的关键参数,本文采用了SFS优化算法来获取径向基宽度δ和惩罚引导因子C.假设在相同的工况下,采集了N把刀具的传感器信号,所提的方法步骤如下:
1) 特征提取和特征筛选.分析传感器直接获得的数据信息,从中提取常见的特征.然后,经过特征量与VB值的相关性计算,筛选出满足相关性要求的特征,组成特征向量.
2) 数据预处理.对特征向量进行归一化处理,使得每个特征值都在[0, 1]区间.此外,为了减小随机噪声的影响,采用滑移平均法对特征向量进行平滑处理.
3) 降维处理.采用主成分分析(principal component analysis,PCA)方法对高维度的特征向量进行降维,所获得的第一主成分作为SVR预测模型的输入.
4) 训练SVR模型.由剩余切削次数与总切削次数的比率来表征刀具的剩余使用寿命,并以此作为SVR模型的输出.应用SFS算法优化SVR预测模型中的关键参数,包括径向基宽度δ和惩罚引导因子C.
5) 交叉验证.采用交叉验证的方法测试SFS- SVR模型的预测性能.将N-1把刀具的信号数据用于训练,余下的1把刀具用于预测,N把刀具不断组合,每把刀具的RUL都会得到预测.
上述方法的流程如图 2所示.
图 2(Fig. 2)
 | 图 2 SFS-SVR方法流程图Fig.2 Flowchart of the SFS-SVR method |
3 刀具的剩余使用寿命预测3.1 特征提取和选择在高速铣削实验中,由传感器所直接获得的信号不但数据量庞大,而且伴随着各种没有价值甚至干扰预测结果的信息,无法直接用于刀具的RUL预测.时域特征能够很好地反映刀具的总体运行状态,具有效率高、变化趋势明显、计算方便等优点[15].为了获得足够的退化信息,本文提取了16种常见的时域特征,其计算公式如表 2所示.
表 2(Table 2)
| 表 2 时域特征计算公式 Table 2 Calculation formula of time-domain feature |
提取的112个时域特征中不乏包含一些不明显的特征,将导致模型预测效果较差,而且过多的特征也会造成模型过于复杂,影响模型的推广.本文探究了这些特征与VB值的相关程度,通过计算两者的相关系数,判断特征在不同磨损状态下的拟合程度,其相关系数的计算公式如下:
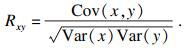 | (13) |
保证特征与刀具磨损量之间的强相关性是保证预测精度的前提.通过计算刀具C1数据中的相关系数,进而筛选出|Rxy|大于0.8的特征,共有50个特征满足要求,其中,23个特征来自切削力信号,27个特征来自振动信号,声发射信号在表征刀具磨损时的相关性较差,特征排序结果如表 3所示.其中,Fx,Fy和Fz分别表示x,y,z方向上的切削力,Vx,Vy和Vz分别表征x,y,z方向上的振动.例如,Xrms_Vy表示y方向上振动信号的均方根.表中粗体的部分是后续预测模型的输入特征,将组成如下4个特征向量:
表 3(Table 3)
| 表 3 影响,如电压波动和机床振动等,采集到的信号往往伴随着随机噪声,严重时甚至能够掩盖掉信号中的关键信息.为了弱化随机噪声的影响,本文对提取的特征进行滑移平均处理,滑动窗口的大小为11. Table 3 The characteristics that meets the relevance requirement | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 | (14) |
在切削加工过程中,由于许多不确定因素的影响,如电压波动和机床振动等,采集到的信号往往伴随着随机噪声,严重时甚至能够掩盖掉信号中的关键信息.为了弱化随机噪声的影响,本文对提取的特征进行滑移平均处理,滑动窗口的大小为11.
经过滑移平均滤波后,降噪效果显著,在时域图上可以明显看出曲线变得更加平滑.其中,滑移平均处理前后z方向切削力的脉冲因子变化如图 3所示.
图 3(Fig. 3)
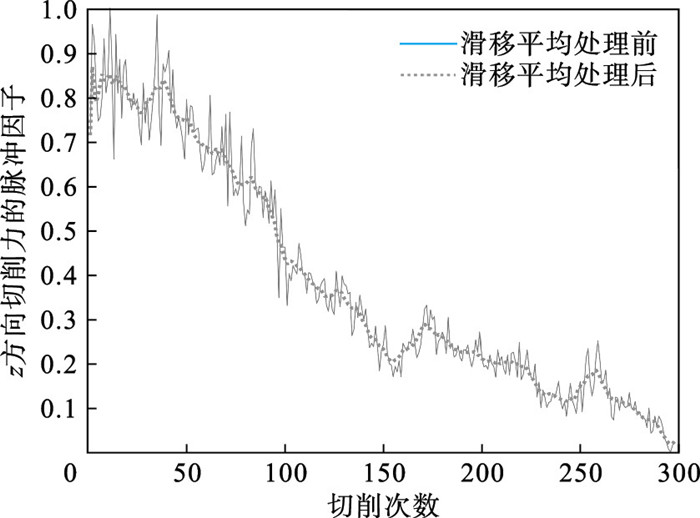 | 图 3 滑移平均处理前后脉冲因子的变化Fig.3 The change of the impulse factor before and after moving average processing |
3.3 基于PCA的降维处理在机器学习的训练和预测中,为了避免“维数灾难”的发生,常采用降维技术将高维度的数据集A转换为低维度的新数据集B,同时保留数据中的大部分细节.PCA方法是目前应用最广泛的降维技术之一,使用PCA方法对时域特征进行降维处理,从而得到了新的数据集,即第一主成分.然后,将此作为SVR模型训练和预测的输入.
3.4 预测模型的训练和性能评估本文采用交叉验证的方法测试SFS-SVR模型的预测性能.将刀具C4和C6作为训练集,刀具C1作为测试集,对当前时刻刀具C1的RUL进行预测.然后,再依次将刀具C4和C6作为测试集,其余的刀具作为训练集,对所提出的预测模型进行反复验证.
特征向量[f1, f2, f3, f4] 经过处理后作为模型的输入,刀具RUL作为输出,分别训练刀具C1,C4和C6的SVR模型.模型中的径向基宽度δ和惩罚引导因子C通过SFS算法寻优得到.作为比较,本文还引入了遗传算法(genetic algorithm,GA),并由均方误差MSE来评价训练模型的回归效果,以及通过寻参时间t来评价参数的求解速度,越小的MSE代表模型的回归能力越好,越小的t代表参数的求解速度越快.参数的优化结果如表 4所示.从表 4可以看出,SFS优化算法具有更快的收敛速度,并且训练出的SVR模型具有更强的回归能力.
表 4(Table 4)
| 表 4 The change of the impulse factor before and after moving average processing Table 4 Results of parameter optimization |
当刀具的磨损量为0.165 mm时,刀具达到失效状态,此时需要及时更换刀具.刀具C1,C4和C6的RUL预测结果如图 4所示,从切削过程的开始到结束,预测值围绕着真实值波动,总体变化大致相似.此外,在C6切削过程的初期和后期,预测误差较稳定阶段都有着明显的增大,不同阶段的RUL预测误差如图 5所示.这是因为在初始阶段时,切削时间短,采集的数据量有限,信号的特征变化不准确,导致模型的预测误差较大.当加工了一段时间后,收集的数据量逐渐增加,预测模型能够更加准确地拟合信号特征随切削次数和数据量增加的变化.因此,在采集了大量数据后,模型对刀具RUL的预测可以达到较小的误差.在加工阶段的后期,虽然已经采集了足够多的数据,但是此阶段的刀具磨损严重,切削力和振动急剧增加,导致预测精度下降.
图 4(Fig. 4)
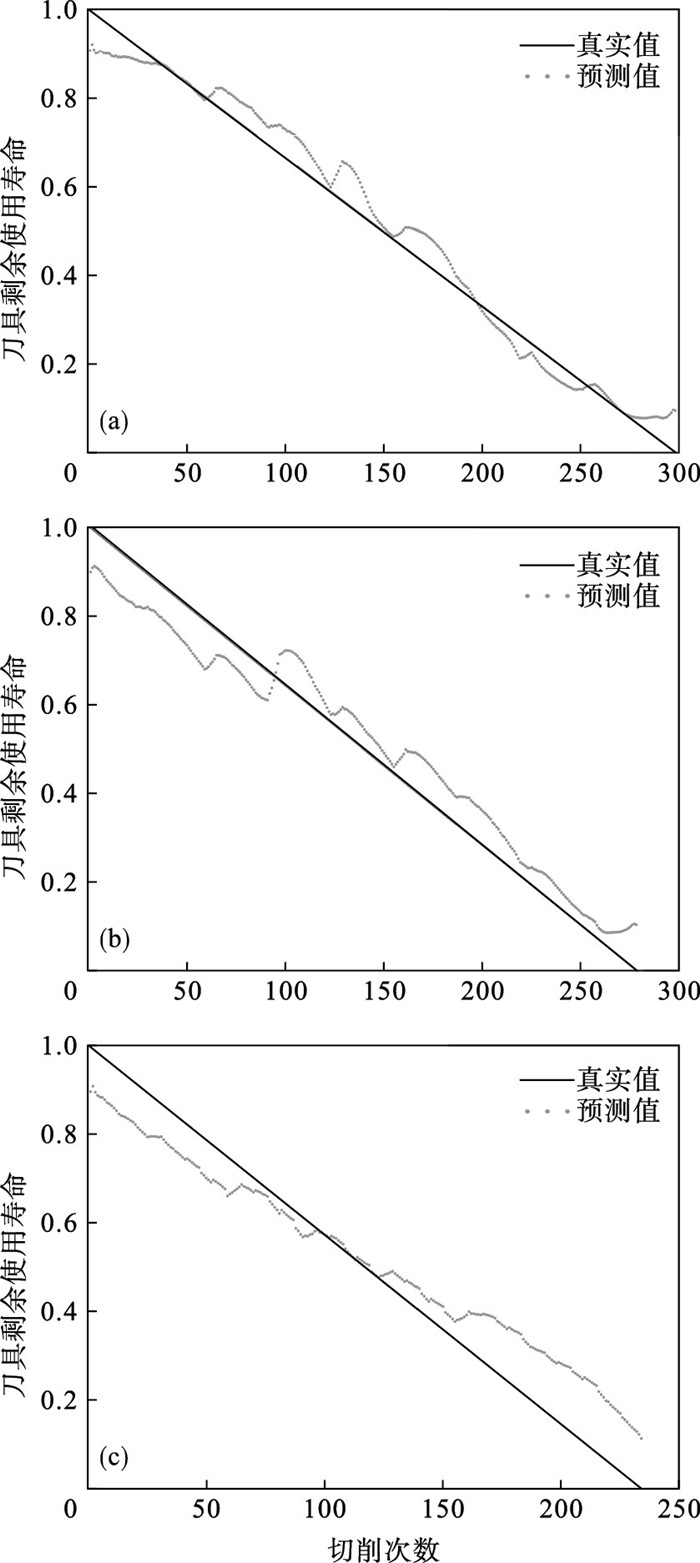 | 图 4 刀具C1,C4和C6的RUL预测Fig.4 RUL prediction of C1, C4 and C6 (a)—C1; (b)—C4; (c)—C6. |
图 5(Fig. 5)
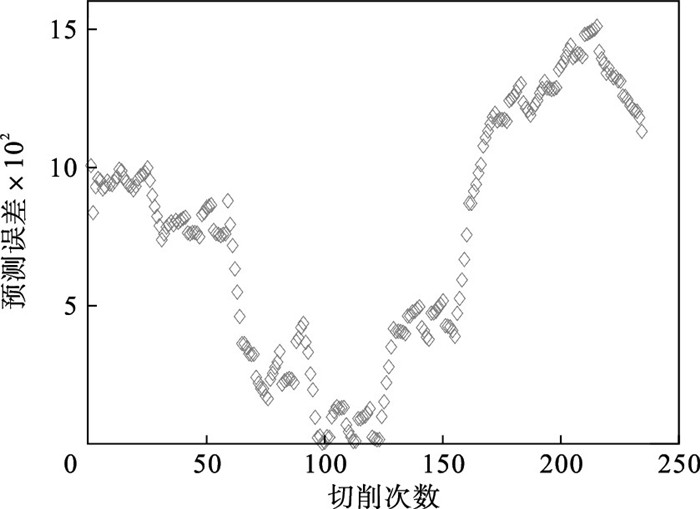 | 图 5 刀具C6的RUL预测误差Fig.5 The error of the RUL prediction results for tool C6 |
为了进一步验证所提方法在刀具RUL预测上的准确性,本文还引入了HMM方法[16]进行对比.使用式(15)定义精确度,作为量化预测性能的评价标准,当精确度等于1时预测性能最好,等于0时预测性能最差.如表 5所示,比较了交叉验证时SFS-SVR方法和HMM方法的预测精确度.SFS-SVR方法在刀具RUL预测上具有明显的优势,刀具C1, C4和C6经SFS-SVR方法预测的结果都比HMM方法预测的精确度高,其平均值可以由0.627 7提高到0.819 9.
表 5(Table 5)
| 表 5 HMM和SFS-SVR的预测精确度 Table 5 Prediction accuracy using HMM and SFS-SVR |
 | (15) |
2) 相比于传统的GA算法,由SFS算法寻参训练出的3个SVR模型,其均方误差MSE平均值由0.004 5减少至0.004 1,寻参时间t平均值由93.86 s降低至2.76 s.结果表明,SFS算法在收敛速度和求解质量上都具有明显的优势.
3) 相比于HMM方法,本文所提出的方法在刀具RUL预测上具有更强的优势.刀具C1,C4和C6在交叉验证时的预测精确度分别为0.884 5,0.819 7和0.755 4.因此,该方法能够有效地预测刀具RUL,有助于操作人员在未来的实际生产中合理更换刀具.
参考文献
| [1] | 卢志远, 马鹏飞, 肖江林, 等. 基于机床信息的加工过程刀具磨损状态在线监测[J]. 中国机械工程, 2019, 30(2): 220-224. (Lu Zhi-yuan, Ma Peng-fei, Xiao Jiang-lin, et al. Online monitoring of tool wear conditions in machining processes based on machine tool data[J]. China Mechanical Engineering, 2019, 30(2): 220-224. DOI:10.3969/j.issn.1004-132X.2019.02.013) |
| [2] | Silva R, Reuben R, Baker K, et al. Tool wear monitoring of turning operations by neural network and expert system classification of a feature set generated from multiple sensors[J]. Mechanical Systems and Signal Processing, 1998, 12(2): 319-332. DOI:10.1006/mssp.1997.0123 |
| [3] | Wang J, Gao R X, Yuan Z, et al. A joint particle filter and expectation maximization approach to machine condition prognosis[J]. Journal of Intelligent Manufacturing, 2019, 30(2): 605-621. DOI:10.1007/s10845-016-1268-0 |
| [4] | Li W J, Liu T S. Time varying and condition adaptive hidden Markov model for tool wear state estimation and remaining useful life prediction in micro-milling[J]. Mechanical Systems and Signal Processing, 2019, 131(15): 689-702. |
| [5] | Sun H B, Pan J L, Zhang J D, et al. Non-linear Wiener process-based cutting tool remaining useful life prediction considering measurement variability[J]. The International Journal of Advanced Manufacturing Technology, 2020, 107: 4493-4502. DOI:10.1007/s00170-020-05264-3 |
| [6] | Huang Y X, Lu Z Y, Dai W, et al. Remaining useful life prediction of cutting tools using an inverse Gaussian process model[J]. Applied Sciences, 2021, 11(11): 5011. DOI:10.3390/app11115011 |
| [7] | Drouillet C, Karandikar J, Nath C, et al. Tool life predictions in milling using spindle power with the neural network technique[J]. Journal of Manufacturing Processes, 2016, 22: 161-168. DOI:10.1016/j.jmapro.2016.03.010 |
| [8] | Huang Q Q, Kang Z, Zhang Y, et al. Tool remaining useful life prediction based on edge data processing and LSTM recurrent neural network[C]//2020 IEEE International Conference on Prognostics and Health Management(ICPHM). Detroit, 2020: 1-5. |
| [9] | Zhang X Y, Lu X, Li W D, et al. Prediction of the remaining useful life of cutting tool using the hurst exponent and CNN-LSTM[J]. The International Journal of Advanced Manufacturing Technology, 2021, 112: 2277-2299. DOI:10.1007/s00170-020-06447-8 |
| [10] | Smola A J, Scholkopf B. A tutorial on support vector regression[J]. Statistics and Computing, 2004, 14: 199-222. DOI:10.1023/B:STCO.0000035301.49549.88 |
| [11] | PHM Society.PHM data challenge 2010[EB/OL].(2010-05-18)[2020-12-10].https://www.phmsociety.org/competition/phm/10. |
| [12] | Huang Z W, Zhu J M, Lei J T, et al. Tool wear predicting based on multisensory raw signals fusion by reshaped time series convolutional neural network in manufacturing[J]. IEEE Access, 2019, 7: 178640-178651. DOI:10.1109/ACCESS.2019.2958330 |
| [13] | Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20: 273-297. |
| [14] | Li Y X, Huang X Z, Zhao C Y, et al. Stochastic fractal search-optimized multi-support vector regression for remaining useful life prediction of bearings[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2021, 43: 1-18. DOI:10.1007/s40430-020-02713-8 |
| [15] | Salimi H. Stochastic fractal search: a powerful metaheuristic algorithm[J]. Knowledge-Based Systems, 2015, 75: 1-18. DOI:10.1016/j.knosys.2014.07.025 |
| [16] | Yu J S, Liang S, Tang D Y, et al. A weight hidden Markov model approach for continuous-state tool wear monitoring and tool life prediction[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91: 201-211. DOI:10.1007/s00170-016-9711-0 |