
 , 周孝洪, 魏德洲
, 周孝洪, 魏德洲 东北大学 资源与土木工程学院,辽宁 沈阳 110819
收稿日期:2022-03-26
基金项目:国家自然科学基金资助项目(51974065,52274257)。
作者简介:孟令国(1994-),男,山东潍坊人,东北大学博士研究生;
高淑玲(1980-),女,河北泊头人,东北大学副教授,博士生导师;
魏德洲(1956-),男,河南南阳人,东北大学教授,博士生导师。
摘要:螺旋溜槽首圈流场特性及其演变对矿物颗粒运动与分离结果具有决定性影响.针对实验室?300 mm螺旋溜槽,采用RNG k-ε湍流模型、VOF和Eulerian Multi-fluid VOF多相流模型,系统考察了入口流量对螺旋溜槽首圈流场演变及赤铁矿和石英颗粒分布的影响.结果表明,增加入口流量会延长外缘处流膜形态、主流及二次环流达到稳定时的历程;随着入口流量的增大,石英和赤铁矿的分层效果得到增强,赤铁矿分布范围相应变宽,而石英向外缘流膜中的迁移量增加;首圈的最大分离效率随入口流量的增大呈现先增大而后渐稳的趋势,适宜的最低入口流量为7 L/min,此时首圈的最大分离效率可达61.45%.
关键词:螺旋溜槽首圈流场演变稳定性颗粒分布分离效率
Influence of the Inlet Flow Rate on Flow Field Evolution and Mineral Particle Distribution in the First Turn of Spiral Separators
MENG Ling-guo, GAO Shu-ling

 , ZHOU Xiao-hong, WEI De-zhou
, ZHOU Xiao-hong, WEI De-zhou School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: GAO Shu-ling, E-mail: gaoshuling@mail.neu.edu.cn.
Abstract: The characteristics and evolution of the flow field in the first turn of the spiral separator play an important role on the movement and separation of mineral particles. For the laboratory-scale spiral separator(?300 mm), the turbulence model of RNG k-ε and the multiphase flow model of the volume of fraction(VOF) as well as the Eulerian Multi-fluid VOF were used to investigate the influence of the inlet flow rate on the flow field evolution and the distribution of hematite and quartz particles in the first turn of spiral separators. With the increase of inlet flow rate, the distance to reach the stability of the flow film shape, primary and secondary flows at the outer trough are prolonged. The stratification performance of quartz and hematite is enhanced. Meanwhile, the hematite ore band is correspondingly widened, and the migration of quartz to the outer trough of the thick flow film region is increased. With the increase of the inlet flow rate, the maximum separation efficiency of the first turn increases first and then gets stable. The suitable inlet flow rate of 7L/min can be obtained with the maximum separation efficiency of 61.45%.
Key words: spiral separatorflow field evolution in the first turnstabilityparticle distributionseparation efficiency
复合力场条件下的流膜分选是处理细粒矿物的一个重要方向,螺旋溜槽凭借其回收粒度下限低、处理量大、操作简单等优势广泛地应用于选矿和选煤作业[1-3].在螺旋溜槽所提供的回转流场中,固体颗粒基于离心惯性力和重力的联合作用做复杂的三维运动,最终根据运动差异实现分离.当颗粒组成一定时,螺旋溜槽的分离性能从根本上取决于颗粒所处的流场环境[4].
螺旋溜槽螺旋圈数的选取与待分选物料性质相关,通常情况下为3~7圈[5].值得注意的是,不同螺旋圈数所发挥的分离作用有所差异.Holland-Batt[6]发现颗粒在径向上的迁移程度会随着螺旋圈数的增加而逐渐降低.Boucher等[7]和Atasoy等[8]认为前几圈是颗粒发生高效分离的主要阶段.由此可见非稳定阶段中颗粒的运动行为对螺旋溜槽的分离性能具有重要影响.对此,研究者对螺旋溜槽非稳定阶段中的流场特性和分离性能展开了相关研究.在早期,黄尚安[9]对螺旋溜槽初始阶段中水流的流膜厚度及平均流速等流场参数进行了实验测量,他认为此阶段水流的主要作用是将轻矿物推移至外缘,将重矿物推至中间带,从而为后续的分带和分选创造有利条件.然而由于测量手段有限,无法获取颗粒的分层及径向迁移等信息.之后,Boucher等[5, 7, 10]采用正电子发射粒子追踪(positron emission particle tracking, PEPT)技术得到了赤铁矿和石英颗粒在螺旋溜槽前两圈内的空间位置和速度等基础信息,然而却并没有阐明流场与颗粒运动行为的相关性.
近年来,计算流体力学(computational fluid dynamics, CFD)的蓬勃发展为螺旋溜槽内流场及颗粒分离过程的可视化和定量化提供了有力的支撑[11-14].黄波等[15]基于CFD-DEM单向耦合的数值模拟方法发现首圈中的水流会依次经过初始区、过渡区和稳定区,在此过程中流膜形态会发生相应波动,颗粒随水流进行回转运动,低密度颗粒悬浮在流膜上层,中高密度颗粒呈滚动或跳跃状态.Meng等[16]采用VOF多相流模型考察了实验室型螺旋溜槽流场的演变过程,结果表明首圈中的流场稳定性较差,不稳定性主要源自流体与外缘边壁的首次碰撞,且碰撞后引发的不平衡内外径向流动是促使二次环流生成的主要原因.上述研究结果为研究人员多方位地认识非稳定阶段流场特性及颗粒分离过程提供了非常有益的帮助.
入口流量是影响螺旋溜槽生产能力和分离效率的重要操作参数[17-18].通常,螺旋溜槽的入口流量是根据待处理的物料性质和对产物的质量要求而决定.当结构参数固定后,可以通过调整入口流量改变螺旋溜槽内部流场从而达到改善分离效果的目的.但是入口流量对螺旋溜槽首圈流场特性及颗粒分离过程的影响机制尚缺乏系统的研究.对此,本研究采用数值模拟方法,系统考察了入口流量对实验室型螺旋溜槽首圈中流膜形态和流型的演变及颗粒分布特性的影响机制.
1 数值模型的建立1.1 物理模型选择实验室型螺旋溜槽作为模拟对象,其外半径为150 mm,内半径为30 mm,螺距为240 mm,螺旋圈数为1圈,断面曲线方程如式(1)所示:
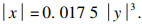 | (1) |
图 1(Fig. 1)
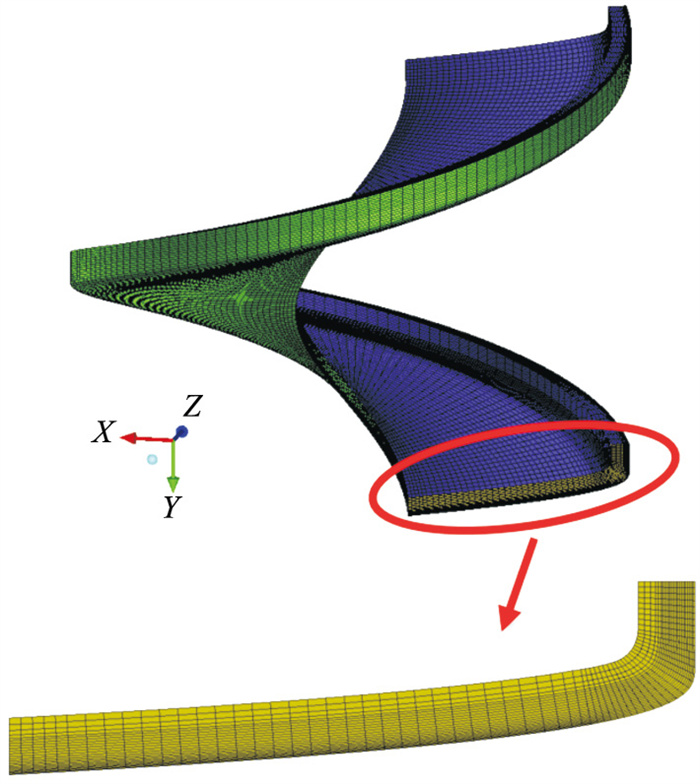 | 图 1 螺旋溜槽计算域网格划分Fig.1 Mesh division of the computational domain of the spiral separator |
1.2 模拟策略与边界条件螺旋溜槽中的分离过程涉及了一种复杂的三维多相无压旋转剪切运动,直接模拟气-液-固多相运动容易造成计算不稳定.因此本研究先用VOF多相流模型和RNG k-ε湍流模型捕捉气液界面并获得稳定的气-液两相流场.在此基础上,采用Eulerian Multi-fluid VOF多相流模型和RNG k-ε湍流模型模拟颗粒分离的情况,模拟策略如图 2所示.Eulerian Multi-fluid VOF多相流模型是一种基于VOF模型和Euler-Euler模型的耦合模型,其特点在于可以根据网格单元中的局部界面扩散值来识别螺旋溜槽计算域中的分层流和混合流,进而采用VOF模型来捕捉处于分层状态的气-液两相之间的界面,同时采用Euler-Euler模型预测固-液混合流中离散相颗粒的运动行为.在动量方程中考虑了Symmetric气-液曳力模型,Gidaspow液-固曳力模型以及修正的拜格诺升力模型,详情可参考文献[19].
图 2(Fig. 2)
 | 图 2 模拟策略Fig.2 Simulation strategy |
具体边界条件和模拟步骤设置如下:
1) 计算域的边界分为进口、出口、上边壁以及槽底壁.其中,入口的边界条件为速度入口,且入口流体的速度方向垂直于入口边界,入口处的径向位置范围为r=40~130 mm.出口采用压力出口边界条件.槽底壁采用无滑移边界条件,近壁面处理采用标准壁面函数.同时,将上边壁设置为自由滑移边界条件.
2) 进行气-液两相流模拟时,首先将螺旋溜槽内充满空气,在入口处设置水的入口速度,然后对计算域初始化并进行计算.
3) 进行气-液-固多相流模拟时,在稳定的气-液流场基础上,注入颗粒相.颗粒形状假设为球形.颗粒相的入口速度与水相一致,且给入方向垂直于入口面.本研究选取鞍山式赤铁矿矿石中的石英和赤铁矿颗粒作为研究对象,密度分别为2 650,4 950 kg/m3,粒度均设置为89.5 μm,按1∶1体积比例混合给入螺旋溜槽,入料质量分数为20 %.
数值模拟的准确性需要物理试验进行验证.需要说明的是,本文采用的气-液两相流以及气-液-固多相流模拟策略已通过相关验证[19-20].
2 模拟结果与分析2.1 入口流量对流膜厚度的影响流膜厚度决定了颗粒的分布空间,首先考察了入口流量对首圈中流膜形态演变的影响,结果如图 3所示.考虑到各径向位置的流膜厚度不同,为简化研究,本文选取的三处旋转半径:r=50,95,140 mm,分别代表了螺旋溜槽的内缘、中部以及外缘.
从图 3可以看出,随着螺旋圈数的增加,内缘和中部区域处流膜厚度自入口给入后便快速下降并在0.4圈附近降到最低值,随后逐渐趋于稳定.在前0.4圈中,流膜厚度与入口流量呈现为正相关,而当螺旋圈数超过0.4圈后,改变入口流量对流膜形态不会造成显著影响.相比之下,外缘区域中流膜的演变过程较为复杂.随着螺旋圈数的增加,流膜厚度呈现为先快速增长而后波动式下降的变化趋势.在这个过程中,流膜厚度每经历一次波动其振幅便逐渐缩小,并最终趋于稳定.随着入口流量的增大,各螺旋圈数处的流膜厚度均有所增加,且流膜厚度的波动程度也更加显著,这说明增加入口流量将会延长外缘区域流膜形态趋于稳定时所经历的行程长度.
图 3(Fig. 3)
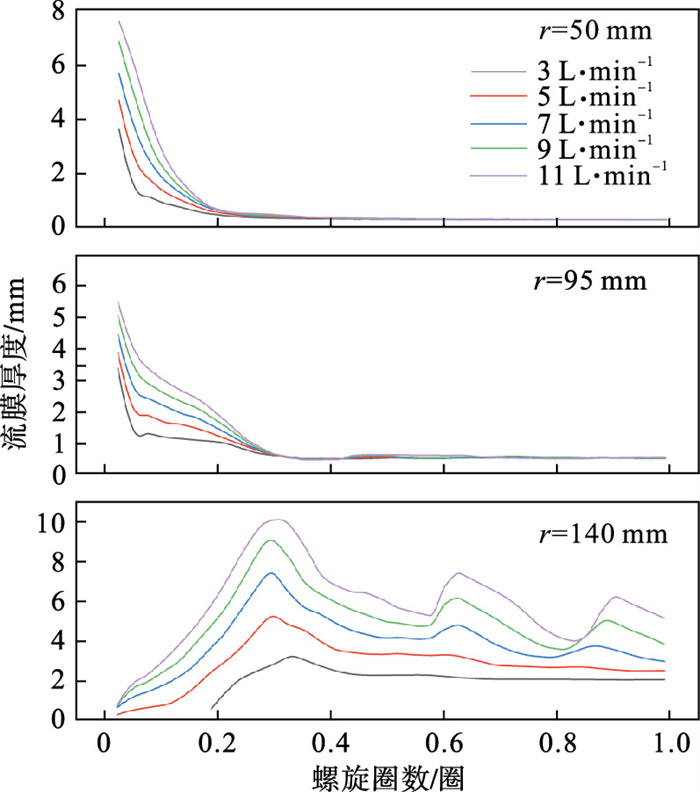 | 图 3 入口流量对流膜形态演变过程的影响Fig.3 Influence of the inlet flow rate on the evolution of flow film shape |
2.2 入口流量对切向流速的影响螺旋溜槽中的主流以切向流速为主,其不但对矿石起着输送、松散分层和分带的作用,而且也是径向流速产生的主要原因.图 4展示了不同入口流量下首圈中三处径向位置(r=50,95,140 mm)的表面切向流速分布.
图 4(Fig. 4)
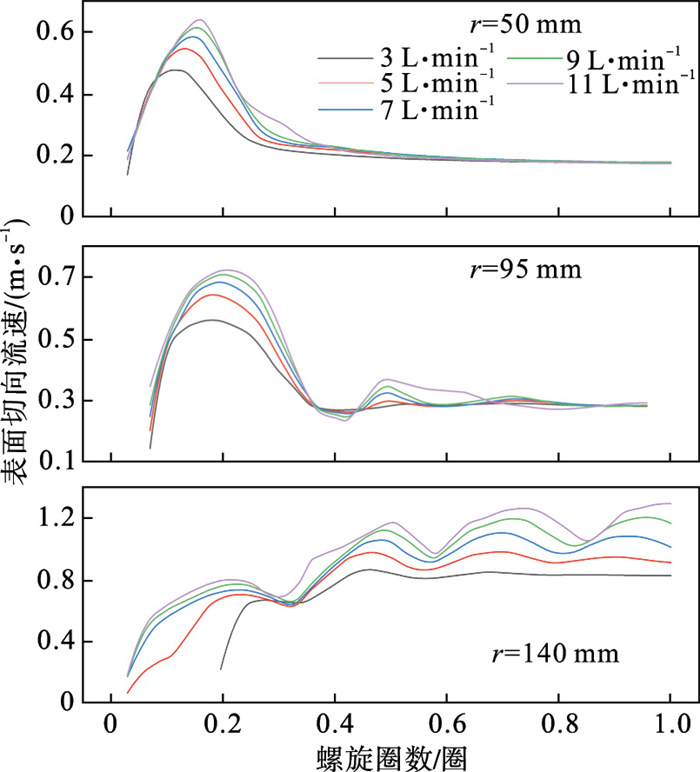 | 图 4 入口流量对不同旋转半径处表面切向流速演变过程的影响Fig.4 Influence of the inlet flow rate on the evolution of surface tangential velocity at different rotation radius |
由图 4可以发现,首圈中部和内缘区域中流膜表面切向流速的演变规律较为相似.在流体发展的前期,表面切向流速经历了较大幅度的波动.这是因为,流体在刚由入口给入时,受到重力的加速作用,表面切向流速会迅速增大.而后随着流膜厚度的减小,壁面的黏滞阻力对流体的阻碍作用愈发显著,因此表面切向流速转变为下降的发展趋势.增加入口流量能够增大速度波动的幅值,这对颗粒的松散悬浮是有利的.而后,随着流体的进一步发展,表面切向流速逐渐趋于平稳,改变入口流量对此阶段中流体表面切向流速的影响并不显著.
在外缘区域中,随着螺旋圈数的增加,流体的表面切向流速呈现为波动式增长的发展趋势.流速的增长幅度与入口流量呈现为正相关,且随着入口流量的增大,表面切向流速的波动程度更加明显,这意味着外缘区域主流的稳定性有所变差.
2.3 入口流量对径向流速的影响二次环流是螺旋溜槽独特的流型特征,其在促进颗粒分带过程中起着重要作用.表层流体的径向流速可以在一定程度上反映二次环流的演变机制.对此,本节提取了不同入口流量下首圈中表面径向流速云图,结果如图 5所示.需要说明的是,径向速度为正值时流体为沿径向向外运动,反之则向内.
图 5(Fig. 5)
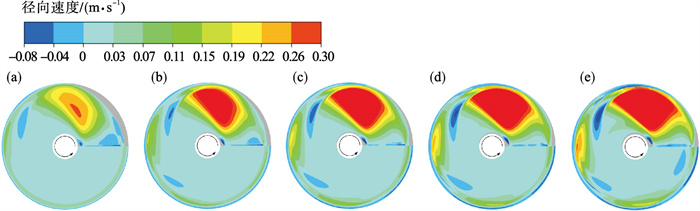 | 图 5 入口流量对首圈表面径向流速演变过程的影响Fig.5 Influence of the inlet flow rate on the evolution of surface radial velocity in the first turn (a)—Q=3 L·min-1; (b)—Q=5 L·min-1; (c)—Q=7 L·min-1; (d)—Q=9 L·min-1; (e)—Q=11 L·min-1. |
通过图 5可以发现,流体自入口给入后,各径向位置处的表层流体均呈现出沿径向向外的运动趋势,并在第0.125至0.375圈之间形成了高速区(红色区域),这主要与流体所受离心力的增大有关.增大入口流量可以显著扩大高速区的范围,这表明流体向外缘的迁移量会随之增大.而随着流体的发展,外缘区域中的表层流体转变为沿径向向内运动.这是因为之前大量向外运动的流体会与外缘边壁相撞,从而促使流体发生折返运动.可以发现,增大入口流量可以加剧外缘区域中流体在径向上运动的不平衡性,但对中部及内缘区域的流体径向运动没有显著影响.
2.4 入口流量对首圈颗粒分布特性的影响在气-液两相流场的基础上,注入石英和赤铁矿颗粒,利用Eulerian Multi-fluid VOF模型对气-液-固多相流进行了数值模拟,从而获得了不同密度的颗粒空间分布特性.入口流量对螺旋溜槽首圈槽面处赤铁矿和石英分布的影响情况分别如图 6和图 7所示.
图 6(Fig. 6)
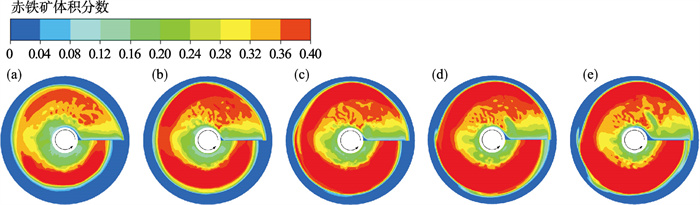 | 图 6 入口流量对首圈槽面处赤铁矿分布的影响Fig.6 Influence of the inlet flow rate on the distribution of hematite in the first turn (a)—Q=3 L·min-1; (b)—Q=5 L·min-1; (c)—Q=7 L·min-1; (d)—Q=9 L·min-1; (e)—Q=11 L·min-1. |
图 7(Fig. 7)
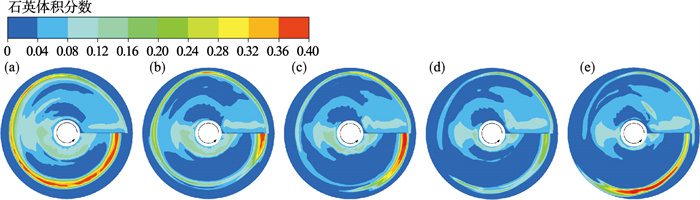 | 图 7 入口流量对首圈槽面处石英分布的影响Fig.7 Influence of the inlet flow rate on the distribution of quartz in the first turn (a)—Q=3 L·min-1; (b)—Q=5 L·min-1; (c)—Q=7 L·min-1; (d)—Q=9 L·min-1; (e)—Q=11 L·min-1. |
槽面处颗粒的体积分数在一定程度上体现了颗粒的沉降行为.由图 6和图 7可知,随着矿浆的铺展,槽面处赤铁矿的体积分数有所增加并逐渐在中部区域形成富集带,石英的体积分数则相对减小,随后在外缘区域产生富集.这意味着大部分中部区域的赤铁矿颗粒先于石英沉降至槽面,有利于形成良好的分层效果.随着入口流量的增大,中部区域槽面处赤铁矿的体积分数相应增大且富集带范围逐渐变宽,而石英的体积分数有所降低,这说明颗粒的分层效果得到了增强.值得注意的是,在内缘区域的槽面上存在小部分的石英颗粒,同时该区域中赤铁矿的体积分数相对较低,这意味着颗粒的分层效果较差,其与该区域中的拜格诺效应有关.在第0.125至0.375圈范围内,由于流体向外的径向流速较高,大部分颗粒呈现为向外运动的趋势,因此内缘区域的固体浓度较低.此外,由于内缘区域中流体的速度梯度较小,从而导致内缘区域拜格诺效应较弱,颗粒的分层结果不理想,增大入口流量有利于改善该区域的分层效果.
为了进一步研究颗粒在流膜中的分布特性,考察了入口流量对螺旋溜槽首圈末流膜中赤铁矿和石英分布的影响情况,分别如图 8和图 9所示.需要说明的是,由于流膜较薄不易分辨颗粒的空间分布,为了增加辨识度,依据颗粒的分布范围对流膜进行了局部放大处理,仅展示了r=50~120 mm处赤铁矿颗粒及r=70~150 mm处石英颗粒的分布情况.
图 8(Fig. 8)
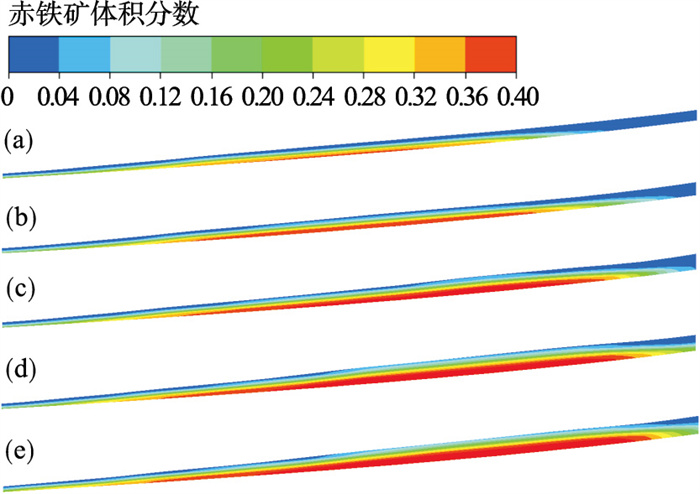 | 图 8 入口流量对首圈末流膜中赤铁矿分布的影响Fig.8 Influence of the inlet flow rate on the distribution of hematite at the end of the first turn (a)—Q=3 L·min-1; (b)—Q=5 L·min-1; (c)—Q=7 L·min-1; (d)—Q=9 L·min-1; (e)—Q=11 L·min-1. |
图 9(Fig. 9)
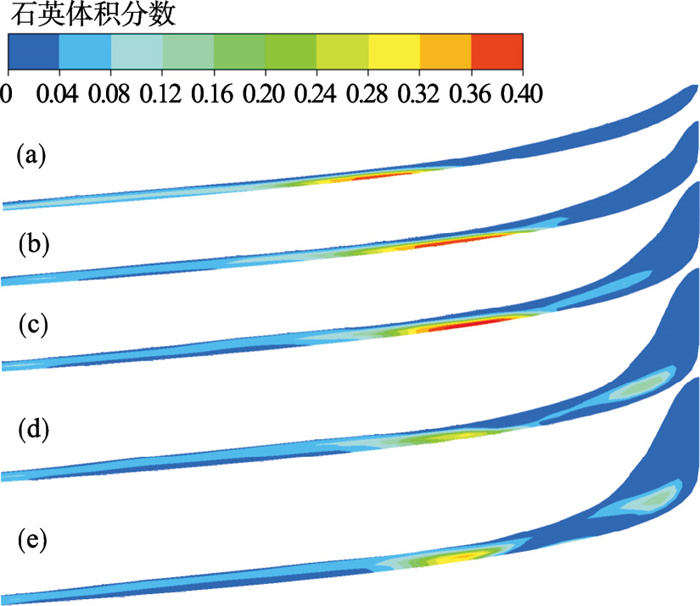 | 图 9 入口流量对首圈末流膜中石英分布的影响Fig.9 Influence of inlet flow rate on the distribution of quartz at the end of the first turn (a)—Q=3 L·min-1; (b)—Q=5 L·min-1; (c)—Q=7 L·min-1; (d)—Q=9 L·min-1; (e)—Q=11 L·min-1. |
由图 8和图 9可以发现,经过首圈的分选后,赤铁矿和石英在空间上形成了初步分离.赤铁矿带出现在中部区域,受到重力的影响,其在流膜中呈现为上稀下稠的分布特性,增大入口流量会促使赤铁矿带向外延伸.相比之下,大部分的石英出现在赤铁矿带的外侧,随着入口流量的增大,石英向外缘厚流膜区域迁移的趋势有所增强,且该区域中的石英受到强烈的湍流脉动作用呈现为悬浮状态.少部分石英出现在中部区域流膜的上层,与下流层中的赤铁矿形成了轴向分离,增加入口流量使得该区域中轴向分离的效果更加显著.
2.5 入口流量对首圈中颗粒分离结果的影响首圈的分离效果对颗粒后续的分离具有重要影响,为了考察螺旋溜槽首圈的分离性能,本文采用了分离效率作为表征方式,其定义为精矿带中目的矿物回收率与脉石矿物回收率之差,表达式如下[21]:
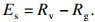 | (2) |
图 10(Fig. 10)
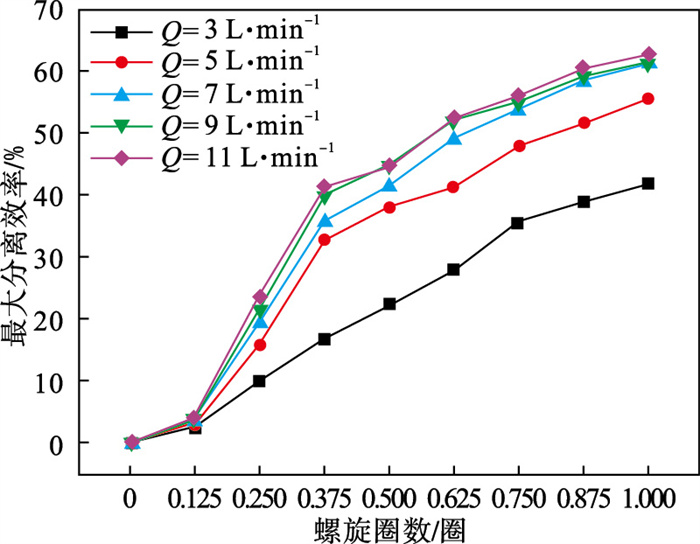 | 图 10 入口流量对各螺旋圈数最大分离效率的影响Fig.10 Influence of inlet flow rate on the maximum separation efficiency with different spiral turns |
由图 10可知,在入口流量为5~11 L/min范围内,最大分离效率在第0.125至0.375圈中增长最快,这说明该阶段中螺旋溜槽的分离效果最好.这是因为在该阶段中,一方面较高的速度梯度使得不同密度的颗粒快速发生法向分层,另一方面流体会带动颗粒向外缘运动,而流膜上层的径向流速较大,因此轻颗粒将先于重颗粒到达槽体外缘处,进一步促使了不同密度颗粒之间的径向分离.
入口流量对螺旋溜槽首圈的分离性能具有重要的影响.当入口流量为3 L/min时,首圈末的最大分离效率仅为41.6%,此条件下螺旋溜槽的分离性能较低,这主要与不理想的颗粒分层效果有关.随着入口流量的增大,各圈末的最大分离效率均有显著提升.然而当入口流量超过7 L/min后,继续增加入口流量对螺旋溜槽分离性能的提升幅度不大.基于首圈分离结果可以初步判定适宜该螺旋溜槽的最低入口流量为7 L/min,此时的最大分离效率为61.45%.在此基础上,继续增大入口流量可以在保证首圈分离性能的前提下扩大生产处理量,这对生产实践是有利的.然而,过大的入口流量将会降低螺旋溜槽的分离性能,这是因为当入口流量较大时,流场参数的稳定性会有所下降.这与Jain等[22]的观点一致,他们认为当入口流量超限后,过大的湍流强度会破坏主流及二次环流的基本流型结构,这对后续的颗粒分离是不利的.因此,确定入口流量的上限值还需结合螺旋溜槽流场稳定性及最终分离指标来综合判断,这有待于进一步的研究.
3 结论1) 随着流膜的演化发展,螺旋溜槽首圈槽面内外缘区域的流膜厚度、切向流速及径向流速呈现为波动式变化,增大入口流量会延长各流场参数达到稳定时所历经的行程;
2) 在槽面中部和内缘区域,随着入口流量的增大,初始阶段的流膜增厚,同时切向流速和径向流速均得到相应提升,随着流膜的进一步发展,不同入口流量下的流场分布特性渐趋一致;
3) 首圈流场中颗粒的法向分层和径向分离同步进行,随入口流量的增大,石英和赤铁矿的分层效果得到增强,赤铁矿分布范围变宽,石英向外缘厚流膜区域的迁移量增加;
4) 随流体纵向行程延长,最大分离效率逐渐提高,第0.125至0.375圈为最佳分离段,且随入口流量的增大,首圈中最大分离效率先明显增大而后渐趋平衡.适宜的最低入口流量为7 L/min,此时首圈的最大分离效率可达61.45%.
参考文献
| [1] | Khanchi A R, Sedighi H, Ansar S, et al. Preconcentration of rare earth elements from Iranian monazite ore by spiral separator using multi-response optimization method[J]. International Journal of Mining Science and Technology, 2014, 24: 117-121. DOI:10.1016/j.ijmst.2013.12.020 |
| [2] | Bazin C, Sadeghi M, Bourassa M, et al. Size recovery curves of minerals in industrial spirals for processing iron oxide ores[J]. Minerals Engineering, 2014, 65: 115-123. DOI:10.1016/j.mineng.2014.05.012 |
| [3] | Holland-Batt A B. The effect of feed rate on the performance of coal spirals[J]. Coal Preparation, 1994, 14: 199-222. DOI:10.1080/07349349408905234 |
| [4] | 高淑玲, 孟令国, 魏德洲, 等. 螺旋溜槽流场特性与分离性能研究进展[J]. 矿产保护与利用, 2020, 40(1): 166-171. (Gao Shu-ling, Meng Ling-guo, Wei De-zhou, et al. Research advance of flow characteristics in spirals and its separation performance[J]. Conservation and Utilization of Mineral Resources, 2020, 40(1): 166-171.) |
| [5] | Boucher D, Deng Z, Leadbeater T, et al. Observation of iron ore beneficiation within a spiral concentrator by positron emission particle tracking of large(?=1 440 μm) and small(?=58 μm) hematite and quartz tracers[J]. Chemical Engineering Science, 2016, 140: 217-232. DOI:10.1016/j.ces.2015.10.018 |
| [6] | Holland-Batt A B. The dynamics of sluice and spiral separations[J]. Minerals Engineering, 1995, 8: 3-21. DOI:10.1016/0892-6875(94)00098-W |
| [7] | Boucher D, Deng Z, Leadbeater T, et al. PEPT studies of heavy particle flow within a spiral concentrator[J]. Minerals Engineering, 2014, 62: 120-128. DOI:10.1016/j.mineng.2013.12.022 |
| [8] | Atasoy Y, Spottiswood D J. A study of particle separation in a spiral concentrator[J]. Minerals Engineering, 1995, 8: 1197-1208. DOI:10.1016/0892-6875(95)00084-4 |
| [9] | 黄尚安. 螺旋溜槽起始段水流运动特性和作用[J]. 中南矿冶学院学报, 1992(6): 665-669. (Huang Shang-an. The characteristics and functions of flowing fluid in the initial region of spiral sluice[J]. Journal of Central-South Institute of Mining and Metallurgy, 1992(6): 665-669.) |
| [10] | Boucher D, Deng Z, Leadbeater T, et al. Speed analysis of quartz and hematite particles in a spiral concentrator by PEPT[J]. Minerals Engineering, 2016, 91: 86-91. DOI:10.1016/j.mineng.2015.09.014 |
| [11] | 高淑玲, 魏德洲, 崔宝玉, 等. 基于CFD的螺旋溜槽流场及颗粒运动行为数值模拟[J]. 金属矿山, 2014(11): 121-126. (Gao Shu-ling, Wei De-zhou, Cui Bao-yu, et al. CFD-based numerical simulation of flow field and particles motion behavior in spiral[J]. Metal Mine, 2014(11): 121-126.) |
| [12] | Ye G, Ma L, Alberini F, et al. Numerical studies of the effects of design parameters on flow fields in spiral concentrators[J]. International Journal of Coal Preparation and Utilization, 2022, 42(1): 67-81. DOI:10.1080/19392699.2019.1579200 |
| [13] | Doheim M A, Abdel G A F, Mahran G M A, et al. Computational prediction of water-flow characteristics in spiral separators: part Ⅱ, the primary and secondary flows[J]. Journal of Engineering Sciences, 2008, 36(4): 951-961. |
| [14] | Doheim M A, Abdel G A F, Mahran G M A, et al. Numerical simulation of particulate-flow in spiral separators: part I.low solids concentration(0.3% & 3% solids)[J]. Applied Mathematical Modelling, 2013, 37: 198-215. DOI:10.1016/j.apm.2012.02.022 |
| [15] | 黄波, 许秋石, 徐宏祥, 等. 螺旋分选机流场及颗粒运动的数值模拟研究[J]. 中国矿业大学学报, 2019, 48(3): 655-661. (Huang Bo, Xu Qiu-shi, Xu Hong-xiang, et al. Numerical simulation of flow field and particle motion behavior in spiral separator[J]. Journal of China University of Mining & Technology, 2019, 48(3): 656-661.) |
| [16] | Meng L, Gao S, Wei D, et al. Investigation on the evolution of flow field stability in a spiral separator[J]. Minerals Engineering, 2021, 174: 107224. DOI:10.1016/j.mineng.2021.107224 |
| [17] | Tripathy S K, Murthy Y R. Modeling and optimization of spiral concentrator for separation of ultrafine chromite[J]. Powder Technology, 2012, 221: 387-394. DOI:10.1016/j.powtec.2012.01.035 |
| [18] | Ye G, Huo Y, Li C, et al. A comparative study of trough profile and operating parameters performance in spiral concentrator[J]. International Journal of Coal Preparation & Utilization, 2021, 41(9): 678-691. |
| [19] | Gao S, Meng L, Zhou X, et al. Design of partial cross-sectional geometry and prediction of separation performance in the spiral separator[J]. Separation Science and Technology, 2022, 57(13): 2127-2144. |
| [20] | Meng L, Gao S, Wei D, et al. Effects of cross-sectional geometry on flow characteristics in spirals separators[J]. Separation Science and Technology, 2021, 56(17): 2967-2977. |
| [21] | Mishra B K, Tripathy A. A preliminary study of particle separation in spiral concentrators using DEM[J]. International Journal of Mineral Processing, 2010, 94: 192-195. |
| [22] | Jain P K, Rayasam V. An analytical approach to explain the generation of secondary circulation in spiral concentrators[J]. Powder Technology, 2017, 308: 165-177. |
