易平涛, 袁建荣, 李伟伟
东北大学 工商管理学院，辽宁 沈阳 110169
收稿日期：2022-03-26
基金项目：国家自然科学基金资助项目(72171040, 72171041)；中央高校基本科研业务费专项资金资助项目(N2006013)。
作者简介：易平涛(1981-)，男，湖南永州人，东北大学教授，博士生导师。

摘要：分层无量纲化方法能够有效去除指标量纲影响的同时解决异常指标造成的数据分布不均衡、区分度低等问题.然而，该方法的使用需要人为指定区间数，使得无量纲化结果受人为因素的干扰，失去客观性.针对该问题，考虑原始数据的分布特征，提出了密度分层无量纲化方法.该方法按照数据分布的疏密程度进行区间划分，客观确定分层级数，同时兼顾分层无量纲化方法的优点，计算相对简单且减少了人为干扰.此外，通过随机模拟发现，该方法对于异常值具有较好的抗干扰性，且无量纲化结果的均衡性受原始数据规模影响.
关键词：无量纲化方法异常值分层无量纲化方法数据密度客观分层
Hierarchical Dimensionless Method Based on Data Distribution Characteristics and Its Equilibrium Analysis
YI Ping-tao, YUAN Jian-rong, LI Wei-wei
School of Business Administration, Northeastern University, Shenyang 110169, China
Corresponding author: YUAN Jian-rong, E-mail: jianrong_yuan@163.comjianrong_yuan@163.com.

Abstract: The hierarchical dimensionless method can effectively remove the effect of different index dimensions, and solve imbalanced data distribution and low discrimination caused by anomalous index values. However, when using this method, it is necessary to artificially specify the number of partition intervals so that the dimensionless results are interfered by human factors and lose objectivity. To solve this problem, a dimensionless method of density hierarchy is proposed considering the distribution characteristics of raw data. This method divides the interval according to the density of data distribution, objectively determines the hierarchical series, and takes into account the advantages of the hierarchical dimensionless method. The calculation is comparatively simple and reduces human factors. In addition, through the stochastic simulation method, it is found that the method has good anti-interference to outliers, and the balance of dimensionless results is affected by the scale of raw data.
Key words: dimensionless methodoutlierhierarchical dimensionless methoddata densityobjective hierarchy
综合评价，是指对被评价对象所进行的公正、客观以及合理的全面评价，广泛应用于经济管理、统计及决策等各领域，具有重大的实用价值和广泛的应用前景^[1-8].作为评价流程中的重要环节，指标的无量纲化过程消除了不同量纲对评价结果的影响^[9-10]，为多属性数据的集结奠定了基础.根据函数特性的不同可将无量纲化方法主要分为两类：线性无量纲化方法和非线性无量纲化方法^[11].由于计算简洁，易于操作，线性无量纲化方法的使用更为广泛^[12-17].
线性无量纲化方法，其最大特点在于能够保留原始数据的分布特征.但是，在综合评价过程中，原始指标数据之间的关系并非都是线性的，其分布也并非都是均匀.数据间分布差异大，甚至存在异常数据的情况时有发生.异常数据的分布远离于大部分评价数据，它的存在间接压缩了其他数据的分布范围，导致评价数据呈现明显的不均匀分布^[18]，使得绝大部分数据之间区分度不高.在存在异常值的情况下，若选择线性无量纲化方法，会导致结果出现分布不均衡的问题^[19]，进而降低指标的区分度，从整体上削弱了评价的差异测度功能.
针对此问题，“分层处理”的思想被引入无量纲化处理过程中.文献[18]首先对原始数据进行异常值判断、识别，然后以极值处理法为基础分别指定异常值和非异常值的无量纲化取值区间，从而进行分层无量纲化处理.文献[20]则省去对异常信息的判别，在尽量保证原始数据分布特征的前提下，基于极值处理法提出了一种根据数据位置分布进行划分区间的分层无量纲化处理方法，即“位置分布处理法”.在此基础上，文献[19]又对该方法做了进一步的优化，对其分层方法展开细化改进，提出了按照原始数据排序值百分比实现区间划分，进而对原始数据实行无量纲化处理，即“序比例诱导分段无量纲化方法”.
然而，上述方法均未给出分层区间的具体划分层数，需要根据评价者自行确定.因此，在实际应用过程中针对异常值存在的情况，评价者往往会直接选择传统的四分位分层无量纲化方法^[20].但将四分位数作为分层区间的依据，也是基于评价者的经验判断所得，无法保证无量纲化结果的客观性.因此，本文在已有研究的基础上，考虑到数据自身的密度特征，即按照数据分布的疏密程度客观地划分分层区间，提出了一种新的基于原始数据分布疏密程度的分层无量纲化方法.此外，本文还对运用该方法进行处理所得结果的均衡性进行对比分析，并提出相关结论.
1 研究基础及问题描述本文在分层无量纲化方法^[20]的基础上进行拓展研究，下面简要介绍分层无量纲化方法.
设n个被评价对象o₁, o₂, …, o_n关于m个指标x₁, x₂, …, x_m的取值矩阵为[x_ij]_n×m，记无量纲化处理后的矩阵X^*=[x_ij^*]_n×m.不失一般性，令m, n≥3.分层无量纲化方法的基本步骤如下：
对某一指标下的原始数据按升序排列，在[0, 1]区间内取l+2个分层点(记为α₀, α₁, …, α_l+1)，将区间划分为l+1个子区间，其中α₀=0, α_l+1=1.不失一般性，令l≥1，子区间分别为[α₀, α₁], (α₁, α₂], …, (α_l, α_l+1].与此同时，依据原始指标数据按照分层点依次计算其相对应的百分位数，记为γ₀, γ₁, …, γ_l+1.在明确分层区间且得到相应的百分位数后，可按式(1)对原始数据进行无量纲化处理：

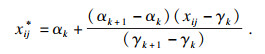(1)

式中，x_ij∈(γ_kj, γ_(k+1)j]，且x_j为极大型指标，k=0, 1, …, l.
分层无量纲化方法的关键是分层区间数的确定，即l值的确定.现有研究中评价者往往直接选用四分位数来划分区间，进而实现分层无量纲化处理，但其合理性和结果的均衡性都无法得到保障.因此，本文聚焦于如何客观合理地确定分层区间数，并将其与传统的四分位分层无量纲化方法进行对比，以突出本文方法的优势.
2 基于密度划分区间的分层无量纲化方法2.1 基于数据密度的分层区间划分本文依据指标数据的分布密度对其进行区间分层，划分的基本思路为：首先，将原始指标数据进行按序排列，并计算前后相邻数据之间的差值；其次，对其差值作标准化处理并进行判断，将不符合条件的差值所对应的数据单独成数据集，同时将符合条件的差值作为划分依据，进行区间的划分；最后，对初次划分的区间进行判断、校正，从而得到最终的分层区间.
2.1.1 原始数据集的初步划分步骤1 指标值的排序.对n个被评价对象关于第j(j=1, 2, …, m)个指标取值{x_1j, x_2j, …, x_nj}，按升序排列，为便于理解，排序后的指标值仍记为{x_1j, x_2j, …, x_nj}.
步骤2 相邻指标间差值的计算.依次计算前后相邻数据间的差值(记为Δ_tj)，如式(2)所示：

(2)

步骤3 差值的标准化处理.计算n－1个差值Δ_tj的平均值Δ_θj和标准差s_θj，并对每个Δ_tj进行标准化处理，即令

(3)

式中，z_tj为“标准分数”统计量，代表Δ_tj偏离平均差值的程度，用于识别Δ_tj中的异常值.
步骤4 分层条件的判断.本文以首个非零差值Δ_1j(Δ_1j≠0)作为比较基准，为防止Δ_1j值过大导致判别条件失效，在进行比较前需对Δ_1j进行异常值判断.若满足|z_1j|<z(z的取值依据拉依达准则进行确定，2.1.2节中给出)，则可将Δ_1j作为判断标准并进入下一步处理；否则，表明该差值异常，需顺次对z_2j进行判断，直至出现满足上述条件的Δ_tj为止.
步骤5 根据分层点，初步得到分层区间.若存在异常差值，则需先将其所处位置作为分层点进行区间划分.然后，以前文正常差值Δ_tj为基准依次作比，若出现Δ_δj>Δ_tj(δ>t)，则将Δ_δj所在位置作为分层点进行区间划分.不失一般性，设原始数据划分为Ω₁={x_1j, x_2j, …, x_μj}, Ω₂={x_(μ+1)j, x_(μ+2)j, …, x_nj}(1≤μ<n)两个子数据集，并将Ω₁和Ω₂数据集的间距定义为Δ_δj(Δ_δj=x_(μ+1)j－x_μj).
步骤6 对数据集Ω₂进行划分.一般地，Ω₂内数据分布密度不均衡，仍需对其进行细致划分.以Δ_δj作为基准，按照前文规则识别其中分层点并以此进行数据分割，得到分层区间Ω₃与Ω₄.依此类推，得到所有分层区间Ω_ρ(1≤ρ≤n).
2.1.2 数据集划分的检验经上述处理，原始数据被划分为若干个区间，为了使划分结果更加精确，需进一步判断和处理每个分层区间.具体过程如下：
步骤1 对已划分好的各个分层区间，分别计算其内部所有差值Δ_σj^*(1<σ<n)的平均值Δ_ρj^*和标准差s_ρj^*，并根据式(3)对各分层区间内的每个Δ_σj^*进行标准化处理，令其标准分数值为z_σj^*(z_σj^*同2.1.1节步骤3中的z_tj含义及作用完全一致).
步骤2 对各个分层区间内的异常差值进行辨识.若分层区间内所有的Δ_σj^*均满足|z_σj^*|<z(此处z同前文一致)，表明前文对于该区间的划分没有问题；否则，若存在Δ_σj^*不满足此条件，则表明前文对该分层区间的划分存在问题，需重新对其进行处理划分，进而转入步骤3.
步骤3 根据异常差值Δ_σj^*的位置，对其所在分层区间Ω_ρ再次分割，并重复步骤1~3，直至所有区间内的z_σj^*满足条件为止，得到最终各分层区间Ω_λ(1≤λ≤n).
根据上述分层区间划分步骤中对于判断差值是否异常的需要，本文选择拉依达准则对差值所对应的标准分数值进行比较.拉依达准则是指对一组数据进行处理得到标准偏差，并按一定概率确定一个区间，若有数据超过该区间，则表明该数据属于异常值应予以剔除^[21].此原则主要对正态或近似正态分布的样本数据进行处理，用于判别数据中是否存在异常值.根据拉依达准则理论，本文中z值取3.另外，运用拉依达准则进行异常值判断时，对于样本量有一定的要求，当样本量较小时，则不适用.
2.2 无量纲化处理经前文处理，原始数据已按分布的疏密程度进行了区间划分，使得区间内部的数据分布相对紧密，而各区间的分布则相对分散，接下来就是无量纲化处理.
步骤1 无量纲化分层点的确定.统计各分层区间Ω_λ内原始数据个数η_ω(ω=1, 2, …, λ)，计算其占全部数据个数的百分比，

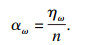(4)

依据其占比确定每个分层区间对应的分层点α_l(l=0, 1, …, λ)，其中α₀=0, α_λ=1.
步骤2 无量纲化分位数的确定.计算相邻分层区间的差值Δ_εj(Δ_εj=x_(φ+1)j－x_φj, 1≤φ≤n-1, ε=1, 2, …, λ－1)，根据相邻数据集的个数对差值Δ_εj进行均分，并依此确定相应的分位数，记为γ_l，

(5)

步骤3 指标值的无量纲化处理.无量纲化处理的具体公式如下：

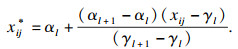(6)

式中x_ij∈(γ_l, γ_l+1]，且x_j为极大型指标.
由于本文的无量纲化方法是基于数据分布特征进行区间划分，因此若原始数据无明显分布特征、数据太过杂乱或者数据分布呈现特殊状态时，可使用四分位分层无量纲化方法进行数据处理.
密度分层无量纲化方法，主要特征是基于指标数据分布的疏密程度划分区间，从而根据分层无量纲化方法的原理进行处理.通过该方法，将分布相近的数据划分在同一区间内，各区间则相距较远；与此同时，还可将异常数据与正常数据划分开，避免了将异常值与正常值划分在同一区间后，正常数据被压缩而无法发挥作用的可能.总的来说，本文方法在保证客观划分分层区间的基础上，提高了无量纲化结果分布的均衡性.
3 均衡性分析在分层无量纲化方法中四分位法最为常用，但其合理性以及结果的均衡性无法得到保证; 而本文方法在分层无量纲化方法的基础上，实现了对分层区间的客观划分.因此，为了突出本文方法的优势，将本文方法与四分位分层无量纲化方法进行均衡性对比.本文采用模拟仿真的方法从原始数据个数、异常值个数和偏离方向入手，探究两种方法下无量纲化结果的分布均衡性.无量纲化后数据分布均衡性的判断，采用文献[19]中的测度值.均衡性测度值越小，表明数据的均衡性越高.
针对异常值主要从以下2种情形进行分析：1)在原始数据的最小值方向生成1个异常值；2)在原始数据的最大及最小值方向分别生成1个异常值，2个异常值方向相反.异常值的产生方式分别为：max{x_ij}+cσt(i=1, 2, …, n)和min{x_ij}－cσt(i=1, 2, …, n).其中：σ为原始指标数据{x_1j, x_2j, …, x_nj}的标准差；c(c<0)为偏离系数，cσ为异常值偏离原始数据的步长；t为步长的个数，取值为自然数.为了能够使产生的异常值足够偏离原始正常数据，本文取c=0.4, t=10.
本文运用模拟仿真技术对无量纲化结果进行均衡性分析，具体仿真过程如下所示.
1) 设置总仿真次数sum、原始数据个数n及其取值区间(设为[a, b]，结果不受a, b取值的影响)，循环变量v(初始值为0)，初始变量s(初始值为0)；2) 令v=v+1，在[a, b]内按正态分布方式随机生成n个原始数据，记为{x₁, x₂, …, x_n}；3) 在原始数据的基础上根据前文所示异常值的生成公式，生成异常数据；4) 对数据进行无量纲化处理，并将处理后的结果记为{x₁^*, x₂^*, …, x_n^*}；5) 计算无量纲化后结果的均衡性测度值，记为V_s；6) 令s = s + V_s，若v=sum，则转7)，否则转2)；7) 求解sum次仿真过程中均衡性测度值的平均偏差，记为s=s/sum，并保存值；8)变动1)中的原始数据个数n的取值和异常值，并重复步骤1)~7)，保存不同n值、不同异常值下取值，退出程序.
按照上述步骤，本文按正态分布的方式随机生成15, 20, 25, 30, 35, 40, 45, 50, 75和100个原始数据，根据异常值的两种情形分别进行模拟，具体结果如图 1和图 2所示.
图 1(Fig. 1)

图 1 1个异常值时不同原始数据个数下无量纲化结果分布的均衡性Fig.1 Equilibrium of dimensionless result distribution under different numbers of raw data with 1 outlier

图 2(Fig. 2)

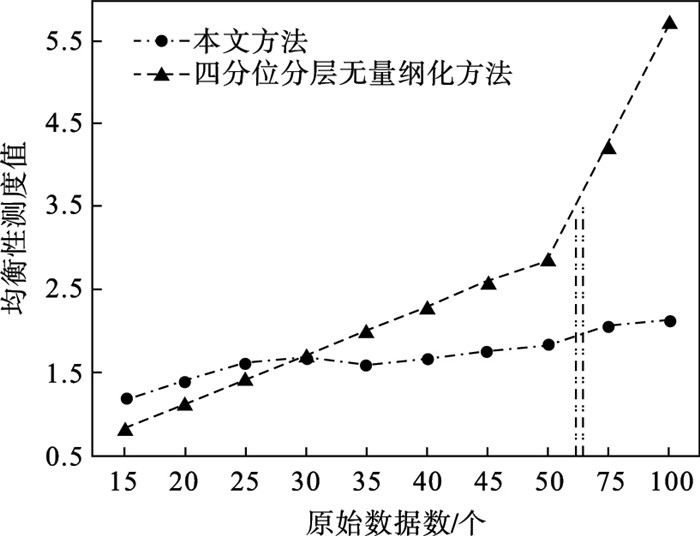图 2 2个正负异常值时不同原始数据个数下无量纲化结果分布的均衡性Fig.2 Equilibrium of dimensionless result distribution under different numbers of raw data with two positive and negative outliers

通过图 1中的数值比较，可以得到如下结果：
1) 当原始数据个数超过30后，运用本文方法对存在异常值的原始指标数据进行无量纲化处理，其结果分布的均衡性明显优于四分位分层无量纲化方法，且差距越来越大.这表明，当原始数据规模超过30后，运用本文方法进行无量纲化处理更为客观合理.
2) 随着原始数据规模的增大，运用四分位分层无量纲化方法进行处理所得结果的均衡性测度值变动幅度较大，而运用本文方法所得均衡性测度值的变动幅度则相对较缓.这表明，本文方法的稳定性优于四分位分层无量纲化方法.
3) 两种方法的均衡性测度值随原始数据规模的增大而增大.这表明，无论使用哪种方法，无量纲化结果分布的均衡性随着原始数据个数的增多而减弱.
当原始数据中存在正负2个异常值时，其结果的均衡性与存在1个异常值时类似，如图 2所示.在此种情形下本文方法的均衡性变动幅度更为平缓，而四分位分层无量纲化方法则相反，这进一步表明本文方法的稳定性更高，能更好地抵抗异常值的干扰.另外，拉依达准则进行异常值识别时，对样本量有一定的要求.也就是说，当原始数据规模越大时，本文方法对于异常值的处理越有效.因此，当原始数据个数超过30后，使用本文方法会更加有效.
综上所述，可以看出，数据分布的均衡性主要受原始数据规模的影响.当存在异常值的原始数据个数超过30后，相较于传统的分层无量纲化方法，运用密度分层无量纲化方法进行无量纲化处理，可以更好地减弱异常值的影响，同时保持更高的结构稳定性.即本文方法对异常值有更好的抗干扰性，且操作简单，在实际应用中有广泛的应用前景.
4 应用算例为验证本文提出的无量纲化方法的有效性，选用2021年《中国城市统计年鉴》数据，采用“人均地区生产总值(x₁)(元)”、“每万人人均工业企业数(x₂)(个)”、“地方一般公共预算收入(x₃)(万元)”和“人均年末金融机构人民币各项存款余额(x₄)(元)”等4个常用指标对东北三省(辽宁省、吉林省和黑龙江省)34个地级以上城市在2020年的经济发展作简要评价，原始数据如表 1所示.
表 1(Table 1)

表 1 原始数据Table 1 Raw data 城市 x1 x2 x3 x4 城市 x1 x2 x3 x4 沈阳市 75 570.00 1.76 7 360 802.00 212 487.65 辽源市 37 171.00 1.04 170 338.00 72 384.70 大连市 94 685.00 2.55 7 026 822.00 208 221.49 通化市 35 113.00 2.56 535 197.00 122 256.38 鞍山市 52 020.00 2.13 1 572 696.00 135 376.80 白山市 44 021.00 1.67 234 385.00 93 543.04 抚顺市 44 137.00 1.40 766 870.00 125 335.53 松原市 27 487.00 0.93 762 000.00 71 258.83 本溪市 60 210.00 1.69 696 616.00 130 603.09 白城市 27 230.00 1.01 407 908.00 65 690.99 丹东市 35 389.00 1.73 776 069.00 120 342.23 哈尔滨市 54 570.00 1.19 3 395 674.00 137 356.22 锦州市 39 332.00 1.25 1 041 364.00 146 676.44 齐齐哈尔市 24 273.00 0.87 745 843.00 64 047.03 营口市 56 777.00 2.92 1 357 770.00 167 462.58 鸡西市 34 031.00 1.40 336 601.00 90 339.21 阜新市 30 541.00 1.27 444 117.00 90 180.22 鹤岗市 34 809.00 1.56 229 843.00 96 170.48 辽阳市 51 792.00 1.55 981 946.00 186 256.19 双鸭山市 35 391.00 1.27 254 147.00 90 058.17 盘锦市 93 802.00 2.32 1 583 723.00 186 800.99 大庆市 84 784.00 1.76 1 528 677.00 115 033.17 铁岭市 27 577.00 1.25 504 085.00 77 094.40 伊春市 26 506.00 0.72 152 430.00 104 755.70 朝阳市 30 371.00 1.13 777 734.00 78 911.08 佳木斯市 35 124.00 1.48 465 923.00 78 518.24 葫芦岛市 31 514.00 1.11 695 178.00 96 758.14 七台河市 26 979.00 1.48 192 536.00 87 423.72 长春市 77 634.00 1.34 4 404 297.00 156 071.66 牡丹江市 33 428.00 1.25 545 433.00 82 286.55 吉林市 35 588.00 1.17 850 129.00 91 313.32 黑河市 39 184.00 0.90 425 270.00 81 550.91 四平市 24 586.00 0.94 337 991.00 99 051.35 绥化市 22 122.00 0.99 674 869.00 56 318.54

表 1 原始数据 Table 1 Raw data

由表 1的数据可以看出，34个城市关于指标x₃的取值中包含2个异常值，即沈阳市(7 360 802.00)和大连市(7 026 822.00)的取值远大于其他城市的取值.表 2展示了采用极值处理法、四分位分层无量纲化方法以及本文方法分别对表 1数据进行无量纲化处理的结果.由表 2可以看出，经由本文方法和四分位分层无量纲化方法处理后，数据分布相较极值处理法更加均衡，且2种方法间的结果更加相近.
表 2(Table 2)

表 2 3种方法的处理结果Table 2 Results processed by three methods 城市 极值处理法 四分位分层无量纲化方法 本文方法 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 绥化市 0.000 0.122 0.072 0.000 0.000 0.173 0.481 0.000 0.000 0.140 0.506 0.000 齐齐哈尔市 0.030 0.066 0.082 0.049 0.065 0.093 0.538 0.076 0.070 0.034 0.577 0.088 四平市 0.034 0.098 0.026 0.274 0.074 0.139 0.179 0.517 0.080 0.094 0.196 0.487 伊春市 0.060 0.000 0.000 0.310 0.132 0.000 0.000 0.555 0.143 0.000 0.000 0.552 七台河市 0.067 0.344 0.006 0.199 0.146 0.614 0.039 0.347 0.158 0.560 0.069 0.354 白城市 0.070 0.129 0.035 0.060 0.154 0.182 0.246 0.092 0.166 0.152 0.259 0.107 松原市 0.074 0.093 0.085 0.096 0.162 0.132 0.550 0.147 0.175 0.086 0.593 0.170 铁岭市 0.075 0.241 0.049 0.133 0.164 0.431 0.331 0.204 0.177 0.364 0.346 0.237 朝阳市 0.114 0.183 0.087 0.145 0.249 0.268 0.562 0.222 0.275 0.255 0.609 0.257 阜新市 0.116 0.250 0.040 0.217 0.256 0.458 0.278 0.393 0.282 0.382 0.292 0.386 葫芦岛市 0.129 0.174 0.075 0.259 0.305 0.247 0.499 0.502 0.319 0.239 0.526 0.461 牡丹江市 0.156 0.242 0.055 0.166 0.401 0.434 0.367 0.259 0.394 0.366 0.383 0.296 鸡西市 0.164 0.306 0.026 0.218 0.432 0.559 0.177 0.396 0.418 0.489 0.195 0.388 鹤岗市 0.175 0.382 0.011 0.255 0.471 0.669 0.074 0.495 0.448 0.632 0.097 0.454 通化市 0.179 0.837 0.053 0.422 0.486 0.928 0.358 0.671 0.460 0.952 0.374 0.665 佳木斯市 0.179 0.346 0.043 0.142 0.487 0.617 0.297 0.218 0.460 0.564 0.311 0.253 丹东市 0.183 0.458 0.087 0.410 0.500 0.759 0.561 0.658 0.471 0.776 0.608 0.655 双鸭山市 0.183 0.247 0.014 0.216 0.500 0.450 0.098 0.391 0.471 0.377 0.119 0.384 吉林市 0.186 0.205 0.097 0.224 0.503 0.330 0.617 0.413 0.478 0.297 0.682 0.399 辽源市 0.207 0.144 0.002 0.103 0.527 0.204 0.017 0.158 0.540 0.181 0.042 0.183 黑河市 0.235 0.079 0.038 0.162 0.557 0.112 0.261 0.248 0.618 0.059 0.275 0.287 锦州市 0.237 0.240 0.123 0.579 0.559 0.431 0.751 0.790 0.624 0.364 0.732 0.796 白山市 0.302 0.433 0.011 0.238 0.630 0.742 0.079 0.450 0.672 0.728 0.101 0.424 抚顺市 0.303 0.307 0.085 0.442 0.632 0.561 0.554 0.691 0.673 0.490 0.598 0.682 辽阳市 0.409 0.376 0.115 0.832 0.747 0.661 0.716 0.916 0.723 0.622 0.723 0.903 鞍山市 0.412 0.640 0.197 0.506 0.750 0.840 0.772 0.754 0.725 0.895 0.805 0.736 哈尔滨市 0.447 0.214 0.450 0.519 0.765 0.357 0.844 0.760 0.746 0.315 0.902 0.746 营口市 0.478 1.000 0.167 0.712 0.778 1.000 0.763 0.856 0.764 1.000 0.778 0.866 本溪市 0.525 0.440 0.075 0.476 0.798 0.751 0.501 0.726 0.791 0.742 0.528 0.710 沈阳市 0.737 0.470 1.000 1.000 0.888 0.764 1.000 1.000 0.895 0.799 1.000 1.000 长春市 0.765 0.280 0.590 0.639 0.900 0.522 0.883 0.820 0.906 0.439 0.919 0.847 大庆市 0.864 0.473 0.191 0.376 0.942 0.766 0.770 0.623 0.946 0.805 0.799 0.626 盘锦市 0.988 0.728 0.199 0.836 0.995 0.879 0.772 0.918 0.995 0.920 0.806 0.905 大连市 1.000 0.831 0.954 0.973 1.000 0.925 0.987 0.986 1.000 0.950 0.988 0.983

表 2 3种方法的处理结果 Table 2 Results processed by three methods

为进一步分析不同无量纲化方法对最终综合评价值的影响，本文分别对经3种方法处理的指标值进行集结.表 3展示了不同无量纲化方法下的评价值(y_i)及序值(r_i)，以此分析本文方法在评价值层面的影响.为简化问题，消除指标权重的影响，在此将指标权重设置为均权，采用算术平均的方法对数据进行集结.首先，对不含异常值的3个指标“人均地区生产总值”、“每万人人均工业企业数”和“人均年末金融机构人民币各项存款余额”分别运用3种方法进行集结；然后，对全部指标进行集结，具体结果如表 3所示.
表 3(Table 3)

表 3 采用不同无量纲化方法得到的评价值及排序值Table 3 Evaluation value and ranking value obtained by different dimensionless methods 城市 不存在异常值的情形 存在异常值的情形 极值处理法 四分位分层无量纲化方法 本文方法 极值处理法 四分位分层无量纲化方法 本文方法 yi ri yi ri yi ri yi ri yi ri yi ri 绥化市 0.041 34 0.058 34 0.047 34 0.049 34 0.164 34 0.162 34 齐齐哈尔市 0.048 33 0.078 33 0.064 33 0.057 33 0.193 31 0.192 31 四平市 0.135 29 0.243 29 0.221 30 0.108 29 0.227 29 0.214 30 伊春市 0.124 30 0.229 30 0.232 29 0.093 30 0.172 32 0.174 32 七台河市 0.203 21 0.369 22 0.357 21 0.154 24 0.286 26 0.285 26 白城市 0.086 32 0.143 32 0.142 32 0.074 32 0.169 33 0.171 33 松原市 0.088 31 0.147 31 0.143 31 0.087 31 0.248 28 0.256 28 铁岭市 0.150 27 0.267 27 0.260 28 0.124 27 0.283 27 0.281 27 朝阳市 0.147 28 0.246 28 0.262 27 0.132 25 0.325 24 0.349 22 阜新市 0.194 22 0.369 21 0.350 23 0.156 22 0.346 23 0.335 24 葫芦岛市 0.188 24 0.351 24 0.340 24 0.160 21 0.388 20 0.386 19 牡丹江市 0.188 23 0.365 23 0.352 22 0.155 23 0.366 21 0.360 21 鸡西市 0.229 17 0.462 17 0.431 17 0.178 17 0.391 19 0.372 20 鹤岗市 0.271 16 0.545 16 0.511 16 0.206 16 0.427 17 0.408 17 通化市 0.480 10 0.695 10 0.692 10 0.373 11 0.611 13 0.613 13 佳木斯市 0.222 18 0.441 19 0.426 18 0.178 19 0.405 18 0.397 18 丹东市 0.350 14 0.639 11 0.634 11 0.284 14 0.619 12 0.627 12 双鸭山市 0.215 19 0.447 18 0.411 19 0.165 20 0.360 22 0.338 23 吉林市 0.205 20 0.415 20 0.391 20 0.178 18 0.466 16 0.464 16 辽源市 0.151 26 0.296 26 0.301 26 0.114 28 0.226 30 0.237 29 黑河市 0.159 25 0.306 25 0.322 25 0.128 26 0.295 25 0.310 25 锦州市 0.352 12 0.593 15 0.595 15 0.295 12 0.633 11 0.629 11 白山市 0.324 15 0.608 14 0.608 13 0.246 15 0.475 15 0.481 15 抚顺市 0.351 13 0.628 12 0.615 12 0.284 13 0.609 14 0.611 14 辽阳市 0.539 7 0.775 7 0.749 7 0.433 8 0.760 8 0.743 8 鞍山市 0.520 8 0.781 5 0.785 6 0.439 7 0.779 6 0.790 6 哈尔滨市 0.394 11 0.628 13 0.602 14 0.408 9 0.682 10 0.677 10 营口市 0.730 4 0.878 4 0.877 4 0.589 4 0.849 4 0.852 4 本溪市 0.480 9 0.758 8 0.748 8 0.379 10 0.694 9 0.693 9 沈阳市 0.735 3 0.884 3 0.898 3 0.802 2 0.913 2 0.923 2 长春市 0.561 6 0.747 9 0.731 9 0.568 5 0.781 5 0.778 7 大庆市 0.571 5 0.777 6 0.792 5 0.476 6 0.775 7 0.794 5 盘锦市 0.850 2 0.931 2 0.940 2 0.687 3 0.891 3 0.907 3 大连市 0.935 1 0.970 1 0.978 1 0.939 1 0.975 1 0.980 1

表 3 采用不同无量纲化方法得到的评价值及排序值 Table 3 Evaluation value and ranking value obtained by different dimensionless methods

为进一步研究各方法在两种情境下(有、无异常值)对最终评价结果的影响，本文引入皮尔逊相关系数及斯皮尔曼等级相关系数分别对评价值以及序值进行分析讨论.本文使用u_j, u_s, u_m分别表示不存在异常值情况下的极值处理法、四分位分层无量纲化方法以及本文方法，使用u_j^*, u_s^*, u_m^*分别表示存在异常数据时的3种方法，r₁, r₂分别表示皮尔逊相关系数与斯皮尔曼等级相关系数.
通过表 4中的信息，可以看出：
表 4(Table 4)

表 4 皮尔逊相关系数矩阵Table 4 Pearson correlation coefficient matrix r1 uj us um uj* us* um* m1+ m1- uj 1.000 0.953 0.959 0.980 0.960 0.961 0.980 0.953 us 0.953 1.000 0.999 0.911 0.972 0.968 0.999 0.911 um 0.959 0.999 1.000 0.918 0.973 0.971 0.999 0.918 uj* 0.980 0.911 0.918 1.000 0.943 0.944 0.980 0.911 us* 0.960 0.972 0.973 0.943 1.000 0.999 0.999 0.943 um* 0.961 0.968 0.971 0.944 0.999 1.000 0.999 0.944 注：m1+, m1-分别表示某方法所有相关系数的最大值和最小值.

表 4 皮尔逊相关系数矩阵 Table 4 Pearson correlation coefficient matrix

1) u_j, u_s与u_m三者间的相关系数关系为r_1ujus(0.953)<r_1ujum(0.959)<r_1usum(0.999)，3种方法间的一致性程度均很高，且相较于四分位分层无量纲化方法，本文方法与极值处理法间的一致性程度更高.这表明在无异常值存在的情况下，运用3种方法对原始数据进行无量纲化处理所得的评价值相近，且本文方法相较于四分位分层无量纲化方法更贴近极值处理法的结果，使得结果能够更好保留原始数据的分布特征.
2) u_j^*, u_s^*与u_m^*间的相关系数存在如下关系：r_1uj^*us^*(0.943)<r_1uj^*um^*(0.944)<r_1us^*um^*(0.999).由此可以看出极值处理法与四分位分层无量纲化方法以及本文方法间的一致性程度相对较低，而后两种方法间的一致性程度较高.这表明当指标中存在异常值时，运用分层无量纲化方法和极值处理法所获得的结果差距较大，而经后两种方法处理后的结果更相近.
3) u_j与u_j^*，u_s与u_s^*以及u_m与u_m^*间的相关系数关系为r_1umum^*(0.971)<r_1usus^*(0.972)<r_1ujuj^*(0.980)，可以看出极值处理法在两种情境下的一致性程度最高，本文方法最低，四分位分层无量纲化方法介于二者之间且与本文方法更加相近.这表明异常值存在前后对于极值处理法的影响最小，当考虑了异常值指标后，由于极值处理法无法兼顾对异常值的处理，使得无量纲化后的绝大部分数据区分度不高，进而使得评价结果变动程度不大，从而无法体现出相应指标的作用，而本文方法则相对较好地克服了这一缺点.
表 5为序值间的等级相关系数，观察表 5可以得出与表 4相似的结论，且相较于评价值本文方法对于序值的影响更大，这里将不再赘述.由表 4和表 5可以看出在无异常值的情况下，运用3种方法对数据进行无量纲化处理得到的评价值及序值相近，且相对于四分位分层无量纲化方法，本文方法更贴近极值处理法的结果，能够更好地保留数据的分布特征；而在考虑了异常值指标后，极值处理法对应的评价值和序值较无异常值存在时变动最不明显，本文方法变动程度最大，四分位分层无量纲化方法介于二者之间.这说明，在本文算例中，相较于其余两种方法，运用本文方法对指标x₃进行处理，更能凸显这2个指标在评价过程中的作用.因此，本文方法不仅保证了分层区间划分的客观性和保留了原始数据的分布特征，同时，保证了该指标在评价过程中的作用.
表 5(Table 5)

表 5 斯皮尔曼等级相关系数矩阵Table 5 Spearman rank correlation coefficient matrix r2 uj us um uj* us* um* m2+ m2- uj 1.000 0.993 0.992 0.992 0.976 0.971 1.000 0.993 us 0.993 1.000 0.998 0.985 0.971 0.966 0.993 1.000 um 0.992 0.998 1.000 0.983 0.970 0.968 0.992 0.998 uj* 0.992 0.985 0.983 1.000 0.991 0.987 0.992 0.985 us* 0.976 0.971 0.970 0.991 1.000 0.997 0.976 0.971 um* 0.971 0.966 0.968 0.987 0.997 1.000 0.971 0.966 注：m2+, m2-分别表示某方法所有相关系数的最大值和最小值.

表 5 斯皮尔曼等级相关系数矩阵 Table 5 Spearman rank correlation coefficient matrix

5 结语本文提出一种新的分层无量纲化方法，即密度分层无量纲化方法.该方法依据数据分布的疏密程度划分区间，同时还能有效处理异常值对无量纲化结果造成的影响.该方法有如下特点：①运用该处理方法操作简单，易于理解；②从数据本身出发，根据数据自身分布特征划分分层区间更加贴合数据特征；③可以很好地解决异常值对最终结果的影响；④适宜编程实现，减少交互环节，可大幅提高数据分析的应用效率.对该问题的进一步研究可以从密度分层无量纲化方法的动态拓展等方面展开深入探讨.
参考文献

[1]	Chen Y, Li W W, Yi P T. Evaluation of city innovation capability using the TOPSIS-based order relation method: the case of Liaoning Province, China[J]. Technology in Society, 2020, 63: 101330. DOI:10.1016/j.techsoc.2020.101330
[2]	Dong Q K, Yi P T, Li W W, et al. Evaluation of city sustainability using the HGRW method: a case study of urban agglomeration on the West Side of the Straits, China[J]. Journal of Cleaner Production, 2022, 358: 132008. DOI:10.1016/j.jclepro.2022.132008
[3]	Chao X R, Kou G, Peng Y, et al. Large-scale group decision-making with non-cooperative behaviors and heterogeneous preferences: an application in financial inclusion[J]. European Journal of Operational Research, 2021, 288(1): 271-293. DOI:10.1016/j.ejor.2020.05.047
[4]	Carli R, Dotoli M, Pellegrino R. Multi-criteria decision-making for sustainable metropolitan cities assessment[J]. Journal of Environmental Management, 2018, 226: 46-61.
[5]	Zhang Z G, Hu X, Liu Z T, et al. Multi-attribute decision making: an innovative method based on the dynamic credibility of experts[J]. Applied Mathematics and Computation, 2021, 393: 125816. DOI:10.1016/j.amc.2020.125816
[6]	Li W W, Yi P T, Li L Y. Superiority-comparison-based transformation, consensus, and ranking methods for heterogeneous multi-attribute group decision-making[J]. Expert Systems with Applications, 2023, 213: 119018. DOI:10.1016/j.eswa.2022.119018
[7]	Liu Y T, Sun Z W, Liang H M, et al. Ranking range model in multiple attribute decision making: a comparison of selected methods[J]. Computers & Industrial Engineering, 2021, 155: 107180.
[8]	Mohammadi M, Rezaei J. Ensemble ranking: aggregation of rankings produced by different multi-criteria decision-making methods[J]. Omega, 2020, 96: 102254. DOI:10.1016/j.omega.2020.102254
[9]	郭亚军, 易平涛. 线性无量纲化方法的性质分析[J]. 统计研究, 2008, 25(2): 93-100. (Guo Ya-jun, Yi Ping-tao. Character analysis of linear dimensionless methods[J]. Statistical Research, 2008, 25(2): 93-100. DOI:10.3969/j.issn.1002-4565.2008.02.017)
[10]	易平涛, 张丹宁, 郭亚军, 等. 动态综合评价中的无量纲化方法[J]. 东北大学学报(自然科学版), 2009, 30(6): 889-892. (Yi Ping-tao, Zhang Dan-ning, Guo Ya-jun, et al. Study on dimensionless methods in dynamic comprehensive evaluation[J]. Journal of Northeastern University(Natural Science), 2009, 30(6): 889-892.)
[11]	胡永宏. 对统计综合评价中几个问题的认识与探讨[J]. 统计研究, 2012, 29(1): 26-30. (Hu Yong-hong. Understanding and discussion of some problems in statistical synthesis evaluation[J]. Statistical Research, 2012, 29(1): 26-30. DOI:10.3969/j.issn.1002-4565.2012.01.006)
[12]	Li W W, Yi P T, Zhang D N. Investigation of sustainability and key factors of Shenyang City in China using GRA and SRA methods[J]. Sustainable Cities and Society, 2021, 68: 102796. DOI:10.1016/j.scs.2021.102796
[13]	Lama N, Boracchi P, Biganzoli E. Exploration of distributional models for a novel intensity-dependent normalization procedure in censored gene expression data[J]. Computational Statistics & Data Analysis, 2009, 53(5): 1906-1922.
[14]	Chakraborty S, Yeh C H. A simulation comparison of normalization procedures for TOPSIS[C]//International Conference on Computers & Industrial Engineering. Troyes: IEEE, 2009: 1815-1820.
[15]	Chen Y, Zhang D N. Evaluation and driving factors of city sustainability in Northeast China: an analysis based on interaction among multiple indicators[J]. Sustainable Cities and Society, 2021, 67: 102721. DOI:10.1016/j.scs.2021.102721
[16]	Altintas K, Vayvay O, Apak S, et al. An extended GRA method integrated with fuzzy AHP to construct a multidimensional index for ranking overall energy sustainability performances[J]. Sustainability, 2020, 12(4): 1602. DOI:10.3390/su12041602
[17]	Awasthi A, Omrani H, Gerber P. Investigating ideal-solution based multicriteria decision making techniques for sustainability evaluation of urban mobility projects[J]. Transportation Research Part A: Policy and Practice, 2018, 116: 247-259.
[18]	李伟伟, 易平涛, 李玲玉. 综合评价中异常值的识别及无量纲化处理方法[J]. 运筹与管理, 2018, 27(4): 173-178. (Li Wei-wei, Yi Ping-tao, Li Ling-yu. Outliers recognition and the dimensionless method in comprehensive evaluation[J]. Operations Research and Management Science, 2018, 27(4): 173-178.)
[19]	易平涛, 李伟伟, 李玲玉. 序比例诱导分段无量纲化方法及其影响因素[J]. 系统管理学报, 2020, 29(5): 866-873. (Yi Ping-tao, Li Wei-wei, Li Ling-yu. A segmented dimensionless method induced by ranking percentage and its influencing factors[J]. Journal of Systems & Management, 2020, 29(5): 866-873.)
[20]	易平涛, 李伟伟, 郭亚军. 线性无量纲化方法的结构稳定性分析[J]. 系统管理学报, 2014, 23(1): 104-110. (Yi Ping-tao, Li Wei-wei, Guo Ya-jun. Structure stability analysis of linear dimensionless methods[J]. Journal of Systems & Management, 2014, 23(1): 104-110.)
[21]	张敏, 袁辉. 拉依达(PauTa)准则与异常值剔除[J]. 郑州工业大学学报, 1997(1): 87-91. (Zhang Min, Yuan Hui. The PauTa criterion and rejecting the abnormal value[J]. Journal of Zhengzhou University of Technology, 1997(1): 87-91.)