
 , 周赛男1, 尹猛2, 樊星1
, 周赛男1, 尹猛2, 樊星1 1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 中国科学院 深圳先进技术研究院,广东 深圳 518055
收稿日期:2022-03-11
基金项目:国家自然科学基金资助项目(51875092); 宁夏自然科学基金资助项目(2020AAC03279)。
作者简介:李小彭(1976-),男,江西宁都人,东北大学教授,博士生导师。
摘要:柔性机械臂系统中的负载柔性、关节柔性会导致输出转速波动,故使用PI控制策略对伺服系统进行控制.根据连续体振动理论和拉格朗日方程建立同时考虑负载和关节两种柔性的动力学模型,并分析了两种柔性对系统传动特性的影响.使用Arnoldi方法对传递函数进行降阶,并对降阶误差进行评价.采用极点配置方法设计控制器参数,讨论了极点阻尼系数、自然频率等对系统动态特性的影响.最后进行双柔性机械臂的仿真分析和转动控制实验,结果表明:适当调整控制器参数可以有效减弱柔性机械臂伺服传动系统末端的转速波动,进而抑制机械谐振现象,使系统趋于稳定.
关键词:双柔性机械臂伺服传动系统关节柔性负载柔性极点配置
PI Control Strategy of Double-Flexible Manipulator's Servo System
LI Xiao-peng1

 , ZHOU Sai-nan1, YIN Meng2, FAN Xing1
, ZHOU Sai-nan1, YIN Meng2, FAN Xing1 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518055, China
Corresponding author: LI Xiao-peng, E-mail: xpli@me.neu.edu.cn.
Abstract: The load flexibility and joint flexibility in the flexible manipulator system will lead to the fluctuation of output speed, so the PI control strategy is used to control the servo system. Based on the continuum vibration theory and Lagrange equation, a dynamic model considering both the load and joint flexibilities is established, and the influence of the two flexibilities on the transmission characteristics of the system is analyzed. The Arnoldi method is used to reduce the order of transfer functions, and the error of order reduction is evaluated. The pole assignment method is used to design the controller's parameters, and the effects of the pole damping coefficient and natural frequency on the system dynamic characteristics are discussed. Finally, the simulation analysis and rotation control experiment of the double-flexible manipulator are carried out. The results show that adjusting the controller's parameters properly can effectively reduce the speed fluctuation of the servo drive system of the flexible manipulator, and then suppress the mechanical resonance phenomenon, so that the system tends to be more stable.
Key words: double-flexible manipulatorservo drive systemjoint flexibilityload flexibilitypole assignment
近年来,柔性机械臂因耗能低、结构紧凑被广泛应用于工业装配、航空航天、医疗辅助等领域[1-2].在机械臂传动系统中,柔性常体现在两方面:一方面是由于机械臂传动机构和关节转轴扭曲变形所造成的存在于传动关节之间的柔性,称为关节柔性,常见于驱动器与负载间传递旋转运动的齿轮、联轴器等[3];另一方面是机械臂长连杆运动过程中引起的连杆自身弹性变形,称为负载柔性.将同时含有关节柔性和负载柔性的机械臂传动系统定义为双柔性机械臂传动系统.
在双柔性机械臂伺服传动系统工作过程中,因柔性因素的存在,不可避免会产生扭曲、弹性形变和剪切变形,这容易引起系统机械谐振,影响其动态精度,严重时甚至会损坏机械臂[4].针对柔性机械臂传动系统的建模及其所引起的机械谐振等问题,国内外研究人员进行了大量的研究.
关于机械臂传动系统的建模,Spong[5]首先提出用两质量系统表示关节柔性,即将电机和负载之间的柔性传动关节等效为一个小阻尼弹簧进行系统动力学建模.文献[6]将巡检机器人传动轴系等效成扭簧进行力学分析.对于具有柔性的负载,文献[7]将其简化为欧拉-伯努利梁,利用悬臂梁的振动理论描述负载末端的弯曲变形,并根据拉格朗日原理建立系统的动力学方程.这种方法适合细长梁模型,且便于求解.文献[8]在柔性机械臂传动系统建模中,既考虑负载柔性又考虑关节柔性,将关节柔性作为负载的一个特殊模态进行建模.但此种建模方法忽略了关节驱动器对系统的影响.此外,有限单元法、基于力学的绝对节点坐标法是目前较为热门的建模方法,但求解也相对复杂.文献[9]基于绝对节点坐标法对新型翘曲三维梁单元进行了高效建模和降阶的研究.
通常柔性机械臂传动系统的控制方法主要包括两大类:主动控制和被动控制.主动控制是通过主动调整PI控制器的参数或结构来消除系统谐振,包括比例-积分控制(即PI控制)、鲁棒控制策略、基于位置反馈的极点配置控制策略、基于加速度反馈的优化控制策略、智能控制等.在伺服传动系统中,文献[10]通过PI控制策略调节速度环,减轻系统机械谐振.文献[11-12]分别采用扰动观测器、负载加速度反馈策略,对伺服系统机械谐振进行了抑制.文献[13]结合滑模控制及模糊理论对六轴机械臂进行高精度定位,以实现系统稳定.文献[14]采用边界控制方法抑制柔性机械臂的残余振动问题.
被动控制是往系统中加入陷波滤波器,常见的有低通滤波器、自适应陷波器等,但被动控制往往需要消耗大量能量,且会影响系统动态性能.在柔性机械臂传动系统中,通过选取合适的解调器参数抑制系统谐振的PI控制是应用较为广泛的控制策略,可使系统获得良好的动态性能.
为了使机械臂传动系统获得稳定的输出转速,本文综合考虑关节柔性、负载柔性,建立了更接近实际工况的双柔性机械臂传动系统动力学方程,为控制策略的实现建立了更精确的数学模型.此外,结合文献[15],使用基于极点配置方法的PI控制策略对伺服系统速度环进行控制,从而实现对机械臂系统更精准地控制.数值仿真和控制实验的结果也进一步验证了本文所提出的极点配置方法整定控制器参数的有效性.
1 系统建模及传递特性分析驱动器的转动惯量由两部分组成,第一部分为电机本身所具有的转动惯量,第二部分是由负载转动惯量所引起的,该部分转动惯量与柔性机械臂的惯性矩阵和减速比有关.因此驱动器的转动惯量为
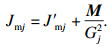 | (1) |
高性能的柔性机械臂传动系统,既需要考虑关节柔性,又需要考虑负载柔性.简化后具有负载柔性和关节柔性的机械臂传动系统如图 1所示,柔性机械臂传动系统参数如表 1所示.
图 1(Fig. 1)
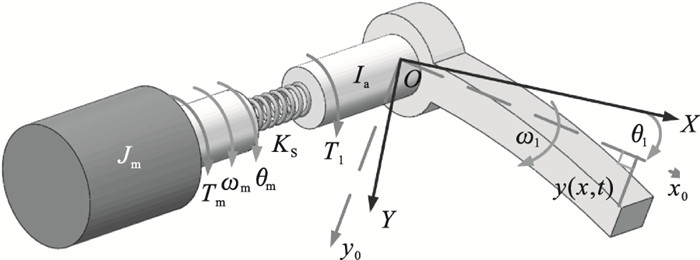 | 图 1 具有关节柔性和负载柔性的伺服驱动系统模型图Fig.1 Model diagram of servo drive system with joint flexibility and load flexibility |
表 1(Table 1)
| 表 1 系统参数 Table 1 System parameters |
建模时,将具有柔性的负载等效为欧拉-伯努利(Euler-Bernoulli)梁,只考虑其横向振动,忽略纵向振动和变形,且不考虑外力的影响,故将负载简化为悬臂梁.
根据梁的振动理论,可得负载横向振动的偏微分方程为
 | (2) |
借鉴文献[16],采用假设模态法建立旋转柔性机械臂的动力学模型,则负载在任意位置x处的变形为
 | (3) |
模态函数和模态坐标可表示为
 | (4) |
负载上任意一点的向量表示为
 | (5) |
 | (6) |
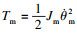
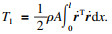
同理可得,双柔性机械臂传动系统的总势能为
 | (7) |
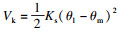

根据拉格朗日动力学方程可得
 | (8) |
最终整理可得到如下形式:
 | (9) |
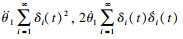
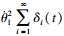
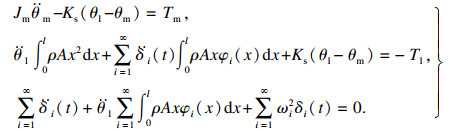 | (10) |
 | (11) |
 | (12) |
 | (13) |
 | (14) |
 | (15) |
 | (16) |
 | (17) |
为便于分析两种柔性的作用关系,进行模态截断,取前三阶模态,则在双柔性伺服驱动系统中,电机转角和电磁转矩、负载转角和电磁转矩之间的传递函数为
 | (18) |
 | (19) |
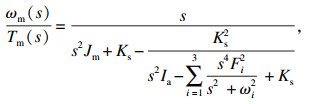 | (20) |
 | (21) |
 | (22) |
 | (23) |
 | (24) |
 | (25) |
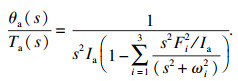 | (26) |
进一步,若不考虑负载柔性的影响,则负载转角到驱动力矩的传递函数为
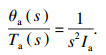 | (27) |
图 2(Fig. 2)
 | 图 2 伺服驱动系统伯德图Fig.2 Servo drive system Bode diagram (a)—电机;(b)—负载. |
通过图 2可知:因关节柔性导致的突变主要发生在低频区;负载柔性的一阶模态所激发的突变同样发生在低频区域;相反,负载柔性的高阶模态所激发的突变发生在高频区.两种柔性共同作用所导致的突变分布在全频域.此外,在驱动力矩与电机端转角、负载端转角的传递关系中,关节柔性主导低频模态突变,其他频域作用甚微,负载柔性在高频区对模态突变起主导作用,关节柔性对系统高频区突变影响很小.
时域分析中,基于以上三种伺服驱动系统中电机转速和电磁转矩之间的传递函数,以单位脉冲输入为激励信号分析系统的脉冲响应,如图 3所示.
图 3(Fig. 3)
 | 图 3 传递函数脉冲响应图Fig.3 Pulse response diagram of transfer functions |
由图 3可以明显看出,刚性工况下,电机端转速先线性增加而后保持稳定;加入柔性因素后,转速仍先增加后稳定在一定范围内,但无论是增加阶段,还是稳定阶段都存在一定波动,这说明柔性因素的存在会导致电机端转速的不稳定,而这可能会引发系统谐振;此外,与关节柔性单独作用相比,关节柔性和负载柔性同时作用会使转速波动幅度增大,也说明了负载柔性是在分析系统抑振策略时不可忽略的重要因素.
2 传递函数的降阶根据文献[18]可知,二阶及以上模态对具有柔性的负载的动力学特性影响很小,可忽略不计.对双柔性伺服驱动系统,仅考虑一阶模态,则驱动器转速与电磁转矩间的传递函数为
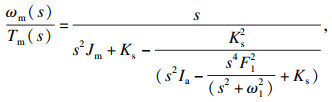 | (28) |
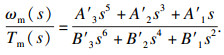 | (29) |
由于式(29)中传递函数属于高阶系统,不利于设计伺服系统的控制参数,需要对传递函数进行降阶处理.本文利用Arnoldi方法对传递函数进行降阶.
首先将单输入单输出系统高阶传递函数写成状态空间方程的形式为
 | (30) |
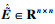
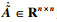
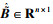
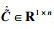
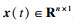
假设
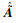
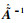
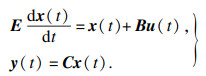 | (31) |
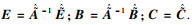
 | (32) |
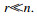
Arnoldi算法本质是对Krylow子空间Kr(E, B)进行标准的Gram-Schmidt正价化过程.应用Arnoldi算法求得子空间Kr(E, B)的标准正交基底矩阵V r=[v1 v2 … vr].v1,vi+1的表达式为
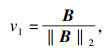 | (33) |
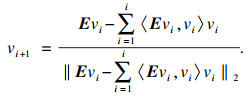 | (34) |
 | (35) |
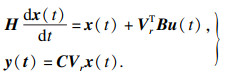 | (36) |
 | (37) |
图 4(Fig. 4)
 | 图 4 降阶前后传递函数响应图Fig.4 Transfer functions' response diagram before and after order reduction (a)—系统传递函数响应;(b)—系统传递函数响应误差. |
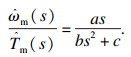 | (38) |
由图 4可以看出:降阶后的传递函数与降阶前的传递函数对于相同的输入,系统响应基本保持一致,且系统误差在一很小的范围内波动,基本可以忽略,为方便设计控制器参数,完全可以用降阶后的传递函数代替降阶前的传递函数.
3 基于极点配置的PI控制策略使用降阶后的传递函数作为伺服驱动系统的被控对象,使用PI调节器进行控制.柔性机械臂传动系统的控制图如图 5所示,ω*表示期望的负载转角.
图 5(Fig. 5)
 | 图 5 柔性机械臂传动系统的控制图Fig.5 Control diagram of the flexible manipulator's transmission system |
柔性机械臂传动系统采用PI调节器时,系统的闭环传递函数为
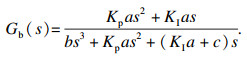 | (39) |
此处借鉴文献[15]中提到的极点配置策略,将式(39)中的分母多项式化成式(40)的形式.
 | (40) |
根据对应项相等,有式(41),式(42)成立.
 | (41) |
 | (42) |
 | (43) |
最大超调量是指在阶跃输入作用下,被调量(根据系统传递函数得到的响应)的瞬时最大偏差值与稳态值之比,它反映了系统的动态精度,最大超调量越小说明系统越平稳.峰值时间是系统输出达到最大值时所用的时间,峰值时间反映了系统响应的快速性.调整时间为系统输出达到稳定时,系统所用的时间.
描述系统动态性能的参数:输出转速、最大超调量、峰值时间、调整时间等都取决于ξa1,ωa1的取值,具体关系如图 6所示.
图 6(Fig. 6)
 | 图 6 极点配置法系统评价指标图Fig.6 System evaluation index diagram of the pole assignment method (a)—输出转速分布图;(b)—最大超调量分布图;(c)—峰值时间分布图;(d)—调整时间分布图. |
从图 6a可知:系统的最终输出值与ωa1密切相关,最终输出值随着ωa1的增大而增大,但ξa1对其影响不大.当ωa1∈(60, 75)时,系统最终的输出值较好.从图 6b可知:系统的最大超调量与ωa1密切相关,最大超调量随着ωa1的增大而减小,说明系统的稳定性逐渐加强.ξa1对最大超调量影响较大,最大超调量随着ξa1的增大而减小,当ξa1取值过小时系统超调量较大,稳定性较低,故ξa1的取值要大于0.6.从图 6c可知:系统的峰值时间与ωa1,ξa1密切相关,峰值时间随着ωa1,ξa1的增大而减小, 说明系统的快速性逐渐加强.从图 6d可知:系统的调整时间与ωa1,ξa1密切相关,调整时间在ξa1取值较小时随着ωa1的增大而减小,当ξa1取值较大时调整时间变化不明显.
4 数值仿真分析4.1 极点阻尼系数、自然频率对系统的影响柔性机械臂传动系统使用极点配置的PI控制策略控制系统速度输出,其关键在于选择PI调节器的参数.可通过选择不同的极点阻尼系数、自然频率系数确定PI调节器参数.所以可通过调整极点阻尼系数、自然频率改变系统的输出转速.这两种参数对柔性机械臂传动系统输出转速的影响如图 7所示.
图 7(Fig. 7)
 | 图 7 极点阻尼系数、自然频率对系统影响Fig.7 Impact of pole damping coefficient and natural frequency on the system (a)—阻尼系数的影响(位姿1);(b)—自然频率的影响. |
由图 7a可知:随着极点阻尼系数的增大,系统转速输出逐渐平稳,与图 6b中的结论相一致.由图 7b可知:随着自然频率系数的增大,柔性机械臂传动系统的输出转速值逐渐提高,与图 6a中的结论相一致.
4.2 柔性机械臂位姿对于系统的影响为探究不同柔性机械臂位姿对传动系统速度环输出转速的影响,分别选择柔性机械臂处于两种不同位姿的参数,具体参数如表 2所示.使用PI控制策略的仿真结果如图 8所示.
表 2(Table 2)
| 表 2 不同位姿系统参数表 Table 2 Parameter table of different pose systems |
图 8(Fig. 8)
 | 图 8 系统输出转速仿真结果(位姿2)Fig.8 Simulation results of system output speed(pose 2) |
对比图 7a和图 8可知,柔性机械臂处于不同位姿的情况下,传动系统的输出转速也发生变化.负载的转动惯量较小时,系统输出速度波动较大,但可通过调整PI调节器参数使系统的输出趋于稳定.
5 双柔性机械臂转动控制实验5.1 实验原理本文搭建了验证双柔性机械臂控制实验平台,如图 9所示.该实验平台主要由伺服电机(自带减速器的舵机ASME-MRB)、套索(直径1 mm的钢丝绳)、柔性梁、NI控制器组成.通过套索将伺服电机产生的驱动力矩传递到柔性梁(即柔性机械臂),驱动柔性梁转动.套索在传动力矩的过程中因具有柔性而发生变形,因此基于套索传动力矩的方式可以等效为关节柔性;柔性梁即为传动系统的负载,在水平面转动.
图 9(Fig. 9)
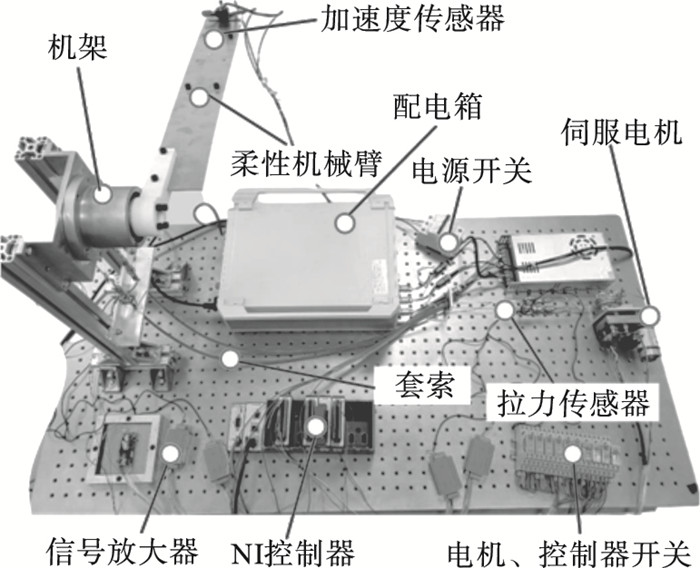 | 图 9 双柔性机械臂控制实验平台Fig.9 Double-flexible manipulator's control experiment platform |
实验平台的控制系统是基于LabVIEW软件进行的实时控制.控制程序通过上位机由LabVIEW软件进行编写,通过接口将程序下载到下位机发出指令.实验平台采用NI-Crio-9053作为下位机.通过传感器采集电机端和负载端的转角、加速度变化信号,经过处理后传入NI-9401数据采集模块.电机控制信号由NI-9264模块输出到电机驱动器,控制电机驱动力矩.
5.2 实验数据分析在双柔性机械臂的控制实验中,用柔性梁模拟柔性机械臂,分别采用长度为1.2,1.6 m的柔性梁模拟不同位姿的柔性机械臂.以正弦信号作为柔性机械臂转角的输入信号,使用两种不同的控制方法开展柔性梁的转角控制实验:传统的PI控制策略和基于极点配置的PI控制策略,并通过机械臂末端安装的加速度传感器,采集柔性梁水平方向的加速度变化信号.由控制实验得到不同位姿柔性梁的转角误差(Δθl)、末端加速度(al)波动情况,如图 10所示.
图 10(Fig. 10)
 | 图 10 双柔性机械臂控制实验结果Fig.10 Double-flexible manipulator's control experimental results (a)—位姿1,转角误差;(b)—位姿2,转角误差;(c)—位姿1,加速度;(d)—位姿2,加速度. |
由图 10可知,使用极点配置策略的控制方法拥有更小的转角误差.在机械臂长度较长时,使用极点配置策略的控制方法能够有效地减少机械臂末端的加速度波动.
6 结论1) 对于柔性机械臂传动系统,同时考虑关节柔性和负载柔性,会使系统转速环开环伯德图在高频区产生大的幅值突变,说明负载柔性在高频区对速度环的影响较大,在系统建模时需要加以考虑.
2) 本文提出基于极点配置的PI调节器对柔性机械臂传动系统进行控制,从仿真结果可以看出:当ωa1∈(60, 75), ξa1的取值大于0.6时,系统评价指标较好.这对实际参数选取,包括系统参数、控制器参数等,均有参考价值和实际应用意义.
3) 通过数值仿真分析可知:系统极点阻尼系数位于0.5~1.2之间时,柔性机械臂传动系统输出转速更快趋于稳定,系统动态性能较好;机械臂控制实验验证了本文基于极点配置的PI调节器参数设计方法的有效性.这为PI控制实际工业落地提供了理论依据和数据支撑.
参考文献
| [1] | Yu Y, Zhang Y. Collision avoidance and path planning for industrial manipulator using slice-based heuristic fast marching tree[J]. Robotics and Computer-Integrated Manufacturing, 2022, 75: 102289. DOI:10.1016/j.rcim.2021.102289 |
| [2] | Jiao C, Zhang L, Su X, et al. Predictive motion control for autonomous capture of a tumbling target with a space manipulator[J]. Journal of the Franklin Institute, 2022, 359(15): 7913-7935. DOI:10.1016/j.jfranklin.2022.08.012 |
| [3] | Li X, Shang D, Li H, et al. Resonant suppression method based on PI control for serial manipulator servo drive system[J]. Science Progress, 2020, 103(3): 1-39. |
| [4] | Oh S, Kong K. High-precision robust force control of a series elastic actuator[J]. IEEE/ASME Transactions on Mechatronics, 2016, 22(1): 71-80. |
| [5] | Spong M. Modeling and control of elastic joint robots[J]. Journal of Dynamic Systems, Measurement, and Control, 1987, 109(1): 310-319. |
| [6] | 李小彭, 尚东阳, 李凡杰, 等. 输电线巡检机器人位姿变化的柔性关节控制策略[J]. 东北大学学报(自然科学版), 2020, 41(11): 1577-1583. (Li Xiao-peng, Shang Dong-yang, Li Fan-jie, et al. Flexible joint control strategy based on posture change of transmission line inspection robots[J]. Journal of Northeastern University(Natural Science), 2020, 41(11): 1577-1583.) |
| [7] | Katsura S, Ohnishi K. Force servoing by flexible manipulator based on resonance ratio control[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 539-547. DOI:10.1109/TIE.2006.888805 |
| [8] | He W, He X, Zou M, et al. PDE model-based boundary control design for a flexible robotic manipulator with input backlash[J]. IEEE Transactions on Control Systems Technology, 2018, 27(2): 790-797. |
| [9] | Tang Y, Tian Q, Hu H. Efficient modeling and order reduction of new 3D beam elements with warping via absolute nodal coordinate formulation[J]. Nonlinear Dynamics, 2022, 109(4): 2319-2354. DOI:10.1007/s11071-022-07547-8 |
| [10] | Zhang G, Furusho J. Speed control of two-inertia system by PI/PID control[J]. IEEE Transactions on Industrial Electronics, 2000, 47(3): 603-609. DOI:10.1109/41.847901 |
| [11] | Li W, Hori Y. Vibration suppression using single neuron-based PI fuzzy controller and fractional-order disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2007, 54(1): 117-126. DOI:10.1109/TIE.2006.888771 |
| [12] | Szabat K, Orlowska-Kowalska T, Dybkowski M. Indirect adaptive control of induction motor drive system with an flexible coupling[J]. IEEE Transactions on Industrial Electronics, 2009, 56(10): 4038-4042. DOI:10.1109/TIE.2009.2022514 |
| [13] | 王宏, 郑天奇. 基于滑模补偿的六轴机械臂RBF网络自适应控制[J]. 东北大学学报(自然科学版), 2017, 38(11): 1601-1606. (Wang Hong, Zheng Tian-qi. RBF network adaptive control based on SMC compensation for six-axis manipulator[J]. Journal of Northeastern University(Natural Science), 2017, 38(11): 1601-1606.) |
| [14] | Entessari F, Ardekany-Najafi A, Alasty A. Boundary control of a vertical nonlinear flexible manipulator considering disturbance observer and deflection constraint with torque and boundary force feedback signals[J]. International Journal of Systems Science, 2022, 53(4): 704-725. DOI:10.1080/00207721.2021.1971793 |
| [15] | Chen Y, Yang M, Long J, et al. Analysis of oscillation frequency deviation in elastic coupling digital drive system and robust notch filter strategy[J]. IEEE Transactions on Industrial Electronics, 2018, 66(1): 90-101. |
| [16] | Shang D, Li X, Yin M, et al. Speed control method for dual-flexible manipulator with a telescopic arm considering bearing friction based on adaptive PI controller with DOB[J]. Alexandria Engineering Journal, 2022, 61(6): 4741-4756. DOI:10.1016/j.aej.2021.10.026 |
| [17] | Shang D, Li X, Yin M, et al. Control method of flexible manipulator servo system based on a combination of RBF neural network and pole placement strategy[J]. Mathematics, 2021, 9(8): 1-32. |
| [18] | Shang D, Li X, Yin M, et al. Dynamic modeling and fuzzy compensation sliding mode control for flexible manipulator servo system[J]. Applied Mathematical Modelling, 2022, 107: 530-556. |
