
 , 刘俊岐, 钟山, 李凌轩
, 刘俊岐, 钟山, 李凌轩 东北大学秦皇岛分校 控制工程学院,河北 秦皇岛 066004
收稿日期:2022-02-28
基金项目:国家自然科学基金资助项目(51905081); 河北省自然科学基金资助项目(E2019501117, E2021501014); 中央高校基本科研业务费专项资金资助项目(N2223028, N2123026)。
作者简介:陈晓哲(1986-), 男, 辽宁沈阳人, 东北大学讲师,博士。
摘要:以偏心转子激励单自由度弹簧质量阻尼系统为分析对象,研究该非理想振动系统由交流电机作原动机时的Sommerfeld效应.引入交流电机电磁力矩公式来建立振动系统的动力学模型.基于小参数平均法,获取了振动系统响应的一次近似解.根据该解推导了稳态的电机力矩平衡方程.数值分析发现电机角速度与供电频率在共振区会出现跳跃现象,并且导致系统振幅与供电频率之间的关系曲线存在硬式非线性特征.通过稳定性判别条件解释了上述现象产生的机制,并且应用时域仿真的方法验证了本文所提理论方法的正确性.最后对关键结构参数进行了定量和定性的讨论.
关键词:非理想振动系统非线性跳跃交流电机稳定性
Sommerfeld Effect of Non-ideal Vibration System Driven by AC Motor
CHEN Xiao-zhe

 , LIU Jun-qi, ZHONG Shan, LI Ling-xuan
, LIU Jun-qi, ZHONG Shan, LI Ling-xuan School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: CHEN Xiao-zhe, E-mail: xzchen1986@163.com.
Abstract: By taking the spring mass damping system of the single degree of freedom excited by the eccentric rotor as the object, Sommerfeld effect of the non-ideal vibration system driven by the AC motor as the prime motor was studied. The electromagnetic torque formula of the AC motor was introduced to establish the dynamic model of the vibration system driven by the AC motor. Based on the small parameter averaging method, the approximate solution of the vibration system response was obtained. According to the solution, the torque balance equation of the motor in steady-state motion was derived. Numerical analysis illustrated that the angular velocity of the motor and the frequency of power will jump in the resonance region, and the relationship between the amplitude of the system and the frequency of power has hard non-linear characteristics. The mechanism of these phenomena was explained by the stability judgment conditions, and the correctness of the theoretical method was verified by the numerical time domain simulation. Finally, the key structural parameters were discussed quantitatively and qualitatively.
Key words: non-ideal vibration systemnon-linearityjumpAC motorstability
利用振动原理工作的振动机械因其采用弹簧质量阻尼系统模型,所设计出来的机器具有结构简单、可靠性高及维修成本低的优点,被广泛应用在工业的各个部门[1].此类机器往往采用交流电机驱动偏心转子作激振器来使机体获得周期性激振力.
在振动机械中,由于偏心转子是固定在机体上并随其一起运动,偏心转子驱动机体运动的同时也会受机体运动的干扰,两者的运动呈现出一种机电耦合状态.在建立数学模型时,对考虑上述机电耦合作用的系统称为非理想振动系统[2].众所周知,任何一台电机能够提供的动力输出都是有限的,所以忽略该作用势必对研究结果产生影响.因为该作用最明显的影响就是电机转速的变化,被称之为Sommerfeld效应[2].因此,在振动机械设计过程中需要考虑Sommerfeld效应.
近年来,Sommerfeld效应吸引了众多****在不同机构中对其开展研究.在单盘转子系统中,Bharti等[3]发现如果将该系统考虑成非理想振动系统,转子在前二阶固有频率处会出现角速度跳跃现象.Samantaray等[4]基于直流电机模型,通过研究发现阻尼对Sommerfeld效应有抑制作用.在此基础上,Jha等[5]采用主动磁轴承来衰减系统内阻尼进而控制转子角速度跳跃现象的发生.上述研究是避免转子系统存在Sommerfeld效应,Felix等[6]利用Sommerfeld效应进行了能量回收方面的研究.为了判断哪些系统参数对是否出现Sommerfeld效应起重要作用,孔祥希等[7]对偏心转子质量与总质量的质量比进行数值讨论,确定质量比的临界条件.
不仅在转子系统中存在Sommerfeld效应,在其他系统中也被发现存在该效应.Sinha等[8]在曲柄滑块模型中,发现往复机构会存在Sommerfeld效应.前面的研究多以线性振动模型作为研究对象,Gonzalez-Carbajal等[9]考虑弹簧的非线性作用,讨论了电机机械特性曲线的斜率对Sommerfeld现象的影响,发现了该系统中存在霍普分岔.Jiang等[10]在悬臂梁系统中采用模态法对梁进行离散后,来研究弹性质体的Sommerfeld效应.
在考虑一台原动机的基础上,Zhang等[11]在两台原动机驱动的双质体振动系统中,在第二阶固有频率处发现了Sommerfeld效应.Kovriguine[12]对比一个原动机和两个原动机关于Sommerfeld效应的不同之处.在弹性矩形板系统中,Djanan等[13]采用两台直流偏心电机对Sommerfeld效应进行了研究,提出了减小弹性板振动的办法.
综上,振动机械中的偏心转子不同于一般转子系统,它是利用质量偏心来获取激振力的,所以其不可避免地存在质量偏心.上述文献的结论大部分采用直流电机作为原动机模型来获得的,因为交流电机的机械特性不同于直流电机,所以相关结果不一定适用于交流电机作原动机的场合.为了弄清楚交流电机驱动振动机械的Sommerfeld效应,以偏心转子激励单自由度弹簧质量阻尼系统为研究对象,来研究该非理想振动系统由交流电机作原动机时的Sommerfeld效应.
1 振动系统的机电耦合动力学模型图 1为偏心转子激励单自由度弹簧质量阻尼系统的动力学模型.图 1a所示交流电机两端输出轴各安装偏心质量块组成偏心转子系统,其中总偏心质量为m0,偏心半径为r,然后将其安装在振动台上组成单质体振动系统,如图 1b所示.振动台质量为m1,系统刚度为k,阻尼为c.为了简化分析,本文只考虑振动台在x方向存在运动.
图 1(Fig. 1)
 | 图 1 动力学模型Fig.1 Dynamic model (a)—交流振动电机;(b)—偏心转子激励弹簧质量阻尼系统. |
通过受力分析可知,当交流电机以一定的角速度Ω带动偏心块旋转,在其产生的激振力作用下,振动台进行往复运动.考虑φ和x两个自由度,应用拉格朗日方程[11],引入交流电机电磁力矩公式[14],得到振动系统的机电耦合数学方程为
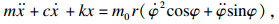 | (1) |
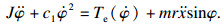 | (2) |
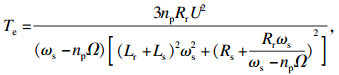 |
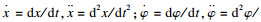
表 1(Table 1)
| 表 1 振动系统仿真参数 Table 1 Simulation parameters of the vibration system |
2 解析过程2.1 非理想振动系统的稳态解由于Sommerfeld效应是指转子在共振区附近的角速度变化,因此可以将式(1)中的阻尼项和外部激励项视为小参数项[15].考虑瞬时角速度
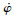
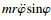
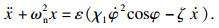 | (3) |
由于系统的幅值A,瞬时角速度
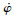
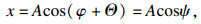 | (4) |
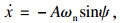 | (5) |
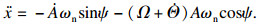 | (6) |
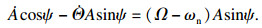 | (7) |
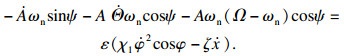 | (8) |
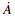
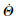
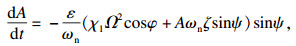 | (9) |
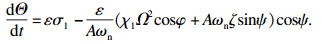 | (10) |
 | (11) |
 | (12) |
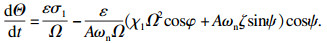 | (13) |
相对时间t作为变量,Ω,A和Θ对于转角φ是缓变函数.因此,可以将它们看作围绕着平均变化量进行小幅的波动,所以将Ω,A和Θ设成如下形式:
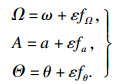 | (14) |
取在一个运动周期2π内Ω,A和Θ的平均值作为平均变化量部分.将式(11)~式(13)进行积分平均得
 | (15) |
 | (16) |
 | (17) |
虽然通过式(14)可以求出系统高阶近似响应,但从摄动法的设解形式来看,各物理量取一次近似已经足够定性分析了.因此当ω′=0,a′=0和θ′=0时,可以得到系统稳态运动时的一次近似解:
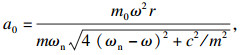 | (18) |
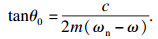 | (19) |
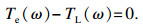 | (20) |
式(20)是关于角速度ω的超越方程,因此无法得到解析解,后面讨论中均采用二分法求数值解.
2.2 稳定性分析对一次近似解进行摄动,得
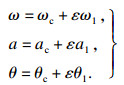 | (21) |
将式(21)代入式(15)~式(17),得到扰动方程:
 | (22) |
对式(22)求解特征根:
 | (23) |
 | (24) |
同理,第二稳定性条件为
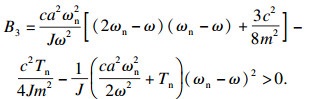 | (25) |
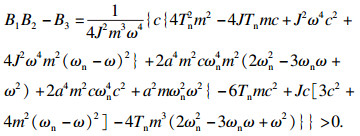 | (26) |
3.1 特性曲线图 2a为不同电机供电频率f下,系统的最大振幅a0随f的变化规律.与线性系统的幅频特性曲线相比较,交流电机驱动的非理想振动系统存在硬式非线性特征,即脊骨线向右弯曲.由于存在非线性特征,导致振动系统在升频时的跳跃点和降频时的跳跃点并不重合,出现时滞特性.具体的描述:随着f的增大,x由a点跳到b点;随着f的减小,x由c点跳到d点.尽管是硬式非线性,但和刚度非线性本质上还是有区别的,这点可以从图 2b中观察到.该非理想系统幅频曲线出现的非线性现象,实际上是由电机角速度ω的频率俘获导致的.因为电机角速度等于外部激振力的激振频率,当接近系统固有频率时,会出现共振现象.众所周知,一旦发生共振,系统振幅急速增加.此时,从能量守恒角度上解释,系统振幅变大所需要的外部输入能量就要更多.但是非理想原动机是不能够提供无限能量的,那就会造成交流电机所有的能量全部用来维持系统共振运动,而没有多余的能量来提高电机角速度.上述分析可以从式(2)得到验证,负载力矩消耗掉所有的电磁力矩后,系统不会产生新的角加速度,因此角速度没有变化.对于实际系统而言,就会出现一种小幅度提升电机供电频率后转子的角速度也不会增加的现象,如图 2b中d点到a点这段曲线,该曲线变化比较平缓.但是,系统这种频率俘获能力不是一直存在的,它存在的前提是要求振幅随供电频率的增加而增加.当振幅超过了共振点a后,振幅就会下降,这就导致了系统振动不再需要原来那么多的能量了.根据式(2),假定还是原来那么多的能量输入,现在系统振动腾出来多余的能量,那这部分能量突然全部施加给电机角加速度了.因此,系统获得了较大的角加速度后,就会出现电机角速度跳跃现象,如图 2b中a点到b点这段变化.
图 2(Fig. 2)
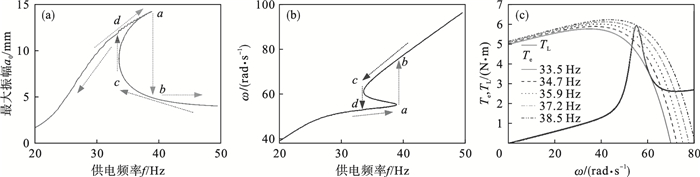 | 图 2 Sommerfeld效应Fig.2 Sommerfeld effect (a)—供电频率-最大振幅曲线;(b)—供电频率-角速度曲线;(c) —角速度-力矩曲线. |
前面分析了电机角速度上升过程中的跳跃,接下来分析供电频率下降过程中的电机角速度变化.如图 2b所示,虽然供电频率在下降过程中经过点b,但是并没有发生跳跃现象.这是由于b点到c点,系统的振幅并没有急速变化,而当供电频率经过c点后,系统的振幅由c点跳到d点,如图 2a所示.振幅突变导致负载力矩急速变大,假定原输入电磁力矩不变的情况下,此时式(2)等式右端出现了负力矩,就会导致产生负角加速度.因此,电机角速度再次出现跳跃现象.但供电频率下降过程中的角速度跳跃并没有出现频率俘获现象,所以系统的频率俘获只发生在升频过程中.由于两次跳跃现象发生在不同的频率点,就造成非理想系统存在响应时滞现象.同时,也发现Sommerfeld效应会导致升频时跳跃幅值差大于降频时幅值差,这将在时域仿真过程中得到验证.
上述数值分析说明了交流电机驱动的非理想振动系统同其他原动机驱动的非理想振动系统一样存在Sommerfeld效应.图 2c给出系统在共振区附近,不同电机供电频率下,电磁力矩和负载力矩的耦合变化规律.从图中可以看出交流电机的电磁力矩曲线是角速度的非线性函数,其不同于直流电机的机械特性.交流电机电磁力矩先随着角速度增加,达到最大电磁力矩值后,随角速度增加而减少,直至与负载力矩相交,此时的交点所对应的角速度满足力矩平衡方程式(20).根据式(18)可知,一次近似振幅也是角速度的非线性函数,在接近共振区会引起力矩曲线出现波峰现象.由于该波峰同时与电磁力矩曲线有3个交点,体现了非线性系统的多解特性.图 2c中存在3个交点的频率区间对应着可以出现Sommerfeld效应的区间,也就是说只有频率在这个区间才会出现Sommerfeld效应,即Sommerfeld效应只可能发生在共振区附近.
对非线性系统存在多个平衡点现象,需要作进一步的稳定性判断.图 3是图 2对应的三大稳定性条件,可以发现第一稳定性条件图 3a和第三稳定性条件图 3c在不同供电频率下都得到了满足,只有第二稳定性条件图 3b出现了不满足情况.因此,交流电机驱动非理想振动系统的稳定性判断条件可以简化为只采用第二稳定性条件来进行判断.
图 3(Fig. 3)
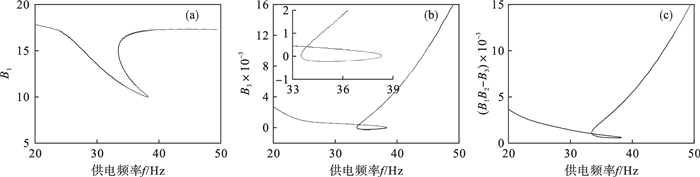 | 图 3 稳定性条件Fig.3 Stability conditions (a)—供电频率-第一稳定性条件;(b)—供电频率-第二稳定性条件;(c)—供电频率-第三稳定性条件. |
由于系统共振导致交流电机负载力矩突变所引起的电机角速度的跳跃现象也可以从图 3b中观察到.如果系统振幅对应的稳定性系数点处于负值,说明该振幅是不稳定的,即实际系统不会存在该状态.虽然在Sommerfeld效应区间内的任意一条电磁力矩曲线与负载力矩曲线均存在3个交点,但是通过稳定判断可知,其中1个交点是不稳定的,这就造成系统最终稳定状态将在这两点中间来选择.当处于临界频率时,即电磁力矩曲线与负载力矩曲线相切时,两条力矩曲线只存在2个交点,并且2个交点都是稳定的.假设系统处于升频临界状态,稍微加一点供电频率,就会导致电机角速度产生跳跃.同理,当系统降频时,稍减少一点供电频率,也会出现跳跃现象.为了更方便观察临界情况,将图 2c中力矩相交的模式换成力矩差的形式来描述,如图 4所示.处于Sommerfeld效应区间的频率所对应的力矩差曲线均有3个零值点.对比图 3b第二稳定性条件,发现力矩差曲线处于上升阶段的零值点是不稳定的,而处于下降阶段的零值点都是稳定的.
图 4(Fig. 4)
 | 图 4 角速度与力矩差Fig.4 Angular velocity and torque difference |
3.2 系统瞬态响应采用数值仿真的方法对式(1)和式(2)进行时域响应的分析,如图 5所示.根据图 2c,取处于Sommerfeld效应区间内的35 Hz作为交流电机的供电频率.然后以2 Hz的频率升频,发现在37~39 Hz之间电机的角速度发生了跳跃现象.这是因为37 Hz仍然处于Sommerfeld效应区间,而39 Hz已经不属于该区间了.系统在升频过程中,当供电频率经过临界频率时,由于稳定性的影响,角速度先发生跳跃,然后再升速,最终稳定在39 Hz.为了验证系统时滞响应,再次以2 Hz的频率降频,发现虽然都是37 Hz,但是存在两种稳定状态.同理,35 Hz也存在两种稳定状态.当频率降至33 Hz,系统仍没有发生角速度跳跃,直至降频离开Sommerfeld效应区间.当频率从33 Hz降至31 Hz时,在该阶段系统发生了角速度跳跃现象.系统的振幅在共振前和共振后均有明显的对比变化,如图 5b所示.特别是升频跳跃时的振幅差大于降频跳跃时的振幅差,这些时域曲线变化规律均和理论解的结果是一致的,证明了理论分析的正确性.
图 5(Fig. 5)
 | 图 5 时域仿真Fig.5 Time domain simulation (a)—电机的角速度;(b)—x方向的位移. |
3.3 关键参数通过3.1节和3.2节理论解与数值解的对比分析,证明了交流电机驱动非理想振动系统也是会发生Sommerfeld效应.本节将对一些关键参数进行定量和定性的分析,进而为该类振动系统的参数设计提供理论依据.本组实验的电机供电频率均为37 Hz,从而保证系统初始状态都存在Sommerfeld效应.
根据振动系统特性可知,单自由度弹簧-质量系统在共振时的振幅是最大的.因为固有频率是参振质量和刚度的函数,接下来研究两者对Sommerfeld效应的影响.图 6a为不同参振质量对Sommerfeld效应的影响.由于参振质量变大会导致固有频率减小,所以不仅共振点左移,而且波峰高度也会下降,进而避免了发生Sommerfeld效应.图 6b为不同刚度对Sommerfeld效应的影响.因为刚度也同样影响着固有频率,导致共振点随着刚度增加而进行右移,这与参振质量的变化正好相反.因此,减小刚度会避免发生Sommerfeld效应.综上,因为刚度与固有频率呈正比例变化,而参振质量与固有频率呈反比例变化.固有频率左移,负载力矩曲线整体缩小,可避免发生Sommerfeld效应.
图 6(Fig. 6)
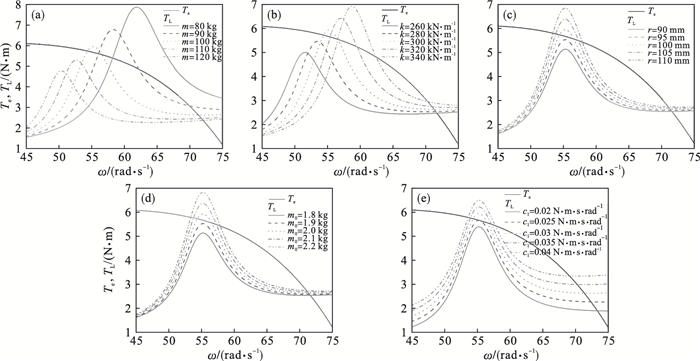 | 图 6 不同参数情况下负载力矩曲线Fig.6 Load torque curves with different parameters (a)—参振质量;(b)—刚度;(c)—偏心半径;(d)—偏心质量;(e)—电机阻尼系数. |
根据式(2)可知,振动力矩是振幅的函数,而振幅是质量与半径乘积的正比例函数.图 6c为偏心半径对Sommerfeld效应的影响.由于偏心半径是属于外部激振力的组成部分,其值的大小会影响着外部振动力的大小.从图中也可以发现,随着偏心半径增大,振幅的波峰值也相应提高.但是共振点并不会因为该外部激振力提高了,发生相应的变化,这符合振动系统特性.因此,适当降低偏心半径,从而降低外部激振力,进而降低负载力矩,可以避免Sommerfeld效应的发生.图 6d为偏心质量对Sommerfeld效应的影响.同偏心半径一样,偏心质量也是外部激振的组成部分,其对Sommerfeld效应影响的变化规律是一致的.综上,偏心质量与偏心半径对负载力矩的影响仅是峰值高度的纵向变化,并不会使共振点移动,这不同于参振质量和刚度.因此,适当减小偏心质量与半径乘积可避免Sommerfeld效应的发生.
由负载力矩TL(ω)=c1ω+cωn2a02/(2ω)可知,第一项为阻尼力矩,其值的变化必定影响负载力矩.图 6e为电机轴承阻尼系数对Sommerfeld效应的影响.不同于外部激励,只对波峰曲线有影响,轴承阻尼变大会导致负载力矩曲线整体平移.但有一点要注意,轴承阻尼和系统阻尼作用不一样,轴承阻尼对于振动机械来讲是作无用功的,因此需要想办法减小其数值.通过图中曲线变化可以发现,减小轴承阻尼系数可以避免发生Sommerfeld效应.
4 结论1) 以小参数平均法推导了系统一次近似解及稳态时的电机力矩平衡方程,基于上述理论结果并且通过数值法分析,验证了该类非理想振动系统以交流电机作为原动机时,当参数条件符合也会发生Sommerfeld效应.
2) 对稳态解进行摄动,推导了满足系统稳定性的3个条件.通过数值分析发现,电机角速度跳跃是由于电机力矩平衡方程是超越方程,存在3个平衡点所导致的.对3个稳定性条件进行作图发现,系统的稳定性取决第二稳定性条件.根据第二稳定性条件得出,当电磁力矩和负载力矩之差处于减函数阶段时的平衡点是稳定的,反之是不稳定的状态.
3) 为了避免发生Sommerfeld效应,对系统关键参数进行了定性的讨论,由于参振质量和刚度可直接改变固有频率,所以对Sommerfeld效应的影响是最大的.而偏心半径和偏心质量由于是外部激振力部分,虽然不会改变共振点,但会影响负载力矩波峰的大小形状,也存在一定的影响.轴承阻尼在本系统中做无用功,因此设计时应尽量减小,同时可避免发生Sommerfeld效应.
参考文献
| [1] | Wen B C, Zhang H, Liu S Y, et al. Theory and techniques of vibrating machinery and their applications[M]. Beijing: Science Press, 2010: 119-120. |
| [2] | Balthazar J M, Tusset A M, Brasil R M L R F, et al. An overview on the appearance of the Sommerfeld effect and saturation phenomenon in non-ideal vibrating systems(NIS) in macro and MEMS scales[J]. Nonlinear Dynamics, 2018, 93(1): 19-40. DOI:10.1007/s11071-018-4126-0 |
| [3] | Bharti S K, Bisoi A, Sinha A, et al. Sommerfeld effect at forward and backward critical speeds in a rigid rotor shaft system with anisotropic supports[J]. Journal of Sound and Vibration, 2019, 442: 330-349. DOI:10.1016/j.jsv.2018.11.002 |
| [4] | Samantaray A K, Dasgupta S S, Bhattacharyya R. Sommerfeld effect in rotationally symmetric planar dynamical systems[J]. International Journal of Engineering Science, 2010, 48(1): 21-36. DOI:10.1016/j.ijengsci.2009.06.005 |
| [5] | Jha A K, Dasgupta S S. Attenuation of Sommerfeld effect in an internally damped eccentric shaft-disk system via active magnetic bearings[J]. Meccanica, 2019, 54(1/2): 311-320. |
| [6] | Felix J L P, Balthazar J M, Rocha R T, et al. On vibration mitigation and energy harvesting of a non-ideal system with autoparametric vibration absorber system[J]. Meccanica, 2018, 53(13): 3177-3188. DOI:10.1007/s11012-018-0881-8 |
| [7] | 孔祥希, 牛俊开, 罗园庆, 等. 考虑感应电动机模型的质量偏心单盘转子系统Sommerfeld效应及不平衡响应分析[J]. 机械工程学报, 2020, 56(17): 137-144. (Kong Xiang-xi, Niu Jun-kai, Luo Yuan-qing, et al. Sommerfeld effect and unbalanced response analysis in single disk rotor system with eccentric mass considering induction motor model[J]. Journal of Mechanical Engineering, 2020, 56(17): 137-144.) |
| [8] | Sinha A, Bharti S K, Samantaray A K, et al. Sommerfeld effect in an oscillator with a reciprocating mass[J]. Nonlinear Dynamics, 2018, 93(3): 1719-1739. DOI:10.1007/s11071-018-4287-x |
| [9] | González-Carbajal J, Domínguez J. Non-linear vibrating systems excited by a nonideal energy source with a large slope characteristic[J]. Mechanical System and Signal Processing, 2017, 96: 366-384. DOI:10.1016/j.ymssp.2017.04.026 |
| [10] | Jiang J, Kong X X, Chen C Z, et al. Dynamic and stability analysis of a cantilever beam system excited by a non-ideal induction motor[J]. Meccanica, 2021, 56(7): 1675-1691. DOI:10.1007/s11012-021-01333-3 |
| [11] | Zhang X L, Li Z M, Li M, et al. Stability and Sommerfeld effect of a vibrating system with two vibrators driven separately by induction motors[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 807-817. DOI:10.1109/TMECH.2020.3003029 |
| [12] | Kovriguine D A. Synchronization and Sommerfeld effect as typical resonant patterns[J]. Archive of Applied Mechanics, 2012, 82(5): 591-604. DOI:10.1007/s00419-011-0574-4 |
| [13] | Djanan A A N, Nbendjo B R N. Effect of two moving non-ideal sources on the dynamic of a rectangular plate[J]. Nonlinear Dynamics, 2018, 93(2): 645-657. |
| [14] | 丁学文. 电力拖动运动控制系统[M]. 北京: 机械工业出版社, 2013: 119-120. (Ding Xue-wen. Electric drive motion control system[M]. Beijing: China Machine Press, 2013: 119-120.) |
| [15] | 闻邦椿. 非线性振动理论中的解析方法及工程应用[M]. 沈阳: 东北大学出版社, 2001: 79-81. (Wen Bang-chun. Analytical methods and engineering applications in nonlinear vibration theory[M]. Shenyang: Northeastern University Press, 2001: 79-81.) |
