黄贤振^1,2, 栾晓刚¹, 朱丽莎³, 刘慧珍¹
1. 东北大学 机械工程与自动化学院，辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室，辽宁 沈阳 110819;
3. 肇庆学院 机械与汽车工程学院，广东 肇庆 526061
收稿日期：2022-03-04
基金项目：国家自然科学基金资助项目(51975511, 51975110, U22B2087)；肇庆学院创新科研团队资助项目。
作者简介：黄贤振(1982-), 男, 山东定陶人, 东北大学教授, 博士生导师;
朱丽莎(1986-), 女，河北南宫人, 肇庆学院教授。

摘要：传统的阀芯位移稳定性是在系统参数确定的前提下进行的，然而，在实际生产的使用过程中，各种系统参数具有不确定性.针对此问题，建立了一个锥阀工作动态过程的有限元分析模型，采用双向流固耦合和重叠网格方法分析求解压力入口下锥阀的动态响应过程.考虑参数随机性的影响，以阀芯稳定后位移是否超过许用位移量为衡量标准建立阀芯位移波动的极限状态方程，通过Monte-Carlo仿真和Kriging方法，对阀芯稳定后位移的波动情况进行了可靠性分析.研究发现，阀芯稳定位移波动范围小于理论值的19%，阀芯稳定位移的可靠度随着入口压力的增大而降低.
关键词：可靠性锥阀流固耦合Monte-Carlo仿真Kriging方法
Displacement Reliability Analysis of Cone Valve Spools Based on Bidirectional Fluid-Solid Coupling
HUANG Xian-zhen^1,2, LUAN Xiao-gang¹, ZHU Li-sha³, LIU Hui-zhen¹
1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems, Ministry of Education, Northeastern University, Shenyang 110819, China;
3. School of Mechanical & Automotive Engineering, Zhaoqing University, Zhaoqing 526061, China
Corresponding author: ZHU Li-sha, E-mail: neulisachu@163.com.

Abstract: The traditional spool displacement stability is carried out on the premise that the system parameters are determined. However, in the process of actual production and use, various system parameters are uncertain. To solve this problem, a finite element analysis model of the cone valve's dynamic process was established, and the dynamic response process of the cone valve under the pressure inlet was analyzed and solved by the bidirectional fluid-solid coupling and the overlapping grid method. Considering the influence of parameter randomness, the limit state equation of the spool displacement fluctuation was established based on whether the displacement after the spool stabilizes exceeds the allowable displacement. The reliability analysis of the displacement fluctuation after the stability of the spool was carried out by the Monte-Carlo method and Kriging method. It was shown that the stable displacement fluctuation range of the spool is 19% less than the theoretical value, and the reliability of the stable displacement of the spool decreases as the inlet pressure increases.
Key words: reliabilitycone valvefluid-solid couplingMonte-Carlo simulationKriging method
锥阀结构简单、响应迅速、密封性好、抗污染能力强，在液压系统中是常用的压力调节阀，工作中与弹簧配合，通过液压力与弹簧力的平衡完成压力调节，既可以单独使用作为直动式压力调节阀调节系统压力，也可以作为先导阀与主阀组成多级压力调节阀工作.国内外****主要采用计算流体动力学(computational fluid dynamics，CFD)仿真、数值模拟和实验分析的方法，针对锥阀的振动特性和动态特性展开了大量研究.通过振动特性分析发现，溢流阀由于内部流体流动不稳定造成的阀芯与阀座发生碰撞冲击产生磨损^[1-2].王海芳等^[3]基于数值模拟的方法对锥阀的振动可靠性和稳态液动力下结合有限元仿真结果对阀芯可靠性进行了分析研究，但研究是基于固定开度进行的，无法模拟阀芯工作的动态过程，具有一定的局限性.采用数值仿真的方法对锥阀建立振动模型，研究发现弹簧刚度、阀芯锥角对锥阀的启动特性有重要的影响.Li等^[4]通过可视化实验方法捕捉阀芯的振动，发现阀芯的位移偏差与压力差成正比，与弹簧压缩量成反比.动态特性方面，Sang等^[5]建立了动态特性分析的二维轴对称模型，采用动态网格研究了锥阀不同设定压力条件下的动态特性.Min等^[6]建立了锥阀流体的流固耦合模型，分析了锥阀分别在阶跃和周期激励信号下的响应.闵为等^[7]通过实验分析得到阀芯位移和系统压力波动曲线，研究发现液体流量、阀芯结构等多种因素影响锥阀开启过程中的阀芯振动.姜万录等^[8]通过建立溢流阀非线性动力学模型，研究发现系统参数对溢流阀动态特性的影响规律.Misra等^[9]采用将管道系统的液压与自动控制阀结构运动耦合的动态模型，确定了引起管道系统自激振动的机理.Moussou等^[10]考虑流固耦合对泄压阀做了一系列实验，观察到阀芯一些振动频率会产生负压降系数，触发动态不稳定性.Bazsó等^[11]通过实验研究了锥阀式溢流阀的静态和动态特性，分析了导致阀不稳定的参数.Chen等^[12]对阀芯轴向和径向振动共存的动力学特性进行研究，发现径向运动会通过阀芯与阀体的碰撞影响轴向运动.Choi等^[13]采用流固耦合方法分析压缩弹簧预设力对阀动态特性的影响.
基于以上分析，本文采用双向流固耦合的方法，仿真分析锥阀不同入口条件下的动态响应.考虑随机因素对锥阀稳定时位移的影响，将锥阀的流固耦合分析模型与锥阀阀芯稳定后位移的波动范围相结合，以阀芯稳定位移的许用波动范围为判断依据建立极限状态方程，提出了一种锥阀阀芯位移稳定性分析的可靠性模型.通过Monte-Carlo仿真和Kriging方法进行可靠性分析，分析锥阀参数对阀芯位移稳定性的影响，为锥阀的定压精度检测提供理论依据.
1 动态特性分析1.1 建立几何模型图 1为锥阀式溢流阀结构简图，其主要结构由阀芯、阀体、弹簧以及弹簧座等组成.常态下锥阀阀芯在弹簧力的作用下紧紧地靠在阀座上，当作用于阀芯表面的流体作用力达到弹簧作用力时，阀芯打开，溢流阀开始工作.考虑溢流阀开启是一个动态变化的过程，在划分网格时，为保证计算精度、提高收敛速度，对整个流场及溢流阀采用更易于收敛的六面体网格.由于整体模型网格节点较多，数据间传递过程复杂，所需时间较长，考虑所研究的溢流阀以及阀内流体为旋转对称模型的特点，为提高计算效率、节省计算时间，在CFD仿真过程，本文采用四分之一模型进行研究.
图 1(Fig. 1)

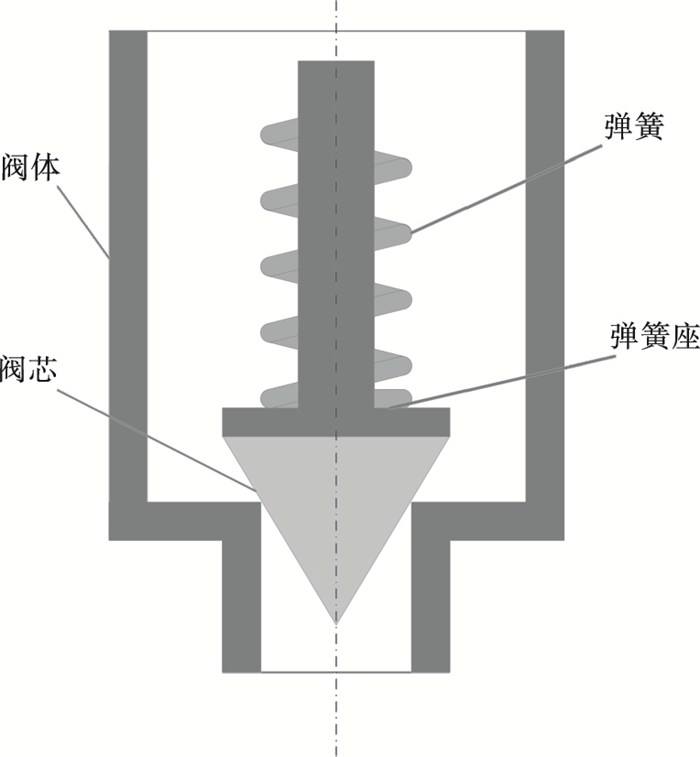图 1 锥阀式溢流阀结构简图Fig.1 Structural diagram of the cone relief valve

1.2 理论分析溢流阀在液压系统中根据连接方式和位置不同可以起到定压溢流、稳压、安全保护等作用.溢流阀阀芯不同工况下的受力不同，从而产生不同的运动状态发挥作用.溢流阀工作时阀芯受力主要包括：弹簧力、流体压力以及阀芯重力，根据阀芯受力可得溢流阀工作时阀芯运动方程如下：

(1)

式中：F_fluid为流体作用力；m为质量；g为重力加速度；F_preset为弹簧预设力；k为弹簧刚度；x为阀芯位移.
由于阀芯运动的复杂性和数值方法的计算代价及自身局限性，基于数值方法求解阀芯运动方程，分析阀芯运动状态和涉及变化流场力的复杂位移计算是很难实现的.此外，数值方法求解忽略了摩擦力、黏性力与实际工况可能存在偏差.因此本文采用CFD仿真，通过流固耦合的方法模拟溢流阀工作时阀芯的运动情况.
1.3 计算方法1.3.1 双向流固耦合流固耦合在分析流体机械方面应用广泛，能够综合分析流体场与固体场的相互作用^[14].与单向流固耦合相比，双向流固耦合中的数据传递是双向的，流场和固体场的计算结果会相互影响，主要应用于固体变形或位移较大的场合.本文主要研究溢流阀工作时阀芯的运动情况，阀芯的位置在流场的作用下不断变化，对应阀芯不同位置的流场也会发生变化，因此本文基于Fluent，Transient Structural和System Coupling模块采用双向流固耦合的方法进行分析计算，旨在提高分析结果的可靠性和精确性.双向流固耦合分析求解流程图如图 2所示.
图 2(Fig. 2)

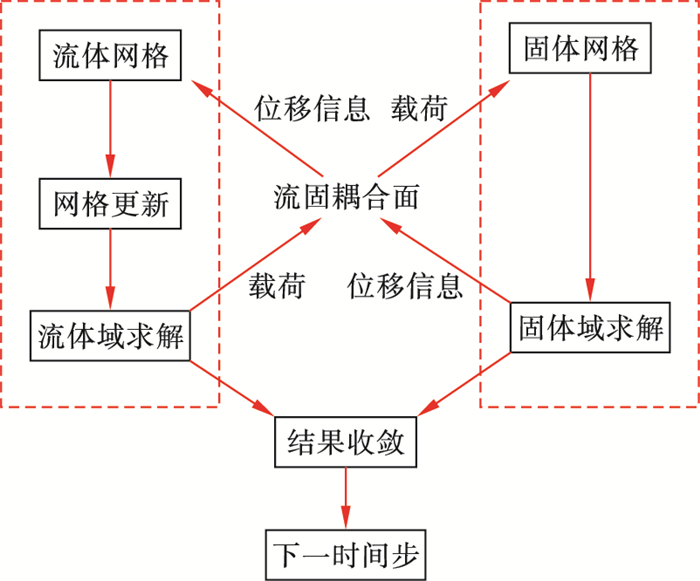图 2 双向流固耦合求解流程图Fig.2 Flow chart of the bidirectional fluid-solid coupling solution

具体步骤如下：
1) 流体域、固体域分别对初始位置分析求解；
2) 流固耦合面数据交换，流体域与固体域分别将载荷信息和位移信息在耦合面上完成传递；
3) 流体域网格根据固体域传来的位移信息进行网格更新；
4) 流体域、固体域分别进行分析求解，如果结果收敛则进行步骤5)，否则重复步骤2)~步骤4)；
5) 进行下一时间步求解，重复步骤2)~步骤4)，直至完成计算.
1.3.2 重叠网格本文应用Fluent重叠网格对阀芯的运动情况进行仿真，重叠网格是由前景网格和背景网格两部分重叠的网格构成，两部分网格空间上相互重叠但二者之间相互独立，不存在联通关系，在仿真计算过程中由前处理软件进行挖洞、建立区域连通性、插值计算^[15].相较传统的动网格方法，重叠网格对不同计算区域可采用最恰当的网格形式；对于位置或位移变化较大的场合，重叠网格可以方便地调整网格的相对位置，避免出现动网格仿真中出现的负体积.流体域网格如图 3所示.
图 3(Fig. 3)

图 3 流体域网格Fig.3 Fluid domain grids

1.4 边界条件及参数设置1) 锥阀入口采用压力入口；
2) 锥阀出口选择压力出口，出口压力设置为101 325 Pa，即出口直接与大气相通；
3) 切面采用对称边界，壁面采用非滑移边界；
4) 选择标准κ-ε湍流模型；
5) 固体求解模块设置相应约束条件并添加弹簧连接.
在Workbench中建立流体、固体和耦合模块的数据传递，最后进行耦合迭代计算.
1.5 网格无关化验证考虑网格数量和质量对于计算结果的影响，分别按照1.5万，2.3万，3.6万，4.5万数量的网格进行网格无关化验证，由图 4可看出，当网格数量小于2.3万时，计算结果变化较大，而网格数量为3.6万和4.5万时，计算结果差异很小，因此网格数量为3.6万即可满足计算要求.
图 4(Fig. 4)

图 4 不同网格数量计算结果对比Fig.4 Calculation results comparison with different grid numbers

1.6 结果处理在仿真计算结果中，提取阀芯的轴向位移变化曲线图，观察阀芯位移的稳定情况，导出阀芯经短暂波动后的稳定位移.
2 可靠性分析在溢流阀工作过程中，无法对液压系统的参数进行确定性描述和精确控制.所以，大多数影响阀芯稳定位移的变量都是随机的.例如，由于制造误差造成的弹簧刚度和液压阀尺寸的随机性；由于工作环境中的不确定性因素(如温度变化对液压油黏度的影响)，弹簧预设力、入口流量参数也是随机的.
对于概率分析，溢流阀工作阀芯稳定位移的可靠性可以描述为多维积分：

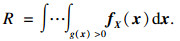(2)

式中：x=[K, F, μ]^T是用于预测溢流阀工作稳定性的特征参数向量；X表示对应于x的随机参数向量；f_X(x)是X的联合概率密度函数.Z=g(x)=b_lim-b是极限状态函数，b是阀芯稳定位移波动范围.如果x∈X，Z=g(x) < 0，则称为失效.这种情况下阀芯稳定位移波动大于极限波动范围，导致系统稳定压力波动较大；如果Z=g(x)>0，则称为可靠.这种情况下阀芯稳定位移波动小于极限波动范围；Z=g(x)=0是极限状态.
在工程实践中，液压系统的参数可以看作是相互独立的，因此，

(3)

式中，f_Xi(x_i)是变量X_i(i=1, 2, 3)的边际概率密度函数.由于高维和复杂的被积函数，解析法和直接的数值方法都很难求解式(3)中所示的多维积分.
2.1 Monte-Carlo仿真Monte-Carlo仿真^[16-18]是一种较为可靠和适用的可靠性方法.该方法涉及基于随机变量均值、方差和概率密度函数的抽样设计空间.可靠性是指安全区域内的样本数量与总样本的比值.使用Monte-Carlo方法对溢流阀阀芯稳定位移进行概率分析的步骤如图 5所示.
图 5(Fig. 5)

图 5 阀芯稳定位移可靠度计算流程图Fig.5 Flow chart of the calculation of the reliability of the stable displacement of the spool

具体步骤如下：
1) 根据随机变量分布情况生成N组样本；
2) 计算符合条件b_lim-b>0的样本数量；
3) 根据计算求得溢流阀的近似可靠性.
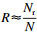
2.2 Kriging代理模型通过有限元计算大量溢流阀参数数据，采用Monte-Carlo仿真计算可靠度需要花费大量时间，因此本文通过建立Kriging代理模型代替上述过程从而提高计算效率.
Kriging模型^[19-20]是一种估计方差最小的无偏估计模型，它可以通过较少的点准确预测出原始模型，对求解强非线性问题有显著优势，因此本文利用Kriging代理模型对函数进行近似，Kriging模型近似表达为一个随机分布函数与一个多项式的和，具体形式为

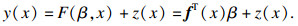(4)

式中：y(x)表示未知的Kriging模型是关于随机变量x的多项式函数，其值表示阀芯稳定后的位移量，随机变量x包括弹簧刚度、弹簧预设力和液压油黏度；F(β, x)为线性回归模型，β为回归系数；f(x)是随机变量的基函数，是模型的全局近似；z(x)是一个随机过程，是模型的局部近似，对整个模型的准确性有重要影响，z(x)是在全局模拟的基础上创建的期望μ=0，方差为σ²的正态分布，其协方差为

(5)

式中：x_i，x_j为任意两个样本点；R(θ, ω, x)为任意两样本点带有参数θ的相关函数，是相关矩阵R的分量，对模型的准确性有直接影响，通常采用高斯函数作为相关函数.
已知点的响应值Y=[y₁, y₂, …，y_n]，根据Kriging理论，在未知点x处的响应估计值为

(6)

式中：β^*为β的估计值；R^-1为R的逆矩阵；F是由n个样本点处的回归模型组成的矩阵；r(x)是预测点与样本点之间的相关向量.β^*和σ²采用极大似然估计可得估计值为

(7)

(8)

采用上述方法即可通过输入变量样本和输出响应值训练得到Kriging代理模型，对预测值进行误差分析后可以利用构建的Kriging模型进行分析计算，提高计算效率.
3 算例分析本算例选用普通的锥阀式溢流阀和46号液压油进行分析研究，其具体参数如表 1所示.
表 1(Table 1)

表 1 锥阀、液压油主要参数Table 1 Main parameters of cone valve and hydraulic oil 参数名称 符号 单位 值 阀座孔径 D mm 6 弹簧刚度 k N·mm-1 12 阀芯半锥角 α (°) 30 油液密度 ρ kg·m-3 880 油液动力黏度 μ Pa·s 0.051

表 1 锥阀、液压油主要参数 Table 1 Main parameters of cone valve and hydraulic oil

3.1 仿真结果分析为分析不同条件下阀芯的运动情况，首先考虑阀芯不受弹簧预设力，弹簧自然长度时不同入口压力下阀芯的运动情况如图 6所示.
图 6(Fig. 6)

图 6 不同入口压力下阀芯位移的波动情况Fig.6 Fluctuation of the spool displacement under different inlet pressures

从图 6可以发现，阀芯在不受弹簧预设力时，阀芯的位移会随着溢流阀入口压力的增大而增大，当压力较小时，阀芯经过短暂的振动后流体压力与弹簧压力达到平衡，阀芯处于稳定状态；当入口压力增大至2 MPa时，阀芯经过振动后仍会处于一个动态平衡的状态.以入口压力为2 MPa，时间步长取1 ms为例，阀芯在2 ms时达到位移最大值，此时由于阀芯在0时刻未打开，弹簧未压缩，仅受流体作用于阀芯表面的力，提供了一个较大的加速度，当阀芯打开，流体通过阀芯与阀座间的间隙后撞击阀体改变流动方向产生漩涡，见图 7，造成部分压力损失；在4 ms时，由于2 ms时弹簧压缩量最大，阀芯在弹簧力的作用下产生趋于关闭的运动，阀芯达到位移最小值.阀芯运动速度在10 ms后达到稳定，阀芯位移波动趋于稳定，如图 8所示.
图 7(Fig. 7)

图 7 流体速度矢量图Fig.7 Fluid velocity vector diagram

图 8(Fig. 8)

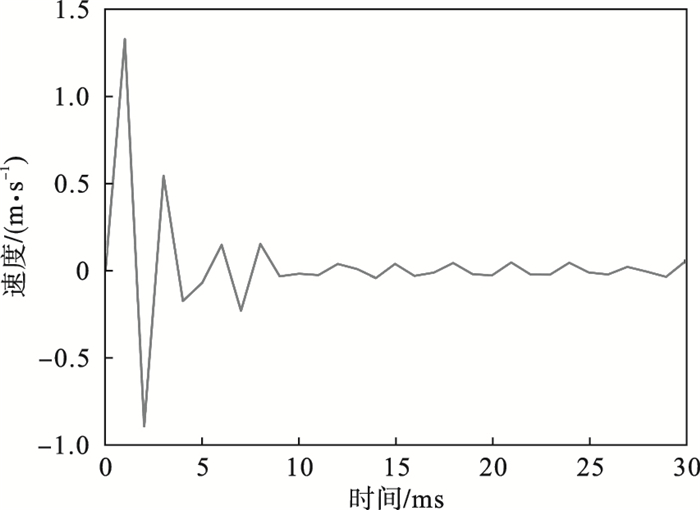图 8 溢流阀工作阀芯速度变化情况Fig.8 Speed change of the working spool of the relief valve

在实际应用中，溢流阀根据弹簧预设力的不同可以调节溢流阀的开启压力，从而使溢流阀可以应用于不同场合.仿真结果显示，在同等条件下，施加弹簧预设力后阀芯位移先达到稳定状态，且阀芯位移相应减小，从而调整溢流阀稳定状态下的定压精度，如图 9所示.
图 9(Fig. 9)

图 9 有、无弹簧预设力下阀芯稳定位移对比Fig.9 Comparison of the stable displacement of the spool with or without spring preset force

根据上述研究发现，溢流阀工作时阀芯的运动情况受多种因素的影响，作为先导阀的锥阀式溢流阀阀芯的位移波动情况对主阀的位移波动有重要影响，以本文所研究的锥阀为例，阀芯稳定后位移每变化0.1 mm，将会引起系统压力产生约0.06 MPa的变化.若阀芯位移波动较大则会造成系统压力的不稳定，产生噪声和冲击，严重时影响系统的稳定性.
3.2 Kriging模型预测结果验证在添加弹簧预设力的情况下，阀芯稳定后位移稳定在0.597 mm处.采用拉丁超立方抽样随机抽取70组以弹簧刚度、弹簧预设力、油液黏度为变量的参数样本，以70组随机变量参数对应的有限元模型计算结果为输出，训练得到Kriging模型.随机抽取10组随机变量参数将其对应的有限元计算结果与Kriging模型计算结果对比分析其准确性，通过式(9)计算相对误差, 见表 2.

(9)

表 2(Table 2)

表 2 Kriging模型与有限元计算值相对误差Table 2 Relative error between Kriging model and finite element calculation 位移/mm 相对误差/% 有限元 Kriging模型 0.652 4 0.662 0 1.47 0.576 7 0.573 8 1.02 0.541 6 0.552 3 1.99 0.599 3 0.563 6 5.97 0.752 7 0.747 4 0.71 0.626 5 0.626 5 0 0.568 2 0.558 9 1.64 0.442 1 0.442 0 0 0.699 5 0.675 4 3.44 0.554 1 0.571 9 3.21

表 2 Kriging模型与有限元计算值相对误差 Table 2 Relative error between Kriging model and finite element calculation

通过对比发现，Kriging模型的计算结果相比于有限元计算结果误差很小，最大不超过6%，从而进一步验证了Kriging模型的准确性.
3.3 阀芯稳定位移可靠性分析根据上述研究，溢流阀在设计参数下工作阀芯的稳定位移为0.597 mm，采用Monte-Carlo仿真，随机抽取10⁶组数据组成样本池，分析计算得到阀芯在设计参数对应稳定位移波动范围为0~20%的概率变化情况如图 10所示.
图 10(Fig. 10)

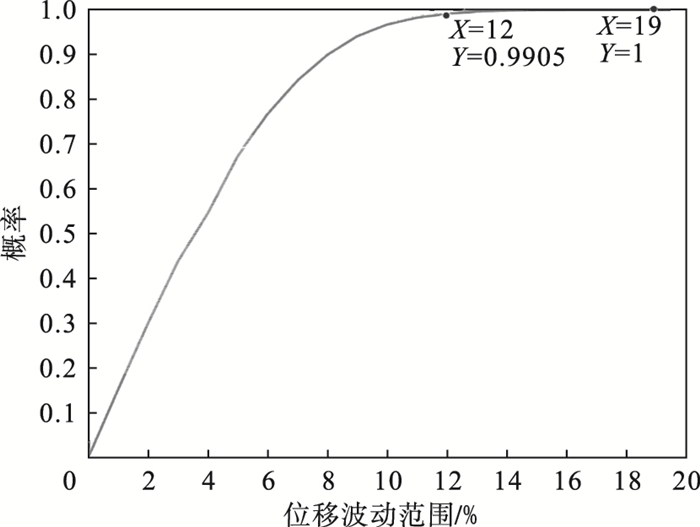图 10 阀芯稳定位移波动范围概率分布Fig.10 Probability distribution of the spool stable displacement fluctuation range

观察图 10发现，阀芯稳定位置一般分布在理论值的附近，在波动范围达到8%以后，分布概率增长趋缓，阀芯稳定位移波动范围不会超过理论值的19%.
为了探究入口压力对阀芯稳定位移波动可靠度的影响，以阀芯稳定后位移波动不超过理想值的5%为限，对入口压力在1.3~2.3 MPa范围内变化进行可靠性分析，得到可靠度随阀芯入口压力的变化规律, 见图 11.
图 11(Fig. 11)

图 11 可靠度随入口压力的变化Fig.11 Change of reliability with inlet pressures

由图 11可知，当入口压力小于1.5 MPa时，可靠度变化较小，当入口压力超过1.5 MPa时，可靠度下降速度增快.整体上随着入口压力的增大，阀芯稳定位移的可靠度降低.
4 结论1) 溢流阀在一定压力范围内工作时，由于惯性力和流场漩涡的作用使阀芯开启时都会经过短暂的波动，一段时间后在液压力和弹簧力的作用下会达到平衡状态.
2) 由阀芯稳定位移可靠度变化分析发现，随机参数变化时阀芯位移基本稳定在理论值的88%至112%范围内，位移波动最大值不超过理论值的19%.对于作为先导阀的溢流阀来说，这种稳定的性能会降低对主阀的影响.
3) 阀芯稳定位移的可靠度会随着入口压力的增大而降低，即随着入口压力的增大，锥阀的定压稳定性变差的概率增加.
参考文献

[1]	李光飞, 刘桓龙, 邓斌, 等. 液动力对锥阀振动特性的影响[J]. 机床与液压, 2014, 42(5): 28-30, 44. (Li Guang-fei, Liu Huan-long, Deng Bin, et al. Effect of flow force to the poppet valve vibration[J]. Machine Tool & Hydraulics, 2014, 42(5): 28-30, 44. DOI:10.3969/j.issn.1001-3881.2014.05.008)
[2]	Morita R, Inada F, Mori M, et al. CFD simulations and experiments of flow fluctuations around a steam control valve[J]. Journal of Fluids Engineering, 2007, 129(1): 48-54. DOI:10.1115/1.2375123
[3]	王海芳, 任明, 王晨炜, 等. 单向阀阀芯的振动可靠性分析[J]. 中国工程机械学报, 2019, 17(1): 89-93, 98. (Wang Hai-fang, Ren Ming, Wang Chen-wei, et al. Vibration reliability analysis of the check valve spool[J]. Chinese Journal of Engineering Machinery, 2019, 17(1): 89-93, 98.)
[4]	Li B B, Yan J W, Zhao Q. Image recognition and diagnosis for vibration characteristics of cone valve core[J]. Advances in Mechanical Engineering, 2020, 12(4): 1-9.
[5]	Sang Y, Wang X, Sun W. The dynamic characteristics of a small hydraulic poppet safety relief valve[J]. International Journal of Fluid Machinery and Systems, 2020, 13(1): 233-240. DOI:10.5293/IJFMS.2020.13.1.233
[6]	Min W, Ji H, Yang L F. Axial vibration in a poppet valve based on fluid-structure interaction[J]. Proceedings of the Institution of Mechanical Engineers.Part C: Journal of Mechanical Engineering Science, 2015, 229(17): 3266-3273. DOI:10.1177/0954406214559999
[7]	闵为, 王东, 郑直, 等. 压力调节锥阀开启过程振动特性研究[J]. 振动与冲击, 2020, 39(18): 181-187. (Min Wei, Wang Dong, Zheng Zhi, et al. Vibration characteristics of a pressure regulating poppet valve during opening process[J]. Journal of Vibration and Shock, 2020, 39(18): 181-187. DOI:10.13465/j.cnki.jvs.2020.18.024)
[8]	姜万录, 朱勇, 杨超. 直动型溢流阀非线性动力学行为研究[J]. 中国机械工程, 2013, 24(20): 2705-2709. (Jiang Wan-lu, Zhu Yong, Yang Chao. Study on nonlinear dynamic behavior of a hydraulic relief valve[J]. China Mechanical Engineering, 2013, 24(20): 2705-2709.)
[9]	Misra A, Behdinan K, Cleghorn W L. Self-excited vibration of a control valve due to fluid-structure interaction[J]. Journal of Fluids and Structures, 2002, 16(5): 649-665. DOI:10.1006/jfls.2002.0441
[10]	Moussou P, Gibert R J, Brasseur G. Instability of pressure relief valves in water pipes[J]. Pressure Vessel Technology, 2010, 132(4): 041308. DOI:10.1115/1.4002164
[11]	Bazsó C, H?s C J. An experimental study on the stability of a direct spring loaded poppet relief valve[J]. Journal of Fluids and Structures, 2013, 42(7): 456-465.
[12]	Chen J, Wang J R, Mo G Y, et al. Instability of a poppet valve: interaction of axial vibration and lateral vibration[J]. International Journal of Advanced Manufacturing Technology, 2018, 94(9): 3065-3074.
[13]	Choi Y S, Lee J H, Jeong W B, et al. Dynamic behavior of valve system in linear compressor based on fluid-structure interaction[J]. Journal of Mechanical Science and Technology, 2010, 24(7): 1371-1377.
[14]	Xu H, Liu H L, Tan M G, et al. Fluid-structure interaction study on diffuser pump with a two-way coupling method[J]. International Journal of Fluid Machinery and Systems, 2013, 6(2): 87-93.
[15]	Zhang H R, Fan J J, Yuan W, et al. Structure overset grid method and its applications to simulation of multi-body separation[J]. Science China (Physics, Mechanics & Astronomy), 2015, 58(9): 1-8.
[16]	曹汝男, 孙志礼, 郭凡逸, 等. 基于Kriging和Monte Carlo的动态可靠性算法[J]. 东北大学学报(自然科学版), 2021, 42(5): 658-664. (Cao Ru-nan, Sun Zhi-li, Guo Fan-yi, et al. Time-dependent reliability algorithm based on Kriging and Monte Carlo[J]. Journal of Northeastern University(Natural Science), 2021, 42(5): 658-664.)
[17]	Melchers R E, Beck A T. Structural reliability analysis and prediction[M]. Hoboken: John Wiley & Sons, 2018.
[18]	Choi S K, Grandhi R V, Canfield R A. Reliability-based structural design[M]. London: Springer, 2007.
[19]	刘阔, 李晓雷, 王健. 一种基于Kriging模型的机械结构可靠性分析方法[J]. 东北大学学报(自然科学版), 2017, 38(7): 1002-1006. (Liu Kuo, Li Xiao-lei, Wang Jian. An analysis method of mechanical structural reliability based on the Kriging model[J]. Journal of Northeastern University(Natural Science), 2017, 38(7): 1002-1006.)
[20]	Sun Z L, Wang J, Li R, et al. LIF: a new Kriging based learning function and its application to structural reliability analysis[J]. Reliability Engineering and System Safety, 2017, 157: 152-165.