
 , 夏搏然1, 唐晓垒1,2
, 夏搏然1, 唐晓垒1,2 1. 北京科技大学 机械工程学院, 北京 100083;
2. 天津大学 机械工程学院, 天津 300354
收稿日期:2022-03-04
基金项目:中央高校基本科研业务费专项资金资助项目(FRF-GF-19-009B)。
作者简介:陈兵(1976-),男,湖北荆州人,北京科技大学副教授。
摘要:拉矫机广泛用于现代冶金企业宽幅薄板带连续生产线,其发展面临的核心问题是对布置于矫直机前后的张紧辊组驱动电机功率的优化匹配.围绕此工程需求,基于功率平衡法、键合图法等理论,建立传动系统功率键合图模型,以某现代钢企冷轧板带产线在役差动式拉矫机为案例,研究其功率传递动态特性.结果表明在拉矫传动系统生产不同规格带钢时,差动式拉矫机传动构型在启动初期低转速阶段,主传动电机功率发生波动概率增大,引发构件变形量增加进而导致设备安全服役概率下降,通过现场工业试验计算得到模型的均值绝对百分比误差为9.3%,验证了模型准确性.
关键词:冷轧拉矫机传动系统功率键合图逆向路径法
Dynamic Modeling and Simulation of Transmission System of Cold Rolling Tension Levelers
CHEN Bing1

 , XIA Bo-ran1, TANG Xiao-lei1,2
, XIA Bo-ran1, TANG Xiao-lei1,2 1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. School of Mechanical Engineering, Tianjin University, Tianjin 300354, China
Corresponding author: CHEN Bing, E-mail: bingchen9803@ustb.edu.cn.
Abstract: Tension levelers are widely used in the continuous production line of wide strips in modern metallurgical enterprises. The core problem of its development is the optimal matching of the power of the drive motor of the tensioning roller group arranged before and after the straightener. Based on the theory of power balance method and bond graph method, the power bond graph model of the transmission system was established. Taking the in-service differential tension straightener for the production line of cold rolling plates in a modern steel company as an example, the dynamic characteristics of power transmission were studied. The results showed that when the tension straightening drive system produces strips of different specifications, the power fluctuation probability of the main transmission motor increases at the early start-up low-speed stage, which leads to the increase of the component deformation and the decrease of the safe service probability of the equipment. The MAPE (mean absolute percentage error) of the model calculated by the field industrial test is 9.3%, which verifies the accuracy of the model.
Key words: cold rollingtension levelertransmission systempower bond graphreverse path method
进入21世纪以来,节能减排及绿色化可持续发展成为时代发展的主题,机电产品选材上表现出轻量化及高强化趋势,但是在对应高强钢和不同规格板带的生产过程中,受制于生产设备出现的电机频繁报警、带钢张力波动大、板材板形质量不稳定等因素影响,常出现生产能力不足的情况,阻碍板带的顺利生产[1].针对以上问题,本文从传动系统功率配置出发,通过对冷轧拉伸矫直机的传动系统结构的运行状态以及驱动电机的承载能力进行研究,为生产设备作业中出现的异常现象提供理论依据.
目前,传动系统驱动功率的研究类型具有较大的局限性,此方面研究主要是针对特定的传动类型或者某一类型传动系统的传动计算.Sauer等[2]通过改变表面张力以及表面结构的方式减小了链传动中的功率损耗;Chen等[3]采用数值计算方法分析齿轮匹配关系和传动特性,建立了各部件的转矩关系和功率比关系,进而计算系统部件之间的功率分配关系.Ye等[4]开发了一种基于实验数据来建模和分析这种混合变速器的功率损耗的方法,并应用总功率损耗模型来估计变速器在各种驾驶模式下的功率损耗;Luo等[5]针对行星齿轮组开发一个基于键合图理论的有效且通用的动态模型,提出了3个子模型:载体行星子模型,环形行星子模型,太阳行星子模型.陈树宗等[6]通过有限元的数值积分方法计算冷轧电机功率, 并采用实验测试回归方法获得电机机械功率损耗;Silva等[7-8]构建了带传输中考虑皮带内部和外部能量损耗的功率损耗模型.
键合图理论[9]被提出主要是以相对简洁易懂的方式建立面向计算机的自动建模与仿真.国内外的一些研究****也利用键合图理论对简单传动系统进行分析.Han等[10]基于履带车辆转向过程的理论分析,结合能量守恒和功率流动特性,将键合图理论应用于效率分析;Liu等[11]利用增广键合图模型,提出了含有状态变量的动态特性和能耗数学模型,并证明了其有效性;Lvanovic等[12]使用键合图对行星自动变速器动力学建模,总结了相关的行星齿轮组的键合图模型;Boudon等[13]使用图形化软件平台模拟多体系统键合图,提出了带有向量键和标量键的模型之间的转换;Tripathi等[14]通过将液压缸视为受安装坐标约束的统一长度的单一体来对液压缸进行建模.Tan等[15]基于键合图模型,对电动汽车的振动特性进行了模态分析, 并验证了此方法的有效性以及准确性.
然而,目前针对差动机构机械式集中驱动系统的功率计算研究较少,且在钢铁企业生产过程中功率传递路径较为复杂.为此,本文利用功率平衡法建立了拉矫机机组传动系统的解析模型,利用键合图法建立传动系统的功率键合图以及状态方程,并结合数值解析法求解系统状态方程,分析了系统功率变化情况.
1 传动系统结构及功率传递原理本文基于我国某钢铁企业的宽幅冷轧薄板酸轧生产线拉矫机传动系统进行分析,利用数值解析法和键合图法对拉矫传动系统的驱动功率建模求解.
拉矫机组采用了带差动机构机械式集中驱动系统,该系统由1台主电机、1台延伸率电机以及2台辅助的扭矩电机组成,入口和出口的两组张紧辊共同组成拉矫机的张紧辊组[16].具体布置如图 1所示.
图 1(Fig. 1)
 | 图 1 拉矫机组简图Fig.1 Schematic diagram of the tension leveler unit |
图 2为拉矫机组传动系统示意图.拉矫传动系统中,出口张紧辊将出口酸洗工艺段张力提升至拉矫出口张力,此时张紧辊为主动辊向外输出功率,电机此时向外输出功率,张紧辊提供的扭矩与转向相同;入口张紧辊则将张力降低至入口活套张力,此时入口张紧辊为制动辊,同时将能量传递回电机使得电动机吸收功率,张紧辊提供的扭矩与转向相反.拉矫机传动过程中的损耗功率和拉矫过程中张力损失所消耗的功率由电机进行补偿.
图 2(Fig. 2)
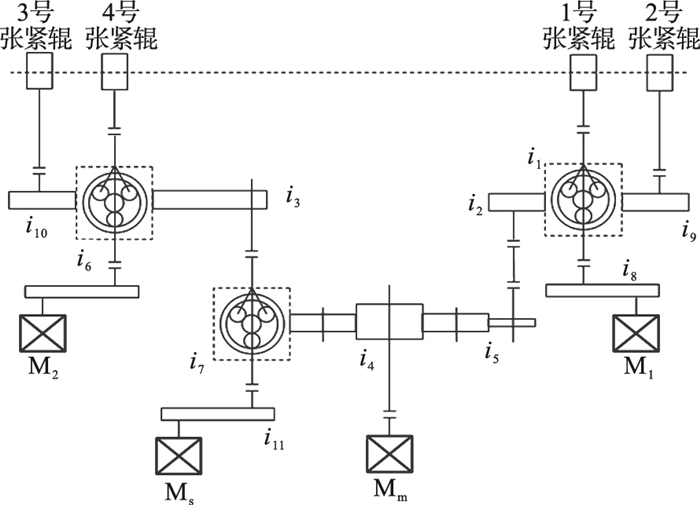 | 图 2 拉矫机组传动系统Fig.2 Transmission system of the tension leveler unit |
系统电机Mm,Ms,M1,M2功率传递路径如图 3所示,传动系统中的功率从M1,Mm,Ms以及M2电机经过传动系统的减速箱、传动轴传递到3,4号张紧辊中,在此传动系统中有如下功率关系式:
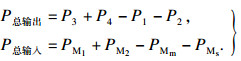 | (1) |
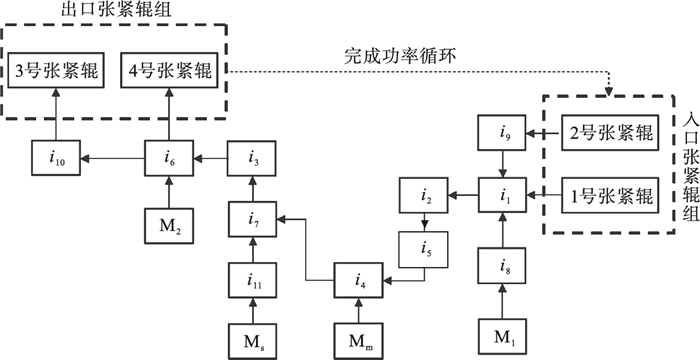 | 图 3 功率传递流程图Fig.3 Power transfer flow chart |
2 传动系统电机功率数学模型为了建立更准确的拉矫机传动系统数学解析模型,本文利用功率在传动系统中逆向路径传递和功率平衡法进行求解.通过利用逆向路径法计算拉矫传动系统中机构的传动效率,进而计算出传动系统各电机功率,其方向为从张紧辊的所受功率出发,与功率传递路径的方向相反.功率平衡法本质为能量守恒原理,利用驱动系统运行时的输入、输出功率守恒关系建立关系式求解所需项.
根据图 4的周转轮系受力示意图,推导出公式(2):
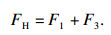 | (2) |
 | 图 4 周转轮系转向及受力示意图Fig.4 Schematic diagram of the steering and force of the epicyclic gear train |
根据力平衡方程和功率平衡方程求解行星齿轮中的受力情况,力平衡方程是基于周转轮系中行星架受力等于内齿轮和外齿圈对行星轮力的和,通过行星轮系输入、输出功率相等为基础建立对应功率平衡方程.
力平衡方程为
 | (3) |
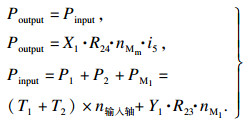 | (4) |
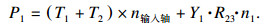 | (5) |
根据图 3所示功率传递流程图,从4个张紧辊处分析,可以分别求解出4个电机功率的计算公式,如式(6)所示:
 | (6) |
在实际生产中,拉矫系统中电机报警问题以及电机功率强烈波动是由在有限的电机功率情况下,生产速度和生产工艺参数没有做到适时调整而导致的,应尽量避免这一情况的发生.
3 传动系统功率键合图模型作为一个典型的非线性刚柔耦合、周期时变的多体系统,冷轧产线拉矫机传动系统的特点在于此传动系统中结构分布以及运动组成较为复杂,因此在此基础上建立的动力学微分方程也较为冗长复杂,而功率键合图理论正是一种适于分析这类复杂系统的通用方法.键合图理论基于工程系统中的功率传输、转换、存储和耗散原理[17].它通过带有特定线条和符号的图形和信息流共同组合进而建立工程系统的能量流动模型,以分析和控制其动态特性[18].键合图理论将多种物理参量整理归纳为4种广义变量,通过规定的符号表示传动系统中的基本原件,通过线条以及箭头的组合直观表示描述系统内部功率能量的流动方向[19].传动系统所用的各基本元件的名称、符号及物理意义如表 1所示.
表 1(Table 1)
| 表 1 键合图基本元件 Table 1 Basic elements of bond graph | |||||||||||||||||||||||||||||||||||||||||||||||||
该齿轮传动系统中1,2,3和4号张紧辊在正常生产时消耗电机功率,4个辊在工作过程中分别将扭矩传递至齿轮箱,齿轮传动系统为带差动机构机械式集中驱动系统,传动系统装置如图 5所示,图中a为太阳轮,b为内齿圈,b′为外齿圈,c为行星轮,t为齿轮,H为行星架.将行星架以及各传动轴视为柔性体,考虑其形变导致的能量损耗,同时考虑齿轮的惯性、弹性和阻尼,同样将考虑阻尼导致的能量损失,输入转矩定义为电动机带动下的主轴转矩,在此基础上根据拉矫机传动系统中的功率流向和转速比关系建立对应的键合图模型,具体模型如图 6所示,图中伴随箭头的编号1~129为根据系统组成构件的相互关系确定的各键的编号,Se为输入转矩, Ri为各齿轮的阻尼,Ii为各齿轮的转动惯量,Ci为各轴及行星架的刚度,ii为各级传动比.
图 5(Fig. 5)
 | 图 5 齿轮传动系统装置示意图Fig.5 Schematic diagram of the gear transmission system |
图 6(Fig. 6)
 | 图 6 齿轮传动系统键合图Fig.6 Bond graph of the gear transmission system |
键合图中广义动量p(t)和广义位移q(t)与势变量e(t)和流变量f(t)存在如下积分关系式:
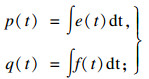 | (7) |
 | (8) |
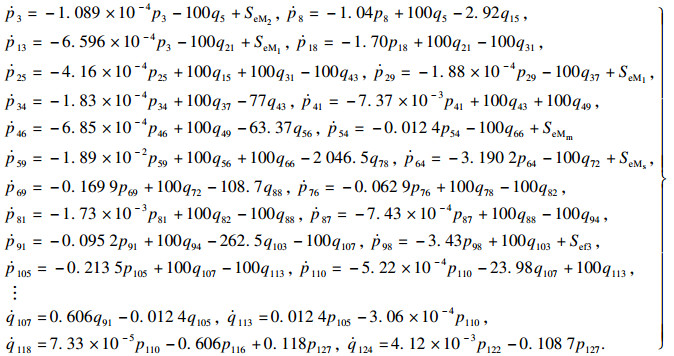 | (9) |
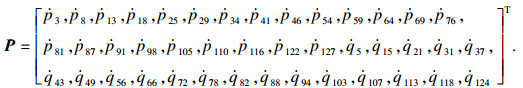 | (10) |
定性分析时,将扭矩定义为恒定输入,求解仿真后可得到传动系统输出转速、转矩以及行星架的位移.为得到系统的真实输出,转速ω通过角动量p(t)与元件的转动惯量I相除得到,转矩通过角位移q(t)与元件的刚度C相除得到,如式(11)所示.
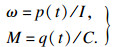 | (11) |
图 7(Fig. 7)
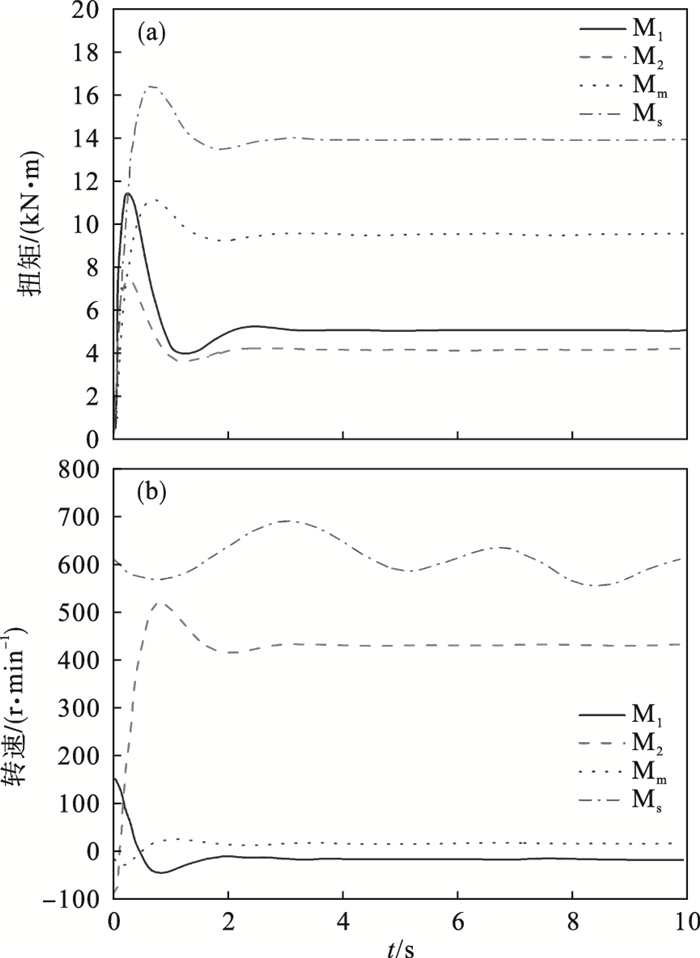 | 图 7 电机输出性能曲线Fig.7 Motor output performance curves (a)—扭矩;(b)—转速. |
前文分析得到MS电机的功率容易波动,因此对功率不稳定情况进行分析.由图 8a可以看出,经过5 s运行时间可以得到传动轴的变形情况,最大变形量为2 mm,由于轴在传动过程中功率不稳定导致系统结构部件存在一定的波动变形,因此保证功率运行稳定有助于设备安全生产.
图 8(Fig. 8)
 | 图 8 Ms电机传动轴的运行数据Fig.8 Operating data of the Ms motor drive shaft (a)—变形量;(b)—扭矩;(c)—转速. |
从图 8中可以发现,当Ms电机功率运行不稳定时,传动系统中轴的扭矩和转速运行非常不稳定相对应会导致图 8a中结构部件的变形,影响设备寿命.
4 功率模型结果验证4.1 数学模型结果验证针对某钢企宽幅冷轧产线拉伸弯曲矫直机组进行现场试验,依据该企业钢铁型号将带材分为6种型号进行试验验证,这6种型号带材的强度等级以及横截面参数如表 2所示.
表 2(Table 2)
| 表 2 6种型号带材的强度等级及横截面参数 Table 2 Strength grade and cross section parameters of six kinds of strips |
依据带材在生产中的要求进行现场试验,当每种型号带材数值解析得到的速度和张量与现场观测的相同时,分析电机功率占比.通过数值解析与试验验证,进而判断传动系统驱动电机功率的准确性.本文采用均值绝对百分比误差(mean absolute percentage error, MAPE)对解析值的准确性进行评估.MAPE越小,表示数值解析对实际值的拟合程度越高.其数学表达式为
 | (12) |

图 9为拉矫生产现场以及生产线监控界面,不同带钢进入拉矫时通过读取电机功率模块中对应电机的功率以及其功率占比,获得本文测试数据.
图 9(Fig. 9)
 | 图 9 拉矫机与电机功率监控界面Fig.9 Tension leveler and motor power monitoring interface |
收集6种型号带材的现场试验数据并将其与数值解析得到的驱动电机功率占比进行对比,得到图 10.由图 10a可看出,6种不同型号带材运行时的Mm电机功率整体趋势一致,其中在现场生产试验中,A型号和D型号与数值解析模型存在一定误差,其他4种型号带材的功率运行趋势一致,MAPE为25.4%;对比图 10b,Ms电机功率运行趋势与实际生产结果一致,并且整体偏差较小,MAPE为3.4%,说明该数值解析模型的准确性.
图 10(Fig. 10)
 | 图 10 不同带材的驱动电机功率占比Fig.10 Power percentage of driving motor for different strips (a)—Mm电机;(b)—Ms电机. |
由图 10对比可以看到Ms电机功率占比比较大,Mm电机功率占比比较小.通过对该企业酸轧拉矫机组传动系统电机功率进行计算,研究结果表明通过本文使用的计算方式计算得到的电机功率来拟合电机的实际功率具有可行性,可以为生产实际中的钢种预生产测试提供理论依据.
4.2 键合图模型结果验证对建立的齿轮传动系统状态方程,利用数值模拟进行求解,采用ODE45算法求解该非线性方程组,选用某一型号带钢通过记录带钢生产过程中的速度以及带钢张力,通过所建立的功率键合图进行求解各电机功率,根据第3节所求解结果与现场生产结果相对比得到图 11.
图 11(Fig. 11)
 | 图 11 各驱动电机功率占比Fig.11 The power percentage of each drive motor |
如图 11所示,利用功率键合图和功率转换公式得到的带材生产过程中电机功率与实际电机运行趋势一致.通过对各驱动电机功率对比,表明用功率键合图方法计算得到的功率占比与现场工业试验记录数据的误差较小,MAPE为9.3%,说明了所建立的齿轮传动键合图模型的正确性,可以为生产实际中的钢种预生产测试提供理论依据.
5 结论1) 提出了一种利用功率平衡法、逆向路径法和键合图法求解传动系统驱动功率方法,并结合冷轧拉矫机组传动系统,建立了传动系统功率求解关系式,Ms电机解析值的均值绝对百分比误差(MAPE)达3.4%,现场测试吻合度较好.
2) 通过建立的解析模型和功率键合图模型,分析冷轧传动系统功率运行情况.得到不同型号带材生产情况下,Ms电机功率更容易出现波动,同时设备更容易产生损坏.
3) 通过建立传动系统的功率键合图求解拉矫机传动系统的性能变化曲线,得到了电机开启阶段的扭矩不稳定会导致张紧辊产生较大变形量,影响设备安全性与寿命的结论,电机功率占比仿真数据解析值的MAPE为9.3%,误差较小,可为实际生产电机功率占比预测提供借鉴.
参考文献
| [1] | Huh H, Lee H W, Park S R, et al. The parametric process design of tension leveling with an elasto-plastic finite element method[J]. Journal of Materials Processing Technology, 2001, 113(1): 714-719. |
| [2] | Sauer B, Krupp F, Becker A. Power loss reduction in timing chain drives by adjusted tensioning and surface structuring[J]. Industrial Lubrication and Tribology, 2019, 71(8): 997-1002. DOI:10.1108/ILT-09-2018-0335 |
| [3] | Chen X, Zhang P, Min X, et al. Study on power split characteristics of planetary multistage face gear transmission device and its effect to drive efficiency under variable speed working condition[J]. Mechanical Sciences, 2020, 11(1): 173-182. DOI:10.5194/ms-11-173-2020 |
| [4] | Ye S, Andreas V, Stephan R. Investigation of the power losses of the hybrid transmission DE-REX based on modeling and measurement[J]. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, 2019, 233(14): 3646-3657. DOI:10.1177/0954407019829655 |
| [5] | Luo Y, Di T. Dynamics modeling of planetary gear set considering meshing stiffness based on bond graph[J]. Procedia Engineering, 2011, 24: 850-855. |
| [6] | 陈树宗, 李旭, 彭文, 等. 基于数值积分与功率损耗测试的冷轧电机功率模型[J]. 东北大学学报(自然科学版), 2017, 38(3): 361-365. (Chen Shu-zong, Li Xu, Peng Wen, et al. Motor power model of cold rolling based on numerical integration and power loss test[J]. Journal of Northeastern University(Natural Science), 2017, 38(3): 361-365. DOI:10.3969/j.issn.1005-3026.2017.03.012) |
| [7] | Silva C A, Manin L, Rinaldi R G, et al. Modeling of power losses in poly-V belt transmissions: hysteresis phenomena(enhanced analysis)[J]. Mechanism and Machine Theory, 2018, 121: 373-397. DOI:10.1016/j.mechmachtheory.2017.10.008 |
| [8] | Silva C A, Manin L, Andrianoely M A, et al. Power losses distribution in serpentine belt drive: modelling and experiments[J]. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, 2019, 233(13): 3424-3437. DOI:10.1177/0954407018824943 |
| [9] | 王中双, 陆念力. 键合图理论及应用研究若干问题的发展及现状[J]. 机械科学与技术, 2008(1): 72-77. (Wang Zhong-shuang, Lu Nian-li. A review of bond graph theory and its application[J]. Mechanical Science and Technology, 2008(1): 72-77.) |
| [10] | Han Y, Hu J J, Hu Z H, et al. Power flow and efficiency analyses of dual planetary coupling machanism based on bond graph theory[J]. Journal of Advanced Mechanical Design Systems & Manufacturing, 2017, 12(2): 10-13. |
| [11] | Liu W, Li L, Cai W, et al. Dynamic characteristics and energy consumption modelling of machine tools based on bond graph theory[J]. Energy, 2020, 212: 118767. DOI:10.1016/j.energy.2020.118767 |
| [12] | Lvanovic V, Tseng H E. Bond graph based approach for modeling of automatic transmission dynamics[J]. SAE International Engineering Journal, 2017, 10(4): 1999-2014. DOI:10.4271/2017-01-1143 |
| [13] | Boudon B, Dang T T, Margetts R, et al. Simulation methods of rigid holonomic multibody systems with bond graphs[J]. Advances in Mechanical Engineering, 2019, 11(3): 1-29. |
| [14] | Tripathi J P, Ghoshal S K, Dasgupta K, et al. Bond graph modelling of a hydraulic cylinder-actuated planar manipulator[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2017, 39(11): 4275-4287. DOI:10.1007/s40430-017-0790-0 |
| [15] | Tan D, Wang Q, Wu Y S. Modal analysis of in-wheel motor-driven electric vehicle based on bond graph theory[J]. Shock and Vibration, 2017, 2017: 6459154. |
| [16] | 及时. 拉弯矫直变形过程与力能参数研究[D]. 沈阳: 东北大学, 2011. (Ji Shi. Research on deformation process and force and energy parameters of the stretch-bending straightening machine[D]. Shenyang: Northeastern University, 2011. ) |
| [17] | Benchouia N E, Elias H A, Khochemane L, et al. Bond graph modeling approach development for fuel cell PEMFC systems[J]. International Journal of Hydrogen Energy, 2014, 39(27): 15224-15231. |
| [18] | 王中双. 键合图理论及其在系统动力学中的应用[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007. (Wang Zhong-shuang. Bond graph theory and its application in system dynamics[M]. Harbin: Harbin Engineering University Press, 2007.) |
| [19] | 孙伟, 董荣梅, 许焕卫. 基于键合图的风电齿轮传动系统稳健优化设计[J]. 中国机械工程, 2009, 20(21): 2549-2553. (Sun Wei, Dong Rong-mei, Xu Huan-wei. Robust optimization design of the gear transmission of wind turbine based on bond graph[J]. Chinese Journal of Mechanical Engineering, 2009, 20(21): 2549-2553.) |
