
 , 徐志博1
, 徐志博1 1. 长安大学 道路施工技术与装备教育部重点实验室,陕西 西安 710064;
2. 比亚迪汽车有限公司,陕西 西安 710118
收稿日期:2022-03-02
基金项目:陕西省科技重大专项(2018zdzx01-01-01);陕西省自然科学基金资助项目(2022JM-295,2022JQ-576)。
作者简介:刘永生(1985-),男,山东菏泽人,长安大学讲师,博士。
摘要:激光扫描获取的曲面零件点云中包含的噪声点将影响零件的曲面拟合精度.提出了一种根据噪声分类分步降噪及光顺方法,利用kd tree结合K-means聚类算法去除离群点噪声,引入采样点曲率改进双边滤波因子,对非离群点噪声进行光顺.利用该方法对液力变矩器导轮叶片点云进行去噪,并与利用三坐标测量机接触式测量获得的叶片局部测量结果配准比较.实验结果表明,70%以上的接触式扫描测量点与利用本文方法去噪后的叶片点云之间的偏差在±10 μm之间.表明该方法可以很好地保留扫描物体的几何特征,获得的点云模型能够满足后续模型重建的精度要求.
关键词:点云处理点云去噪K-means聚类改进双边滤波液力变矩器
Point Cloud Denoising Algorithm Based on Hybrid Filtering and Improved Bilateral Filtering
LIU Yong-sheng1, CAI Shi-yang1,2, CHEN Yi-xin1

 , XU Zhi-bo1
, XU Zhi-bo1 1. Key Laboratory of Road Construction Technology & Equipment, Ministry of Education, Chang'an University, Xi'an 710064, China;
2. BYD Automotive Co., Ltd., Xi'an 710118, China
Corresponding author: CHEN Yi-xin, E-mail: chenyx@chd.edu.cn.
Abstract: The point cloud of curved parts obtained by laser scanning contains noise points, that may affect the surface fitting accuracy of the parts. A denoising and smoothing method based on noise classification was proposed. The kd tree algorithm and K-means clustering algorithm were combined to remove the outlier noise. The curvature of the sampling points was substituted to improve the bilateral filter factor, and the improved bilateral filtering algorithm was used to smooth the non-outlier noise. The proposed method was used to denoise the point cloud of the blade of the guide pulley of the hydraulic torque converter, and compared with the measurement results obtained by coordinate measuring machine. The experimental results showed that the deviations between more than 70% of the measurement points and the denoised point cloud is within ± 10 μm. It was found that the proposed method can well preserve the geometric features of the scanned object, and the denoised point cloud can meet the accuracy requirements of the model reconstruction.
Key words: point cloud processingpoint cloud denoisingK-means clusteringimproved bilateral filteringhydraulic torque converter
三维激光扫描技术在逆向工程、零件建模、零件修复等领域应用广泛.利用三维激光扫描仪器获取的零部件点云数据中,不可避免地存在噪声点,直接影响零部件逆向重建模型的表面质量及重建精度,因此在进行逆向重建前需要去除噪声点.
目前,有许多国内外****对点云模型的去噪平滑提出了不同的算法.Yu等[1]提出了一种局部熵度值更新网格顶点,保持模型细节和尖锐特征,但是这种方法会产生过度光顺问题.焦亚男等[2]采用半径滤波结合改进具有噪声的基于密度的聚类方法(density-based spatial clustering of applications with noise, DBSCAN)算法以及改进双边滤波算法对点云进行去噪,同时用八叉树并行优化提高双边滤波速度.Wei等[3]对网格表面的面法向量或顶点法向量进行集合,提出一种用于网格去噪的法向双边滤波算法,该方法在几何特征多样、曲面采样不规则的情况下有良好的效果.Zhang等[4]基于法向量和L1中值建立了一种优化算法,在提取环锻件原始点云截面线时去除点云噪声.Sun等[5]利用一阶信息的稀疏性去噪,很好地保留了点云表面尖锐特征,但在平滑的弯曲区域会出现阶梯效果.Zheng等[6]将引导法向量滤波方法扩展到点云处理领域,提出尖锐特征保持的点云引导去噪方法.夏毅敏等[7]利用距离阈值点云去噪方法及低频随机噪声点过滤方法去除隧道截面点云噪声,提高了隧道截面的曲线拟合及缺陷检测精度.Li等[8]提出了一种估计散乱点云法线的新方法,在去噪过程中不受点云尖锐特征的影响.文献[9]在考虑相邻点间的距离及沿法线方向距离的基础上,利用双边滤波器实现点云噪声的去除.Kawasaki等[10]在构造B样条曲面时,利用双边滤波对点云数据进行去噪,可有效地平滑B样条曲面,同时保留其特征.Zhang等[11]提出一种基于主成分分析结合改进双边滤波算法,对点云数据中不同尺度的噪声进行去除.Zou等[12]采用主成分分析-小波函数双边滤波方法,通过粒子群优化方法搜索最佳邻域中两点间的距离,实现点云噪声的高效去除.秦亚光等[13]利用曲率-弦长比复合判据实现点云数据高频噪声的处理,运用随机滤波法实现低频噪声的去除.文献[14]利用法线张量投票进行网格去噪,并通过曲率拉普拉斯更新定点,使含噪声的点云数据更具有鲁棒性,且去噪后能保持尖锐特征.Li等[15]提出使用L0梯度最小化方法直接生成具有尖锐特征的曲面,可有效去除点云噪声.但是上述噪声点去除方法未兼顾曲率变化对特征点的影响,导致特征点保持不好或去噪效率不高.
本文首先利用kd tree算法结合K-means聚类算法对离群噪声点进行去除,然后对点云数据进行法向与曲率估计,并对双边滤波算法进行改进,提高其特征保持性能,然后利用改进的双边滤波算法对非离群噪声点进行光顺去噪.利用本文的方法对液力变矩器导轮叶片点云进行去噪处理,并与接触式测量结果进行对比,验证去噪算法的有效性.
1 kd tree结合K-means聚类去噪算法离群噪声点主要指漂浮在主体点云上方的稀疏点或小而密集的片状点云,以及超出预先设定的扫描区域的多余数据点.K-means聚类算法可根据距离标准剔除点云中的离群点,原理简单高效,但对噪声和离群孤立点敏感,且需事先确定初始值K.由于点云的数据量大且分布不规律,本文将kd tree算法与K-means算法相结合去除离群噪声点,改进后的算法先用kd tree算法过滤出数据集中的孤立离群点,以减少类数从而间接减少K值,再用K-means算法剔除离群噪声点,从而可以快速有效地去除离群噪声点.
1.1 kd tree粗去噪算法扫描得到的三维点云原始数据是散乱无序的,根据kd tree算法建立点云拓扑关系,计算得到的点云任意一点与邻域内各点的平均距离服从高斯分布,均值μ,标准差δ.若某一点与其邻域内所有点的平均距离超过设定阈值μ+λδ,则判定该点为噪声点,从点云中剔除.
利用kd tree算法搜索邻域点之前,需要进行k初值和标准差倍数参数λ设定.k值的选取直接影响点云模型的噪声点去除效果.
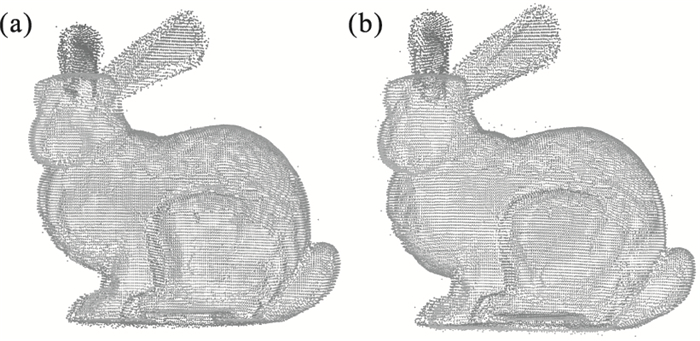
将1 700个随机噪声点加入斯坦福大学兔子(Bunny)点云,产生含噪声点的Bunny点云模型,如图 1所示.选取不同的k值,对点云进行去噪处理,去噪后的点云数量随k值的变化如图 2所示.
图 1(Fig. 1)
 | 图 1 含噪声点的Bunny点云Fig.1 Point cloud of Bunny with noise points |
图 2(Fig. 2)
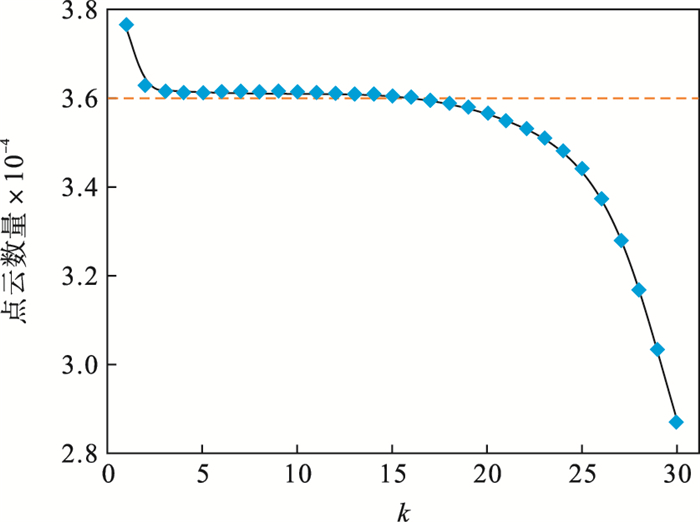 | 图 2 点云数量随k值变化曲线图Fig.2 Curve of point cloud number with k value |
由图 2可知,当k值小于5时,点云去噪效果不明显,当k值大于15时,随着k值增大,点云数量急剧下降,出现真值被剔除的现象.因此k值的选取范围应为[5, 15],即该曲线水平区域.
1.2 K-means聚类去噪算法K-means聚类算法对点云数据Ci进行聚类,根据点到聚类中心的欧氏距离判断该点是否为噪声点.K-means参数的最优解以成本函数最小化为目标,每个类的点p与类内重心点mi的距离平方和称为畸变程度,成本函数为各个类的畸变程度之和,如式(1)所示:
 | (1) |
图 3(Fig. 3)
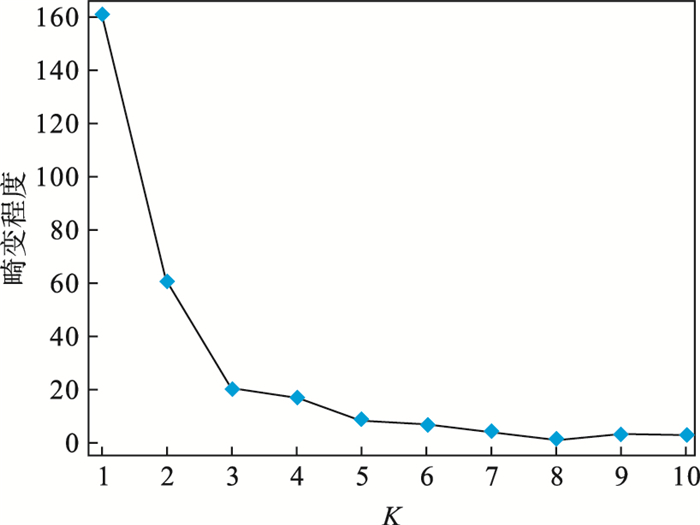 | 图 3 畸变程度随K值变化曲线Fig.3 Curve of distortion degree with K value |
由图 3可知,在K=3时,畸变程度得到大幅改善,可以考虑选取K=3作为最佳聚类数量.
1.3 kd tree结合K-means聚类算法参数分析采用kd tree结合K-means聚类算法进行去噪过程中,为了得到合适的滤波参数,选取表 1中6组不同参数对含噪声点Bunny点云进行去噪实验,结果如图 4所示.
表 1(Table 1)
| 表 1 kd tree结合K-means聚类算法对Bunny点云模型去噪的参数选择 Table 1 Parameters of noise removal of Bunny by kd tree and K-means clustering algorithm |
图 4(Fig. 4)
 | 图 4 kd tree结合K-means聚类算法的去噪效果Fig.4 Denoising effect of kd tree and K-means clustering algorithm (a)—k=5, λ=0.1; (b)—k=5, λ=2; (c)—k=10, λ=0.1; (d)—k=15, λ=0.1; (e)—k=15, λ=1; (f)—k=15, λ=2. |
由图 4可以看出,基于kd tree结合K-means聚类算法能够有效剔除离群噪声点,将图 4各图进行对比可知,标准差倍数值λ过小,尖锐区域离群点易被误判为特征点,去除不彻底,当λ过大,容易出现过去噪,将尖锐区域特征点误认为噪声点去除掉.
2 改进双边滤波去噪算法利用kd tree结合K-means聚类算法去噪后,点云中还存在与主体点云数据混合在一起的小尺度噪声点,难以用常见的基于欧氏距离和点云密度判断的方法剔除,影响后续三维模型曲面重建精度,需要对其进行光顺处理.点云数据集是一组没有拓扑关系的坐标点,利用双边滤波可得到点云的法向量与曲率,但其对于点云模型的尖锐区域区分不明显,会导致过光顺问题[11].本文将采样点曲率ωi作为参数,改进双边滤波因子,以增强特征保持性,并将其用于非离群噪声点的光顺.
2.1 法向及曲率估计表面法线是几何体表面的重要属性,通过拟合出点云的局部曲面,可很好地估计法向量[12].本文采用主成分分析法来估计采样点的法向量.对采样点pi进行k近邻搜索,获得k个邻域点N(pi)来近似代替点pi的局部邻域曲面S,即pi∈S,对邻域点构建协方差矩阵C如式(2)所示:
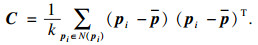 | (2) |

点云中任意采样点处的曲率可用该点及其邻域点拟合的局部曲面曲率来表征,可以用主成分分析方法来估计,点pi处的曲率ωi可表示为
 | (3) |
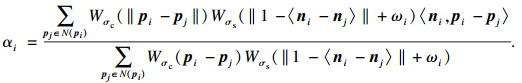 | (4) |
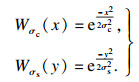 | (5) |
 | (6) |
1) 初始化k值,构建kd tree,计算点云数据点pi的k个邻近点;
2) 利用PCA估计点云的法向量ni和曲率值ωi;
3) 利用式(7)计算各采样点pi光顺平滑权重Wσc参数x和特征域权重Wσs参数y;
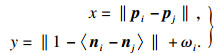 | (7) |
5) 将Wσc和Wσs代入式(4)计算双边滤波因子αi;
6) 利用式(6)计算点pi的几何位置,得到去噪后的点云数据模型.
选择不同的双边滤波参数对Bunny点云中非离群噪声点进行去噪,结果如图 5所示.
图 5(Fig. 5)
 | 图 5 双边滤波光顺效果图Fig.5 Smoothing effect by bilateral filtering (a)—σc=5, σs=0.01; (b)—σc=5, σs=0.1; (c)—σc=5, σs=5; (d)—σc=15, σs=0.1; (e)—σc=25, σs=0.1. |
通过对比图 5a,图 5b,图 5c可以看出,当σc一定时,随着σs增大,点云局部几何特征保持较好,但在较平坦区域,光顺性较差;通过对比图 5b,图 5d,图 5e可以看出,当σs一定时,随着σc增大,点云模型光顺性较好,但是局部几何特征保持性不好.由实验得到利用双边滤波去除Bunny非离群噪声点的最佳参数为σc=5,σs=0.1.
针对图 1所示含噪声点的Bunny点云,利用统计滤波结合双边滤波算法以及DBSCAN聚类结合快速双边滤波算法进行处理,结果如图 6所示.
图 6(Fig. 6)
 | 图 6 不同去噪算法效果图Fig.6 Denoising effect by different algorithms (a)—统计滤波+双边滤波; (b)—DBSCAN+快速双边滤波. |
图 6a显示该算法可以去除大部分噪声点,但距离主体较近的噪声无法有效去除.图 6b显示该算法可以去除大部分噪声点并保留了点云的特征,但尖锐区域的噪声点不容易去除.而图 5b所显示的本文设计的算法可以在较好去除离群及非离群噪声点的同时,较好地保留了点云的局部几何特征.
3 液力变矩器导轮叶片点云去噪实验利用本文所设计的改进双边滤波去噪方法对液力变矩器导轮的叶片点云进行实际去噪实验,得到去噪后的叶片点云.利用三坐标测量机对该叶片进行接触式测量,将接触式测量结果通过曲面配准的方法投影到去噪处理后的叶片点云上,通过误差分析结果验证叶片点云的去噪效果.
3.1 导轮叶片点云的获取液力变矩器导轮如图 7所示,利用三坐标测量机搭载Header LS60激光扫描测头对导轮的一个叶片进行扫描,得到导轮叶片的三维点云如图 8所示.
图 7(Fig. 7)
 | 图 7 液力变矩器导轮Fig.7 Guide pulley of the hydraulic torque converter |
图 8(Fig. 8)
 | 图 8 导轮叶片原始点云Fig.8 Original point cloud of the guide pulley blade (a)—叶片正面;(b)—叶片背面. |
由图 8可以看出,导轮叶片的原始点云数据中存在着离群及非离群噪声点,影响叶片点云数据的后续处理.
3.2 导轮叶片点云去噪利用本文所提出的去噪算法对导轮叶片点云的离群及非离群噪声点进行去噪处理,通过多次实验,得到算法的最佳参数为k=25,λ=0.8,K=10,σc=5,σs=0.2,导轮叶片点云去噪处理后的效果如图 9所示.
图 9(Fig. 9)
 | 图 9 去噪处理后的导轮叶片点云Fig.9 Point cloud of the guide pulley blade after denoising (a)—叶片正面;(b)—叶片背面. |
由图 9可以看出,利用本文算法可以有效地对导轮叶片的三维点云数据进行去噪和平滑,同时很好地保留了模型的几何特征.
3.3 导轮叶片点云去噪误差分析利用三坐标测量机对图 10所示导轮叶片的5个局部区域进行接触式扫描测量.
图 10(Fig. 10)
 | 图 10 导轮叶片接触式测量区域示意图Fig.10 Measurement area of the guide pulley blade (a)—叶片正面;(b)—叶片背面. |
将每个区域的扫描测量结果与经过本文算法处理后的叶片点云进行配准,如图 11所示.计算各接触式测量点与导轮叶片点云之间的偏差,如图 12所示.
图 11(Fig. 11)
 | 图 11 叶片接触式测量与点云配准结果Fig.11 Matching results between measurement and point cloud of the guide pulley blade (a)—区域A;(b)—区域B;(c)—区域C;(d)—区域D;(e)—区域E. |
图 12(Fig. 12)
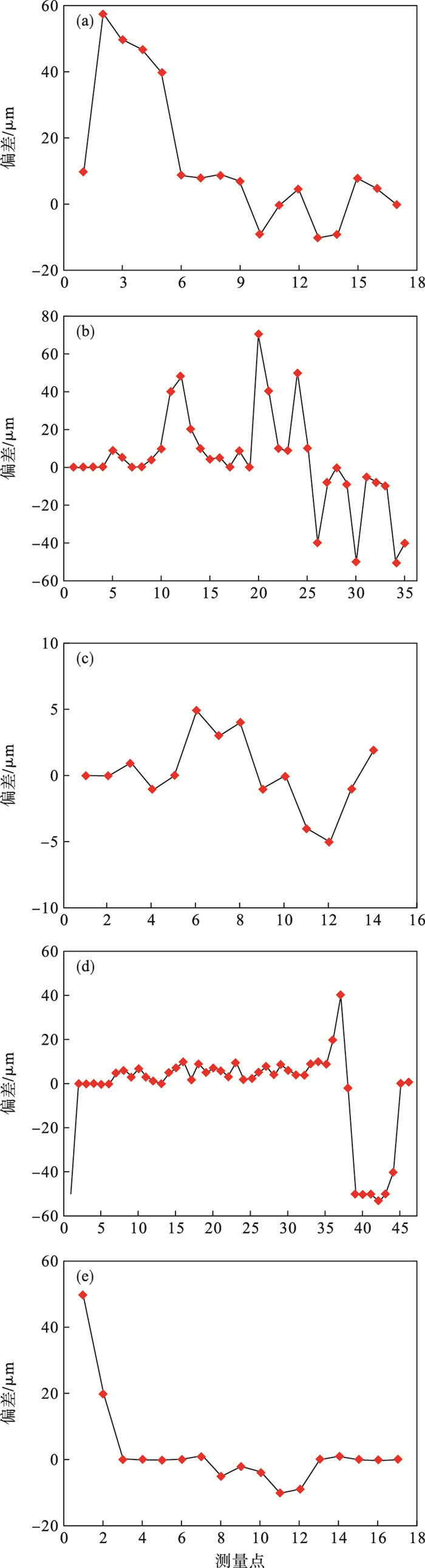 | 图 12 叶片接触式测量与点云之间偏差图Fig.12 Deviations between measurement and point cloud of the guide pulley blade (a)—区域A;(b)—区域B;(c)—区域C;(d)—区域D;(e)—区域E. |
由图 12可知,70%以上的接触式扫描测量点与利用本文方法进行离群及非离群噪声点去噪后的叶片点云之间的偏差在±10 μm之间,表明经过本文方法处理后的点云能保持较高的精度,很好地保留了扫描物体的几何特征,获得的点云模型满足后续三维重建精度要求,为后续的三维重建模型奠定了基础.
4 结论本文利用kd tree滤波结合K-means滤波对点云离群噪声点进行去除,引入采样点曲率以改进双边滤波因子,利用改进双边滤波算法对点云非离群点进行光顺处理.此方法去噪效果好,能够有效保持模型的尖锐区域特征.利用此方法对液力变矩器导轮叶片点云进行去噪,且与导轮叶片局部接触式扫描测量结果进行配准,并对利用本方法去噪后的叶片点云与接触式扫描测量结果之间的偏差进行分析.实验结果表明,70%以上测量点与叶片点云之间的偏差在±10 μm之间,表明本文的方法可以很好地保留扫描物体的几何特征,获得的点云模型满足后续三维重建精度要求.
参考文献
| [1] | Yu J Z, Wei M Q, Qin J, et al. Feature-preserving mesh denoising via normal guided quadric error metrics[J]. Optics and Lasers in Engineering, 2014, 62(6): 57-68. |
| [2] | 焦亚男, 马杰, 钟斌斌. 一种基于尺度变化的点云并行去噪方法[J]. 武汉大学学报(工学版), 2021, 54(3): 277-282. (Jiao Ya-nan, Ma Jie, Zhong Bin-bin. Point cloud parallel denoising algorithms based on scale change[J]. Engineering Journal of Wuhan University, 2021, 54(3): 277-282.) |
| [3] | Wei M Q, Yu J Z, Pang W M, et al. Bi-normal filtering for mesh denoising[J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(1): 43-55. DOI:10.1109/TVCG.2014.2326872 |
| [4] | Zhang Y C, Wang X J, Li Q, et al. A new section line extraction method of ring forgings based on normal vector and L1-median[J]. Measurement, 2021, 184: 109894. DOI:10.1016/j.measurement.2021.109894 |
| [5] | Sun Y J, Schaefer S, Wang W P. Denoising point sets via L0 minimization[J]. Computer Aided Geometric Design, 2015, 35/36: 2-15. DOI:10.1016/j.cagd.2015.03.011 |
| [6] | Zheng Y L, Li G Q, Wu S H, et al. Guided point cloud denoising via sharp feature skeletons[J]. The Visual Computer, 2017, 33: 857-867. DOI:10.1007/s00371-017-1391-8 |
| [7] | 夏毅敏, 郭子泺, 邓朝辉, 等. 基于点云的TBM隧道成型质量检测方法及应用[J]. 东北大学学报(自然科学版), 2021, 42(6): 864-870. (Xia Yi-min, Guo Zi-luo, Deng Chao-hui, et al. TBM tunnel shaping quality detection method and its application based on point cloud[J]. Journal of Northeastern University(Natural Science), 2021, 42(6): 864-870.) |
| [8] | Li B, Schnabel R, Klein R, et al. Robust normal estimation for point clouds with sharp features[J]. Computers & Graphics, 2010, 34(2): 94-106. |
| [9] | Digne J, de Franchis C. The bilateral filter for point clouds[J]. Image Processing on Line, 2017, 7: 278-287. DOI:10.5201/ipol.2017.179 |
| [10] | Kawasaki T, Jayaraman P K, Shida K, et al. An image processing approach to feature-preserving B-spline surface fairing[J]. Computer-Aided Design, 2018, 99: 1-10. DOI:10.1016/j.cad.2018.01.003 |
| [11] | Zhang F, Zhang C, Yang H M, et al. Point cloud denoising with principal component analysis and a novel bilateral filter[J]. Traitement Du Signal, 2019, 36(5): 393-398. DOI:10.18280/ts.360503 |
| [12] | Zou B C, Qiu H D, Lu Y F. Point cloud reduction and denoising based on optimized downsampling and bilateral filtering[J]. IEEE Access, 2020, 8: 136316-136326. DOI:10.1109/ACCESS.2020.3011989 |
| [13] | 秦亚光, 罗周全, 汪伟, 等. 采空区三维激光扫描点云数据处理技术[J]. 东北大学学报(自然科学版), 2016, 37(11): 1635-1639. (Qin Ya-guang, Luo Zhou-quan, Wang Wei, et al. Cavity three-dimensional laser scanning point cloud data processing technology[J]. Journal of Northeastern University(Natural Science), 2016, 37(11): 1635-1639.) |
| [14] | Tsuchie S, Higashi M. Surface mesh denoising with normal tensor framework[J]. Graphical Models, 2012, 74: 130-139. DOI:10.1016/j.gmod.2012.03.010 |
| [15] | Li H B, Li Y B, Yu R X, et al. Surface reconstruction from unorganized points with L0 gradient minimization[J]. Computer Vision and Image Understanding, 2018, 169: 108-118. DOI:10.1016/j.cviu.2018.01.009 |
