
 , 石伟川, 孔瑞, 郭家繁
, 石伟川, 孔瑞, 郭家繁 东北大学 深部金属矿山安全开采教育部重点实验室,辽宁 沈阳 110819
收稿日期:2022-02-23
基金项目:国家自然科学基金资助项目(51779045); 中央高校基本科研业务费专项资金资助项目(N2001026); 辽宁省‘兴辽英才计划’项目(XLYC1807029)。
作者简介:王者超(1980-),男,山东高唐人,东北大学教授,博士生导师。
摘要:基于真三轴试验机对取自某储气库、埋深3 600 m的试样开展了一系列砂岩真三轴压缩试验.研究了真三向应力作用下深部砂岩的强度、变形特征,并将深部砂岩与浅部砂岩的弹性模量、黏聚力、摩擦角和峰值破坏强度进行了对比.结果表明:在一定范围内随着中间主应力的增加,深部砂岩的峰值强度也会增加,深部砂岩的起裂应力和损伤应力也随之增加,峰值处的中间主应变呈现减小的趋势.随着砂岩深度的增加,砂岩的弹性模量、黏聚力和摩擦角均呈现增大的趋势.浅部砂岩峰值破坏强度的八面体剪应力与有效平均正应力表现为非线性关系,而深部砂岩峰值破坏强度的八面体剪应力与有效平均正应力表现为线性关系,且Mogi-Coulomb准则更适用于表述深部砂岩破坏时的强度特征.
关键词:深部砂岩真三轴试验变形特征应力分界点Mogi-Coulomb准则
Mechanical Properties of Deep Sandstone Under True Triaxial Stress
WANG Zhe-chao

 , SHI Wei-chuan, KONG Rui, GUO Jia-fan
, SHI Wei-chuan, KONG Rui, GUO Jia-fan Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Zhe-chao, E-mail: wang_zhechao@hotmail.com.
Abstract: A series of true triaxial compression tests on sandstone were carried out based on the true triaxial testing machine. The sandstone samples were taken from a gas storage facility, with a buried depth of 3 600 meters. The strength and deformation characteristics of deep sandstone under true triaxial stress were studied, and the elastic modulus, cohesion, friction angle and peak failure strength of deep sandstone and shallow sandstone were compared. The results show that with the increase of the intermediate principal stress, the peak strength of the deep sandstone will also increase, the crack initiation stress and the damage stress of the deep sandstone will also increase, and the intermediate principal strain at the peak will decrease. With the increase of sandstone depth, the elastic modulus, cohesion and friction angle of sandstone all show an increasing trend. The octahedral shear stress of the peak failure strength of the shallow rock and the effective mean normal stress show a nonlinear relationship, while the octahedral shear stress of the peak failure strength of the deep rock has a linear relationship with the effective mean normal stress. And the Mogi-Coulomb criterion is more suitable for reflecting the strength characteristics of deep sandstone at failure.
Key words: deep sandstonetrue triaxial testdeformation characteristicsstress breakpointMogi-Coulomb criterion
岩石在常规三轴应力作用下的力学行为得到了大量的研究,但是根据地应力测量的结果显示,地下的岩石工程实际上处于三向应力不相等的状态,即σ1>σ2>σ3[1].目前国内天然气、煤炭、石油的开采和储存已经进入地层深部阶段.深部岩石大多处于围压不相等的高地应力条件下,砂岩作为沉积岩又是深部岩石工程中最常见的岩体.因此,研究真三向应力作用下深部砂岩的力学特性对深部岩石工程的结构变形和破坏有着重要的指导价值.
如今国内外****对真三向应力作用下岩石的变形和强度特征的研究取得了一定的进展.Mogi[2]设计了真三轴压缩试验仪器,并根据岩石的试验结果提出了Mogi-Coulomb强度准则.Feng等[3]对砂岩和花岗岩试样进行了一系列真三轴压缩试验,研究发现岩石的破裂和变形呈现应力诱导的各向异性,从广义三轴压缩到广义三轴拉伸应力状态,岩石强度随中间主应力的变化呈非对称变化的特征.Ma等[4-5]通过真三轴压缩试验,分析了在不同的应力路径下中间主应力对岩石变形、强度与破坏特征的影响,研究发现,当岩石以剪切破坏为主时,破坏所需的剪应力随平均主应力的增大而增大,破坏角随平均主应力和洛德角的增大而减小.Haimson等[6]对岩石进行了一系列的真三轴压缩试验,研究发现岩石在峰值破坏时的八面体剪应力与剪切面上的平均有效正应力呈现幂指数的关系,但这一结果无法描述岩石在压缩破坏时与拉伸破坏时的变形和强度的不同.Zhao等[7]利用真三轴仪研究了岩石在真三轴卸荷时的力学特性和破坏模式.研究发现,在卸荷状态下岩石的破坏形式表现为脆性破坏,而且在卸荷时岩石主要为拉-剪复合破坏,并不是简单的剪切破坏.
然而,目前****对真三向应力作用下岩石力学特性的研究大部分都是基于地下3 000 m以上的岩石,对在地层深部3 000 m以下取出的岩石的力学性质的研究还较少.在实际工程中,深部岩石与浅部岩石本身性质也有差异,因此在真三向应力作用下深部岩石与浅部岩石表现出的力学特性也会有所不同.因此,本文以地层深部3 600 m的砂岩为研究对象,通过东北大学自主研发的真三轴试验机开展了一系列真三轴压缩试验,研究了深部砂岩在真三向应力作用下的力学特性,从而为深部石油、天然气等开采和储存过程中岩石的稳定性控制提供一定的基础理论依据.
1 试验方法1.1 试样制备本文试验所用砂岩取自某地下储气库直接盖层(埋深3 600 m)的同一段岩心,并且取样方向保持一致.将岩心制作成25 mm×25 mm×50 mm的试样.试验前,对砂岩的各个方向进行了波速测量,选出声速接近的9块试样.图 1为制备好的砂岩试样.
图 1(Fig. 1)
 | 图 1 用于真三轴试验的砂岩试样Fig.1 Sandstone specimens for true triaxial test |
1.2 试样设备试验采用东北大学自主研发的新型Mogi式伺服试验系统(Lavender 508)[8],如图 2所示.试验系统主要有刚性加载框架、压力室、液压加载模块、数据采集与控制模块等主模块组成.水平加载框架最大输出力为3 000 kN,竖直加载框架最大输出力为6 000 kN,压力室内的油压最大可达100 MPa.采用LVDT传感器测量加载过程中试样的变形,传感器精度为0.1%.为了能够得到试样的全应力-应变曲线,在真三轴压缩试验过程中,静水压力加载阶段和中间主应力加载阶段采用应力控制,在最大主应力加载阶段,在试样的应力达到70%~80%的峰值强度时,将应力控制转变为最小主应力方向上的应变信号进行位移控制,以获得岩石的峰后曲线.
图 2(Fig. 2)
 | 图 2 Mogi式真三轴压缩测试系统Fig.2 The Mogi type of the true triaxial testing system |
1.3 试验方案真三轴压缩试验的典型加载路径分为3个阶段:静水压力加载阶段,中间主应力加载阶段,最大主应力加载阶段.图 3为真三轴压缩试验的加载路径,在本试验中,首先,以0.1 MPa/s的加载速率施加静水压力,直到达到目标值,且σ1=σ2=σ3.然后,保持σ3恒定,以0.5 MPa/s的加载速率同时将σ1和σ2增加到目标值,且σ1=σ2.最后,在保持σ3和σ2不变的情况下,施加σ1.为了获得砂岩峰后变形,在应力达到峰值强度的70%~80%时,采用最小主应变(ε3)进行反馈控制,应变率为5×10-6 s-1.
图 3(Fig. 3)
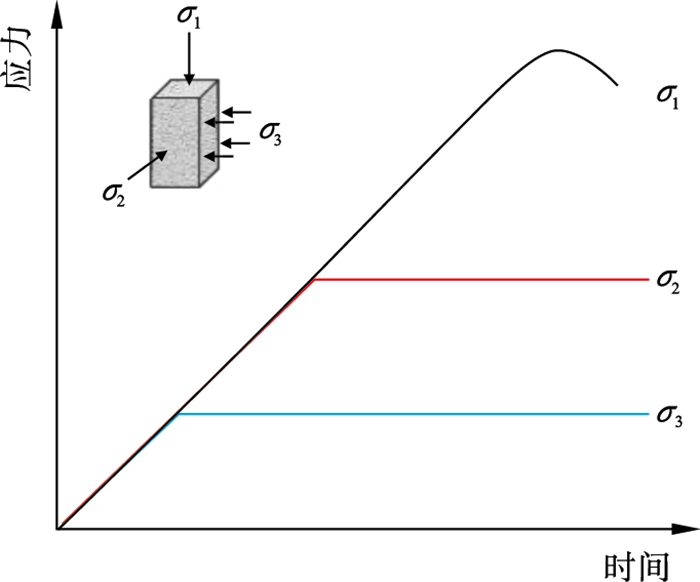 | 图 3 真三轴压缩试验加载路径Fig.3 Loading paths of the true triaxial compression test |
该地下储气库直接盖层厚度约为150 m,地层温度为92.5 ℃,岩性为泥岩和砂岩,平均孔隙度和渗透率分别为4.1%和2.8× 10-6 μm2,直接盖层钻取岩心试样处的最小水平主应力σ3=66 MPa,垂向主应力σ2=83 MPa,最大水平主应力σ1=91 MPa[9].在土体材料的有效应力原理基础上,Biot[10]引入了有效应力系数,得到了适用于岩石材料的有效应力公式:
 | (1) |
有效应力系数有多种获取方法,例如,声波动态法、排水试验法和Cross-Plotting法[11]等.根据某储气库盖层砂岩的孔隙率、孔隙几何形状及工程经验,确定有效应力系数的取值为0.6[12].该储气库的孔隙压力梯度为10 kPa/m,可以得到盖层岩心试样处的孔隙压力为36 MPa.因此,经计算可得直接盖层钻取岩心试样处的有效应力分别为σ3=44.4 MPa,σ2=61.4 MPa,σ1=69.4 MPa.
根据盖层岩心处的实际有效应力,设置试样的最小主应力取值范围σ3=(45±5)MPa,中间主应力的取值范围σ2=(60±20) MPa.将选取的9个试样分为3组,每组恒定σ3,具体试验工况见表 1,表中应力为有效应力.
表 1(Table 1)
| 表 1 真三轴压缩试验工况 Table 1 True triaxial compression test conditions |
2 试验结果分析2.1 深部砂岩真三轴变形全过程应力-应变曲线根据试验结果,真三向应力作用下深部砂岩的应力-应变关系曲线如图 4所示.
图 4(Fig. 4)
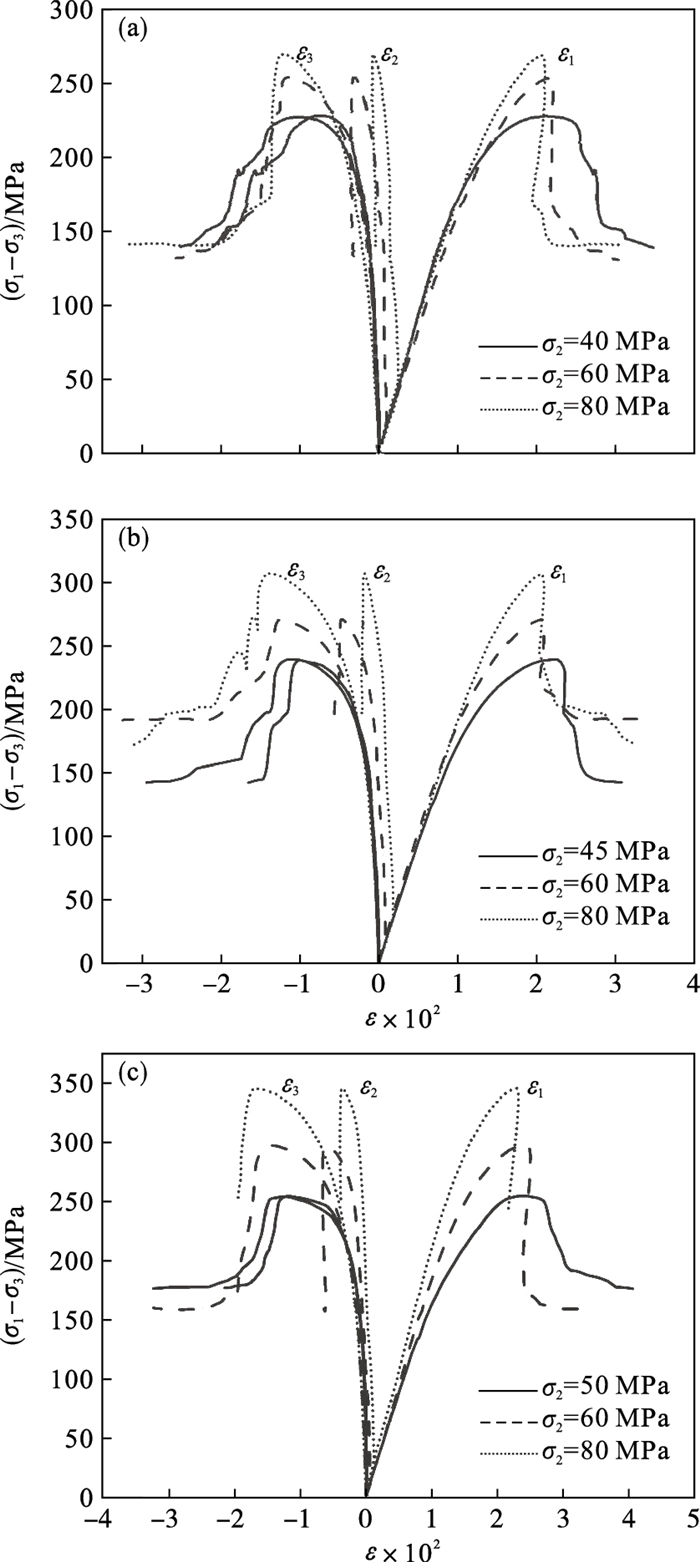 | 图 4 真三向应力作用下砂岩应力-应变曲线Fig.4 Stress-strain curves of sandstone under the true three-dimensional stress (a)—σ3=40 MPa;(b)—σ3=45 MPa;(c)—σ3=50 MPa. |
从图中的最大主应变ε1曲线可以看出,恒定最小主应力条件下,峰值处的最大主应变ε1随着中间主应力的增大呈现出减小的趋势,在σ3=40 MPa条件下,ε1从σ2=40 MPa时的2.18%逐渐降低到σ2=80 MPa时的2.05%,降低了约5.96%;同理,在σ3=45 MPa时,ε1从σ2=45 MPa时的2.27%逐渐降低到σ2=80 MPa时的2.06%,降低了约9.25%;在σ3=50 MPa时,ε1从σ2=50 MPa时的2.47%逐渐降低到σ2=80 MPa时的2.29%,降低了约7.29%.
从图 4中的中间主应变ε2曲线可以看出,恒定最小主应力条件下,随着中间主应力σ2的增加,中间主应变ε2曲线与最小主应变ε3曲线从开始的重合到差异性越来越大,这是因为中间主应力方向上岩石裂隙的张开和扩展受到了更大的约束.在峰值应力位置,当σ3=40 MPa时,ε2从σ2=40 MPa时的0.77%减小到σ2=80 MPa时的0.07%,降低了约90.9%;同理,在σ3=45 MPa时,ε2从σ2=45 MPa时的1.00%减小到σ2=80 MPa时的0.18%,降低了约82%;在σ3=50 MPa时,ε2从σ2=50 MPa时的1.2%减小到σ2=80 MPa时的0.37%,降低了约69%.
从图 4中最小主应变ε3曲线可看出,恒定最小主应力条件下,由于中间主应力σ2的增加,岩样侧向膨胀主要沿最小主应力σ3方向[13].在峰值应力位置,当σ3=40 MPa时,ε3从σ2=40 MPa时的1.02%增大到σ2=80 MPa时的1.23%,增加了约20.6%;同理,在σ3=45 MPa时,ε3从σ2=45 MPa时的1.15%增大到σ2=80 MPa时的1.40%,增加了约21.7%;在σ3=50 MPa时,ε3从σ2=50 MPa时的1.32%增加到σ2=80 MPa时的1.68%,增加了约27.3%.
图 5给出了最小主应力σ3=45 MPa时不同中间主应力条件下深部砂岩偏应力(σ1-σ3)与体积应变(εV)关系曲线.可以看出,εV先是近似呈线性增加,当σ1增加到一定值后,体积应变逐渐偏离线性段,并且向负向弯曲,此时砂岩由压缩进入扩容状态[14].
图 5(Fig. 5)
 | 图 5 真三向应力作用下砂岩应力-体积应变曲线Fig.5 Stress-volumetric strain curves of sandstone under the true three-dimensional stress |
2.2 深部砂岩强度分界点的确定与阶段划分在真三向应力作用下,砂岩的变形特性有一定的自相似性,因此可选用最小主应力σ3=45 MPa,中间主应力σ2=60 MPa下的深部砂岩应力-应变曲线进行强度分界点的划分.岩石的强度分界点依次为闭合应力σcc、起裂应力σci与损伤应力σcd.当最大主应力达到闭合应力σcc时,岩石内部由孔隙和微裂纹压密状态向岩石的弹性阶段过渡.当最大主应力达到起裂应力σci时,岩石内部开始出现微裂纹,σci为岩石开始出现损失时的阈值.当最大主应力达到损伤应力σcd时,岩石内部产生裂纹的速度加快,且裂纹开始扩张、汇合、贯通.目前****对这三种应力的确定提出了多种方法,比较认可的有裂纹体积应变法和声发射法[15].本文采用裂纹体积应变法确定闭合应力σcc、起裂应力σci与损伤应力σcd.并通过这3个强度分界点将深部砂岩的应力-应变曲线划分为4个阶段:孔隙压密段Ⅰ(0~σcc)、弹性变形段Ⅱ(σcc~σci)、稳定裂纹扩展段Ⅲ(σci~σcd)和非稳定裂纹扩展段Ⅳ(σcd~σc).
将砂岩试样视为各向同性材料,砂岩颗粒连续均质,弹性阶段符合广义胡克定律.体积应变εV为岩石的总应变,因此体积应变εV为最大主应变ε1、中间主应变ε2和最小主应变ε3的三者之和:
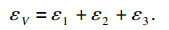 | (2) |
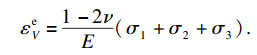 | (3) |
另一部分是岩样加载过程中新裂纹的张开和扩展形成的体积变化εVc:
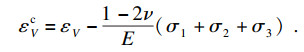 | (4) |
图 6(Fig. 6)
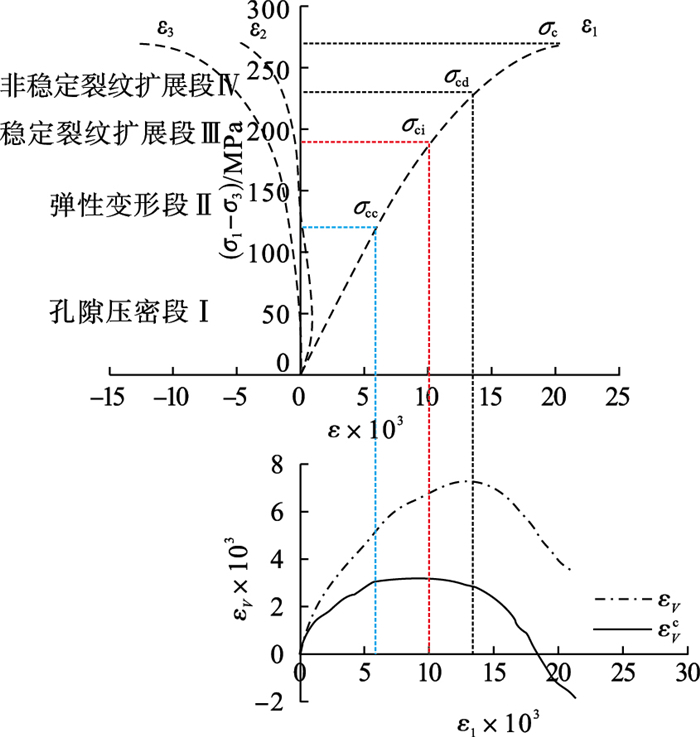 | 图 6 真三轴条件下砂岩强度分界点Fig.6 Sandstone strength boundary point under true triaxial conditions |
图 7为在不同的最小主应力σ3下,中间主应力σ2对深部砂岩起裂应力σci和损伤应力σcd的影响结果.从图中可以看出,在最小主应力σ3恒定的情况下,随着中间主应力σ2的增大,岩石的起裂应力σci和损伤应力σcd呈现近似线性增加的趋势;同时,在中间主应力σ2恒定的情况下,随着最小主应力σ3的增加,砂岩的起裂应力σci和损伤应力σcd呈现增加的趋势.
图 7(Fig. 7)
 | 图 7 中间主应力对起裂应力、损伤应力的影响Fig.7 Influence of intermediate principal stress on crack initiation stress and damage stress (a)—恒定σ3下,σ2对起裂应力σci的影响;(b)—恒定σ3下,σ2对损伤应力σcd的影响. |
3 深部砂岩强度特性分析3.1 峰值强度在真三轴应力条件下深部岩石的强度受3个主应力的影响,表现出复杂的特性.表 2为真三轴压缩下深部砂岩的峰值强度和破坏角.在最小主应力恒定的条件下,在一定范围内砂岩的峰值强度随中间主应力的增加而变大,中间主应力对砂岩起到保护作用.在σ3=40 MPa时,随着σ2从40 MPa增加到80 MPa,峰值强度σ1从268 MPa增加到了310 MPa,增加了15.67%;在σ3=45 MPa时,随着σ2从45 MPa增加到80 MPa,峰值强度σ1从285 MPa增加到了352 MPa,增加了23.51%;在σ3=50 MPa时,随着σ2从50 MPa增加到80 MPa,峰值强度σ1从306 MPa增加到了397 MPa,增加了29.74%.
表 2(Table 2)
| 表 2 真三轴压缩下砂岩的峰值强度和破坏角 Table 2 Peak strength and failure angles of sandstone under true triaxial compression |
在中间主应力恒定的条件下,在一定范围内砂岩的峰值强度随最小主应力的增大而变大.在σ2=60 MPa时,随着σ3从40 MPa增加到50 MPa,峰值强度σ1从293 MPa增加到了347 MPa,增加了18.43%;在σ2=80 MPa时,随着σ3从40 MPa增加到50 MPa,峰值强度σ1从310 MPa增加到了397 MPa,增加了28.06%.最小主应力对深部砂岩的强化作用高于中间主应力的作用.
3.2 力学参数根据深部砂岩应力-应变曲线,由式(5),式(6)计算出砂岩弹性模量E=22.9 GPa,泊松比ν=0.13.
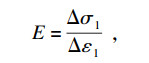 | (5) |
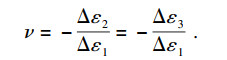 | (6) |
图 8(Fig. 8)
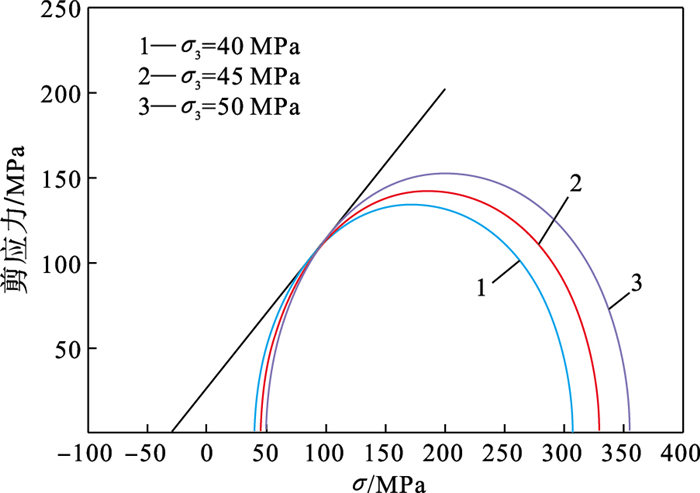 | 图 8 Mohr-Coulomb包络图Fig.8 Mohr-Coulomb envelope diagram |
为了探究不同深度对砂岩力学参数的影响,将本文砂岩与云南砂岩[16]、石柱砂岩[17]的弹性模量、黏聚力和摩擦角进行对比,见表 3.三种砂岩的主要矿物成分中石英和长石的含量有所差别,但砂岩本身是一种多孔介质,孔隙率较高.在这里假设砂岩的固体颗粒不会发生变形,砂岩的变形是由孔隙空间的变化引起的.因此可以忽略矿物成分对砂岩力学行为的影响.
表 3(Table 3)
| 表 3 不同深度下砂岩力学参数 Table 3 Sandstone mechanical parameters at different depths |
从表 3中可以看出,随着深度的增加,砂岩的弹性模量呈现出略微增大的趋势,这是因为岩石的埋深越深,所处的地应力也就越高,将岩石从深部取出后相当于一次高应力的卸载,应力卸载后会有一定的残余塑性应变.岩石的埋深越深,取出后的残余塑性应变也就越大.因此,当再次对岩石进行真三轴加载时,根据弹性模量计算式(5)可知,深部岩石在应力-应变曲线上计算得到的弹性模量要稍大于浅部岩石.随着深度的增加,砂岩的黏聚力和摩擦角均呈现出逐渐增大的趋势,这是由于深部岩石长期处于高地应力条件下,岩石颗粒骨架被压缩从而导致颗粒密度增加,更为致密,因此深部砂岩的黏聚力和摩擦角要稍大于浅部砂岩的黏聚力和摩擦角.
图 9为深部的本文砂岩与浅部的云南砂岩的应力-最大主应变对比图,从图中可知,在相同的最大主应力条件下,深部砂岩的最大主应变要小于浅部砂岩的最大主应变,这是因为深部砂岩长期处于高地应力环境中,岩石颗粒之间更为致密,孔隙空间略小,从深部取出后有一定的残余塑性应变,因此再次进行真三轴加载时深部砂岩的变形要小于浅部砂岩的变形.
图 9(Fig. 9)
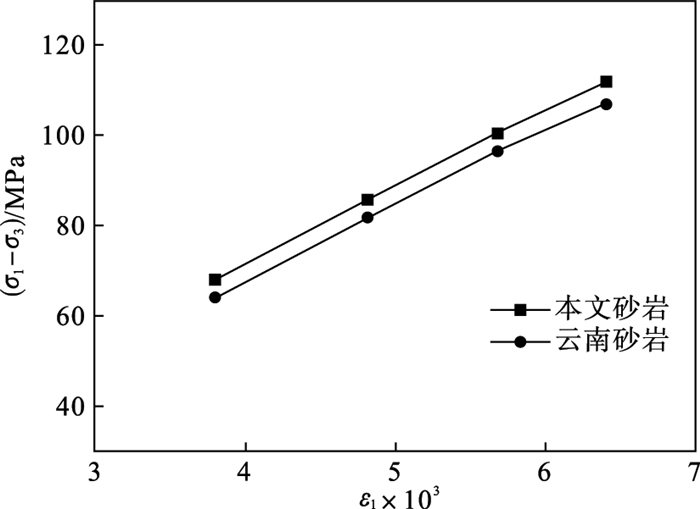 | 图 9 应力-最大主应变对比情况Fig.9 Stress-maximum principal strain comparison |
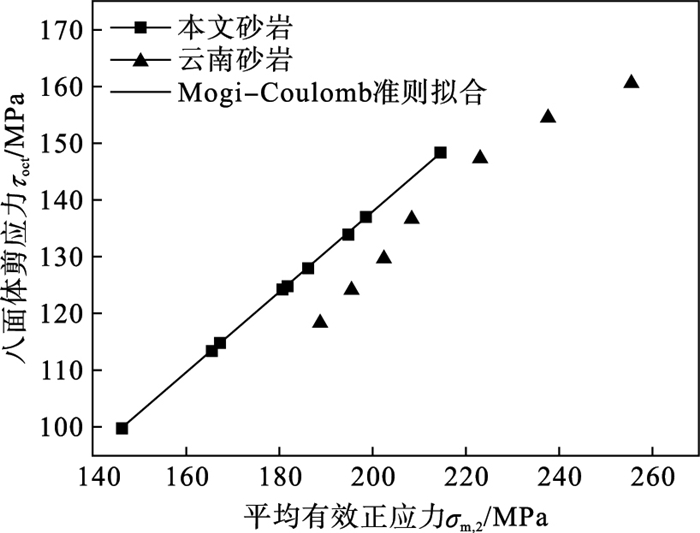
3.3 强度准则由于Mohr-Coulomb,Griffith,Hoek-Brown等经典的二维强度准则未反映中间主应力效应.因此本文采用Mogi-Coulomb准则和Drucker-Prager准则对真三向应力作用下不同深度的岩石强度进行对比分析.
Mogi-Coulomb强度准则可以表示为八面体剪应力τoct和剪切面上的平均有效正应力σm, 2之间的线性函数[18-19],表达式如下:
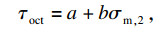 | (7) |
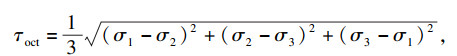 | (8) |
 | (9) |
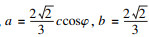
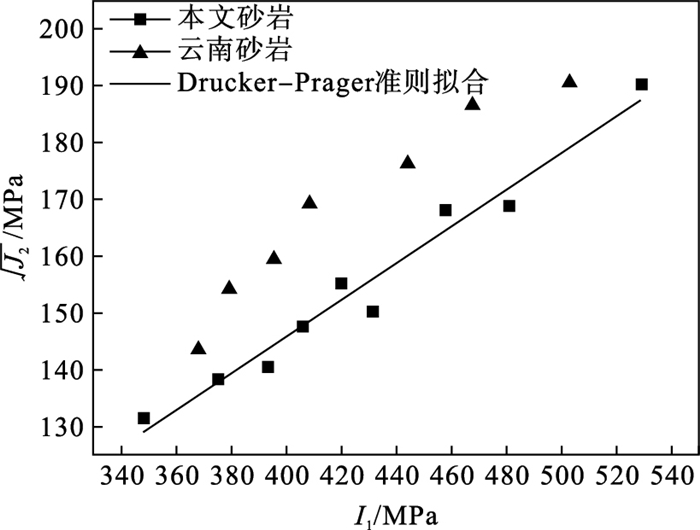
Drucker-Prager准则表示为
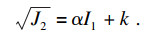 | (10) |
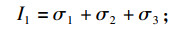 | (11) |
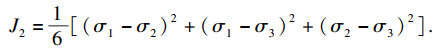 | (12) |
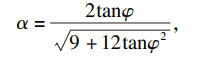 | (13) |
 | (14) |
图 10(Fig. 10)
 | 图 10 Mogi-Coulomb准则Fig.10 Mogi-Coulomb criterion |
图 11为Drucker-Prager准则描述深部的本文砂岩与浅部的云南砂岩的破坏强度曲线,从图 11中可以看出,浅部的云南砂岩的破坏强度的非线性要明显强于深部的本文砂岩.从图 10与图 11的拟合效果对比可以发现,对于深部砂岩,Mogi-Coulomb强度准则拟合的效果强于Drucker-Prager准则.这表明Mogi-Coulomb强度准则更适合描述真三向应力作用下的深部岩石的破坏强度特征.
图 11(Fig. 11)
 | 图 11 Drucker-Prager准则Fig.11 Drucker-Prager criterion |
4 结论1) 在真三向应力作用下,随着中间主应力的增加,深部砂岩中间主应变呈现减小的趋势,深部砂岩的起裂应力和损伤应力随之增加,砂岩的峰值强度呈现增大的趋势.
2) 在真三向应力作用下,随着砂岩深度的增加,砂岩的弹性模量、黏聚力和摩擦角均呈现增大的趋势.这是由于深部的砂岩长期处于高地应力条件下,砂岩颗粒骨架被压缩从而导致颗粒密度增加,更为致密.浅部砂岩的峰值破坏强度的八面体剪应力与平均有效正应力表现为非线性关系,而深部砂岩的峰值破坏强度的八面体剪应力与平均有效正应力表现为线性关系,且Mogi-Coulomb准则更适用于表述深部砂岩破坏时的强度特征.
参考文献
| [1] | Brace W F, Kohlstedt D L. Limits on lithospheric stress imposed by laboratory experiments[J]. Journal of Geophysical Research, 1980, 85(11): 6248-6252. |
| [2] | Mogi K. Fracture and flow of rocks under high triaxial compression[J]. Journal of Geophysical Research, 1971, 76(5): 1255-1269. DOI:10.1029/JB076i005p01255 |
| [3] | Feng X T, Kong R, Yang C X, et al. A three-dimensional failure criterion for hard rocks under true triaxial compression[J]. Rock Mechanics and Rock Engineering, 2019, 53(12): 103-111. |
| [4] | Ma X, Rudnicki J W, Haimson B C. Failure characteristics of two porous siltstones subjected to true triaxial stresses: applied through a novel loading path[J]. Journal of Geophysical Research, 2017, 122(4): 2525-2540. DOI:10.1002/2016JB013637 |
| [5] | Ma X, Rudnicki J W, Haimson B C. The application of a Matsuoka-Nakai-Lade-Duncan failure criterion to two porous sandstones[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 92: 9-18. DOI:10.1016/j.ijrmms.2016.12.004 |
| [6] | Haimson B C, Chang C. A new true triaxial cell for testing mechanical properties of rock, and its use to determine rock strength and deformability of Westerly granite[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1): 285-296. |
| [7] | Zhao X G, Wang J, Cai M, et al. Influence of unloading rate on the strainburst characteristics of Beishan granite under true-triaxial unloading conditions[J]. Rock Mechanics & Rock Engineering, 2014, 47(2): 467-483. |
| [8] | Feng X T, Zhang X, Kong R, et al. A novel Mogi type true triaxial testing apparatus and its use to obtain complete stress-strain curves of hard rocks[J]. Rock Mechanics and Rock Engineering, 2016, 49(5): 1649-1662. DOI:10.1007/s00603-015-0875-y |
| [9] | 廖伟, 刘国良, 陈如鹤, 等. 气藏型地下储气库动态密封性评价——以新疆H地下储气库为例[J]. 天然气工业, 2021, 41(3): 133-141. (Liao Wei, Liu Guo-liang, Chen Ru-he, et al. Evaluation on the dynamic sealing capacity of underground gas storages rebuilt from gas reservoirs: a case study of Xinjiang H underground gas storage[J]. Natural Gas Industry, 2021, 41(3): 133-141.) |
| [10] | Biot M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. DOI:10.1063/1.1712886 |
| [11] | 乔丽苹, 王者超, 李术才. 基于Tight gas致密砂岩储层渗透率的有效应力特性研究[J]. 岩石力学与工程学报, 2011, 30(7): 1422-1427. (Qiao Li-ping, Wang Zhe-chao, Li Shu-cai. Effective stress law for permeability of Tight gas[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1422-1427.) |
| [12] | 曹锡秋. 新疆某地衰竭气藏地下储气库地应力特征研究[D]. 北京: 中国地质大学(北京), 2013. (Cao Xi-qiu. A research on reservoir geomechanic features of a gas storage in Xinjiang after natural deletion[D]. Beijing: China University of Geosciences(Bejing), 2013. ) |
| [13] | Li Z L, Wang L G, Lu Y L, et al. Experimental investigation on true triaxial deformation and progressive damage behaviour of sandstone[J]. Scientific Reports, 2019, 9(1): 3386. DOI:10.1038/s41598-019-39816-9 |
| [14] | 尹光志, 鲁俊, 李星, 等. 中间主应力对砂岩扩容及强度特性影响[J]. 煤炭学报, 2017, 42(4): 879-885. (Yin Guang-zhi, Lu Jun, Li Xing, et al. Influence of intermediate principal stress on dilation and strength characteristics of sandstone[J]. Journal of China Coal Society, 2017, 42(4): 879-885.) |
| [15] | 陈世万, 杨春和, 王贵宾, 等. 不同围压下花岗岩σcc, σci和σcd的确定[J]. 东北大学学报(自然科学版), 2016, 37(12): 1789-1793, 1799. (Chen Shi-wan, Yang Chun-he, Wang Gui-bin, et al. Experimental study on the determination method of σcc, σci and σcd for granite under different confining pressures[J]. Journal of Northeastern University(Natural Science), 2016, 37(12): 1789-1793, 1799.) |
| [16] | Feng X T, Kong R, Zhang X W, et al. Experimental study of failure differences in hard rock under true triaxial compression[J]. Rock Mechanics and Rock Engineering, 2019, 52(7): 2109-2122. DOI:10.1007/s00603-018-1700-1 |
| [17] | Lu J, Yin G Z, Zhang D M, et al. True triaxial strength and failure characteristics of cubic coal and sandstone under different loading paths[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 135: 104439. DOI:10.1016/j.ijrmms.2020.104439 |
| [18] | Vachaparampil A, Ghassemi A. Failure characteristics of three shales under true-triaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 100: 151-159. DOI:10.1016/j.ijrmms.2017.10.018 |
| [19] | Singh A, Rao K S, Ayothiraman R. An analytical solution to wellbore stability using Mogi-Coulomb failure criterion[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2019, 11(6): 1211-1230. DOI:10.1016/j.jrmge.2019.03.004 |
