杨金金^1,2, 王者超^1,2, 乔丽苹^1,2, 李崴^1,2
1. 东北大学 资源与土木工程学院，辽宁 沈阳 110819;
2. 东北大学 深部金属矿山安全开采教育部重点实验室，辽宁 沈阳 110819
收稿日期：2022-02-23
基金项目：国家自然科学基金资助项目(42177157)。
作者简介：杨金金(1988-)，女，河南巩义人，东北大学博士研究生;
王者超(1980-)，男，山东高唐人，东北大学教授，博士生导师。

摘要：为探究粗糙裂隙内细观流动结构演化过程及影响因素，用COMSOL Multiphysics可视化了不同条件下粗糙裂隙渗流场中的流动结构.基于响应面法建立多因素与涡旋结构面积的二阶多项式回归方程，并进行了方差分析和显著性检验，探讨多因素间交互作用对裂隙内涡旋结构的影响.结果表明：粗糙裂隙内细观流动结构演化过程包括涡旋结构发生、发展、破裂和稳定；回归模型的显著性和适应性良好，可以较为有效确定影响因素的重要程度；多因素交互作用对涡旋结构的影响程度中平均开度最大，速度次之，裂隙粗糙度最小.研究结果对揭示裂隙非线性渗流细观机理有重要意义.
关键词：岩体裂隙粗糙度涡旋结构演化特征响应面
Analysis of Evolution Characteristics and Influencing Factors of Vortex Structure in Rough-Walled Fracture
YANG Jin-jin^1,2, WANG Zhe-chao^1,2, QIAO Li-ping^1,2, LI Wei^1,2
1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Zhe-chao, E-mail: wangzhechao@mail.neu.edu.cn.

Abstract: To study the evolution characteristics and influencing factors of vortex structure in rough-walled fracture, COMSOL Multiphysics is used to simulate the flow field under different conditions, and the meso-flow structure is visualized. Based on the response surface methodology (RSM), a second-order polynomial regression equation is established, and the variance analysis and significance test of the regression equation are carried out, and the effect of multi-factor interaction on vortex structure is discussed. The results show that the evolution process of meso-flow structure in rough-walled fracture includes the generation, development, rupture and stability. The regression model has good significance and adaptability, which can effectively determine the significance of influencing factors. The influencing degree of multi-factor interaction on vortex structure is as follows: average aperture is the largest, followed by velocity, and roughness is the smallest. The results are of great significance to reveal the mesoscopic mechanism of nonlinear seepage in fractures.
Key words: rock fractureroughnessvortex structureevolution characteristicsresponse surface
天然岩体是经历长期地质构造作用形成的，内部由岩块和裂隙共同组成.因具有强透水性，裂隙成为了地下水流动的主要通道，其对页岩气开采、地下水封油库、地热资源开发等领域的渗流问题具有关键控制作用.因此对岩体裂隙中流体流动特性进行深入研究对指导地下工程建设和促进地质科学理论发展具有重要意义.
目前，研究岩体裂隙渗流规律的基本理论为线性立方定律，该定律是基于光滑平行板模型和达西层流假设建立的^[1].但绝对光滑平行的裂隙几乎不存在，且天然岩体裂隙表面形貌总是粗糙迂曲，开度分布随机性很大，还可能有充填物和接触，使岩体裂隙渗流规律偏离线性立方定律而呈现非线性特征^[2-3].为探究非线性渗流特性与裂隙几何特征的关系，Liu等^[4]用节理粗糙度系数(joint roughness coefficient，JRC)表征裂隙表面粗糙度，开展了大范围雷诺数条件下粗糙单裂隙渗流试验，发现裂隙渗流的非线性程度与JRC呈正相关，并建立了考虑JRC的单裂隙渗流模型.Xiong等^[5]研究了接触对天然粗糙三维裂隙非线性渗流特性的影响，发现随着雷诺数增加，裂隙接触和粗糙度容易导致复杂的非线性流动现象.Dong等^[6]采用一种考虑局部开度权重的方法对具有分形特征的对称裂隙渗流特性进行了数值分析，发现与等开度裂隙相比，变开度裂隙存在明显非线性渗流特性，并提出了考虑开度变化的局部立方律.周新等^[7]用分形维数表征裂隙表面粗糙度，建立了基于分形维数和开度均值、标准差的非线性渗流模型.除此之外，还有部分研究者关注了外部因素对非线性渗流特性的影响，如剪切位移、法向应力和围压等.Javadi等^[8]研究了剪切过程中粗糙裂隙渗流特征由线性转向非线性的临界雷诺数，给出了一种定量非线性流动转捩的判据.Chen等^[9]开展了不同围压下花岗岩裂隙渗流试验，发现惯性效应、裂隙膨胀和固水相互作用诱发的三种典型的非线性流动行为.Zhang等^[10]通过数值计算研究了剪切位移、粗糙度和压力梯度对自仿射裂隙非线性流动的综合影响，发现裂隙内非线性渗流特征随着剪切位移和压力梯度的增加愈加显著.上述研究裂隙内流体介质多为牛顿流体，还有****研究了裂隙内非牛顿流体的渗流特征，如王者超等^[11]进行了大范围压力梯度下不同流变参数的宾汉姆流体在粗糙裂隙中的渗流特性，发现宾汉姆流体的渗流特性受表面粗糙度和流变参数的影响十分显著.
上述研究主要从宏观层面对粗糙裂隙内非线性渗流特性进行分析.与此同时，有部分****的研究表明粗糙裂隙内宏观非线性渗流现象与细观涡旋结构的出现密切相关.如Zhou等^[12]用格子玻尔兹曼方法(lattice Boltzmann method，LBM)求解了不同水动力学条件下粗糙裂隙的渗流场，发现当惯性效应不可忽略时宏观非线性层流的出现与裂隙中涡旋结构的增长有关，其剪切过程增强了这种非线性现象.Guo等^[13-14]开展了粗糙人工裂隙的微流场渗流试验，发现水流涡旋结构束窄了主流动通道的过流面积，裂隙整体水力传导能力下降，使得水流流动表现出宏观非线性现象.综上分析，尽管对岩体粗糙裂隙的非线性渗流特征进行了很好的揭示，但在不同条件下对其内部水流涡旋结构的发生条件、演化特征及其影响因素还缺乏深入研究.
针对以上问题，本文用COMSOL Multiphysics模拟不同条件下均匀粗糙裂隙内渗流场，对渗流场中细观流动结构进行可视化，分析均匀粗糙裂隙内细观涡旋结构演化特征，确定影响涡旋结构演化的因素.基于响应面法，建立多因素与涡旋结构面积的回归方程，对方程进行方差分析和显著性检验，探讨因素间的交互作用对裂隙内涡旋结构面积的影响.
1 研究方法1.1 数值分析粗糙裂隙中不可压缩、黏滞系数恒定的牛顿流体稳态流动满足Navier-Stokes方程和连续性方程：

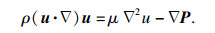(1)

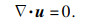(2)

式中：ρ为流体密度；u为速度矢量；μ为动力黏滞系数；P为流体压力；?为哈密顿算子.研究中流体为水，对应的ρ和μ分别取1 000 kg/m³，0.001 Pa·s.
COMSOL Multiphysics是模拟流体流动的有效工具，它不仅可以灵活添加边界条件，而且能够对流体的微观流动行为进行可视化分析.因此本文用其求解Navier-Stokes方程，模拟粗糙裂隙中涡旋结构演化特征.
如图 1所示，粗糙裂隙壁面为无滑移边界条件，进口为速度边界，速度为0.001~9 m/s，出口为压力边界，压力为0 Pa.考虑求解精度、计算成本和求解所需时间，裂隙模型网格由COMSOL模拟器物理场控制，同时使用三角形网格和矩形网格，网格在进口、出口和壁面局部加密，其他区域采用较为稀疏的网格.粗糙裂隙模型长30 mm，每个模型对应有3个平均开度，分别为0.98，1.48和1.97 mm，壁面粗糙元均为三角形，具体见表 1.
图 1(Fig. 1)

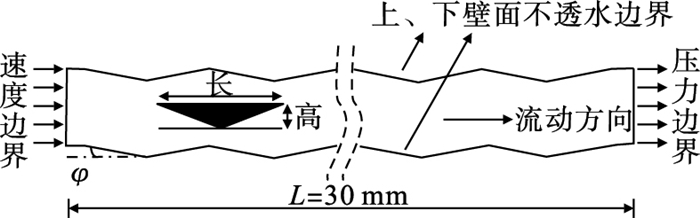图 1 粗糙裂隙模型和边界条件示意图Fig.1 Schematic diagram of rough-walled fracture model and boundary conditions

表 1(Table 1)

表 1 粗糙裂隙数值模型参数Table 1 Numerical model parameters of rough-walled fractures 裂隙模型 A1 26.57 1 0.25 A2 14.04 1 0.5 A3 9.46 1 1 B1 45 2 0.25 B2 26.57 2 0.5 B3 18.43 2 1 C1 63.43 3 0.25 C2 45 3 0.5 C3 33.69 3 1

表 1 粗糙裂隙数值模型参数 Table 1 Numerical model parameters of rough-walled fractures

1.2 试验分析1.2.1 单因素单一影响因素主要考察某因素对涡旋结构演化特征的影响，其他因素保持不变.本研究在平均开度和裂隙粗糙度不变时，进口速度在0.1~9 m/s内取10组.在平均开度和速度不变时，裂隙粗糙度在0.162~0.172内取6组.在进口速度和裂隙粗糙度不变时，平均开度在0.25~2 mm内取7组.研究中裂隙粗糙度用统计参数一阶导数均方根Z₂表征，其值越大表明裂隙壁面越粗糙^[4].
1.2.2 响应面法响应面法(reponse surface method, RSM)是对指定空间内的样本点集合进行有限试验设计，进而用回归出的输出变量的全局逼近来代替真实值.在某个范围的设计变量通常采用低阶多项式近似响应面模型，如一阶和二阶多项式近似模型，二者的基函数分别为

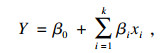(3)

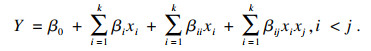(4)

式中：Y表示预测响应面；x_i和x_j为独立设计变量；k为设计变量的数量；β₀，β_i，β_ii分别是偏移项、线性偏移和二阶偏移系数；β_ij是交互作用系数.
实际上大多数RSM问题都可用以上两个模型中的一个或两个解决.本次主要采用二阶多项式近似响应面模型，确定裂隙内涡旋结构演化主要影响因素.
1.2.3 试验设计箱形本肯设计(box-Behnken design，BBD)是响应面法常用设计方法，适用于2~5个因素.BBD设计法每个因素取3个水平，以(-1，0，1)编码，以0为中心点，+1，-1分别是立方点相对应的高值和低值.以三因素为例，BBD设计的试验点分布情况如图 2所示.
图 2(Fig. 2)

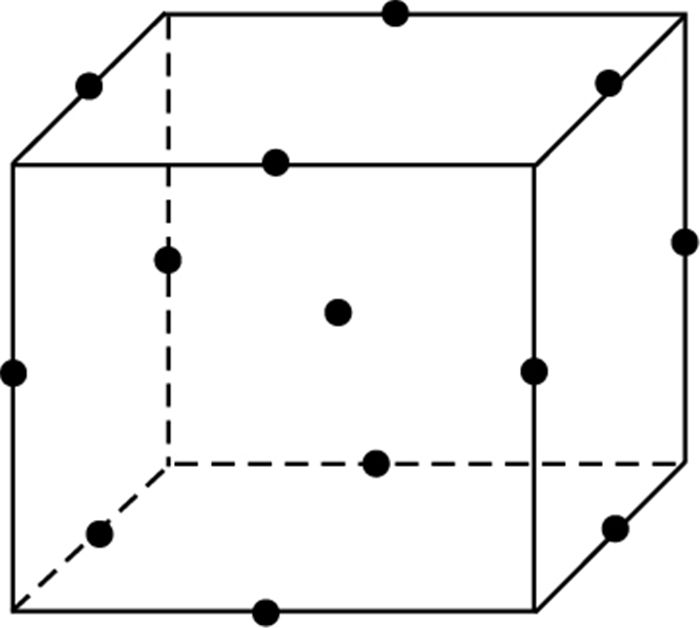图 2 BBD试验设计试验点分布情况Fig.2 Distribution of test sites in BBD experiment design

本次采用Design-Export软件中的Box-Behnken组合设计法，结合单因素水平分析结果设计响应面试验因素和水平，遵循优先选取对涡旋结构影响显著的因素，水平值的设计原则遵循响应值(涡旋结构面积)的最大值或涡旋结构面积的趋势突变处对应的水平值为该水平的中间值.涡旋结构面积是指涡旋结构与主流动通道的交界面与裂隙壁面围成的封闭图形的面积，计算方法可参考文献[15-16].本次设计因素、水平值及其编码条件见表 2.编码后经软件设计，共计需要17次计算，包括零点计算5次以及预估误差和析因点计算12次.
表 2(Table 2)

表 2 BBD试验设计因素与水平Table 2 Factors and levels of BBD experiment design 因素 变量 水平编码 -1 0 1 进口速度/(m·s-1) x1 0.3 3 9 裂隙粗糙度 x2 0.162 0.167 0.171 平均开度/mm x3 0.5 1.0 1.5

表 2 BBD试验设计因素与水平 Table 2 Factors and levels of BBD experiment design

2 结果与分析2.1 涡旋结构演化特征图 3展示了在不同水力条件下，平均开度为0.98 mm的裂隙模型C3内涡旋结构的演化过程.在进口速度较小时，裂隙内流线整体上分布较为均匀，没有明显紊乱，也没有涡旋结构发生(图 3a)；速度逐渐增大，在裂隙壁面处流线局部小范围开始偏离主流向，发生涡旋结构(图 3b)；随着速度不断增大，壁面处较大范围流线显著偏离主流向，形成完整的逐渐增大的封闭涡旋结构(图 3c，图 3d)；速度继续增大，初次形成的封闭涡旋结构破裂(图 3e)；速度增大至1 m/s后，破裂后的涡旋结构发展成熟并稳定(图 3f).在涡旋结构演化过程中，涡旋结构首先沿展向扩张形成展向涡，随后展向涡沿主流动方向移动形成流向涡，同时涡核顺应涡旋结构形态变化先沿展向移动后沿流向移动.受流动方向影响，涡旋结构演化过程中上边界处涡旋结构始终逆时针旋转，下边界处涡旋结构始终顺时针旋转.在演化过程中，涡旋结构始终粘附在裂隙壁面，这是因为在固体壁面附近的边界层中，流体速度由主流的速度值快速下降为零，导致薄层中速度梯度变化很大，形成了明显的涡旋运动.
图 3(Fig. 3)

图 3 裂隙模型C3内涡旋结构演化过程中流线分布Fig.3 Streamline distribution of vortex structure evolution in C3 fracture model (a)—无涡旋结构；(b)—涡旋结构发生；(c)，(d)—涡旋结构发展；(e)—涡旋结构破裂；(f)—涡旋结构稳定.

表 3展示了不同裂隙模型内涡旋结构演化过程及对应的临界速度.对裂隙模型A3，B3和C3，涡旋结构经历了相对充分完整的演化，其他裂隙模型内涡旋结构演化过程会有所缺失.如裂隙模型B2，涡旋结构仅经历了发生、发展，几乎都没有破裂和稳定.裂隙模型A1发生了涡旋结构，此后涡旋结构经过充分发展，没有破裂就稳定了下来.在裂隙模型平均开度和粗糙元长度相同时，随着粗糙元高度增大和起伏角减小，在进口速度较小时就能发生涡旋结构，且涡旋结构演化过程趋于完整.结合表 1，在平均开度和粗糙元高度相同时，随着粗糙元长度和起伏角增大，在进口速度足够大时才会在裂隙内激发出涡旋结构，涡旋结构演化过程亦趋于完整.另外，对粗糙元尺寸相同的裂隙模型，随着平均开度增大，涡旋结构发生时进口速度逐渐减小，演化过程整体逐渐缺失.
表 3(Table 3)

表 3 裂隙模型内涡旋结构演化过程及临界速度Table 3 Evolution process of vortex structure and critical velocity in fracture models 裂隙模型 临界速度/(m·s-1) 涡旋发生 涡旋破裂 涡旋稳定 0.98 0.05 — 0.4 A1 1.48 0.05 — 0.6 1.97 0.05 — 0.7 0.98 ＜0.001 — 3 A2 1.48 ＜0.001 — 4 1.97 ＜0.001 — 4.5 0.98 ＜0.001 0.3 1.5 A3 1.48 ＜0.001 1 2 1.97 ＜0.001 — 3 0.98 0.2 — 1 B1 1.48 0.2 — 2 1.97 0.2 — 3.5 0.98 0.02 0.9 — B2 1.48 0.02 — — 1.97 0.02 — — 0.98 ＜0.001 0.08 0.2 B3 1.48 ＜0.001 0.25 0.9 1.97 ＜0.001 1.5 4 0.98 0.4 — 2 C1 1.48 0.4 — 3 1.97 0.4 — 4.5 0.98 0.06 0.9 — C2 1.48 0.05 2.5 — 1.97 0.05 — — 0.98 0.01 0.2 1 C3 1.48 0.008 0.2 1.5 1.97 0.005 0.25 —

表 3 裂隙模型内涡旋结构演化过程及临界速度 Table 3 Evolution process of vortex structure and critical velocity in fracture models

综上分析，裂隙内涡旋结构完整演化过程包括发生、发展、破裂和稳定阶段，这样演化过程中涡旋结构数量可能会经历从无到有、增多或减少的剧烈变化，直观上看其演化过程与流线的变形有密切联系.但是，不是每个裂隙模型内涡旋结构都会经历完整的演化过程，不同裂隙模型内涡旋结构演化过程存在差异性.另外，通过对均匀粗糙裂隙内涡旋结构演化特征分析，初步发现影响涡旋结构演化特征的因素主要有进口速度、裂隙粗糙度和平均开度.
2.2 涡旋结构演化的影响因素2.2.1 单因素影响设置不同进口速度，选取具有不同粗糙度和平均开度的裂隙模型，绘制裂隙内涡旋结构面积与3个单因素的变化曲线，如图 4所示.随着进口速度增加，涡旋结构面积逐渐增大，在进口速度增加至3 m·s^-1后，涡旋结构面积开始趋于稳定(图 4a).随着裂隙粗糙度的增加，涡旋结构面积逐渐增大，在裂隙粗糙度增加至0.169后，涡旋结构面积相对稳定(图 4b).在图 4a和图 4b中，裂隙进口速度较大或粗糙度较高时，涡旋结构面积稍微下降，这是由裂隙内涡旋结构发生、发展稳定后，继续增加裂隙粗糙度和进口速度，稳定后的涡旋结构几何形态破裂引起的.随着裂隙平均开度增加，涡旋结构面积逐渐增大，没有明显稳定趋势，这与宏观流动规律趋势近似(图 4c).因此，在进行分析时，进口速度取0.3~9 m·s^-1，裂隙粗糙度取0.162~0.171，平均开度取0.5~1.5 mm.
图 4(Fig. 4)

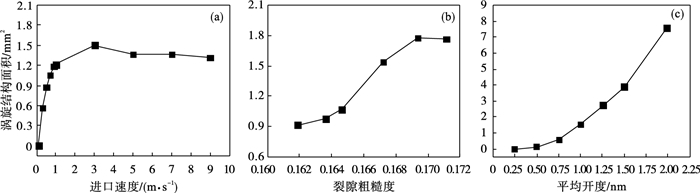图 4 不同因素对裂隙内涡旋结构面积的影响Fig.4 Effect of different factors on the area of vortex structure in fractures (a)—平均开度1 mm，裂隙粗糙度0.167；(b)—平均开度1 mm，进口速度3 m·s-1；(c)—进口速度3 m·s-1，裂隙粗糙度0.167.

2.2.2 多因素影响涡旋结构面积的回归方程为

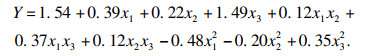(5)

对回归方程进行方差分析及显著性检验，结果见表 4.由表 4可见：模型的F值为76.81，P＜0.000 1，说明模型非常显著.模型的失拟项中F值为5.46，P=0.067 3>0.05，失拟项不显著，说明拟合模型良好，其预测值可以较为有效确定裂隙内涡旋结构面积大小的影响因素的重要性.因素水平中的进口速度(x₁)和平均开度(x₃)在一阶项、二阶项和平方项中的P值均小于0.05，具有统计学差异，说明进口速度和平均开度是裂隙内涡旋结构面积的显著影响因素.
表 4(Table 4)

表 4 响应值回归方程的方差分析Table 4 Analysis of variance of regression equation of response value 类型 SS DF MS F值 P 显著性 模型 21.53 9 2.39 76.81 ＜0.000 1 非常显著 x1 1.19 1 1.19 38.13 0.000 5 显著 x2 0.383 9 1 0.383 9 12.33 0.009 8 显著 x3 17.71 1 17.71 568.59 ＜0.000 1 非常显著 x1x2 0.053 2 1 0.053 2 1.71 0.232 4 不显著 x1x3 0.546 9 1 0.546 9 17.56 0.004 1 显著 x2x3 0.056 6 1 0.056 6 1.82 0.219 5 不显著 x12 0.973 4 1 0.973 4 31.25 0.000 8 显著 x22 0.163 9 1 0.163 9 5.26 0.055 5 不显著 x32 0.511 6 1 0.511 6 16.42 0.004 9 显著 残差 0.218 0 7 0.031 1 — — — 失拟项 0.175 2 3 0.058 4 5.46 0.067 3 不显著 纯误差 0.042 8 4 0.010 7 — — — 注：SS为变差平方和；DF为自由度；MS为均方.

表 4 响应值回归方程的方差分析 Table 4 Analysis of variance of regression equation of response value

对拟合出的回归方程进行误差统计分析，发现响应值Y的相关系数R²等于0.990，接近1，相关性好，表明模型拟合良好；调整后相关系数0.977的平方与预测相关系数0.898的平方之差为0.15，满足小于0.2的要求，说明回归模型能识别裂隙内涡旋结构面积的显著影响因素；变异系数(coefficient of variation，CV)为12.76%，满足10%＜CV＜20%，说明回归模型整体具有弱变异性，可信度和精确度符合标准；模型精度为27.68>4，满足检验要求.图 5是回归模型中涡旋结构面积的残差、预测值和实际值分布图.残差分布、预测值同实际值的分布线性良好，残差与预测值之间关系以中心线为准分布无规律但相对均匀.以上分析均表明利用响应面法拟合影响裂隙内涡旋结构面积的回归模型适应性较好.
图 5(Fig. 5)

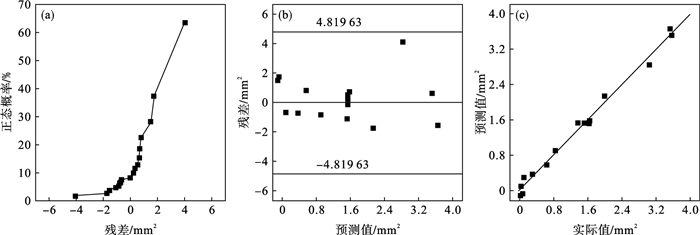图 5 涡旋结构面积的残差、预测值和实际值分布Fig.5 Residual, predicted and actual distribution of the area of vortex structure (a)—残差的正态概率分布；(b)—残差与预测值关系；(c)—预测值与实际值关系.

图 6为不同因素间交互作用的三维响应面和等高线图，考察在其他因素固定不变的情况下，两个因素间的交互作用对裂隙内涡旋结构面积的影响.等高线的形状趋于椭圆表明二者间的交互作用显著，趋于圆形则表明二者间的交互作用不显著，等高线轮廓线的曲率越大相互作用越强^[17-18].图 6a中进口速度和裂隙粗糙度对涡旋结构面积共同作用的等高线图形状为椭圆形，说明进口速度和裂隙粗糙度间有强烈的交互作用，改变裂隙粗糙度，最大涡旋结构面积对应的最佳进口速度会发生相应改变；从三维响应面图可以看出，涡旋结构面积随进口速度的增大而增大，随裂隙粗糙度的增加而增加，增加速率逐渐减小，这与单因素实验结果基本一致，证明了所建模型的可靠性.进口速度和裂隙粗糙度的响应面趋于平坦，但整体上裂隙粗糙度的影响略高于进口速度.图 6b是进口速度与平均开度共同作用的等高线图和响应面图，二者之间的作用显著，在涡旋结构面积不变时增加平均开度可适当降低进口速度，曲面陡峭说明几何平均开度的影响大于进口速度的影响.由图 6c可知，当进口速度不变时，裂隙粗糙度和平均开度的响应面曲线也较陡峭，平均开度的影响大于裂隙粗糙度的影响，二者也具有交互作用，但是与图 6b相比，进口速度对平均开度的交互作用比裂隙粗糙度对平均开度的交互作用强烈.
图 6(Fig. 6)

图 6 不同因素间交互作用对裂隙内涡旋结构面积的影响Fig.6 Effect of different factors interaction on the area of vortex structure in fractures (a)—进口速度和裂隙粗糙度对涡旋面积的影响；(b)—进口速度和平均开度对涡旋面积的影响；(c)—裂隙粗糙度和平均开度对涡旋面积的影响.

3 结论1) 在进口速度逐渐增大过程中，裂隙内完整涡旋结构演化过程包括发生、发展、破裂和稳定阶段，其演化过程与流线的变形有密切联系，具有不同几何特征和水动力学条件的裂隙模型内涡旋结构演化过程存在差异性.
2) 随着进口速度和裂隙粗糙度增加，涡旋结构面积均是先增大后趋于稳定.随着平均开度增加，涡旋结构面积逐渐增大，但无明显稳定趋势.
3) 二次多项式回归模型的显著性和适应性良好，可以较为有效地确定涡旋结构影响因素的显著程度.
4) 多因素交互作用对涡旋结构面积的影响程度为：平均开度最大，进口速度次之，裂隙粗糙度最小.
参考文献

[1]	Zimmerman R W, Bodvarsson G S. Hydraulic conductivity of rock fractures[J]. Transport in Porous Media, 1996, 23(1): 1-30.
[2]	Konzuk J S, Kueper B H. Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture[J]. Water Resources Research, 2004, 40(2): 1-17.
[3]	Chen Z, Qian J Z, Zhan H B, et al. Effect of roughness on water flow through a synthetic single rough fracture[J]. Environmental Earth Sciences, 2017, 76(4): 1-17.
[4]	Liu J, Wang Z, Qiao L, et al. Transition from linear to nonlinear flow in single rough fractures: effect of fracture roughness[J]. Hydrogeology Journal, 2021, 29: 1343-1353. DOI:10.1007/s10040-020-02297-6
[5]	Xiong F, Jiang Q, Ye Z, et al. Nonlinear flow behavior through rough-walled rock fractures: the effect of contact area[J]. Computers and Geotechnics, 2018, 102: 179-195. DOI:10.1016/j.compgeo.2018.06.006
[6]	Dong J, Ju Y. Quantitative characterization of single-phase flow through rough-walled fractures with variable apertures[J]. Geomechanics and Geophysics for Geo-energy and Geo-resources, 2020, 6(3): 1-14. DOI:10.1007/s40948-020-00166-w
[7]	周新, 盛建龙, 叶祖洋, 等. 岩体粗糙裂隙几何特征对其Forchheimer型渗流特性的影响[J]. 岩土工程学报, 2021, 43(11): 2075-2083. (Zhou Xin, Sheng Jian-long, Ye Zu-yang, et al. Effects of geometrical feature on Forchheimer-flow behavior through rough-walled rock fractures[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2075-2083.)
[8]	Javadi M, Sharifzadeh M, Shahriar K, et al. Critical Reynolds number for nonlinear flow through rough-walled fractures: the role of shear processes[J]. Water Resources Research, 2014, 50(2): 1789-1804. DOI:10.1002/2013WR014610
[9]	Chen Y, Zhou J, Hu S, et al. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J]. Journal of Hydrology, 2015, 529: 993-1006. DOI:10.1016/j.jhydrol.2015.09.021
[10]	Zhang Y, Chai J, Cao C, et al. Combined influences of shear displacement, roughness, and pressure gradient on nonlinear flow in self-affine fractures[J]. Journal of Petroleum Science and Engineering, 2021, 198: 108229. DOI:10.1016/j.petrol.2020.108229
[11]	王者超, 张浩炜, 龙求喜, 等. 岩体裂隙中宾汉姆流体渗流模型[J]. 东北大学学报(自然科学版), 2021, 42(10): 1459-1466. (Wang Zhe-chao, Zhang Hao-wei, Long Qiu-xi, et al. Bingham fluid seepage model in rock fractures[J]. Journal of Northeastern University(Natural Science), 2021, 42(10): 1459-1466. DOI:10.12068/j.issn.1005-3026.2021.10.013)
[12]	Zhou J, Wang M, Wang L, et al. Emergence of nonlinear laminar flow in fractures during shear[J]. Rock Mechanics and Rock Engineering, 2018, 51(11): 3635-3643.
[13]	Guo P, Wang M, He M, et al. Experimental investigation on macroscopic behavior and microfluidic field of nonlinear flow in rough-walled artificial fracture models[J]. Advances in Water Resources, 2020, 142: 103637.
[14]	Guo P, Wang M, Gao K, et al. Influence of fracture surface roughness on local flow pattern: visualization using a microfluidic field experiment[J]. Hydrogeology Journal, 2020, 28: 2373-2385.
[15]	Zou L, Jing L, Cvetkovic V. Roughness decomposition and nonlinear fluid flow in a single rock fracture[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 75: 102-118.
[16]	Zhou J, Wang L, Chen Y, et al. Mass transfer between recirculation and main flow zones: is physically based parameterization possible?[J]. Water Resources Research, 2019, 55(1): 345-362.
[17]	Mukhopadhyay S, Mukherjee S, Adnan N F, et al. Ammonium-based deep eutectic solvents as novel soil washing agent for lead removal[J]. Chemical Engineering Journal, 2016, 294: 316-322.
[18]	Mohammadi R, Mohammadifar M A, Mortazavian A M, et al. Extraction optimization of pepsin-soluble collagen from eggshell membrane by response surface methodology(RSM)[J]. Food Chemistry, 2016, 190: 186-193.