
 , 张淼, 张石
, 张淼, 张石 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169
收稿日期:2022-02-16
基金项目:国家自然科学基金资助项目(U21A20387);中央高校基本科研业务费专项资金资助项目(N171604011)。
作者简介:王宝宇(1981-), 男, 辽宁朝阳人, 东北大学博士研究生;
张石(1963-), 男, 辽宁抚顺人, 东北大学教授, 博士生导师。
摘要:为了提高超声虚源次序波束形成的成像分辨率, 提出一种基于虚源的延时乘累加波束形成算法, 即VS-DMAS(delay multiply and sum beamforming based on virtual source)算法.该算法将DMAS的思想引入虚源次序波束形成的第二阶段, 利用DMAS算法中相乘耦合运算的特点, 充分考虑信号之间的相干性, 以抑制低回声区域伪影的产生, 提高超声成像的分辨率和对比度.对该算法进行了点目标仿体仿真以及实体数据成像实验.结果表明, 相较于常规的聚焦方式, VS-DMAS算法具有更低的旁瓣和更窄的主瓣, 能够更好地将点目标从背景噪声中分离出来, 随着深度的增加, 依然有着较高的成像分辨率.且随着算法中p值适当增大, 成像分辨率和对比度均有一定的提升.
关键词:波束形成算法虚源延时乘累加超声成像图像重建
Delay Multiply and Sum Beamforming Algorithm Based on Virtual Source
WANG Bao-yu, LIU Rui-lin

 , ZHANG Miao, ZHANG Shi
, ZHANG Miao, ZHANG Shi School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: LIU Rui-lin, E-mail: 2001686@stu.neu.edu.cn.
Abstract: In order to improve the imaging resolution in ultrasonic sequential beamforming based on virtual source, a delay multiply and sum beamforming algorithm based on virtual source, namely VS-DMAS algorithm, is proposed. The algorithm introduces the idea of DMAS into the second stage of sequential beamforming based on virtual source, taking advantage of the characteristics of multiplication coupling operation in DMAS algorithm, with the consideration of the coherence between signals, in order to suppress the generation of artifacts in low echo areas and improve the resolution and contrast of ultrasonic imaging. The point target phantom simulation and entity data imaging experiment are carried out. The results show that compared with the conventional focusing method, VS-DMAS algorithm has lower side lobe and narrower main lobe and can better separate the point target from the background noise, with the increase of depth as well as a higher imaging resolution. And with the appropriate increase of p value in the algorithm, the imaging resolution and contrast are improved to a certain extent.
Key words: beamforming algorithmvirtual sourcedelay multiply and sumultrasonic imagingimage reconstruction
虚源(virtual source, VS)成像的概念源于合成孔径超声成像.受合成孔径雷达技术的启发[1-2], 合成孔径超声成像近年来已经得到了广泛的研究[3-4].合成孔径成像的合成效果可以等价于收发双向的理想聚焦, 从而提升超声成像的分辨率[5], 但其对超声成像系统硬件要求较高, 在一定程度上限制了该方法的工程化应用.因此, 诸多****对合成孔径技术进行了进一步的研究和改进.
Passmann等[6]基于合成孔径技术提出了虚源的概念.随后, Frazier等[7]和Bae等[8]进一步研究了合成发射孔径中的虚源成像, 结果表明, 虚源与声场的焦点重合, 并且可以实现深度独立的成像分辨率.Sutcliffe等拓宽了虚源成像在工业检测领域的应用[9].Golfetto等将典型相干平面波复合成像与具有相似帧率和发射功率的虚源成像进行了比较, 结果表明, 特别是在流体成像方面, 虚源成像可能产生更高的信噪比[10].
Kortbek等[11]提出了虚源次序波束形成合成孔径成像, 将虚源成像过程放在第二阶段波束形成中完成, 在减少对系统要求的同时, 仍然保持了合成孔径成像的优点.该算法在第二阶段波束形成中对信号只是进行了简单的延时累加(delay and sum, DAS), 然而实际应用中并非总能满足信号能够相干累加这一前提, 非相干信号的累加会导致低回声区域伪影的产生[12].
文献[13]提出了一种非线性波束形成算法——延时乘累加(delay multiply and sum, DMAS), DMAS中的相乘耦合运算与空间自相关函数的运算步骤等价, 因此能够充分考虑信号之间的相干性, 从而抑制非相干信号的影响, 在分辨率和对比度方面都优于经典的延时累加(delay and sum, DAS)波束形成算法.因此本文考虑将DMAS的思想引入虚源次序波束形成的第二阶段, 提出一种基于虚源的延时乘累加(virtual source-DMAS, VS-DMAS)波束形成算法.
1 方法1.1 虚源次序波束形成虚源次序波束形成将虚源概念和DAS波束形成相结合, 并采用两阶段独立的聚焦波束形成.
第一阶段利用子孔径进行固定焦点的发射和接收聚焦, 将接收的通道数据进行DAS波束形成, 构建并存储一组低分辨率的图像线.焦点被视为发射一定角度球面波的虚拟声源, 多个虚拟声源组成一个虚拟阵列.第二阶段将第一阶段的聚焦图像线作为输入数据, 并利用虚拟阵列进行第二次DAS波束形成, 这一过程中, 相邻图像线间进行相干累加, 最终得到了高分辨率的图像线.该方法能够动态扩展虚拟阵列的尺寸;并在发射和接收过程中进行动态聚焦, 提高了穿透深度, 与常规超声成像的发射固定聚焦、接收动态聚焦相比, 能够提高横向分辨率;与完全合成孔径相比, 每次发射只需要存储一条图像线, 能够大大降低对系统的需求.
图 1给出了三次不同子孔径发射的声场几何模型, 三个子孔径分别为LA, LB和LC, 对应焦点即虚源分别为A, B, C, 焦距为zf, 相邻虚源之间横向距离为d.图中粗虚线表示子孔径LB所对应的虚源B发射的球面波声场覆盖区域.细虚线分别表示子孔径LA, LC所对应的虚源A, C发射的球面波声场覆盖区域.
图 1(Fig. 1)
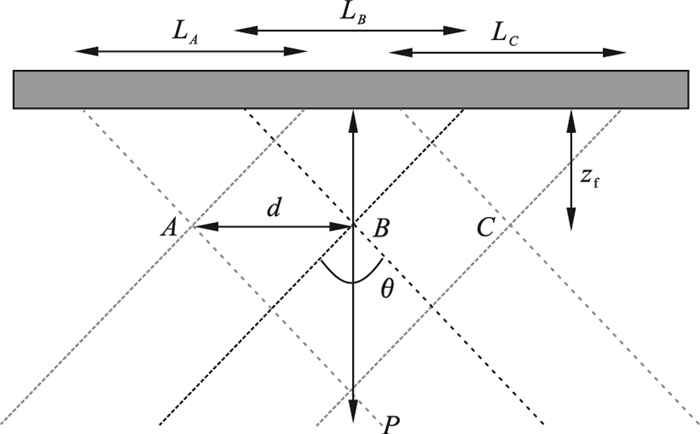 | 图 1 声场几何模型Fig.1 Geometric model of sound field |
从图 1中可以看出, 对于虚源B下方的成像点P, 该点也被虚源A, C的声场所覆盖, 因此其信息不仅在虚源B所对应的图像线中存在, 而且也在虚源A和C所对应的图像线中存在.这一现象就会在低分辨率图像中表现为P点成像区域的扩散, 导致分辨率和对比度下降, 特别是随着深度的增加, 包含P点信息的图像线越来越多, 但每条图像线的能量减弱, 成像分辨率和对比度会大幅度下降.
将子孔径LB的中心设为原点, 成像点P的坐标设为(x, z), 由于第一阶段波束形成进行固定焦点的接收聚焦, 因此对于虚源B, 声波到达P点的往返传播时间为
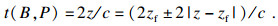 | (1) |
 | (2) |
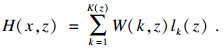 | (3) |
从图 1中可以看出, 在虚源近似声场中, K(z)可表示为
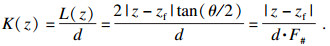 | (4) |
该方法假设了一个具有无限个阵元的孔径, 当实际成像深度足够大时, K(z)将超过第一阶段图像线的数量, 此时合成的孔径将不再随着深度而增加, F#将会增加.
低分辨率图像线中包含的不同散射信号信息, 可以通过式(2)计算特定延时进行提取, 即
 | (5) |
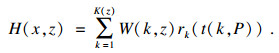 | (6) |
Hollman等[14]提出了空间相干系数(coherence factor, CF)的概念:
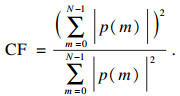 | (7) |
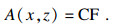 | (8) |
 | (9) |
1.3 DMAS算法DMAS最初在雷达成像领域被提出, 后经改进应用于超声成像[13], 该算法可用公式表示为
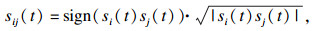 | (10) |
 | (11) |
由于DMAS算法包含了大量的相乘耦合运算, 算法复杂度较高, 因此文献[15]提出一种低计算成本的公式, 并在实时研究扫描仪上得到了实现.文献[16]提出将有符号的p次方根应用DAS, 再使用p次方恢复原始的信号维数, 对公式进行了推广和进一步简化, 简化后的p-DMAS输出可表示为
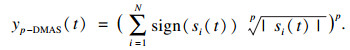 | (12) |
最后, 为了在包络检波前恢复单频信号, 波束形成的信号要经过带通滤波器以消除非线性运算可能引入的不期望的谐波成分.如果p是奇数, 带通滤波器应该以f0为中心;如果p是偶数, p次方信号不再有符号, 所以它的频谱包含偶次谐波, 带通滤波器应该以2f0为中心, 滤波后的输出信号可表示为
 | (13) |
 | (14) |
1.4 VS-DMAS算法本文考虑将DMAS的思想引入虚源次序波束形成的第二阶段, DMAS算法中的相乘耦合运算与空间自相关函数的运算步骤等价, 能够充分考虑信号之间的相干性, 抑制低回声区域伪影的产生.因此将简化后的DMAS算法与自适应虚源次序波束形成相结合, 提出一种VS-DMAS波束形成算法.
将式(5)中的射频数据进行有符号的p次方根运算, 记为Rk(t(k, P)):
 | (15) |
 | (16) |
2 实验结果2.1 点目标仿体仿真为了验证VS-DMAS算法的成像效果优越性以及不同p值对成像的影响, 通过超声仿真平台Field II[18]进行点目标仿体仿真, 并与固定焦点的发射和接收聚焦(fixT-fixR)、固定焦点发射聚焦、动态接收聚焦(fixT-dynR)的仿真成像结果进行对比.其中fixT-fixR在发射和接收的过程中均采用固定焦点聚焦, 只需计算单个焦点的几何参考系, 并通过递推关系或特定延时参数表来获得其他位置的延时值, 因此复杂度较低, 但相应的成像效果较差;fixT-dynR是目前超声系统常用的聚焦方式, 该方法在接收的过程中采用动态聚焦, 即所需进行聚焦的点包括位于声束轴线上的多个甚至所有点, 因此复杂度较高, 但相比fixT-fixR, 能够在发射焦点附近得到更高的分辨率, 然而随着成像深度增加, 波束的主瓣宽度增加, 成像分辨率会降低;VS-DMAS在fixT-fixR的基础上利用虚源的思想以及DMAS的相乘耦合运算, 能够大幅度提高成像分辨率和对比度, 且在理论上能够实现深度独立的成像分辨率, 随着深度的增加, 依然有着较高的成像分辨率.
设置传感器采用线阵扫描的方式, 为了使用高频来突出VS-DMAS算法的优越性, 中心频率设为7.5 MHz, 采样频率为30 MHz, 阵元数为128, 每次扫描开放的有效阵元数为64.焦点深度为20 mm.将12个点目标仿体设置为两排, 深度间隔为5 mm, 分布在10~35 mm, 横向间隔为2 mm.图 2展示了点目标仿体的仿真图像结果, 分别由fixT-fixR,fixT-dynR,VS-DMAS(p=1),VS-DMAS(p=2),VS-DMAS(p=3)重建形成, 所有图像均显示在60 dB动态范围.图 2a为fixT-fixR重建的图像, 即VS-DMAS算法第一阶段的低分辨率图像, 图 2a中的点除焦点位置外, 存在严重的伪影, 难以分辨清楚;图 2b中的点基本能够分辨, 但相邻的点之间存在着粘连, 且随着深度增加, 成像点越来越模糊;图 2c中相邻的点之间粘连基本消失, 所有的点能够清晰分辨, 且随着深度增加, 成像点依然十分清晰, 但在点的附近出现了虚源带来的伪影;图 2d中的伪影现象有了一定改善;图 2e中的伪影现象有了很大改善, 相邻点之间的粘连完全消失.
图 2(Fig. 2)
 | 图 2 点目标仿体仿真图像Fig.2 Simulation images of point target phantom (a)—fixT-fixR; (b)—fixT-dynR; (c)—VS-DMAS(p=1); (d)—VS-DMAS(p=2); (e)—VS-DMAS(p=3). |
从图 2中可以看出VS-DMAS算法相比常规的fixT-dynR聚焦方式, 能够大幅度减少相邻点目标之间的粘连, 且随着p值的增大, 伪影现象也有了很大的改善.图 3为35mm处的横向响应图, 能够进一步验证VS-DMAS在深度较深时的成像效果优越性, 此外在不同深度下也能得到相似的横向响应图.从图 3中可以看出VS-DMAS算法的旁瓣以及两组峰之间的波谷都远低于常规的fixT-dynR聚焦方式, 且随着p值的增大, 旁瓣以及伪影幅度都有了一定程度的降低, VS-DMAS算法也有着更窄的主瓣宽度以及更高的主瓣幅度, 这些都说明了该算法相比常规的fixT-dynR聚焦方式, 有着更高的分辨率和更好的成像效果.
图 3(Fig. 3)
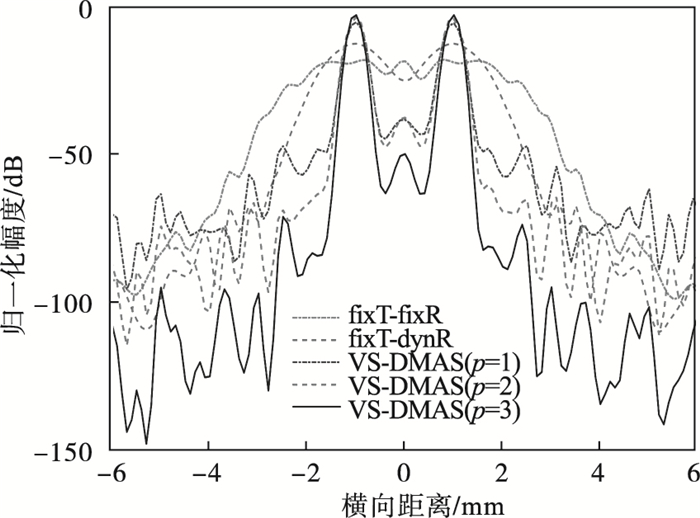 | 图 3 横向响应图Fig.3 Horizontal response diagram |
2.2 实体数据成像实验为了验证VS-DMAS算法在真实环境的成像效果, 本文利用来自医学超声平台(东软医疗系统有限公司)获得的Model ATS 539超声模体射频数据进行了成像实验, 超声模体实物如图 4所示, 该模体可用于临床成像频率2~18 MHz范围内的综合性评估实验, 本文实验中的垂直距离组部分, 初始深度为10 mm, 深度间隔也为10 mm.该实验数据由128阵元0.22 mm阵元间距的线阵传感器采集得到, 其发射中心频率为7.5 MHz, 采样频率设置为30 MHz, 每次扫描开放的有效阵元数为64.超声信号的发射和接收均设置为固定焦点聚焦, 焦点深度46 mm约为图像的中心位置, 可以验证VS-DMAS在两个方向的成像效果, 不同波束形成方法重建的图像如图 5所示, 10 mm深度处的横向响应图如图 6所示.从图 5和图 6可以看出, 相较于常规的fixT-dynR聚焦方式, VS-DMAS算法展示了更高的对比度, 能够更好地将点目标从背景噪声中分离出来, 且随着p值的增大, 对背景噪声以及伪影的抑制效果也在逐渐增强.
图 4(Fig. 4)
 | 图 4 超声模体Model ATS 539Fig.4 Ultrasonic phantom Model ATS 539 |
图 5(Fig. 5)
 | 图 5 实体数据图像Fig.5 Images of entity data (a)—fixT-fixR; (b)—fixT-dynR; (c)—VS-DMAS(p=1); (d)—VS-DMAS(p=2); (e)—VS-DMAS(p=3). |
图 6(Fig. 6)
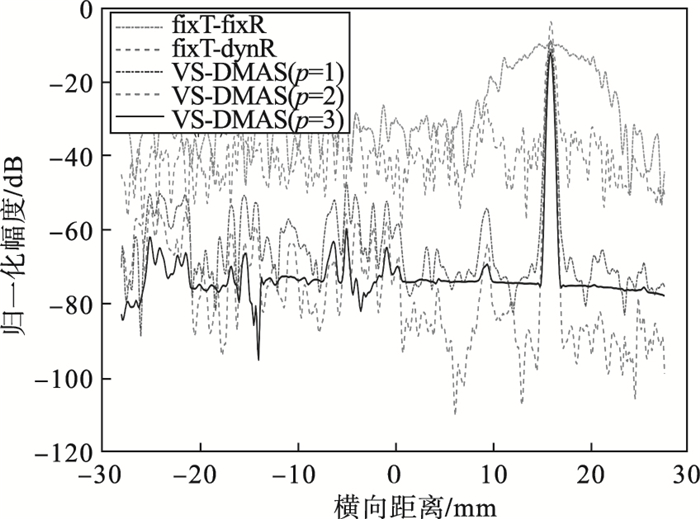 | 图 6 横向响应图Fig.6 Horizontal response diagram |
但从图 5中也可以看出, 随着成像深度增加, 分辨率在逐渐下降, 未能达到仿真中深度独立的成像分辨率, 造成这种差异的原因是, 超声实体数据受多种因素影响, 如系统参数的准确性、发射声波的能量、声波在组织中的声束衰减以及声场发散导致不满足虚源假设等, 这些均会导致聚焦误差和在深度较深时的成像分辨率和信噪比下降, 此外, 当p值大于等于3时, 信号通过带通滤波器后会丢失一部分频率分量, 这也会影响最终的成像分辨率, 因此在成像深度较深时, 横向响应图的效果较差, 图 6只展示了10 mm深度处的横向响应图.后续考虑将原始射频信号解调到基带以避免使用额外的带通滤波器, 同时对算法进行其他的适应性改进, 对系统参数的准确性、声束衰减等因素进行综合考虑, 得到更好的成像效果以应用于实际医学超声成像系统.
对比图 3和图 6可以发现, 在图 3中VS-DMAS归一化幅值最高, 而在图 6中fixT-dynR归一化幅值最高, 造成这种差异的原因是上文提到的超声实体数据受多种因素影响, 导致聚焦误差使得VS-DMAS第二阶段在低分辨率图像线中未能提取到散射信号的峰值.另外, 随着p值的增大, 在焦点附近的点目标强度也受到了一定的抑制, 这种现象主要是由于在焦点附近参与累加的虚源声场数过少, 因此, 虽然实体数据成像实验能够进一步证明VS-DMAS算法在真实环境中能够提高成像分辨率和对比度, 但距离仿真的结果还有一定的差距, 后续仍需要对算法进行适应性的改进.
在横向响应图的基础上可以采用PSL和FWHM两个参数来定量评价VS-DMAS算法的成像质量, PSL代表第一个旁瓣的幅度, FWHM代表最大幅度一半处的主瓣宽度.表 1给出了10 mm深度处相应的结果, 可以看出VS-DMAS算法具有最低的旁瓣幅度和主瓣宽度, 且随着p值的增大, 旁瓣幅度和主瓣宽度也在逐渐降低, 定量地说明了VS-DMAS算法在成像分辨率和对比度方面的优越性.在旁瓣幅度降低的同时, VS-DMAS算法主瓣的归一化幅度并没有明显变化, 因此随着p值的增大, 信噪比也在逐渐提升.
表 1(Table 1)
| 表 1 实体数据图像中不同波束形成方法的PSL和FWHM值 Table 1 PSL and FWHM values of different beamforming methods in entity data images | ||||||||||||||||||||||||||||
3 结论1) 为了提高超声虚源次序波束形成的成像分辨率, 本文考虑将DMAS的思想引入虚源次序波束形成的第二阶段, 提出一种VS-DMAS波束形成算法.该算法在点目标仿体仿真和实体数据成像实验中均表现出较好的成像性能, 且随着算法中p值的适当增大, 成像性能可以进一步提高.在不同的波束形成聚焦方式以及不同的p值中, p=3时VS-DMAS算法具有最低的旁瓣幅度-68.76 dB以及最窄的主瓣宽度0.49 mm.
2) 由于算法本身的制约以及实际环境的复杂性, 后续仍需要对算法进行适应性的改进以应用于实际医学超声成像系统.如算法中的p次方根在输出信号频谱中引入了谐波成分, 同时高于奈奎斯特频率, 原始射频信号可能提前被过采样, 因此VS-DMAS算法在处理实际射频信号时, 可能会因为数据量过大而导致成像帧率的降低, 而且当p值大于等于3时, 信号通过带通滤波器后会丢失一部分的频率分量, 这也会影响最终的成像分辨率, 因此考虑在算法处理前, 将原始射频信号解调到基带, 以避免过采样和使用额外的带通滤波器.
参考文献
| [1] | Cutrona L J, Vivian W E, Leith E N, et al. A high-resolution radar combat-surveillance system[J]. IRE Transactions on Military Electronics, 1961, 5(2): 127-131. |
| [2] | Sherwin C W, Ruina J P, Rawcliffe R D. Some early developments in synthetic aperture radar systems[J]. IRE Transactions on Military Electronics, 1962, 6(2): 111-115. |
| [3] | Karaman M, Li P C. Synthetic aperture imaging for small scale systems[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 1995, 42(3): 429-442. DOI:10.1109/58.384453 |
| [4] | Jensen J A, Nikolov S I, Gammelmark K L, et al. Synthetic aperture ultrasound imaging[J]. Ultrasonics, 2006, 44: e5-e15. DOI:10.1016/j.ultras.2006.07.017 |
| [5] | Pedersen M H, Gammelmark K L, Jensen J A. In-vivo evaluation of convex array synthetic aperture imaging[J]. Ultrasound in Medicine and Biology, 2007, 33(1): 37-47. DOI:10.1016/j.ultrasmedbio.2006.07.041 |
| [6] | Passmann C, Ermert H. A 100-MHz ultrasound imaging system for dermatologic and ophthalmologic diagnostics[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 1996, 43(4): 545-552. DOI:10.1109/58.503714 |
| [7] | Frazier C H, O'Brien W D. Synthetic aperture techniques with a virtual source element[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 1998, 45(1): 196-207. DOI:10.1109/58.646925 |
| [8] | Bae M H, Jeong M K. A study of synthetic-aperture imaging with virtual source elements in B-mode ultrasound imaging systems[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2000, 47(6): 1510-1519. DOI:10.1109/58.883540 |
| [9] | Sutcliffe M, Weston M, Charlton P, et al. Virtual source aperture imaging for non-destructive testing[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2012, 54(7): 371-379. DOI:10.1784/insi.2012.54.7.371 |
| [10] | Golfetto C, Ekroll I K, Top H, et al. Retrospective transmit beamforming and coherent plane-wave compounding for microvascular doppler imaging: a comparison study[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2020, 68(4): 1105-1116. |
| [11] | Kortbek J, Jensen J A, Gammelmark K L. Sequential beamforming for synthetic aperture imaging[J]. Ultrasonics, 2013, 53(1): 1-16. DOI:10.1016/j.ultras.2012.06.006 |
| [12] | 李遥, 吴文焘, 李平, 等. 超声虚源成像中自适应双向空间逐点聚焦方法[J]. 声学学报, 2016, 41(3): 287-295. (Li Yao, Wu Wen-tao, Li Ping, et al. Adaptive bidirectional spatial point-by-point focusing method in ultrasonic virtual source imaging[J]. Acta Acustica, 2016, 41(3): 287-295.) |
| [13] | Matrone G, Savoia A S, Caliano G, et al. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging[J]. IEEE Transactions on Medical Imaging, 2015, 34(4): 940-949. DOI:10.1109/TMI.2014.2371235 |
| [14] | Hollman K W, Rigby K W, O'Donnell M. Coherence factor of speckle from a multi-row probe[C]//1999 IEEE International Ultrasonics Symposium(IUS). Lake Tahoe, 1999: 1257-1260. |
| [15] | Ramalli A, Scaringella M, Matrone G, et al. High dynamic range ultrasound imaging with real-time filtered-delay multiply and sum beamforming[C]//2017 IEEE International Ultrasonics Symposium(IUS). Washington, D C, 2017: 6-9. |
| [16] | Polichetti M, Varray F, Matrone G, et al. A computationally efficient nonlinear beamformer based on p-th root signal compression for enhanced ultrasound B-mode imaging[C]//2017 IEEE International Ultrasonics Symposium (IUS). Washington, D C, 2017: 1-4. |
| [17] | Shen C C, Hsieh P Y. Ultrasound base band delay-multiply-and-sum (BB-DMAS) nonlinear beamforming[J]. Ultrasonics, 2019, 96: 165-174. DOI:10.1016/j.ultras.2019.01.010 |
| [18] | Jensen J A, Svendsen N B. Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 1992, 39(2): 262-267. DOI:10.1109/58.139123 |
