张露文, 刘洪娟
东北大学 软件学院, 辽宁 沈阳 110819
收稿日期：2022-02-07
基金项目：国家自然科学基金青年基金资助项目(61902057)；辽宁省自然科学基金资助项目(2020-MS-083)。
作者简介：张露文(1998-), 女, 辽宁鞍山人, 东北大学硕士研究生;
刘洪娟(1980-), 女, 山东胶南人, 东北大学副教授。

摘要：基于SEIR模型, 引入自我防护和隔离两个仓室, 提出一个更加通用的传染病传播模型.通过对模型进行定性分析, 计算模型的基本再生数, 通过特征值理论和Routh-Hurwitz判据, 分析模型的无病平衡点和地方病平衡点的局部渐近稳定性.数值模拟和COVID-19病毒真实数据拟合结果表明, 所提出的SEIQRP模型能够有效地描述传染病的动态传播过程.模型中防护率、潜伏期隔离率和感染者隔离率这三个参数对疾病的传播起着非常关键的作用.提高人们加强自我防护意识、重点排查潜伏期患者和对感染者进行隔离治疗可以有效降低传染病的传播.
关键词：传染病传播模型自我防护基本再生数稳定性拟合
Modeling and Analysis of Infectious Disease Transmission Considering Protection and Isolation
ZHANG Lu-wen, LIU Hong-juan
School of Software, Northeastern University, Shenyang 110819, China
Corresponding author: LIU Hong-juan, E-mail: liuhj@swc.neu.edu.cn.

Abstract: Based on the SEIR model, two compartments for self-protection and isolation are introduced, and a more general infectious disease transmission model is proposed. Through qualitative analysis of the model, the basic reproduction number of the model is calculated, and the local asymptotic stability of the disease-free equilibrium point and the endemic equilibrium point of the model is analyzed through eigenvalue theory and Routh-Hurwitz criterion. The numerical simulation and fitting results of COVID-19 virus show that the proposed SEIQRP model can effectively describe the dynamic transmission process of the infectious disease. In the model, the three parameters, i.e. protection rate, incubation period isolation rate, and infected person isolation rate play a very critical role in the spread of the disease. Raising people's awareness of self-protection, focusing on screening for patients in the incubation period, and isolating and treating infected people can effectively reduce the spread of infectious diseases.
Key words: infectious disease spread modelself-protectionbasic reproduction numberstabilityfitting
由于各种传染病的存在, 各个国家遭受了人口的死亡、经济的萧条和社会结构的改变.因此, 建立传染病的传播模型对疾病的评估、预测和控制起着至关重要的作用.早期模型一般只考虑感染者、易感者和康复者几种基础的状态.但随着时代的发展, 研究发现有必要加入一些其他参数和变量, 以便更精确地描述不断变种的传染病的特征.研究者们根据不同的传染病特征, 提出了不同的数学模型来描述传染病的动态变化.
结核病目前仍然是世界卫生组织的巨大挑战, 每年世界卫生组织都会对结核病进行全面评估.Kim等建立了一个结核病模型, 研究各种干预措施和控制策略的有效性，结果表明, 加强远程控制措施可以降低易感者的接触, 减少感染者的出现^[1].Liu等提出带有新生儿疫苗接种的结核病传播模型, 从理论上证明了接种疫苗对控制传播的有效性^[2].
2002年底, 中国出现严重的急性呼吸系统综合症(SARS)患者, Chowell等创建了SEIJR模型, 预测隔离措施对多伦多、香港和新加坡疫情的影响, 分析三个城市传播状态的不同^[3].文献[4]在SEIJR模型的基础上加入了扩散, 研究干预措施对SARS传播的影响.
2019年底, 新型冠状病毒(COVID-19)患者在中国武汉市出现.Fanelli等提出加入死亡仓室的传播模型, 研究三个国家的新冠病毒的传播动态, 预测了疫情高峰期的时间和规模^[5].文献[6-7]对短期内累计感染人数进行了预测.研究发现, 隔离和政府管控措施都会减少疫情的传播.Khajanchi等提出了一个比较全面的符合新冠病毒特点的传播模型, 为研究病毒的传播、控制和预测提供重要依据^[8].
然而, 在现有大部分传染病模型中, 并没有同时考虑隔离和采取防护措施两类人群.而在抵抗大部分传染病疫情时, 易感者对自身采取的防护措施, 政府对潜伏者和感染者进行的隔离治疗, 都能有效地控制传染病的传播.只有充分考虑这些因素, 建立的传染病模型才能更加精确地描述疾病的传播过程, 进而更好地预测传染病未来的传播趋势.因此, 本文在SEIR模型的基础上, 提出一个更加通用的传染病传播模型, 加入了隔离治疗和加强防护两类人群.对提出的模型进行定性分析, 计算基本再生数, 研究了无病平衡点和地方病平衡点的局部渐进稳定性.数值模拟和COVID-19病毒真实数据拟合结果表明, 所提出的模型能够有效地描述传染病的动态传播过程.
1 数学模型当有传染病存在时, 人们会采取相应的防护措施, 如戴口罩、减少外出、勤洗手、消毒等.此外, 由于传染病传播能力非常强, 要对潜伏者和感染者进行隔离和治疗.本文创建的传染病模型考虑了加强防护措施和隔离治疗两个因素, 在任意时刻t，人们被分为6个群体，分别为：易感者S(t)、潜伏者E(t)、感染者I(t)、隔离和治疗者Q(t)、康复者R(t)、受保护者P(t)，该模型被称为SEIQRP模型.其中，潜伏者表示没有确诊，但是具有传染能力的人群，受保护者为加强防护措施和减少外出的人群.N(t)表示人口的总数，可以表示为

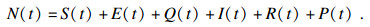(1)

6个群体之间会进行状态的变换, 这些群体之间的动态传播情况如图 1所示.
图 1(Fig. 1)

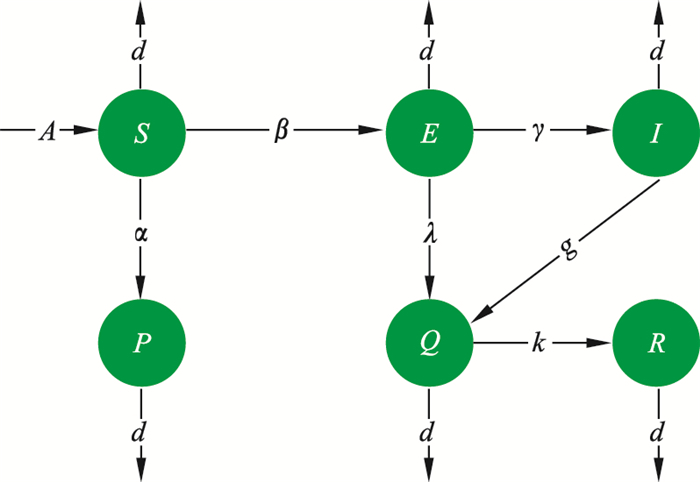图 1 传染病动态传播图Fig.1 Dynamic map of the spread of infectious diseases

根据图 1的传染病动态传播图, 可以写出SEIQRP模型的非线性动力学系统方程式为

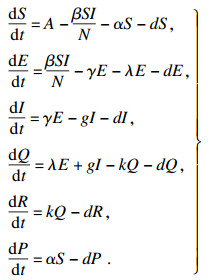(2)

式中: A为出生人口数；d为自然死亡率；β为疾病的传播率；α为人们自我防护的防护率，这里假设人们采取防护措施后将不会感染病毒；γ为感染率；λ为潜伏者的隔离率；g为感染者的隔离治疗率；k为康复率.据统计，对于大部分传染病来说，感染者治愈之后再次感染病毒的概率非常小，所以该模型没有考虑传染病复发的情况.
2 系统的定性分析对系统(2)进行定性分析, 研究系统的正性、有界性、基本再生数、无病平衡点和地方病平衡点的稳定性.
2.1 系统的正性实际情况下, 模型的初始值应该为非负数, 即S(0)≥0，E(0)≥0，Q(0)≥0，I(0)≥0，R(0)≥0，P(0)≥0.
定理1??当t>0时, 系统(2)的解保持正性.
证明??由系统(2)的动力学方程可以得出

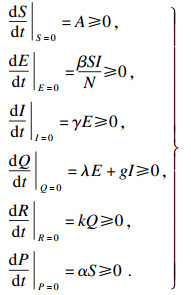(3)

即系统(2)的解保持正性，证毕.
2.2 系统的有界性定理2??系统(2)是有界的.
证明??为了证明模型的有界性, 将系统(2)中的6个动力学方程相加.由于N=S+E+Q+I+R+P, 可得

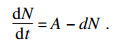(4)

根据定理1的证明可以得出，所以，因此得到可行区域为
这一结果表明, 在有限的时间内, 没有一个个体是无限增长或指数增长的, 也就是有界的, 证毕.
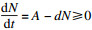
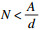
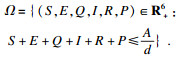2.3 系统的基本再生数在传染病模型中, 基本再生数表示将单个感染个体引入易感人群时, 所产生的二次感染数, 可以用来表示一种病毒是否继续存在或消失^[9].因此, 制定控制策略使R₀ < 1是至关重要的.这里采用下一代矩阵的方法计算基本再生数.系统(2)中涉及疾病传染的仓室有E，I和Q, 相关的动力学方程为

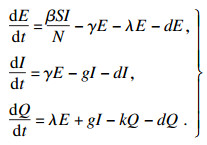(5)

构造矩阵Φ和矩阵Ψ:
系统(2)有无病平衡点(, 0, 0, 0，0，), 其中, α是人们自我防护的防护率.矩阵Φ和Ψ的雅可比矩阵分别表示为F和V：
由公式R₀=ρ(FV^－1)可以求出系统(2)的基本再生数为

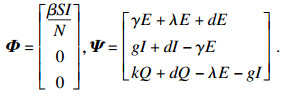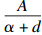
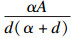
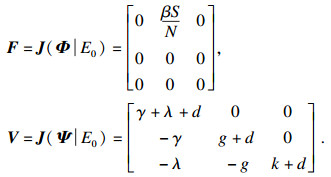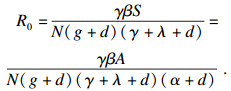(6)

其中, ρ(FV^－1)表示下一代矩阵的光谱半径^[10].
2.4 稳定性分析研究系统的无病平衡点和地方病平衡点的局部渐进稳定性.
定理3??当R₀ < 1时, 无病平衡点是局部渐进稳定的；当R₀>1时, 无病平衡点是不稳定的.
证明??系统(2)在无病平衡点的雅可比矩阵表示为
根据J₁雅可比矩阵, 系统(2)的无病平衡点的特征方程可以表示为

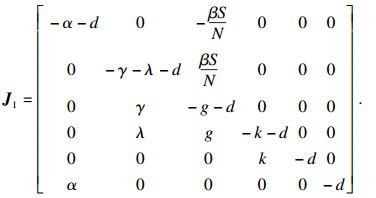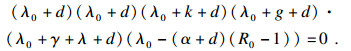(7)

通过式(7)特征方程可以得知, 当R₀ < 1时, 所有的特征值λ₀都为负值, 系统是局部渐进稳定的；否则系统是不稳定的, 证毕.
定理4??当R₀>1时, 地方病平衡点局部渐进稳定, 否则, 地方病平衡点不稳定.
证明??地方病平衡点即为系统一直存在传染病的情况.这里采用文献[6]给出的方法进行证明, 首先求出地方病平衡点, 进而判断地方病平衡点的稳定性.
当系统(2)存在地方病平衡点时, 可以得出

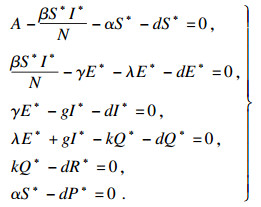(8)

通过式(8)可以得出地方病平衡点为

(9)

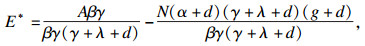(10)

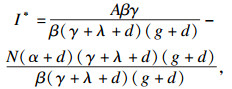(11)

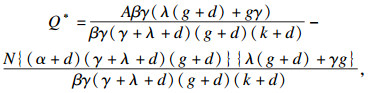(12)

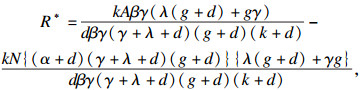(13)

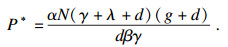(14)

地方病平衡点的雅可比矩阵为
雅可比矩阵J₂的特征方程为

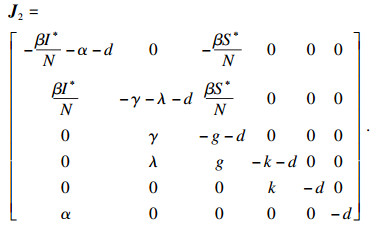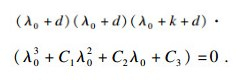(15)

通过计算特征方程的解来判断地方病平衡点的稳定性, 由特征多项式的公式计算C₁, C₂和C₃可得

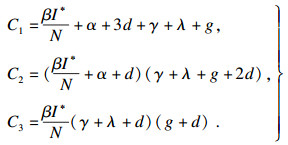(16)

J₂的特征方程的前3个根为负值, 分别为-d, -d和-k-d.根据劳斯-赫尔维茨稳定性判据(Routh-Hurwitz判据)可得, 当参数取任意值时, C₁, C₂, C₃和C₁C₂-C₃都为正数.因此, 系统(2)是局部渐进稳定的.
3 数值模拟与分析使用模拟数据来验证传染病模型的有效性, 分析结果的正确性.模拟数据的初始值设置为E₀=10, Q₀=5, I₀=1, R₀=0, P₀=0和N=500.无病平衡点的参数设置如表 1所示, 所对应的R₀为0.484 < 1, 即存在无病平衡点.
表 1(Table 1)

表 1 无病平衡点的参数设置Table 1 Parameter setting of disease-free equilibrium point 参数 描述 值 A 出生率 dN α 防护措施的概率 0.053 k 恢复率 0.235 β 传播率 1.2 d 自然死亡率 0.05 γ 感染率 0.36 g 感染者的隔离率 0.52 λ 潜伏期的隔离率 0.35

表 1 无病平衡点的参数设置 Table 1 Parameter setting of disease-free equilibrium point

地方病平衡点的参数设置如表 2所示, 所对应的R₀为1.28>1, 即存在地方病平衡点.
表 2(Table 2)

表 2 地方病平衡点的参数设置Table 2 Parameter setting of endemic equilibrium point 参数 描述 值 A 出生率 dN α 防护措施的概率 0.065 k 恢复率 0.231 β 传播率 2.56 d 自然死亡率 0.12 γ 感染率 0.36 g 感染者的隔离率 0.52 λ 潜伏期的隔离率 0.25

表 2 地方病平衡点的参数设置 Table 2 Parameter setting of endemic equilibrium point

当R₀=0.484 < 1时, 系统(2)存在无病平衡点, 采用表 1参数值模拟的传播结果如图 2所示.
图 2(Fig. 2)

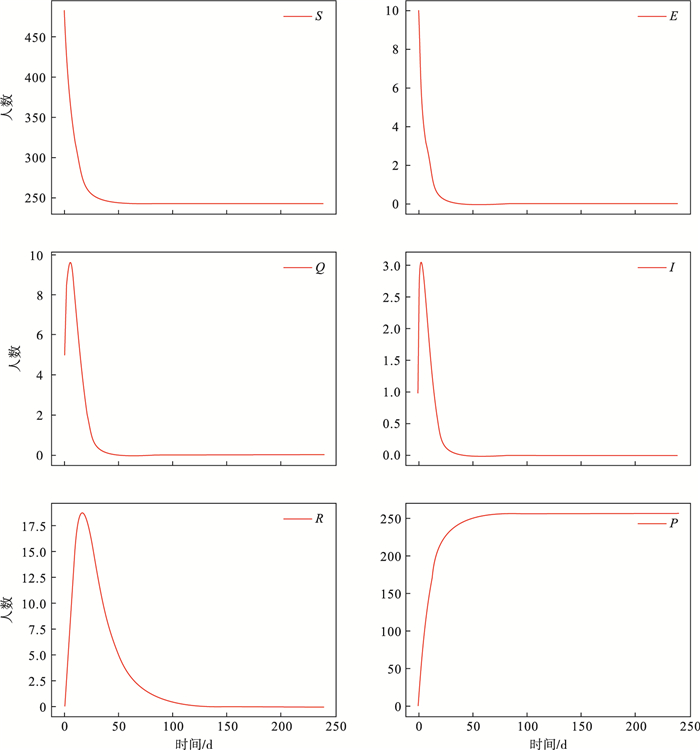图 2 存在无病平衡点时的传播结果Fig.2 Transmission outcomes when there is a disease-free equilibrium

观察图 2可以得出, 当R₀ < 1时, 无病平衡点为(231.48, 0, 0, 0, 0, 268.5), 此时的特征值为-0.05, -0.05, -0.285, -0.57, -0.76, -0.053 15.由于所有的特征值都是负数, 无病平衡点在R₀ < 1时是局部渐进稳定的.
当R₀=1.28>1时, 系统(2)存在地方病平衡点, 采用表 2参数值模拟的传播结果如图 3所示.
图 3(Fig. 3)

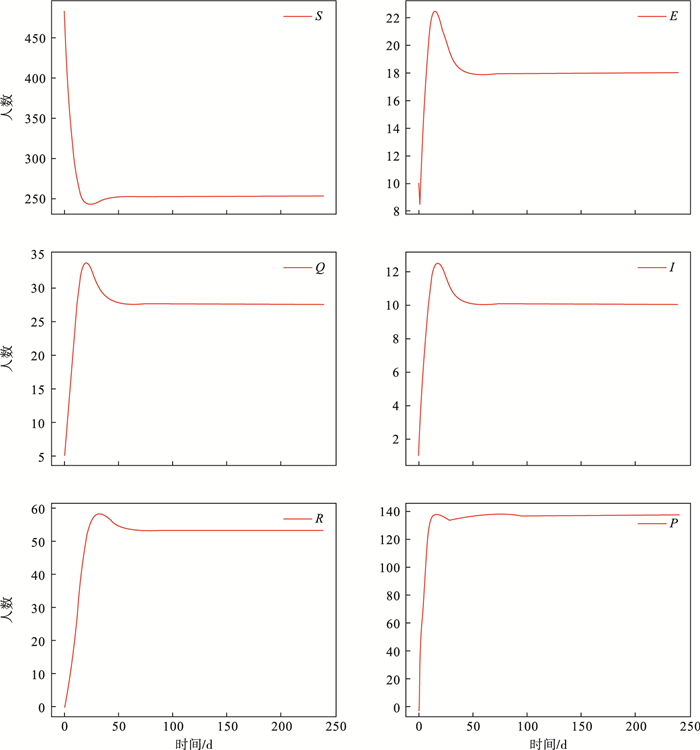图 3 存在地方病平衡点时的传播结果Fig.3 Transmission outcomes when there is an endemic equilibrium point

观察图 3可以得出, 当R₀>1时, 地方病平衡点为(253.47, 17.96, 27.75, 10.1, 53.42, 137.297), 此时3个特征值为-0.12, -0.12, -0.351, 相应地, C₁=1.606 7>0, C₂=0.324 3>0, C₃=0.024 2>0, C₁C₂-C₃=0.496 9>0.因此, 地方病平衡点是局部渐进稳定的.
分析在R₀>1的情况下, 传播模型中防护率、潜伏期隔离率、感染患者隔离率这三个参数对感染人数的影响.
系统在不同防护率下感染人数的变化情况如图 4所示, 可以看出, 当防护率越大时, 感染人数的峰值越低, 感染人数越少, 进一步地, 当防护率增大到0.075时, 传染病逐渐消失.
图 4(Fig. 4)

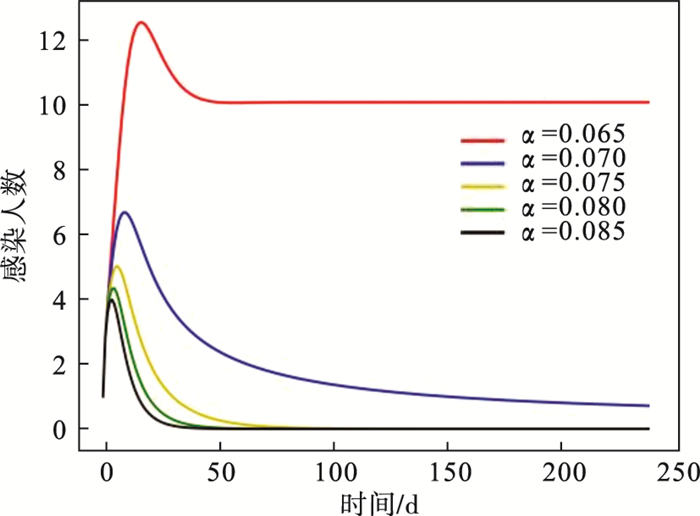图 4 防护率对感染人群数目的影响Fig.4 Effect of protection rate on the number of infected people

不同潜伏期隔离率下的传染病患者数量的变化情况如图 5所示.随着潜伏期隔离率的增大, 感染者的数量和感染者的峰值都会逐渐降低, 当潜伏者的隔离率增加到0.4时, 感染者病例趋近于零.
图 5(Fig. 5)

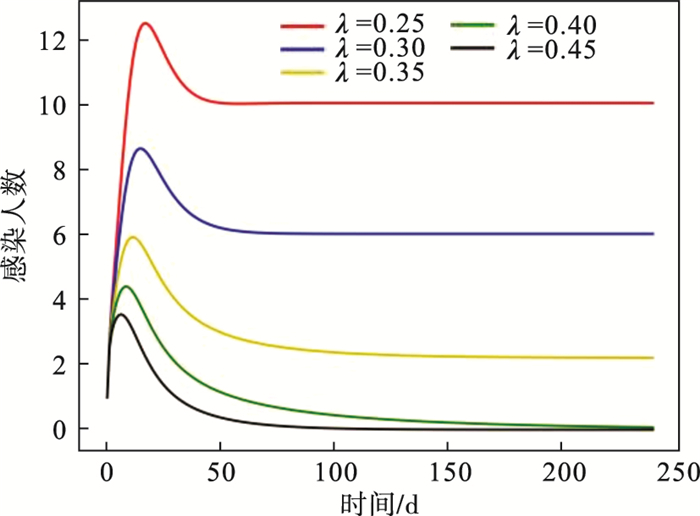图 5 潜伏期的隔离率对感染人群数目的影响Fig.5 Impact of the isolation rate during the incubation period on the number of infected people

不同感染者隔离率下的感染者数量的变化情况如图 6所示.随着感染者隔离率的不断增加, 感染者的数目和峰值不断减少.
图 6(Fig. 6)

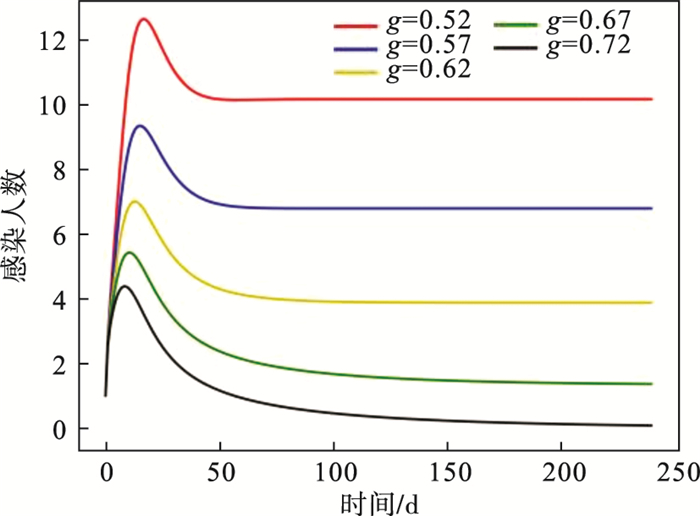图 6 感染者的隔离率对感染人数的影响Fig.6 Impact of the isolation rate of infected people on the number of infected people

综上分析可得, 当传染病来临时, 人们要做好防护措施, 如戴口罩、增大社交距离、减少出行、勤消毒等, 这样可以最大程度地降低病毒的传播.当人们已经感染病毒或处在潜伏期时, 应该有意识地进行自我隔离, 禁止病毒进一步扩散.通过研究图 4~图 6的实验结果可以进一步得出, 加强对处于潜伏期患者的隔离比对感染者的隔离对于控制传染病的传播更加有效.政府也应该加大宣传力度, 尽量让每个人都做好防护措施, 加大对潜伏者的排查和隔离的力度, 防止潜伏者与易感者人群接触, 即使没有疫苗和治疗, 只要人们充分配合, 疾病也可以随着时间逐渐消失.
4 模型在COVID-19中的应用将提出的SEIQRP传播模型运用在新冠病毒的传播中, 采用目前还在大规模暴发的印度两个邦的数据, 分别是马哈拉施特拉邦和泰米尔纳德邦，前者是疾病暴发最严重的邦, 后者是人口最密集的邦.通过真实数据估计模型的参数, 观察拟合的结果使用2020年3月9日至2020年7月23日的累计确诊病例数和恢复病例数的真实数据进行拟合, 该数据集由Our World in Data维护的COVID-19数据集合提供^[10].对于马哈拉施特拉邦, 人口初始值设置为：N=120 837 347，E₀=350，R₀=0，I₀=2，Q₀=2，P₀=0，S₀=N－E₀－R₀－I₀－Q₀－P₀.针对泰米尔纳德邦，人口初始值设置为：N=38 472 769，E₀=3，R₀=0，I₀=1，Q₀=1，P₀=0，S₀=N－E₀－R₀－I₀－Q₀－P₀.
模型的参数通过与真实数据进行拟合估计得到.运用Matlab软件工具, 使用最小二乘的方法, 使用lsqcurvefit函数进行拟合.该函数定义为x=lsqcurvefit(fun, x₀, xdata, ydata, lb, ub, option), 其中, fun为要拟合的函数, x₀为拟合参数的初始值, xdata为时间, ydata为输入的真实数据, lb为参数的下界, ub为参数的上界, option为优化参数.采用龙格-库塔法对模型进行数值求解.对模型的参数进行估计的结果如表 3所示.
表 3(Table 3)

表 3 马哈拉施特拉邦和泰米尔纳德邦的参数值Table 3 Parameter values for Maharashtra and Tamil Nadu 参数 马哈拉施特拉邦 泰米尔纳德邦 引用 A dN dN 文献[11] α 0.011 2 0.005 7 估计 k 0.043 5 0.079 6 估计 β 1.823 4 0.789 4 估计 d 0.005 8 0.007 1 文献[6] γ 0.033 2 0.579 4 估计 g 0.178 5 0.456 3 估计 λ 0.068 4 0.000 179 估计

表 3 马哈拉施特拉邦和泰米尔纳德邦的参数值 Table 3 Parameter values for Maharashtra and Tamil Nadu

采用马哈拉施特拉邦实际康复病例数和累计确诊病例数的数据, 使用表 3中给出的参数值, 真实数据与模型演化数据的拟合结果如图 7和图 8所示.实际数据用红色圆圈表示, 模型演化数据用黑色线形表示.
图 7(Fig. 7)

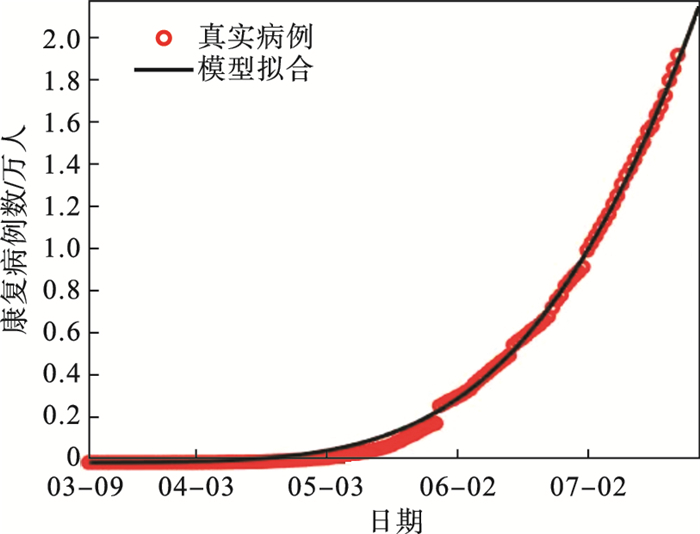图 7 马哈拉施特拉邦康复病例数的拟合结果Fig.7 Fitting results of the number of recovered cases in Maharashtra

图 8(Fig. 8)

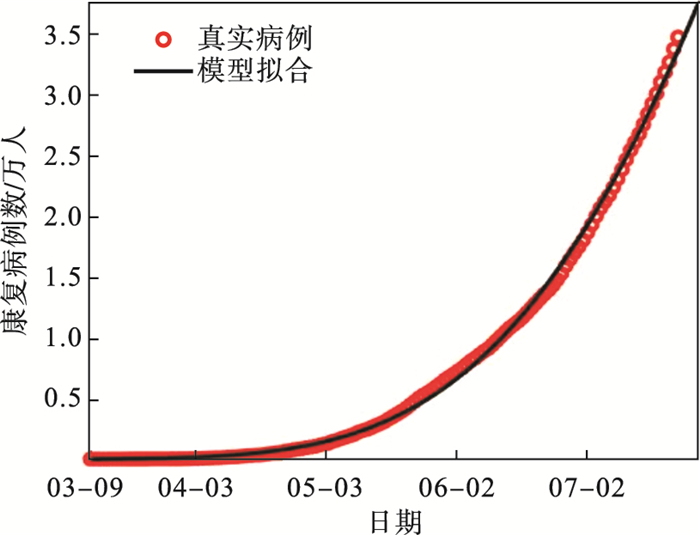图 8 马哈拉施特拉邦累计确诊病例数的拟合结果Fig.8 Fitting results of cumulative number of confirmed cases in Maharashtra

采用泰米尔纳德邦实际康复病例数和累计确诊病例数的数据, 使用表 3中给出的参数值, 真实数据与模型演化数据的拟合结果如图 9和图 10所示.实际数据用蓝色圆圈表示, 模型演化数据用黑色线形表示.
图 9(Fig. 9)

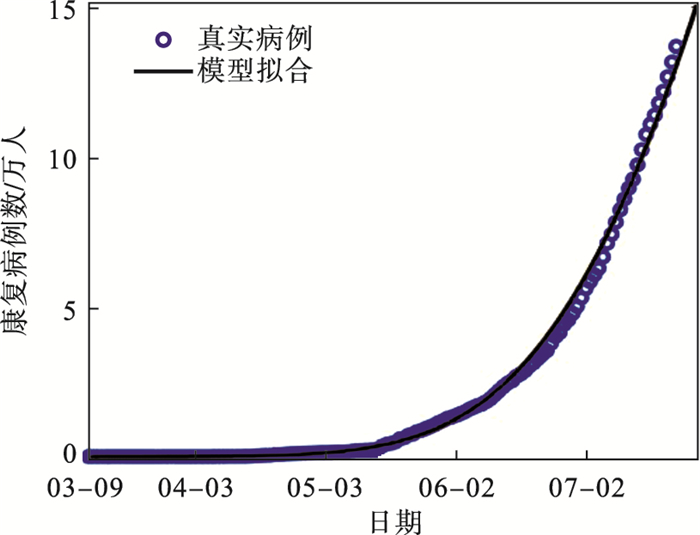图 9 泰米尔纳德邦康复病例数的拟合结果Fig.9 Fitting results of the number of recovered cases in Tamil Nadu

图 10(Fig. 10)

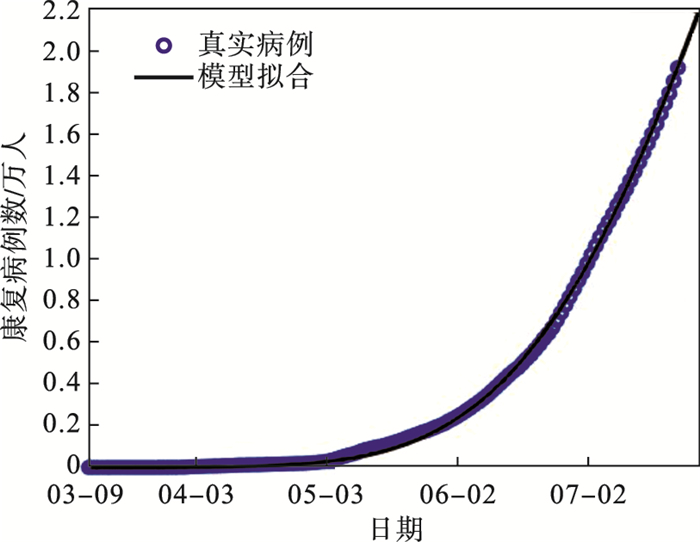图 10 泰米尔纳德邦累计确诊病例数的拟合结果Fig.10 Fitting results of cumulative number of confirmed cases in Tamil Nadu

图 7~图 10的实际累计确诊病例数和康复病例数的拟合实验结果表明, 两个邦的数据均呈现为增长状态, 拟合结果比较准确.其中, 马哈拉施特拉邦的基本再生数R₀>1, 也就是说, 该传染病将长时间存在于该邦中, 与事实情况相符.泰米尔纳德邦的初期感染病例数较少, 但随着时间的推移, 病例数迅速增加, 感染病例的数量仅次于马哈拉施特拉邦.此外, 模型演化数据与真实数据的拟合结果有少许偏差, 这是由传染病的突然爆发以及政府所采取的隔离、防护和治疗等措施影响所致.
为了进一步证明传播模型的优势和有效性, 与文献[12]中提出的SEIQR模型进行对比分析.以马哈拉施特拉邦为例进行拟合, 使用完全相同的马哈拉施特拉邦真实累计确诊病例数和康复病例数, 拟合结果如图 11和图 12所示.
图 11(Fig. 11)

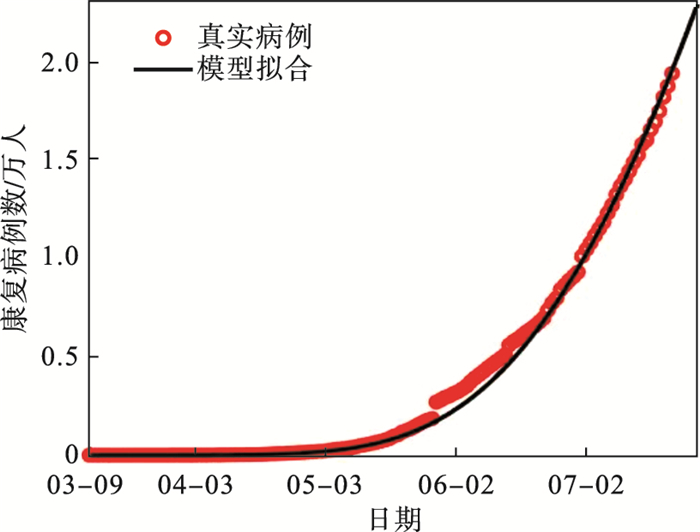图 11 SEIQR模型康复病例数的拟合结果Fig.11 Fitting results of the number of recovered cases by SEIQR model

图 12(Fig. 12)

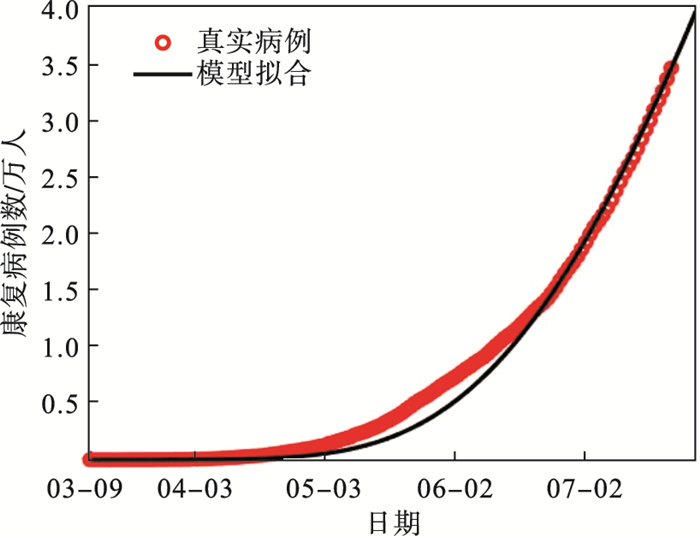图 12 SEIQR模型累计确诊病例数的拟合结果Fig.12 Fitting results of cumulative number of confirmed cases by SEIQR model

观察图 11和图 12的拟合结果可以看出, 与图 7和图 8的结果相比, 当感染者和康复者的病例数出现拐点时, SEIQR模型的拟合效果不理想, 而本文所提模型的拟合结果更加准确.综上可知, 本文提出的模型能够更准确地描述传染病的传播过程.
5 结语为了更精确地描述传染病的传播过程, 本文提出了一个考虑防护措施和隔离措施的传播模型.数值模拟结果表明, 做好防护措施, 加强感染者隔离和潜伏期患者隔离, 可以最大程度地控制病毒的传播.特别地, 尽早识别潜伏者进行隔离比对感染者进行隔离对于控制病毒传播更有效.针对COVID-19病毒, 对印度最具有代表性的两个邦进行真实数据拟合的结果表明, 所提出的SEIQRP模型能够有效地描述传染病的动态传播过程.虽然该模型能够较好地描述现有的传染病, 今后还将考虑接种疫苗、病毒变种、治疗策略以及环境变化等因素, 进一步完善该传染病模型.
参考文献

[1]	Kim S, de los Reyes A, Jung E. Mathematical model and intervention strategies for mitigating tuberculosis in the Philippines[J]. Journal of Theoretical Biology, 2018, 443: 100-112. DOI:10.1016/j.jtbi.2018.01.026
[2]	Liu S, Bi Y, Liu Y. Modeling and dynamic analysis of tuberculosis in mainland China from 1998 to 2017:the effect of DOTS strategy and further control[J]. Theoretical Biology and Medical Modelling, 2020, 17(1): 1-10. DOI:10.1186/s12976-019-0118-0
[3]	Chowell G, Fenimore P W, Castillo-Garsow M A, et al. SARS outbreaks in Ontario, Hong Kong and Singapore: the role of diagnosis and isolation as a control mechanism[J]. Journal of Theoretical Biology, 2003, 224: 1-8. DOI:10.1016/S0022-5193(03)00228-5
[4]	Naheed A, Singh M, Lucy D. Numerical study of SARS epidemic model with the inclusion of diffusion in the system[J]. Applied Mathematics & Computation, 2014, 229: 480-498. DOI:10.3969/j.issn.1008-5513.2014.05.007
[5]	Fanelli D, Piazza F. Analysis and forecast of COVID-19 spreading in China, Italy and France[J]. Chaos, Solitons & Fractals, 2020, 134: 109761.
[6]	Mandal M, Jana S, Nandi S K, et al. A model based study on the dynamics of COVID-19:prediction and control[J]. Chaos, Solitons & Fractals, 2020, 136: 109889.
[7]	Wang K, Lu Z, Wang X, et al. Current trends and future prediction of novel coronavirus disease (COVID-19) epidemic in China: a dynamical modeling analysis[J]. Mathematical Biosciences and Engineering, 2020, 17(4): 3052-3061. DOI:10.3934/mbe.2020173
[8]	Khajanchi S, Sarkar K. Forecasting the daily and cumulative number of cases for the COVID-19 pandemic in India[J]. Chaos, 2020, 30(7): 071101. DOI:10.1063/5.0016240
[9]	Van den Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1/2): 29-48.
[10]	Hasell J, Mathieu E, Beltekian D, et al. A cross-country database of COVID-19 testing[J]. Scientific Data, 2020, 7: 345. DOI:10.1038/s41597-020-00688-8
[11]	Pekpe K M, Zitouni D, Gasso G, et al. From SIR to SEAIRD: a novel data-driven modeling approach based on the grey-box system theory to predict the dynamics of COVID-19[J]. Applied Intelligence, 2022, 52(1): 71-80. DOI:10.1007/s10489-021-02379-2
[12]	Hussain T, Ozair M, Ali F, et al. Sensitivity analysis and optimal control of COVID-19 dynamics based on SEIQR model[J]. Results in Physics, 2021, 22(8): 103956.