单泉¹, 潘帅¹, 于学荞¹, 马廉洁²
1. 东北大学秦皇岛分校 控制工程学院, 河北 秦皇岛 066004;
2. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819
收稿日期：2022-01-25
基金项目：国家自然科学基金资助项目(51975113)；河北省自然科学基金资助项目(E2018501078)。
作者简介：单泉(1977-), 男, 江西赣州人, 东北大学副教授;
马廉洁(1970-), 男, 内蒙古赤峰人, 东北大学教授, 博士生导师。

摘要：将频率视为一种新的特征参数来分析振动特性.首先提出了振动特征频率提取原理, 通过快速点磨削振动特征提取试验获得了特征频率函数, 随后分析了加工/空载状态下不同水平的工艺参数对磨削振动的影响, 并结合砂轮与工件间的接触和能量传递关系分析了特征频率的变化规律.结果表明, 加工特征频率始终小于空载特征频率, 特征频率的相对偏差随砂轮线速度的增大而减小, 随磨削深度、进给速度的增大而增大, 同时比较了各工艺参数对特征频率的影响权重, 提出了改善加工效率的思路.
关键词：磨削振动特征频率工艺参数快速点磨削相对偏差
Effect of Quick-Point Grinding Technological Parameters on Grinding Vibration Frequency
SHAN Quan¹, PAN Shuai¹, YU Xue-qiao¹, MA Lian-jie²
1. School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China;
2. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China
Corresponding author: PAN Shuai, E-mail: psiyxq@163.com.

Abstract: In this paper, frequency is regarded as a new characteristic parameter to analyze vibration features. Firstly, the principle of vibration signal feature extraction was proposed, and the characteristic frequency function was obtained through the vibration feature extraction test of quick-point grinding. Then, the influence of different levels of technological parameters on grinding vibration under the machining or idle condition was analyzed. And the variation law of characteristic frequency was analyzed by comparing the contact and energy transfer relationship between the grinding wheel and workpiece. The results showed that the machining characteristic frequency is always smaller than the idle and the relative deviation of characteristic frequency decreases with the increase of the grinding wheel's linear velocity, and increases with the increase of grinding depth and feed velocity. At the same time, the influence weight of each technological parameter on the characteristic frequency was compared, and the idea of improving the machining efficiency was put forward.
Key words: grinding vibrationcharacteristic frequencytechnological parameterquick-point grindingrelative deviation
快速点磨削作为一种融合了CBN超硬磨料与CNC柔性加工的超高速磨削技术已广泛应用于国内外制造行业^[1], 因其具有超高线速度和点接触特性, 使磨削力大幅下降^[2], 磨削比能小, 产热少, 同时实现了精加工和高磨除率.磨削振动是使加工表面恶化的关键因素之一, 受工艺参数、机床刚度和加工系统不平衡程度等影响, 充分了解快速点磨削工艺与磨削振动的关系对实现高质量加工有重要意义.
目前, 关于机械加工振动的影响因素及快速点磨削工艺特性, 国内外****已经开展了诸多研究.Thomas等^[3]研究了车削过程中工艺条件对刀具振动的影响, 收集并分析了不同加工水平和几何参数下的刀具振动数据.Li等^[4]通过建立刀尖运动轨迹方程证明了车削加工表面粗糙化源于切削振动和进给量的共同作用.Zahia等^[5]针对切削用量和刀具振动对硬车表面粗糙度的综合影响建立了数学模型, 得出振动对表面质量的影响权重低于切削用量.Vikas等^[6]利用加工振动参数建立了钛合金车削表面粗糙度的一阶多元回归模型.Kim等^[7]提出了金刚石车削的表面生成模型, 解释了刀具振动在微观上对表面轮廓的拓扑效应.Elango等^[8]利用人工神经网络对不同参数水平下的刀具振动和刀具寿命进行了预测.马廉洁等^[9-11]通过快速点磨削振动特性试验, 分析了加速度信号的时频域特征, 证明了工艺参数对磨削振动的影响显著, 利用多算法改进BP神经网络对工程陶瓷快速点磨削工艺参数进行了优化.周培培等^[12]研究了钛合金外圆车削中切削用量与切削振动的关系, 证明了切削深度对振动的影响最大.
磨削振动的产生机理非常复杂, 目前的研究以振幅表征振动为主.为多角度探究振动机理, 优化磨削工艺, 需要开展振动特征参数提取工作.本文针对快速点磨削工艺参数对振动特征频率的影响展开研究, 提出了特征频率提取原理, 设计了不同参数水平下的特征频率提取试验, 获得了工艺参数对磨削振动的具体影响.
1 振动特征频率及提取原理机械加工过程中, 振动往往表现为受迫位置产生的小范围加速度波动, 如图 1所示, 这种波动本身极为复杂, 无法直接获取振动特征, 目前多用加速度信号振幅的均值进行表征^[12], 而将振幅均值后, 杂乱无序的波形近似成了当量形式的恒加速度, 会丢失信号的波动性.为了深入研究振动特性, 需在加速度信号中提取新的特征量.考虑将频率视为一种新的特征参数, 既实现了复杂波形的量化, 又保留了信号的波动特性.
图 1(Fig. 1)

图 1 振动信号时域波形图Fig.1 Time spectrum of vibration signal

为获取特征频率, 将加速度信号视为特殊的周期函数f(t)：

(1)

其中: c₀, l为常实数; g(x)为任一周期为2l的函数; ω_k为特征频率的整数倍; φ_k为初相.
现确定f(t)具体形式.根据完备正交系的性质, 任意周期函数都可以写成基本三角函数系的叠加, 所以可将三角函数系视为一组基, 在该数系下将振动信号函数f(t)展开成正余弦函数的线性组合.对于基本三角函数系, 其形式如下：
将f(t)展开得

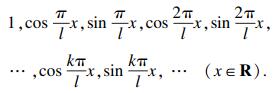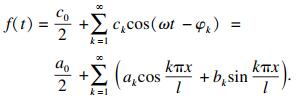(2)

其中：a_k, b_k, c_k为常实数.

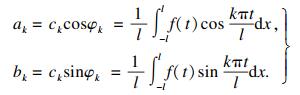(3)

即f(t)的频率变量, 为探究ω的变化规律, 需构造特征频率函数F(ω).
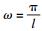
将式(3), ω_k=kω, cosθ=, sinθ=代入式(2)得

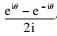
(4)

将式(4)推广, 取l→+∞, 有Δω_k→dω, 得

(5)

取F(ω)为

(6)

上述过程即为特征频率提取原理, 利用式(6)对图 1的时域信号进行特征提取可得到特征频率函数图, 如图 2所示.不同频率余弦波的叠加系数在谱图中表现为细而尖的峰, 把某一频率及其倍频均出现明显幅值的波峰称为特征峰, 对应的频率即为特征频率ω.
图 2(Fig. 2)

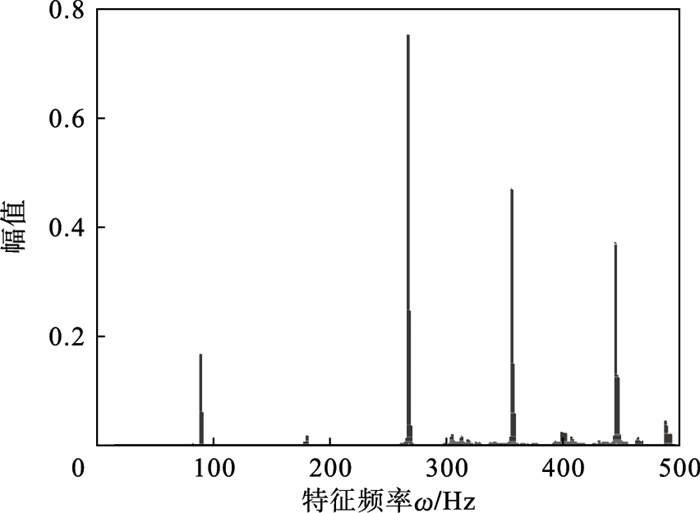图 2 振动信号频域波形图Fig.2 Frequency spectrum of vibration signal

将式(6)代入式(5)得

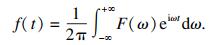(7)

式(7)说明特征频率函数持有原信号的全部信息, 验证了特征频率ω用于表征振动的充分性.
2 试验设计快速点磨削振动特征提取试验来研究工艺参数对特征频率的影响, 选用MK9025A型曲线磨床进行加工, 其主要参数为：砂轮转速3 000~6 600 r/min, 最大磨削深度35 mm, 最大砂轮直径180 mm.工件材料为低膨胀微晶玻璃, 主要组成元素为碳、氧、钛等.作为一种典型的难加工硬脆材料, 为降低加工成本, 提高加工效率, 宜采用快速点磨削工艺^[13].采用SD1413三向加速度传感器采集振动时域信号, 并利用DH5920-1394动态信号采集分析系统对信号进行处理, 试验装置如图 3所示.
图 3(Fig. 3)

图 3 快速点磨削振动特征提取试验装置Fig.3 Equipment in tests of vibration feature extraction in quick-point grinding

为研究磨削工艺的共性问题, 本文主要考察了砂轮线速度v_s, 磨削深度a_p及工件进给速度v_w对快速点磨削振动特征频率的影响, 并针对以上三要素设计了多水平简单单因素试验, 试验条件如表 1所示.
表 1(Table 1)

表 1 快速点磨削振动特征提取试验条件Table 1 Tests conditions of vibration feature extraction in quick-point grinding 序号 vs/(m·s-1) ap/mm vw/(mm·min-1) 1 32~64 0.05 15 2 48 0.015~0.15 15 3 48 0.05 5~55

表 1 快速点磨削振动特征提取试验条件 Table 1 Tests conditions of vibration feature extraction in quick-point grinding

3 工艺参数对特征频率的影响信号采集过程中, 系统将实时记录振动时域信号, 并对加工时段进行筛选, 利用特征频率提取原理从该部分信号中获得各参数水平下的特征频率函数, 并识取特征值来分析各工艺参数与ω的关系.
3.1 砂轮线速度对特征频率的影响快速点磨削作为超高速磨削技术的应用之一, 其砂轮线速度大, 变化范围广, 对磨削振动影响显著.在加工试验中, 设置a_p=0.05 mm, v_w=15 mm/min, v_s=32~64 m/s, 将采集的时域信号经特征提取获得特征频率ω, 如图 4所示.可观察到ω与v_s具有明显的线性关系, 这是由于ω存在与主轴转速成正比的基础值, 该值可从同工况的空载试验中提取, 因此将其定义为空载特征频率ω_b.
图 4(Fig. 4)

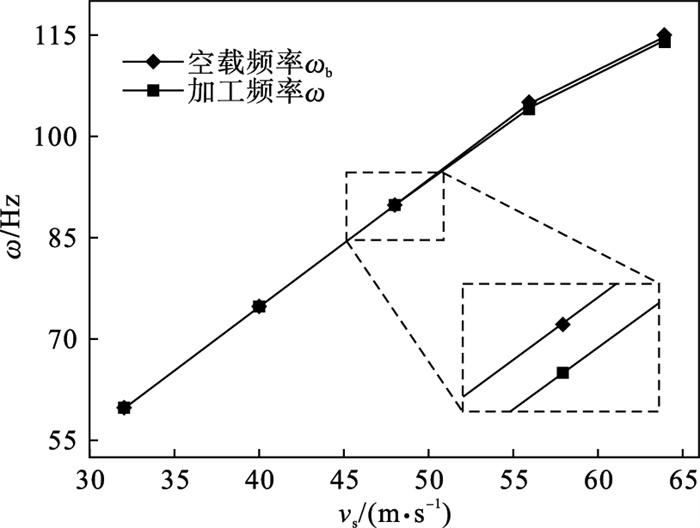图 4 砂轮线速度对特征频率的影响Fig.4 Effect of the grinding wheel's linear velocity on characteristic frequency

为探究工艺参数对ω的影响, 测定信号时, 记录了相应的空载信号并提取了ω_b, 如图 4所示.引入最大影响率ε衡量不同工艺参数对ω的影响权重, 同时计算了ω_b与ω的相对偏差e_r(ω)来表征工艺参数对ω的实际影响程度, 如图 5所示, 计算方式如下：
图 5(Fig. 5)

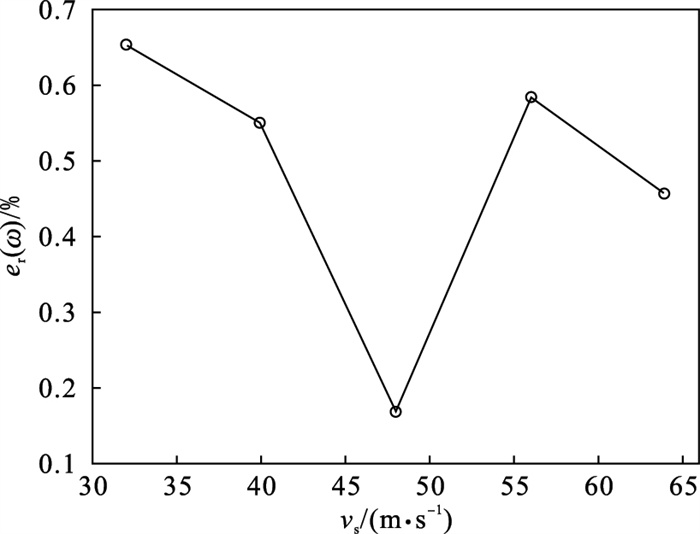图 5 砂轮线速度对相对偏差的影响Fig.5 Effect of the grinding wheel's linear velocity on relative deviation

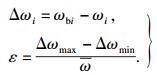(8)

(9)

其中: ω_i为任一工艺下的特征频率; ω_bi为与ω_i同工况的空载特征频率; ω为ω_i平均值; Δω_max, Δω_min分别为式(8)中Δω_i的最大值和最小值.
经计算, v_s的最大影响率=0.516 2%.结合图 4分析可知, 在不同的v_s下, 始终有ω_b>ω, ω与v_s存在明显的线性关系, 因此, 砂轮线速度对特征频率的影响显著.根据图 5可知, 随着v_s增大, e_r(ω)整体呈下降趋势, 但其中出现了上升的反常阶段, 考虑工件产生了谐振, 谐振是指系统在谐振频率下从周围环境吸收更多能量的现象, 在该状态下, 振动传递给工件的能量激增, 导致ω的相对偏差增大.
3.2 磨削深度对特征频率的影响磨削深度a_p对加工质量有明显影响.试验过程中, 在v_w=15 mm/min, v_s=48 m/s的工艺条件下, 在区间0.015~0.15 mm内改变a_p, 可获得ω, ω_b和e_r(ω)随a_p变化的曲线, 如图 6和图 7所示.
图 6(Fig. 6)

图 6 磨削深度对特征频率的影响Fig.6 Effect of grinding depth on characteristic frequency

图 7(Fig. 7)

图 7 磨削深度对相对偏差的影响Fig.7 Effect of grinding depth on relative deviation

经计算, a_p的最大影响率ε_ap=0.079 5%, 可见磨削深度对特征频率的影响较小, 图中e_r(ω)变化呈波动状, 无明显特征, 趋势线斜率为很小的正值, 数据点离散程度较大, 认为a_p对ω的影响可视为正相关, 但权重较小, 故易受其他因素干扰, 这一结论也与现有理论相符^{[5, 9]}.
3.3 进给速度对特征频率的影响进给速度对表面质量的影响最为显著^[14], 且与磨削深度共同决定了磨除效率, 是权衡加工质量和效率的另一重要参数.试验设置v_s=48 m/s，a_p=0.05 mm, v_w变化区间为32~64 mm/min, 得到ω，ω_b和e_r(ω)随v_w的变化曲线, 如图 8和图 9所示.
图 8(Fig. 8)

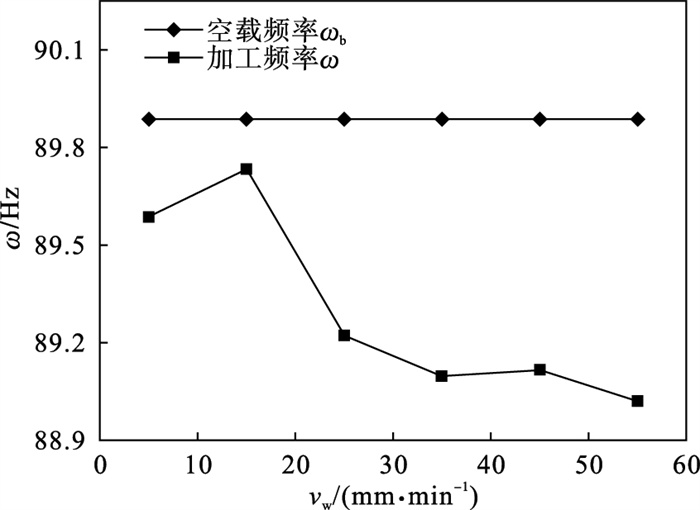图 8 进给速度对特征频率的影响Fig.8 Effect of feed velocity on characteristic frequency

图 9(Fig. 9)

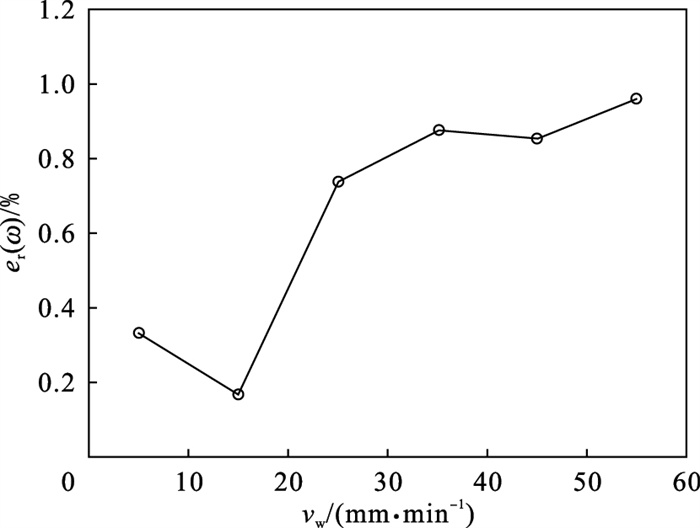图 9 进给速度对相对偏差的影响Fig.9 Effect of feed velocity on relative deviation

类比对a_p的分析, 计算v_w最大影响率ε_vw=0.797 1%, 其值约为ε_ap的10倍, 可见v_w对快速点磨削加工振动特性的影响远大于a_p, e_r(ω)数据离散程度小, 与v_w呈现明显的正相关, 可实现利用ω对v_w进行表征.
随着v_w增大, e_r(ω)的增长速率下降, 这是由于磨削温度上升, 导致工件材料受热软化, 加工阻力减小, 降低了载荷的增长速率, 使振动机械能的消耗减缓, 但磨削温度升高时温度场梯度过大会使升温速度下降, 所以当v_w继续升高, 磨削温度超过临界值时, e_r(ω)的增长速度开始恢复.
综合分析上述试验现象可知, 砂轮线速度v_s主要决定特征频率ω的基准, 进给速度v_w是ω下降的主要因素, 磨削深度a_p对ω的影响较小, 其效果易湮没于其他干扰中.对比快速点磨削加工过程和空载过程, ω总是小于ω_b, 这是由于砂轮与工件间的接触总会消耗能量从而削弱振动产生的工件材料去除, 不考虑能量传递时, 特征频率将被维持.而实际接触中, 砂轮与工件间产生阻力, 振动传递到工件上, 部分维持振动的能量被工件吸收转化为新的表面能, 因此接触后振动频率总是降低的.
分析不同工艺水平下e_r(ω)的变化趋势可知, 在高转速、小切深、小进给向低转速、大切深、大进给变化过程中, 磨削载荷增大, 材料去除方式由塑性流动变为脆性断裂, 表面及亚表面裂纹增多, 振动的机械能转化为裂纹生成的表面能, 振动的能量被消耗; 材料产生脆性去除后在工件表面形成凹坑, 导致砂轮与工件表面的微凸体接触概率降低, 挤压产生的弹性变形被削减, 维持振动的弹性势能减少; 当工件材料内部出现裂纹时, 其刚度会降低, 使工件的固有频率降低, 导致特征频率的相对偏差增大.由于上述原因, 振动的特征频率难以维系, 宏观表现为e_r(ω)增大.
4 结论1) 利用振动信号特征提取原理求解出特征频率函数F(ω), 证明该函数能继承振动信号函数f(t)的全部信息.
2) 特征频率ω存在基础值ω_b, 与主轴转速成正比, 且ω_b始终大于ω, ω的相对偏差e_r(ω)随砂轮线速度v_s增大而减小, 随磨削深度a_p、进给速度v_w增大而增大, 但与a_p的线性关系不明显.
3) 提出最大影响率ε, 并研究了三种工艺参数对特征频率ω的影响权重, 其中v_w的影响最大, v_s次之, a_p影响最小, 仅为v_w的10%, 因此为了抑制振动的影响, 提高加工效率, 可在合理范围内增大磨削深度.
参考文献

[1]	Ma L J, Gong Y D, Chen X. Study on surface roughness model and surface forming mechanism of ceramics in quick point grinding[J]. International Journal of Machine Tools and Manufacture, 2014, 77: 82-92. DOI:10.1016/j.ijmachtools.2013.11.001
[2]	T?nissen S, Klocke F, Feldhaus B, et al. Residual stress prediction in quick point grinding[J]. Production Engineering, 2012, 6(3): 243-249. DOI:10.1007/s11740-012-0382-x
[3]	Thomas M, Beauchamp Y, Youssef A Y, et al. Effect of tool vibrations on surface roughness during lathe dry turning process[J]. Computers & Industrial Engineering, 1996, 31(3): 637-644.
[4]	Li J, Wang C. Effect of the feed rate on three-dimensional topography of Ti-6Al-4V based on dynamic mechanical model analysis in cutting process[J]. The International Journal of Advanced Manufacturing Technology, 2019, 105: 1539-1547. DOI:10.1007/s00170-019-04373-y
[5]	Hessainia Z, Belbah A, Yallese M A, et al. On the prediction of surface roughness in the hard turning based on cutting parameters and tool vibrations[J]. Measurement, 2013, 46(5): 1671-1681. DOI:10.1016/j.measurement.2012.12.016
[6]	Upadhyay V, Jain P K, Mehta N K. In-process prediction of surface roughness in turning of Ti-6Al-4V alloy using cutting parameters and vibration signals[J]. Measurement, 2013, 46(1): 154-160. DOI:10.1016/j.measurement.2012.06.002
[7]	Kim D, Chang I, Kim S. Microscopic topographical analysis of tool vibration effects on diamond turned optical surfaces[J]. Precision Engineering, 2002, 26(2): 168-174. DOI:10.1016/S0141-6359(01)00115-5
[8]	Elango M, Annamalai A, Praveen Raju A. Production of cutting tool vibration in turning using artificial neural network[J]. IOP Conference Series: Materials Science and Engineering, 2021, 1013(1): 12003. DOI:10.1088/1757-899X/1013/1/012003
[9]	马廉洁. 工程陶瓷点磨削表面质量建模及其演化机理的研究[D]. 沈阳: 东北大学, 2014. (Ma Lian-jie. Research on modeling and evolution mechanism of surface quality of engineering ceramics in point grinding[D]. Shenyang: Northeastern University, 2014. )
[10]	马廉洁, 曹小兵, 巩亚东, 等. 基于遗传算法与BP神经网络的微晶玻璃点磨削工艺参数优化[J]. 中国机械工程, 2015, 26(1): 102-106. (Ma Lian-jie, Cao Xiao-bing, Gong Ya-dong, et al. Optimization of glass-ceramic spot grinding process parameters based on genetic algorithm and BP neural network[J]. China Mechanical Engineering, 2015, 26(1): 102-106.)
[11]	马廉洁, 陈杰, 巩亚东, 等. 基于PSO算法改进BP神经网络的氟金云母点磨削工艺参数优化[J]. 中国机械工程, 2016, 27(6): 761-766. (Ma Lian-jie, Chen Jie, Gong Ya-dong, et al. Optimization of fluoride mica spot grinding process parameters based on PSO algorithm to improve BP neural network[J]. China Mechanical Engineering, 2016, 27(6): 761-766. DOI:10.3969/j.issn.1004-132X.2016.06.010)
[12]	周培培, 李金泉, 许立福, 等. TA15钛合金切削振动与表面质量关系研究[J]. 工具技术, 2016, 50(5): 21-25. (Zhou Pei-pei, Li Jin-quan, Xu Li-fu, et al. Study on the relationship between cutting vibration and surface quality of TA15 titanium alloy[J]. Tool Engineering, 2016, 50(5): 21-25.)
[13]	Ma L, Yu A, Gu L, et al. Mechanism of compound fracture and removal in grinding process for low-expansion glass ceramics[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91: 2303-2313. DOI:10.1007/s00170-016-9915-3
[14]	Asiltürk ?, Akku?, H. Determining the effect of cutting parameters on surface roughness in hard turning using the Taguchi method[J]. Measurement, 2011, 44(9): 1697-1704.