1. 东北大学 资源与土木工程学院, 辽宁 沈阳 110819;
2. 辽河油田勘探开发研究院, 辽宁 盘锦 124010;
3. 东北大学 深部金属矿山安全开采教育部重点实验室，辽宁 沈阳 110819
收稿日期：2022-02-07
基金项目：国家自然科学基金资助项目(42177157)；国家重点研发计划项目(ZX20210496)；沈阳市中青年人才支持计划项目(RC210405)；中央高校基本科研业务费专项资金资助项目(N2101005, N2101037)。
作者简介：乔丽苹(1982-), 女, 山西晋城人, 东北大学副教授;
王者超(1980-)，男，山东高唐人，东北大学教授。
摘要：结构面的几何参数和力学参数随机分布导致岩体工程的稳定性具有高度不确定性.以我国某地下水封石油储备库项目为背景, 把结构面倾向、倾角、黏聚力及内摩擦角作为随机变量, 运用可靠度理论, 在数值模拟的基础上, 研究了围岩块体稳定性和支护系统可靠性, 并对支护参数进行检验与优化.结果表明：Ⅰ~Ⅳ级围岩块体稳定性可靠度指标分别为4.23，1.68，0.65和-0.07；对Ⅱ级、Ⅲ级和Ⅳ级围岩块体采取支护措施后, 可靠度指标分别为3.3，3.0和2.0；并对其支护间排距进行优化, 推荐值分别为2.8，2.0和1.6 m.
关键词：地下水封洞库参数不确定性Monte Carlo法失效概率支护可靠度参数检验与优化
Reliability Analysis of Rock Block Stability and Support for Underground Water-Sealed Storage Caverns
QIAO Li-ping1, LU Wei-li1, MIN Zhong-shun2, WANG Zhe-chao3
1. School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China;
2. Liaohe Oilfield Exploration and Development Research Institute, Panjin 124010, China;
3. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang 110819, China
Corresponding author: WANG Zhe-chao, E-mail: wangzhechao@mail.neu.edu.cn.
Abstract: The stochastic distribution of geometrical and mechanical parameters of rock joints causes a high degree of uncertainty in the stability of rock mass engineering. Taking a project of underground water-sealed storage caverns as an example, and considering the uncertainty of dip directions, dip angles, cohesion and friction angles, the reliability of surrounding rock block stability and support system are studied using the reliability theory and numerical simulation, and the support parameters are tested and optimized. The results show that the reliability indexes of the surrounding rock blocks of Grade Ⅰ to Ⅳ are 4.23, 1.68, 0.65 and -0.07, respectively. After the support system is applied to Grade Ⅱ, Ⅲ and Ⅳ surrounding rocks, the reliability indexes of the surrounding rock blocks are 3.3, 3.0 and 2.0, respectively. The row spacing between supports is optimized, and the recommended values are 2.8, 2.0 and 1.6 m for the surrounding rock blocks of Grade Ⅱ, Ⅲ and Ⅳ, respectively.
Key words: underground water-sealed storage cavernparameter uncertaintyMonte Carlo methodfailure probabilitysupport reliabilityparameter inspection and optimization
石油是现代工业的“血液”, 是国民经济和社会发展的重要战略资源.因此, 建立石油储备库, 拥有充足的石油储备, 对保障国家经济发展及国防安全有着不可估量的作用[1-2].相比地上储备库, 地下水封洞库具有储量大、安全性高、造价低、节约土地资源等优点, 被全球公认为“具有高度战略安全的储备库”[3-4].地下水封洞库一般建在硬质岩中[5], 天然岩体在其形成和存在的整个地质历史过程中, 经受了各种复杂的地质作用, 产生了大量的节理、断层等结构面[6], 且这些结构面的几何和力学参数具有随机分布的特点, 传统的确定性分析方法已不能准确地反映块体的稳定性和支护强度, 因此****们将可靠度理论引入到块体稳定性和支护系统中来解决此类工程问题[7-14].
对于地下工程支护系统可靠度的研究, 李健等[15]将隧道支护设计中锚杆间排距作为随机变量, 采用中心点法评估了可靠度指标.王卫军等[16]将岩体力学参数作为随机变量, 采用验算点法进行了可靠度指标的求解, 并分析了间排距对可靠度的影响.侯晓琳等[17]考虑力学参数随机性, 将优化求解法和Monte Carlo法相结合研究了可靠度理论.杨军伟等[18]采用Monte Carlo法研究了锚杆支护系统可靠度, 并分析了锚杆间排距和长度对可靠度的影响.Low等[19]结合一次二阶矩方法提出基于概率可靠性的隧道支护设计方法, 分析了楔形块体稳定性的两种安全系数定义不一致性的问题, 然后扩展了锚杆加固隧道的确定性公式使其可以进行锚杆可靠性设计.Lü等[20]采用一阶可靠性方法和响应面方法对可靠度指标进行求解, 并分析了锚杆长度对可靠性的影响.Oreste[21]提出了考虑岩体力学参数和支护材料力学参数概率分布的隧道初衬设计的概率数值分析方法.目前, 对于地上结构可靠度研究已有很多标准, 但地下结构还没有统一的标准, 对于地下水封洞库的相关研究仍处于摸索阶段.目前根据工程实践可以提出不同围岩经验性支护参数, 并控制其稳定性, 但基于可靠度的支护参数并不明确, 为了提高设计的科学性, 有必要从可靠度方面分析支护系统的参数设计是否合理.
本文以某地下水封石油洞库项目为背景, 在分析了结构面几何参数和力学参数不确定性的基础上, 研究了地下水封洞库各级围岩块体的稳定性, 采用Monte Carlo法计算各级围岩块体稳定性可靠度和锚杆支护可靠度, 并对支护参数进行检验与优化.
1 地下结构可靠度分析方法1.1 地下结构可靠度计算原理地下结构可靠度分析是将影响地下结构设计的各种主要变量视为非确定性的随机变量, 并应用概率论来研究这些随机变量的概率模型及其取值的统计规律.通过建立随机模型, 在分析模型中直接考虑随机变量的影响, 并基于变量的随机特性探讨结构的稳定性, 最终进行工程设计.针对地下水封洞库, 失稳破坏形式主要以块体失稳为主.因此, 在分析中通常采用安全系数Fs来反映块体的稳定性, 即当Fs>1时, 地下水封洞库处于稳定状态；当Fs=1时, 地下水封洞库处于极限状态；当Fs < 1时, 地下水封洞库失稳破坏.块体的滑动模式主要分为三种, 即直接垮落、沿单结构面滑动和沿双结构面滑动, 其安全系数公式分别如下：
 | (1) |
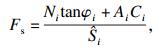 | (2) |
 | (3) |
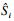
针对以上分析地下水封洞库围岩块体滑动的三种模式, 建立式(4)功能函数，x1, x2, …, xn为n个具有一定分布、统计独立的随机变量.在本文中, 分析块体可靠度时xn分别为结构面倾向、倾角、黏聚力和内摩擦角, 分析块体支护可靠度时xn分别为结构面倾向、倾角、黏聚力、内摩擦角和锚杆间排距.
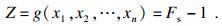 | (4) |
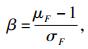 | (5) |
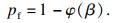 | (6) |
1.2 可靠度计算方法在本文可靠度分析中, 主要采用Monte Carlo法计算地下水封洞库可靠度指标.Monte Carlo法是一种依据统计抽样理论, 利用计算机研究随机变量的数值计算方法.该方法首先生成随机变量的样本, 然后将随机变量的样本输入获得功能函数的样本, 再统计失效区样本的数量从而统计失效概率.随机数的产生是实施Monte Carlo法的基础, 通过计算机程序产生[0, 1]一系列均匀分布的随机数μi, 将这些均匀分布的随机数代入随机变量x的模拟模型中, 则可得符合Fx(x)的随机变量的大量模拟样本系列：
 | (7) |
实践证明, Monte Carlo法的精度只与试验次数有关, 而与随机变量无关, 且试验次数越多, 随机变量的频率分布越接近于真实的概率分布.在实际中, 试验次数一般取频率分布收敛时所对应的数值, 在本文中试验次数取值为1000, 通过分析计算, 符合精度要求.
2 块体稳定性可靠度评价2.1 工程概况某地下水封洞库工程如图 1所示, 主要由7条主洞室、8条水幕巷道、2条施工巷道及1条操作巷道组成.主洞室为直边墙圆拱洞, 按NE70°向平行设置, 跨度为20 m, 高度为30 m, 洞室底板高程-60 m, 顶板高程-30 m.库址区岩体主要为二长花岗岩, 平均重度为28.63 kN/m3.根据岩土工程勘探报告确定结构面的几何参数, 结构面倾向、倾角主要根据整个库址区结构面极点等密度图、走向玫瑰花图统计出15 000余组倾向、倾角数据, 得到3组主要优势结构面, 并对这些数据进行概率统计.选择正态分布函数对结构面倾向、倾角进行概率密度拟合, 拟合优度R2均大于0.95, 可以得出倾向、倾角拟合效果较好.结构面黏聚力和内摩擦角根据《工程岩体分级标准》GB50218—2014确定, 其分布概型和特征值从相关文献获得.通过上述方法获得各级岩体结构面几何参数和力学参数主要特征值如表 1所示.
图 1(Fig. 1)
 | 图 1 地下结构布置图Fig.1 Layout diagram of underground structure |
表 1(Table 1)
 表 1 结构面和围岩统计参数Table 1 Statistical parameters of rock fracture and surrounding rock
| 表 1 结构面和围岩统计参数 Table 1 Statistical parameters of rock fracture and surrounding rock | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.2 可靠度计算在块体稳定性可靠度分析中, 考虑把结构面倾向、倾角、黏聚力和内摩擦角作为主要影响因素.将表 1中各级围岩结构面几何参数和力学参数代入块体分析程序Unwedge 3.0中, 建立块体分析模型, 如图 2所示.由主洞室与优势结构面产生的块体信息得知, 块体主要分布在洞室的顶部、底部和边墙, 且顶部块体6有沿单结构面滑动的趋势, 选择该块体为主要分析对象.
图 2(Fig. 2)
 | 图 2 各级围岩下地下水封洞库块体分布图Fig.2 Block distribution diagram of underground water-sealed storage caverns of surrounding rocks in all grades (a)—Ⅰ级；(b)—Ⅱ级；(c)—Ⅲ级；(d)—Ⅳ级. |
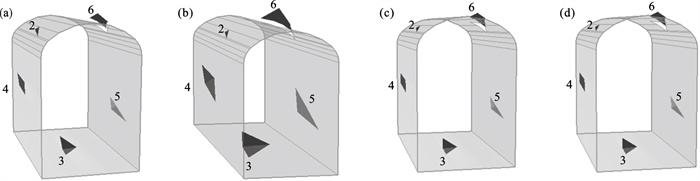
根据上述的可靠度计算方法, 可以得到各级围岩顶部块体的安全系数, 并采用频率直方图的方式对其进行数据拟合, 获得安全系数分布概型和特征值, 并将其均值和标准差代入式(5)和式(6)计算得出可靠度指标和失效概率.各级围岩块体安全系数频率直方图如图 3所示, 可以看出安全系数主要集中在0~5之间, 且随着围岩级别的升高, 小于1的安全系数越来越多, 即不稳定块体数量越来越多.各级围岩块体可靠度评价如表 2所示, 可以看出随着围岩级别的升高, 安全系数平均值逐级减小, 可靠度指标逐级降低, 失效概率逐级增加.相邻级别围岩安全系数平均值减小幅度分别为1.68，0.22和0.38, 相邻级别围岩可靠度指标降低幅度分别为2.55，1.03和0.72, 相邻级别围岩失效概率大幅增加, 且Ⅳ级围岩的失效概率高达0.573, 极大地威胁了地下水封洞库的稳定性.从以上对各级围岩块体安全系数分析得知, 除了Ⅰ级岩体可靠度指标比较高, 失效概率比较低, 不会对工程稳定性产生危害外, 其他三类岩体可靠度指标都比较低, 失效概率较高, 均超过一般所允许的风险水平(0.01), 在一定程度上对工程稳定性产生了危害.因此, 需对这三类围岩采取相应支护措施, 提升支护可靠度.
图 3(Fig. 3)
 | 图 3 各级围岩安全系数频率直方图Fig.3 Frequency histogram of surrounding rock safety factors in all grades (a)—Ⅰ级；(b)—Ⅱ级；(c)—Ⅲ级；(d)—Ⅳ级. |
表 2(Table 2)
表 2 各级围岩块体可靠度评价表Table 2 Reliability evaluation table of surrounding rock blocks in all grades
| 表 2 各级围岩块体可靠度评价表 Table 2 Reliability evaluation table of surrounding rock blocks in all grades |
为了验证本文试验次数的可靠性, 以Ⅱ级围岩为例, 统计分析了1 000次样本试验结果, 做出如图 4所示的失效概率收敛图.从图中可以看出, 曲线呈现先上升后平稳的趋势, 当试验次数达到600次时, 曲线开始逐渐收敛, 说明本文试验次数取值为1 000满足精度要求.
图 4(Fig. 4)
 | 图 4 失效概率收敛图Fig.4 Convergence diagram of failure probability |
3 锚杆支护参数检验与优化锚杆支护参数的检验与优化是在块体稳定性可靠度分析的基础上, 首先根据设计标准中的支护参数计算块体支护可靠度, 对各级围岩支护参数进行验证, 然后通过调整锚杆布置的间排距把各级围岩的可靠度指标分别调整为2，3和4, 得到合理的支护参数, 避免围岩支护过剩或不足.一般岩体工程可允许的风险水平不超过1%, 表 3为部分可靠度指标与失效概率的对应关系, 可知在可靠度指标为3左右时对应的失效概率符合要求, 可以据此对设计标准中各级围岩支护参数进行验证.
表 3(Table 3)
表 3 部分可靠度指标与失效概率对照Table 3 Comparison of partial reliability indexes and failure probability
| 表 3 部分可靠度指标与失效概率对照 Table 3 Comparison of partial reliability indexes and failure probability |
在设计标准中, Ⅱ级、Ⅲ级和Ⅳ级围岩的锚杆支护间排距分别为2.5，2.0和2.0 m, 锚杆长度为4.0 m.根据此支护参数计算的各级围岩锚杆支护可靠度见表 4, 当Ⅱ级围岩间排距为2.5 m时, 可靠度指标为3.3, 对应失效概率为5.19×10-4, 远小于0.01, 可知Ⅱ级围岩支护间排距采用2.5 m时会造成支护过剩, 增加工程造价；而Ⅳ级围岩间排距为2.0 m时, 可靠度指标为2, 失效概率为2.28×10-2, 大于0.01, 可知Ⅳ级围岩支护间排距采用2.0 m时会造成支护不足, 对工程稳定性产生一定的危害；而当Ⅲ级围岩间排距为2.0 m时, 可靠度指标为3.0, 失效概率为1.30×10-3, 满足一般岩体工程要求的风险水平, 可知Ⅲ级围岩支护间排距采用2.0 m较为合理.
表 4(Table 4)
表 4 设计标准中各级围岩支护参数评价表Table 4 Evaluation table of supporting parameters of surrounding rocks in all grades
| 表 4 设计标准中各级围岩支护参数评价表 Table 4 Evaluation table of supporting parameters of surrounding rocks in all grades |
通过以上分析可知, 设计标准中给出的支护参数并非完全合理, 由此可以对照可靠度指标与失效概率的关系表, 通过不断调整支护间排距来合理优化支护参数, 并给出各级围岩不同可靠度指标下的支护参数推荐值(见表 5)以供地下水封洞库施工参考.
表 5(Table 5)
表 5 各级围岩支护间排距推荐值Table 5 Recommended supporting row spacing of surrounding rocks in all grades?
| 表 5 各级围岩支护间排距推荐值 Table 5 Recommended supporting row spacing of surrounding rocks in all grades? | |||||||||||||||||||||||||||||||||||||||||||||||||
从部分可靠度指标与失效概率的关系表中可知, 若需满足一般岩体工程要求的风险水平, 即可靠度指标为3, Ⅱ级、Ⅲ级和Ⅳ级围岩支护间排距推荐值分别为2.8，2.0和1.6 m；若要提升工程可靠度, 即可靠度指标为4, Ⅱ级、Ⅲ级和Ⅳ级围岩支护间排距推荐值分别为2.0，1.2和0.6 m；若要降低工程可靠度, 即可靠度指标为2, Ⅱ级、Ⅲ级和Ⅳ级围岩支护间排距推荐值分别为4.0，2.4和2.0 m.对设计标准中Ⅱ级、Ⅲ级和Ⅳ级围岩支护间排距优化后取值分别为2.8，2.0和1.6 m.
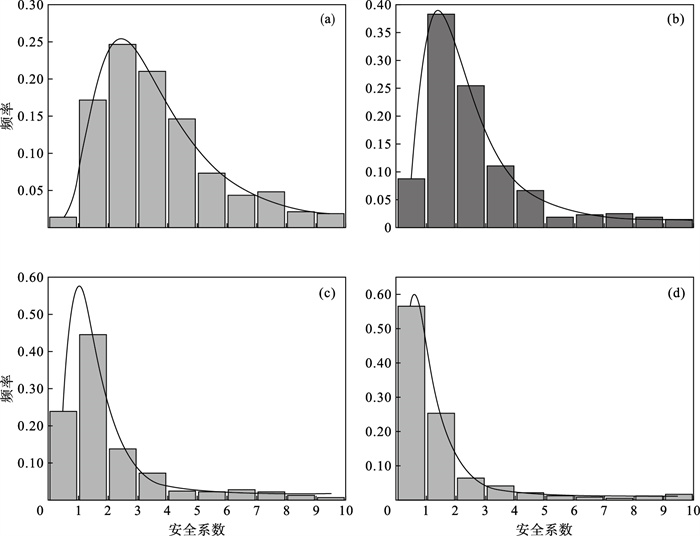
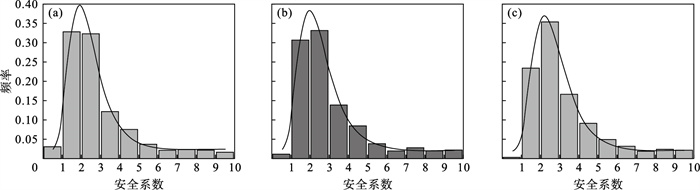
各级围岩安全系数频率直方图如图 5~图 7所示, 随着可靠度指标的增大, 安全系数小于1的块体逐渐减少, 说明优化支护措施后有了显著效果, 支护间排距推荐值比较合理.
图 5(Fig. 5)
 | 图 5 Ⅱ级围岩可靠度指标分别为2，3和4时安全系数频率直方图Fig.5 Frequency histogram of safety factor when the reliability index of Grade Ⅱ surrounding rocks is 2, 3 and 4 (a)—可靠度指标为2；(b)—可靠度指标为3；(c)—可靠度指标为4. |
图 6(Fig. 6)
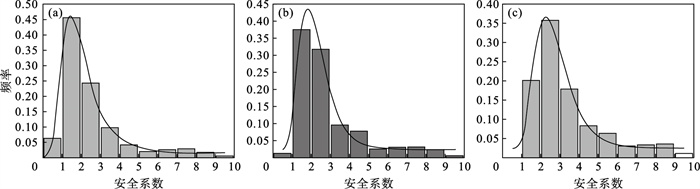 | 图 6 Ⅲ级围岩可靠度指标分别为2，3和4时安全系数频率直方图Fig.6 Frequency histogram of safety factor when the reliability index of Grade Ⅲ surrounding rocks is 2, 3 and 4 (a)—可靠度指标为2；(b)—可靠度指标为3；(c)—可靠度指标为4. |
图 7(Fig. 7)
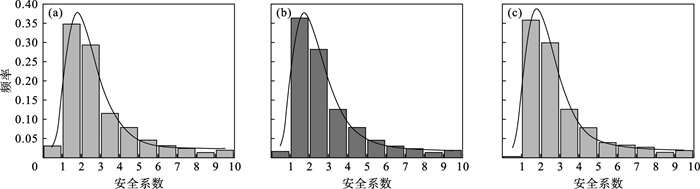 | 图 7 Ⅳ级围岩可靠度指标分别为2，3和4时安全系数频率直方图Fig.7 Frequency histogram of safety factor when the reliability index of Grade Ⅳ surrounding rocks is 2, 3 and 4 (a)—可靠度指标为2；(b)—可靠度指标为3；(c)—可靠度指标为4. |
4 结论1) 采用数值模拟的方法对地下水封洞库各级围岩块体稳定性进行分析, 得知块体主要分布在洞室的顶部、底部和边墙, 且顶部的块体最不稳定, 有沿单结构面滑动的趋势.
2) 采用Monte Carlo法计算Ⅰ~Ⅳ级围岩块体稳定性可靠度指标分别为4.23，1.68，0.65和-0.07, 失效概率分别为1.17×10-5，4.65×10-2，0.258和0.573, 除了Ⅰ级围岩满足工程要求的风险水平外, 其余三级围岩均超过一般岩体工程要求的风险水平, 需要采取相应的支护措施.
3) 采用设计标准中的支护间排距计算支护可靠度指标分别为3.3，3.0和2.0, 可知Ⅱ级围岩支护过剩, 需要增大间排距, Ⅳ级围岩支护不足, 需要减小间排距, Ⅲ级围岩支护满足一般工程要求, 则对Ⅱ级和Ⅳ级围岩支护参数进行优化, 间排距推荐值分别为2.8和1.6 m.
参考文献
| [1] | Liu H, Qiao L, Wang S, et al. Quantifying the containment efficiency of underground water-sealed oil storage caverns: method and case study[J]. Tunnelling and Underground Space Technology, 2021, 110: 103797. DOI:10.1016/j.tust.2020.103797 |
| [2] | Zhao X D, Deng L, Zhang S J. Stability analysis of underground water-sealed oil storage caverns in China: a case study[J]. Energy Exploration & Exploitation, 2020, 38(6): 2252-2276. |
| [3] | Xue Y G, Ning Z X, Qiu D H, et al. A study of water curtain parameters of underground oil storage caverns using time series monitoring and numerical simulation[J]. Journal of Zhejiang University: Science A, 2021, 22(3): 165-181. DOI:10.1631/jzus.A2000130 |
| [4] | 王者超, 陆宝麒, 李术才, 等. 地下水封石油洞库施工期安全风险评估研究[J]. 岩土工程学报, 2015, 37(6): 1057-1067. (Wang Zhe-chao, Lu Bao-qi, Li Shu-cai, et al. Risk assessment for an underground crude oil storage facility with water-curtaining system during construction phase[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(6): 1057-1067.) |
| [5] | Qiao L P, Wang Z C, Li S C, et al. Assessing containment properties of underground oil storage caverns: methods and a case study[J]. Geosciences Journal, 2017, 21(4): 579-593. DOI:10.1007/s12303-016-0063-4 |
| [6] | Zhang B, Wang H, Wang L, et al. Large-scale field test on abandoned deep anhydrite mine-out for reuse as crude oil storage—a case study[J]. Engineering Geology, 2020, 267: 105477. DOI:10.1016/j.enggeo.2020.105477 |
| [7] | Langford J C, Diederichs M S. Reliability based approach to tunnel lining design using a modified point estimate method[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60: 263-276. DOI:10.1016/j.ijrmms.2012.12.034 |
| [8] | Xu Z H, Gao B, Li S C, et al. A groundwater seal evaluation method based on water inflow for underground oil storage caverns[J]. Tunnelling and Underground Space Technology, 2018, 82: 265-277. DOI:10.1016/j.tust.2018.08.030 |
| [9] | Hoek E. Reliability of Hoek-Brown estimates of rock mass properties and their impact on design[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(1): 63-68. DOI:10.1016/S0148-9062(97)00314-8 |
| [10] | Li Z, Xue Y, Li S, et al. An analytical model for surrounding rock classification during underground water-sealed caverns construction: a case study from eastern China[J]. Environmental Earth Sciences, 2019, 78(20): 1-11. |
| [11] | 王者超, 李术才, 乔丽苹, 等. 地下石油洞库水封性评价方法体系及应用[J]. 岩土工程学报, 2016, 38(11): 2033-2042. (Wang Zhe-chao, Li Shu-cai, Qiao Li-ping, et al. Assessment methods for containment properties of underground crude oil storage caverns and their applications[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(11): 2033-2042. DOI:10.11779/CJGE201611013) |
| [12] | Li Z K, Lu B, Zou J, et al. Design and operation problems related to water curtain system for underground water-sealed oil storage caverns[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8(5): 689-696. DOI:10.1016/j.jrmge.2016.06.003 |
| [13] | Li H Z, Low B K. Reliability analysis of circular tunnel under hydrostatic stress field[J]. Computers and Geotechnics, 2010, 37(1/2): 50-58. |
| [14] | Goh A T C, Zhang W. Reliability assessment of stability of underground rock caverns[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 55: 157-163. DOI:10.1016/j.ijrmms.2012.07.012 |
| [15] | 李健, 郭忠平, 郭嘉兴. 基于中心点法的井下巷道锚杆支护可靠性分析[J]. 煤矿安全, 2019(4): 237-240. (Li Jian, Guo Zhong-ping, Guo Jia-xing. Reliability analysis of underground roadway bolt support based on central point method[J]. Safety in Coal Mines, 2019(4): 237-240.) |
| [16] | 王卫军, 侯朝炯. 回采巷道煤帮锚杆支护可靠性分析[J]. 岩石力学与工程学报, 2001, 20(6): 813-816. (Wang Wei-jun, Hou Chao-jiong. Reliablity analysis on coal wall bolting of extraction callery[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 813-816. DOI:10.3321/j.issn:1000-6915.2001.06.013) |
| [17] | 侯晓琳, 郑怀昌, 张晓君. 矩形巷道锚杆支护系统可靠度分析研究[J]. 煤炭科学技术, 2016, 44(sup 1): 31-34. (Hou Xiao-lin, Zheng Huai-chang, Zhang Xiao-jun. Reliability analysis of bolting support system in rectangular tunnels[J]. Coal Science and Technology, 2016, 44(sup 1): 31-34.) |
| [18] | 杨军伟, 苏静, 刘泽. 基于可靠性分析的沿空留巷顶板支护效果研究[J]. 矿业安全与环保, 2013, 40(2): 62-65. (Yang Jun-wei, Su Jing, Liu Ze. Research of roof support effect for gob-side retained roadway based on reliability analysis[J]. Mining Safety & Environmental Protection, 2013, 40(2): 62-65. DOI:10.3969/j.issn.1008-4495.2013.02.020) |
| [19] | Low B K, Einstein H H. Reliability analysis of roof wedges and rockbolt forces in tunnels[J]. Tunnelling and Underground Space Technology, 2013, 38: 1-10. DOI:10.1016/j.tust.2013.04.006 |
| [20] | Lü Q, Xiao Z P, Ji J, et al. Reliability based design optimization for a rock tunnel support system with multiple failure modes using response surface method[J]. Tunnelling and Underground Space Technology, 2017, 70: 1-10. DOI:10.1016/j.tust.2017.06.017 |
| [21] | Oreste P P. A probabilistic design approach for tunnel supports[J]. Computers and Geotechnics, 2005, 32(7): 520-534. |
