沙成满, 王星, 杨慧敏
东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期：2022-01-21
基金项目：“十三五”国家重点研发计划项目(2016YFC0801603, 2017YFC1503105)。
作者简介：沙成满(1964-), 男, 黑龙江哈尔滨人, 东北大学副教授。

摘要：为研究潜水面升降对充水采空区渗透系数的影响, 根据立方定律推导以应变为参数的3个渗透主方向上的等效渗透系数, 通过FISH函数完善FLAC^3D的非饱和渗流计算功能, 基于FLAC^3D的流固耦合计算模式, 对采动岩体的等效连续介质流固耦合模型非饱和单元进行修正, 实现充水采空区渗流场与应力场的模拟计算.通过主渗透系数比与1差值的绝对值反映渗流场对应力场的影响程度, 对比模型修正前后矿柱中部单元的计算结果可知：该值随潜水面升高而增大；模型修正前渗流场对应力场的影响大于修正后；模型修正后最大和最小主应变的变化曲线在饱和度为1后出现拐点.因修正前渗流模型参数与饱和渗流参数相同, 由此可验证修正后的模型更符合非饱和渗流理论.最后通过与实际工况中地下水渗流量的数据对比, 验证了修正后的模型更符合实际.
关键词：充水采空区流固耦合渗透系数渗流模型FLAC^3D
Seepage Model of Water-Filled Goaf Based on Fluid-Solid Interaction
SHA Cheng-man, WANG Xing, YANG Hui-min
School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: SHA Cheng-man, E-mail: shachengman@mail.neu.edu.cn.

Abstract: In order to study the influence of the rise and fall of the water table on the permeability coefficients of the water-filled goaf, the equivalent permeability coefficients in three main permeability directions with strain as parameters were derived according to the cubic law. FISH function was used to improve the unsaturated seepage calculation function of FLAC^3D based on the fluid-solid coupling calculation model, and the unsaturated element of the equivalent continuous medium fluid-solid coupling model of mining rock mass was modified to realize the simulation calculation of the seepage field and stress field of water-filled goaf. The influence of the seepage field on the stress field was reflected by the absolute value of the difference between principal permeability coefficient ratio and 1. By comparing the calculation results of pillar central unit before and after model modification, it could be seen that: the value increases with the rise of the water table. The effect of seepage field on stress field before model modification is greater than that after model modification. After model modification, the maximum and minimum principal strain curves show an inflection point when the saturation is 1. Since the parameters of the seepage model before modification are the same as those of saturated seepage, it can be verified that the modified model is more consistent with the unsaturated seepage theory. Finally, by comparing the data of the groundwater seepage flow in actual working conditions, the modified model is verified to be more consistent with the reality.
Key words: water-filled goaffluid-solid couplingpermeability coefficientseepage modelFLAC^3D
弓长岭老岭矿区水文工程地质环境复杂, 岩体质量普遍较差, 矿体与围岩接触, 并出现破碎.采空区多位于潜水面以下, 处于充水状态, 受渗流场影响较大.矿区经多年水文地质勘察和流量测试, 通过水头损失确定采空区渗流场为非饱和渗流场.在充水采空区治理过程中, 因泄水导致潜水面降低形成非饱和区, 计算采空区渗流场需考虑非饱和渗流.
在众多岩土、水利、能源工程等领域均涉及饱和-非饱和渗流分析, 如降雨导致岩体边坡滑坡、水位变化时的土坝渗流、矿产资源二次开采等.但目前非饱和渗流模型多基于非饱和土渗流理论, 只适用于非饱和土渗流, 不能直接应用于裂隙岩体渗流.国内外****已对采空区流固耦合渗流模型进行深入研究：Biot^[1]建立三维固结理论, 奠定多孔介质模型与流体流固耦合作用的理论基础；耿克勤等^[2]根据节理岩体的力学本构关系, 推导出岩体的等效渗透系数与应力、应变的耦合关系；白国良等^[3]建立采动岩体的等效连续介质流固耦合模型, 研究了采空区围岩渗透系数变化的普遍规律.但等效连续介质流固耦合模型在进行渗流计算过程中, 因FLAC^3D在非饱和计算功能中的非饱和区的饱和度被强制为1, 渗透系数与饱和区相同, 这与非饱和渗流理论相悖.
本文基于等效连续介质模型, 通过修正渗透系数与饱和度, 完善其非饱和渗流计算功能.通过对比简单三维模型修正前后的计算结果, 及弓长岭老岭矿区的充水采空区泄水后非饱和渗流的实测流量, 验证修正后模型更符合实际工况.
1 修正等效连续介质模型1.1 非饱和渗流基本原理对于多孔连续介质模型, 饱和-非饱和渗流方程为

(1)

式中：q_i为单位流量, m·s^-1；k_il为饱和渗透系数, m·s^-1；k_r(s)为相对渗透系数；h_j为水力梯度,%.
由式(1)可知, 非饱和渗流不同于饱和渗流, 渗透系数随饱和度变化.而FLAC^3D在渗流计算过程中采用达西定律.因此等效连续介质模型在裂隙岩体中的渗流方程可假定为^[4]

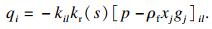(2)

式中：ρ_f为流体密度, kg·m^-3; x_j为笛卡尔坐标分量, m；g_j为重力加速度分量, m·s^-2；p为孔隙水压力, Pa.
1.2 非饱和渗流计算功能的完善等效连续介质模型中, 裂隙岩体与均质土体具有相似的渗透规律, 可通过FISH函数完善FLAC^3D的非饱和渗流计算功能^[5-6], 实现采动岩体的等效连续介质流固耦合模型的计算^[7-8].
对于非饱和土中的含水率, Van Genuchten于1980年提出了体积含水率与负压的关系方程^[9]：

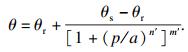(3)

式中：θ为体积含水率,%；θ_r为残余体积含水率,%；θ_s为饱和体积含水率,%；ɑ，n′，m′为拟合参数.
体积含水率与饱和度关系式为θ=nS，n为孔隙率.将其代入式(3)可得饱和度与负孔隙水压力的关系式^[10]：

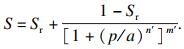(4)

式中：S为饱和度,%；S_r为残余饱和度,%.
岩体的拟合参数可采用GEO-Slope软件的默认值, 即：ɑ=10, n′=2, m′=1.根据上述公式, 通过FISH函数内置变量的单元孔隙水压力.
1.3 等效渗透系数的修正在等效连续介质模型中, 岩体的初始渗透系数可假设为各项同性.岩体受采动影响后, 非连续介质模型可用各向异性介质模型等效代替.在FLAC^3D中, 可通过不同方向上的应变反映在流固耦合计算过程中, 因岩体屈服或脆性破坏导致各方向渗透系数的变化规律^[11-12].
对于二维裂隙岩体, z方向上渗透系数K_z与x方向上应变Δε_x的关系式为^[13]

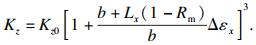(5)

式中：b为裂隙宽度, mm；L_x为裂隙间距, m；R_m为模量比, 控制岩块应变与裂隙应变的比值, 0≤R_m≤1.
对于各向异性渗流模型中的6个渗透系数, 可转移到3个渗透主方向上得到3个主渗透系数K_x，K_y，K_z^[14].根据式(5), 某一方向上主渗透系数的变化可表示为其他两个方向上的采动应变函数.3个主渗透系数可表示如下：

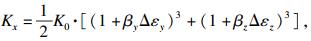(6)

(7)

(8)

式中：β_x=1+L_x(1-R_m)/b_x；β_y=1+L_y(1-R_m)/b_y；β_z=1+L_z(1-R_m)/b_z.
修正后非饱和单元渗透系数k=k_sat·k_r(s), k_sat为饱和单元渗透系数, k_r(s)为单元相对渗透系数.根据相对渗透系数计算公式k_r(s)=S²·(3-2S), 可得修正后非饱和单元的3个主方向渗透系数与饱和度关系式：

(9)

(10)

(11)

2 修正前后模型计算结果对比2.1 简单三维模型建立和模型参数取值为验证对模型修正后充水采空区围岩渗透系数比修正前更符合实际, 建立三维模型.模型建立步骤如下：
1) 在FLAC^3D中建立三维模型, 模型长50 m, 宽50 m, 高70 m, 设置采空区位于模型正中央偏下, 为边长10 m的正立方体.采空区附近围岩单元加密, 共计88 000个单元, 数值模型如图 1所示.
图 1(Fig. 1)

图 1 数值模型Fig.1 Numerical model

2) 力学模型采用摩尔-库仑模型, 平衡地应力后开挖采空区.模型上表面为自由边界, 其他边界均约束相应方向上的位移.
3) 通过FISH函数修正渗透系数与饱和度.设置额外变量主渗透系数比K_x/K₀, K_y/K₀, K_z/K₀, 可用于反映主渗透系数变化情况和潜水面对渗透系数变化规律的影响.设置孔隙水为潜水, 埋藏在第一个稳定隔水层之上, 使采空区内充满水.设置数值模型渗流边界为不透水边界, 建立流固耦合模型.
4) 力学模型参数选取：为确保简单三维模型计算结果符合实际, 力学模型参数取何家采区和大砬子采区处地质勘测数据.
通过对矿区岩芯进行采样加工, 进行岩石模量与强度实验, 获得岩石体抗压强度、弹性模量等物理参数.考虑岩石样品不能完全代表岩体, 采用面波法, 利用面波的频散曲线, 得到不同深度的面波传播速度关系, 再将面波速度换算成纵波速度, 参照《工程岩体分级标准》(GB50218—2014), 可以得到不同深度的岩体完整性指数.岩体力学参数取值以实验为参考, 以剪切波束的测定为主要依据.A组和B组取自不同分级与分区(见图 1和表 1), B区受到爆破影响较破碎级别低, A区为基本不受爆破影响的正常岩体.
表 1(Table 1)

表 1 数值模型力学参数Table 1 Mechanical parameters of numerical model 分组 重力密度 变形模量 泊松比 内摩擦角 黏聚力 kN·m-3 GPa (°) MPa A 26.12 17.34 0.259 5 47.91 1.384 B 22.54 1.394 0.349 27.24 0.21

表 1 数值模型力学参数 Table 1 Mechanical parameters of numerical model

渗流模型参数选取：流体体积模量取常温下水文地质勘测数据, 孔隙率、裂隙间距和宽度取均值, 选取弓长岭铁矿床老岭矿区2线某工作面采空区泄水时, 根据现场实验观测数据计算得到的渗透系数k_h, 按公式k=k_h×1.02×10^-6换算为FLAC^3D中所需的单位, 见表 2.
表 2(Table 2)

表 2 渗流模型流体和裂隙参数Table 2 Fluid and fracture parameters of seepage model 孔隙率 流体密度 体积模量 渗透系数 裂隙间距 裂隙宽度 kg·m-3 GPa m2·Pa-1·s-1 m mm 0.35 1000 2.05 2.5×10-8 0.5 0.2

表 2 渗流模型流体和裂隙参数 Table 2 Fluid and fracture parameters of seepage model

2.2 模型修正前后的主渗透系数比在流固耦合计算中, 改变潜水面高度会导致模型中渗流场的改变, 且随着潜水面的升高, 渗流场对应力场影响逐渐增大.为方便比较, 可采用主渗透系数比与1差值的绝对值表示渗透系数变化率, 用以反映渗流场对采空区应力场的影响程度, 其绝对值越大, 渗流场对应力场影响越大.
为证明修正后模型比修正前更符合实际, 选取潜水面高度从20 m上升至30 m的阶段分析渗透系数变化规律, 即潜水面从采空区底板上升至顶板.根据潜水面高度分为11个工况, 潜水面每升高1 m监测记录一次数据.选取y坐标为25的截面中采空区顶板中部, 即左侧第5单元分析.模型修正前后, 采空区顶板中部3个方向上的主渗透系数变化率随潜水面高度变化规律如图 2所示.
图 2(Fig. 2)

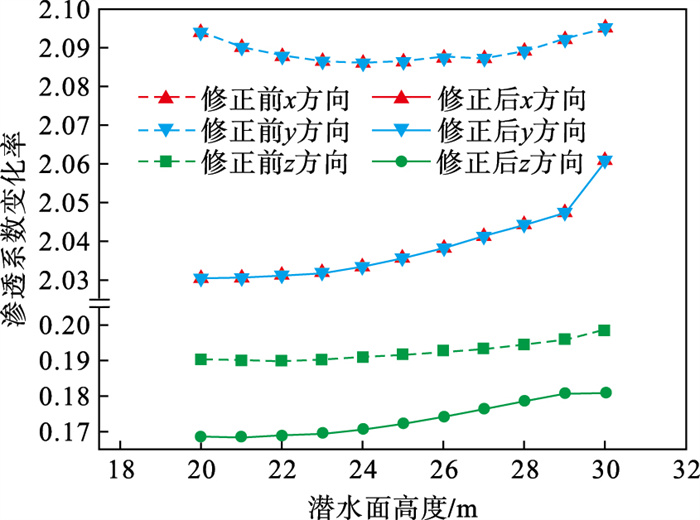图 2 顶板中部主渗透系数变化率曲线Fig.2 Change rate curves of main permeability coefficients in the middle of the roof

通过对比修正前后采空区顶板中部的渗透系数变化率曲线可知：渗透系数变化率随潜水面升高而增大, 且模型修正后的渗透系数变化率低于修正前.但模型修正前的x与y方向上的渗透系数变化率先增大后减小, 不符合此规律.
在潜水面上升过程中, 潜水面高度低于30 m时, 所选取的单元位于非饱和区, 计算结果受潜水面高度影响较小, 曲线上升幅度较小.潜水面升高至30 m, 即潜水面淹没采空区时, 模型修正后x与y方向上的渗透系数变化率明显增大.因此模型修正后的曲线变化规律更符合理论值.
选取采空区左侧矿柱中部, 即底部第5单元分析, 3个方向上的主渗透系数变化率随潜水面高度变化规律如图 3所示.
图 3(Fig. 3)

图 3 矿柱中部主渗透系数变化率曲线Fig.3 Change rate curves of main permeability coefficients in the middle of the pillar

通过对比修正前后采空区矿柱中部的渗透系数变化率曲线可知：与采空区顶板中部单元相同, 模型修正前的渗透系数变化率同样随潜水面升高而增大, 且模型修正前的变化率大于修正后.
在潜水面上升过程中, 在潜水面高度低于25 m时, 渗透系数变化率曲线较平缓, 其值基本不受潜水面变化影响.而在潜水面高度超过25 m后, 所选取的矿柱中部单元位于潜水面之下, 由非饱和单元变为饱和单元.此时模型修正后的渗透系数变化率明显增大.与之相比, 模型修正前的渗透系数变化率基本无变化, 不能反映单元由非饱和状态转化为饱和状态的过程.因此模型修正后的曲线变化规律更符合理论值.
2.3 模型修正前后的最大和最小主应变为证明修正后模型比修正前更符合实际, 除对比不同潜水面高度下的主渗透系数比外, 还需对比无地下水影响的力学模型变量.可选取模型修正前后和无地下水影响的条件下, 采空区围岩的最大和最小主应变进行对比.
选取y坐标为25的截面上采空区左侧矿柱中部, 即矿柱底部第5单元分析.模型修正前后, 采空区矿柱中部最大和最小主应变随潜水面变化规律如图 4和图 5所示.
图 4(Fig. 4)

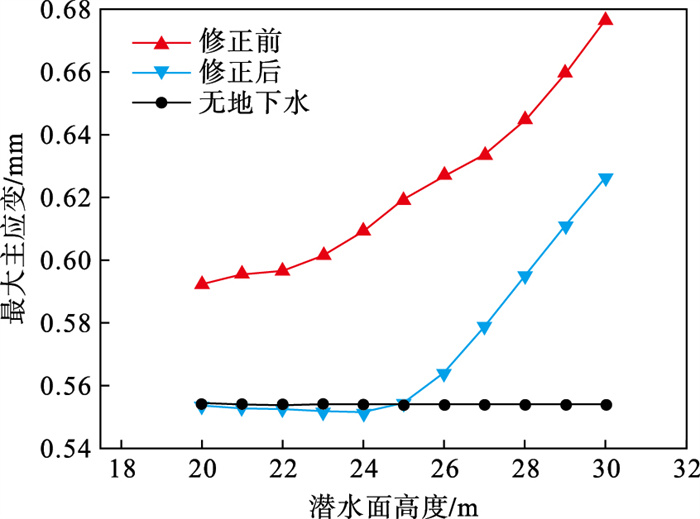图 4 潜水面对矿柱中部最大主应变影响Fig.4 Influence of groundwater level on maximum principal strain in the middle of the pillar

图 5(Fig. 5)

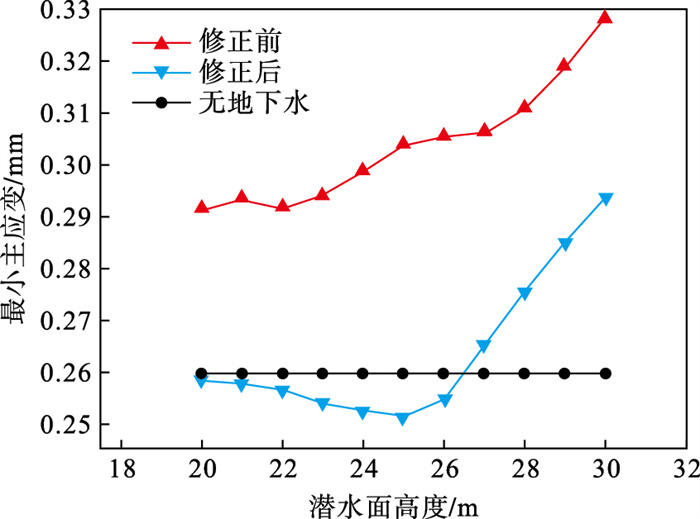图 5 潜水面对矿柱中部最小主应变影响Fig.5 Influence of groundwater level on minimum principal strain in the middle of the pillar

通过对比修正前后采空区矿柱中部的最大和最小主应变曲线可知：对于修正前的模型, 矿柱中部单元的最大和最小主应变均大于修正后, 其值随潜水面升高而增大.
而对于修正后的模型, 在潜水面低于25 m时, 矿柱中部单元位于非饱和区, 受负孔隙水压力的影响, 最大和最小主应变均略小于无地下水影响的工况.而在潜水面高于25 m后, 矿柱中部单元位于饱和区, 最大和最小主应变迅速增长且逐渐超过无地下水影响的工况.
由此可知, 修正后的模型可区分饱和渗流与非饱和渗流对应力场的影响, 而修正前的模型不具备此功能, 可初步从理论上验证修正后的模型比修正前更符合实际.
3 工程实例分析为从实际工程角度验证修正后模型更符合实际, 以弓长岭铁矿床老岭矿区2线某工作面为原型, 参考地质剖面图建立三维流固耦合模型, 模型长200 m, 宽80 m, 最高点207 m, 共计89 656个单元, 岩层简化为三层.采空区为马蹄形, 围岩附近模型单元细化, 如图 6所示.
图 6(Fig. 6)

图 6 老岭矿区数值模型Fig.6 Numerical model of Laoling mining area

设置力学模型为摩尔-库仑模型, 平衡地应力后开挖采空区, 模型上表面为自由边界, 其他边界均约束相应方向上的位移.力学模型参数获取方式与表 1相同, 取弓长岭铁矿床老岭矿区2线地质勘测数据, 力学模型岩体参数取值见表 3.
表 3(Table 3)

表 3 老岭矿区各岩层力学参数Table 3 Mechanical parameters of strata in Laoling mining area 岩层 重力密度 变形模量 泊松比 内摩擦角 黏聚力 kN·m-3 GPa (°) MPa A 24.90 8.800 0.290 0 41.20 0.860 B 24.52 6.140 0.299 5 39.11 0.708 C 24.26 5.436 0.306 0 37.56 0.640

表 3 老岭矿区各岩层力学参数 Table 3 Mechanical parameters of strata in Laoling mining area

设置渗流模型为各向异性, 模型底部和边缘设置不透水边界, 渗流模型参数同表 2, 利用流固耦合功能计算模型中初始孔隙水压力, 建立与真实工况相近的初始孔压场.
充水采空区的治理需对其进行泄水处理, 可通过约束采空区的孔隙水压力模拟采空区泄水过程.为保证渗透系数在泄水过程中实时更新, 设置每隔0.001更新一次渗透系数.取y坐标为40的截面分析, 模型修正前, 采空区泄水后各单元在3个主渗透方向上的渗流量分布如图 7所示.
图 7(Fig. 7)

图 7 模型修正前采空区流量分布Fig.7 Contours of goaf seepage flow before model modification (a)—x方向；(b)—y方向；(c)—z方向.

模型修正前, 受采空区开挖方向的影响, y方向上的渗流量最大值远小于x与z方向的渗流量最大值, 且采空区围岩中渗流量较大的单元分布不规律, 与实际工况不符.模型修正后, 采空区泄水后各单元在3个主渗透方向上的渗流量分布如图 8所示.
图 8(Fig. 8)

图 8 模型修正后采空区渗流量分布Fig.8 Contours of goaf seepage flow after model modification (a)—x方向；(b)—y方向；(c)—z方向.

模型修正后, 采空区围岩在x和z方向上的渗流量分布规律基本一致, 其渗流量最大单元的流量小于修正前的渗流量；而在y方向上的渗流量最大单元的流量则大于修正前.
选取上方采空区顶部单元z方向上的渗流量与实测值对比.因该单元底部面积约2 m², 将计算结果换算为采空区顶部每平方米的渗流量, 对比结果如表 4和图 9所示.
表 4(Table 4)

表 4 采空区上方泄水后顶部观测孔渗流量变化Table 4 Change of seepage flow rate of observation hole at the top after drainage above the goaf? m3·d-1 时间/h 修正前 修正后 实测值 1 24.645 384 0.011 110 0.013 1 2 20.125 886 0.011 106 0.012 9 3 18.662 832 0.011 110 0.012 9 4 16.862 731 0.011 113 0.012 7 5 16.048 454 0.011 113 0.012 8 6 15.412 810 0.011 113 0.012 8 7 14.855 011 0.011 113 0.012 6 8 14.428 152 0.011 113 0.012 6 9 14.124 370 0.011 113 0.012 7 10 13.856 270 0.011 114 0.012 6

表 4 采空区上方泄水后顶部观测孔渗流量变化 Table 4 Change of seepage flow rate of observation hole at the top after drainage above the goaf?

图 9(Fig. 9)

图 9 采空区上方泄水后顶部观测孔流量变化曲线Fig.9 Flow curves of observation hole at the top of the goaf after drainage

通过对比采空区顶部观测孔流量的变化曲线可知：模型修正前, 采空区顶部单元的渗流量从24.645 384 m³·d^-1降低到13.856 270 m³·d^-1, 与实测值相差甚远.因渗透系数和饱和度仍与饱和区单元相同, 实际上在进行饱和渗流计算.
而模型修正后, 位于非饱和区的采空区顶部单元的地下水渗流量基本不变, 约为0.011 m³·d^-1, 与实测值相近.因泄水过程完成, 采空区围岩内仅残余少量水, 孔隙水压力降低, 其渗流量趋于稳定.计算结果更接近实测值, 符合非饱和渗流理论, 证明修正后的模型比修正前更符合实际.
上述结果表明, 通过对等效连续介质模型的渗透系数和饱和度进行修正，可进一步完善对采动岩体的饱和-非饱和渗流的计算与研究.对采空区的泄水处理能有效地使充水型采空区围岩内孔隙水压力释放, 泄水后地下水渗流量较低且趋于稳定, 对避免发生涌水和突水等灾害具有显著效果.
4 结论1) 通过推导以应变为参数的等效连续介质模型和完善FLAC^3D的非饱和渗流功能, 建立采动岩体饱和-非饱和渗流的流固耦合计算模型.通过对比非饱和渗流参数修正前后的计算结果和实际工程中的渗流量, 验证模型的合理性.
2) 通过对比修正非饱和渗流参数前后的计算结果可知, 修正后的模型具有区分饱和渗流与非饱和渗流的功能, 单元由非饱和状态变为饱和状态后, 模型对该单元的渗流计算方式可转换为饱和渗流计算.
3) 采空区泄水后围岩内孔隙水压力释放, 地下水渗流量较低且趋于稳定.通过与实际工程中泄水后的采空区渗流量对比, 可验证修正渗流参数后的模型对非饱和单元渗流量的计算结果更接近实测值.而修正前的模型仍在对非饱和单元进行饱和渗流计算, 计算结果远大于实测值且随时间变化明显.
参考文献

[1]	Biot M A. General solutions of the equations of elasticity and consolidation for a porous material[J]. Journal of Applied Mechanics, 1956, 78: 91-96.
[2]	耿克勤, 刘光廷, 陈兴华. 节理岩体的渗透系数与应变、应力的关系[J]. 清华大学学报(自然科学版), 1996, 36(1): 107-112. (Geng Ke-qin, Liu Guang-ting, Chen Xing-hua. Coupling relationship of percolation coefficient of fractured rock masses to strain and stress[J]. Journal of Tsinghua University(Science and Technology), 1996, 36(1): 107-112.)
[3]	白国良, 梁冰, 李树志. 采动影响下等效连续介质水岩耦合数学模型及应用[J]. 煤炭学报, 2009, 34(4): 461-465. (Bai Guo-liang, Liang Bing, Li Shu-zhi. An equivalent porous media water-rock coupling model impacted by coalmining and its application[J]. Journal of China Coal Society, 2009, 34(4): 461-465.)
[4]	郭震山, 赵建斌, 赵紫阳. 降雨入渗条件下抗滑桩加固边坡稳定性分析[J]. 土木工程与管理学报, 2017, 34(4): 47-52. (Guo Zhen-shan, Zhao Jian-bin, Zhao Zi-yang. Stability analysis of the slope reinforced with anti-slide pile under the condition of rainfall infiltration[J]. Journal of Civil Engineering and Management, 2017, 34(4): 47-52. DOI:10.3969/j.issn.2095-0985.2017.04.008)
[5]	Ye Z Y, Jiang Q H, Zhou C B, et al. Numerical analysis of unsaturated seepage flow in two-dimensional fracture networks[J]. International Journal of Geomechanics, 2017, 17(5): 04016118. DOI:10.1061/(ASCE)GM.1943-5622.0000826
[6]	Tran K M, Bui H H, Nguyen G D. DEM modelling of unsaturated seepage flows through porous media[J]. Computational Particle Mechanics, 2021, 9(4): 135-152.
[7]	李毅, 伍嘉, 李坤. 基于FLAC3D的饱和-非饱和渗流分析[J]. 岩土力学, 2012, 33(2): 617-622. (Li Yi, Wu Jia, Li Kun. Saturated-unsaturated seepage analysis based on FLAC3D[J]. Rock and Soil Mechanics, 2012, 33(2): 617-622.)
[8]	Song Z P, Jiang A N, Zhang J. Studying the rock seepage parameters identification method based on finite element method and difference evolution arithmetic[J]. Key Engineering Materials, 2011, 474/475/476: 933-937.
[9]	Van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x
[10]	蒋中明, 熊小虎, 曾铃. 基于FLAC3D平台的边坡非饱和降雨入渗分析[J]. 岩土力学, 2014, 35(3): 855-861. (Jiang Zhong-ming, Xiong Xiao-hu, Zeng Ling. Unsaturated seepage analysis of slope under rainfall condition based on FLAC3D[J]. Rock and Soil Mechanics, 2014, 35(3): 855-861.)
[11]	Li C, Zhou T Q, Jiang S S, et al. Finite element analysis for the stress field and seepage field interaction within Qingdao submarine tunnel rockmass[J]. Applied Mechanics and Materials, 2013, 408: 1278-1282.
[12]	Chen G, Ma L, Gong H S, et al. Numerical calculation method of aperture function for rough rock fracture flow[J]. IOP Conference Series: Earth and Environmental Science, 2021, 861(3): 032010.
[13]	白国良. 基于FLAC3D的采动岩体等效连续介质流固耦合模型及应用[J]. 采矿与安全工程学报, 2010, 27(1): 106-110. (Bai Guo-liang. Fluid solid coupling model of equivalent continuous medium in overburden rock based on FLAC3D and its application[J]. Journal of Mining & Safety Engineering, 2010, 27(1): 106-110.)
[14]	薛娈鸾, 陈胜宏. 岩石裂隙渗流与法向应力耦合的复合单元模型[J]. 岩石力学与工程学报, 2007, 26(sup 1): 2613-2619. (Xue Luan-luan, Chen Sheng-hong. Composite element model of seepage-normal stress coupling for rock fractures[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(sup 1): 2613-2619.)