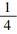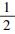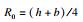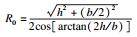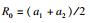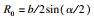, 王鑫, 柏谦 东北大学 资源与土木工程学院, 辽宁 沈阳 110819
收稿日期：2022-02-15
基金项目：国家自然科学基金资助项目(51878127)。
作者简介：孙大增(1994-), 男, 辽宁本溪人, 东北大学博士研究生;
赵文(1962-), 男, 内蒙古乌兰察布人, 东北大学教授, 博士生导师。
摘要：为了评估既有隧道扩建开挖的应力扰动程度和重分布特征, 以南岭单线铁路隧道原位扩建工程为研究背景, 基于经典弹塑性理论, 结合Mohr-Coulomb屈服准则, 推导扩建过程围岩径、环向应力变化量计算式, 分析不同地层条件、初始应力、等代圆计算方法对应力变化的影响规律.结果表明：二次开挖导致径向应力较扩建前不同程度减小, 环向应力先减小后增加, 最后趋于原应力状态；围岩应力分布状态与围岩条件、初始应力、等代圆计算方法均相关, 采用1/4高度与跨度之和的等代圆计算简化方法, 对单线隧道原位扩建的围岩应力变化量求解具有较好的适用性；通过围岩环向应力演化特征的现场实测, 验证了应力变化量计算式的准确性, 为扩建隧道开挖方案设计及支护参数优化提供理论依据.
关键词：隧道工程原位扩建二次扰动应力演化变化特征敏感性分析
Stress Change Characteristics of the Existing Tunnel Surrounding Rocks by In-situ Expansion
SUN Da-zeng, ZHAO Wen
, WANG Xin, BAI Qian School of Resources & Civil Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: ZHAO Wen, E-mail: wenneu@163.com.
Abstract: In order to evaluate the stress disturbance degree and redistribution characteristics of the expansion and excavation of existing tunnels, taking the in-situ expansion project of the Nanling single-track railway tunnel as the research background, based on the classical elastic-plastic theory, and combined with the Mohr-Coulomb yield criterion, the calculation formulas of the surrounding rock diameter and circumferential stress change during the expansion process were deduced, and the influences of different formation conditions, initial stress, and equal-circle calculation methods on stress change were analyzed. The results showed that the second excavation causes the radial stress to decrease in varying degrees compared with that before the expansion, and the circumferential stress first decreases and then increases, and finally remains in the original stress state; the surrounding rock stress distribution state is closely related to the surrounding rock conditions, initial stress, equal-circle calculation methods, and the simplified calculation method of the equal-circle calculation of the sum of 1/4 height and span has good applicability to the calculation of the stress change of the surrounding rocks for the in-situ expansion of a single-line tunnel. The on-site measurement has verified the accuracy of the calculation formula of stress change, and provided a theoretical basis for the design of the excavation scheme of expansion tunnels and the optimization of the support parameters.
Key words: tunnel engineeringin-situ expansionsecond disturbancestress evolutionchange characteristicssensitivity analysis
随着人口增长和经济社会的发展, 隧道等地下空间工程使用需求不断提高[1-2], 现有工程超负荷运行情况严重, 亟需采取相应措施以增加可利用空间. 隧道原位扩建以既有隧道为施工基础, 破除原有衬砌结构进行开挖, 最后重新施作衬砌, 扩大断面尺寸[3-4].目前各地均存在大量新建隧道工程, 在未经历工程扰动的原岩上新建隧道, 研究围岩应力分布特征规律已经十分成熟[5-7], 原位扩建隧道的应力变化规律较新建隧道复杂得多, 扩建卸荷过程会打破初次开挖形成的应力分布状态并演化形成新的应力平衡, 围岩受二次开挖扰动作用明显, 塑性区继续发育扩展.设计的扩建隧道半径处于既有隧道的塑性区或弹性区范围时应力特征又大为不同, 因此分析原位扩建过程中既有隧道的围岩应力变化情况, 揭示扩建隧道围岩应力演化特征及空间分布规律已经成为目前研究的重要问题.
当前开展隧道改扩建型式、施工工法步序以及支护设计的研究较多, 针对应力变化特征开展的研究相对较少.黄伦海等[8]通过相似模拟和数值计算得到了大帽山大断面隧道不同扩建方案应力随施工步序的S形演化规律.来弘鹏等[9]分析5种工况扩建前后衬砌受力特征和围压分布情况.张俊儒等[10]分析四车道马尾隧道“回填-台阶法”扩建阶段变形及动态施工力学.Jia等[11-12]采用相似材料模型分析了浅埋单洞隧道扩建为双连拱隧道开挖过程中围岩和隧道结构的力学响应.Yang等[13]研究了隧道扩建坍塌段CRD法的施工动态力学特性.杨宾等[14]结合复变函数理论Schwarz交替法引入支反力作用应力进一步完善了单侧扩挖围岩力学特性的解析解, 并验证了其适用性.
现有研究主要集中在扩建阶段应力具体形式的求解, 难以全面评估二次扩挖对既有隧道围岩的应力扰动程度以及围岩应力的动态演化过程.本文以原位全断面扩挖单线南岭隧道工程为研究背景, 基于经典弹塑性理论, 结合Mohr-Coulomb屈服准则, 分析隧道在原位扩建不同阶段围岩径、环向应力的变化特征, 以期为扩建开挖方案设计及后续的支护参数优化提供理论指导.
1 工程概况南岭隧道地处辽宁省北票市上园镇与大板镇交界位置, 总体呈近东南至西北向展布.既有南岭隧道为单线铁路隧道, 起讫里程DK85+696.5~DK86+883.6, 全程1 187.1 m, 最大埋深37.75 m.地质勘察显示，表覆为第四系全新统残坡积层(Q4el+dl)粗角砾土, 下伏侏罗系上统(J3)泥质砂岩, 泥质砂岩按照风化程度分为全风化、强风化以及弱风化, 地质纵断面如图 1所示.隧道历年大修和病害统计资料显示, 南岭隧道局部限界不能满足电气化铁路隧道的要求, 衬砌开裂、错动、腐蚀以及漏水现象十分严重, 必须扩挖并重新施作衬砌.
图 1(Fig. 1)
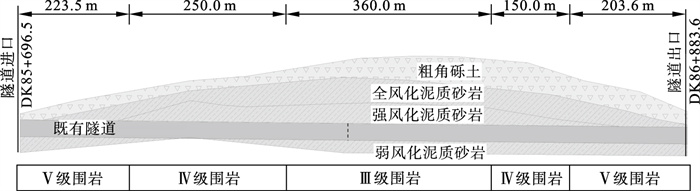 | 图 1 南岭隧道地质纵断面Fig.1 Longitudinal profile of Nanling tunnel |
既有隧道为直墙拱形结构, 拱部条石衬砌, 直墙C20混凝土, 平均强度仅为15.6 MPa, 原衬砌基本丧失对围岩的支护作用.原隧道宽度5.5 m, 高度8.1 m, 断面面积41.3 m2.扩建型式为原位四周扩建模式, 扩挖后宽度7.15 m, 高度9.25 m, 断面面积64.9 m2, 扩大57.1%, 满足使用要求, 隧道扩建如图 2所示.由于原衬砌和围岩强度均较低, 扩建采用全断面钻爆施工工艺, 衬砌拆除与围岩扩挖同步进行, 爆破采用浅孔弱爆的方式, 最大限度依托既有隧道内轮廓面作为爆破自由面, 局部风镐凿除.
图 2(Fig. 2)
 | 图 2 南岭隧道扩建施工Fig.2 Nanling tunnel expansion project |
2 围岩应力变化量的弹塑性解在原岩上修建隧道, 围岩受到开挖卸荷扰动后达到应力平衡状态, 而原位扩建隧道需要打破这种平衡重新稳定, 围岩经历二次扰动的影响, 所以围岩应力演化规律较新建隧道复杂得多.分析扩建过程中围岩应力的二次变化规律, 对于控制围岩稳定十分重要.本文采用传统弹塑性计算方法, 结合Mohr-Coulomb屈服准则, 推导原位四周扩建引起的围岩应力变化量计算式.
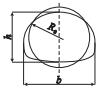
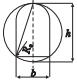
地下工程的围岩弹塑性理论中, 对圆形隧道断面的研究较成熟, 开挖后形成的围岩应力分布状态见图 3, 受开挖卸荷影响环向应力先升高后降低最后趋于原岩应力, 规定环向应力变化量为0的位置为扩建隧道压力拱内边界, 环向应力恢复到变化量仅为既有隧道围岩应力10%的位置作为扩建隧道压力拱外边界.四周扩建前后的断面简化为等代圆, 同时假定围岩为均一、连续、各向同性的理想弹塑性介质, 初始应力为静水应力.将隧道扩建引起的围岩应力重分布视作二维轴对称问题, 采用弹塑性力学开展原位扩建既有隧道围岩弹塑性分析, 计算模型如图 4所示.
图 3(Fig. 3)
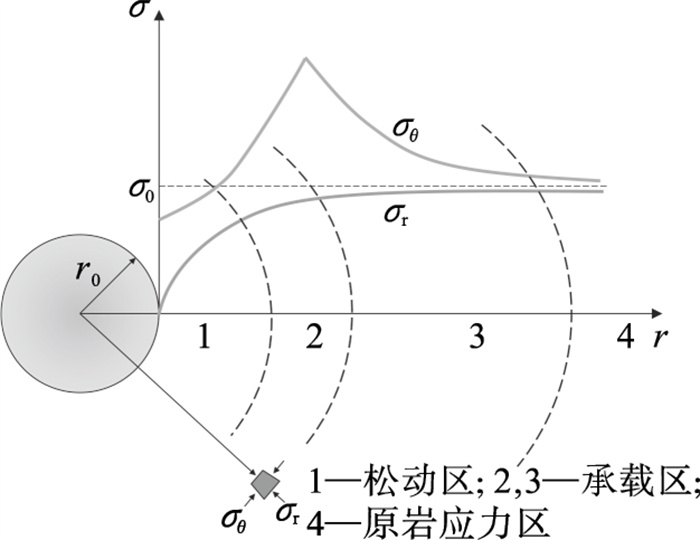 | 图 3 圆形隧道围岩弹塑性应力分布状态Fig.3 Elastic-plastic stress distribution state in circular tunnel envelope |
图 4(Fig. 4)
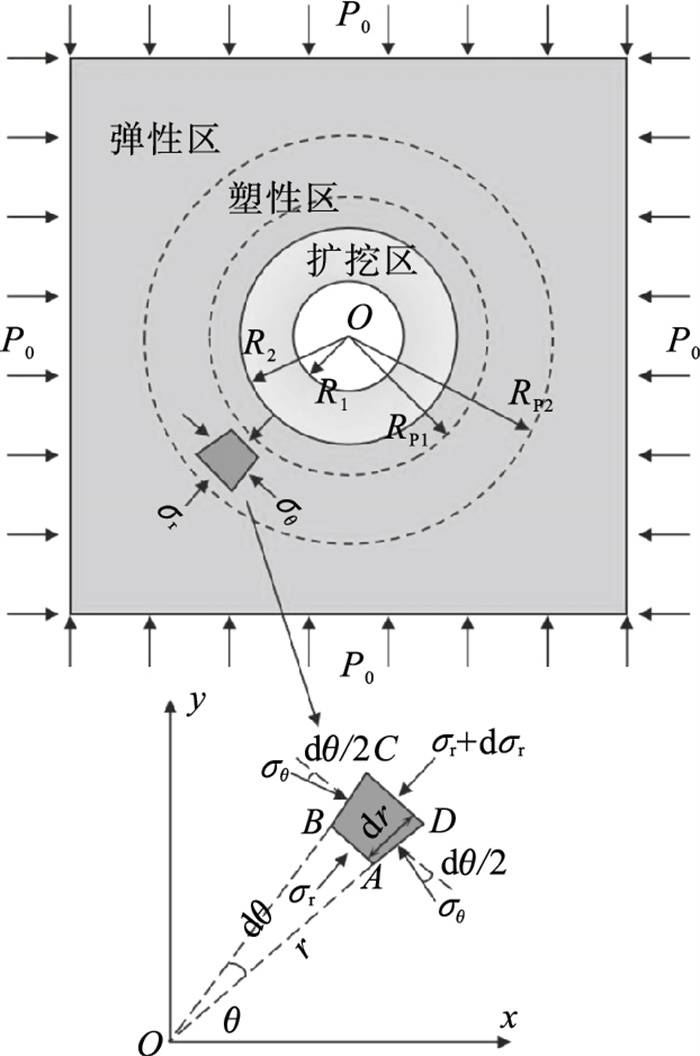 | 图 4 原位扩建既有隧道围岩应力计算模型Fig.4 Stress calculation model of existing tunnel surrounding rocks by in-situ expansion |
设既有隧道半径R1, 塑性区发育半径RP1；扩建隧道半径R2, 扩建引起的塑性区发育半径RP2.对任一位置的微元体(ABCD), 需满足应力平衡方程和对应的弹塑性条件, 位于弹塑性交界位置需同时满足塑性条件和弹性条件.沿垂直隧道轴线方向取单位厚度, 其径向受力平衡：
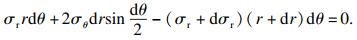 | (1) |
 | (2) |
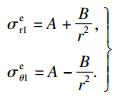 | (3) |
弹性区外边界条件：r→∞(远离隧道内边界),
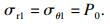 | (4) |
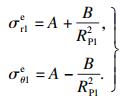 | (5) |
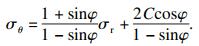 | (6) |
塑性区外边界条件：r=RP1,
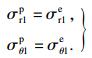 | (7) |
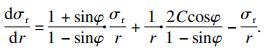 | (8) |
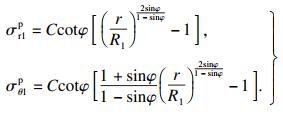 | (9) |
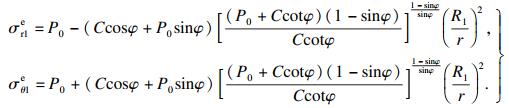 | (10) |
 | (11) |
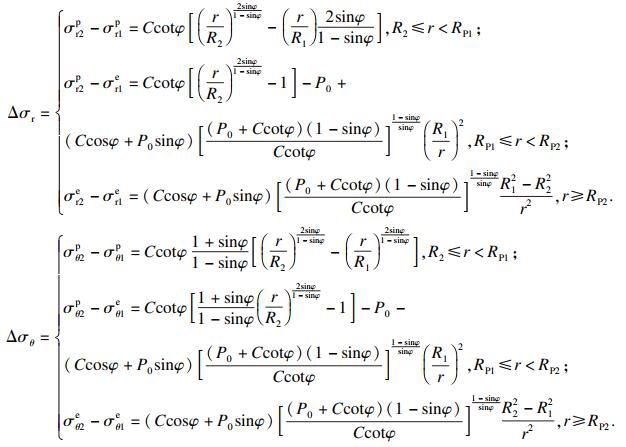 | (12) |
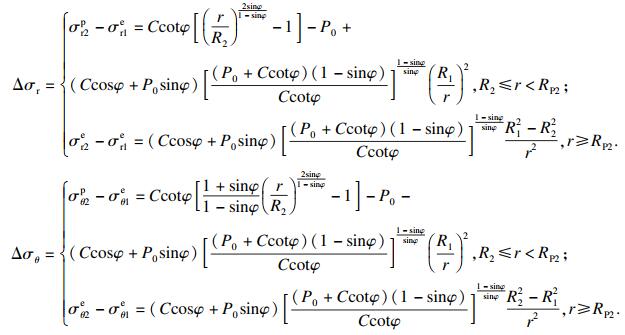 | (13) |
图 5(Fig. 5)
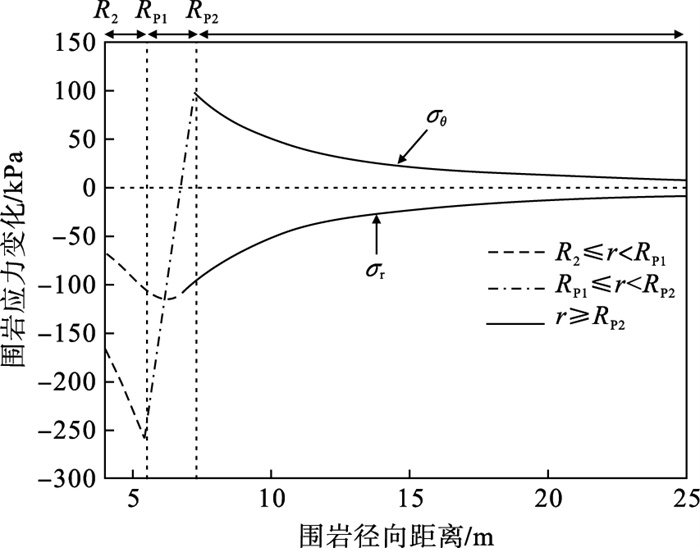 | 图 5 R1＜R2≤RP1时围岩应力变化量曲线Fig.5 Stress change of surrounding rocks when R1＜R2≤RP1 |
当R1＜R2≤RP1时, 围岩应力变化趋势为：较扩建前径向应力不同程度减小, 环向应力沿径向先减小后增加, 最后逐渐趋于既有隧道围岩应力状态.R2≤r＜RP1时, 原位扩建重复扰动已处于塑性区内的围岩, 径、环向应力均线性减小；RP1≤r＜RP2时, 由于扩挖施工增大了隧道断面, 围岩塑性区进一步扩展, 径向应力逐渐减小并达到最小值峰值状态, 环向应力减小程度随径向距离的增大而降低, 并在临近RP2时, 由应力释放状态转化为应力集中状态, 最终达到最大值峰值点；r≥RP2时, 随着径向距离的增大, 径、环向应力逐渐恢复至既有隧道围岩应力状态.
设R2=6 m, 其他变量取值不变, 此时符合第二种情况.通过式(13)得出原位扩建引起的围岩应力变化量曲线, 如图 6所示.当R2＞RP1时, 围岩应力的整体变化趋势为：随着径向距离的增大, 径向应力持续减小, 环向应力较扩建前先减小后增大.R2≤r＜RP2时, 原位扩建使原处于弹性区的围岩发生应力重分布, 围岩径向应力减小, 环向应力减小量随径向距离的增大而减小, 最终由应力释放状态转化为应力集中状态；r≥RP2时, 随着径向距离的增大, 径、环向应力逐渐恢复至既有隧道围岩应力状态.
图 6(Fig. 6)
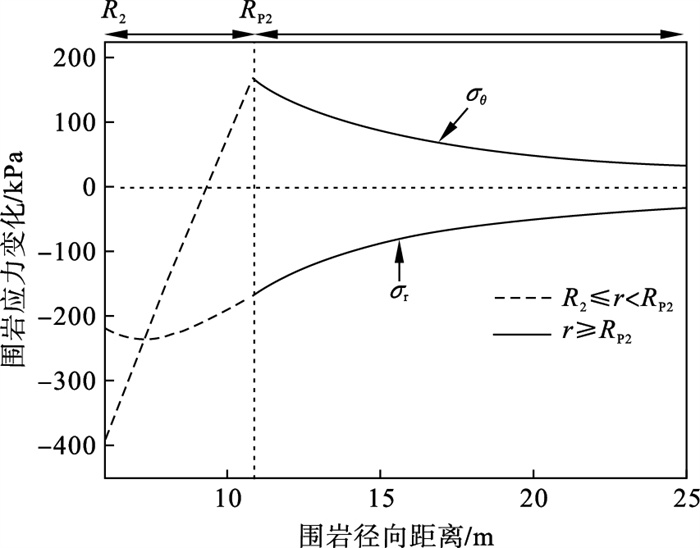 | 图 6 R2＞RP1时围岩应力变化量曲线Fig.6 Stress change of surrounding rocks when R2 > RP1 |
3 围岩应力变化量计算式的参数敏感性分析3.1 围岩条件的影响南岭隧道位于辽宁西部山地丘陵区, 地势存在较大起伏, 属低山丘陵地貌, 冲沟较为发育.隧道处地层为表覆第四系全新统残地层粗角砾土, 下伏侏罗系上统泥质砂岩.分析全风化、强风化、弱风化泥质砂岩等三种不同围岩条件下, 原位扩建引起的围岩径、环向应力变化情况, 围岩物理力学参数如表 1所示.
表 1(Table 1)
 表 1 围岩物理力学计算参数Table 1 Physical and mechanical calculation parameters of surrounding rocks
| 表 1 围岩物理力学计算参数 Table 1 Physical and mechanical calculation parameters of surrounding rocks |
由图 7可知, 围岩条件越好, 既有隧道开挖后形成的RP1越小, 围岩的自承能力越好.全风化、强风化、弱风化泥质砂岩中原位扩建引起的围岩径向应力的释放峰值分别为-98.22，-116.67，-169.79 kPa, 环向应力的集中峰值分别为83.10，100.18，154.15 kPa, 压力拱内边界分别为8.71，6.51，4.31 m.围岩条件越好, 围岩应力重分布范围越向隧道内部集中, 扩挖施工对围岩的影响范围越小, 原位扩建的稳定性越好.
图 7(Fig. 7)
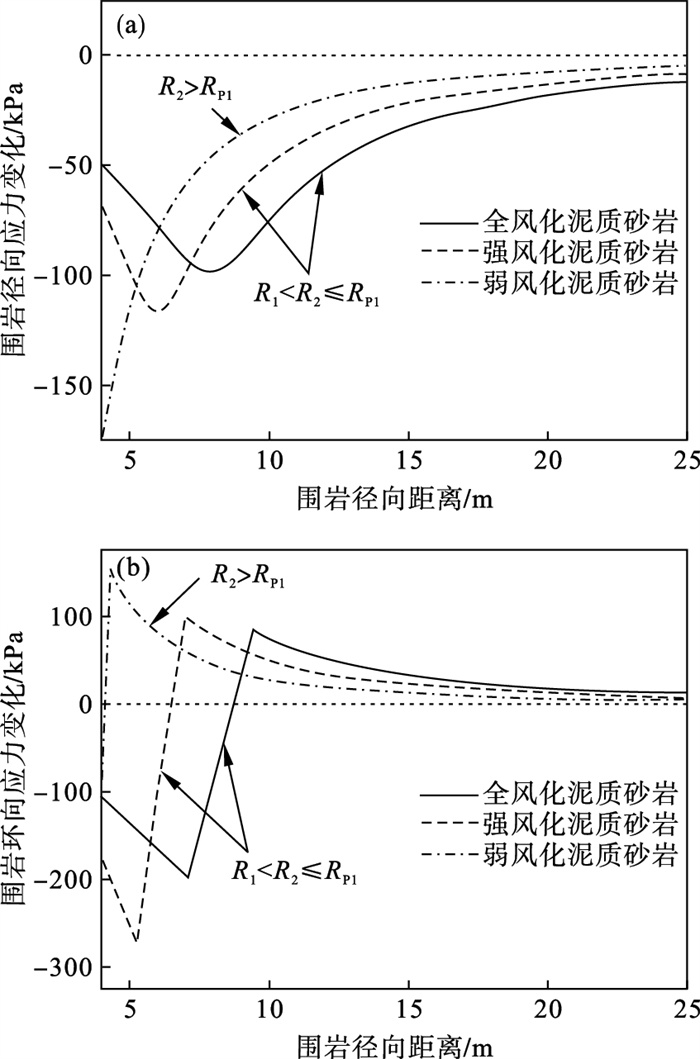 | 图 7 不同围岩条件下围岩应力变化曲线Fig.7 Stress change of surrounding rocks under different surrounding rock conditions (a)—径向应力变化；(b)—环向应力变化. |
3.2 初始应力的影响为考虑初始应力对原位扩建引起的围岩应力变化量的影响, 分别取P0为200，400，600 kPa进行计算, 围岩条件取为强风化泥质砂岩.由图 8可知, 隧道所处位置初始应力越大, 扩建引起的应力重分布影响范围越广.P0为200，400，600 kPa时, 原位扩建引起的围岩径向应力的释放峰值分别为-72.38，-116.67，-161.35 kPa, 环向应力的集中峰值分别为59.83，100.18，138.53 kPa, 压力拱内边界分别为4.76，6.51，7.99 m.围岩径、环向应力的变化幅值及范围均随初始应力的增大而增大.
图 8(Fig. 8)
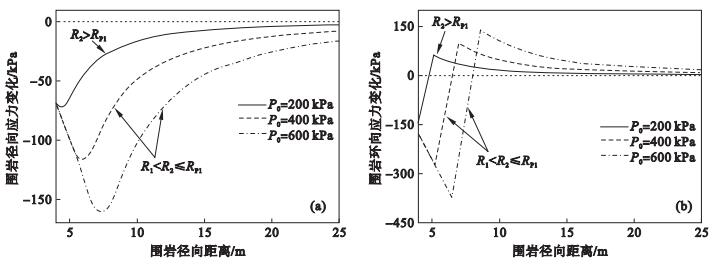 | 图 8 不同初始应力下围岩应力变化曲线Fig.8 Stress change of surrounding rocks under different ground stress (a)—径向应力变化；(b)—环向应力变化. |
3.3 等代圆计算方法的影响等代圆方法是按照一定标准采用等效圆形表示不同形式断面的过程, 采用四种简化方法得到等代圆的半径, 如表 2所示, 不同计算方法得到的等代圆半径存在较大差异, 其中采用方法4得到的等代圆半径最小, 方法1, 3得到的等代圆半径相同, 方法2得到的等代圆半径最大.
表 2(Table 2)
表 2 不同等代圆计算方法Table 2 Different equal-circle calculation methods
| 表 2 不同等代圆计算方法 Table 2 Different equal-circle calculation methods |
考虑等代圆半径的计算方法对原位扩建引起的围岩应力变化量的影响, 将表 2中不同计算方法得到的R1，R2代入围岩应力变化量计算式进行比较, 围岩条件(C, φ)根据地勘报告等资料选取, 通过围岩容重和隧道埋深换算得出初始应力P0=γH=609 kPa.式中：γ为围岩容重；H为隧道埋深.方法1和方法3的计算结果相同, 因此仅将方法1，2，4的计算结果进行对比分析.由图 9可知, 不同等代圆计算方法得到的围岩应力变化趋势相同, 采用方法1，2，4得到的围岩径向应力释放峰值分别为-79.13，-65.14，-103.65 kPa, 环向应力的集中峰值分别为68.39，59.73，90.49 kPa, 压力拱内边界分别为6.84，8.35，5.88 m.由此可知扩建后隧道半径越大, 塑性区发育半径RP2越大.
图 9(Fig. 9)
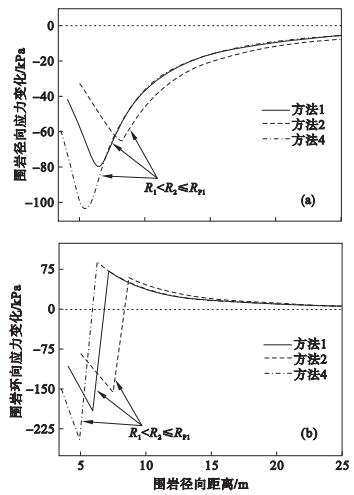 | 图 9 不同等代圆半径计算方法下围岩应力变化曲线Fig.9 Stress change of surrounding rocks under different equal-circle radius (a)—径向应力变化；(b)—环向应力变化. |
4 工程实例分析4.1 围岩环向应力现场监测在既有隧道DK86+523位置设置监测断面, 将振弦式钻孔应力计布置在左侧拱脚和边墙处, 采集扩建进程中围岩内部的环向应力数据, 分析环向应力演化规律.施工钻孔长1.8 m，孔径42 mm, 利用清孔工具和动力风清孔后将振弦式钻孔应力计埋入对应监测位置的基岩中, 如图 10所示.
图 10(Fig. 10)
 | 图 10 监测断面测点布置Fig.10 On-site monitoring point layout drawing |
监测围岩环向应力随扩建推进的变化情况, 图 11为DK86+523断面的环向应力变化量曲线, 规定监测断面所在位置为横坐标原点, 当掌子面位于监测断面后方时, 横坐标为负值.随着掌子面前移, 拱脚、边墙处围岩的环向应力均随之增大.当掌子面开挖至距监测断面7 m时, DK86+523断面的围岩应力增速明显且边墙增速较拱脚更明显, 说明此时发生剧烈的应力演化.当掌子面至监测断面前方1 m处, 拱脚环向应力增大至0.202 MPa, 边墙环向应力增大至0.215 MPa, 此后钻孔应力计因爆破施工损坏.从应力平衡角度分析, 隧道开挖扰动打破了原始应力平衡, 导致开挖边界处围岩径向卸荷, 此时径向应力释放, 环向产生应力集中现象, 与监测结果保持一致.
图 11(Fig. 11)
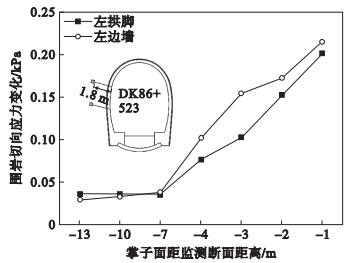 | 图 11 DK86+523断面环向应力变化曲线Fig.11 Circumferential stress variation curve of DK86+523 cross-section |
4.2 围岩应力变化量计算式准确性验证为了验证本文推导得到的围岩应力变化量计算式的准确性, 将计算值与依托工程的围岩环向应力变化监测值对比分析.由图 12可知, 采用方法1，2，4简化隧道断面后得到的环向应力变化量分别为217，176，272 kPa.3种计算方法与拱脚实测值的相对误差分别约为7.4%，12.9%，34.6%, 与边墙实测值的相对误差为1.0%，18.1%，26.5%.综合比较发现：采用等代圆计算方法1即取高度与跨度之和的1/4计算结果与实测值吻合性更好, 验证了本文提出的围岩应力变化量推导方法的合理性.
图 12(Fig. 12)
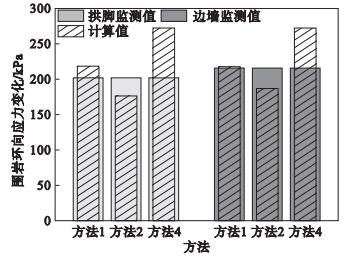 | 图 12 监测值与计算值对比Fig.12 Comparison of monitoring values calculated values |
5 结论1) 基于Mohr-Coulomb屈服准则, 采用二维轴对称弹塑性解法, 推导原位四周扩建引起的围岩应力变化量计算式.原位扩建引起的围岩应力变化趋势为, 随着径向距离的增大, 围岩径向应力不同程度减小, 环向应力先减小后增加.
2) 围岩条件越好, 隧道扩建对围岩的扰动影响越小, 应力重新分布范围越小, 原位扩建的稳定性越好.围岩径、环向应力的变化幅值及范围均随初始应力的增大而增大, 扩建隧道的半径越大, 原位扩建后形成的塑性区半径越大.
3) 隧道拱脚、边墙处围岩的环向应力均随掌子面前移而增大, 扩挖距监测断面1倍洞径时, 环向应力增速明显增加.采用取高度与跨度之和的1/4简化方法, 所得计算值与依托工程的监测值较吻合, 适用于原位四周扩建单线铁路隧道的围岩应力变化量求解.
参考文献
| [1] | Chen Z L, Chen J Y, Liu H, et al. Present status and development trends of underground space in Chinese cities: evaluation and analysis[J]. Tunnelling and Underground Space Technology, 2018, 71: 253-270. DOI:10.1016/j.tust.2017.08.027 |
| [2] | Cui J Q, Broere W, Lin D. Underground space utilisation for urban renewal[J]. Tunnelling and Underground Space Technology, 2021, 108: 103726. DOI:10.1016/j.tust.2020.103726 |
| [3] | 彭念. 原位扩建隧道围岩力学响应机理研究[D]. 重庆: 重庆大学, 2010. (Peng Nian. Research on mechanical response mechanism of surrounding rock of in-situ extension tunnel[D]. Chongqing: Chongqing University, 2010. ) |
| [4] | Peng N, Zhang Y X, Wang C. Study on mechanical properties of surrounding rock during tunnel construction with in-situ expansion step excavation method[J]. Disaster Advances, 2010, 3(4): 194-199. |
| [5] | Nikadat N, Marji M F. Analysis of stress distribution around tunnels by hybridized FSM and DDM considering the influences of joints parameters[J]. Geomechanics and Engineering, 2017, 11(2): 269-288. |
| [6] | Gao C L, Zhou Z Q, Li Z H, et al. Peridynamics simulation of surrounding rock damage characteristics during tunnel excavation[J]. Tunnelling and Underground Space Technology, 2020, 97: 103289. DOI:10.1016/j.tust.2020.103289 |
| [7] | Zhao K, Bonini M, Debernardi D, et al. Computational modelling of the mechanised excavation of deep tunnels in weak rock[J]. Computers and Geotechnics, 2015, 66: 158-171. DOI:10.1016/j.compgeo.2015.01.020 |
| [8] | 黄伦海, 钱七虎. 公路隧道大断面改扩建施工开挖方案研究[J]. 现代隧道技术, 2016, 53(5): 145-153, 160. (Huang Lun-hai, Qian Qi-hu. Study on excavation schemes for the redevelopment construction of highway tunnels with large sections[J]. Modern Tunnelling Technology, 2016, 53(5): 145-153, 160.) |
| [9] | 来弘鹏, 徐学深, 常瑞成, 等. 公路隧道扩建力学特征研究[J]. 中国公路学报, 2014, 27(1): 84-93. (Lai Hong-peng, Xu Xue-shen, Chang Rui-cheng, et al. Study on mechanical characteristics of highway tunnel expansion[J]. China Journal of Highway and Transport, 2014, 27(1): 84-93.) |
| [10] | 张俊儒, 史博然, 汪家雷, 等. 塌方段原位扩建四车道公路隧道"回填-台阶法"施工力学及安全分析[J]. 中国公路学报, 2021, 34(6): 109-124. (Zhang Jun-ru, Shi Bo-ran, Wang Jia-lei, et al. Construction mechanics and safety analysis of"backfill-bench method"for in-site expansion of four-land highway tunnel in collapsed section[J]. China Journal of Highway and Transport, 2021, 34(6): 109-124.) |
| [11] | Jia Y L, Ouyang A H, Wang S Y, et al. Development and application of model test system for reconstruction and expansion of existing shallow single-hole tunnel into twin-arch tunnel[J]. Advances in Civil Engineering, 2021, 2021: 6656165. |
| [12] | Jia Y L, Xia Y X, Chen X D, et al. Force and deformation characteristics during the reconstruction and expansion of shallow single-tube tunnels into large-span multiarch tunnels[J]. Advances in Materials Science and Engineering, 2019, 2019: 2783784. |
| [13] | Yang S, Shi B R, Liu H. Study on construction mechanics of in-situ expansion of ultra-large flat tunnel in collapse section of an existing tunnel[J]. IOP Conference Series: Earth and Environmental Science, 2020, 570(2): 022068. |
| [14] | 杨宾, 林从谋, 张在晨, 等. 隧道原位单侧扩挖围岩力学特性解析分析[J]. 地下空间与工程学报, 2018, 14(6): 1458-1465. (Yang Bin, Lin Cong-mou, Zhang Zai-chen, et al. Mechanical characteristics analysis of surrounding rock of unilateral expansion tunnels in situ[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(6): 1458-1465.) |
