1. 东北大学 医学与生物信息工程学院, 辽宁 沈阳 110169;
2. 东北大学 计算机科学与工程学院, 辽宁 沈阳 110169;
3. 辽宁省大数据管理与分析重点实验室, 辽宁 沈阳 110169
收稿日期：2022-01-14
基金项目：国家自然科学基金资助项目(62072089)；中央高校基本科研业务费专项资金资助项目(N2116016, N2104001, N2019007, N2224001-10)。
作者简介：李婵(1994-), 女, 河北邯郸人, 东北大学硕士研究生;
信俊昌(1977-), 男, 辽宁辽阳人, 东北大学教授, 博士生导师;
王之琼(1980-), 女, 黑龙江哈尔滨人, 东北大学教授, 博士生导师。
摘要：为了解决目前用于构建基因调控网络的方法中所存在的网络构建准确率低、网络构建时间过长等问题, 以及减小网络构建的复杂度, 提高网络构建效率, 提出了一种基于潜在调控因子筛选的高阶动态贝叶斯网络建模方法(high-order dynamic Bayesian network modeling method based on potential regulatory factor screening, PRS-HO-DBN).该方法将关联模型与高阶动态贝叶斯网络模型相结合, 首先利用潜在调控因子筛选的方法在不同的时间延迟下删除与目标基因关联程度较低的基因, 保留与目标基因关联程度较高的基因并作为目标基因的潜在调控因子集, 以减小搜索空间; 然后利用高阶动态贝叶斯模型进行结构学习, 以提高网络构建的精确率.与其他的网络构建模型方法相比, 该方法可以极大地缩短网络构建的时间, 提升效率和精确度.
关键词：基因调控网络潜在调控因子高阶动态贝叶斯网络关联模型结构学习
High-Order Dynamic Bayesian Network Modelling Method Based on Potential Regulatory Factors Screening
LI Chan1, QU Lu-xuan1, XIN Jun-chang2,3, WANG Zhi-qiong1
1. College of Medicine & Biological Information Engineering, Northeastern University, Shenyang 110169, China;
2. School of Computer Science & Engineering, Northeastern University, Shenyang 110169, China;
3. Key Laboratory of Big Data Management and Analytics(Liaoning Province), Shenyang 110169, China
Corresponding author: WANG Zhi-qiong, E-mail: wangzq@bmie.neu.edu.cn.
Abstract: In order to solve the problems of low network construction accuracy and long network construction time in the current methods used to construct gene regulatory networks, so as to reduce the complexity of network construction and improve the efficiency of network construction, a method called high-order dynamic Bayesian network modelling method based on potential regulatory factors screening (PRS-HO-DBN) was proposed. The method combines the correlation model with the high-order dynamic Bayesian network model. Firstly, the potential regulatory factor screening method is used to delete the genes with low association with the target gene under different time delays, and retain the genes with high association with the target gene as the potential regulatory factor set of the target gene to reduce the search space. Then the high-order dynamic Bayesian model is used for structure learning to improve the accuracy of network construction. Compared with other methods, the method can greatly reduce network construction time and improve efficiency and accuracy.
Key words: gene regulatory networkspotential regulatory factorshigh-order dynamic Bayesian networkcorrelation modelstructure learning
基因通过表达传输遗传信息, 基因之间相互影响、相互制约的调控关系, 形成了复杂的基因调控网络.该网络可以帮助人们在面对由于基因异常表达所导致的恶性肿瘤等疾病时, 从遗传层面上了解疾病发生的原因, 以实现对于治疗靶点的精准用药[1].因此, 构建具有高精确度的基因调控网络在疾病诊断治疗方面具有重要意义.传统用于构建基因调控网络的模型大多针对非时序基因表达数据, 这不符合生物学意义, 也不能精确地描述基因之间的调控关系.基因表达是随时间变化的, 不同基因表达后调控其他基因表达的时间延迟也是不同的, 因此，基于时间维度去构建基因调控网络才能更真实地还原基因之间的调控关系.而如何更有效地利用时序基因表达数据构建包含更多真阳边，同时更高效地构建基因调控网络成为一种挑战.
随着基因调控网络建模方法研究的不断进步, 产生了各种各样的模型.这些模型从不同角度对基因调控网络进行抽象, 其中动态贝叶斯网络模型[2]由于可以处理时序基因表达数据进而构建基于时间维度的基因调控网络而被广泛使用.关联模型[3]因为可以精确地寻找到不同基因之间的关联程度，也被广泛应用在基因调控网络构建中.关联模型虽然可以寻找到不同基因之间的关联程度强弱, 但是该模型所构建的网络是无向图; 而动态贝叶斯模型时间复杂度高, 且只能寻找一个时间延迟的调控关系.如果增加阶数, 为目标基因寻找父节点的搜索空间呈指数级上升, 而且所构建的网络结构中假阳边较多, 使得网络构建效率降低.
基于此, 本文将关联模型与高阶动态贝叶斯网络模型相结合, 提出了基于潜在调控因子筛选的高阶动态贝叶斯基因调控网络构建方法(high-order dynamic Bayesian network modeling method based on potential regulatory factor screening, PRS-HO-DBN). 首先，利用关联模型方法计算目标基因与不同时间延迟下其他基因之间的关联程度强弱, 为了筛选出更符合要求的基因, 使用节点自动选择技术, 根据时序基因表达数据之间的关系自动选择阈值来筛选潜在调控因子集, 目的是为进行网络结构学习时缩小搜索空间; 然后, 利用高阶动态贝叶斯模型进行结构学习, 去构建基因调控网络；最后，通过实验证明该方法在保证真阳边数量的同时大大缩短了网络的构建时间, 提高了计算效率, 使利用高阶动态贝叶斯网络模型进行大规模基因调控网络的构建成为可能.
1 潜在调控因子筛选的高阶动态贝叶斯网络建模1.1 相关工作为了准确找到目标基因与其他基因之间的关系, 本文采用关联模型中互信息(mutual information, MI)和皮尔逊相关系数(Pearson correlation coefficient, PCC)两种方法来计算基因间的关联程度, 但这两种方法只能确定基因之间是否有关联, 无法确定基因之间的关联程度.为了获得合理的阈值, 使用预测最小描述长度(predictive minimum description length, PMDL)和基于假设检验的断点检测两种方法分别为互信息和皮尔逊相关系数两种方法确定阈值, 以实现对目标基因潜在调控因子的筛选.
1.1.1 互信息互信息[4]是求两个随机变量之间相互依赖的程度, 在基因调控网络中, 互信息描述基因之间相互关联的程度, 互信息值越高表明两个基因之间关联程度越强.在时序基因表达数据中, 基因的表达水平被表示成变量X, X={X1, …, Xn}, n为基因数量, {Xi[1], …, Xi[t]}表示X中第i个基因在t个时刻内的表达值; Xi[t]表示X中第i个基因在第t时刻的表达值; 而在X中所有基因{X1, …, Xn}在第t时刻的表达值可以表示为X[t]={X1[t], …, Xn[t]}.
对于一个离散变量X, 它的熵H(X)是指X接收的每条消息中所包含信息的平均值, 即所接收的消息随机性越大熵就越大, 可表示为
 | (1) |
X和Y的联合熵(joint entropy，JE)可表示为
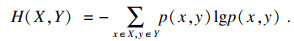 | (2) |
互信息以熵的形式可表示为
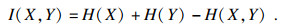 | (3) |
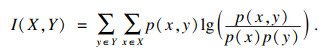 | (4) |
1.1.2 皮尔逊相关系数皮尔逊相关系数用于度量两个变量间的线性相关程度, 相关系数的绝对值越大, 表明变量之间的相关度越高[5].在基因调控网络中, 通过基因表达数据去计算基因之间的线性相关程度.
在基因调控网络构建过程中，基因之间皮尔逊相关系数的计算可由式(5)表示.
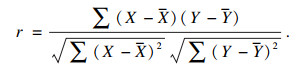 | (5) |
1.1.3 预测最小描述长度要实现潜在调控因子的筛选, 需要确定筛选阈值, 选择预测最小描述长度[6]方法来计算通过互信息获取基因之间关联程度的阈值, 该方法适用于时间序列数据.该方法只对数据点建模, 因此计算代码长度只涉及数据.将代码长度设为文献[7]中给出的数据长度.由于基因调控网络的概率特性, 当一个基因从一个时刻转换到另一个时刻时, 它可以取任何值, 而每个状态转换都会带来新的信息, 这些信息由条件熵来衡量:
 | (6) |
给定基因X在t个时间序列样本点的表达值(X1, …, Xt), 则其总熵为
 | (7) |
 | (8) |
因此将寻找目标基因的潜在调控因子的问题转化为断点检测问题, 利用假设检验来解决.首先基于式(5)计算出所有目标基因和具有不同时间延迟下所有其他基因的皮尔逊相关系数矩阵P0, 并将每一目标基因所对应的所有值升序排序, 根据上述分析, 得到原假设和备择假设:
H0: 原假设——没有断点存在.
H1: 备择假设——存在一个重要的断点.
即矩阵P0的每一行中有一个位置可以将该行中的节点分为相关节点和无关节点两部分.
在原假设下, 目标基因与其他基因的皮尔逊系数值都来自同一分布, 其概率为lg(p(M1:m|δ)).而在备择假设下, 在目标基因与其他基因的皮尔逊相关系数所形成的向量中存在一个断点在位置k, 两种类型的节点来自不同的分布, 构造似然函数:
 | (9) |
检测P0每行中存在的断点, 构造测试统计量Q:
 | (10) |
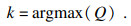 | (11) |
1.2 总体框架高阶动态贝叶斯网络描述基因之间多个时间延迟的调控关系, 解决了动态贝叶斯网络只能描述一个时间延迟的问题.动态贝叶斯网络中基因间相互调控的时间延迟为1, 满足一阶马尔科夫原理[9], 即P(X[t]|X[1], …, X[t-1])=P(X[t]|X[t-1]).高阶动态贝叶斯网络在d个时间延迟下寻找基因之间调控关系, 满足d阶马尔科夫原理[10], 即P(X[t]|X[1], …, X[t-1])= P(X[t]|X[t-d], …, X[t-1]).其P(X[t]|X[t-d], …, X[t-1])表示基因X在t时刻的状态仅与从[t-1]到[t-d]时刻的状态有关, 与其他状态无关.因此在结构学习时一个基因节点只需在[t-d, t]范围内寻找父节点.
利用时序基因表达数据构建高阶动态贝叶斯基因调控网络时, 首先要进行数据预处理, 高阶动态贝叶斯网络要在不同的时间延迟下寻找父节点, 因此将数据进行离散化和数据对齐[10], 具体对齐规则如图 1b中数据对齐所示.
图 1(Fig. 1)
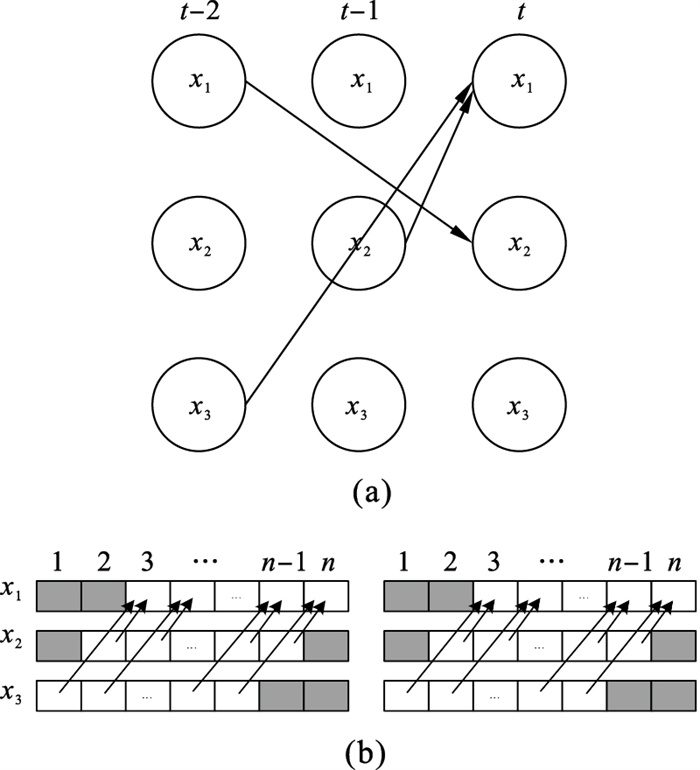 | 图 1 数据对齐Fig.1 Data alignment (a)—2阶转移网络；(b)—x1的数据对齐. |
高阶动态贝叶斯模型进行网络结构学习是在多个时间片内为目标基因寻找父节点, 其结构学习的时间复杂度极高.为了加快学习, 在进行结构学习前先寻找潜在的调控因子集, 缩小父节点的搜索空间.本文使用了两种方法, 从不同的角度对基因之间的关联程度进行分析, 以便在缩小搜索空间的同时保留更多可能存在调控关系的基因, 如图 2中潜在调控因子筛选部分所示.在图 2中以t时刻基因X1作为目标基因为例, 为其所寻找的是2阶转移网络.
图 2(Fig. 2)
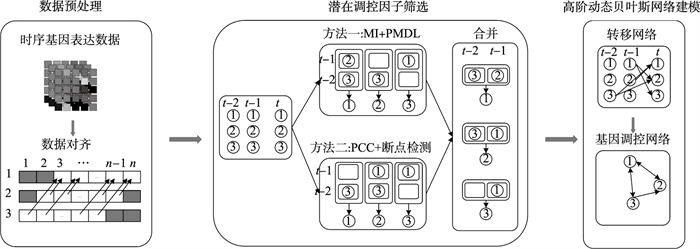 | 图 2 总体框架Fig.2 Overall framework |
在方法一中, 使用互信息去计算t时刻目标基因X1和与其具有不同时间延迟的其他基因X2和X3之间的关联程度, 为了确定到底是哪些基因应该被保留下来, 使用预测最小描述长度原理进行阈值的确定, 选择与目标基因X1关联程度大于阈值的基因作为目标基因X1的潜在调控因子.
在方法二中, 使用皮尔逊相关系数寻找t时刻目标基因X1和不同时间延迟的X2和X3之间的关联程度, 为了筛选出可能相关基因, 使用断点检测方法确定阈值, 使得与目标基因X1关联程度大于阈值的基因作为目标基因X1的潜在调控因子.最后, 将上述两种方法分别为目标基因X1寻找到的潜在调控因子取并集, 作为目标基因X1的潜在调控因子集.
潜在调控因子筛选后, 将潜在调控因子集作为网络结构学习时目标基因父节点的搜索空间, 构建高阶动态贝叶斯基因调控网络.以图 2中的目标基因X1为例, 原本其父节点寻找范围是[t-2, t]时间内的所有基因节点, 使用潜在调控因子筛选算法后, 目标基因X1的父节点寻找范围变成了[t-2, t]时间内目标基因X1的潜在调控因子集.为了得到最优的网络结构, 在进行网络结构学习时对每个目标基因的父节点搜索空间中所有可能的组合进行遍历, 通过评分函数进行评分, 得分最高的组合作为目标基因的父节点.本文使用的评分函数是互信息测试(mutual information tests, MIT)[10].与传统的评分函数相比, 该评分函数计算复杂度低, 可以在多项式时间内实现全局最优的网络结构学习.合并取得所有目标基因的最优父节点集后, 得到高阶动态贝叶斯网络的转移网络.最后将转移网络进行合并, 得到基因调控网络.网络构建的总体框架如图 2所示.
通过图 2可以看到, 基于潜在调控因子筛选的高阶动态贝叶斯基因调控网络构建方法的总体流程: 首先, 将时序基因表达数据进行预处理并进行数据对齐; 然后, 利用关联模型中互信息和皮尔逊相关系数两种方法计算处于不同时间延迟的其他基因与目标基因之间的关联程度, 通过节点自动选择技术中预测最小描述长度和断点检测实现阈值的自动选择, 保留与其关联程度强的基因并作为潜在调控因子; 接下来，将两种方法为目标基因所寻找的潜在调控因子合并作为目标基因的潜在调控因子集; 最后, 将目标基因的潜在调控因子集作为目标基因进行网络结构学习的搜索空间, 利用高阶动态贝叶斯模型进行结构学习, 并通过评分函数来得到目标基因的最优父节点集, 最后将所得到的网络结构进行合并, 得到高阶动态贝叶斯的基因调控网络.
1.3 算法描述本文提出的建模方法主要包括两部分, 即潜在调控因子筛选和网络结构学习.
潜在调控因子筛选包括两个方法：方法一是基于互信息的预测最小描述长度算法；方法二是基于皮尔逊相关系数的断点检测算法, 具体过程如算法1所示.算法的输入是时序基因表达数据X, 输出矩阵Pa, 其中n是基因数量, d是阶数, 矩阵中每个元素P(i, j)表示基因j是基因i的潜在调控因子, 两基因之间的时间延迟是P(i, j).在完成数据预处理后, 分别利用式(4)和式(5)计算基因i和基因j的互信息和皮尔逊相关系数, 形成一个n×(d×n)矩阵I0(第7行)和矩阵P0(第8行).然后利用预测最小描述长度原理确定互信息矩阵I0的阈值并进行筛选, 以矩阵I0中的每个互信息值分别为阈值形成一个模型矩阵C, 利用式(8)去计算最小描述长度LD, 选使得矩阵C具有最小LD值所对应的MI值, 以该MI值作为阈值去对整个互信息矩阵进行筛选, 大于阈值的互信息值保留下来, 小于阈值的设为0, 最终形成矩阵M (第12~16行).接着利用断点检测方法来确定皮尔逊系数矩阵P0的阈值并进行筛选, 对比目标基因i与其他基因j在每一个时间片中所计算出来的皮尔逊系数值, 选其中最大的作为i与j的皮尔逊系数值, 形成一个矩阵P1, 然后利用式(9)构造似然函数, 利用式(11)寻找断点θ, 将所找到的断点θ分别与矩阵P0中的值进行对比, 大于断点值的保留, 小于断点值的设为0, 形成最终的矩阵P(第17~20行).最后将矩阵M和矩阵P取并集作为目标基因的潜在调控因子集Pa并输出(第21~22行).
算法1??潜在调控因子集筛选
输入: 时序基因表达数据X∈{Xi[t]}i=1n.
输出: 潜在调控因子集Pa.
1) ??for i=1 to n do
2) ????{Yj[t-1], …, Yj[t-d]}j=1n-1
3) ????{Yj[t-d]}j=1n-1={X1[t-d], …, Xi-1[t-d], Xi+1[t-d], …, Xn[t-d]}
4) ???? for r=1 to d do
5) ??????分别计算平均值X[t]和Y[t-r];
6) ??????for j=1 to n-1 do
7) ????????由式(4)计算并得到互信息矩阵I0;
8) ????????由式(5)计算并得到PCC矩阵P0;
9) ??for i=1 to n do
10) ????for r=1 to d do
11) ?????? for k=1 to n-1 do
12) ????????以I0中每个元素Ii, k×r分别作为阈值;
13) ????????筛选得到模型矩阵C;
14) ????????由式(8)计算模型长度LD;
15) ????????选LD取最小值所对应的Ii, k×r为阈值α;
16) ????????筛选I0中的元素, 得到矩阵M;
17) ????????选取最大的Pi, k×r作为i和j的PCCs值;
18) ????????将所有值进行升序排列, 形成P1;
19) ????????由式(11)利用P1计算断点θ;
20) ??????将θ作为阈值筛选P0得到矩阵P;
21) ??计算潜在调控因子集Pa= M ∪P;
22) ??输出矩阵Pa.
网络结构学习过程如算法2所示.在进行网络结构学习时, 输入时序基因表达数据X, 目标基因的潜在调控因子集Pa, 设定网络结构中最大的父节点个数p.输出基因调控网络G, 矩阵中每个元素的值代表父节点的阶数.首先, 根据每个目标基因的潜在调控因子集计算每个目标基因的潜在父节点个数形成矩阵A (第1行).然后计算目标基因Xi[t]父节点集为空的MIT分数为最优得分(第3行), 根据目标基因Xi[t]的最大父节点个数p, 从Pa中依次随机选取1-p个基因作为父节点集, 并计算不同父节点集所对应的MIT得分, 将该分数与初始得分进行对比, 若优于初始得分, 将最优得分进行更新, 直到遍历完所有可能的父节点集组合, 最后将最优得分以及最优得分所对应的父节点集作为目标基因p最终的父节点集, 并将其保存在best_Pa(i)和best_MIT(i)中(第5~11行); 最后, 重复上述步骤, 计算出所有基因的结构及其所对应的MIT得分, 输出最终的基因调控网络G.
算法2??高阶动态贝叶斯网络结构学习
输入: 时序基因表达数据X∈{Xi[t]}i=1n, 矩阵Pa, 父节点个数p
输出: 基因调控网络G
1) ??计算目标基因潜在调控因子集个数矩阵A;
2) ??for i=1 to n do
3) ????计算父节点集为空的MIT分数best_MIT(i);
4) ????设置最优父节点集best_Pa(i);
5) ????for k=1 to p do
6) ??????计算所有可能的父节点组合数
7) ??????for q=1 to all_pa do
8) ??????????计算组合为Paq的MIT分数s_MIT;
9) ????????if s_MIT>best_MIT(i)
10) ????????best_Pa(i)=Paq;
11) ????????best_MIT(i)=s_MIT;
12) ????best_score_arr(i)=best_MIT(i);
13) ????Gi=best_Pa(i);
14) ????将Gi添加到G;
15) ??输出G.
2 实验结果及分析2.1 实验设置该实验使用的是DREAM4数据集[11]中insilico_size10和insilico_size100的时序基因表达数据, 每个数据集包含5个网络.实验目标是2阶转移网络, 所以PRS(potential regvllatory factor screening)方法在时间延迟分别为t-1和t-2的情况下为目标基因筛选潜在调控因子集, 同时对比不同时间延迟下所寻找到的真阳边的数量.并对本文所提出的基于潜在调控因子筛选的PRS-HO-DBN, HO-DBN(high-order DBN)方法以及globalMIT[9]和globalMIT+[10]两种经典方法的性能进行评估, 其中HO-DBN方法是基本方法, 在进行网络结构学习前不进行潜在调控因子筛选; 方法globalMIT构建的是一阶DBN, 即FO-DBN; 方法globalMIT+构建的是允许有多个时间延迟的高阶DBN, 即HO-DBN.在进行性能评价时, 选用TPR和FPR两个评估指标, 对比网络结构的AUC和运行时间, 验证了网络构建的效率和准确率.
2.2 实验结果表 1给出了PRS方法在不同时间延迟下对基因筛选潜在调控因子集, 同时对比TP边数量的实验结果.结果表明, 10个和100个基因的网络在使用PRS方法时, t-2都可以比t-1获取更多的真阳边.
表 1(Table 1)
 表 1 10基因和100基因在不同阶数下PRS方法寻找到的TP数量对比Table 1 Comparisons of the number of TP found by PRS method under different orders for 10 genes and 100 genes
| 表 1 10基因和100基因在不同阶数下PRS方法寻找到的TP数量对比 Table 1 Comparisons of the number of TP found by PRS method under different orders for 10 genes and 100 genes |
表 2和表 3给出了使用HO-DBN和PRS-HO-DBN构建的基因调控网络的评估指标的对比.结果表明，PRS-HO-DBN构建的基因调控网络中TPR与HO-DBN大致相同, 但FPR却低于HO-DBN, 使得由PRS-HO-DBN构建的基因调控网络在AUC评估指标上要优于HO-DBN, 这在基因数量为10的网络中尤为明显.这表明潜在调控因子筛选可以有效保留关联性强的基因作为其潜在调控因子, 缩小结构学习时的搜索空间, 降低网络结构中假阳边的比例, 提高AUC的值.
表 2(Table 2)
表 2 HO-DBN网络构建评估指标Table 2 Evaluation indexes of network construction for HO-DBN
| 表 2 HO-DBN网络构建评估指标 Table 2 Evaluation indexes of network construction for HO-DBN |
表 3(Table 3)
表 3 PRS-HO-DBN网络构建评估指标Table 3 Evaluation indexes of network construction for PRS-HO-DBN
| 表 3 PRS-HO-DBN网络构建评估指标 Table 3 Evaluation indexes of network construction for PRS-HO-DBN |
图 3对比了PRS-HO-DBN与3种对比方法在构建基因调控网络时所使用的时间.结果表明, 不管基因个数是10还是100, PRS-HO-DBN的运行时间远远小于globalMIT+和globalMIT, 因为PRS-HO-DBN在结构学习前对目标基因进行了潜在调控因子的筛选, 减少了寻找父节点进行遍历组合时的基数, 使得搜索空间减小, 运行时间缩短.而globalMIT+虽然在结构学习前也进行了基因节点的筛选, 但筛选后的搜索空间仍远大于PRS-HO-DBN; 而globalMIT在结构学习之前未进行潜在调控因子的筛选, 其寻找父节点的搜索空间是所有的基因节点, 在网络结构学习时其搜索空间最大, 学习时间远高于前者.而且随着基因个数的增加, 其运行时间的增长趋势也会远高于PRS-HO-DBN.因此可以得出, PRS-HO-DBN在保证网络构建准确度的前提下可以明显缩短网络构建的运行时间, 提高构建效率.同时, 通过图 3还能发现, 只要进行潜在调控因子筛选再去构建基因调控网络, 都会使得网络的构建时间小于HO-DBN, 证明结构学习前筛选潜在调控因子能提高网络的构建效率.
图 3(Fig. 3)
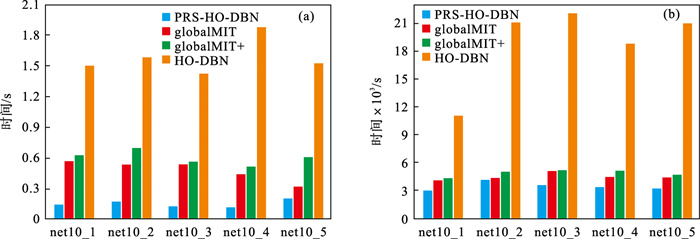 | 图 3 PRS-HO-DBN，globalMIT，globalMIT+和HO-DBN网络构建运行时间的对比Fig.3 Comparison of running time for PRS-HO-DBN, globalMIT, globalMIT+ and HO-DBN (a)—10基因；(b)—100基因. |
表 4和表 5分别给出了使用PRS-HO-DBN和两种经典方法对基因数量为10和100的各5个网络进行基因调控网络构建, 并对比各评估指标的结果.由表可知，基因数量为10或100, 用PRS-HO-DBN所构建的网络其评估结果普遍优于对比方法.与globalMIT相比, PRS-HO-DBN从2个时间延迟内为目标基因寻找父节点, 可以找到更多潜在父节点, 因此PRS-HO-DBN构建的网络结构的TPR普遍高于globalMIT; 与globalMIT+相比, PRS-HO-DBN在筛选潜在调控因子时可以保留更多真阳边, 同时删除无关基因, 使得网络的各项指标值优于globalMIT+.
表 4(Table 4)
表 4 10基因的PRS-HO-DBN，globalMIT和globalMIT+三种方法网络构建评估指标对比Table 4 Comparisons of the performance indices for PRS-HO-DBN, globalMIT and globalMIT+for 10 genes
| 表 4 10基因的PRS-HO-DBN，globalMIT和globalMIT+三种方法网络构建评估指标对比 Table 4 Comparisons of the performance indices for PRS-HO-DBN, globalMIT and globalMIT+for 10 genes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 5(Table 5)
表 5 100基因的PRS-HO-DBN，globalMIT和globalMIT+三种方法网络构建评估指标对比Table 5 Comparisons of the performance indices for PRS-HO-DBN, globalMIT and globalMIT+for 100 genes
| 表 5 100基因的PRS-HO-DBN，globalMIT和globalMIT+三种方法网络构建评估指标对比 Table 5 Comparisons of the performance indices for PRS-HO-DBN, globalMIT and globalMIT+for 100 genes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3 结论1) 本文选用关联模型中的互信息和皮尔逊相关系数两种方法从不同的角度对基因之间的关联程度进行衡量, 在目标基因筛选潜在调控因子时可以对候选基因进行全面的评估, 同时也可以有效地防止在进行网络结构学习时对真阳边的遗漏.
2) 本文采用关联模型与节点自动选择技术相结合的方法为目标基因实现潜在调控因子的自动筛选, 缩小了在进行网络结构学习时为目标基因寻找父节点的搜索空间, 解决了在利用高阶动态贝叶斯网络模型进行基因调控网络构建时所存在的网络构建时间过长的问题, 使得利用高阶动态贝叶斯网络模型进行大规模网络结构构建成为可能.
3) 通过使用DREAM4数据集中的时序基因表达数据进行实验, 实验表明PRS-HO-DBN方法在构建基因调控网络方面具有较好的性能.
参考文献
| [1] | Castelletti F, Rocca L L, Peluso S, et al. Bayesian learning of multiple directed networks from observational data[J]. Statistics in Medicine, 2020, 39(30): 4745-4766. DOI:10.1002/sim.8751 |
| [2] | Chai L E, Mohamad M S, Deris S, et al. A dynamic Bayesian network-based model for inferring gene regulatory networks from gene expression data[J]. International Journal of Bio-science & Bio-technology, 2015, 6(1): 41-52. |
| [3] | 曲璐渲, 郭上慧, 王之琼, 等. 基因调控网络的父节点筛选贝叶斯建模方法[J]. 东北大学学报(自然科学版), 2020, 41(2): 158-162. (Qu Lu-xuan, Guo Shang-hui, Wang Zhi-qiong, et al. Modelling of gene regulatory networks by parent node screening-based Bayesian method[J]. Journal of Northeastern University(Natural Science), 2020, 41(2): 158-162.) |
| [4] | Zhang X, Jian Y, Xu Z. A semi-supervised learning algorithm for predicting four types MiRNA-disease associations by mutual information in a heterogeneous network[J]. Genes, 2018, 9(3): 139-154. DOI:10.3390/genes9030139 |
| [5] | Qu L, Wang Z, Li C, et al. Dynamic Bayesian network modeling based on structure prediction for gene regulatory network[J]. IEEE Access, 2021, 9: 123616-123634. DOI:10.1109/ACCESS.2021.3109133 |
| [6] | Chaitankar V, Ghosh P, Perkins E J, et al. A novel gene network inference algorithm using predictive minimum description length approach[J]. BMC Systems Biology, 2010, 4(sup1): S1-S7. |
| [7] | Zhao W, Serpedin E, Dougherty A E R. Inferring gene regulatory networks from time series data using the minimum description length principle[J]. Bioinformatics, 2006, 22(17): 2129-2135. DOI:10.1093/bioinformatics/btl364 |
| [8] | Xing L, Guo M, Liu X, et al. Gene regulatory networks reconstruction using the flooding-pruning hill-climbing algorithm[J]. Genes, 2018, 9(7): 342. DOI:10.3390/genes9070342 |
| [9] | Vinh N X, Chetty M, Coppel R, et al. GlobalMIT: learning globally optimal dynamic Bayesian network with the mutual information test criterion[J]. Bioinformatics, 2011, 27(19): 2765-2766. DOI:10.1093/bioinformatics/btr457 |
| [10] | Vinh N X, Chetty M, Coppel R, et al. Gene regulatory network modeling via global optimization of high-order dynamic Bayesian network[J]. BMC Bioinformatics, 2012, 13: 131. DOI:10.1186/1471-2105-13-131 |
| [11] | Schaffter T, Marbach D, Floreano D. GeneNetWeaver: in silico benchmark generation and performance profiling of network inference methods[J]. Bioinformatics, 2011, 27(16): 2263-2270. DOI:10.1093/bioinformatics/btr373 |
