李海燕¹, 熊立昌¹, 郭磊¹, 李海江²
1. 云南大学 信息学院，云南 昆明 650000;
2. 云南交通投资建设集团有限公司，云南 昆明 650001
收稿日期：2022-01-07
基金项目：国家自然科学基金资助项目(62266049，61861045)；云南省****“教学名师”；云南省高校重点实验室建设计划项目(202101AS070031)。
作者简介：李海燕(1976-)，女，云南红河人，云南大学教授，博士生导师。

摘要：为了有效修复背景复杂、大面积不规则缺失区域，得到合理的结构和精细的纹理，提出了基于U-net边缘生成和超图卷积的两阶段修复算法.首先，将缺失图像输入基于U-net门控卷积的粗修复网络，通过跳跃连接将图像的上下文信息向深层传播，获取丰富的图像细节信息，下采样提取缺失区域边缘特征，上采样还原缺失区域边缘细节，同时使用混合空洞卷积增大信息感受野，获取细节纹理信息.然后，将粗修复结果输入含超图卷积的细修复网络，捕获和学习输入图像中的超图结构，使用空间特征的互相关矩阵捕获空间特征结构，改善结构完整性并提升细节细粒度.最后，将细修复结果输入鉴别器进行判别优化，进一步优化修复结果.在国际公认数据集上进行实验仿真，结果显示：本文提出的算法在修复大面积不规则缺失时，可以生成合理的结构和丰富的纹理细节，修复的视觉效果，PSNR，SSIM和L1损失优于对比算法.
关键词：图像修复U-net边缘生成超图卷积混合空洞卷积两阶段网络
Two-Stage Inpainting Algorithm Based on U-net Edge Generation and Hypergraphs Convolution
LI Hai-yan¹, XIONG Li-chang¹, GUO Lei¹, LI Hai-jiang²
1. School of Information Science and Engneering, Yunnan University, Kunming 650000, China;
2. Yunnan Communications Investment and Construction Group Co., Ltd., Kunming 650001, China
Corresponding author: LI Hai-yan, E-mail: leehy@ynu.edu.cn.

Abstract: In order to implement reasonable structure inpainting and fine texture reconstruction for large irregular missing areas with complex background, a two-stage network inpainting algorithm based on U-net edge generation and hypergraphs convolution is proposed. Firstly, the image to be repaired is fed into a coarse inpainting network based on U-net gated convolution where the context information of the image is propagated to a deeper layer through jump connection to obtain rich image detail information. Down-sampling is applied to extract the edge features of the missing area, and up-sampling is performed to restore the edge details of the missing area while hybrid dilated convolution is adopted to increase the information receptive field and further obtain image detailed texture information. Subsequently, the coarse inpainting results are inputted into the refine inpainting network with hypergraphs convolution to capture and learn the hypergraphs structure in the input image, and the cross-correlation matrix of spatial features is implemented to capture the spatial feature structure as well as to further improve the structural integrity and fine-grained details. Finally, the refined inpainting results are input into the discriminator for discrimination optimization to further improve the inpainting results. The experimental simulation is carried out on the internationally published dataset. The experimental results demonstrate that the proposed algorithm can generate a reasonable structure with good color consistency and abundant detail texture under the condition of large-area loss, and the visual effect, PSNR, SSIM and L1 loss are superior over those of the compared algorithms.
Key words: image inpaintingU-net edge generationhypergraphs convolutionhybrid dilated convolutiontwo-stage network
图像修复旨在填充图像的缺失区域，生成完整的图像.现有的图像修复算法主要可以分为两类：传统修复算法和基于深度学习的算法.传统修复算法^[1-3]主要从非孔像素复制内容或纹理填充缺失区域，在背景复杂时很难得到合理的结构，也无法修复较大损坏区域.TV算法^[4]利用图像的平滑特性填充缺失区域，可修复破损较小的区域，但破损面积大时，易出现结构扭曲和纹理不连续.Patch match算法^[5]从图像中搜索相似区域，迭代填充缺失像素，可生成较合理的细节纹理，但无法识别图像的全局语义结构，导致修复的结构语义一致性差.
为解决传统修复算法的不足，基于深度学习的修复算法应运而生.Pathak等^[6]提出上下文编码器修复算法，采用编码器-解码器架构对抗训练网络，编码器将缺失区域映射到低维特征空间，解码器利用低维特征空间构建输出图像，可修复小面积规则缺失区域，但由于全连接层的信息瓶颈，在修复大面积缺失时会出现伪影和边缘模糊.为解决此问题，Iizuka等^[7]提出全局与局部一致性的图像修复算法，用空洞卷积代替全连接层并减少下采样层数以期解决信息瓶颈，用全局鉴别器评估整体结构一致性，用局部鉴别器确保生成细节的完整性，该算法修复小面积缺失效果不错，但缺失区域面积大时，无法兼顾整体与局部的语义一致性.Yang等^[8]提出多尺度神经补丁合成修复算法，引入已训练好的VGG网络^[9]，从周围环境中传播结构纹理信息，迭代多尺度优化算法填充缺失区域，能修复较大面积的规则缺失，获得精细的结构及纹理，但将其应用于实际的随机不规则缺失修复时，性能急剧下降.为了有效修复随机不规则缺失区域，Liu等^[10]提出用部分卷积代替普通卷积的修复算法，利用有效像素通过自动掩码更新机制推断并修复缺失区域，能处理背景简单、随机不规则的小面积缺失区域，但背景复杂、缺失区域过大时，修复结果缺乏整体与局部信息的语义一致性.Nazeri等^[11]提出基于边缘生成器与图像生成器的修复算法，边缘生成器估计不规则缺失区域的边缘，在背景简单时，可得到逼真的细节纹理，但无法重建复杂背景的大面积不规则缺失图像.为有效修复随机不规则缺失，Zheng等^[12]提出由重建路径和生成路径组成的多元补全算法(PIC)，重建路径获取缺失区域的先验分布，生成路径预测缺失区域的潜在先验分布，然后采样生成修复结果，但该算法修复背景复杂的随机缺失区域时，存在结构扭曲且颜色一致性差等不足.Peng等^[13]提出基于分层变分自编码器的修复算法(VQ-VAE)，使用结构注意力模块，捕获结构特征的远距离相关性，能生成高度多样化的合理结构，但在修复大面积不规则缺失时，生成的图像细节模糊、纹理错乱.Wadhwa等^[14]提出粗修复-精修复两阶段修复算法(HII)，首次将图卷积用于不规则缺失区域修复，能生成合理的结构信息与纹理细节，保持图像整体颜色的一致性，但在背景复杂且缺失面积增大到30 % 及以上时，性能急剧下降.
综上所述，现有算法在修复背景复杂、大面积不规则缺失区域时，难以兼顾结构全局性与纹理细节的精细度.为解决此不足，本文提出基于U-net边缘生成和超图卷积的两阶段修复算法，主要创新点：①粗修复网络是门控卷积的U-net边缘生成架构，跳跃连接编码器与解码器，使解码器更好地捕获图像的细节纹理，下采样提取缺失图像的边缘特征，再结合上采样的信息和下采样的各层纹理特征生成精细的图像边缘；②首次在细修复网络中使用超图卷积，捕获学习图像中的超图结构，提出使用空间特征的互相关矩阵学习长期的内部空间依赖性，更好地捕获空间结构特征，提升结构一致性；③用混合空洞卷积代替空洞卷积，扩大信息感受野，捕获更多的图像细节.
1 基于U-net边缘生成和超图卷积的两阶段图像修复算法基于U-net边缘生成和超图卷积的两阶段修复算法如图 1所示.首先, 将待修复图像输入门控卷积定义的U-net边缘生成网络，捕获细节特征，下采样将图像信息向网络的深层传递，上采样结合输入信息和下采样各层信息还原图像细节信息，生成精细的轮廓边缘.然后, 将粗修复结果输入到含有超图卷积的细修复网络，学习图像中的超图结构信息，使用空间特征的互相关计算每个节点在每条超边中的贡献，捕获图像的空间结构特征，完善修复图像的结构及纹理细节.最后，将细修复结果输入鉴别器判别优化，并在鉴别器中引入门控卷积，加强预测图像的局部一致性.
图 1(Fig. 1)

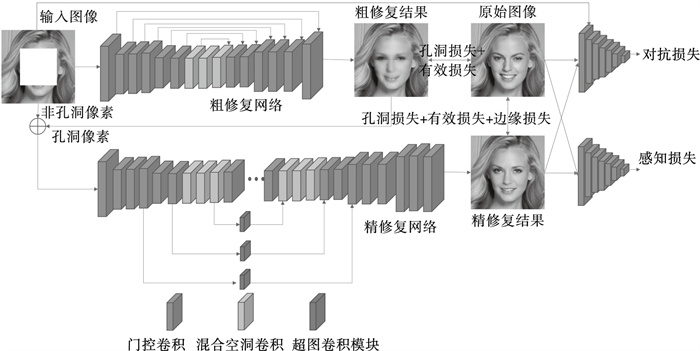图 1 提出的算法模型Fig.1 The proposed algorithm model

1.1 粗修复网络为了尽可能捕获图像纹理细节，生成大面积不规则缺失的边缘，本文提出的粗修复网络基于U-net架构^[15]包含上采样与下采样：下采样逐步捕获图像信息；上采样结合下采样各层的图像信息和上采样的输入还原缺失区域的结构和纹理细节，提高修复精度.U-net边缘生成网络中的编码器与解码器通过跳跃连接，使解码器更好地捕获缺失区域的纹理细节，生成合理的图像边缘.编码器第一层的卷积核为7×7，其余的卷积核均为3×3，步长分别为1，2，1，1，1，1.解码层卷积核大小均为3×3，步长为1，1，1，1，2，1.编码层和解码层采用门控卷积代替普通卷积，避免常规卷积将图像的所有像素视为有效像素的不足，为所有层中每个空间位置的通道提供可学习的动态特征选择机制泛化部分卷积，使网络捕获更精准的细节纹理.为进一步增大信息感受野且避免图像信息的不连续性，使用混合空洞卷积(HDC)^[16]代替空洞卷积，空洞率分别为1，2和5.其中，门控卷积定义为

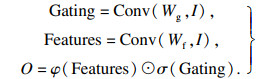(1)

其中：W_g和W_f是卷积运算的两个可学习参数；I是输入图像；σ是Sigmoid激活函数；φ是非线性激活函数.本文算法使用ELU激活函数，并在卷积过程中删除归一化，避免降低修复结果的颜色一致性^[7].
1.2 细修复网络为了捕获精细的纹理细节，细修复网络也用门控卷积代替普通卷积，用混合空洞卷积代替空洞卷积，且在细修复网络中加入超图卷积，从输入图像中学习超图结构，改善修复结果的结构以及纹理信息.
超图卷积结构如图 2所示.超图结构可对数据的高阶约束进行建模，而这些约束是传统图结构中无法容纳的.超图包含可以连接两个或多个顶点的超边，定义为G=(V, E, W), 其中V={v₁, …, v_N}是顶点集，E={e₁, …, e_M}是超边集合，W∈R^m×m是包含每条边权重的对角矩阵.超图G可以用关联矩阵H∈R^n×m表示.
图 2(Fig. 2)

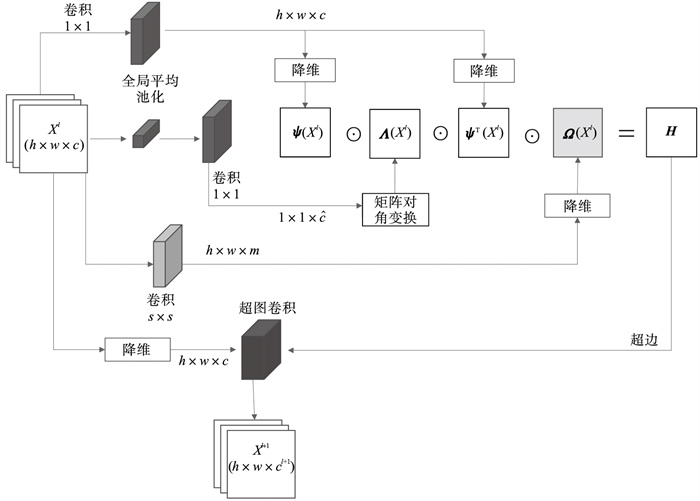图 2 超图卷积空间特征示意图Fig.2 The hypergraph convolution on the spatial features

为克服CNN架构的有限接受域，将空间特征图转换为基于图的结构，并执行图卷积捕获数据间的全局关系^[17-19].简单图作为超图的一种特殊情况，每条超边仅连接两个节点，可以很容易表示数据之间的成对关系，但很难表示图像空间特征之间的复杂关系，因此本文算法使用超图代替图卷积网络.为了将空间特征F^I∈ R^h×w×c转换为超图的结构，本文算法将每个空间特征视为具有维度c的特征向量节点且X^I∈ R^h×w×c.为了更好地捕捉图像的内部空间结构，提出了改进的关联矩阵H，可学习捕获长期的内部空间依赖性.提出算法使用空间特征的互相关计算每个节点在每条超边中的贡献，而不是空间特征之间的欧几里德距离^[20].关联矩阵H包含每个节点在每条超边中的贡献信息，表示为

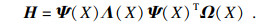(2)

其中，Ψ(X)，Λ(X)和Ω(X)都是数据相关矩阵. Ψ(X)∈ 是输入特征的线性嵌入，由输入特征的1×1卷积实现. 是线性嵌是对角矩阵，由通道全局平均池化后经过1×1卷积，再用Sigmoid将其归一化到[0, 1]的范围，将此值作为尺度乘到X的c个通道上，作为下一级的输入数据，通过控制尺度的大小，增强重要特征，减弱次要特征，使提取的特征指向性更强，为关联矩阵H学习节点之间更好地度量距离. Ω(X)∈ R^n×m用于捕获特征的全局关系以选择更好的超边(本文算法使用7×7滤波器实现)，确定每个节点对超边的贡献.
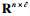
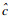
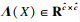
如图 2所示，关联矩阵H^I定义为

(3)

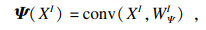(4)

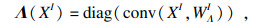(5)

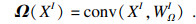(6)

其中：是输入特征全局池化后的特征图；W_Ψ^I, W_Λ^I和W_Ω^I是线性嵌入的可学习参数；H^I用于产生最终的输出特征；为了避免关联矩阵H出现负值，导致矩阵中的虚值，本文算法对关联矩阵求绝对值，然后将空间特征的超图卷积层定义为

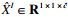
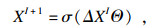(7)

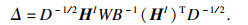(8)

其中: Θ∈ R^cI×cl+1是可学习参数; σ是非线性激活; X^I是输入特征; D为顶点度; B为超边度; X^I+1为输出特征.
1.3 损失函数本文提出算法使用由内容损失、对抗性损失、感知损失和边缘保留损失的组合损失训练网络.为了保证像素级的语义一致性，提出算法在粗修复I_coarse和细修复I_refine输出上使用L1损失，将内容损失定义为

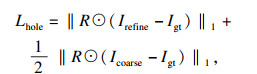(9)

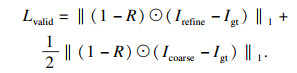(10)

其中：I_coarse和I_refine分别表示粗修复网络和细修复网络；R表示二进制掩码；I_gt表示真实图像；L_hole是孔像素值的损失；L_valid是非孔像素值的损失.
对抗性损失可有效生成逼真且全局一致的图像^[21]，对抗性损失定义为最小-最大问题：

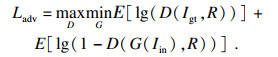(11)

其中：G是图像修复网络；I_refine为预测细修复结果；D是鉴别器.
对于给定输入x，令φ_I(x)表示预训练网络第I激活层的高维特征，则感知损失定义为

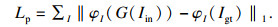(12)

以此计算最终预测I_refine的感知损失，将非孔像素设置为真实值.
为了有效预测图像中的边缘，提出算法使用边缘保留损失^[22]:

(13)

其中，E(·)是Sobel滤波器.因此总损失L_total定义为

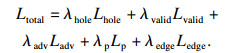(14)

其中，λ_hole，λ_valid，λ_adv，λ_p和λ_edge分别是平衡孔洞、有效、对抗、边缘保留损失的权重，可由掩码大小动态学习以均衡损失，根据实验测试.将L_hole, λ_valid, L_adv, L_p和L_edge的值分别设置为0.2，1，0.05，0.002，0.000 1.
2 实验结果与分析在CelebA-HQ, Places2和Paris-street三个数据集上，对本文算法和现有的3种算法进行实验对比.CelebA-HQ, Places2和Paris-street分别包含各种高清人脸、自然风景和街景图像.在CelebA-HQ和Places2中选取20 000张图像，其中19 000张用于训练，900张用于测试，100张用于验证.在Paris-street中选取14 000张图像用于训练，800张用于测试，100张用于验证.设备参数为CPU：Intel i7-9700K，GPU：RTX2080Ti.代码在Tensorflow深度学习框架下运行，将本文算法与PIC算法^[12]，VQ-VAE算法^[13]和HII算法^[14]进行对比，掩码为规则掩码以及不规则掩码.
2.1 实验结果为了保证比较的公平性，所有模型的迭代次数相同.图 3为各算法在CelebA-HQ, Places2和Paris-street数据集上叠加规则掩码的修复结果.第一组图中，PIC算法能保持修复结果的整体结构性，但修复细节有瑕疵，眼睛的纹理错乱，鼻子部位出现修复斑点.VQ-VAE算法和HII算法的修复性能较PIC算法有改进，但VQ-VAE算法在眼睛部位无法生成合理结构，HII算法修复的眼睛纹理细节欠精细.相对而言，本文提出算法修复的整体结构清晰，眼睛和鼻子的纹理细节精致.
图 3(Fig. 3)

图 3 规则掩码修复结果Fig.3 Inpainting results of regular masks (a)—原图；(b)—输入图像；(c)—PIC算法；(d)—VQ-VAE算法；(e)—HII算法；(f)—本文算法.

第二组图中，PIC算法修复的眼睛严重失真，鼻子部位有明显修复边界.VQ-VAE算法得到的结构一致性好，但鼻子处部分细节丢失.HII算法修复的鼻子部位细节丰富，但眼睛处出现黑色，颜色一致性差.相较而言，本文提出算法得到的结构纹理更合理且丰富，颜色一致性好.
第三组图中，PIC算法修复的墙体有较好的线条，但门处出现修复光影，整体效果一般.VQ-VAE算法修复的整体效果较好，但标记部位结构错乱.HII算法在门处能保持较好的结构完整性，但墙体线条丢失，修复效果较好.本文提出算法不仅能保持整体语义结构的一致性，且生成细节丰富的墙体线条，修复效果好.
第四组图中，PIC算法修复结果差，出现大面积的修复伪影.VQ-VQE算法在标记处出现不合理结构，颜色一致性差，修复效果一般.HII算法在标记处也出现了小面积修复伪影.而本文提出算法可保持整体结构、局部语义结构以及颜色一致性.
图 4为各算法在CelebA-HQ, Places2和Paris-street数据集上叠加不规则掩码的修复结果, 输入图像缺失面积较大，达35 % 及以上.第一组图中，PIC算法可以生成合理的面部结构，但无法保持整体颜色一致性，出现大面积色差.VQ-VAE算法修复大面积缺失时，结构与语义一致性极差，无法生成合理的纹理.HII算法可以保持整体的颜色一致性，但面部及头发边缘轮廓丢失，结构性差.相较而言，本文提出算法兼顾颜色一致性与结构合理性，面部结构完整，修复效果好.
图 4(Fig. 4)

图 4 不规则掩码修复结果Fig.4 Inpainting results of irregular masks (a)—原图；(b)—输入图像；(c)—PIC算法；(d)—VQ-VAE算法；(e)—HII算法；(f)—本文算法.

第二组图中，PIC算法和HII算法的修复结果均出现伪影，PIC算法的修复结果存在颜色失真.HII算法能够保持整体颜色一致性，但无法生成精细的细节纹理.VQ-VAE算法出现大面积修复痕迹，且颜色一致性差.而本文提出算法可减少色差，避免色彩大幅丢失，保持结构和纹理一致性.
第三组和第四组中，缺失面积达45 % 及以上，且背景复杂.PIC算法修复的门拱结构不合理且存在颜色失真，柱子线条边缘轮廓丢失，且包含大量修复斑点，纹理细节错乱.VQ-VAE算法的修复结果出现大面积结构扭曲，无法生成合理的结构，纹理严重畸变.HII算法能保持整体的语义结构和颜色一致性，但窗户的纹理细节模糊.本文提出算法能兼顾语义结构和颜色一致性，在色彩、结构及细节纹理上与未损坏区域一致性好，与原图相似度高.
2.2 定量评估表 1为各算法在CelebA-HQ和Paris-street数据集上叠加规则掩码和不规则掩码的定量实验对比.由表 1的结果可知：本文算法的PSNR(峰值信噪比)、SSIM(结构相似性)和L1损失3个指标比3种对比算法的好.叠加规则掩码时，在CelebA-HQ数据集上，本文提出算法的PSNR比HII算法的提高2.91，SSIM提高0.038，L1损失降低0.6.在Paris-street数据集上，本文提出算法的PSNR比HII算法提高2.63，SSIM提高0.028，L1损失降低0.57.叠加不规则掩码时，在CelebA-HQ数据集和Paris-street数据集上，本文提出算法的PSNR比HII算法分别提高3.42和2.68，SSIM分别提高0.052和0.07，L1损失分别降低0.54和0.46.实验结果说明：本文提出算法采用U-net边缘生成以及混合空洞卷积和超图卷积网络能提高修复精度，改善整体颜色的一致性，对大面积不规则缺失的修复效果优于对比算法.
表 1(Table 1)

表 1 定量实验对比Table 1 Quantitative experimental comparisons 类型 指标 CelebA-HQ Paris-street PIC VQ-VAE HII 本文 PIC VQ-VAE HII 本文 规则 PSNR 23.35 24.86 25.25 28.16 22.05 21.38 24.59 27.22 SSIM 0.867 0.896 0.91 0.948 0.816 0.833 0.858 0.886 L1 3.12 2.77 2.28 1.68 3.95 3.47 2.89 2.32 不规则 PSNR 16.84 18.89 21.46 24.88 15.94 14.78 20.86 23.54 SSIM 0.75 0.73 0.85 0.902 0.69 0.63 0.82 0.89 L1 4.82 5.36 3.58 3.04 5.38 5.69 4.54 4.08

表 1 定量实验对比 Table 1 Quantitative experimental comparisons

2.3 消融实验一为验证本文提出算法中混合空洞卷积、U-net边缘生成以及超图卷积的作用，对修复模型进行消融实验.图 5a~图 5f分别为原图、待修复图、基础模型、叠加混合空洞卷积模型、再叠加U-net边缘生成的模型和完整模型.当仅叠加HDC时，相较于基础模型结果，左眼细节更丰富，鼻子结构更完整.叠加U-net边缘生成网络后，图 5f较图 5d眼睛更清晰明亮.完整模型的结果更合理，眼睛黑白分明，鼻子部位完整，缺失区域和未缺失区域有更好的语义结构和纹理一致性.
图 5(Fig. 5)

图 5 重要模块消融实验结果图Fig.5 The ablation experiment results of important modules (a)—原图；(b)—输入图像；(c)—基础模型；(d)—HDC；(e)—HDC+U-net边缘生长；(f)—HDC+U-net边缘生成+超图模型.

表 2为在CelebA-HQ数据集上叠加规则掩码的重要模块消融实验定量对比.可以看出，仅叠加HDC时，PSNR较基础模型提高了0.9，SSIM提高了0.015，L1损失降低了0.32.再叠加U-net时，较仅叠加HDC的结果，PSNR又提高了0.81，SSIM提高了0.011，L1损失降低了0.13.完整模型相较于叠加U-net边缘生成和HDC的结果，3个指标又分别改善了1.2，0.012，0.15.综上所述，本文提出算法中的HDC，U-net边缘生成以及超图卷积均能改善修复效果.
表 2(Table 2)

表 2 重要模块消融实验定量指标对比Table 2 Comparison of quantitative indexes in the ablation experiment of important modules 指标 基础模型 HDC HDC+U-net边缘生成 HDC+U-net边缘生成+超图模型 PSNR 25.25 26.15 26.96 28.16 SSIM 0.91 0.925 0.936 0.948 L1 2.28 1.96 1.83 1.68

表 2 重要模块消融实验定量指标对比 Table 2 Comparison of quantitative indexes in the ablation experiment of important modules

2.4 消融实验二为验证本文提出算法中对抗性损失和边缘保留损失等损失函数的作用，对模型进行消融实验.图 6a~图 6h分别为原图、待修复图像、去孔像素值损失后的结果、去非孔像素值损失后的结果、去对抗性损失后的结果、去边缘保留损失后的结果、去边缘损失后的结果以及本文提出算法的结果.可以看出，相较于图 6h，去L_hole后眼睛部位细节不够精细，面部轮廓过于平滑.去L_valid后眼睛黑白不分明，无法生成合理的结构.去L_adv后眼部虽然生成了黑白分明的结构，但纹理细粒度欠佳.去L_p后眼睛部位颜色严重丢失，出现明显的黑色像素，嘴唇以及鼻子部位结构轻微扭曲.去L_edge后眉毛和眼睛部分结构混合，损失了面部的结构一致性.如图 6h所示，完整模型不仅保持面部整体结构一致性，而且兼顾了纹理与颜色的一致性，结构与原图更贴合.
图 6(Fig. 6)

图 6 损失函数消融实验结果图Fig.6 Ablation experiment results of the loss function (a)—原图；(b)—输入图像；(c)—去Lhole；(d)—去Lvalid；(e)—去Ladv；(f)—去Lp；(g)—去Ledge；(h)—本文算法.

表 3为在CelebA-HQ数据集上叠加规则掩码时损失函数的消融实验定量指标对比，去掉L_hole，L_valid，L_adv，L_p和L_edge后，相较于完整模型，PSNR分别降低了0.5，1.18，0.14，1.67和0.42；SSIM分别降低了0.03，0.092，0.015，0.106和0.024；L1分别提高了0.36，0.6，0.13，0.71和0.25.综上所述，对抗性损失和边缘保留损失等损失函数均能优化模型修复结果.
表 3(Table 3)

表 3 损失函数消融实验定量指标对比Table 3 Qantitative indexes comparisons of loss function ablation experiments 指标 去Lhole 去Lvalid 去Ladv 去Lp 去Ledge 完整模型 PSNR 27.66 26.98 27.92 26.49 27.74 28.16 SSIM 0.918 0.856 0.933 0.842 0.92 0.948 L1 2.04 2.28 1.81 2.39 1.93 1.68

表 3 损失函数消融实验定量指标对比 Table 3 Qantitative indexes comparisons of loss function ablation experiments

3 结语本文提出了基于U-net边缘生成和超图卷积的两阶段修复算法，首先，将待修复图像输入以U-net边缘生成为架构、门控卷积为基础的粗修复网络，通过混合空洞卷积增加信息感受野，对待修复图像进行粗修复.然后，将待修复图像与粗修复图像输入含有超图卷积模块的细修复网络，通过超图卷积模块捕获精细的图像结构和细节纹理.最后，将细修复结果输入以门控卷积定义的鉴别器进行判别优化.实验表明，本文提出算法在修复大面积不规则缺失时，可生成合理的结构和丰富的纹理细节，优于对比算法.
参考文献

[1]	Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting[C]//Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2000: 417-424.
[2]	Ballester C, Bertalmio M, Caselles V, et al. Filling-in by joint interpolation of vector fields and gray levels[J]. IEEE Transactions on Image Procession, 2001, 10(8): 1200-1211. DOI:10.1109/83.935036
[3]	Esedoglu S, Shen J. Digital inpainting based on the Mumford-Shah-Euler image model[J]. European Journal of Applied Mathematics, 2002, 13(4): 353-370.
[4]	Wang T, Qin Z, Zhu M. An ELU network with total variation for image denoising[C]//International Conference on Neural Information Processing. Cham: Springer, 2017: 227-237.
[5]	Barnes C, Shechtman E, Finkelstein A, et al. Patch match: a randomized correspondence algorithm for structural image editing[J]. ACM Transactions on Graphics(TOG), 2009, 28(3): 1-11.
[6]	Pathak D, Krahenbuhl P, Donahue J, et al. Context encoders: feature learning by inpainting[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, 2016: 2536-2544.
[7]	Iizuka S, Simo-Serra E, Ishikawa H. Globally and locally consistent image completion[J]. ACM Transactions on Graphics(TOG), 2017, 36(4): 107.
[8]	Yang C, Lu X, Lin Z, et al. High-resolution image inpainting using multi-scale neural patch synthesis[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Puekto Rico, 2017: 6721-6729.
[9]	Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[C]//International Conference on Learning Representations. San Diego: ICLR, 2015: 1150-1210.
[10]	Liu G, Reda F, Shih K, et al. Image inpainting for irregular holes using partial convolutions[C]//Proceedings of the European Conference on Computer Vision(ECCV). Puerto Rito, 2018: 85-100.
[11]	Nazeri K, Ng E, Joseph T, et al. Edge-connect: generative image inpainting with adversarial edge learning[C]//ICCV Workshops. Seoul: ICCV, 2019: 5833-5841.
[12]	Zheng C, Cham T J, Cai J. Pluralistic image completion[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 1438-1447.
[13]	Peng J, Liu D, Xu S, et al. Generating diverse structure for image inpainting with hierarchical VQ-VAE[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Montreal, 2021: 10775-10784.
[14]	Wadhwa G, Dhall A, Murala S, et al. Hyperrealistic image inpainting with hypergraphs[C]//Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. New York, 2021: 3912-3921.
[15]	Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation[C]//International Conference on Medical Image Computing and Computer-Assisted Intervention. Athens, 2015: 234-241.
[16]	李海燕, 吴自莹, 郭磊, 等. 基于混合空洞卷积网络的多鉴别器图像修复[J]. 华中科技大学学报(自然科学版), 2021, 49(3): 40-45. (Li Hai-yan, Wu Zi-ying, Guo Lei, et al. Multi-discriminator image inpainting algorithm based on hybird dilated convolution network[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2021, 49(3): 40-45. DOI:10.13245/j.hust.210308)
[17]	Chen Y, Rohrbach M, Yan Z, et al. Graph-based global reasoning networks[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, 2019: 433-442.
[18]	Li Y, Gupta A. Beyond grids: learning graph representations for visual recognition[J]. Advances in Neural Information Processing Systems, 2018, 31: 9225-9235.
[19]	Liang X, Hu Z, Zhang H, et al. Symbolic graph reasoning meets convolutions[J]. Advances in Neural Information Processing Systems, 2018, 31: 1853-1863.
[20]	Yadati N, Nimishakavi M, Yadav P, et al. HyperGCN: a new method of training graph convolutional networks on hypergraphs[C]//Advances in Neural Information Processing Systems(NeurIPS). Puerto Rico, 2019: 1509-1520.
[21]	Nah S, Kim T H, Lee K M. Deep multi-scale convolutional neural network for dynamic scene deblurring[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Puerto Rico, 2017: 3883-3891.
[22]	Pandey R K, Saha N, Karmakar S, et al. MSCE: an edge-preserving robust loss function for improving super-resolution algorithms[C]//International Conference on Neural Information Processing. Cham: Springer, 2018: 566-575.