
 , 刘军祥
, 刘军祥 东北大学 冶金学院,辽宁 沈阳 110819
收稿日期:2022-01-14
基金项目:国家重点研发计划项目(2017YFB0603603);辽宁省“兴辽英才计划”项目(XLYC1802003)。
作者简介:刘中元(1997-),男,湖北十堰人,东北大学博士研究生;
于庆波(1966-),男,山东莱阳人,东北大学教授,博士生导师。
摘要:针对难以确定制取铁合金一定粒径下的工艺参数,基于飞溅板雾化原理,引入圆盘边缘处液膜厚度和流速为中间变量,将全过程分为圆盘内铺展和圆盘外破碎两个连续阶段,在圆盘内液膜铺展阶段建立气-液两相流数学模型,在圆盘外液膜破碎阶段建立液膜表面扰动波数学模型,研究了液流流速、液流直径和圆盘直径对液膜铺展及破碎特性的影响规律.结果表明,当介质为Sn-58Bi,液流流速为3 m/s,圆盘直径为200 mm,改变液流直径为50~100 mm时,形成液滴直径为7.5~10 mm;液流直径增加或圆盘直径减小时,破碎形成的液滴直径增大;液流流速增加时,液膜破碎时刻提前,对液滴直径的影响较小.
关键词:飞溅板雾化粒化液膜破碎多相流铁合金
Research on Spreading and Breaking Characteristics of Liquid Flow Impact Flat Disc
LIU Zhong-yuan, YU Qing-bo

 , LIU Jun-xiang
, LIU Jun-xiang School of Metallurgy, Northeastern University, Shenyang 110819, China
Corresponding author: YU Qing-bo, E-mail: yuqb@smm.neu.edu.cn.
Abstract: Because of the difficulty in determining the process parameters under a specific particle size, based on the principle of splash plate atomization, the liquid film thickness and flow velocity at the edge of the disk are used as intermediate variables, and the entire process is divided into two correlations: spreading inside the disk and breaking outside the disk. The gas-liquid two-phase flow mathematical model was established for the liquid film spreading process inside the disc, and the liquid film surface disturbance wave mathematical model was established for the liquid film breaking process outside the disc. The effects of flow velocity, flow diameter, and disc diameter on the spreading and breaking characteristics of the liquid film were studied. The results show that when the medium is Sn-58Bi, the liquid flow rate is 3 m/s, the diameter of the disc is 200 mm, and the liquid flow diameter is changed to 50~100 mm, the diameter of the formed droplet is 7.5~10 mm; when the liquid flow diameter increases or the disc diameter decreases, the droplet diameter increases; when the liquid flow velocity increases, the breaking time decreases, and the effect on the droplet diameter is small.
Key words: splash plate atomizationgranulationliquid film breakupmultiphase flowferroalloy
飞溅板雾化是指通过液流冲击飞溅板,在飞溅板内铺展形成液膜,液膜脱离壁面后由于与空气的相互作用破碎形成液滴的雾化方式[1].这种雾化方式能量损失较小,可以较好地控制液膜运动轨迹、速度和液滴直径[2],广泛应用于内燃机的雾化器和锅炉喷嘴中[3].
对液膜铺展特性的研究中,Inamura等[2, 4]使用层流边界层模型分析了飞溅板上液膜厚度,与实验数据进行对比,验证了理论的正确性.对液膜破碎特性的研究中,Dombrowski等[5]研究了扇型喷嘴产生的自由液膜在不同环境密度下的失稳性,实验结果表明,液滴直径随着环境密度的增大而减小.Dombrowski等[6]建立了自由液膜表面扰动波的数学模型,较好地预测了液膜破碎形成液滴的尺寸及破碎位置.Ahmed等[7]研究了液体黏度对液流冲击飞溅板雾化特性的影响,指出自由液膜雾化过程受Rayleigh-Plateau(R-P)和Rayleigh-Taylor(R-T)非稳定性控制.在液膜铺展及破碎特性的研究中,Thunivumani等[8]建立了液膜运动模型,研究了液流的韦伯数和冲击角度对液滴直径的影响,较好地预测了液膜的破碎位置.
在炼钢过程中,加入粒径适中的铁合金颗粒,保证颗粒有一定量穿过熔渣层,降低铁合金在钢液中的熔化时间,提高合金元素在钢液中分布的均匀性.粒径要求与铁合金的种类、炼钢工艺及工况有关,中国武汉某钢铁公司转炉炼钢过程要求的粒径为3~15 mm[9].现国内制粒通常采取先浇铸成块,再人工或机械破碎的方法,效率低、合金成分偏析大、粒径不均匀、污染较大.新型的铁合金直接粒化工艺能耗低、污染较小、粒径均匀,具有较好的应用前景[10-11].该工艺中通过熔融金属液流冲击圆盘生成金属液滴的粒化过程,是典型的飞溅板雾化.目前对飞溅板雾化的研究多以雾化器或喷嘴为背景,重点多集中于自由液膜破碎过程,缺少对液流冲击圆盘后铺展、破碎连续过程的研究,研究的尺度较小,所建立的模型难以对上述粒化过程进行计算.若运用CFD技术对工业尺度下整个冲击破碎的非稳态过程进行模拟,计算资源耗费大、计算时间长且难以保证精度.本文引入圆盘边缘处液膜流速和液膜厚度作为中间变量,将整个过程分为液膜在圆盘内的铺展和在圆盘外的破碎两个连续过程.基于耦合的水平集-流体体积法(coupled level set and volume of fluid,CLSVOF)对圆盘内过程运用Fluent软件进行建模并数值模拟,得到液流流速、液流直径、圆盘直径对圆盘边缘处液膜流速、液膜厚度的影响;基于扰动波理论对圆盘外过程运用Python语言编程,进行建模并数值计算,得到圆盘边缘处液膜流速、液膜厚度对液膜破碎时刻、液滴直径的影响.本研究为设计生产不同种类、不同粒径的铁合金粒化装置提供理论指导.
1 模型构建图 1为液流冲击圆盘铺展及破碎过程示意图.其中:d0为液流直径,m;v0为液流流速,m/s;H为液流入口距离圆盘的高度,m;d1为圆盘直径,m;h为圆盘边缘处液膜厚度,m;v1为圆盘边缘处液膜流速,m/s;dd为液滴直径,m.从图中可以看出,液流垂直冲击圆盘中心,在圆盘内铺展形成液膜,速度方向由垂直于壁面方向变为沿壁面方向,液膜继续运动脱离壁面后,由于与空气相互作用,在液膜边缘处发生破碎形成液丝,最后液丝断裂形成液滴.
图 1(Fig. 1)
 | 图 1 液流冲击圆盘铺展及破碎过程示意图Fig.1 Schematic diagram of the spreading and breaking process of the liquid impact disk |
1.1 圆盘内液膜的铺展过程1.1.1 数学模型图 1虚线框内为圆盘内液膜铺展过程的物理模型.该过程是典型的气-液两相流问题,难点在于对气-液界面的捕捉.CLSVOF法将VOF(volume of fluid)法与Level-Set法耦合,在保证质量守恒下,提高相界面捕捉的精度[12].该方法使用混合相对连续方程和动量方程求解,减小了运算成本.通过引入体积分数φq来对相界面进行捕捉,假设流体相不相互渗透,则在大多数计算单元中,φq为1或0,在相界面位置,0 < φq < 1.通过求解各相的体积分数方程来跟踪相界面, 具体控制方程如下:
连续方程为
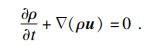 | (1) |
 | (2) |
 | (3) |
 | (4) |
 | (5) |
 | (6) |
为精确捕捉出现剧烈形变的相界面,构造距离函数φ:
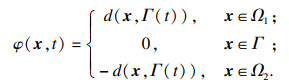 | (7) |
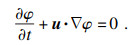 | (8) |
图 2(Fig. 2)
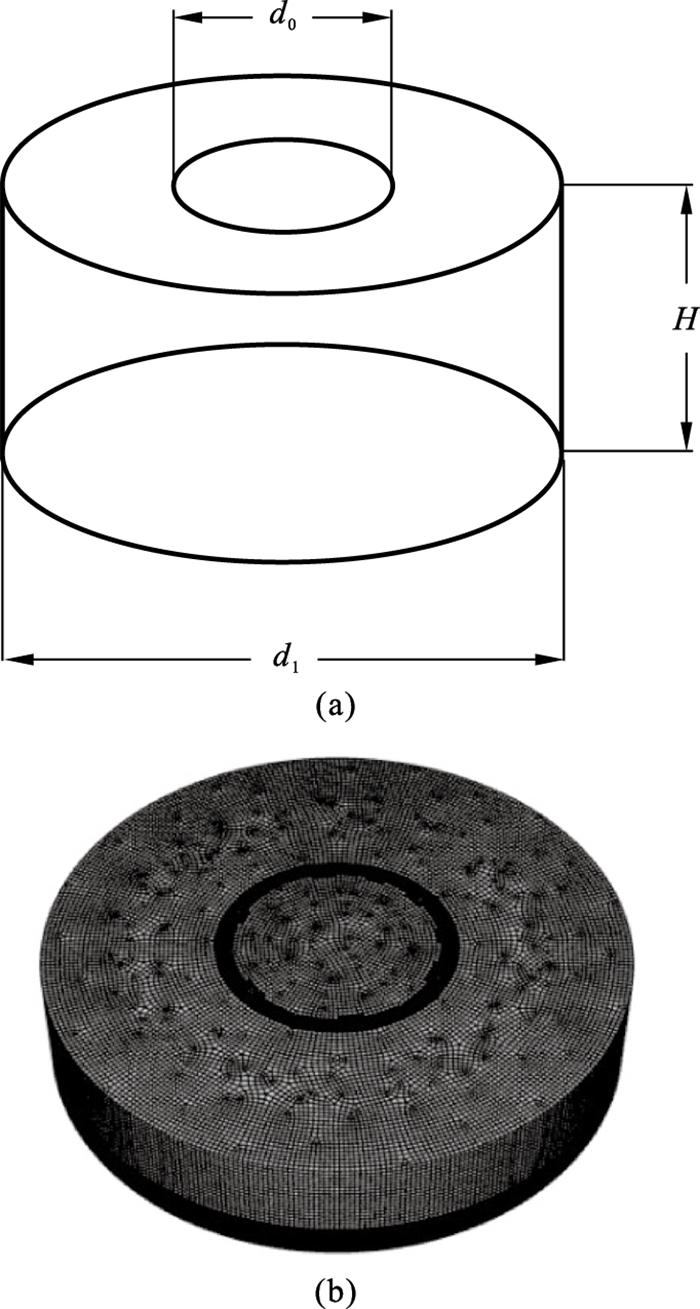 | 图 2 模拟计算域和网格划分示意图Fig.2 Schematic diagram of simulation calculation domain and meshing (a)—模拟计算域;(b)—网格划分. |
1.2 圆盘外液膜的破碎过程图 1虚线框外所示为圆盘外液膜的破碎过程.图 3为膜状破碎过程.从图中可以看出,液膜运动到圆盘外形成自由液膜后,液膜表面扰动波逐渐生长,当扰动波振幅达到临界值时液膜断裂成带状液丝,带状液丝断裂形成液滴[6].
图 3(Fig. 3)
 | 图 3 膜状破碎过程Fig.3 Process of disintegration of film formation |
在空气扰动下,液膜表面的正弦波动可以表示为[13]
 | (9) |
扰动波振幅的增长率为[5]
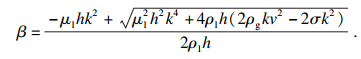 | (10) |
液膜脱离壁面t时刻表面扰动波振幅Am与初始时刻表面扰动波振幅A0存在如式(11)的关系:
 | (11) |
 | (12) |
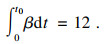 | (13) |
带状液丝的一个完整的波断裂成液滴,液丝破碎成液滴的直径为[15]
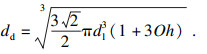 | (14) |
 | (15) |
2 结果分析2.1 液流流速对圆盘内液膜铺展特性的影响在考察液流流速对圆盘内液膜铺展特性的影响时,液流直径为80 mm,圆盘直径为200 mm,改变液流流速为0.5~2 m/s.
图 4为圆盘边缘处液膜厚度、圆盘边缘处液膜流速与液流流速之间的关系.从图中可以看出,当液流流速增加时,圆盘边缘处液膜流速增加.当液流流速增加时,圆盘边缘处液膜厚度增加;当流速增加至1.25 m/s,圆盘边缘处液膜厚度约为7.2 mm;流速继续增加时,圆盘边缘处液膜厚度增速减缓,进一步增加流速对于圆盘边缘处液膜厚度的影响较小.原因是当液流流速较低时,液膜铺展速度较低,壁面阻力占主导作用,随着液流流速逐渐增大,液膜铺展速度逐渐增大,流体的黏性力逐渐占主导作用,圆盘边缘处液膜厚度增加,且增加幅度逐渐减小.
图 4(Fig. 4)
 | 图 4 圆盘边缘处液膜厚度、液膜流速与液流流速之间的关系Fig.4 Relationship between the thickness, velocity of the liquid film at the edge of the disc and the liquid flow velocity |
2.2 液流直径和圆盘直径对圆盘内液膜铺展特性的影响在考察液流直径和圆盘直径对圆盘内液膜铺展特性的影响时,液流流速为1.5 m/s,改变液流直径为80~140 mm,改变圆盘直径为200~300 mm.
图 5为圆盘边缘处液膜厚度与液流直径、圆盘直径的关系.从图中可以看出,当液流直径不变,圆盘直径增大时,液膜厚度减小;当圆盘直径不变,液流直径减小时,液膜厚度减小;改变液流直径相较于改变圆盘直径对圆盘边缘处液膜厚度的影响较大.原因是当液流流速不变,液流直径减小时,流量减小,由质量守恒可知,圆盘边缘处液膜厚度减小;当流量不变,圆盘直径增大时,由质量守恒可知,圆盘边缘处液膜厚度减小.
图 5(Fig. 5)
 | 图 5 圆盘边缘处液膜厚度与液流直径、圆盘直径之间的关系Fig.5 Relationship between the thickness of the liquid film at the edge of the disc and the diameter of the liquid flow, the diameter of the disc |
为量化该过程,引入无量纲数k′:
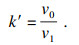 | (16) |
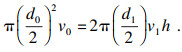 | (17) |
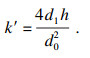 | (18) |
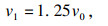 | (19) |
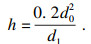 | (20) |
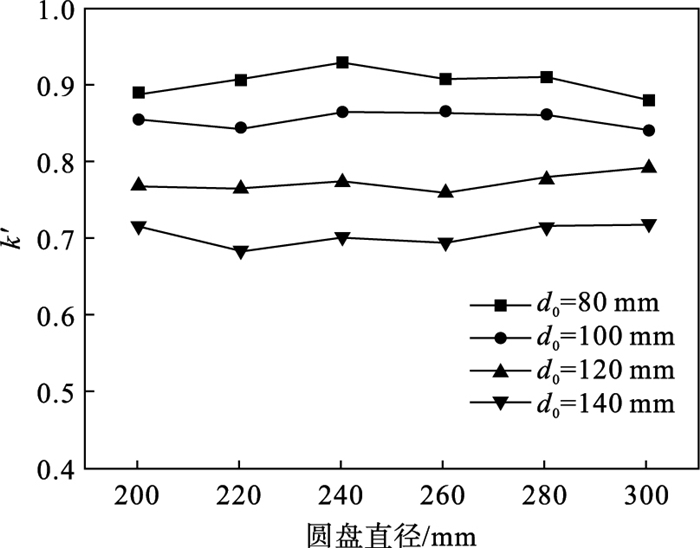 | 图 6 k′与液流直径、圆盘直径之间的关系Fig.6 Relationship between the k′ and the diameter of the liquid flow, the diameter of the disc |
2.3 圆盘边缘处液膜流速对圆盘外液膜破碎特性的影响在考察圆盘边缘处液膜流速对圆盘外液膜破碎特性的影响时,圆盘的直径为200 mm,圆盘边缘处液膜的厚度为7 mm,改变液膜流速为0.5~7 m/s.
图 7为液膜破碎时间、液滴直径与圆盘边缘处液膜流速的关系.从图中可以看出,当液膜流速在0.5~2 m/s时,液膜破碎时间约为0.5 s,当液膜流速继续增大,液膜破碎时刻提前.原因是自由液膜的稳定性随流速的增大而减弱.当液膜流速从0.5 m/s增加到1.5 m/s时,液滴的直径增加,增加幅度很小;当液膜流速继续增大时,液滴直径减小.在本文研究的参数范围内,液滴直径变化较小,大多在8~10 mm.
图 7(Fig. 7)
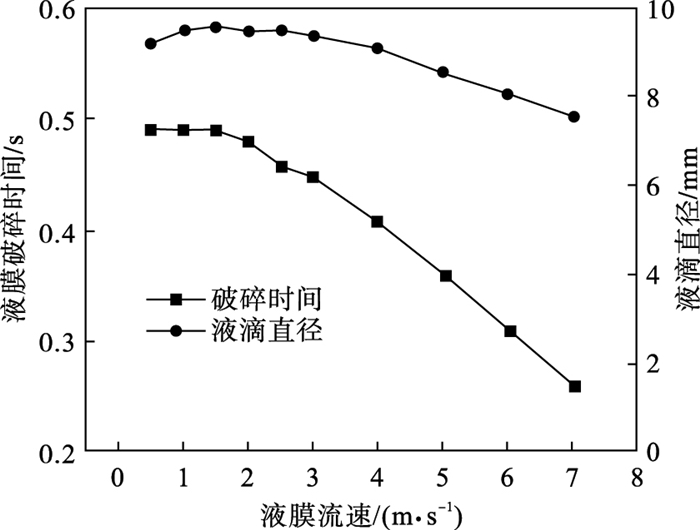 | 图 7 液膜破碎时间、液滴直径与圆盘边缘处液膜流速的关系Fig.7 Relationship between breaking time, droplet diameter and the liquid film flow rate at the edge of the disc |
2.4 圆盘边缘处液膜厚度对圆盘外液膜破碎特性的影响在考察圆盘边缘处液膜厚度对圆盘外液膜破碎特性的影响时,圆盘的直径为200 mm,液膜流速为3 m/s,改变液膜厚度为3~9 mm.
图 8为液膜破碎时间、液滴直径与圆盘边缘处液膜厚度之间的关系.从图中可以看出,随着液膜厚度的增加,液膜破碎时间延迟,原因是自由液膜的稳定性随着厚度的增加而增强.但整体上,改变液膜厚度对液膜破碎时间的影响较小,对液膜的运动轨迹和破碎位置的影响可以忽略.当液膜厚度增加时,液滴直径增加,可近似拟合成一次函数为
 | (21) |
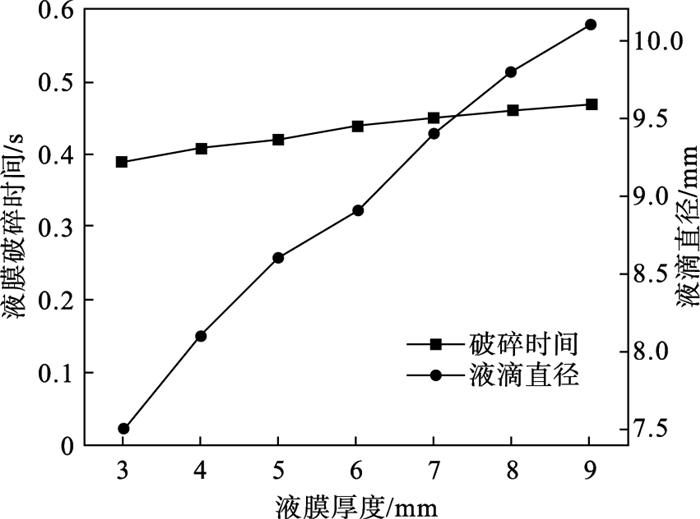 | 图 8 液膜破碎时间、液滴直径与圆盘边缘处液膜厚度之间的关系Fig.8 Relationship between breaking time, droplet diameter and the thickness of the liquid film at the edge of the disc |
3 结论1) 在本文研究的参数范围内,圆盘边缘处液膜流速约等于液流流速的1.25倍;改变液流直径、圆盘直径对圆盘边缘处液膜厚度的影响较大.
2) 圆盘边缘处液膜流速增加时,液膜破碎时间提前,对破碎形成的液滴直径的影响较小;圆盘边缘处液膜厚度与破碎形成的液滴直径近似呈一次函数关系.
3) 当液流流速为3 m/s,液流直径为80 mm,圆盘直径为200 mm时,圆盘边缘处液膜厚度约为6.4 mm,液膜破碎得到的液滴直径约为9.2 mm.可以通过改变液流直径或圆盘直径,进而改变圆盘边缘处的液膜厚度,实现对液滴直径的控制.改变液流流速对液滴直径的影响较小,即在保证液流直径和圆盘直径不变的条件下,增加流量,对液滴直径的改变较小.
参考文献
| [1] | Inamura T, Endo S, Okabe T, et al. Characteristics of liquid upwash formed on a splash plate[J]. International Journal of Multiphase Flow, 2018, 99(1): 446-453. |
| [2] | Inamura T, Yanaoka H, Tomoda T. Prediction of mean droplet size of sprays issued from wall impingement injector[J]. AIAA Journal, 2004, 42(3): 614-621. DOI:10.2514/1.9112 |
| [3] | Yin L, E J Q, Ding J, et al. An experimental study on the spray characteristics of splash platelet injector[J]. Acta Astronautica, 2021, 181(8): 377-383. |
| [4] | Inamura T. Upwash formation on splash plate atomization[J]. International Journal of Multiphase Flow, 2016, 85(1): 67-75. |
| [5] | Dombrowski N, Hooper P C. The effect of ambient density on drop formation in sprays[J]. Chemical Engineering Science, 1962, 17(4): 291-305. DOI:10.1016/0009-2509(62)85008-8 |
| [6] | Dombrowski N, Johns W R. The aerodynamic instability and disintegration of viscous liquid sheets[J]. Chemical Engineering Science, 1963, 18(3): 203-214. DOI:10.1016/0009-2509(63)85005-8 |
| [7] | Ahmed M, Amighi A, Ashgriz N, et al. Characteristics of liquid sheets formed by splash plate nozzles[J]. Experiments in Fluids, 2007, 44(1): 125-136. DOI:10.1007/s00348-007-0381-4 |
| [8] | Thunivumani G, Gadgil H. Dynamics of liquid sheet breakup in splash plate atomization[J]. Journal of Fluids Engineering, 2018, 140(1): 1-41. |
| [9] | 李雪琴, 潘飞飞, 贺文超, 等. 硅铁合金离心粒化工艺[J]. 中国冶金, 2018, 28(9): 77-82. (Li Xue-qin, Pan Fei-fei, He Wen-chao, et al. Centrifugal granulation process for ferrosilicon alloy[J]. China Metallurgy, 2018, 28(9): 77-82.) |
| [10] | Beskow K, Vesterberg P, Dupon E. Granshot granulation process for optimized ironmaking operations[J]. Stahl und Eisen, 2010, 130(12): 27-35. |
| [11] | 刘军祥, 于庆波, 谢华清, 等. 冶金渣颗粒余热回收的实验研究[J]. 东北大学学报(自然科学版), 2014, 35(2): 245-248. (Liu Jun-xiang, Yu Qing-bo, Xie Hua-qing, et al. Experimental study on waste heat recovery for metallurgical slag particles[J]. Journal of Northeastern University(Natural Science), 2014, 35(2): 245-248. DOI:10.3969/j.issn.1005-3026.2014.02.021) |
| [12] | Sussman M, Puckett E G. A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows[J]. Journal of Computational Physics, 2000, 162(2): 301-337. DOI:10.1006/jcph.2000.6537 |
| [13] | Kamiya T. An analysis of the ligament-type disintegration of thin liquid film at the edge of a rotating disk[J]. Journal of Chemical Engineering of Japan, 1972, 5(4): 391-396. DOI:10.1252/jcej.5.391 |
| [14] | Weber C. Disintegration of liquid jets[J]. Zamm-Zeitschrift fur Angewandte Mathematik and Mechanik, 1931, 1(1): 136-159. |
| [15] | Liu J, Yu Q, Qin Q. Numerical study on film disintegration by centrifugal atomisation using rotating cup[J]. Powder Metallurgy, 2013, 56(4): 288-294. |
