

1. 东北大学 机械工程与自动化学院,辽宁 沈阳 110819;
2. 中国北方车辆研究所,北京 100072;
3. 东北大学 航空动力装备振动及控制教育部重点实验室,辽宁 沈阳 110819
收稿日期:2021-12-29
基金项目:国家重点基础研究发展计划项目(20195208003)。
作者简介:徐宏阳(1992-),男,河北石家庄人,东北大学博士研究生;
马辉(1978-),男,河北安平人,东北大学教授,博士生导师。
摘要:轴承不对中可能导致保持架断裂和滚珠分布误差.为了分析不对中及滚珠分布误差对轴承刚度波动的影响,考虑外载荷及内、外圈不对中耦合情况,提出了一种含滚珠分布误差的深沟球轴承拟静力学模型.基于所提模型,进一步分析了外载荷及内、外圈不对中状态下,滚珠分布误差对深沟球轴承径向、轴向及倾覆刚度波动特性的影响.结果表明:外载荷及外圈不对中情况下,轴承刚度以滚珠通过外圈周期,即变柔度(VC,variable compliance)振动为周期进行波动.此时,滚珠分布误差的存在,会使轴承刚度以保持架转动周期进行规律性大幅波动.随主轴旋转的内圈不对中会使轴承刚度以一半的内圈转动周期进行波动,且滚珠分布误差会使刚度波动幅值增加.
关键词:不对中滚珠分布误差球轴承刚度拟静力学模型
Stiffness Fluctuation Characteristics of Ball Bearings with Misalignment and Ball Distribution Error
XU Hong-yang1, YANG Yang2, WANG Peng-fei1, MA Hui1,3


1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. China North Vehicle Research Institute, Beijing 100072, China;
3. Key Laboratory of Vibration and Control of Aero-Propulsion System, Ministry of Education, Northeastern University, Shenyang 110819, China
Corresponding author: MA Hui, E-mail: mahui_2007@163.com.
Abstract: Bearing misalignment may result in cage fractures and ball distribution errors. In order to analyze the effects of misalignments and ball distribution errors on the bearing stiffness fluctuation, considering the external loads and misalignments of inner and outer races, a quasi-static model of deep groove ball bearings with ball distribution errors is proposed. Based on the proposed model, the effects of ball distribution errors on the fluctuation characteristics of radial, axial and overturning stiffness of deep groove ball bearings under the condition of misaligned inner and outer races and external loads are further analyzed. The results show that the stiffness of the bearings fluctuates with the period of the ball passing through the outer race, that is, VC (variable compliance) vibration under the condition of the misaligned outer race and external loads. At this time, because of the existence of ball distribution errors, the bearing stiffness significantly fluctuates with the cage rotation period. The misalignments of the inner race rotating with the spindle cause the bearing stiffness to fluctuate by half of the inner race rotation period. The stiffness fluctuation amplitude increases due to the ball distribution errors.
Key words: misalignmentball distribution errorball bearingstiffnessquasi-static model
深沟球轴承作为旋转机械中的常用关键元件,其在工作状态下通常仅承受径向外载荷.然而,由于轴承座歪斜、轴套加工误差以及暴力安装等原因时常会导致轴承的外圈或内圈在运转状态之前就存在不对中.过大的不对中会导致深沟球轴承除了径向力之外,还会承受一定的轴向力及倾覆力矩,加速轴承的失效.通常,轴承套圈的不对中会导致保持架铆钉的绷断,使得保持架部分丧失了约束滚珠方位的功能.因此轴承在运转过程中,部分滚珠会滚出兜孔,引起滚珠分布误差.为了分析轴承在套圈不对中及滚珠分布误差状态下的刚度波动特性,首先需要建立深沟球轴承的拟静力学模型.
在球轴承的拟静力学模型研究方面,Jones等[1-2]最早建立了组合载荷下的球轴承多自由度拟静力学模型.然而Jones-Harris模型主要基于滚道控制假设,通常在高转速条件下使用外滚道控制假设,低转速工况下使用内滚道控制假设,需要根据转速工况进行合理判断应该选用哪种滚道控制假设,因此,滚道控制假设具有明显的局限性.为了解决这一问题,Wang等[3]建立了无滚道控制假设的球轴承拟静力学模型.基于拟静力学模型,众多****对轴承的接触[4]、寿命[5-6]、刚度[7-9]、可靠性[10]、承载能力[11]、生热[12]及摩擦[13]等特性展开了深入的研究.
在含不对中状态轴承特性的研究方面,Tong等[14]考虑角不对中,建立了联合载荷作用下角接触球轴承的拟静力学模型,在此基础上进一步研究了轴向力与位移预紧情况下,倾斜角对运行扭矩的影响.Oktaviana等[15]考虑惯性力,提出了一种不对中及外载荷作用下角接触球轴承的拟静力学模型,并研究了角度偏差对轴承载荷分布及打滑的影响.Xu等[16-17]提出了一种含不对中的双列角接触球轴承的五自由度解析模型,研究了不对中角对轴承刚度的影响.此外,更多****进一步将不对中轴承拟静力学模型与转子系统进行了耦合,探讨了轴承不对中对转子系统刚度及疲劳寿命及动态特性的影响[18-21].
然而,多数****主要以角接触球轴承为研究对象,对深沟球轴承的研究相对较少.此外,根据前文分析可以知道,深沟球轴承保持架断裂的重要因素即为套圈不对中.因此,保持架断裂导致的滚珠分布误差与不对中共同影响轴承的运行状态.但是,目前对于含不对中及滚珠分布误差的轴承特性方面的研究是较为罕见的.轴承座安装误差会导致外圈不对中,而轴承内圈与主轴的装配误差以及主轴变形会导致内圈产生不对中[19, 22].多数****主要关注外圈不对中,对于跟随主轴转动的内圈不对中的研究较少.
鉴于以上问题,本文主要针对径向外载荷作用下,含有内、外圈不对中及滚珠分布误差的深沟球轴承提出一种拟静力学轴承模型及刚度计算方法.基于所提模型,进一步对轴承的刚度波动特性进行分析.基于本文的研究,可为轴承及转子系统动力学及故障诊断提供技术支持.
1 深沟球轴承拟静力学建模1.1 滚珠分布误差情况下不对中导致的非正常预紧力含有滚珠分布误差的深沟球轴承示意图如图 1所示.正常状态下,滚珠j的分布角为φj.然而,由于保持架失效引起的滚珠分布误差为φe.因此,滚珠的实际分布角φ′j可以表示为
 | (1) |
 | 图 1 滚珠分布误差示意图Fig.1 Diagram of ball distribution errors |
假设轴承外圈固定,内圈随主轴旋转,将套圈的角不对中视为非正常预紧状态,深沟球轴承外圈和内圈的不对中状态如图 2所示.图中,θto和θti分别代表外圈和内圈的不对中倾斜角度,φto和φti分别代表外圈和内圈的不对中轴线的方位角.由于假设轴承外圈固定内圈旋转,因此,外圈不对中轴线的方位角φto为一固定值,而内圈不对中轴线的方位角φti随主轴及内圈一起转动.
图 2(Fig. 2)
 | 图 2 深沟球轴承套圈不对中示意图Fig.2 Diagram of ring misalignments of the deep groove ball bearings (a)—外圈不对中;(b)—内圈不对中. |
在外圈不对中状态下,内滚道曲率中心的相对轴向位移B1j可表示为
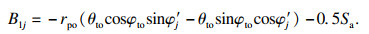 | (2) |
在内圈不对中状态下,内滚道曲率中心的相对轴向位移B1j可表示为
 | (3) |
在不对中状态下,内滚道曲率中心的相对径向位移B2j为
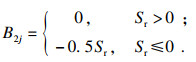 | (4) |
内、外滚道曲率中心与轴承中心之间的径向距离rpi和rpo可以表示为
 | (5) |
位于承载区和非承载区滚珠的变形协调关系如图 3和图 4所示.正常状态下,轴承的内、外滚道曲率中心和滚珠中心分别为Oi, Oo和Ob.初始接触状态下,内滚道曲率中心和滚珠中心分别为O′i和O′b.当深沟球轴承承受异常预紧力及外载荷时,内滚道曲率中心和滚珠中心分别变为O″i和O″b.
图 3(Fig. 3)
 | 图 3 承载区滚珠的变形协调关系Fig.3 Deformation coordination relation of the ball in the load-bearing area |
图 4(Fig. 4)
 | 图 4 非承载区滚珠的变形协调关系Fig.4 Deformation coordination relation of the ball in the non-load-bearing area |
在异常预紧及外载荷耦合作用状态下,对于承载区的滚珠,内滚道曲率中心O′i和O″i之间的轴向距离B1j和径向距离B2j可以分别表示为
 | (6) |
 | (7) |
内、外滚道曲率中心O″i和Oo之间的轴向及径向距离A1j和A2j可以表示为
 | (8) |
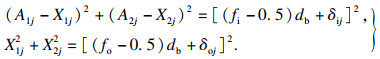 | (9) |
对于位于非承载区的滚珠,其变形协调关系可以表示为
 | (10) |
图 5(Fig. 5)
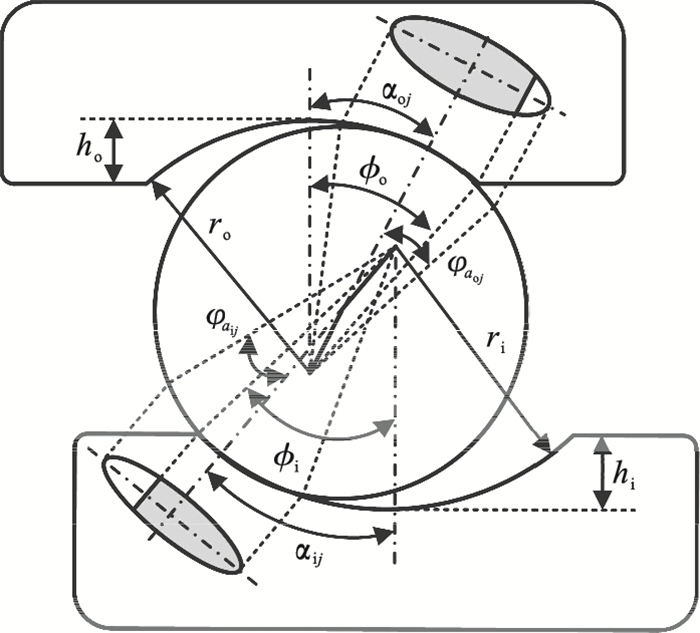 | 图 5 被截断的接触椭圆示意图Fig.5 Diagram of truncated contact ellipse |
滚珠与内、外滚道之间的接触椭圆截断率Rij/ojet可以由式(11)计算得到
 | (11) |
当Rij/ojet≥1时,滚珠脱离滚道,可以将其视为非承载区的滚珠;当0 < Rij/ojet < 1时,接触刚度Kij/oj可以被表示为
 | (12) |
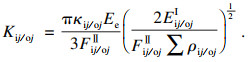 | (13) |
滚珠与内、外滚道之间的接触载荷Qij/oj可以表示为
 | (14) |
 | (15) |
 | (16) |
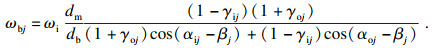 | (17) |
离心力Fcj和陀螺力矩Mgj可以由式(18)计算得到
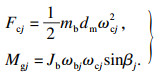 | (18) |
滚珠的受力分析如图 6所示.由于转速引起的滚珠的离心效应,造成承载区滚珠与内、外滚道的接触角大小不一致,并产生陀螺力矩Mgj.为了抵消陀螺力矩Mgj,滚珠与内、外滚道接触点产生切向摩擦力.对于非承载区的滚珠,在离心力Fcj的作用下,滚珠仅与外滚道接触,离心力Fcj完全被滚珠与外滚道之间的接触力抵消.
图 6(Fig. 6)
 | 图 6 轴承滚珠的受力分析Fig.6 Force analysis of balls in the bearing (a)—承载区滚珠受力分析;(b)—非承载区滚珠受力分析. |
承载区滚珠的力平衡方程可以表示为
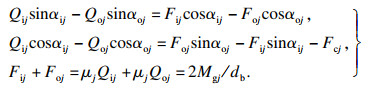 | (19) |
非承载区滚珠的力平衡方程可以表示为
 | (20) |
 | (21) |
1.2 轴承的刚度矩阵计算除了不对中引起的非正常预紧力之外,在工作状态下,轴承还会承受一定的外载荷,轴承的变形是由非正常预紧力及外载荷共同决定的.因此,不对中及滚珠分布误差状态下,轴承内圈的力平衡方程可以表示为
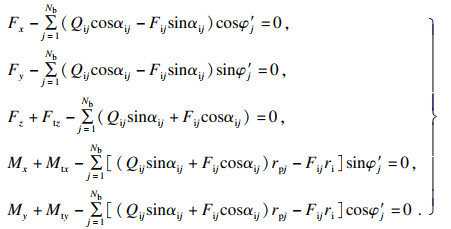 | (22) |
不对中及滚珠分布误差状态下,深沟球轴承的五维刚度矩阵Kb可以表示为
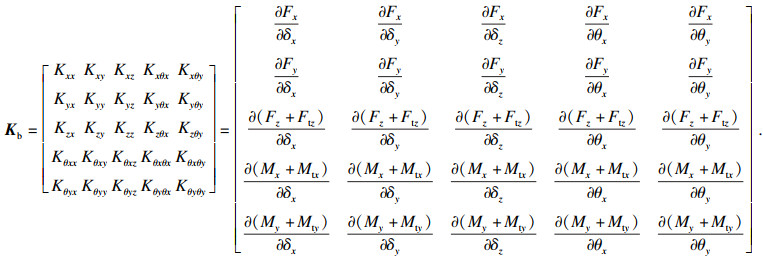 | (23) |
图 7(Fig. 7)
 | 图 7 模型求解流程Fig.7 Model solving process |
与传统模型不同的是,本文所建立的拟静力学模型将陀螺力矩方向的力矩平衡方程引入到滚珠的力平衡方程组中.因此该模型是一个具有5Nb+5个未知变量的非线性方程组.在非线性方程组求解过程中,采用基于解析雅可比矩阵的双层Newton-Raphson迭代方法,该算法对初值要求较低.在本文工况下,滚珠平衡方程组未知变量X1j,X2j,δij,δoj和μj的初值均选为0.内圈平衡方程组未知变量δx,δy,θx和θy的初值同样选为0,而δz的初值选取为0.1 mm.
2 结果与讨论2.1 含滚珠分布误差的轴承刚度波动本文所建立的球轴承拟静力学模型的准确性在文献[11]中已经得到了较好的验证,这里不再赘述.本节主要研究径向外载荷作用下,滚珠分布误差对刚度波动的影响.取深沟球轴承SKF6011作为研究对象,轴承参数如表 1所示.
表 1(Table 1)
| 表 1 深沟球轴承SKF6011参数表 Table 1 Parameters of the deep groove ball bearing SKF6011 |
作用在轴承内圈的外载荷分别设为Fy=-1 000 N,Fx=Fz=Mx=My=0.转速设为5 000 r/min.取内圈旋转周期数为10,每个旋转周期划分为500个时刻.假设轴承某一滚珠存在分布误差,且分布误差分别设为φe=0°,5°和10°.后续的研究中,主要探讨径向刚度Kyy、轴向刚度Kzz和倾覆刚度Kθxθx的波动特性.
径向外载荷作用下,不同滚珠分布误差对轴承刚度波动的影响如图 8所示,其FFT频谱如图 9所示.从图中可以看出,在健康状态下,即φe=0时,轴承的径向刚度Kyy、轴向刚度Kzz和倾覆刚度Kθxθx均以一个固定的频率进行周期性波动.这个频率即为轴承的变柔度(VC,variable compliance)振动频率fvc,其周期为Tvc=1/fvc.在含有滚珠分布误差状态下,轴承的径向刚度Kyy、轴向刚度Kzz和倾覆刚度Kθxθx除了呈现出以VC振动周期Tvc的波动之外,还呈现出明显的周期性冲击. 该周期即为保持架的公转周期Tcage,所体现出来的频率即为保持架频率fcage,并且Tcage=NbTvc,fcage=fvc/Nb.对于SKF6011轴承,Tcage=13Tvc,fcage=fvc/13.此外,随着滚珠分布误差的增大,刚度波动的幅值变大,刚度频谱中的保持架频率及其倍频成分幅值也随之增加.
图 8(Fig. 8)
 | 图 8 不同滚珠分布误差对刚度波动的影响Fig.8 Effects of different ball distribution errors on stiffness fluctuation (a)—径向刚度波动;(b)—轴向刚度波动;(c)—倾覆刚度波动. |
图 9(Fig. 9)
 | 图 9 不同滚珠分布误差下的刚度FFT频谱Fig.9 FFT spectrum of stiffness under different ball distribution errors (a)—径向刚度频谱;(b)—轴向刚度频谱;(c)—倾覆刚度频谱. |
2.2 外圈不对中下含滚珠分布误差的轴承刚度波动本节主要研究径向外载荷及外圈不对中耦合作用下,滚珠分布误差对刚度波动的影响.轴承参数、外载荷、转速、时间以及滚珠分布误差工况与第2.1节相同.此外,轴承外圈不对中轴线方位角φto设为0,外圈的不对中倾斜角度θto设为3×10-3 rad.
径向外载荷及外圈不对中耦合作用下,不同滚珠分布误差对轴承刚度波动的影响如图 10所示,其FFT频谱如图 11所示.可以看出,在仅含有外载荷及不对中耦合作用下,轴承的径向刚度Kyy、轴向刚度Kzz和倾覆刚度Kθxθx同样仅呈现出以Tvc为周期的规律性波动.然而,当存在滚珠分布误差时,轴承的刚度同样呈现出周期性冲击现象,该周期为保持架的公转周期Tcage.但与第2.1节结论(即每一个保持架的公转周期Tcage内仅会出现一次刚度冲击)不同的是,本节中,每一个保持架的公转周期Tcage会出现一大一小两次冲击.这是因为,在仅含有外载荷情况下,轴承在滚珠分布角的360°范围内仅存在一个承载区.含分布误差的滚珠公转一周经过一次承载区,因此引入一次刚度冲击.然而,在同时含有外载荷和外圈不对中耦合的情况下,轴承在滚珠分布角的360°范围内存在一大一小两个承载区.此时,含分布误差的滚珠公转一周会经过两次承载区,因此引入一大一小共两次刚度冲击.从刚度频谱上可以体现为二倍保持架频率(2fcage)相对较高.此外,滚珠分布误差越大,刚度波动的幅值也就越大,刚度频谱中的保持架频率及其倍频成分幅值也越大.
图 10(Fig. 10)
 | 图 10 外圈不对中下不同滚珠分布误差对刚度波动的影响Fig.10 Effects of different ball distribution errors on stiffness fluctuation under the misalignment of the outer race (a)—轴向刚度波动;(b)—径向刚度波动;(c)—倾覆刚度波动. |
图 11(Fig. 11)
 | 图 11 外圈不对中及不同滚珠分布误差下的刚度FFT频谱Fig.11 FFT spectrum of stiffness under the misalignment of the outer race and different ball distribution errors (a)—径向刚度频谱;(b)—轴向刚度频谱;(c)—倾覆刚度频谱. |
2.3 内圈不对中下含滚珠分布误差的轴承刚度波动本节主要研究径向外载荷及内圈不对中耦合作用下,滚珠分布误差对刚度波动的影响.轴承参数、外载荷、转速、时间以及滚珠分布误差工况与第2.1和2.2节相同.此外,轴承内圈不对中轴线的方位角φti随内圈转动,内圈的不对中倾斜角度θti设为3×10-3 rad.
径向外载荷及内圈不对中耦合作用下,不同滚珠分布误差对轴承刚度波动的影响如图 12所示,其FFT频谱如图 13所示.可以看出,在外载荷及内圈不对中耦合作用下,轴承的径向刚度Kyy、轴向刚度Kzz和倾覆刚度Kθxθx主要呈现出以内圈及主轴转动周期的一半,即0.5Tinner为周期的规律性波动,体现为2倍内圈转动频率2finner.对于径向刚度Kyy和倾覆刚度Kθxθx而言,轴承的Tvc和Tcage周期基本被内圈不对中引入的0.5Tinner的幅值所掩盖.随着滚珠分布误差变大,仅能看出径向刚度Kyy和倾覆刚度Kθxθx波动幅值的微弱增加.然而对于轴向刚度Kzz的波动,从刚度频谱可以看出fcage和finner出现了调制现象.这是因为,径向外载荷和内圈不对中主要对径向刚度Kyy和倾覆刚度Kθxθx的影响较大,对轴向刚度Kzz的影响相对较小.因此,轴承的轴向刚度Kzz的波动可以看出明显的Tvc和Tcage.
图 12(Fig. 12)
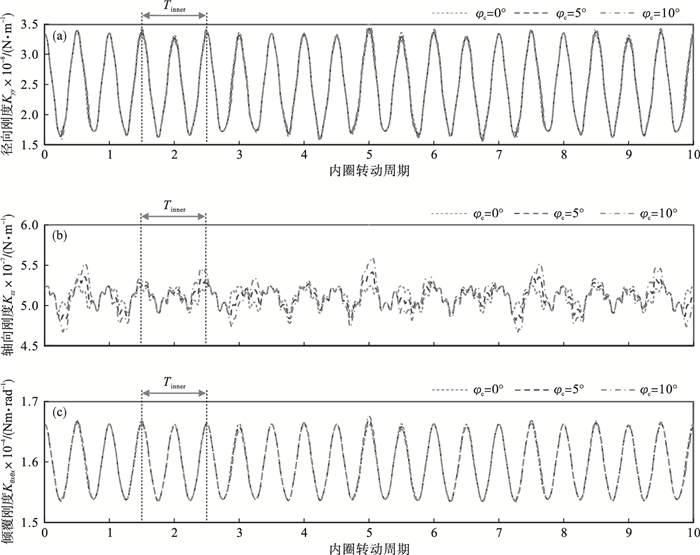 | 图 12 内圈不对中下不同滚珠分布误差对倾覆刚度波动的影响Fig.12 Effects of different ball distribution errors on overturning stiffness fluctuation under the misalignment of the inner race (a)—径向刚度波动;(b)—轴向刚度波动;(c)—倾覆刚度波动. |
图 13(Fig. 13)
 | 图 13 内圈不对中及不同滚珠分布误差下的刚度FFT频谱Fig.13 FFT spectrum of stiffness under the misalignment of the inner race and different ball distribution errors (a)—径向刚度频谱;(b)—轴向刚度频谱;(c)—倾覆刚度频谱. |
3 结论1) 外载荷及外圈不对中状态下,轴承刚度主要以VC振动周期Tvc进行规律性波动;内圈不对中状态下,轴承刚度主要以一半的内圈转动周期0.5Tinner进行规律性波动.
2) 如果存在滚珠分布误差,那么在外载荷状态下,每隔一个保持架周期Tcage刚度会产生一次大幅波动,体现为保持架频率fcage;外圈不对中状态下,每隔一个保持架周期Tcage刚度会产生两次波动,体现为二倍保持架频率2fcage相对较高;内圈不对中状态下,轴承刚度仍然主要以一半的内圈转动周期0.5Tinner进行规律性波动,体现为二倍内圈转频2finner较高,且滚珠分布误差会使刚度波动幅值及保持架频率幅值增加.
参考文献
| [1] | Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions[J]. Journal of Fluids Engineering, Transactions of the ASME, 1960, 82(2): 309-320. |
| [2] | Harris T A. Ball motion in thrust-loaded, angular contact bearings with coulomb friction[J]. Journal of Tribology, 1971, 93(1): 32-38. |
| [3] | Wang W Z, Hu L, Zhang S G, et al. Modeling angular contact ball bearing without raceway control hypothesis[J]. Mechanism and Machine Theory, 2014, 82: 154-172. DOI:10.1016/j.mechmachtheory.2014.08.006 |
| [4] | Li X, Yu K, Ma H, et al. Analysis of varying contact angles and load distributions in defective angular contact ball bearing[J]. Engineering Failure Analysis, 2018, 91: 449-464. DOI:10.1016/j.engfailanal.2018.04.050 |
| [5] | Zhang Y, Zhang M, Xie L, et al. The effect of the uncertain initial angular misalignment on fatigue life of spindle-bearing system[J]. Forschung im Ingenieurwesen, 2020, 85(1): 39-56. |
| [6] | Zhang Y, Liu Y. Research on the rolling contact fatigue life of the bearing considering the friction effect[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2021, 235(12): 2238-2264. DOI:10.1177/0954406220951214 |
| [7] | Xu H, He D, Ma H, et al. A method for calculating radial time-varying stiffness of flexible cylindrical roller bearings with localized defects[J]. Engineering Failure Analysis, 2021, 128: 105590. DOI:10.1016/j.engfailanal.2021.105590 |
| [8] | Fang B, Wan S, Zhang J, et al. Research on the influence of clearance variation on the stiffness fluctuation of ball bearing under different operating conditions[J]. Journal of Mechanical Design, 2021, 143(2): 023403. DOI:10.1115/1.4047903 |
| [9] | Fang B, Yan K, Hong J, et al. A comprehensive study on the off-diagonal coupling elements in the stiffness matrix of the angular contact ball bearing and their influence on the dynamic characteristics of the rotor system[J]. Mechanism and Machine Theory, 2021, 158: 104251. DOI:10.1016/j.mechmachtheory.2021.104251 |
| [10] | 黄贤振, 朱会彬, 姜智元, 等. 角接触球轴承打滑可靠性灵敏度分析[J]. 东北大学学报(自然科学版), 2021, 42(12): 1731-1738. (Huang Xian-zhen, Zhu Hui-bin, Jiang Zhi-yuan, et al. Reliability sensitivity analysis of angular contact ball bearing skidding[J]. Journal of Northeastern University (Natural Science), 2021, 42(12): 1731-1738. DOI:10.12068/j.issn.1005-3026.2021.12.009) |
| [11] | Xu H, Wang P, Ma H, et al. Analysis of axial and overturning ultimate load-bearing capacities of deep groove ball bearings under combined loads and arbitrary rotation speed[J]. Mechanism and Machine Theory, 2022, 169: 104665. DOI:10.1016/j.mechmachtheory.2021.104665 |
| [12] | 赵春雨, 侯森林, 李朕均. 进给系统成对安装的角接触球轴承热分析[J]. 东北大学学报(自然科学版), 2020, 41(5): 700-705. (Zhao Chun-yu, Hou Sen-lin, Li Zhen-jun. Thermal analysis toward pair-installed angular contact ball bearings in feed systems[J]. Journal of Northeastern University(Natural Science), 2020, 41(5): 700-705.) |
| [13] | 张宇, 谢里阳, 胡智勇, 等. 弹性流体动力润滑状态下滚动轴承摩擦的分析[J]. 东北大学学报(自然科学版), 2015, 36(7): 1000-1004. (Zhang Yu, Xie Li-yang, Hu Zhi-yong, et al. Analysis of elastohydrodynamic lubrication friction of rolling element bearing[J]. Journal of Northeastern University(Natural Science), 2015, 36(7): 1000-1004. DOI:10.3969/j.issn.1005-3026.2015.07.019) |
| [14] | Tong V C, Hong S W. Study on the running torque of angular contact ball bearings subjected to angular misalignment[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2018, 232(7): 890-909. DOI:10.1177/1350650117732921 |
| [15] | Oktaviana L, Tong V C, Hong S W. Skidding analysis of angular contact ball bearing subjected to radial load and angular misalignment[J]. Journal of Mechanical Science & Technology, 2019, 33(2): 837-845. |
| [16] | Xu T, Yang L, Wang K. Characteristics of duplex angular contact ball bearing with combined external loads and angular misalignment[J]. Applied Sciences, 2020, 10(17): 5756. DOI:10.3390/app10175756 |
| [17] | Xu T, Yang L, Wu W, et al. Effect of angular misalignment of inner ring on the contact characteristics and stiffness coefficients of duplex angular contact ball bearings[J]. Mechanism and Machine Theory, 2021, 157: 104178. DOI:10.1016/j.mechmachtheory.2020.104178 |
| [18] | Li X, Lu Y, Yan K, et al. Study on the influence of thermal characteristics of rolling bearings and spindle resulted in condition of improper assembly[J]. Applied Thermal Engineering, 2017, 114: 221-233. DOI:10.1016/j.applthermaleng.2016.11.194 |
| [19] | Zhang Y, Fang B, Kong L, et al. Effect of the ring misalignment on the service characteristics of ball bearing and rotor system[J]. Mechanism and Machine Theory, 2020, 151: 103889. DOI:10.1016/j.mechmachtheory.2020.103889 |
| [20] | Zhang Y, Zhang M, Wang Y, et al. Fatigue life analysis of ball bearings and a shaft system considering the combined bearing preload and angular misalignment[J]. Applied Sciences, 2020, 10(8): 2750. |
| [21] | Wen B C, Wang M, Han Q K, et al. Effect of ball bearing misalignment on dynamic characteristics of rotor system[C]//IOP Conference Series: Materials Science and Engineering. Guangzhou: IOP Publishing, 2021: 012014. |
| [22] | Harris T A, Kotzalas M N. Advanced concepts of bearing technology: rolling bearing analysis[M]. Boca Raton: CRC Press, 2006. |
