陈小辉, 刘明月, 刘世纪, 田育松
东北大学秦皇岛分校 控制工程学院，河北 秦皇岛 066004
收稿日期：2022-01-05
基金项目：中央高校基本科研业务费专项资金资助项目(N2123028)；河北省自然科学基金青年基金资助项目(E2021501011)。
作者简介：陈小辉(1982-), 女, 河北秦皇岛人, 东北大学副教授。

摘要：为更好地描述Z2CDN18.12N奥氏体不锈钢的单轴棘轮行为, 在统一黏塑性循环本构理论框架下, 改进了Abdel-Karim-Ohno模型. 将塑性应变记忆面引进各向硬化率中, 之后进行模型参数确定, 进而用Abdel-Karim-Ohno模型和改进Abdel-Karim-Ohno模型对Z2CDN18.12N奥氏体不锈钢在室温下的单轴棘轮效应进行研究.利用两种模型分别研究了平均应力、应力幅值、应力率及加载历史等对Z2CDN18.12N奥氏体不锈钢单轴棘轮行为的影响. 结果表明: 在恒定的加载率条件下, 单轴棘轮应变水平随平均应力和应力幅值的增大而提高; 随应力率的增大而降低, 而且对较低的应力率更为敏感; 单轴棘轮行为受加载历史影响显著.通过对比两种模型对材料的单轴棘轮行为的预测结果与试验数据, 证明了本文改进模型的有效性.
关键词：棘轮效应塑性应变记忆面Abdel-Karim-Ohno模型各向同性硬化随动硬化
Modified Abdel-Karim-Ohno Model and Ratcheting Effect Prediction of Z2CDN18.12N Stainless Steel
CHEN Xiao-hui, LIU Ming-yue, LIU Shi-ji, TIAN Yu-song
School of Control Engineering, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: CHEN Xiao-hui, E-mail: chenxh@neuq.edu.cn.

Abstract: In order to better describe the uniaxial ratcheting behavior of Z2CDN18.12N austenitic stainless steel, the Abdel-Karim-Ohno model was improved under the framework of the unified viscoplastic cyclic constitutive theory. By introducing a plastic strain memory surface into the isotropic hardening rule, the model parameters were determined. Further, the Abdel-Karim-Ohno model and the improved Abdel-Karim-Ohno model were used to predict the uniaxial ratcheting effect behavior of Z2CDN18.12N austenitic stainless steel at the room temperature. The influences of mean stress, stress amplitude, stress rate and loading history on the uniaxial ratcheting strain of Z2CDN18.12N austenitic stainless steel were studied by the two models, respectively. The uniaxial ratcheting strain level increased with the increasing mean stress and stress amplitude, decreased with the increasing stress rate, being more sensitive to the lower stress rate, and the loading history had great influence on the ratcheting behavior. Comparison of the prediction results of the two models with the experimental data proved the effectiveness of the improved model.
Key words: ratcheting effectplastic strain memory surfaceAbdel-Karim-Ohno modelisotropic hardeningkinematic hardening
棘轮效应是指材料在非对称应力循环中产生累积塑性应变的现象^[1]，棘轮效应会导致预期寿命缩短或导致结构不稳定而无法正常工作，因此其早已成为国内外****研究的热点和难点.近年来，众多研究人员对材料的棘轮实验和本构关系进行了大量的探索.Yoshida等^[2-4]在实验中发现：室温下，304不锈钢具有很强的黏性，应力率对材料的棘轮效应有很大影响，并且讨论了在650℃下应力率和应力比的变化对304不锈钢棘轮现象的影响.Kang等^[5]在中温(350℃)和高温(700℃)条件下通过大量的单轴和多轴实验，研究了304奥氏体不锈钢的循环硬化特性和时相关性. McDowell^[6]讨论了应力率对轨道用钢棘轮现象的影响；在室温下，Shi等^[7]通过大量的1Cr18Ni9Ti不锈钢单轴棘轮实验，研究了应力率对其棘轮应变的影响.在650 ℃下，Lissenden等^[8]发现TIMETAL21S钛合金在应力循环实验中表现出明显的率相关性；此外，Krempl等^[9]，Maciucescul等^[10]和Tachibana等^[11-13]提出了无屈服面的VBO(viscoplasticity theory based on overstress)模型，为了改善VBO模型对非比例多轴加载的描述能力，Krempl等^[9]修正了表征各向同性应力的演变关系的参数，研究了路径相关性、幅值、及加载历史对材料循环强化的影响.Maciucescu等^[10]发现材料并不发生各向同性强化，用幂函数代替了各项同性强化，并且用一个标量代替了VBO模型中的形状函数.McDowell等^[14]的蠕变-塑性统一型本构模型是在唯象学理论上发展起来的，适用于静态恢复、蠕变-塑性交互等材料特性的描述，对金属材料的温度相关性和率相关性的描述也取得了较好的效果.Kang等^[15]在Abdel-Karim-Ohno^[16]随动硬化率的基础上改进了三种率相关模型，而且不同的温度下研究了304不锈钢的时相关棘轮特性.陈小辉等^[17]和梁婷^[18]对Z2CDN18.12N奥氏体不锈钢进行了大量的实验和本构模型研究，但并没有考虑黏性对材料棘轮行为的影响.于敦吉^[19]采用率相关模型在室温下对Z2CDN18.12N奥氏体不锈钢的棘轮行为进行了研究.
本文在Abdel-Karim-Ohno^[16]非线性随动硬化模型的基础上，引入塑性应变记忆面来描述塑性应变幅值的影响，并研究Z2CDN18.12N奥氏体不锈钢在不同应力率、平均应力、应力幅值和多步加载条件下的单轴棘轮变形行为.
1 黏塑性本构模型的描述在室温下Z2CDN18.12N奥氏体不锈钢具有黏性^[19-20]：当应变率增大时，应力也随之增大，两者呈正相关; 其还具有循环硬化特性，并且高应变幅值的加载历史会提高低应变幅值的应力响应，即Z2CDN18.12N材料具有塑性应变记忆效应.
1.1 主控方程和随动硬化律黏塑性本构模型的方程：

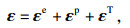(1)

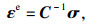(2)

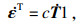(3)

(4)

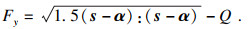(5)

其中：ε，ε^e和ε^p分别为总应变张量、弹性应变张量和非弹性应变张量；为非弹性应变率张量；为热应变率张量；C为弹性矩阵；为相对于参考温度的温度变化率；K和n为表黏性常数；c为各向同性热膨胀系数；s为偏应力张量；α为背应力张量；Q为各向同性变形抗力；〈〉为McCauley括号，其含义为当x≤0时，〈x〉=0；当x＞0时，〈x〉=1.
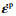
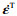
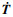
Abdel-Karim和Ohno^[16]将Armstrong Frederick^[21]和Ohno-Wang^[22]模型(OWⅠ模型)叠加，合并为

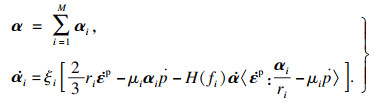(6)

其中：M为背应力个数；ξ_i和r_i代表材料参数；H(f_i)代表Heaviside阶跃函数.当f_i≥0时，H(f_i)=1；当f_i < 0时，H(f_i)=0.当μ_i=0时，该模型将退化为OWⅠ模型，这使得动态恢复项仅在临界面上起作用，且在单轴和多轴的循环加载条件下，OWⅠ比AF模型预测的棘轮效应要小得多.当μ_i=1时，该模型将变成AF模型.
Abdel-Karim-Ohno模型无法兼顾描述单轴和多轴棘轮效应，Kang^[23]改进了Abdel-Karim-Ohno模型背应力的表达式：

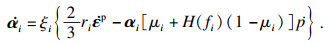(7)

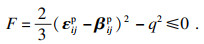1.2 塑性应变幅值记忆效应已有的研究^[20]表明，Z2CDN18.12N在室温下具有明显的塑性应变记忆效应.描述塑性应变幅值记忆效应的方程可表达为

(8)

其中：β_ij^p是塑性应变空间中记忆面的中心；F是塑性应变空间指示面；q代表塑性应变记忆参数.

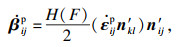(9)

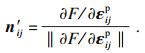(10)

其中：H(F)代表Heaviside函数，当F≥0时，H(F)=1；当F < 0时，H(F)=0.n′_kl表示当前应力点在屈服面f上的法向量；n′_ij表示ε_ij^p在F面上的单位法向量.

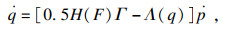(11)

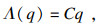(12)

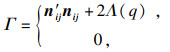(13)

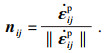(14)

式中：C是非零常数；Γ是一个标量.
1.3 各向同性硬化Z2CDN18.12N不锈钢在室温下具有循环硬化特性^[19]，因此本文将利用各向同性硬化的演化方程来描述材料的棘轮硬化现象，进而改善新建本构模型的预测能力.本文采用Chaboche^[24]提出的硬化准则：

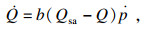(15)

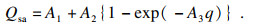(16)

式中：Q_sa为各向同性变形抗力的饱和值；参数b反映Q的演化速率；A₁，A₂和A₃是记忆参数.
2 模型参数确定上述的本构模型中包含众多的材料参数，但是确定方法比较容易，大部分可由单轴实验数据就得到，本文所用的实验数据均来自文献[19].
2.1 参数K和n参数K和n可以由单轴拉伸实验数据确定，见图 1.图中的AKO模型均指的是Abdel-Karim-Ohno模型.在不同应变率的单轴拉伸曲线上取同样的应变值的三个点A，B和C，其中任意两个点的应力与累积塑性应变率符合以下方程：

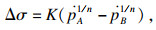(17)

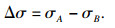(18)

图 1(Fig. 1)

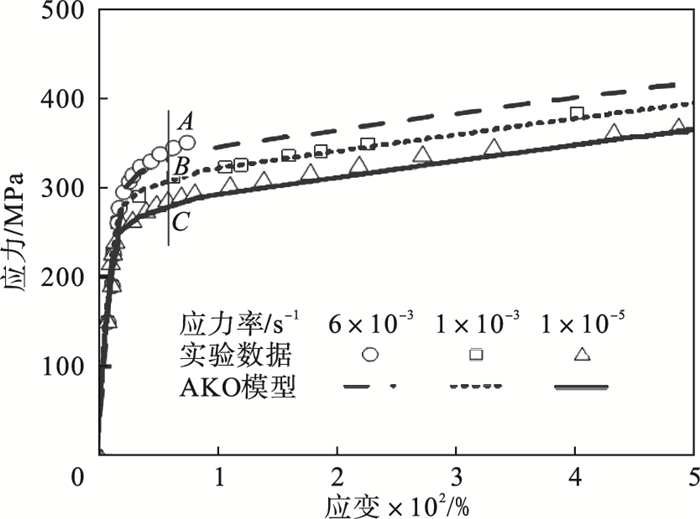图 1 三种不同应力率下的单轴拉伸实验Fig.1 Uniaxial tensile experiment under three different strain rates

2.2 参数ξ_i和r_iξ_i和r_i通过多线性曲线逼近的思想^[25]，可以很容易地由去除了各项同性硬化影响的单轴拉伸曲线得到.

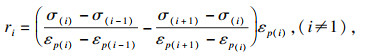(19)

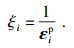(20)

图 2显示的是在室温下、应变率为6×10^-3 s^-1和应变幅值为±1%条件下，材料Z2CDN18.12N材料单轴应变循环实验的仿真结果.由图 1和图 2可知，改进模型较好地描述了应力-应变滞回曲线，与实验结果吻合得较好.此外，从图中可以发现，改进模型较好地预测了材料的循环硬化行为.
图 2(Fig. 2)

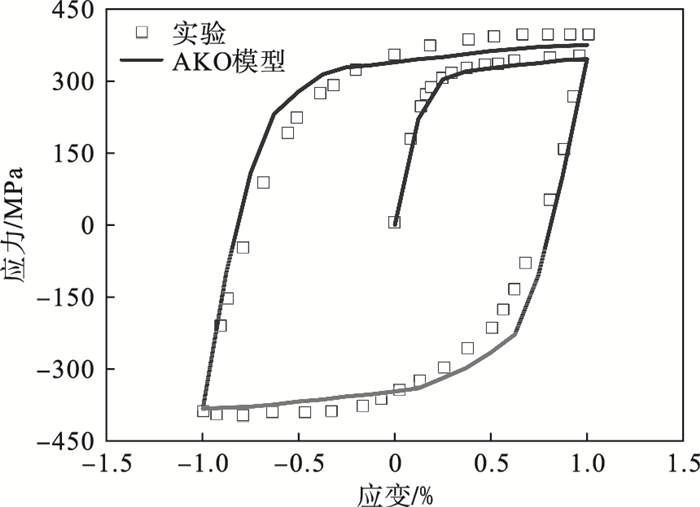图 2 应变幅值为1%应变循环实验仿真结果Fig.2 Simulation results of the strain amplitude of 1% strain cycle experiment

图 3表示的是在室温下，材料Z2CDN18.12N在前20圈峰值应力和循环圈数的仿真结果.从图 3可知，仿真结果较好地预测了峰值应力与循环圈数的关系.
图 3(Fig. 3)

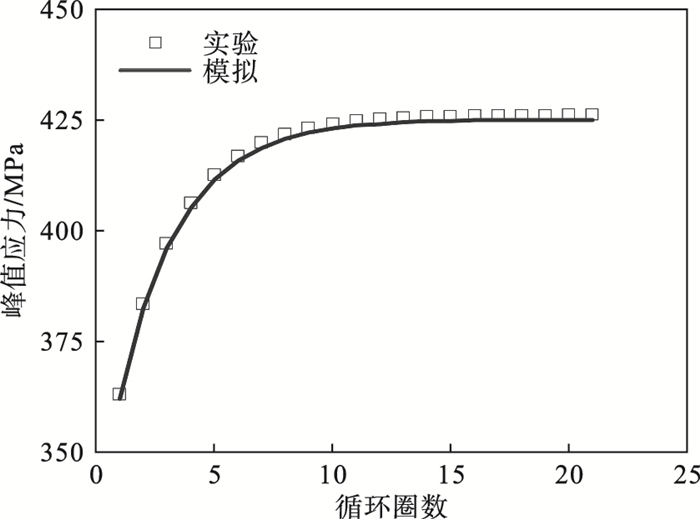图 3 峰值应力与循环圈数模拟结果Fig.3 Simulation results of peak stress and number of cycles

2.3 各向同性硬化参数的确定在确定上述两组参数之后，已知材料的非弹性应变幅值q、给定温度T后，应变循环曲线上的点满足以下方程:

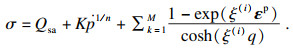(21)

由式(21)可以得出Q_sa的值.然后改变q的值，由式(17)可以得到A₁，A₂和A₃的值.此外，式(16)中参数b可以通过单轴循环实验数据求得，其含义是材料达到循环饱和时的速率.
2.4 参数μ和C参数μ是利用单轴棘轮曲线，由试错法确定；C由实验获得.
本文采用如表 1所示的模型参数进行仿真.
表 1(Table 1)

表 1 改进模型的Z2CDN18.12N材料参数Table 1 Z2CDN18.12N material parameters of the improved model 温度 材料参数值 20 ℃ M=6;E=195 GPa, ν=0.3;K=220 MPa, n=7;μ=0.15 ξ(1)=8 000, ξ(2)=4 000, ξ(3)=2 000, ξ(4)=500, ξ(5)=150, ξ(6)=20 r(1)=16, r(2)=34, r(3)=39, r(4)=15, r(5)=18, r(6)=100 A1=240, A2=280, A3=16, b=6;C=2

表 1 改进模型的Z2CDN18.12N材料参数 Table 1 Z2CDN18.12N material parameters of the improved model

3 单轴棘轮效应3.1 平均应力对单轴棘轮效应的影响图 4a给出了室温下应力率为100 MPa/s, 应力幅值σ_a=150 MPa，平均应力σ_m分别为125，150和175 MPa时，Z2CDN18.12N奥氏体不锈钢单轴棘轮应变与循环圈数的演化关系曲线.图 4b给出了室温下应力率为100 MPa/s, 应力幅值σ_a=200 MPa，平均应力σ_m分别为100，125和150 MPa时，Z2CDN18.12N奥氏体不锈钢单轴棘轮应变演化趋势.从图中可以看出，相同应力幅值下，平均应力增大，棘轮应变也随之增大；改进模型增强了Abdel-Karim-Ohno模型对单轴棘轮效应预测能力.
图 4(Fig. 4)

图 4 平均应力对棘轮效应的影响Fig.4 Influence of average stress on the ratcheting effect (a)—σa=150 MPa；(b)—σa=200 MPa.

3.2 应力幅值对单轴棘轮效应的影响图 5表示的是室温下应力率为100 MP/s，平均应力σ_m=125 MPa，应力幅值σ_a分别为150，175和200 MPa时，Z2CDN18.12N奥氏体不锈钢单轴棘轮应变与实验数据的对比图.从图 5不难看出，相同平均应力下，应力幅值随着棘轮应变值的增大而增大；改进模型与原模型的预测结果相比较，其与实验结果吻合得更好一些.
图 5(Fig. 5)

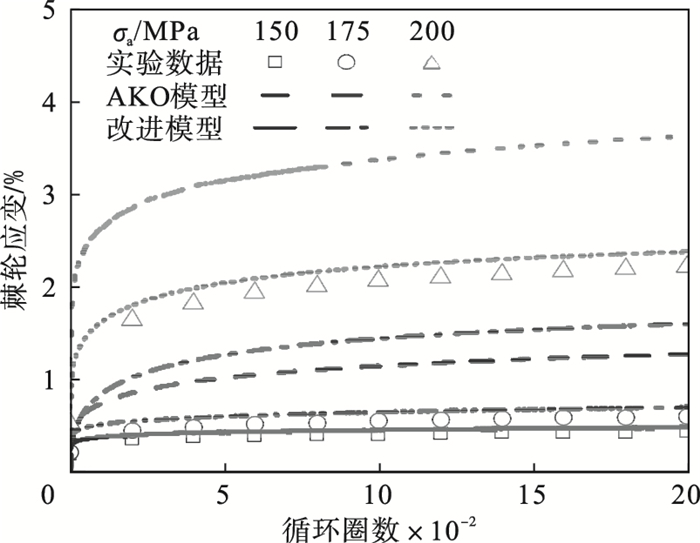图 5 应力幅值对棘轮应变的影响Fig.5 Effect of stress amplitude on the ratcheting strain

3.3 应力率对单轴棘轮效应的影响图 6给出的是室温下在σ_m=150 MPa和应力幅值σ_a=150 MPa的条件下，应力率分别为10, 100和1 000 MPa/s时，Z2CDN18.12N奥氏体不锈钢的单轴棘轮应变和循环圈数的演化关系图.从图 6可以看出，相同平均应力和应力幅值条件下，当应力率增大时，单轴棘轮应变随之减小；改进模型的预测结果比原模型更接近实验值.
图 6(Fig. 6)

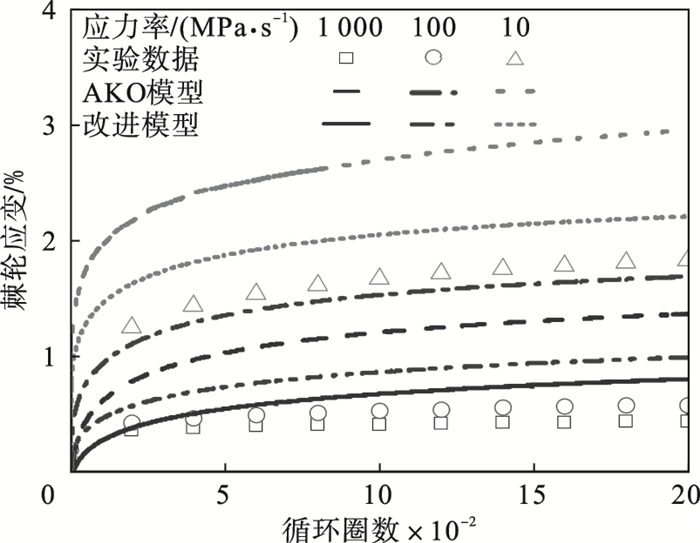图 6 应力率对棘轮效应的影响Fig.6 Effect of stress rate on the ratcheting effect

3.4 加载历史对棘轮效应的影响图 7a表示的是室温下恒定平均应力σ_m=125 MPa，不同应力幅值(σ_a=150→175→200 MPa)下的单轴棘轮实验与仿真结果对比图.从图中可以看到，改进模型相较于原模型改善了单轴棘轮应变值的预测精度；在应力幅值从小到大的变化过程中，材料的棘轮应变显著增大，同时棘轮应变累积速率也增大.
图 7(Fig. 7)

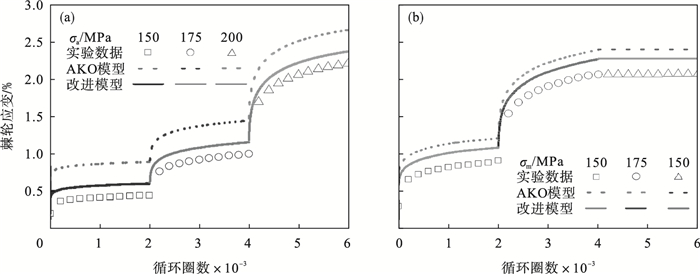图 7 多步加载对棘轮效应的影响Fig.7 Influence of multi-step loading on the ratcheting effect (a)—σm=125 MPa；(b)—σa=150 MPa.

图 7b表示的是室温下恒定应力幅值σ_a=150 MPa，不同平均应力(σ_m=150→175→150 MPa)下的单轴棘轮实验与仿真结果对比关系.从图中可以看出，当平均应力增大时，材料Z2CDN18.12N的单轴棘轮应变值也增大而累积速率继续累积；随着平均应力减小到最初的应力值，棘轮应变则不再继续累积；改进模型的预测值与实验结果更为吻合.
图 8给出的是应力幅值和平均应力均恒定，加载不同应力率下Z2CDN18.12N奥氏体不锈钢的单轴棘轮实验数据和预测结果的对比关系.从图 8a中可以看出，第一步以较小的应力率加载，棘轮应变随着循环圈数增加而增加；随着应力率的增大，棘轮应变不再变化，趋于稳定；从图 8b中可以看出，第一步以较大的应力率加载，棘轮应变随着循环圈数增加而缓慢增加；随着应力率的减小，棘轮应变以更大的速率增加；改进模型的预测值与实验结果更为吻合一些.
图 8(Fig. 8)

图 8 不同应力率的多步加载棘轮效应Fig.8 Ratcheting effect of multi-step loading under different stress rates (a)—低应力率；(b)—高应力率.

4 结论1) 本文对Abdel-Karim-Ohno模型进行了改进，通过引入塑性应力记忆效应来考虑塑性应力幅值对单轴棘轮的影响，改进模型能在一定程度上对Z2CDN18.12N奥氏体不锈钢的单轴棘轮行为给出较合理的预测.
2) 改进模型研究了室温下平均应力、应力幅值、应力率及加载历史等对单轴棘轮行为的影响.结果揭示了改进模型对材料的棘轮应变预测结果比原模型效果更好一些，且与实验数据较吻合.
3) 本文仅针对室温下Z2CDN18.12N奥氏体不锈钢的单轴棘轮行为，下一步应该对不同材料或非室温条件下本文改进模型的普适性进行研究.
参考文献

[1]	康国政. 非弹性本构理论及其有限元实现[M]. 成都: 西南交通大学出版社, 2010: 115. (Kang Guo-zheng. Inelastic constitutive theory and its finite element realization[M]. Chengdu: Southwest Jiaotong University Press, 2010: 115.)
[2]	Yoshida F, Kondo J, Kikuchi Y. Viscoplastic behavior of SUS304 stainless steel under cyclic loading at room temperature[J]. JSME International Jounal: A, 1989, 32: 136-141.
[3]	Yoshida F. Uniaxial and biaxial creep-ratchetting behaviour of SUS304 stainless steel at room temperature[J]. International Journal of Pressure Vessels Pipings, 1990, 44: 207-223. DOI:10.1016/0308-0161(90)90130-A
[4]	Yoshida F. Ratchetting behaviour of 304 stainless steel at 650℃ under multiaxially strain-controlled and uniaxially/multiaxially stress-controlled conditions[J]. European Journal of Mechanics/Solid, 1995, 14: 97-117.
[5]	Kang G Z, Kan Q H, Zhang J, et al. Time-dependent ratcheting experiments of SS304 stainless steel[J]. International Journal of Plasticity, 2006, 22: 858-894. DOI:10.1016/j.ijplas.2005.05.006
[6]	McDowell D L. Stress state dependence of cyclic ratcheting behavior of two rail steels[J]. International Journal of Plasticity, 1995, 11: 397-421. DOI:10.1016/S0749-6419(95)00005-4
[7]	Shi Z, Gao Q, Kang G Z, et al. Experimental study on uniaxial time-dependent ratcheting behavior of 1Cr18Ni9 stainless steel at room temperature[C]// Proceedings of ICMEM2005. Nanjing, 2005: 964-968.
[8]	Lissenden C J, Doraiswamy D, Arnold S M, et al. Experimental investigation of cyclic and time-dependent deformation of titanium alloy at elevated temperature[J]. International Journal of Plasticity, 2007, 23: 1-24. DOI:10.1016/j.ijplas.2006.01.006
[9]	Krempl E, McMahon J J, Yao D, et al. Viscoplasticity based on overstress with a differential growth law for the equilibrium stress[J]. Mechanics of Materials, 1986, 5(1): 35-48. DOI:10.1016/0167-6636(86)90014-1
[10]	Maciucescu L, Sham T L, Krempl E, et al. Modeling the deformation behavior of a Sn-Pb solder alloy using the simplified viscoplasticity theory based on overstress(VBO)[J]. ASME Journal of Electronic Packaging, 1999, 121(2): 92-98. DOI:10.1115/1.2792673
[11]	Tachibana Y, Krempl E. Modeling of high homologous temperature deformation behavior using the viscoplasticity theory based on overstress(VBO): part Ⅰ—creep and tensile behavior[J]. Journal of Engineering Materials and Technology, 1995, 117(4): 456-461. DOI:10.1115/1.2804739
[12]	Tachibana Y, Krempl E. Modeling of high homologous temperature deformation behavior using the viscoplasticity theory based on overstress(VBO): part Ⅱ— characteristics of the VBO model[J]. Journal of Engineering Materials and Technology, 1997, 119(1): 1-6. DOI:10.1115/1.2805967
[13]	Tachibana Y, Krempl E. Modeling of high homologous temperature deformation behavior using the viscoplasticity theory based on overstress(VBO): part Ⅲ—a simplified model[J]. Journal of Engineering Materials and Technology, 1998, 117(3): 193-196.
[14]	McDowell D L, Miller M P, Brooks D C, et al. A unified creep-plasticity theory for solder alloys[J]. Fatigue Testing of Electronic Materials, 1994, 1153: 42-59.
[15]	Kang G Z, Kan Q H. Constitutive modeling for uniaxial time-dependent ratcheting of SS304 stainless steel[J]. Mechanics of Materials, 2007, 39: 488-499. DOI:10.1016/j.mechmat.2006.08.004
[16]	Abdel-Karim M, Ohno N. Kinematic hardening model suitable for ratchetting with steady-state[J]. International Journal of Plasticity, 2000, 16(3): 225-240.
[17]	陈小辉, 陈旭. 核电站压力直管道在位移控制下的棘轮效应[J]. 东北大学学报(自然科学版), 2016, 37(7): 990-993. (Chen Xiao-hui, Chen Xu. Ratcheting effect of pressurized straight pipe under displacement control[J]. Journal of Northeastern University(Natural Science), 2016, 37(7): 990-993. DOI:10.3969/j.issn.1005-3026.2016.07.017)
[18]	梁婷. 热老化作用下Z2CND18.12N管材棘轮效应及棘轮疲劳性能研究[D]. 天津: 天津大学, 2014. (Liang Ting. A study on the ratcheting effect and ratcheting-fatigue behavior of Z2CND18.12N piping material after thermal aging process[D]. Tianjin: Tianjin University, 2014. )
[19]	于敦吉. 奥氏体不锈钢Z2CDN18.12N单轴棘轮行为研究[D]. 天津: 天津大学, 2010. (Yu Dun-ji. Study of micro-mechanisms and macro-constitutive modeling of the cyclic plasticity of austenitic stainless steels[D]. Tianjin: Tianjin University, 2010. )
[20]	邢睿思. 压水堆一回路主管道材料316L/ 316LN不锈钢的多轴循环变形及其本构描述[D]. 天津: 天津大学, 2020. (Xing Rui-si. Multiaxial cyclic deformation and constitutive description of 316L/ 316LN stainless steel for the primary loop of the PWR primary circuit[D]. Tianjin: Tianjin University, 2020. )
[21]	Armstrong P J, Frederick C O. A mathematical representation of the multiaxial Bauschinger effect[J]. Materials at High Temperature, 2007, 24(1): 1-26. DOI:10.3184/096034007X207589
[22]	Ohno N, Wang J D. Kinematic hardening rules with critical state of dynamic recovery, part Ⅱ: application to experiments of ratchetting behavior[J]. International Journal of Plasticity, 1993, 9: 391-403. DOI:10.1016/0749-6419(93)90043-P
[23]	Kang G Z. A visco-plastic constitutive model for ratcheting of cyclically stable materials and its finite element implementation[J]. Mechanics of Materials, 2004, 36: 299-312.
[24]	Chaboche J L. Constitutive equations for cyclic palsticity and cyclic viscoplasticity[J]. International Journal of Plasticity, 1989, 5(3): 247-302.
[25]	Kang G Z, Gao Q, Yang X J, et al. A viscoplastic constitutive model incorporated with cyclic hardening for uniaxial/multiaxial ratcheting of SS304 stainless steel at room temperature[J]. Mechanics of Materials, 2002, 34: 521-531.