赵飞翔, 迟世春
大连理工大学 水利工程学院，辽宁 大连 116024
收稿日期：2022-01-07
基金项目：国家重点研发计划项目(2016YFB0201001)。
作者简介：赵飞翔(1991-)，男，山东临沂人，大连理工大学博士研究生;
迟世春(1964-)，男，山东高密人，大连理工大学教授，博士生导师。

摘要：依据天然堆石颗粒的破碎特性，构建了子颗粒粒径随机的碎片替换模式，即立方体替换模式.采用立方体替换模式可得到符合天然堆石颗粒破碎特性的子颗粒粒径分布.单轴压缩模拟试验表明，与子颗粒粒径固定的4球和18球替换模式相比，立方体替换模式能提高试样级配曲线的连续性，并改善中间粒径缺失的问题.对比不同子颗粒数量替换模式的模拟结果可知，立方体替换模式对应试样的接触数目和平均接触力分布符合替换模式子颗粒数量对分布的影响规律；剔除无接触和单接触颗粒后，3种替换模式的细观力学特性的变化规律一致，表明立方体替换模式可以用于模拟粗粒土的颗粒破碎.
关键词：离散元粗粒土碎片替换模式粒径分布细观力学特性
A Simulation Method for Particle Breakage with Random Fragment Size Based on Discrete Element Method
ZHAO Fei-xiang, CHI Shi-chun
School of Hydraulic Engineering, Dalian University of Technology, Dalian 116024, China
Corresponding author: CHI Shi-chun, E-mail: schchi@dlut.edu.cn.

Abstract: Based on the breakage characteristics of natural rockfill particles, a fragment replacement mode with random sub-particle sizes, namely cube replacement model is established. The simulation test using the cube replacement mode can obtain a size distribution of sub-particles that obeys the breakage characteristic of natural rockfill particles. Uniaxial compression simulations show that, compared with the 4-ball and 18-ball replacement modes with fixed sub-particle sizes, the cube replacement mode can improve the continuity of specimen gradation curve and the problem of missing particles with intermediate sizes. Comparing the simulations of replacement modes with different sub-particle number, the distributions of contact number and mean contact force obtained by cube replacement mode comply with the influence of sub-particle number on the distributions. After removing the non-contact and single-contact particles from specimen, the change rules of micromechanical characteristics of different replacement modes are consisted. It is indicated that the cube replacement mode can be used to simulate the particle breakage of coarse-grained soils.
Key words: discrete element methodcoarse grained soilfragment replacement modeparticle size distributionmicromechanical characteristic
离散单元法在研究岩土材料变形和破坏的细观机理方面具有一定的优越性，近些年在粗粒土的数值模拟中得到了广泛的应用，如堆石料^[1-2]和道砟^[3]等.天然岩石颗粒具有受力会发生破碎的特性，颗粒破碎会改变颗粒集合体的粒径分布，进而影响其力学特性^[4].因此在应用离散元法模拟粗粒土的变形和力学行为时，合理地模拟颗粒破碎十分重要.
基于离散元(PFC3D)模拟颗粒破碎的方法主要有两种：碎片替换法和颗粒黏结法^[5], 本文主要研究前者.碎片替换法采用单个圆球单元代表颗粒，当颗粒所受外力满足破碎准则时，破碎发生.发生破碎的颗粒立刻被删除，并生成特定数量和尺寸的小圆球来模拟颗粒破碎后的碎片.发生破碎的原始颗粒通常被称为母颗粒，用来替换母颗粒的小球称为子颗粒.子颗粒替换母颗粒的具体方式称作碎片替换模式，包括子颗粒的数量、尺寸和位置等.Astrom等^[6]提出了构建碎片替换模式的3个准则：①为保证计算效率，替换所用子颗粒数目不宜过多；②应能模拟破碎发生后局部应力突降的现象；③颗粒破碎特性应与实际情况相符.然而上述3个准则很难同时满足.
McDowell等^[7]构建了等粒径两球、三球和四球替换模式，破碎前后满足质量守恒原则.然而，圆球的几何特性决定了单纯依靠圆球不可能完全填满原始颗粒所占空间.因此若要满足破碎前后质量守恒，而且又限制子颗粒在母颗粒轮廓范围内生成的话，子颗粒间的重叠在所难免.在PFC3D中，颗粒重叠通常意味着存在接触力，因此子颗粒重叠策略违背了前文所述的准则②.Ciantia等^[8]构建了多种子颗粒无重叠但不满足质量守恒的替换模式，但质量损失策略不满足准则③，而且可能会影响动力等模拟试验的结果.Tsoungui等^[9]采用在母颗粒周边空隙中填充小颗粒的方法减小质量损失，但空隙检索会降低计算效率，尤其在数值试样的空隙率较低时.此外，国内外****还提出了线性膨胀法^[10]、变密度法^[11]等替换模式.每种替换模式都具有一定的优势和局限性，因此在实际应用时，需要结合具体研究目的、对象和计算效率等合理地选择或构建碎片替换模式.
从天然颗粒破碎特性的角度上看，现有的多数替换模式的子颗粒粒径是固定的，或者说子颗粒与母颗粒粒径的比值是固定的.而天然岩石颗粒破碎后产生的碎片尺寸往往是随机的，因此子颗粒尺寸固定的策略违背了准则③.徐琨等^[5]提出依据真实颗粒的破碎特性构建具有不同尺寸碎片的替换模式是开展精细模拟研究的基本需求.Brosh等^[12]构建了一种子颗粒粒径随机的替换模式，在满足质量守恒的前提下，基于试错法逐个生成子颗粒，子颗粒粒径由服从指定分布的随机数确定，该替换模式适用于微粒子的冲击破碎.目前尚未见到适用于粗粒土的子颗粒粒径随机的碎片替换模式.
综上所述，本文将依据天然堆石颗粒(石灰岩)的破碎特性，建立子颗粒粒径随机且满足质量守恒原则的碎片替换模式，即立方体替换模式.采用立方体替换模式开展堆石料的单轴压缩模拟试验，并与粒径固定的4球和18球替换模式的结果进行比较，分析子颗粒粒径随机对试样级配曲线的影响.最后，讨论了立方体替换模式对应单轴压缩试样的接触数目和平均接触力分布的合理性.
1 立方体碎片替换模式1.1 碎片粒径的确定方法设有一个单位立方体，立方体的一个顶点与直角坐标系的原点重合，如图 1所示.在立方体内取一随机点(a, b, c)，过该点且平行于立方体表面作三次不同方向的切割，可将立方体切割为8个小块体.其中一个小块体(记为1号块体)的体积k₁为

(1)

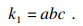图 1(Fig. 1)

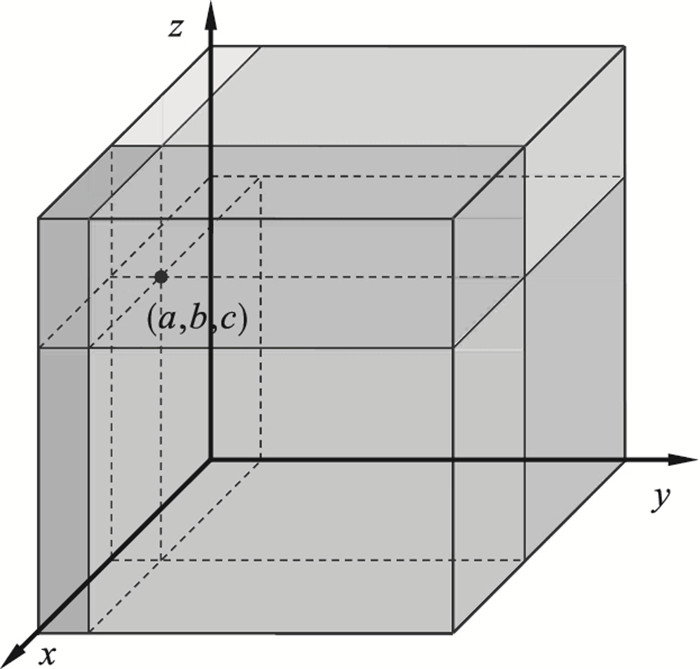图 1 立方体替换模式示意图Fig.1 Schematic of cube replacement mode

式中，a, b, c为随机点的三个坐标值，三者相互独立且均服从(0, 1)区间上的均匀分布.同理可算出其余7个小块体的体积.因为单位立方体的体积V等于1，所以式(1)中的k₁也可表示小块体体积与立方体体积之比.
8个小块体对应8个子颗粒，所以立方体替换模式理论上有8个子颗粒.若母颗粒的半径为R₀，1号块体对应1号子颗粒的体积v₁为

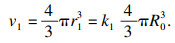(2)

式中，r₁为1号子颗粒的半径.同理可求出其余子颗粒的半径.由式(1)确定的8个小块体的体积之和等于1，因此由式(2)确定的8个子颗粒的体积之和就等于母颗粒体积，即立方体替换模式满足破碎前后质量守恒.
1.2 子颗粒尺寸分布单个天然堆石颗粒破碎后的碎片尺寸分布通常有很大的离散性.但大量同粒径的堆石颗粒破碎后碎片具有一定的统计规律，子颗粒粒径服从正态分布^[13].使用PFC3D软件模拟单粒破碎，首先生成100个粒径为28~30 mm(均匀分布)的颗粒，然后采用立方体替换模式替换这些颗粒，最后统计所有子颗粒的粒径数据，结果如图 2所示.图中除单粒试验数据(柱状图)外，还有三组使用了不同随机切割点的模拟试验结果，其中(a², b², c²)表示由随机数平方值构成的切割点，(a³, b³, c³)为三次方切割点.对比图 2中不同切割点的模拟结果可知，随切割点指数的增大，粒径分布的峰值逐渐向右偏移.由三组模拟结果和试验数据的对比可知，二次方切割点与试验数据的拟合度最好.
图 2(Fig. 2)

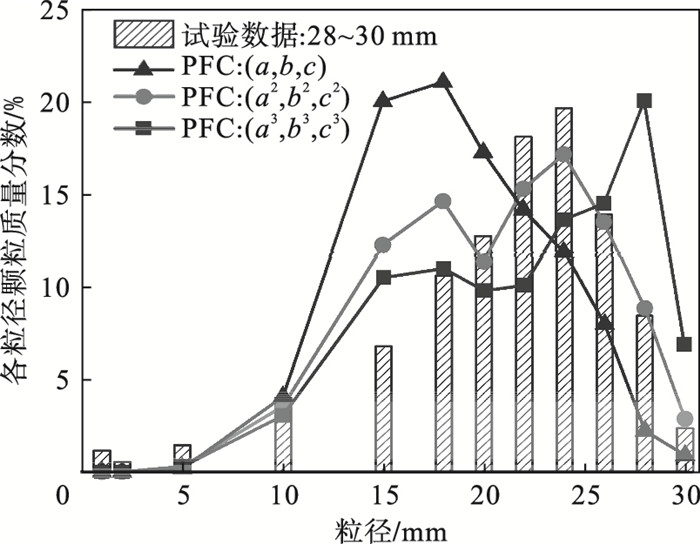图 2 采用立方体替换模式得到的粒径分布与实验数据的对比Fig.2 Comparison of particle size distribution obtained by cube replacement mode with experimental data

为探究切割点的随机性对碎片尺寸分布的影响，再次采用二次方切割点重复10次单粒模拟试验，每次使用不同的随机种子，结果如图 3所示.受切割点随机性的影响，10次模拟结果各不相同.但由这11次模拟结果(包括图 2的二次方数据)可知碎片的粒径分布是在一定范围内的波动，而整体上与实验数据仍有较好的拟合度.
图 3(Fig. 3)

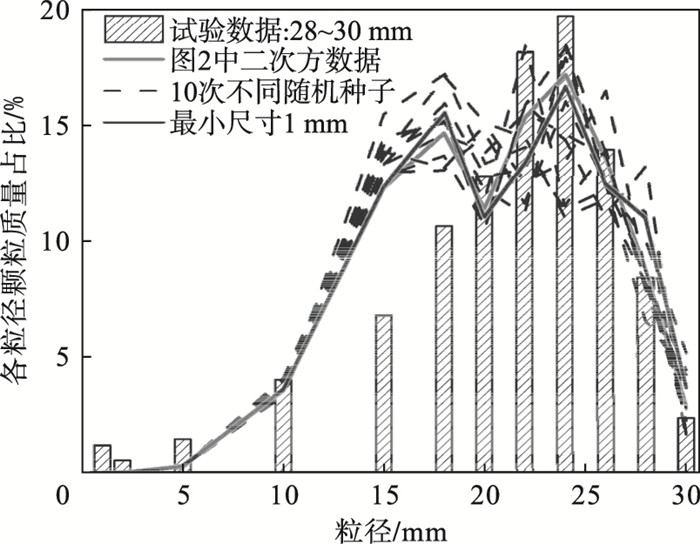图 3 切割点的随机性对碎片尺寸分布的影响Fig.3 Effect of randomness of the cutting point on the fragments size distribution

图 4为粒径范围20~40 mm，且每隔2 mm划分一个粒组的单粒模拟试验结果.图中横坐标的d_max表示各粒组粒径区间的上限值，比如28~30 mm粒组的d_max为30.由图 4可知，原横坐标粒径除以各粒组的d_max后，所有粒组的子颗粒尺寸分布几乎相同，说明基于立方体替换模式的碎片尺寸分布特性不受粒径变化的影响.此外，图 4的离散元模拟结果与天然堆石颗粒的单粒破碎试验^[13]具有相同的分布特性，说明立方体替换模式符合真实颗粒的破碎特性.
图 4(Fig. 4)

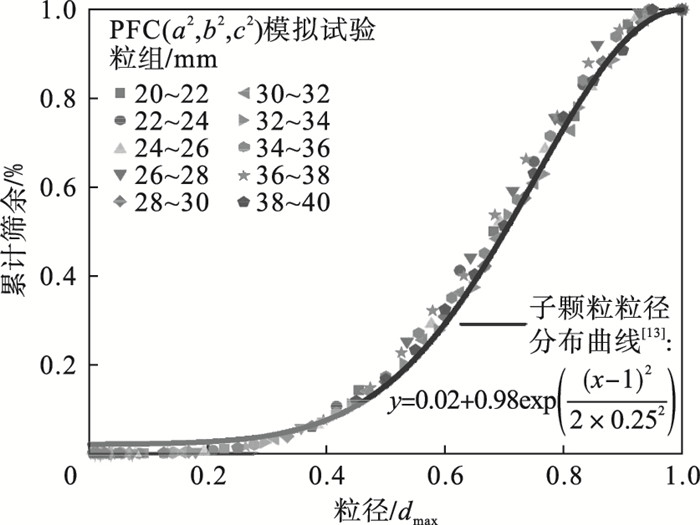图 4 不同粒组的单粒模拟试验结果Fig.4 Results of single particles simulation test of different size fractions

2 碎片替换模式对级配曲线的影响颗粒破碎是离散元模拟试验中改变试样级配的主要甚至唯一途径，不同的碎片替换模式最终会得到不同的级配曲线^[14].本节将开展单轴压缩模拟试验以分析碎片替换模式对试样级配曲线的影响.
2.1 子颗粒位置的确定满足质量守恒原则的碎片替换模式应尽可能地减小子颗粒间的重叠.由于立方体替换模式的子颗粒粒径是随机的，子颗粒位置固定的策略不再适用，本文结合子颗粒粒径和等分轴线来确定子颗粒的位置.如图 5a所示，图中最大球为母颗粒，c₀(c_x, c_y, c_z)为其球心.连接c₀和内接立方体顶点可作8条等分轴线，子颗粒的球心就分别位于这8条等分线上.例如其中一个子颗粒的球心c₁为c₀+R₀-r₁，其中R₀为母颗粒球心指向内接立方体顶点的向量，r₁为子颗粒的球心指向同一顶点的向量.同理可求出其余子颗粒的球心位置.图 5b为使用PFC3D软件实现的三维替换实例，图中半透明球壳为母颗粒轮廓.图中子颗粒间有一定的重叠，满足质量守恒的同时又限制圆球子颗粒在母颗粒轮廓内生成，重叠是不可避免的.
图 5(Fig. 5)

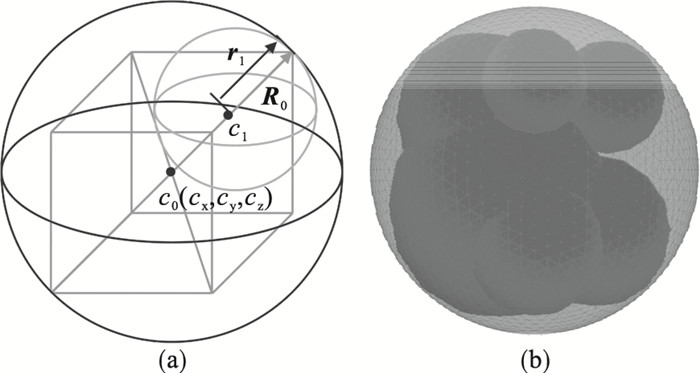图 5 子颗粒位置确定方法示意图和实例Fig.5 Schematic diagram and example of the method of placing sub-particles (a)—示意图；(b)—三维实例.

2.2 破碎极限和允许最小尺寸由式(1)可知，小块体的体积可能会随机取到一个非常小的值，也就对应一个尺寸很小的颗粒.试样内最小颗粒的尺寸是影响模拟试验计算效率的重要因素之一，因此有必要设置一个允许最小尺寸d_M，以限制试样内允许颗粒生成的最小尺寸.若由式(2)求出的子颗粒粒径小于d_M，则标记该子颗粒为无效颗粒，反之为有效颗粒.为保证质量守恒，待8个子颗粒的粒径全部确定后，统计所有无效子颗粒的质量，然后将其分配给尺寸最小的有效颗粒.采取此措施后，最终生成的子颗粒数量可能会少于8个.
允许最小尺寸d_M的选取可根据破碎极限尺寸d_L确定.破碎极限尺寸是允许发生破碎的最小尺寸，设置d_L是为了避免颗粒不断的破碎，导致颗粒尺寸不断变小，进而影响计算效率.d_L的取值目前尚无统一的准则，一般取d_L/d₅₀=0.25^{[7-9, 11-12]}，其中d₅₀为试样的中值粒径.参考堆石料三轴试验所用的级配数据^[15]，破碎极限尺寸d_L可设为5 mm.d_M的取值可参考d_M/d_L=0.25，由此关系式确定d_M并取整，本文将d_M设为1 mm.如图 3所示，设置允许最小尺寸为1 mm后，单粒模拟试验的子颗粒尺寸分布没有出现显著差异，说明d_M选取策略是可行的.
2.3 颗粒破碎准则和接触模型De Bono等^[16]使用4种不同的颗粒破碎准则开展离散元数值模拟试验，结果表明八面体切应力和最大接触力破碎准则都能得到合理的试样级配和正确的应力应变行为.Russell等^[17]分析了颗粒在理想堆积体中的应力状态后发现，颗粒的破碎主要由最大接触力F_M控制.因此本文使用最大接触力破碎准则^[18]：

(3)

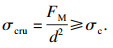式中：σ_cru表示外力引起的颗粒内部破坏应力；d为颗粒粒径；σ_c为颗粒的特征强度.颗粒特征强度为材料属性，可通过单粒破碎试验获得^[13].
接触模型采用PFC3D内置的滚动阻力线性模型(rolling resistance linear model，RRLM)^[19].该接触模型在线性接触模型的基础上，对颗粒在接触点处的滚动进行限制，能模拟堆石颗粒的休止角.该接触模型的相关参数见表 1，其中μ_r为颗粒在斜面上与自重达到极限静力平衡时的斜面倾角的正切值^[1].
表 1(Table 1)

表 1 颗粒接触模型和模拟参数Table 1 Parameters of particle contacts model and simulation 法向刚度kn/(N·m-1) 法向刚度ks/(N·m-1) 摩擦系数μ 滚动阻力系数μr 7.0×107 6.0×107 0.40 0.70

表 1 颗粒接触模型和模拟参数 Table 1 Parameters of particle contacts model and simulation

2.4 单轴压缩试验的级配曲线除立方体替换模式外，参考McDowell等^[7]构建的4球替换模式，以及参考Ciantia等^[8]采用的方法构建了18球替换模式.基于PFC3D的4球和18球替换模式实例如图 6所示.其中4球替换模式满足质量守恒原则，18球替换模式不满足质量守恒原则但子颗粒间无重叠.分别使用这3种替换模式开展单轴压缩模拟试验，分析替换模式对试样级配曲线的影响.
图 6(Fig. 6)

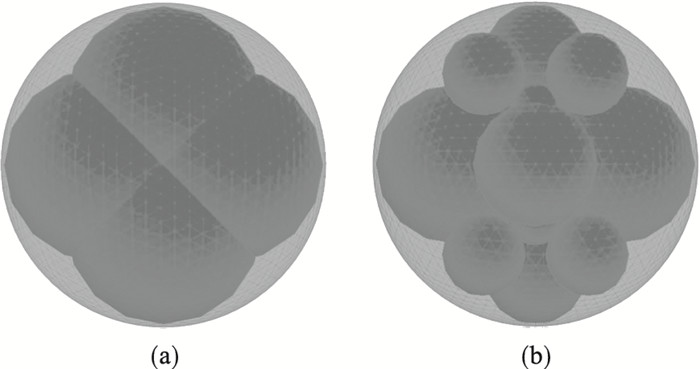图 6 4球和18球替换模式实例Fig.6 Examples of 4-ball and 18-ball replacement modes (a)—4球；(b)—18球.

单轴压缩模拟试验使用单一粒径的初始级配，初始试样仅含粒径为40 mm的颗粒，此时粒径分布的变化可直接反映替换模式对级配曲线演化的影响.不同替换模式的模拟试验采用相同的试验条件.试验结束后，统计不同替换模式对应试样的粒径分布，结果如图 7所示，图中横坐标(粒径)的采样间距为2 mm.4球和18球替换模式对应的级配曲线均出现多个水平段，整体呈阶梯状，说明级配曲线缺失大量中间粒径的颗粒.此时试样内只有几种特定粒径的颗粒，而且这几种特定粒径可根据替换模式和初始级配预先算出.相比较而言，立方体替换模式对应的级配曲线较平滑，未出现平台段，整体为连续型级配.Wood等^[20]指出级配曲线的形状可能比具体颗粒尺寸更重要，而且连续型级配曲线更符合真实土体级配的演化规律.相比较而言，立方体替换模式对应试样的级配更合理.
图 7(Fig. 7)

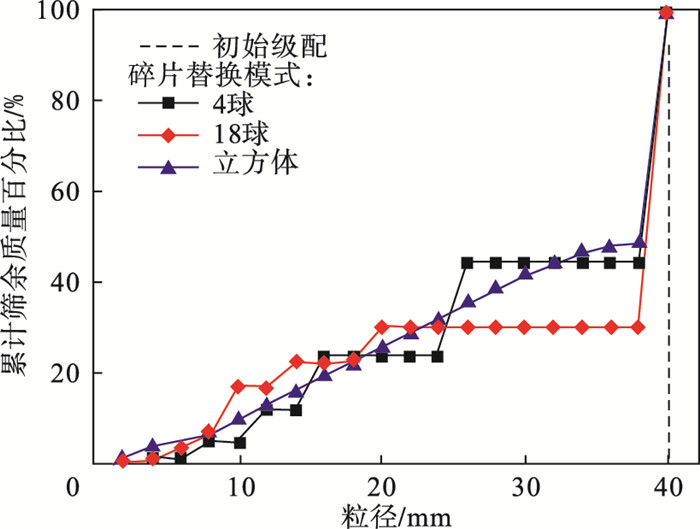图 7 碎片替换模式对试样级配曲线的影响Fig.7 Influence of replacement mode on gradation curves

此外，图 7表明当试样初始级配为单一粒径时，替换模式对试样级配曲线的变化有重要影响.虽然单一粒径的初始级配属于极端情况，但这也能说明初始级配越均匀，越不能忽视碎片替换模式的影响.
3 替换模式对细观力学特性的影响碎片替换模式对颗粒堆积体的细观力学特性有重要影响^[21].为了研究子颗粒粒径随机的策略是否会改变细观力学接触特性的分布规律，选用物理三轴试验制样后的级配作为初始级配^[15]，使用立方体、4球和18球替换模式开展单轴压缩模拟试验，其他条件和参数与前文一致，结果如图 8~图 11所示(原始分布曲线).
图 8(Fig. 8)

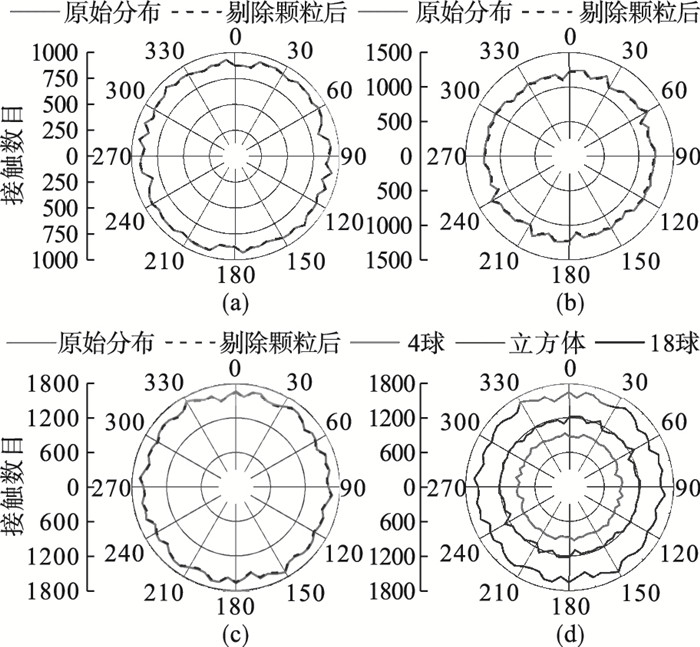图 8 接触数目在水平投影面上的分布Fig.8 Distributions of contact number on horizontal projection (a)—4球；(b)—立方体；(c)—18球；(d)—3种替换模式的对比.

图 9(Fig. 9)

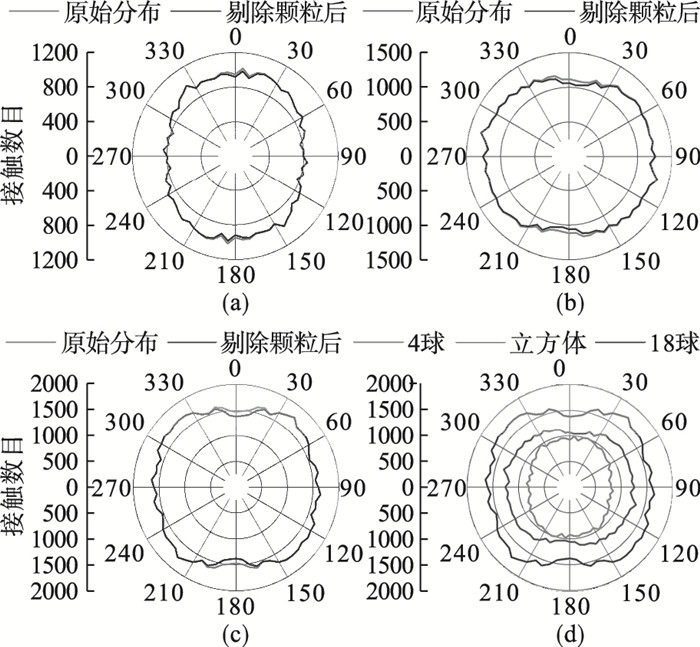图 9 接触数目在竖直投影面上的分布Fig.9 Distributions of contact number on vertical projection plane (a)—4球；(b)—立方体；(c)—18球；(d)—3种替换模式的对比.

图 10(Fig. 10)

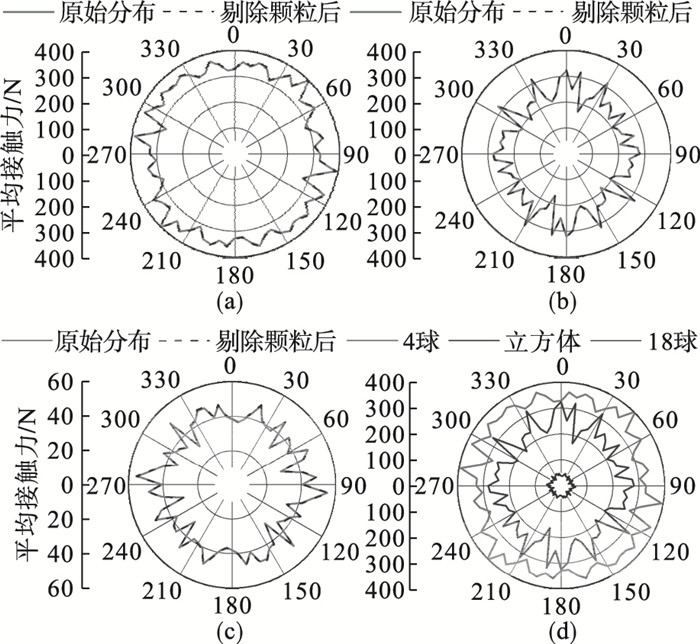图 10 平均接触力在水平投影面上的分布Fig.10 Distributions of mean contact force on horizontal projection plane (a)—4球；(b)—立方体；(c)—18球；(d)—3种替换模式的对比.

图 11(Fig. 11)

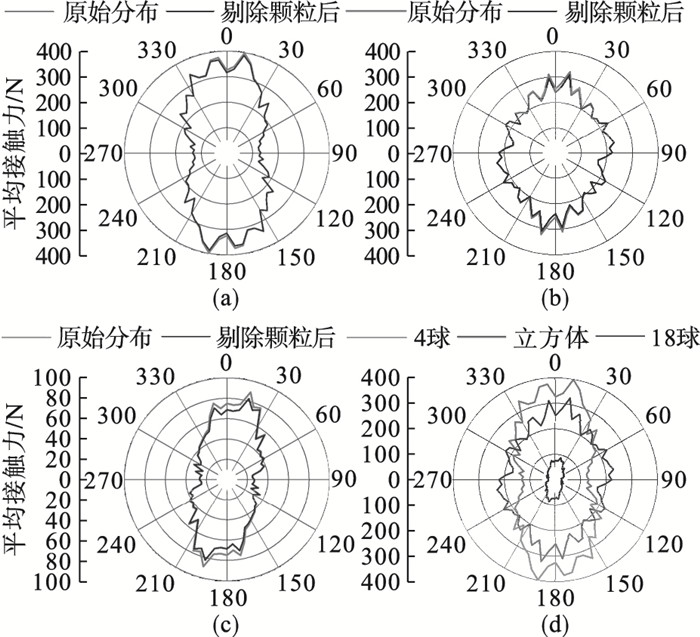图 11 平均接触力在竖直投影面上的分布Fig.11 Distributions of mean contact force on vertical projection plane (a)—4球；(b)—立方体；(c)—18球；(d)—3种替换模式的对比.

3.1 接触数目和平均接触力的分布图 8为接触数目在水平投影面上的分布，3种替换模式对应的分布均表现为各向同性.由图 8d可知，接触数目随子颗粒数量的增加而增多.接触数目在水平投影面上的各向同性说明将其向竖直面投影时，投影结果和角度无关.如图 9所示，3种替换模式的接触数目在竖直投影面上的分布均表现出一定的各向异性，而且接触数目同样与子颗粒数量正相关.
图 10为平均接触力在水平投影面上的分布，虽然分布曲线的光滑性较差，但整体而言，3种替换模式对应的平均接触力分布可认为是各向同性的.如图 10d所示，平均接触力随子颗粒数目的增加而减小.此外，18球的平均接触力要远小于4球和立方体替换模式.造成这种差异的原因：一方面是18球对应的试样有更多的颗粒(图 8d)；另一方面18球替换模式存在质量损失且子颗粒间无重叠，颗粒有更大的空间来调整位置.以上两方面因素使18球对应试样的外力和接触力能更均匀地在颗粒间传递.图 11为平均接触力在竖直投影面上的分布，3种替换模式都表现出明显的各向异性.但三者又存在共性，即平均接触力在0°，180°及附近(试样轴向，即外力方向)相对较大，在90°，270°及附近(水平方向)较小.
3.2 无力学贡献颗粒对细观力学特性的影响Thornton^[22]认为颗粒集合体内存在一些无接触和单接触的颗粒，这些颗粒对结构的整体稳定没有力学贡献，由此提出了不考虑无力学贡献颗粒的力学平均配位数C_m.参考C_m的概念，将无力学贡献的颗粒剔除后，再次绘制接触数目和平均接触力的分布，结果如图 8~图 11所示(剔除颗粒后对应曲线).
由图 8和图 10可知，在水平投影面上，剔除无力学贡献颗粒后，接触数目和平均接触力在各方向上均匀地减小，但变化十分微小.由图 9和图 11可知，在竖直投影面上，剔除无力学贡献颗粒后，接触数目和平均接触力的变化主要在0°，180°及附近，在90°，270°及附近几乎无变化.造成这种变化的原因如下：无接触颗粒(悬浮状态)不会影响接触数目和平均接触力的分布；单接触颗粒大多是落入试样底部的小颗粒，这些颗粒的接触力方向与重力方向、三轴试验加载方式一致，因此剔除单接触颗粒主要影响0°，180°及附近的接触数目和平均接触力分布.另一方面，单接触颗粒的接触力等于自身重力，而这类颗粒的尺寸一般很小，因此剔除单接触颗粒对接触数目和平均接触力分布的影响并不显著.
结合图 8~图 11和以上分析可知，3种替换模式的接触数目和平均接触力的分布虽有差异，但也基本符合替换模式所含子颗粒数量对这两种细观力学特性的影响规律^[21].剔除无力学贡献颗粒后，3种替换模式对应分布的变化也是一致的.以上分析说明基于立方体替换模式的单轴压缩模拟试验，数值试样的接触数目和平均接触力分布是具有一定合理性的.
4 结论1) 构建了一种子颗粒粒径随机且破碎前后质量守恒的碎片替换模式，即立方体替换模式.采用立方体替换模式模拟颗粒破碎可以得到与单粒破碎试验拟合度较好的子颗粒粒径分布.
2) 单一粒径初始级配的单轴压缩模拟试验表明，采用立方体替换模式可以得到连续性更好的子颗粒粒径分布曲线，改善中间粒径的缺失.因此立方体替换模式适合模拟粗粒土的颗粒破碎.
3) 不同碎片替换模式的单轴压缩模拟试验结果表明，立方体替换模式对应试样的接触数目和平均接触力在竖直和水平投影面上分布特性，与子颗粒粒径固定的4球和18球替换模式的一致.
4) 剔除无力学贡献颗粒后，接触数目和平均接触力在水平投影面上的变化十分微小.立方体替换模式对应试样的细观接触特性的变化规律与另两种替换模式相同.
参考文献

[1]	Shao X Q, Chi S C, Tao Y, et al. DEM simulation of the size effect on the wetting deformation of rockfill materials based on single-particle crushing tests[J]. Computers and Geotechnics, 2020, 123: 103429. DOI:10.1016/j.compgeo.2019.103429
[2]	Zhang P T, Sun X J, Zhou X J, et al. Experimental simulation and a reliable calibration method of rockfill microscopic parameters by considering flexible boundary[J]. Powder Technology, 2022, 396: 279-290. DOI:10.1016/j.powtec.2021.10.061
[3]	Zhou W, Yang L, Ma G, et al. DEM analysis of the size effects on the behavior of crushable granular materials[J]. Granular Matter, 2016, 18(3): 1-11.
[4]	Xiao Y, Liu H L, Chen Y M, et al. Strength and deformation of rockfill material based on large scale triaxial compression tests.Ⅱ: influence of particle breakage[J]. Journal Geotechnical and Geoenvironmental Engineering, 2014, 140(12): 04014071. DOI:10.1061/(ASCE)GT.1943-5606.0001177
[5]	徐琨, 周伟, 马刚, 等. 基于离散元法的颗粒破碎模拟研究进展[J]. 岩土工程学报, 2018, 40(5): 880-889. (Xu Kun, Zhou Wei, Ma Gang, et al. Review of particle breakage simulation based on DEM[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 880-889.)
[6]	Astrom J A, Herrmann H J. Fragmentation of grains in a two-dimensional packing[J]. European Physical Journal B-Condensed Matter and Complex Systems, 1998, 5(3): 551-554. DOI:10.1007/s100510050476
[7]	McDowell G R, de Bono J P. On the micro mechanics of one-dimensional normal compression[J]. Géotechnique, 2013, 63(11): 895-908. DOI:10.1680/geot.12.P.041
[8]	Ciantia M O, Arroyo M, Calvetti F, et al. An approach to enhance efficiency of DEM modelling of soils with crushable grains[J]. Géotechnique, 2015, 65(2): 91-110. DOI:10.1680/geot.13.P.218
[9]	Tsoungui O, Vallet D, Charmet J C. Numerical model of crushing of grains inside two-dimensional granular materials[J]. Powder Technology, 1999, 105(1): 190-198.
[10]	Ben-Num O, Einav I. The role of self-organization during confined comminution of granular materials[J]. Philosophical Transactions of the Royal Society A: Mathematical Physical and Engineering Sciences, 2010, 368(1910): 231-247. DOI:10.1098/rsta.2009.0205
[11]	杨贵, 许建宝, 刘昆林. 粗粒料颗粒破碎数值模拟研究[J]. 岩土力学, 2015, 36(11): 3301-3306. (Yang Gui, Xu Jian-bao, Liu Kun-lin. Numerical simulation of particle breakage of coarse aggregates[J]. Rock and Soil Mechanics, 2015, 36(11): 3301-3306.)
[12]	Brosh T, Kalman H, Levy A. Fragments spawning and nteraction models for DEM breakage simulation[J]. Granular Matter, 2011, 13(6): 765-776. DOI:10.1007/s10035-011-0286-z
[13]	赵飞翔, 迟世春, 米晓飞. 基于颗粒破碎特性的堆石材料级配演化模型[J]. 岩土工程学报, 2019, 41(9): 1707-1714. (Zhao Fei-xiang, Chi Shi-chun, Mi Xiao-fei. Gradation evolution model based on particle breakage characteristics for rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1707-1714.)
[14]	Li H Q, McDowell G, Lowndes I. Discrete element modelling of a rock cone crusher[J]. Powder Technology, 2014, 263: 151-158. DOI:10.1016/j.powtec.2014.05.004
[15]	贾宇峰, 王丙申, 迟世春. 堆石料剪切过程中的颗粒破碎研究[J]. 岩土工程学报, 2015, 37(9): 1692-1697. (Jia Yu-feng, Wang Bing-shen, Chi Shi-chun. Particle breakage of rockfill during triaxial tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1692-1697.)
[16]	De Bono J, McDowell G. Particle breakage criteria in discrete-element modelling[J]. Géotechnique, 2016, 66(12): 1014-1027. DOI:10.1680/jgeot.15.P.280
[17]	Russell A R, Wood D M, Kikumoto M. Crushing of particles in idealized granular assemblies[J]. Journal of the Mechanics and Physics of Solids, 2009, 57(8): 1293-1313. DOI:10.1016/j.jmps.2009.04.009
[18]	Marketos G, Bolton M D. Compaction bands simulated in discrete element models[J]. Journal of Structural Geology, 2009, 31(5): 479-490. DOI:10.1016/j.jsg.2009.03.002
[19]	Ai J, Chen J F, Rotter J M, et al. Assessment of rolling resistance models in discrete element simulations[J]. Powder Technology, 2011, 206(3): 269-282.
[20]	Wood D M, Maeda K. Changing grading of soil: effect on critical states[J]. Acta Geotechnica, 2008, 3(1): 3-14.
[21]	张科芬, 张升, 腾继东, 等. 离散元中破碎自组织对颗粒破碎影响研究[J]. 岩土工程学报, 2018, 40(4): 743-751. (Zhang Ke-fen, Zhang Sheng, Teng Ji-dong, et al. Influences of self-organization of granular materials on particle crushing based on discrete element method[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 743-751.)
[22]	Thornton C. Numerical simulations of deviatoric shear deformation of granular media[J]. Géotechnique, 2000, 50(1): 43-53.