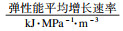纪洪广^1,2, 陈东升^1,2, 苏晓波^1,2, 权道路^1,2
1. 北京科技大学 土木与资源工程学院，北京 100083;
2. 北京科技大学 城市地下空间工程北京市重点实验室，北京 100083
收稿日期：2022-01-14
基金项目：国家重点研发计划项目(2016YFC0600801)；国家自然科学基金资助项目(52074021)。
作者简介：纪洪广(1963-)，男，山东青州人，北京科技大学教授，博士生导师。

摘要：为了研究岩体的变形特征和能量特征与其所处应力状态之间的关系，开展了5种围压下花岗岩的三轴循环加卸载试验.基于应力-应变曲线，计算了循环加卸载过程中花岗岩的弹性模量和能量密度，分析了应力状态对弹性模量及能量演化规律的影响.研究结果表明：轴向弹性模量随围压的增大而增大，随轴向应力的增大先增大后减小.轴向弹性模量与最大、最小主应力呈现良好的二次函数关系.随着围压的增大，能量密度与弹性能占比(弹性能与输入总能量之比)均显著增大，岩石储能能力提高；随着轴向应力增大，弹性能占比先增大后减小.弹性能占比减小阶段即岩石损伤加剧阶段，围压的增加延长了岩石的损伤演化过程.最后讨论了应力状态、岩石力学参数及能量状态的关联性.
关键词：岩石力学三轴循环加卸载弹性模量能量演化特征蓄能水平
Analysis of Elastic Modulus Variation and Energy Evolution of Granite Based on Triaxial Loading and Unloading Test
JI Hong-guang^1,2, CHEN Dong-sheng^1,2, SU Xiao-bo^1,2, QUAN Dao-lu^1,2
1. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Beijing Key Laboratory of Urban Underground Space Engineering, University of Science and Technology Beijing, Beijing 100083, China
Corresponding author: CHEN Dong-sheng, E-mail: beikecds@163.com.

Abstract: To investigate the relationship between the deformation and energy characteristics of the rock mass and the stress state, triaxial cyclic loading and unloading tests on granite under five types of confining pressure were carried out. Based on the stress-strain curves, the elastic modulus and energy density of the granite were calculated during cyclic loading and unloading, and the influence of the stress state on the evolution of the elastic modulus and energy was analyzed. The results show that the axial modulus of elasticity increases with the increase of the confining pressure, and increases first and then decreases with the increase of the axial stress. The axial modulus of elasticity shows a good quadratic function with the maximum and minimum principal stresses. The energy density and the proportion of elastic energy (the ratio of elastic energy to total energy input) increase significantly as the confining pressure increases, and the energy storage capacity of the rock increases. The proportion of elastic energy increases first and then decreases as the axial stress increases. The decrease in the proportion of elastic energy is the stage of increased damage to the rock, and the increase in the confining pressure prolongs the process of damage evolution. Finally, the correlation between stress state, rock mechanical parameters, and energy state is discussed.
Key words: rock mechanicstriaxial cyclic loading and unloadingelastic modulusenergy evolution characteristicsenergy storage levels
随着浅部矿产资源逐渐枯竭，地下工程不断向深部发展^[1-4].深部岩体处于高应力的三轴压缩状态，受地下工程活动如开挖、爆破等影响，深部岩体力学行为较浅部岩体更为复杂.岩体是一种蓄能体，在深部高压状态下，岩体内部可积蓄巨大的弹性能，这部分能量突然释放，会给地下工程带来巨大的灾难^[5-8].岩体储能状态不易直接测得，一般方法是通过岩体所处应力状态和岩体的力学参数(弹性模量、泊松比)进行间接计算，因此明确岩体力学参数变化规律对判断深部岩体储能状态及评价岩体稳定性具有重要意义.
大量试验和研究表明，岩石的力学参数与工程扰动和应力状态有关^[9-15]：谢和平等^[9-10]通过测井数据反演发现岩石的弹性模量、泊松比、内摩擦角等随着深度改变呈非线性变化；Meng等^[11-12]进行循环加卸载试验发现岩石弹性模量随着轴向应力的增加先增大后减小，随围压增大而增大；Jiang等^[13]分析了不同围压下岩石力学参数的统计特征, 发现弹性模量和泊松比服从随机的对数正态分布；Ray等^[14]、Zhao等^[15]通过循环加卸载试验研究了加卸载速率对岩石力学行为和破裂特征的影响，发现弹性模量随应变速率的增大而增大.
岩石能量方面，国内外****主要以试验和理论分析两种方法对岩石能耗规律和破坏准则两个主要问题进行研究.①试验方面: Hua等^[16]通过岩石卸围压试验探究了岩石能量特征，得出岩石自蓄能量可以导致岩石结构破坏的结论；Li等^[17]通过动静组合荷载试验，发现组合荷载条件下声发射能量相对于纯动、静荷载条件下更大；牛双建等^[18]采用能量耗散的方法分析了不同加载路径下砂岩破坏模式及能耗规律；He等^[19]通过声发射试验，探究了声发射及能量特征随着应力路径的变化；孟庆彬等^[20]、Bagde等^[21]通过三轴循环加卸载试验发现围压抑制岩样破裂时能量的释放，提高了峰后蓄能水平.②能量准则及损伤本构方面：谢和平等^[22]基于能量耗散建立了岩石的损伤演化方程和岩体单元的整体破坏准则；Cornetti等^[23]从断裂力学的角度分析了裂纹能量的破坏准则；Gaziev^[24]根据最大应变能理论探讨了应变能和强度之间的关系；孙梦成等^[25]基于最小耗散能原理建立了岩石的损伤本构模型；Li等^[26]从能量耗散的角度建立了裂隙岩体的损伤模型；张志镇等^[27]基于弹性能的积聚机制建立了能量演化模型.上述****对岩石力学参数及能耗特征进行了大量的研究，但是多数****在能耗分析中常将岩石的力学参数设成常数，没有充分考虑岩石参数随应力水平改变的差异性影响.
三轴加卸载试验能够获得岩石三向应力条件下的力学参数和能量特征，本文设计了5种围压下花岗岩的循环加卸载试验，计算各循环下的弹性模量，获得其与最大、最小主应力的关系；分析了不同应力路径下花岗岩的输入总能量、可释放弹性能、耗散能等的演化规律，从能量积聚与耗散的角度分析了受载花岗岩的损伤演化；采用与主应力相关的岩石力学参数对岩石弹性能进行计算，更精确地揭示了深部岩体蓄能水平，为根据围岩应力状态评估深部工程围岩稳定性提供了依据.
1 试验设备和程序1.1 试样制备试验所选用花岗岩岩样取自山东省某金属矿勘探钻孔，埋深1 200 m，以钻取到较为完整且质地、颗粒分布均匀的岩芯加工成直径50 mm，高100 mm的标准圆柱岩样，岩样上、下端面不平整度小于0.05 mm，岩样轴向偏差小于0.25°，波速区间5.1~5.21 km·s^-1，密度区间2.61~2.64 g·cm^-3，物性参数的离散度较小，满足试验要求.
1.2 试验过程围压30 MPa已达千米深地应力的量级，故本文设计的5种围压分别为1，5，10，20，30 MPa.采用TAW2000三轴刚性试验机(最大轴向荷载2 000 kN)进行加卸载试验，采用引伸计来测量岩样的轴向应变和环向应变.加卸载时采用位移控制的方式，加载速率为0.01 mm·min^-1，卸载速率为0.04 mm·min^-1.试验过程采用分级增加轴向位移的加载方式，每次循环最大位移较上一循环增加0.1 mm.具体过程：先以0.5 MPa·s^-1的加载速率对试样施加围压到预定值，保持围压恒定，对轴向位移、轴向应变ε₁和环向应变ε₃进行重置，而后采用图 1所示路径进行加卸载至岩石破坏.
图 1(Fig. 1)

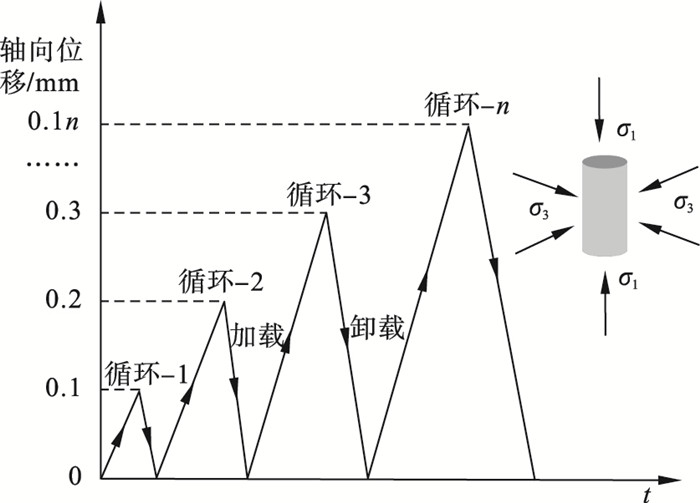图 1 三轴循环加卸载应力路径图Fig.1 Triaxial cyclic loading and unloading stress path diagram

1.3 试验结果分析5种围压下花岗岩应力-应变曲线如图 2所示.围压的增加，提高了裂隙之间的摩擦力，抑制了破裂面的滑移，岩样的峰值强度和残余强度显著增大.岩样的卸载曲线与加载曲线不重合，卸载曲线总是低于本次循环的加载曲线，形成了一个闭合的滞回环，这是由于花岗岩是一种天然的非均质材料，其内部矿物成分、粒度、几何形态、方位分布、裂隙孔洞、节理等因素导致了岩样在外荷载作用下并非理想弹性体.滞回环的产生伴随着能量的耗散，其面积与试样内部裂纹闭合、扩展、联合等耗散能量有关.随着循环应力增大，滞回环的面积也相应地增大.在初始压密阶段和弹性变形阶段，滞回环面积较小，试样损伤和能量耗散相应较小；随着应力增大至裂纹起裂应力，滞回环的面积显著增大，岩石内部裂纹发育、能量耗散增大；峰值应力时，滞回环的面积为最大值，岩石内部裂纹扩展贯通，损伤和耗散能最大；在峰后阶段，滞回环的面积逐渐减小.滞回环累计面积随着围压的增大而增大，围压抑制了岩样的破坏，岩样峰值破坏时消耗更多的能量.
图 2(Fig. 2)

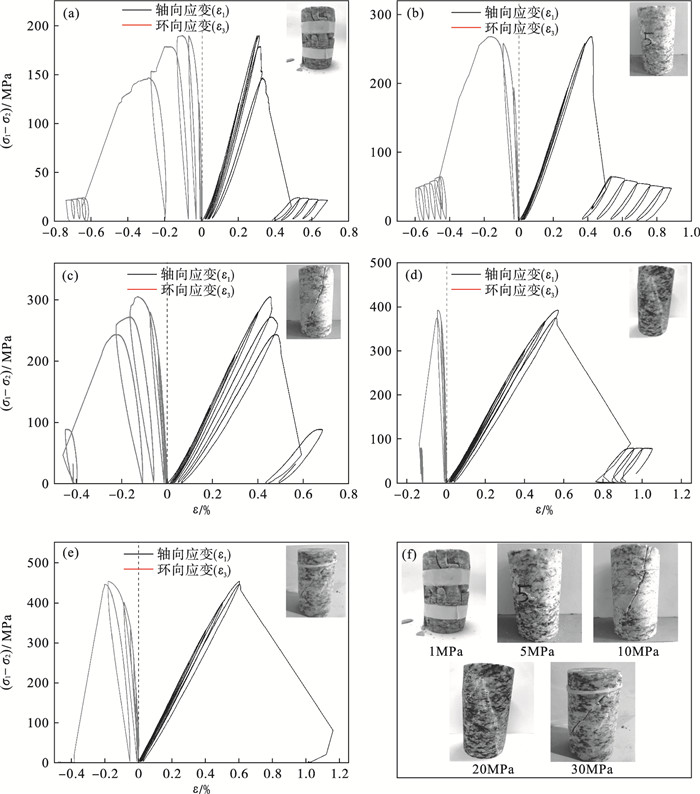图 2 三轴循环加卸载条件下岩样应力-应变曲线及破坏模式.Fig.2 Stress-strain curves and failure modes of rock samples under triaxial cyclic loading and unloading conditions (a)—1 MPa; (b)—5 MPa; (c)—10 MPa; (d)—20 MPa; (e)—30 MPa; (f)—破坏形态.

2 花岗岩弹性模量演化规律岩石在卸载过程中主要发生弹性变形，岩石内部无损伤破裂产生，其变形为岩石储蓄的弹性能释放引起的弹性恢复，卸载应力-应变曲线近似为一条直线，因此以卸载曲线的斜率作为轴向弹性模量(以下简称弹性模量).花岗岩弹性模量随应力状态变化曲线如图 3所示，随着围压的增加，岩样的弹性模量显著增加，这是由于岩石内部原有微裂纹在围压的作用下闭合使岩石刚度增大，且侧向约束的存在抑制了岩样内部裂纹的产生与滑移，减小了轴向位移.从图 3b可以看出，平均弹性模量随着围压的变化率随围压的增大而降低，在低围压下，围压的改变对弹性模量的影响显著，高围压下，弹性模量对围压变化的敏感性不高.为了获得弹性模量随围压的变化规律，采用插值的方法将1~30 MPa围压范围内的平均弹性模量拟合为式(1)，相关系数为0.99.

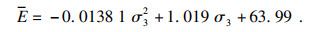(1)

图 3(Fig. 3)

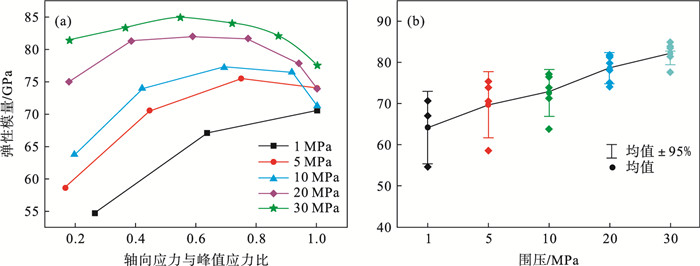图 3 花岗岩弹性模量随应力状态变化曲线.Fig.3 Curves of elastic modulus of granite with stress state (a)—5种围压下弹性模量-轴向应力变化曲线；(b)—平均弹性模量-围压变化曲线.

从图 3a可以看出，围压一定时，弹性模量随轴向应力的变化趋势为先增大后减小，这和单轴循环加卸载条件下岩石弹性模量一直降低有所不同，其原因有以下两种：①由于花岗岩是一种多相的非均质材料，包含着刚度较高的长石和石英，也包含刚度较低的云母及内部原生裂纹、弱结构面等.围压和轴向应力的作用使其内部裂纹压密、软弱结构强化，加载初期岩石刚度增加，弹性模量会有短暂的增大.②岩石非理想弹性体，应力作用下呈现滞弹性，卸载曲线中的应变包括瞬时的弹性应变和与时间相关的滞弹性应变两个部分，在初始压密阶段，滞弹性应变与弹性应变比值更大，滞弹性现象更加明显，因此导致初期弹性模量较低.当岩石进入微裂隙发展阶段，岩石内部裂纹发育、岩石的损伤增大，弹性模量逐渐降低.当岩石进入非稳定破裂阶段，岩石内部的裂纹联合、扩展、岩石损伤加剧，弹性模量迅速降低.
花岗岩弹性模量受应力状态影响较大，为随最大、最小主应力变化而改变的状态量：E=f(σ₁, σ₃)，为了表征应力状态对弹性模量的影响，对试验结果进行插值拟合为式(2)，相关系数为0.92，弹性模量与最大、最小主应力呈现良好的二次函数关系.

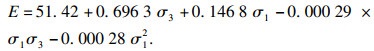(2)

根据式(2)，可以估计弹性模量开始降低时的应力状态，也即岩石损伤开始加剧的应力状态.
3 花岗岩能量演化规律及分配规律3.1 能量计算方法三轴加卸载试验过程中，外部系统(液压机)输入的能量大于岩石内部实际积蓄的能量.峰前阶段，试验机输入的能量大部分以可释放弹性能的形式储存在岩石中，弹性能密度U^e可以表示为^[22]

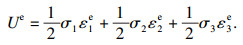(3)

且对于弹性变形：

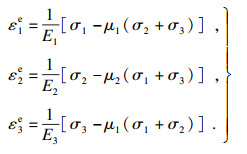(4)

其中: σ_i分别为3个主应力; ε_i^e, E_i, μ_i分别为3个主应力方向上的弹性应变、弹性模量和泊松比.假设岩石均质且各向同性，对于三轴试验：σ₂=σ₃，则联立式(3)、式(4)得岩石弹性能密度：

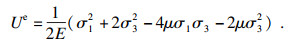(5)

加载过程中σ₃不变，以弹性模量E和轴向应力σ₁为变量，对式(5)求微分得

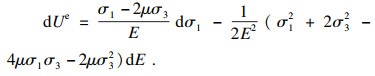(6)

卸载过程中岩石主要发生弹性变形，dE≈0，且，则式(6)可化简为

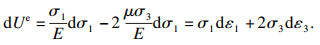(7)

所以卸载释放的弹性能(图 4)可表示为

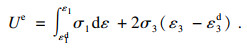(8)

图 4(Fig. 4)

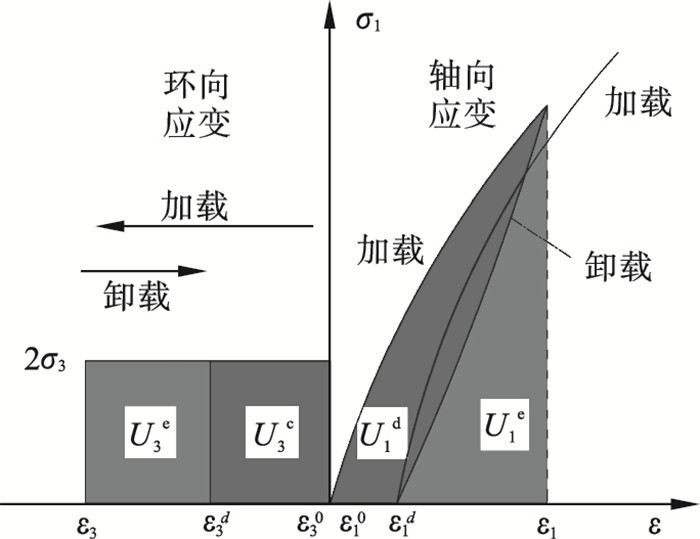图 4 试样能量密度计算示意图Fig.4 Schematic diagram of energy density calculation of sample

其中: ε₁, ε₃分别为卸载时的轴向、环向应变; ε₁^d, ε₃^d分别为卸载后的轴向、环向应变.
岩石内部裂隙的发育，裂纹面的扩展等结构损伤都需要消耗能量，这一部分能量称为耗散能，在不考虑与试验机进行热交换的情况下，耗散能等于试验机输入的总能量减去岩石储存的弹性能：

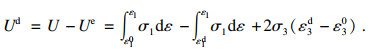(9)

其中，ε₁⁰, ε₃⁰分别为加载开始时的轴向、环向应变.
3.2 花岗岩能量演化通过式(8)、式(9)计算得到三轴循环加卸载条件下花岗岩各能量密度，5种围压下能量密度演化曲线如图 5所示.从图 5中可以看出随着循环应变的增加，不同围压下花岗岩各能量密度均增大，且增长曲线为凹型曲线.试验机输入的能量主要以弹性能的形式储蓄在岩样之中，输入总能量中弹性能所占的比例范围为0.78至0.94.由储存弹性能所占比例可将峰前分为三个阶段：增长期、保持稳定期、迅速减少期，这与岩石峰前的压密阶段、弹性阶段和裂纹扩展阶段(屈服阶段)是密切相关的.如图 5所示，围压作用下循环加卸载过程中的能量演化过程如下：①压密阶段，各能量增长速率均较小.轴向变形较大，轴向应力增长缓慢，试样储存的弹性能较低，输入能量转化为孔隙、裂纹压密等不可逆形变引起的耗散能较多，弹性能占比(弹性能密度与总能量密度之比)随轴向应力增加逐渐增大.②弹性变形阶段，由图 3可知，与压密阶段相比，弹性变形阶段的弹性模量更大，在此阶段，岩石主要发生弹性变形，弹性能占比较大且保持稳定.③非稳定变形至峰值应力阶段，岩石内部裂纹大量产生，岩石损伤加剧，新裂纹的产生、联合、扩展导致耗散能快速增大，储存弹性能的比例迅速降低；但随着应变的增加，弹性能密度仍在增大，达到峰值应力时，弹性能密度达到最大值.
图 5(Fig. 5)

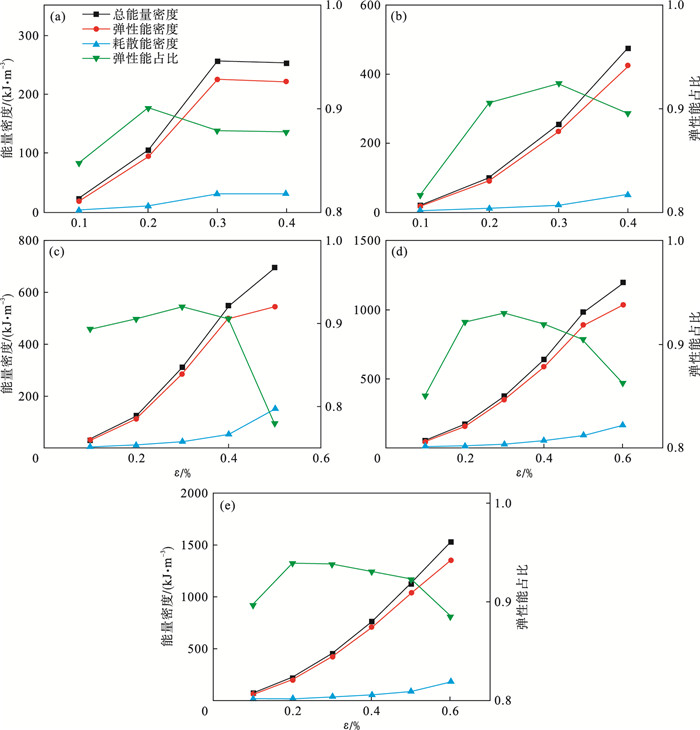图 5 5种围压下花岗岩能量密度演化曲线Fig.5 Energy density evolution curves of granite under five confining pressures (a)—1 MPa; (b)—5 MPa; (c)—10 MPa; (d)—20 MPa; (e)—30 MPa.

表 1为花岗岩能量演化及分配表.由图 5和表 1可知花岗岩弹性能密度的平均增长速率范围：1.17~2.95 kJ·MPa^-1·m^-3，随围压的增大而增大.对于式(6)考虑加载过程中弹性模量变化对弹性能的影响，且

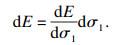(10)

表 1(Table 1)

表 1 花岗岩能量演化及分配表Table 1 Energy evolution and distribution table in granite ηmax k 1 189 1.17 221.3 0.90 0.63 5 267 1.59 424.4 0.92 0.75 10 304 1.79 543.3 0.92 0.69 20 392 2.64 1 035.2 0.93 0.59 30 459 2.95 1 353.9 0.94 0.37

表 1 花岗岩能量演化及分配表 Table 1 Energy evolution and distribution table in granite

则将式(5)、式(10)代入式(6)可得

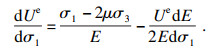(11)

由式(11)可知，围压一定时，弹性能增长速率影响因素可分为两部分：(σ₁-2μσ₃)/E与主应力有关，随轴向应力σ₁的增加而增加；U^edE/2Edσ₁与弹性模量有关，由图 3a可知，dE/dσ₁随σ₁的增大先为正后为负.且由图 5可知，U^e/2E随轴向应力σ₁增大而增大.所以在应力水平较低时，试样弹性能增长速率dU^e/dσ₁较小，在高应力状态下，弹性能增长速率大，能量受应力变化扰动大.
耗散能平均增长速率范围为0.16~0.38 kJ·MPa^-1·m^-3，其随围压增大而增大.压密阶段和弹性阶段，耗散能的增长速率较为稳定.非稳定破裂发展至峰值应力阶段，由于不可逆变形、裂隙扩展等因素，耗散能增长速率显著增大，达到0.4~0.65 kJ·MPa^-1·m^-3.
岩石峰值应力时的弹性能密度可视为岩样极限储能密度，通过表 1和图 6可以看出，围压从1 MPa提高到30 MPa，花岗岩的极限储能密度增大了约6倍，围压的存在提高了花岗岩的储能能力.
图 6(Fig. 6)

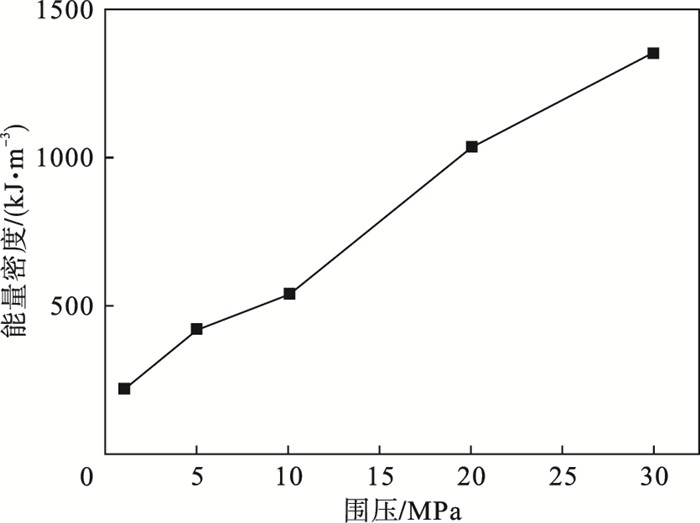图 6 花岗岩极限储能密度与围压的变化曲线Fig.6 Variation curve between energy storage density limit and confining pressure of granite

3.3 能量分配规律各围压下弹性能占比如图 7a所示，围压的存在抑制了裂纹的发育和不可逆形变，随着围压的增大，弹性能占比更高.由图 7a可知弹性能占比η与轴向应力占峰值应力之比σ₁/σ_f之间并非线性关系，而为先增大后减小的变化趋势.当加载到37%~75%峰值应力时，弹性能占比达到最大，而后弹性能占比降低.耗散能与总能量之比变化趋势与之相反.
图 7(Fig. 7)

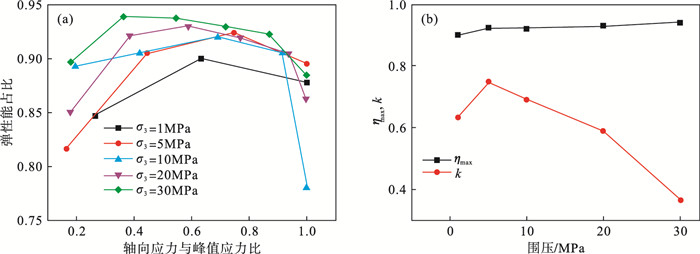图 7 5种围压下花岗岩弹性能占比及k演化曲线Fig.7 Elastic energy proportion and k evolution curves of granite under five confining pressures (a)—弹性能占比演化曲线; (b)—ηmax及k与围压关系曲线.

弹性能占比的降低伴随着花岗岩的弹性模量的降低、能量耗散和损伤加剧.定义最大弹性能占比η_max时轴向应力为损伤加剧应力σ_ηmax，其与峰值应力比值为损伤加剧应力比k=σ_ηmax/σ_f.当轴向应力比峰值应力大于k时，虽然储能能力仍在增加，但是弹性能占比η降低，耗散能迅速增大，损伤加剧.因此应力状态k可以看作是岩样内部结构破坏和损伤显著增加的节点，也可以作为地下空间工程中评估岩体安全的判别因素之一.各围压下η_max及k如图 7b和表 1所示.η_max范围为0.9~0.94，k范围为0.37~0.75.随着围压增大，η_max略有提高，k显著降低，损伤加剧应力比更小.围压抑制了裂纹的滑移，裂纹起裂应力与岩样峰值强度之比更低，高围压下，耗散能在轴向应力与峰值应力之比较低(k更小)时就对岩样的破坏发挥作用，损伤演化过程延长，岩样破裂过程需要更多的耗散能.
4 讨论岩体受载状态、结构状态及蓄能状态等是评价岩体稳定性的基础参数.理论上岩体结构状态与受载状态存在相关性，比如说应力状态可以决定岩体结构中节理裂隙的开、闭，岩体结构内节理裂隙的存在又决定了应力分布的不均匀性.进入深部以后，岩体的自蓄能状态是岩体评价的重要指标之一，岩体受载状态、结构状态、蓄能状态三者关系如图 8所示.深井建设前，可以通过水压致裂或滞弹性恢复等方法完成地应力测定，而对勘探孔岩芯所测岩体力学参数与原位状态必然存在差异性，因此需要模拟原位状态下的受载条件，进而获得原位状态下岩体的力学参数，如此才能更加准确评估深部原位状态下岩石的自蓄能水平.
图 8(Fig. 8)

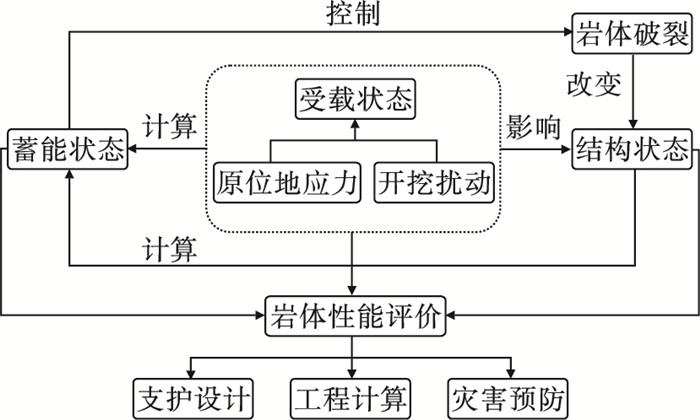图 8 岩体受载状态、结构状态及蓄能状态关系图Fig.8 Relation diagram of rock mass loading state, structure state and energy storage state

目前室内试验条件下侧重于模拟第一主应力影响，由于第二、第三主应力均较小，所以可以忽略泊松比的影响，本文仅考虑轴向弹性模量影响.如若第二、第三主应力与第一主应力相差不大，泊松比的影响不可忽略，这要在真三轴、高围压条件下进行分析.
将弹性模量作为随主应力σ₁, σ₃变化的函数E=f(σ₁, σ₃)，则代入式(5)可得

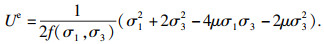(12)

将式(2)代入式(12)，得到花岗岩弹性能密度变化函数为

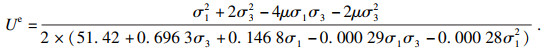(13)

为了对比本文方法与传统弹性模量为常量计算弹性能密度方法，以σ₃=10 MPa为例，泊松比μ=0.25，平均弹性模量E=72.5 GPa，若以弹性模量为常数代入式(5)有

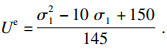(14)

采用随主应力改变的弹性模量对弹性能密度计算：

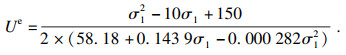(15)

两种方法计算弹性能密度变化曲线如图 9所示，以σ₁=279 MPa为例，试验弹性能密度为498.4 kJ·m^-3，传统计算方法为527.4 kJ·m^-3，
图 9(Fig. 9)

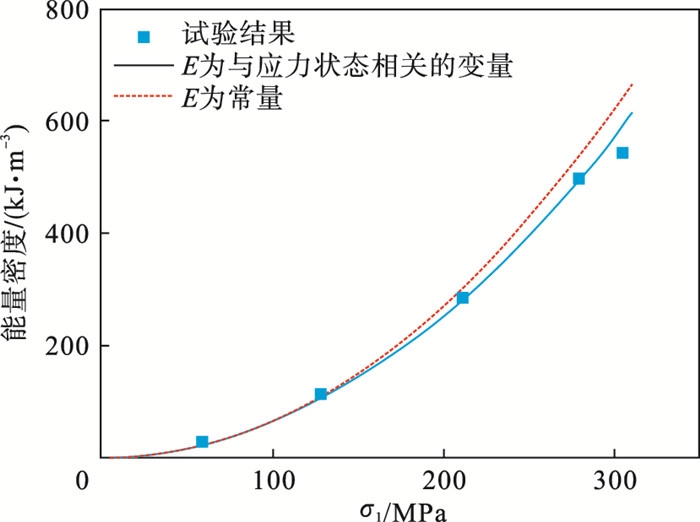图 9 围压10 MPa花岗岩弹性能密度预测与试验结果对比Fig.9 Comparison between prediction and experimental results of elastic energy density of granite with confining pressure of 10 MPa

相对误差为5.81%，本文方法计算弹性能密度为492.3 kJ·m^-3，相对误差为1.22%，式(12)计算结果更符合试验实际测得，采用随主应力改变的弹性模量计算岩体能量密度更加精确.在深部临界条件下，岩爆失稳在轻微的扰动下就会发生，因此更精确的蓄能状态计算方法对深地工程建设有一定的指导意义.
5 结论1) 试验表明花岗岩弹性模量与应力状态有关，其随围压的增大而增大，随着轴向应力增大呈先增大后减小的变化，弹性模量与最大、最小主应力呈现良好的二次函数关系.
2) 循环加卸载应力-应变曲线呈现明显的滞回环，滞回环的面积与耗散能大小有关，其随围压增大而增大，随轴向应力变化趋势为峰前增大、峰后减小.峰前阶段，花岗岩各能量密度随着围压和轴向应力的增大而增大，能量增长速率也呈现相同趋势.围压的增大提高了岩石的极限蓄能水平，高应力条件下岩石的能量密度对应力改变的敏感性更高.
3) 最大弹性能占比为90%~94%.定义了最大弹性能占比时轴向应力与峰值应力之比为损伤加剧应力比k，随着围压增大，弹性能占比略有增大，k显著降低，高围压下花岗岩损伤加剧应力比更低，围压延长了岩石的损伤演化过程.
4) 岩体蓄能水平与岩体参数及应力条件有关，且岩体参数为应力状态的函数.采用本文与最大、最小主应力相关的弹性模量对蓄能水平进行计算，其精度更高，本文的研究对根据岩体应力计算分析岩体参数和蓄能状态具有一定价值.
参考文献

[1]	Wagner H. Deep mining: a rock fngineering challenge[J]. Rock Mechanics and Rock Engineering, 2019, 52(4): 1417-1446.
[2]	Xie H, Gao M, Ru Z, et al. Study on the mechanical properties and mechanical response of coal mining at 1000m or deeper[J]. Rock Mechanics and Rock Engineering, 2019, 52: 1-16. DOI:10.1007/s00603-018-1570-6
[3]	Lu J, Zhang D, Huang G, et al. Effects of loading rate on the compound dynamic disaster in deep underground coal mine under true triaxial stress[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 134(10): 104453.
[4]	谢和平. 深部岩体力学与开采理论研究进展[J]. 煤炭学报, 2019, 44(5): 1283-1305. (Xie He-ping. Research review of the state key research development program of China: deep rock mechanics and mining theory[J]. Journal of China Coal Society, 2019, 44(5): 1283-1305.)
[5]	Wang C, He B, Hou X, et al. Stress-energy mechanism for rock failure evolution based on damage mechanics in hard rock[J]. Rock Mechanics and Rock Engineering, 2019, 53(3): 1021-1037.
[6]	Chen B R, Feng X T, Li Q P, et al. Rock burst intensity classification based on the radiated energy with damage intensity at Jinping Ⅱ Hydropower Station, China[J]. Rock Mechanics and Rock Engineering, 2015, 48(1): 289-303. DOI:10.1007/s00603-013-0524-2
[7]	Weng L, Huang L Q, Taheri A, et al. Rockburst characteristics and numerical simulation based on a strain energy density index: a case study of a roadway in Linglong Gold Mine, China[J]. Tunnelling and Underground Space Technology, 2017, 69: 223-232. DOI:10.1016/j.tust.2017.05.011
[8]	Lindin G L, Lobanova T V. Energy sources of rockbursts[J]. Journal of Mining Science, 2013, 49(1): 36-43. DOI:10.1134/S106273914901005X
[9]	谢和平, 李存宝, 高明忠, 等. 深部原位岩石力学构想与初步探索[J]. 岩石力学与工程学报, 2021, 40(2): 217-232. (Xie He-ping, Li Cun-bao, Gao Ming-zhong, et al. Conceptualization and preliminary research on deep in situ rock mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(2): 217-232.)
[10]	Xie H P, Li C, He Z Q, et al. Experimental study on rock mechanical behavior retaining the in situ geological conditions at different depths[J]. International Journal of Rock Mechanics and Mining Sciences, 2021, 138: 104548. DOI:10.1016/j.ijrmms.2020.104548
[11]	Meng Q B, Liu J F, Ren L, et al. Experimental study on rock strength and deformation characteristics under triaxial cyclic loading and unloading conditions[J]. Rock Mechanics and Rock Engineering, 2021, 54(2): 777. DOI:10.1007/s00603-020-02289-8
[12]	Meng Q B, Liu J F, Pu H, et al. Mechanical properties of limestone after high-temperature treatment under triaxial cyclic loading and unloading conditions[J]. Rock Mechanics and Rock Engineering, 2021, 54(12): 6413-6437. DOI:10.1007/s00603-021-02638-1
[13]	Jiang Q, Zhong S, Cui J, et al. Statistical characterization of the mechanical parameters of intact pock under triaxial compression: an experimental proof of the Jinping marble[J]. Rock Mechanics and Rock Engineering, 2016, 49(12): 4631-4646. DOI:10.1007/s00603-016-1054-5
[14]	Ray S K, Sarkar M, Singh T N. Effect of cyclic loading and strain rate on the mechanical behaviour of sandstone[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(4): 543-549. DOI:10.1016/S0148-9062(99)00016-9
[15]	Zhao Y, Bi J, Wang C, et al. Effect of unloading rate on the mechanical behavior and fracture characteristics of sandstones under complex triaxial stress conditions[J]. Rock Mechanics and Rock Engineering, 2021, 54(9): 4851-4866. DOI:10.1007/s00603-021-02515-x
[16]	Hua A Z, You M Q. Rock failure due to energy release during unloading and application to underground rock burst control[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 241-246. DOI:10.1016/S0886-7798(01)00046-3
[17]	Li X B, Zhou Z L, Lok T S, et al. Innovative testing technique of rock subjected to coupled static and dynamic loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 45(5): 739-748.
[18]	牛双建, 靖洪文, 梁军起. 不同加载路径下砂岩破坏模式试验研究[J]. 岩石力学与工程学报, 2011, 30(sup2): 3966-3974. (Niu Shuang-jian, Jing Hong-wen, Liang Jun-qi. Experimental study of failure mode of sandstone under different loading paths[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(sup2): 3966-3974.)
[19]	He M C, Miao J L, Feng J L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 286-298. DOI:10.1016/j.ijrmms.2009.09.003
[20]	孟庆彬, 王从凯, 黄炳香, 等. 三轴循环加卸载条件下岩石能量演化及分配规律[J]. 岩石力学与工程学报, 2020, 39(10): 2047-2059. (Meng Qing-bin, Wang Cong-kai, Huang Bing-xiang, et al. Rock energy evolution and distribution law under triaxial cyclic loading and unloading conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(10): 2047-2059.)
[21]	Bagde M N, Petros V. Fatigue and dynamic energy behaviour of rock subjected to cyclical loading[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(1): 200-209. DOI:10.1016/j.ijrmms.2008.05.002
[22]	谢和平, 鞠杨, 黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学报, 2005, 24(17): 3003-3010. (Xie He-ping, Ju Yang, Li Li-yun. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003-3010. DOI:10.3321/j.issn:1000-6915.2005.17.001)
[23]	Cornetti P, Pugno N, Carpinteri A, et al. Finite fracture mechanics: a coupled stress and energy failure criterion[J]. Engineering Fracture Mechanics, 2006, 73(14): 2021-2033. DOI:10.1016/j.engfracmech.2006.03.010
[24]	Gaziev E. Rupture energy evaluation for brittle materials[J]. International Journal of Solids and Structures, 2001, 38(42): 7681-7690.
[25]	孙梦成, 徐卫亚, 王苏生, 等. 基于最小耗能原理的岩石损伤本构模型研究[J]. 中南大学学报(自然科学版), 2018, 49(8): 2067-2075. (Sun Meng-cheng, Xu Wei-ya, Wang Su-sheng, et al. Study on damage constitutive model of rock based on principle of minimum dissipative energy[J]. Journal of Central South University(Science and Technology), 2018, 49(8): 2067-2075.)
[26]	Li T T, Pei X J, Wang D P, et al. Nonlinear behavior and damage model for fractured rock under cyclic loading based on energy dissipation principle[J]. Engineering Fracture Mechanics, 2019, 206: 330-341.
[27]	张志镇, 高峰. 单轴压缩下岩石能量演化的非线性特性研究[J]. 岩石力学与工程学报, 2012, 31(6): 1198-1207. (Zhang Zhi-zhen, Gao Feng. Research on nonlinear characteristics of rock energy evolution under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1198-1207.)